2. 中国科学院声学研究所,北京 100097
2. Institute of Acoustics, Chinese Academy of Sciences, Beijing 100097, China
在声呐系统的设计过程中,波束形成是一个核心基础环节,利用一定几何形状的基阵和信号处理技术,使发射和接收的信号形成指向性波束。在发射信号时,通过指向性波束提高声呐的作用距离;在接收信号时,在空间域中抑制环境噪声和混响干扰,提高声呐接收机输入端的信噪比,获得更好的声呐图像和目标的分辨率,其直接表征为旁瓣级,旁瓣级越低,系统抑制旁瓣区域的干扰能力越强。
在没有水下弹道测量系统的条件下,设计测量水下高速小目标末弹道的声呐成像系统的主要考虑:1)目标接近成像系统的方向未知,可能从任一方向接近;2)目标运动速度快,回波多普勒偏移量大,可能达到宽带信号的标准;3)目标距离近,成像系统受到混响的干扰强等因素的限制[1]。在声呐系统的阵型设计中,只有使用均匀排布的圆形阵列,才具有
由于声信号到达基阵各个阵元的距离不同,导致各个阵元输出的信号也不同,需要通过延时等信号处理方法补偿差异,这是常规波束形成的基本思想[2 – 3]。假设入射信号是平面波,基阵是N个阵元组成。以其中某个阵元为参考点,设第
| $D(\theta ) = {\left\{ {E{{\left( {\sum\limits_{i = 0}^{N - 1} {s\left[ {t + {\tau _i}(\theta ) - {\tau _i}({\theta _0})} \right]} } \right)}^2}} \right\}^{\frac{1}{2}}}{\text{。}} $ | (1) |
再经过归一化处理得到
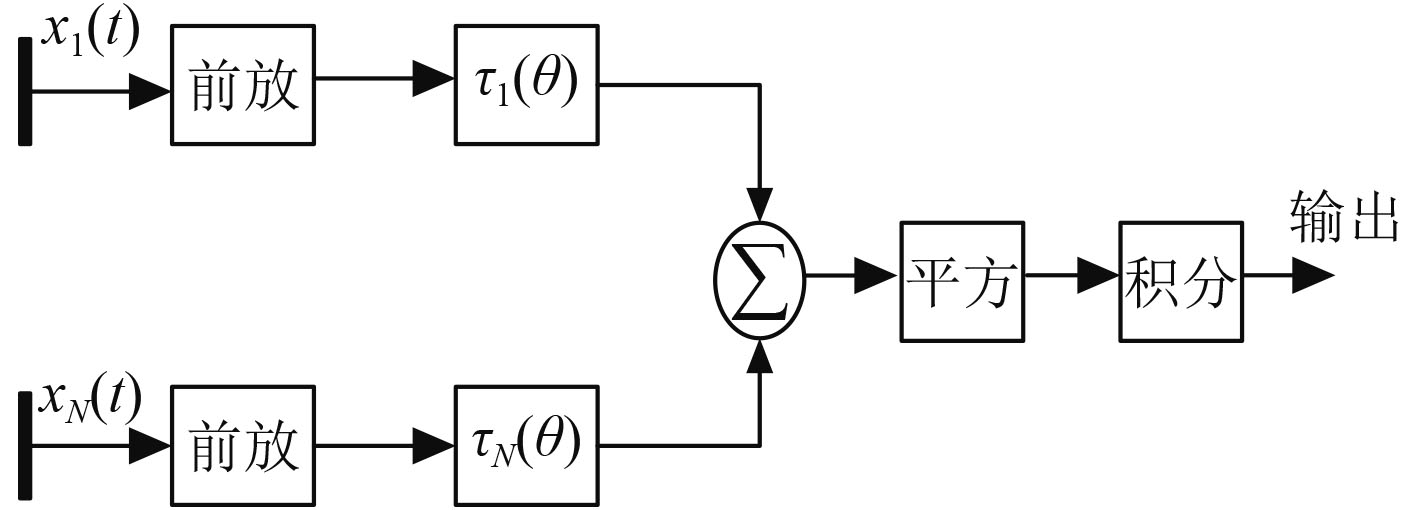
|
图 1 常规波束形成模型 Fig. 1 Conventional beamforming model |
目前,阵元发射信号受到换能器谐振频点的限制,一般只能发射窄带信号。接收信号则根据信号的不同分为窄带信号模型和宽带信号模型,通常当目标回波信号带宽大于信号中心频率的1/10时,被认为是宽带信号,由于发射信号和接收信号的波束形成原理相同[3],文中以接收的信号模型为例说明。
被测目标到成像系统的距离一般是远大于成像系统的圆阵直径,阵元接收的信号属于远场窄带信号。假设回波信号为
| $s(t) = a(t)\cos [2{\text{π}} {f_0}t + \varphi (t)]{\text{,}} $ | (2) |
式中,
| $\mathop {\tilde{s}} (t) = a(t){e^{j[2{\text{π}} {f_0}t + \varphi (t)]}}{\text{,}} $ | (3) |
假设接收信号的时延量为
| $\mathop {\tilde{s}} (t{\rm{ - }}\tau ) = a(t{\rm{ - }}\tau ){e^{j[2{\text{π}} {f_0}(t{\rm{ - }}\tau ) + \varphi (t)]}}{\text{。}} $ | (4) |
但是,窄带信号的幅度是慢变化的,则
| ${{\tilde{s}} _i}(t) = \mathop {\tilde{s}} (t{\rm{ - }}{\tau _i}) \approx \mathop {\tilde{s}} (t){e^{j2{\text{π}} {f_0}{\tau _i}}}{\text{,}} $ | (5) |
圆阵在第
| $S{{(n) = }}s(n)\left[ {\begin{array}{*{20}{c}} {{e^{ - j2{\text{π}} {f_0}{\tau _1}}}} \\ \vdots \\ {{e^{ - j2{\text{π}} {f_0}{\tau _N}}}} \end{array}} \right] = s(n)\Phi {\text{,}} $ | (6) |
式中,
假设圆阵半径为

|
图 2 均匀圆阵阵元分布图 Fig. 2 Distribution of uniform circular array elements |
可知,参考阵元的坐标向量为
| $ {{\tau }_{i}}=-\frac{\Delta R}{c}=\frac{\left\langle {{p}_{m}},l \right\rangle }{c}=\frac{l}{c}\sin \theta \cos \left( \phi -\frac{2{\text{π}} i}{N} \right), \;\;\;\; i=1,2,\cdots ,N{\text{。}} $ | (7) |
其中,
| ${\phi _i}(\theta ,\varphi ) = 2{\text{π}} {f_0}{\tau _i} = \frac{{2{\text{π}} }}{\lambda }R\sin \theta \cos \left(\varphi - \frac{{2{\text{π}} i}}{N}\right){\text{,}} $ | (8) |
整个均匀圆阵的波束响应可以表示为:
| $B(\theta ,\varphi ) = \sum\limits_{i = 0}^{N - 1} {{s_i}(\theta ,\varphi ){\omega _i}} {\text{,}} $ | (9) |
式中,
在均匀圆阵上,采用均匀加权法进行波束形成,则有:
| ${\omega _i}{\rm{ = }}\frac{1}{N}{\text{,}} $ | (10) |
整个均匀圆阵的波束响应可以表示为:
| $B(\theta ,\varphi ) = \sum\limits_{i = 0}^{N - 1} {\frac{1}{N}{s_i}(\theta ,\varphi )} {\text{。}} $ | (11) |
通过Dolph-Chebyshev加权法抑制旁瓣高度,改善圆阵波束形成的性能,但是以上加权法只适用于线性阵列,故需要通过相位模式激励法将圆阵等效成线列阵,再进行后续的波束形成[4 – 5]。
为了方便讨论波束性能,令
| ${\left[ {a(\varphi )} \right]_i} = {\alpha _i}(\varphi ){e^{jkR\cos (\varphi - \frac{{2{\text{π}} i}}{N})}},i = 0,1, \cdots ,N - 1 $ | (12) |
式中,波数
将各个阵元接收信号响应乘上最大相位模数为
| $h \approx \frac{{2{\text{π}} R}}{\lambda }{\text{,}} $ | (13) |
最大相位模数矩阵
| $B_{JF}^H{\rm{ =}} J \cdot {F}{\text{,}} $ | (14) |
定义矩阵
| $ J{\rm{ = diag}}\left\{ \left[{{{j}}^n}\sqrt M {{{J}}_n}(kR)\right]{^{{\rm{ - }}1}}\right\},n{\rm{ = - }}h, \cdots ,0, \cdots ,{{h}}{\text{,}} $ | (15) |
| $F{\rm{ = }}\frac{1}{{\sqrt N }}\left[ {\begin{array}{*{20}{c}} 1&{{\omega ^{{\rm{ - }}h}}}&{{\omega ^{{\rm{ - 2}}h}}}& \cdots &{{\omega ^{{\rm{ - (}}N - 1{\rm{)}}h}}} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1&{{\omega ^{{\rm{ - 1}}}}}&{{\omega ^{{\rm{ - 2}}}}}& \cdots &{{\omega ^{{\rm{ - (}}N - 1{\rm{)}}}}} \\ 1&1&1& \cdots &1 \\ 1&{{\omega ^1}}&{{\omega ^2}}& \cdots &{{\omega ^{(N - 1)}}} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1&{{\omega ^h}}&{{\omega ^{2h}}}& \cdots &{{\omega ^{(N - 1)h}}} \end{array}} \right]{\text{,}} $ | (16) |
式中,
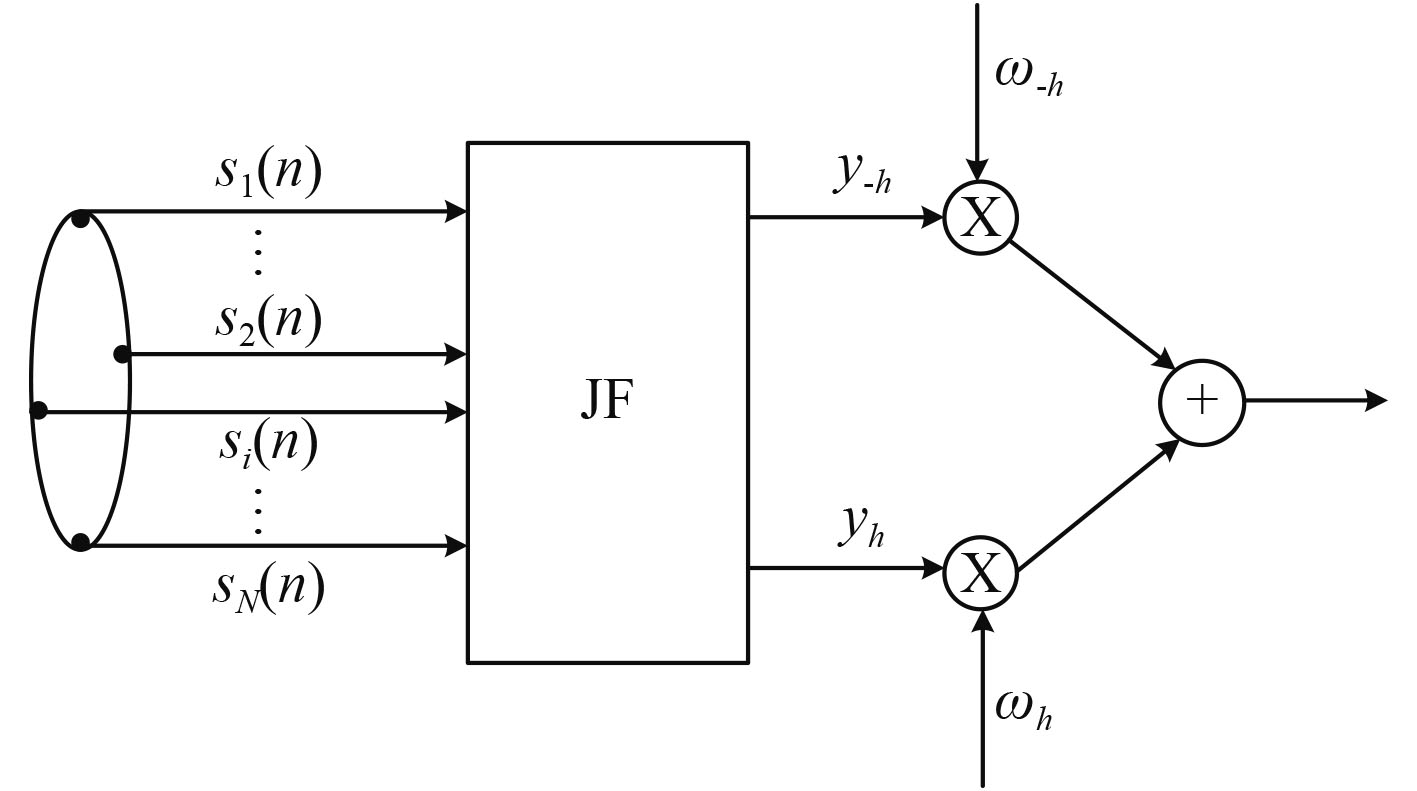
|
图 3 圆阵响应模式转换模型图 Fig. 3 Model diagram of response mode transformation of circular array |
经过转化后,阵元信号响应矩阵为:
| $ {{a}_{v}}(\varphi )=B_{JF}^{H}\centerdot a(\varphi )\approx {{\left[{{e}^{-jh\varphi }},\cdots ,1,\cdots ,{{e}^{jh\varphi }}\right]}^{\rm{T}}}{\text{。}} $ | (17) |
形成了线列阵的响应模式,具有范德蒙行列式的结构形式,在此基础上,可以按照Dolph-Chebyshev加权法对输出信号
| $W = \mathop {\tilde J} {a_v}({\varphi _1}){\text{,}} $ | (18) |
式中,
| $\mathop {\tilde J} {\rm{ = }}diag({I_{ - h}}, \cdots ,{I_{ - 1}},2{I_0},{I_1}, \cdots ,{I_h}){\text{,}} $ | (19) |
则整个整理的波束响应为:
| $ B(\varphi )={{W}^{H}}\centerdot {{a}_{v}}(\varphi )=2{{I}_{0}}+\sum\limits_{n=1}^{h}{{{I}_{-n}}{{e}^{-jn({{\varphi }_{1}}-\varphi )}}}+\sum\limits_{n=1}^{h}{{{I}_{n}}}{{e}^{jn({{\varphi }_{1}}-\varphi )}}{\text{。}} $ | (20) |
根据对角矩阵
| $ B(\varphi )={{W}^{H}}\centerdot {{a}_{v}}(\varphi )=2\sum\limits_{n=0}^{h}{{{I}_{n}}\cos [2nu(\varphi )]}{\text{,}} $ | (21) |
式中,
| $\cos [2nu(\varphi )]{\rm{ = }}{\sum\limits_{q = 0}^n {b_{2q}^{2n}[\cos (u(\varphi ))]} ^{2q}}{\text{,}} $ | (22) |
即,波束响应
| $B(\varphi ){\rm{ = }}2{\sum\limits_{q = 0}^h {\sum\limits_{n = q}^h {{I_n}b_{2q}^{2n}[\cos (u(\varphi ))]} ^{2q}} }{\text{,}} $ | (23) |
令
| ${T_{2h}}(z) = \sum\limits_{q = 0}^h {b_{2q}^{2h}{z^{2q}}} {\text{,}} $ | (24) |
式中,
| $2\sum\limits_{n = q}^h {{I_n}b_{2q}^{2n} = b_{2q}^{2h}z_0^{2q}} {\text{。}} $ | (25) |
对角矩阵
| $B(\varphi ) = {W^H}{a_v}(\varphi ) = {T_{2h}}(z){\text{,}} $ | (26) |
圆阵响应模式可表示为:
| ${\left| {{W^H}{a_v}(\varphi )} \right|^2} = {\left| {{a_v}(\varphi )\mathop {\tilde J} {a_v}(\varphi )} \right|^2} = {\left| {{T_{2h}}({z_0}\cos (u(\varphi )))} \right|^2}{\text{。}} $ | (27) |
此时,圆阵波束响应模式已经等效为均匀线列阵Dolph-Chebyshev多项式的响应模式。因为
值得注意的是上述阵列模式等效转换需要满足矩阵
仿真实验1:假设均匀圆阵共有33个各向同性的阵元,圆阵半径为

|
图 4 均匀加权圆阵三维波束形成图 Fig. 4 Uniform weighted circular array three-dimensional beamforming |
由图4可知,圆阵三维波束形成图可以获得均匀加权圆阵的俯仰角和方位角信息,反映了均匀加权波束形成性能。但是,实孔径声呐成像系统和被测目标基本在同一深度,故方位角信息更值得关注。为了方便分析圆阵波束形成水平方向的指向性特征及讨论不同阵元数和半径的波束指向性能。
仿真实验2:实验1中,其他假设条件不变,令俯仰角
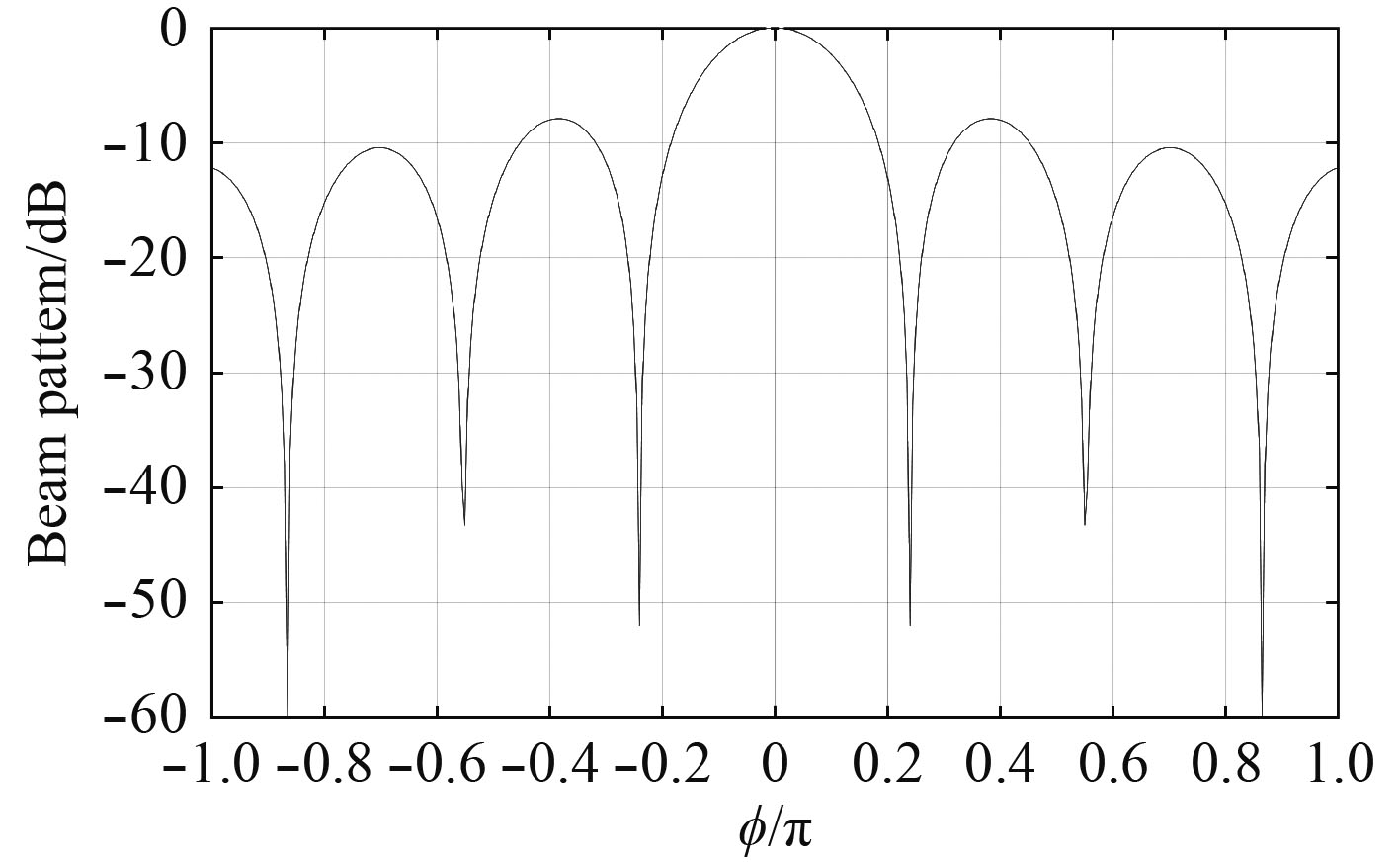
|
图 5 均匀加权圆阵二维波束形成图 Fig. 5 Two-dimensional beamforming of uniformly weighted circular array |
由图5可知,均匀加权圆阵水平方向的半功率波束宽度
仿真实验3:其他实验假设条件不变,保持
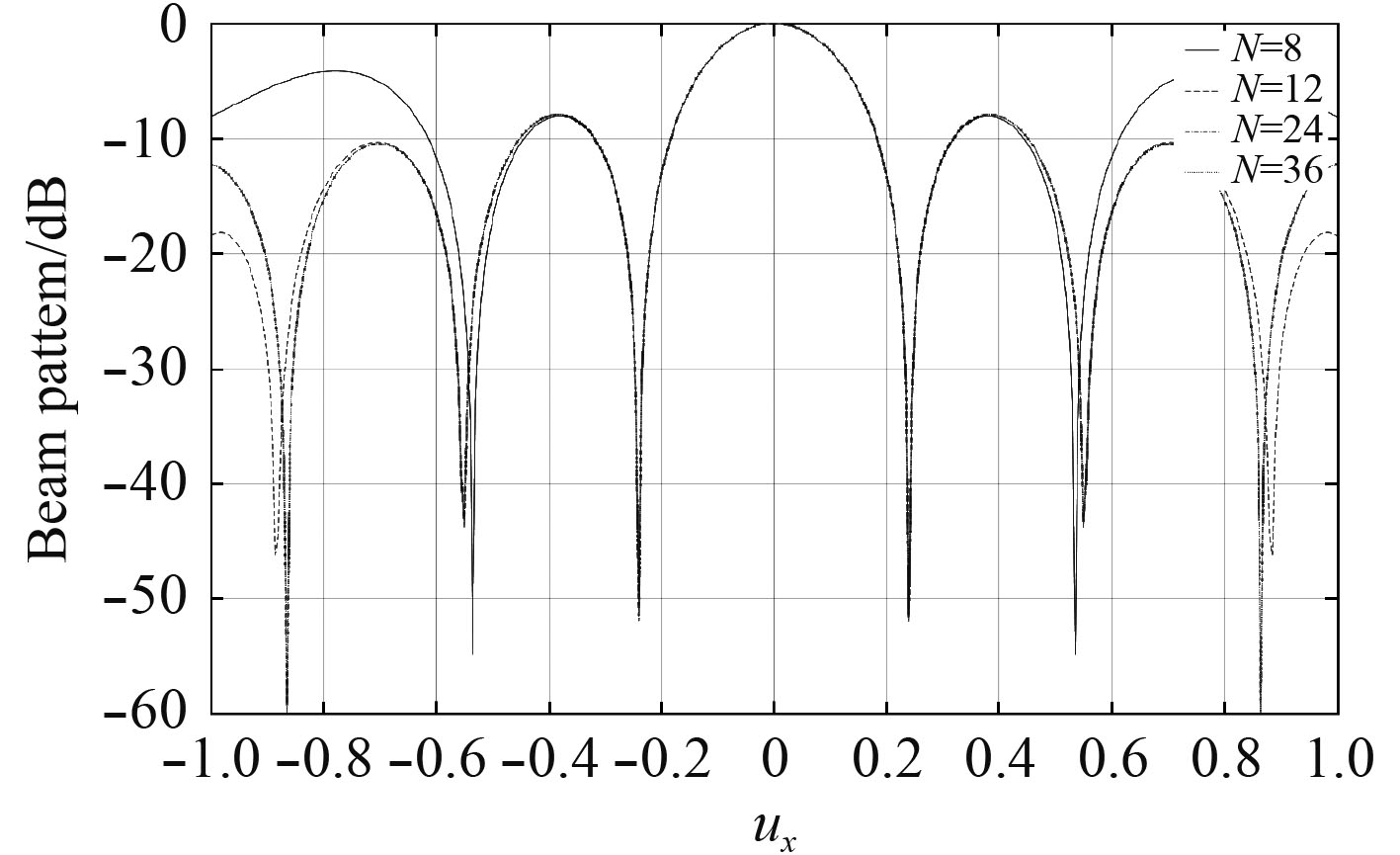
|
图 6 信号频率一定不同阵元数圆阵二维波束形成图 Fig. 6 Two-dimensional beamforming of circular arrays with different signal frequencies |
由图6可知,由于圆阵的非线性特点,在调整圆阵半径和接收信号波长比值不变的情况下,无论怎样改变圆阵阵元的数量,均匀加权圆阵的第一旁瓣高度总是约为–8 dB,明显高于线列阵的第一旁瓣–13.5 dB的高度。高旁瓣会引起高的虚警概率,造成大的弹道测量误差,应当在设计中采用适当的方法抑制旁瓣,保证测量精度。
仿真实验4:实验1的其他假设条件不变,改变圆阵接收信号频率,即改变圆阵的半径和信号波长比

|
图 7 圆阵半径一定不同频率信号二维波束形成图 Fig. 7 Two-dimensional beamforming of signals with certain circular array radius and different frequencies |
由图7所示,在圆阵阵形固定的条件下,提高发射信号频率可以减小波束形成的主瓣宽度,改善波束指向性能,但是最大旁瓣高度仍为–8 dB左右,虚警概率和轨迹测量依然较大,且提高发射信号频率会导致信号吸收损失的增强,限制了声呐系统的作用距离,需要慎重选择发射频率。
仿真实验5:设圆阵具有32个均匀排布的阵元且阵元各向同性,半径波长比
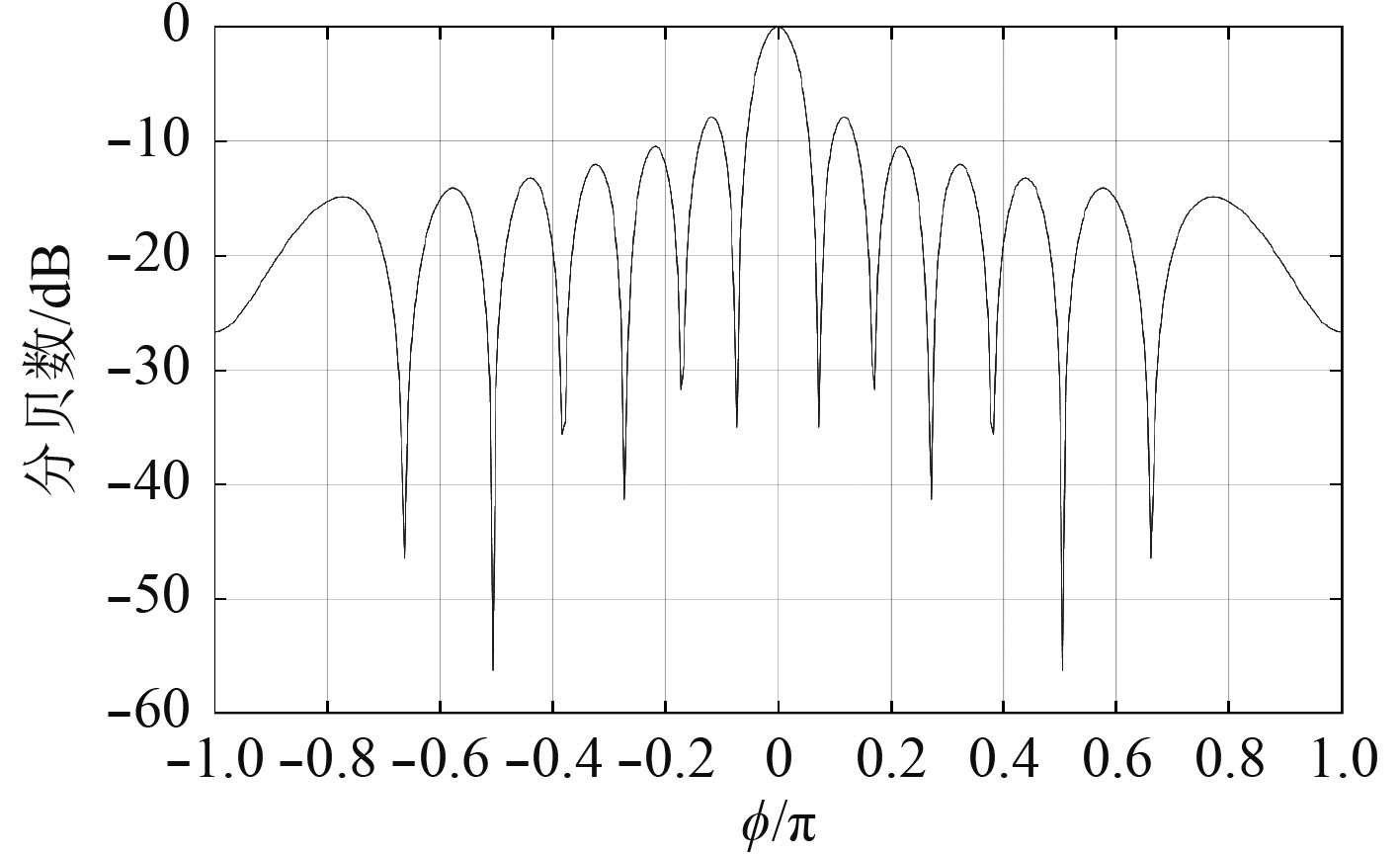
|
图 8 均匀加权圆阵二维波束形成图 Fig. 8 Two-dimensional beamforming diagram of uniform weighted circular array |
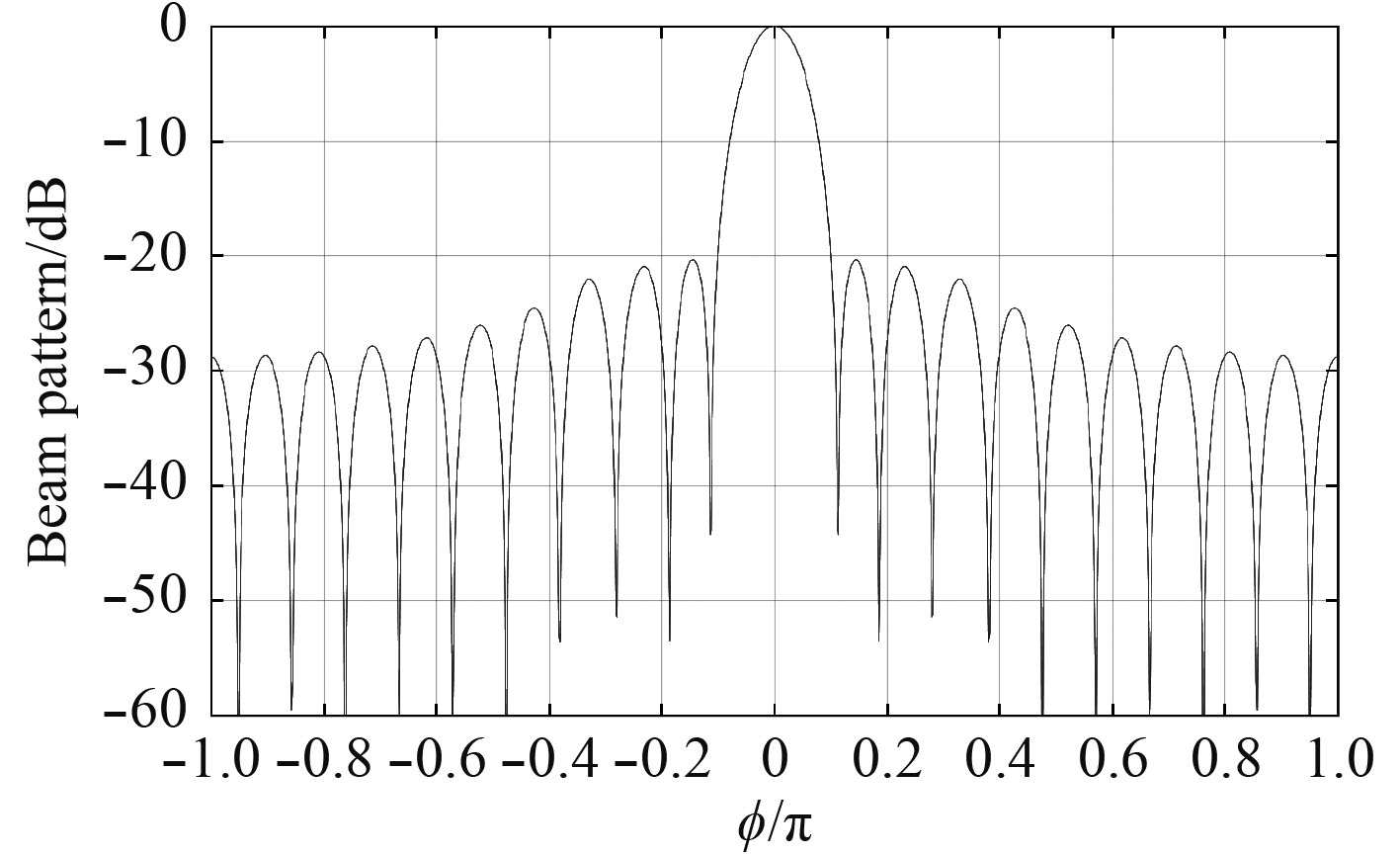
|
图 9 Dolph-Chebyshev加权圆阵二维波束形成图 Fig. 9 Dolph-Chebyshev weighted circular array 2-D beamforming |
由仿真实验5可知,当圆阵满足
设计基于水下高速小目标末弹道测量的实孔径成像声呐应该优先考虑均匀排布的圆阵,保证没有观测盲区,提高观测效率。在圆阵做波束形成时,Dolph-Chebyshev加权法能够有效抑制旁瓣高度,克服均匀加权圆阵波束形成旁瓣高的缺陷,同时能够保证在各个波束方向上,波束响应的幅值相同,为后续图像信号处理提供高质量的输入信号。但是,圆阵阵元数必须满足
| [1] |
李想. 水下高速运动目标轨迹测量技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [2] |
田坦. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2016.
|
| [3] |
李启虎. 声呐信号处理引论[M]. 北京: 科学出版社, 2006.
|
| [4] |
赵龙龙. 矢量传感器三维末段轨迹测量技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [5] |
杨娟. 水下动目标被动跟踪关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
 2019, Vol. 41
2019, Vol. 41
