2. 中国舰船研究院,北京 100192;
3. 哈尔滨工业大学仪器科学与工程学院,哈尔滨 150001
2. China Ship Research and Development Academy, Beijing 100192, China;
3. School of Instrument Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
由于惯性导航系统(Inertal Navigation System,INS)与全球定位系统(Global Positioning System,GPS)组合可以提供较高精度的速度、位置信息,所以INS/GPS组合系统被广泛应用在船舶、飞机、导弹等领域。但因INS/GPS组合系统量测信息仅包括位置和速度信息,缺少姿态信息观测量,导致系统的可观测性较差,容易造成系统在长时间导航应用中精度不高,甚至姿态信息发散的问题[1 – 3]。
天文导航系统(Celestial Navigation System,CNS)采用星体敏感器测量天体方位信息,在经过解算后输出载体姿态信息,其特点是姿态测量精度高、测量误差误差不随时间积累、系统可靠性高,是一种新型的高精度姿态测量系统[4 – 6]。
为增加INS/GPS组合系统的量测信息,提高系统导航精度,改善系统航向误差发散的问题,将CNS与传统INS/GPS系统组合是目前的研究热点。张科设计了基于联邦滤波的INS/GPS/CNS组合导航算法,但由于其采用的是线性卡尔曼滤波框架,不能很好适应INS/GPS/CNS这类典型非线性系统,造成滤波结果精度较低;吴坤峰考虑到CNS可能存在输出不连续的问题,利用GPS和CNS输出的高精度导航信息,分别设计了GPS/INS和CNS/INS滤波方案,在获得滤波后的导航信息后,将其作为全信息观测量进行二次滤波,最终获得高精度的导航信息。该方法计算较为繁琐,且二次滤波会造成系统实时性变差的问题,不宜开展算法的工程化应用[7 – 8]。
针对上述问题,本文提出一种基于扩展卡尔曼滤波(Extended Kalman filter,EKF)的INS/GPS/CNS全信息导航滤波算法,利用GPS和CNS输出的高精度导航信息,结合非线性扩展卡尔曼滤波框架,设计全观测量的滤波算法,通过研制的INS/GPS/CNS三组合导航系统进行试验验证,验证了所提算法的高精度和长时间工作条件下的稳定性。
1 INS/GPS/CNS滤波模型根据INS,GPS和CNS的系统特点,建立INS/GPS/CNS系统的数学模型。
1.1 状态方程模型根据文献[9],建立INS数学模型如下:
1)速度误差模型
| $\begin{split} \delta {{\dot{ V}}^n} = {{{f}}^n} \times {{\bf{\varphi }}^n} - \left( {2{\bf{\omega }}_{ie}^n + {\bf{\omega }}_{en}^n} \right) \times \delta {{{V}}^n}+ \\ \;\;\;\;\;{{{V}}^n} \times \left( {2\delta {\bf{\omega }}_{ie}^n + \delta {\bf{\omega }}_{en}^n} \right) + {{{\nabla}} ^n}\text{。} \end{split}$ | (1) |
式中:
| ${\bf{\omega }}_{ie}^n = {\left[ {\begin{array}{*{20}{c}} 0&{{\omega _{ie}}\cos L}&{{\omega _{ie}}\sin L} \end{array}} \right]^{\rm T}}\text{,}$ | (2) |
| ${\bf{\omega }}_{en}^n = {\left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{{V_N}}}{{R + h}}}&{\displaystyle\frac{{{V_E}}}{{R + h}}}&{\displaystyle\frac{{{V_E}}}{{R + h}}\tan L} \end{array}} \right]^{\rm T}}\text{,}$ | (3) |
| $\delta {\bf{\omega }}_{ie}^n = {\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _{ie}}\sin L\delta L}&{{\omega _{ie}}\cos L\delta L} \end{array}} \right]^{\rm T}}\text{,}$ | (4) |
| $\delta {\bf{\omega }}_{en}^n = \left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{\delta {V_N}}}{{R + h}} + \frac{{{V_N}\delta h}}{{{{\left( {R + h} \right)}^2}}}} \\ {\displaystyle\frac{{\delta {V_E}}}{{R + h}} - \frac{{{V_E}\delta h}}{{{{\left( {R + h} \right)}^2}}}} \\ {\displaystyle\frac{{\delta {V_E}}}{{R + h}}\tan L - \frac{{{V_E}\tan L\delta h}}{{{{\left( {R + h} \right)}^2}}} + - \frac{{{V_E}{{\sec }^2}L\delta L}}{{R + h}}} \end{array}} \right]\text{。}\!\!\!\!\!$ | (5) |
其中:
2)平台失准角误差方程
| ${{\dot{\bf \varphi }}^n} = \delta {\bf{\omega }}_{in}^n - ({\bf{\omega }}_{ie}^n + {\bf{\omega }}_{en}^n) \times {{\bf{\varphi }}^n} + {{\bf{\varepsilon }}^n}\text{。}$ | (6) |
式中:
3)位置误差方程
| $\begin{split} &\delta {{\dot{ P}}^n} = \left[ {\begin{array}{*{20}{c}} 0&{\displaystyle\frac{1}{{R + h}}}&0 \\ {\displaystyle\frac{{\sec L}}{{R + h}}}&0&0 \\ 0&0&1 \end{array}} \right] \cdot \delta {{{V}}^n}+\\ &\quad \left[ {\begin{array}{*{20}{c}} 0&0&{ - \displaystyle\frac{{{V_N}}}{{{{\left( {R + h} \right)}^2}}}} \\ {\displaystyle\frac{{{V_E}\sec L\tan L}}{{R + h}}}&0&{ - \displaystyle\frac{{{V_E}\sec L}}{{{{\left( {R + h} \right)}^2}}}} \\ 0&0&0 \end{array}} \right] \cdot \delta {{{P}}^n} \end{split}\text{。}$ | (7) |
式中:
基于上述分析,选用INS模型作为INS/CNS/GPS系统滤波的基础框架,可获得状态模型如下:
| ${\dot{ X}} = {{AX}} + {{BW}}\text{。}$ | (8) |
其中:
| $ \begin{align} & {\bf X}=[\begin{matrix} \delta \lambda & \delta L & \delta h & \delta {{V}_{E}} & \delta {{V}_{N}} & \delta {{V}_{U}} & {{\varphi }_{E}} & {} & {} \\ \end{matrix} \\ & \begin{matrix} \ \ {{\varphi }_{N}} & {{\varphi }_{U}} & \varepsilon _{x}^{b} & \varepsilon _{y}^{b} & \varepsilon _{z}^{b} & \nabla _{x}^{b} & \nabla _{y}^{b} & \nabla _{z}^{b} \\ \end{matrix}{{]}^{\rm T}}\text{。} \\ \end{align} $ | (9) |
其中:
1)INS/GPS量测方程
由于GPS可提供高精度的位置和速度信息,所以取INS和GPS输出的位置和速度信息之差作为INS/GPS系统的观测量,定义量测方程为:
| ${Z_1} = \left[ {\begin{array}{*{20}{c}} {{L_I} - {L_G}} \\ {{\lambda _I} - {\lambda _G}} \\ {{h_I} - {h_G}} \\ {{v_{xI}} - {v_{xG}}} \\ {{v_{yI}} - {v_{yG}}} \\ {{v_{zI}} - {v_{zG}}} \end{array}} \right] = {{ H}_1}X + \gamma \text{。}$ | (10) |
式中:
2)INS/CNS量测方程
由于INS输出为机体系下姿态(
| $ {\varPhi _{In}} = { C}_b^n{\varPhi _{Ib}}\;{\varPhi _{Cn}} = { C}_i^n{\varPhi _{Ci}}\text{。} $ | (11) |
式中:
获得量测方程如下:
| ${{ Z}_2} = \left[ {\begin{array}{*{20}{c}} {{\varPhi _{EIn}} - {\varPhi _{ECn}}} \\ {{\varPhi _{NIn}} - {\varPhi _{NCn}}} \\ {{\varPhi _{UIn}} - {\varPhi _{UCn}}} \end{array}} \right] = {{ H}_2}X + \kappa $ | (12) |
式中:
3)INS/GPS/CNS量测方程
基于上述量测方程,构建INS/GPS/CNS全信息观测量方程,如下:
| ${ Z} = \left[ {\begin{array}{*{20}{c}} {{L_I} - L} \\ {{\lambda _I} - \lambda } \\ {{h_I} - h} \\ {{v_{xI}} - {v_x}} \\ {{v_{yI}} - {v_y}} \\ {{v_{zI}} - {v_z}} \\ {{\varPhi _{EIn}} - {\varPhi _{En}}} \\ {{\varPhi _{NIn}} - {\varPhi _{Nn}}} \\ {{\varPhi _{UIn}} - {\varPhi _{Un}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varPhi _{EIn}} - {\varPhi _{ECn}}} \\ {{\varPhi _{NIn}} - {\varPhi _{NCn}}} \\ {{\varPhi _{UIn}} - {\varPhi _{UCn}}} \end{array}} \right] = { H}X + \eta \text{。}$ | (13) |
式中:
将式(8)和式(13)离散化获得系统离散化模型:
| $\left\{ \begin{array}{l} {{{{\dot X}}}_k}{{ = }}{{{A}}_{k|k - 1}}{{{X}}_{k - 1}}{{ + }}{{{B}}_{k - 1}}{{{W}}_{k - 1}} \text{,} \\ {Z_k} = {H_k}{X_k} + {\eta _k} \text{。}\\ \end{array} \right.$ | (14) |
根据上述离散化模型建立扩展卡尔曼滤波方程如下:
| ${{\hat{\rm X}}_{k|k - 1}}{\rm{ = }}{{{F}}_{k|k - 1}}{{\hat{\rm X}}_{k - 1}}\text{,}$ | (15) |
| ${{{P}}_{k|k - 1}}{{ = }}{{{F}}_{k|k - 1}}{{{P}}_{k - 1}}{{{F}}_{k|k - 1}^{\rm T}} + {G_{k - 1}}{Q_{k - 1}}G_{k - 1}^{\rm T}\text{,}$ | (16) |
| ${{{K}}_k}{{ = }}{{{P}}_{k|k - 1}}H_k^{\rm T}{\left( {H_k^{}{{\rm{P}}_{k|k - 1}}H_k^{\rm T} + {Q_k}} \right)^{\rm T}}\text{,}$ | (17) |
| ${{\hat{\rm X}}_k}{\rm{ = }}{{\hat{\rm X}}_{k|k - 1}} + {K_k}\left( {{Z_k} - {H_k}{{{\hat{\rm X}}}_{k|k - 1}}} \right)\text{,}$ | (18) |
| ${{{P}}_k} = \left( {I - {{{K}}_k}H_k^{}} \right){{{P}}_{k|k - 1}}{\left( {I - {{{K}}_k}H_k^{}} \right)^{\rm T}} + {K_k}{{ Q}_k}K_k^{\rm T}\text{。}$ | (19) |
其中:
在初始状态向量
为验证本文提出的基于EKF全信息导航算法的有效性,搭建INS/GPS/CNS三组合导航系统进行精度验证,系统由激光惯导(陀螺漂移
| ${A_k} = \frac{{{e_k}}}{{{e_0}}}\text{。}$ | (20) |
|
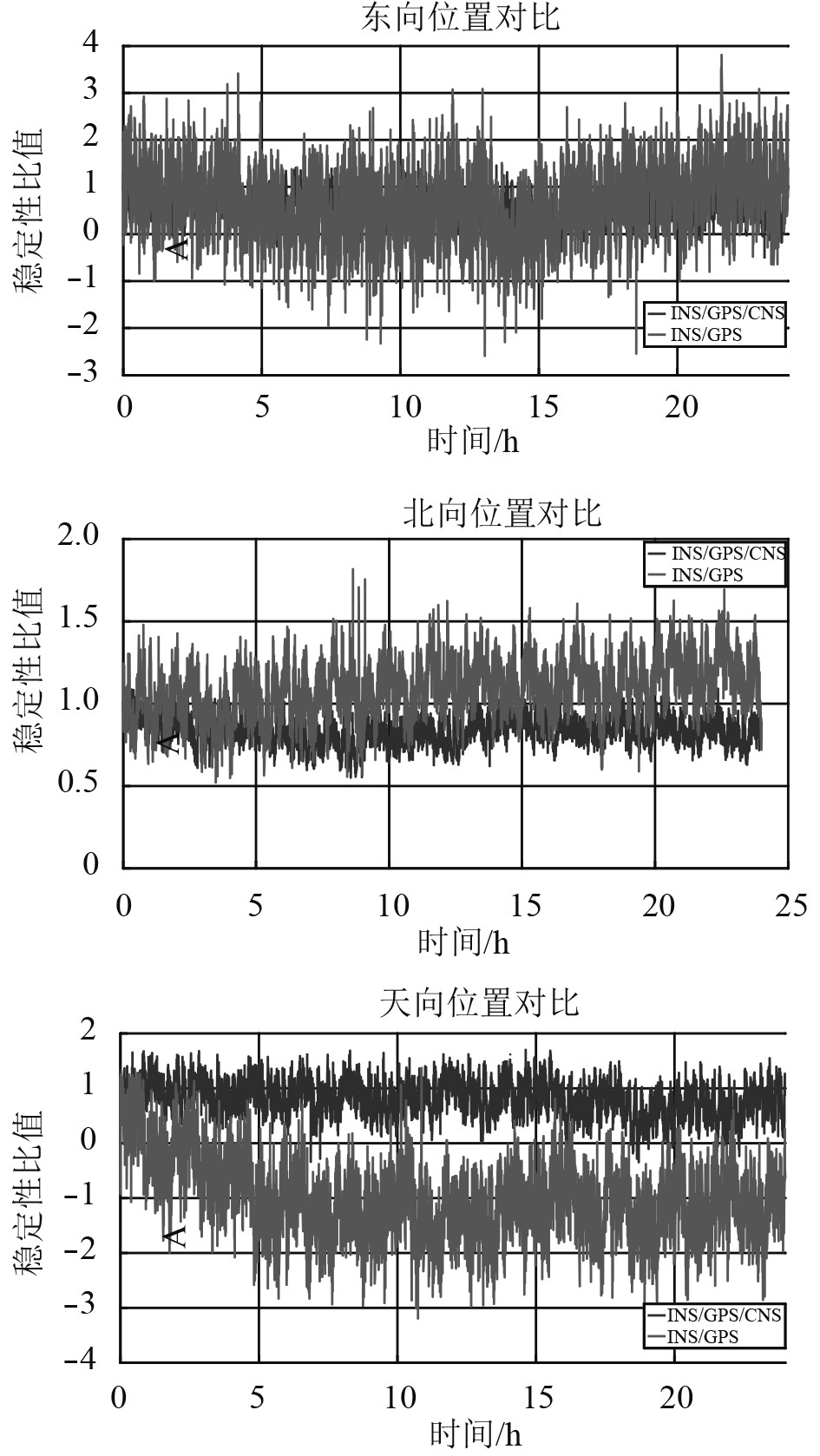
图 1 位置误差试验结果对比图 Fig. 1 Comparison of position error test results |

|
图 2 速度误差试验结果对比图 Fig. 2 Comparison of speed error test results |
|
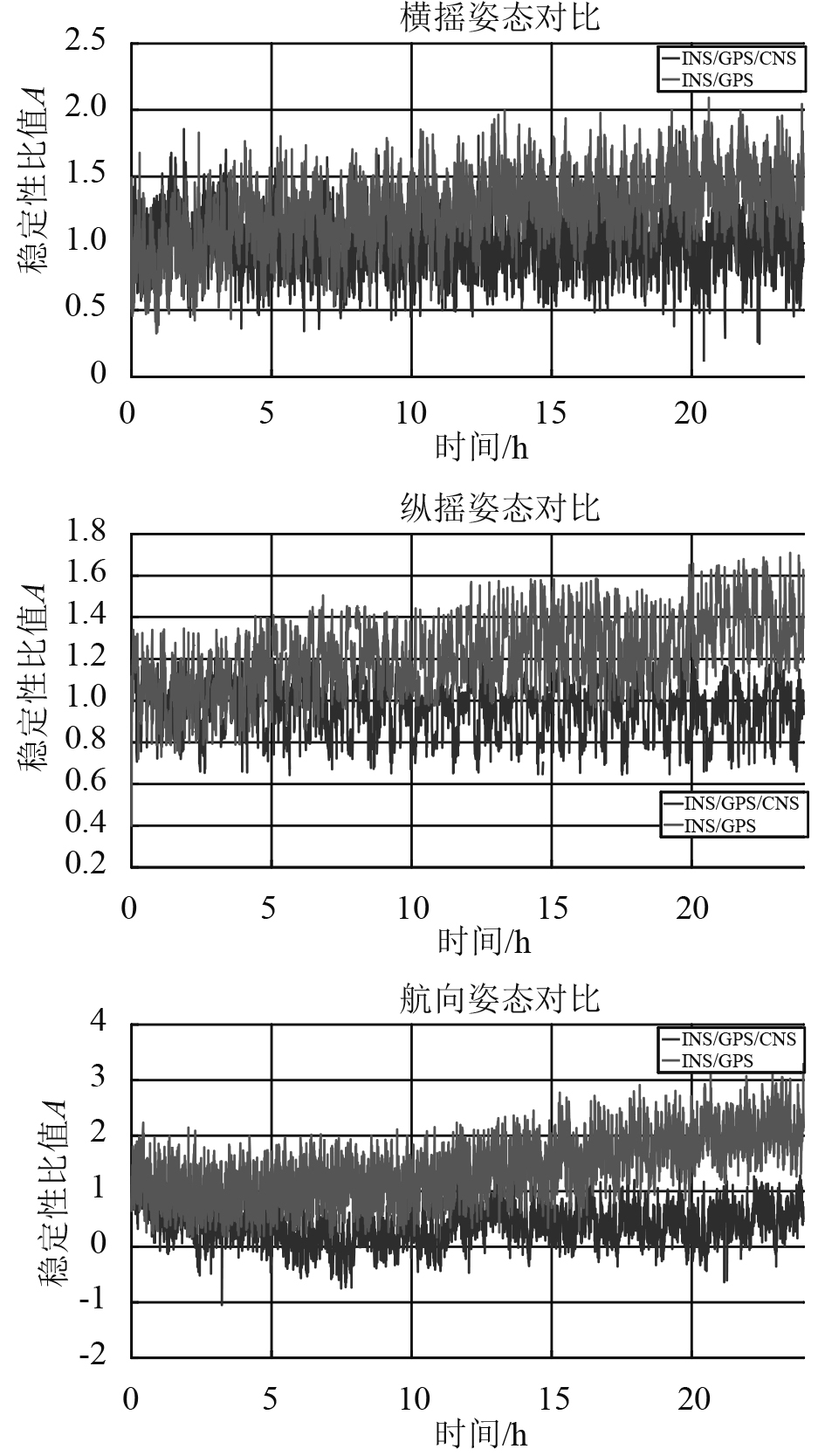
图 3 姿态误差试验结果对比图 Fig. 3 Comparison of attitude error test results |
由图1可知,2种滤波算法的处理结果均收敛,但从数据波动程度来看,两组合算法波动较大,且根据稳定性比值峰峰值,三组合算法峰峰值较小,证明算法稳定性较好。由图2东向速度试验结果,三组合算法误差收敛很快,误差远小于两组合结果,证明三组合算法精度较高。由图3姿态误差试验结果可知,在长航时条件下,姿态信息有不同程度的发散,这是由于INS等效东向陀螺漂移的长期稳定性很难保证所致,在增加了CNS的姿态信息作为观测量后,滤波效果得到明显改善,姿态信息收敛且保持稳定。所以,相较于传统的INS/GPS两组合扩展卡尔曼滤波算法,INS/GPS/CNS三组合扩展卡尔曼滤波算法结果精度更高,长航时工作条件下稳定性更好。
4 结 语本文针对INS/GPS两组合系统长航时条件下姿态精度发散、导航精度较低、系统稳定性较差的问题,引入CNS系统的姿态信息,构建一种基于INS/GPS/CNS的全信息导航滤波模型,提出一种基于EKF的INS/GPS/CNS滤波算法。搭建INS/GPS/CNS三组合系统对算法有效性进行验证,试验结果表明,相较于传统INS/GPS两组合算法,所提算法在长航时条件下稳定性强、收敛性好且精度高,工程应用意义较大。
| [1] |
CHRISTOPHER, MOORE, TERRY, et al. Adaptive Kalman filtering for low-cost INS/GPS[J]. Journal of Navigation, 2003, 56(1): 143-152. DOI:10.1017/S0373463302002151 |
| [2] |
NEMRA A, AOUF N. Robust INS/GPS sensor fusion for UAV localization using SDRE nonlinear filtering[J]. IEEE Sensors Journal, 2010, 10(4): 789-798. DOI:10.1109/JSEN.2009.2034730 |
| [3] |
ABDOLKARIMI E S, ABAEI G, MOSAVI M R. A wavelet-extreme learning machine for low-cost INS/GPS navigation system in high-speed applications[J]. Gps Solutions, 2018, 22(1): 15. DOI:10.1007/s10291-017-0682-x |
| [4] |
WANG H, CAI Y. Study on INS/GPS/CNS integrated navigation systems considering of ship′s deformation[J]. Journal of Jiangsu University of Science & Technology, 2008. |
| [5] |
GAO B, HU G, GAO S, et al. Multi-sensor optimal data fusion for INS/GNSS/CNS integration based on unscented Kalman filter[J]. International Journal of Control Automation & Systems, 2018, 16(1): 129-140. |
| [6] |
WANG D, LV H, JIE W. A novel SINS/CNS integrated navigation method using model constraints for ballistic vehicle applications[J]. Journal of Navigation, 2017, 70(6): 1-23. |
| [7] |
张科, 刘海鹏, 李恒年, 钱山. SINS/GPS/ CNS组合导航联邦滤波算法[J]. 中国惯性技术学报, 2013, 21(2): 226-230. DOI:10.3969/j.issn.1005-6734.2013.02.019 |
| [8] |
吴坤峰, 杨峰, 梁彦, 张共愿, 程咏梅. INS/GPS/CNS组合导航系统仿真[J]. 火力与指挥控制, 2010, 35(7): 13-19. DOI:10.3969/j.issn.1002-0640.2010.07.004 |
| [9] |
ZHANG Tong, CHEN Kang, FU Wen-xing. Optimal two-iteration sculling compensation mathematical framework for SINS velocity updating[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 1065-1071. DOI:10.1109/JSEE.2014.00122 |
| [10] |
严恭敏. 捷联惯导系统动基座初始对准及其它相关问题研究[D]. 西安: 西北工业大学. 2008.
|
 2019, Vol. 41
2019, Vol. 41
