2. 海军大连舰艇学院水武与防化系,辽宁 大连 116018
2. Department of Underwater Weaponry and Chemical Denfense, Dalian Navy Academy, Dalian 116018, China
随着各国海洋利益的不断扩展,水下安全形势越来越复杂,水下目标辐射噪声级不断降低,隐蔽性随之增强。近场区域警戒和近海岸的港口防御等军事需求越来越迫切。针对近场声目标定位问题,聚焦波束形成是常见的方法之一,其原理是根据目标声源到各个阵元曲率半径不同,补偿球面波传播模型下的时延差。该时延差考虑的是声源距离和方位的二维函数,在扫描平面上对不同位置点进行扫描,获得该平面的声强图,当扫描点与目标位置重合时,聚焦波束形成输出会出现峰值,即可得到目标的距离和方位。科研人员基于均匀线列阵,对近场聚焦波束形成方法展开了比较深入的研究,2012年,陈欢等[1]提出了基于幅度补偿的直线阵近场聚焦波束形成方法,该方法有效提高了基阵对于低频信号的空间分辨能力,并进一步抑制了高频信号的空间混叠,但是直线阵对目标进行方位估计时会出现方位模糊等问题针对小基阵的近场目标定位问题,2014年,陈泓宇等[2]提出了基于半圆阵的近场聚焦波束形成方法,通过仿真结果来看,半圆阵虽然克服了直线阵对目标进行方位估计时出现的“左右舷模糊”问题,但是基于半圆阵的近场聚焦波束形成方法旁瓣级比较高,使得空间分辨率降低。从目前的研究情况来看,近场目标的定位研究主要集中于方位估计或方位与俯仰角估计,针对基于空间阵的目标距离、方位、俯仰角三维同时定位需要进行更深入的研究。研究也表明,定位性能与基阵的布设、定位的方法等都有比较大的关系,如何设计更合理的小尺寸基阵实现对近场目标的准确定位仍然是需要解决的问题。
本文提出圆台阵设计的构想,推导了圆台阵的接收信号模型,提出了近场三维声聚焦波束形成的实现框架,通过对切割球面上聚焦点的扫描,得到目标方位角和俯仰角,再通过对不同扫描球面上最大输出功率的比较得到目标距离,从而实现了对近场目标距离、方位角、俯仰角的估计,并采用MVDR波束形成方法仿真分析了圆台阵阵型对目标三维定位性能的影响,可为优化圆台阵的阵形设计提供一定支撑。
1 圆台阵近场信号接收模型如图1所示,圆台阵由4条线型子阵组成,每条子线阵的阵元数为

|
图 1 圆台阵阵列模型 Fig. 1 Circular matrix array model |
根据图1和几何关系,运用三角形余弦定理可得
| $\tiny \left\{ \begin{align} & {{r}_{{\rm 1}i}}{\rm =}\\ &\sqrt{\begin{align} & {{\left( r\cos \left( \theta \right) \right)}^{{\rm 2}}}{\rm +}{{\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{1}} \right)}^{2}}-2r\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{{\rm 1}}} \right)\cos \left( \theta \right)\cos \left( \varphi \right) +{{\left( \left( i-1 \right)\frac{d}{m}\sin \left( {{\theta }_{z}} \right){\rm +}r{\rm sin}\left( \theta \right) \right)}^{2}} {\text{,}}\\ \end{align}}\\& {\text{ 第一个子阵}}{\rm }i=1,2,.....,m {\text{,}}\\ &{{r}_{{\rm 2}i}}{\rm =}\\& \sqrt{\begin{align} &{{\left( r\cos \left( \theta \right) \right)}^{{\rm 2}}}{\rm +}{{\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{1}} \right)}^{2}}-2r\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{{\rm 1}}} \right)\cos \left( \theta \right)\cos \left( {\rm 90}-\varphi \right) +{{\left( \left( i-1 \right)\frac{d}{m}\sin \left( {{\theta }_{z}} \right){\rm +}r{\rm sin}\left( \theta \right) \right)}^{2}}{\text{,}} \\ \end{align}}\\& {\text{第二个子阵}}{\rm }i=1,2,.....,m {\text{,}}\\ &{{r}_{{\rm 3}i}}{\rm =}\\ & \sqrt{\begin{align} & {{\left( r\cos \left( \theta \right) \right)}^{{\rm 2}}}{\rm +}{{\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{1}} \right)}^{2}}-2r\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{{\rm 1}}} \right)\cos \left( \theta \right)\cos \left( 180-\varphi \right) +{{\left( \left( i-1 \right)\frac{d}{m}\sin \left( {{\theta }_{z}} \right){\rm +}r{\rm sin}\left( \theta \right) \right)}^{2}} {\text{,}}\\ \end{align}}\\ &{\text{ 第三个子阵}}{\rm }i=1,2,.....,m \\ &{{r}_{{\rm 4}i}}{\rm =} \\& \sqrt{\begin{align} & {{\left( r\cos \left( \theta \right) \right)}^{{\rm 2}}}{\rm +}{{\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{1}} \right)}^{2}}-2r\left( i\frac{d}{m}\cos \left( {{\theta }_{z}} \right){\rm +}{{l}_{{\rm 1}}} \right)\cos \left( \theta \right)\cos \left( 360-\varphi \right) +{{\left( \left( i-1 \right)\frac{d}{m}\sin \left( {{\theta }_{z}} \right){\rm +}r{\rm sin}\left( \theta \right) \right)}^{2}} {\text{,}}\\ \end{align}}\\ &{\text{第四个子阵}}{\rm }i=1,2,.....,m{\rm } \\ \end{align} \right. $ | (1) |
第
| ${\tau _{ki}}{\rm{ = }}\frac{{{r_{ki}} - r}}{c}{\text{,}}$ | (2) |
则第
| ${x_{ki}}\left( t \right) = s\left( t \right){e^{ - 2{\text{π}} jf{\tau _{ki}}}}{\rm{ + }}{n_{ki}}\left( t \right){\text{,}}$ | (3) |
表示为矩阵形式为:
| ${ X}\left( t \right) = { A}\left( {r,\theta ,\varphi } \right)s\left( t \right) + { N}\left( t \right){\text{。}}$ | (4) |
式中:
| $\tiny \begin{align} & A\left( {r,\theta ,\varphi } \right) =\\ & \left[ \begin{array}{l} \!\! \!\! \!\!{e^{\dfrac{{ - j2{\text{π}} \left( {\sqrt {{{\left( {r\cos \left( \theta \right)} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {\frac{d}{m}\cos \left( {{\theta _z}} \right){\rm{ + }}{l_1}} \right)}^2}\!\! - 2r\left( {\frac{d}{m}\cos \left( {{\theta _z}} \right){\rm{ + }}{l_1}} \right)\cos \left( \theta \right)\cos \left( \varphi \right) + {{\left( {r{\rm{sin}}\left( \theta \right)} \right)}^2}} \!\!- r} \right)}}{\lambda }}} \\ \!\! \!\! \!\! \vdots \\ \!\! \!\! \!\! {e^{\dfrac{{ - j2{\text{π}} \left( {\sqrt {{{\left( {r\cos \left( \theta \right)} \right)}^{\rm{2}}}{\rm{ \!+\! }}{{\left( {i\frac{d}{m}\cos \left( {{\theta _z}} \right){\rm{ \!+\! }}{l_1}} \right)}^2} \!\!\!-\! 2r\left( {i\frac{d}{m}\cos \left( {{\theta _z}} \right){\rm{ \!+\! }}{l_1}} \right)\cos \left( \theta \right)\cos \left( {{\rm{90}} \!-\! \varphi } \right) \!+\! {{\left( {\left( {i \!-\! 1} \right)\frac{d}{m}\sin \left( {{\theta _z}} \right){\rm{ \!+\! }}r{\rm{sin}}\left( \theta \right)} \right)}^{\rm{2}}}} \!\! \!-\! r} \right)}}{\lambda }}} \!\!\!\! \!\! \\ \!\! \!\! \!\! \vdots \\ \\ \!\! \!\! \!\!{e^{\dfrac{{ - j2{\text{π}} \left( {\sqrt {{{\left( {r\cos \left( \theta \right)} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {d\cos \left( {{\theta _z}} \right){\rm{ + }}{l_1}} \right)}^2} - 2r\left( {d\cos \left( {{\theta _z}} \right){\rm{ + }}{l_1}} \right)\cos \left( \theta \right)\cos \left( {360 - \varphi } \right) + {{\left( {d\sin \left( {{\theta _z}} \right){\rm{ + }}r{\rm{sin}}\left( \theta \right)} \right)}^2}} - r} \right)}}{\lambda }}} \!\! \!\!\!\! \end{array} \!\!\! \right]\text{。}\end{align}$ | (5) |
常规的聚焦波束形成,就是根据目标噪声源到各个阵元的声传播距离不同,补偿球面波传播模型下的时延差,再对补偿后的阵元信号进行加权、求和,其传统方法的时延差是声源距离和方位的二维函数,在扫描平面上对不同位置点进行扫描,获得该平面的声强图,当扫描点与目标位置重合时,聚焦波束形成输出会出现峰值,即可得到目标的距离和方位估计[3 – 4]。
本文在常规聚焦波束形成的基础上,提出三维声聚焦波束形成的实现框架,其基本原理如图2所示。
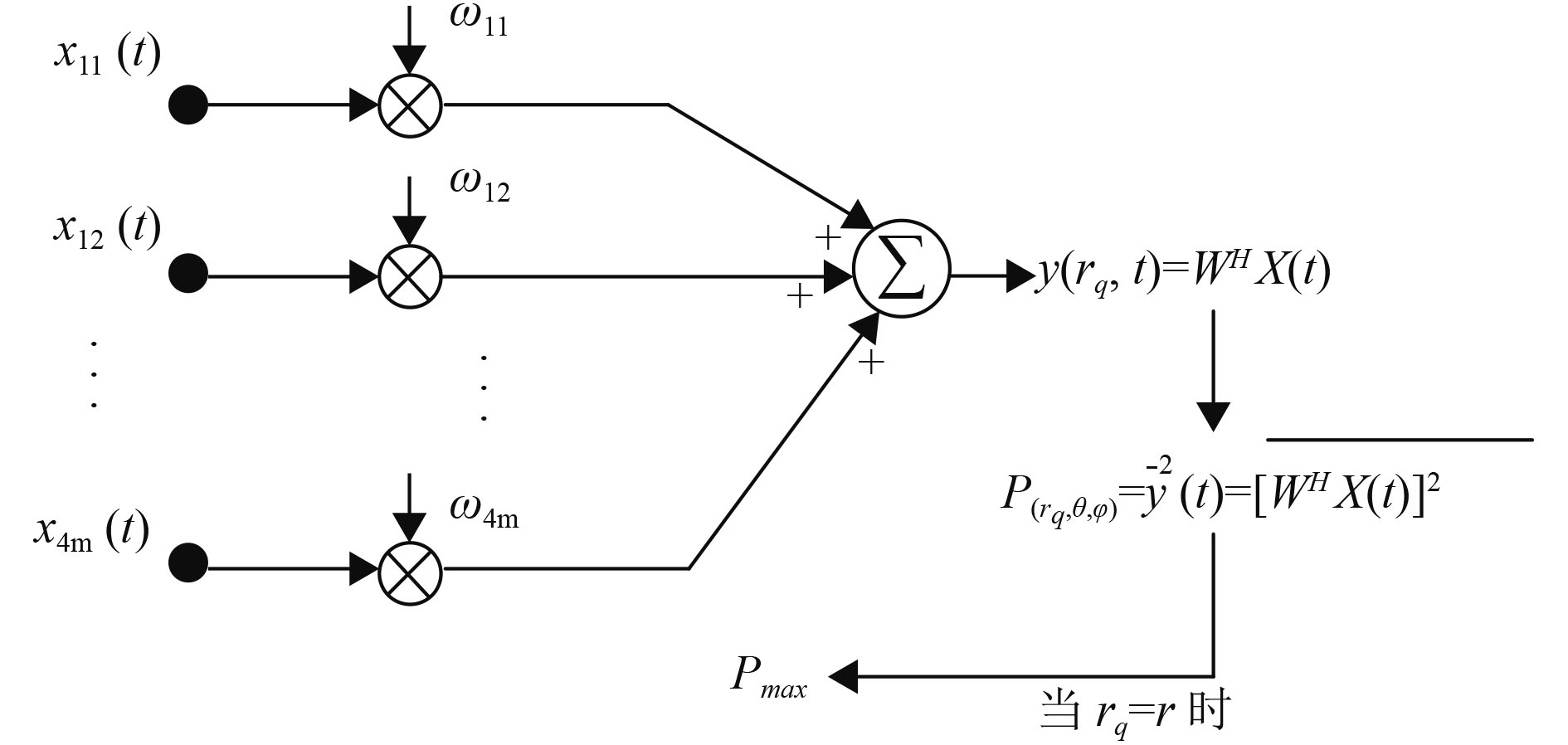
|
图 2 三维声聚焦波束形成原理 Fig. 2 The principle of three-dimensional acoustic focusing beamforming |
首先,将三维空间以参考点为中心,以搜索目标的距离范围将搜索空间切割为

|
图 3 扫描球面 Fig. 3 Scanning sphere |
对
| $y\left( {{r_q},t} \right) = {{ W}^H}{ X}\left( t \right){\text{。}}$ | (6) |
相应
| ${P_{\left( {{r_q},\theta ,\varphi } \right)}} = {\overline y ^2}\left( t \right) = \overline {{{\left[ {{{ W}^H}{ X}\left( t \right)} \right]}^2}} {\text{。}}$ | (7) |
本文采用最小方差无失真响应(MVDR)波束形成方法实现入射位置处信号的输出功率不变,使扫描空间其他位置点的信号输出功率最小。在近场条件下,MVDR三维声聚焦波束形成可以转化为求解如式(8)所示的优化问题[5 – 9]。
| $\left\{ \begin{array}{l} {{ W}^H}{ A}\left( {{r_q},\theta ,\varphi } \right) = 1 {\text{,}} \\ P\left( {{r_q},\theta ,\varphi } \right) = \min {{ W}^H}{ RW} {\text{。}}\\ \end{array} \right.$ | (8) |
式中:
| ${{ W}_{opt}} = \frac{{{{ R}^{ - 1}}{ A}\left( {{r_q},\theta ,\varphi } \right)}}{{{ A}{{\left( {{r_q},\theta ,\varphi } \right)}^H}{{ R}^{ - 1}}{ A}\left( {{r_q},\theta ,\varphi } \right)}}$ | (9) |
相应
| ${P_{MVDR}}\left( {{r_q},\theta ,\varphi } \right) \!= \!{ W}_{opt}^H{ R}{{ W}_{opt}}\! =\! \frac{1}{{{ A}{{\left( {{r_q},\theta ,\varphi } \right)}^H}{{ R}^{ - 1}}{ A}\left( {{r_q},\theta ,\varphi }\! \right)}}\text{。}$ | (10) |
利用上式,代入不同的
仿真验证中假设单条线阵长度
实验1:假设目标俯仰角为
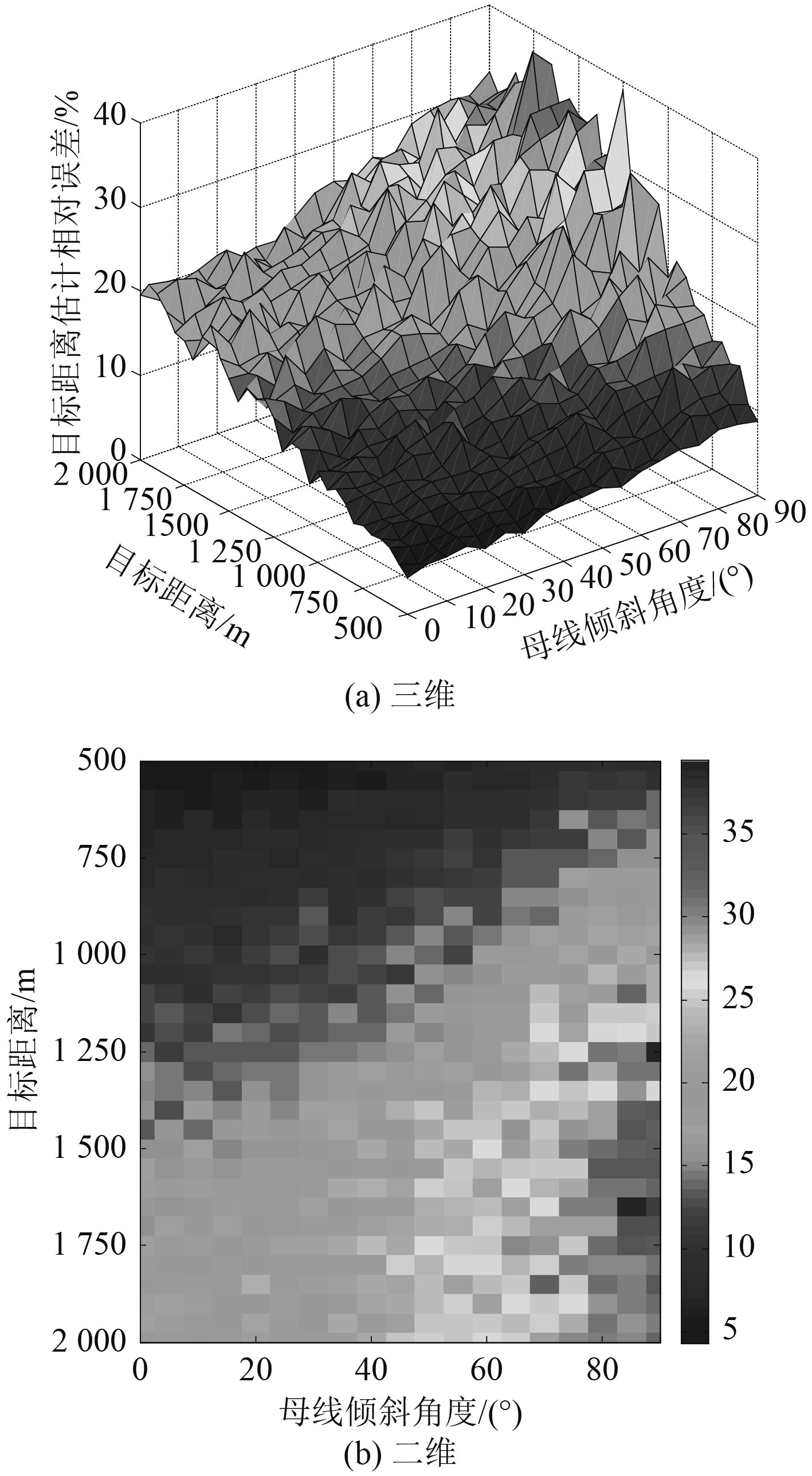
|
图 4 不同母线倾斜角度、不同距离目标下的目标距离估计相对误差 Fig. 4 Relative error of target distance estimation under different bus inclination angle and different target distance |
从图4可以看出,圆台阵的母线倾斜角度对不同距离目标下的距离估计误差影响比较大,总的来看,倾斜角度值越小,由于此时阵越接近平面阵,相当于孔径变大,使得同一距离目标的距离估计越准确,也就是当4个线阵接近于同一平面时,测距性能越好。另外,同一倾斜角度值下,目标距离越远,距离估计误差越大。同时通过取值分析可以得到,当母线倾斜角度小于
实验2:假设目标俯仰角为
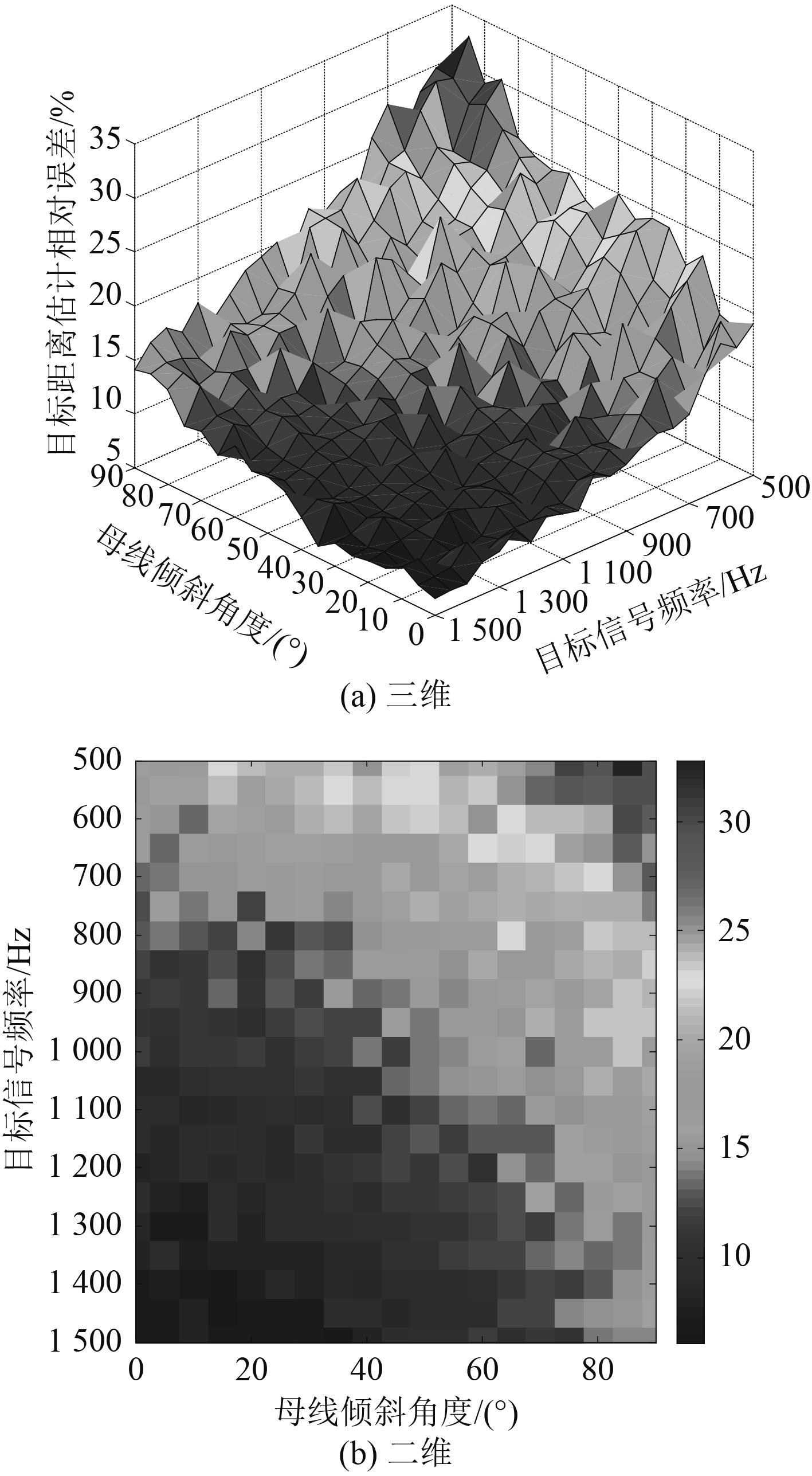
|
图 5 不同母线倾斜角度、不同频率目标下的目标距离估计相对误差 Fig. 5 Relative error of target distance under different frequency targets with different bus inclination angles |
从图5可以看出,圆台阵的母线倾斜角度对不同频率目标下的距离估计误差影响比较大,总的来看,倾斜角度值越小,由于此时阵越接近平面阵,相当于孔径变大,使得同一频率目标的距离估计越准确,也就是当4个线阵接近于同一平面时,测距性能越好,与仿真实验1得到的结果一致。另外,同一倾斜角度值下,目标信号频率越高,距离估计误差越小。同时通过取值分析可以看出,当频率大于1 000 Hz时,目标距离估计误差可均小于
聚焦空间分辨率即聚焦波束在半功率点处的波束宽度值,该值反映的是分辨2个空间位置相近点声源的能力,是衡量近场聚焦波束形成定位性能的重要指标之一[10]。当2个声源之间的角度差大于聚焦波束半功率点处时可分辨。
实验1:假设目标方位角为
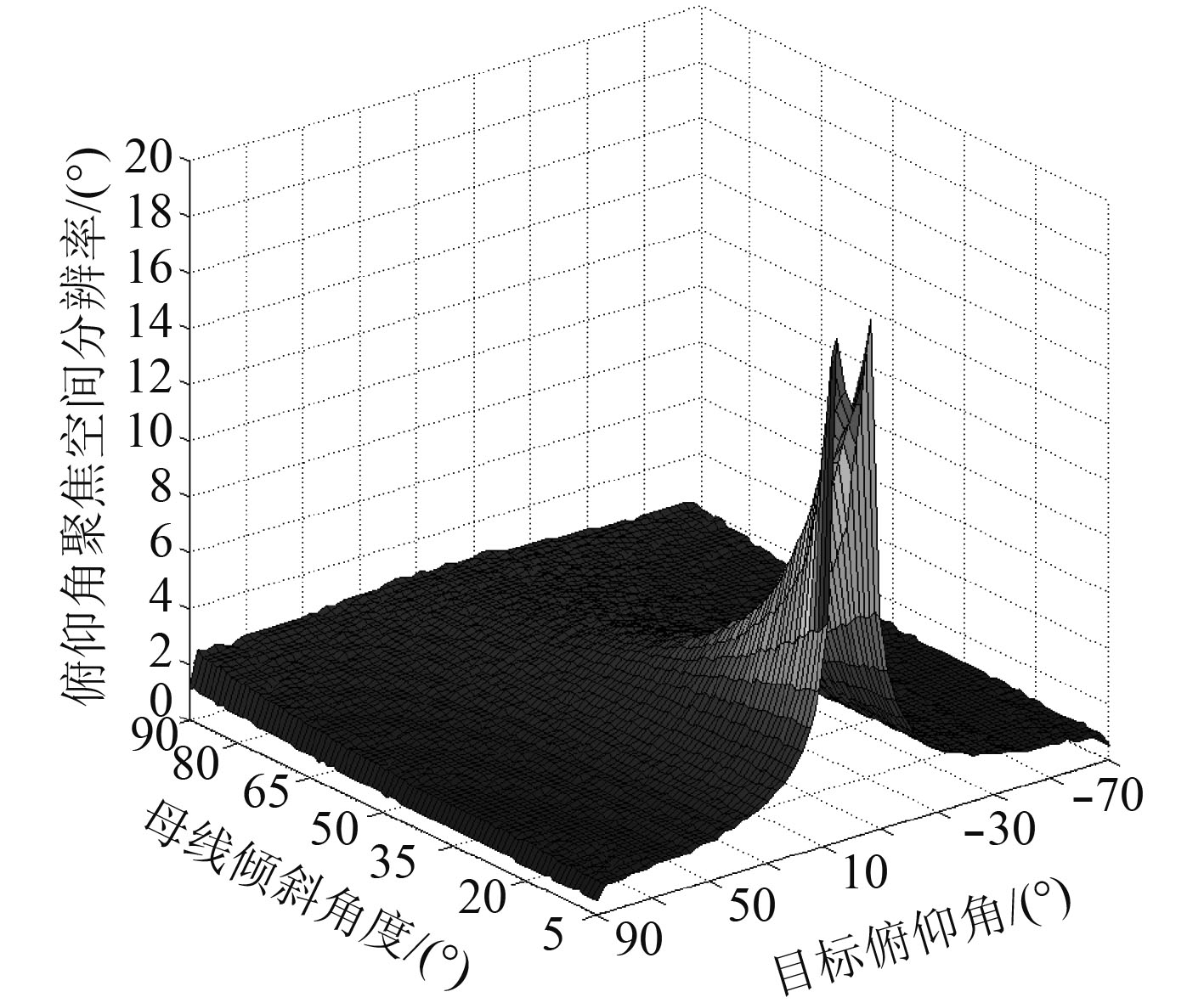
|
图 6 不同母线倾斜角度、不同俯仰角下的俯仰角聚焦空间分辨率 Fig. 6 Focusing spatial resolution of pitch angle at different bus tilt angle and pitch angle |
可以看到,当圆台阵母线倾斜角度较小时,俯仰角在
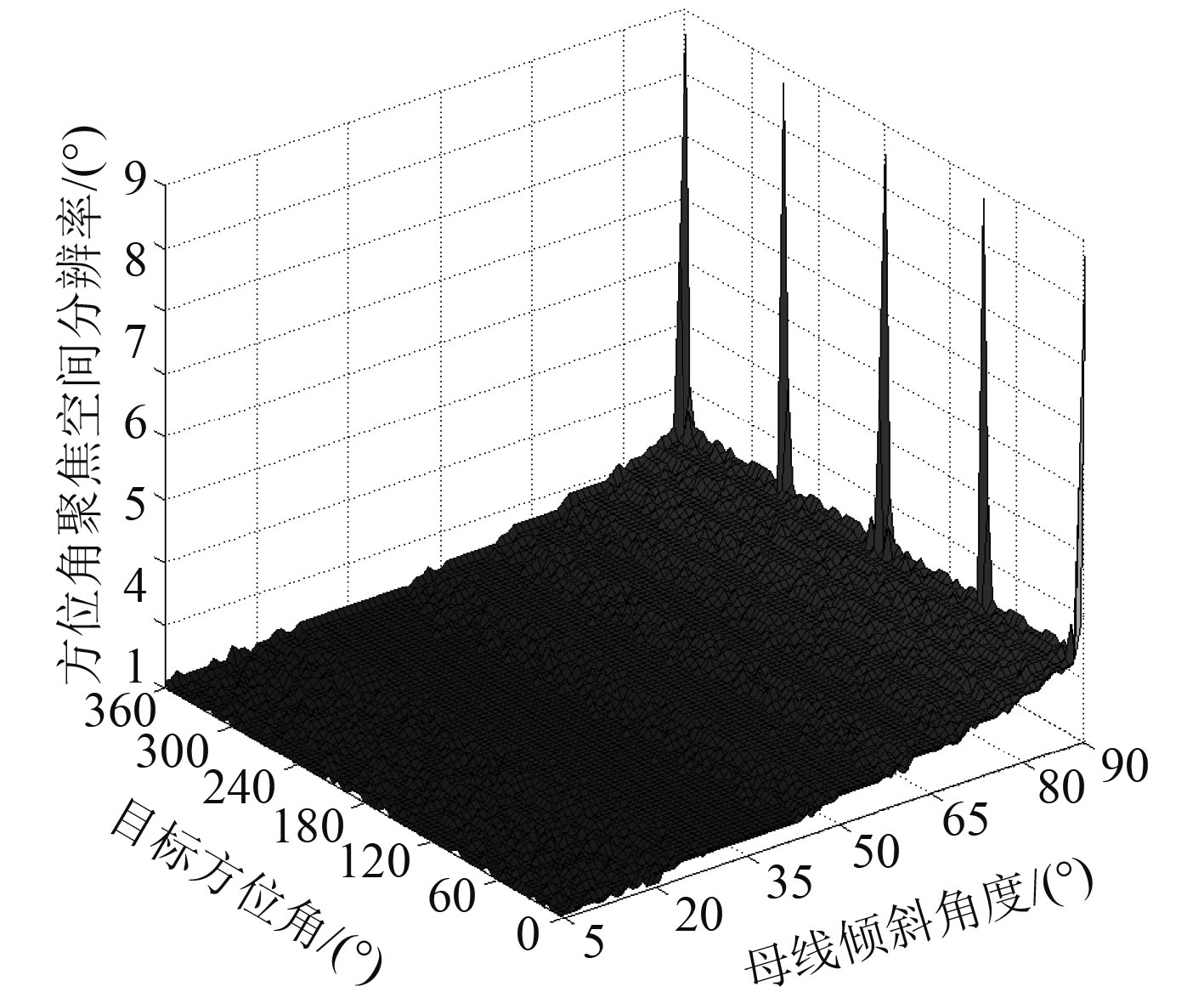
实验 2:假设目标俯仰角为
|
图 7 不同母线倾斜角度、不同方位角下的目标方位角聚焦空间分辨率 Fig. 7 Spatial resolution of target azimuth focusing at different bus tilt angle and azimuth angle |
可以看出,母线倾斜角度越小,目标方位角聚焦空间分辨率越高。同一母线倾斜角度下,不同方位目标的聚焦空间分辨率基本相同。当母线倾斜角度接近
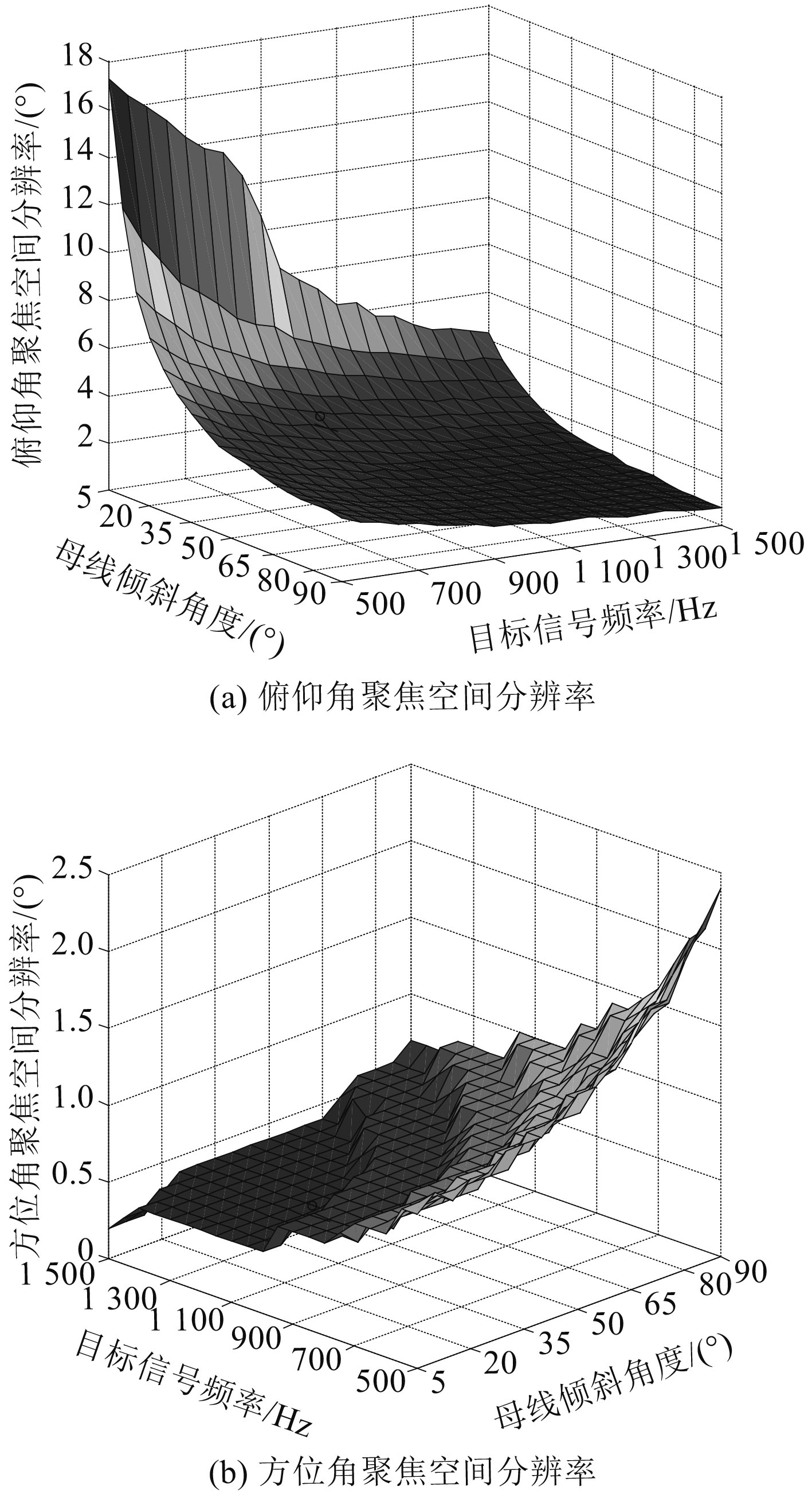
实验3:假设目标距离为2 000 m,俯仰角为
|
图 8 不同母线倾斜角度、不同频率目标下聚焦空间分辨率 Fig. 8 Different bus tilt angle and different frequency target focus spatial resolution |
从图8(a)可以看出,母线倾斜角度不变,信号频率越高,俯仰角聚焦空间分辨率值越小,分辨目标能力越强。信号频率不变,母线倾斜角度越大,俯仰角聚焦空间分辨率值越大,分辨目标能力越弱。
从图8(b)可以看出,母线倾斜角度不变,信号频率越高,方位角聚焦空间分辨率值越小,分辨目标能力越强。信号频率不变,母线倾斜角度越小,方位角聚焦空间分辨率值越小,分辨目标能力越强。
综合图6~图8可以看出,方位角聚焦空间分辨率明显高于俯仰角聚焦空间分辨率,且无论母线倾斜角度等于多少,方位角聚焦空间分辨率均小于3o。但要想保证目标俯仰角的估计精度,母线倾斜角必须增大,对于信号频率为500 Hz的目标而言,要想保证俯仰角聚焦空间分辨率小于5o,母线倾斜角需要大于45o。
4 结 语本文推导了圆台阵近场信号接收模型和三维声聚焦波束形成方法,研究了圆台阵近场MVDR三维声聚焦波束形成被动定位的性能。从仿真数据分析发现,母线倾斜角度对定位性能的影响比较大,母线倾斜角度越小,测距性能就越好,方位角空间分辨率就越高。但是对于俯仰角较低的目标而言,母线倾斜角度越小,俯仰角空间分辨率就越差。要想保证目标俯仰角的估计精度,母线倾斜角必须增大。也就是说,如果只要求目标方位和距离估计性能,则圆台阵可摆放成平面阵型,如果需要对目标实现距离、方位、俯仰三维声定位,则圆台阵的母线倾斜角必须增大到合适的角度。对于中高频目标而言,当指标要求距离估计相对误差10%,方位角和俯仰角误差5o时,母线倾斜角为
| [1] |
陈欢, 何良, 杨德森, 等. 基于幅度补偿德MVDR水下噪声源近场定位识别方法研究[J]. 振动与冲击, 2012, 31(2). DOI:10.3969/j.issn.1000-3835.2012.02.029 |
| [2] |
陈泓宇, 吴伟伟, 王明宇. 基于近场聚焦波束形成方法的声场定位研究[J]. 计算机仿真, (2014)1006-9348;
|
| [3] |
吴一飞, 惠娟, 牛芳, 等. 基于水平直线阵的近场目标被动定位方法研究[J]. 声学技术, 33, 5 Pt. 2 Oct, 2014, 33(10).
|
| [4] |
丁浩. 可识别声源深度的三维声聚焦波束形成方法研究[D]. 杭州: 浙江工业大学, 2013.
|
| [5] |
丁浩, 李春晓, 金江明, 等. 可识别声源深度的三维声聚焦波束形成方法[J]. 传感技术学报, 2013, 26(2): 175-181. DOI:10.3969/j.issn.1004-1699.2013.02.007 |
| [6] |
JUN LI, QIU-HUA LIN, CHUN-YU KANG. Performance analysis for focused beamformers in passive underwater acoustic localization, digital object identifier [EB/oL] 10.1109/ACCESSC.2018.2821766.
|
| [7] |
DONG ZHANG, YONG SHUN ZHANG. Two-dimensional direction of arrival estimation for coprime planar arrays via polynomial root finding technique, Digital Object Identifier [EB/oL] 10.1109/ACCESS.2018.2821919.
|
| [8] |
Wen-Qin WANG, Nested array receiver with time-delayers for joint target range and angle estimation. doi: 10.1049/iet-rsn.2015.0450
|
| [9] |
刘凯, 梁国龙. 基于矩阵空域预滤波的近场聚焦波束形成[J]. 华中科技大学学报(自然科学版), 2014, 42(1): 58-61. |
| [10] |
陈欢. 直线阵潜艇噪声源高分辨定位识别方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
