2. 海军工程大学 动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
叶片在压气机中起到能量转换的重要作用,在燃气轮机各工作环境下承受着很大的负荷。如果转子叶片的强度不足以承受各工况下的受力情况,将产生裂纹、断裂等故障,转子叶片的碎片甚至会飞出,打坏邻近的叶片和机匣,导致燃气轮机紧急停车甚至更严重的事故[1]。燃气轮机中转子叶片数量很大,少则几百片,多达几千片。因此,转子叶片强度计算的意义是为了保证所设计的转子叶片能可靠工作,又使其尽可能轻。
曲文浩[2]针对某型发动机压气机叶片,建立三维有限元分析模型,评价叶片的静强度储备是否满足设计准则的要求,进而对叶片结构进行强度设计优化。Ralsto等[3]运用有限元分析软件得到燃气轮机压气机叶片的高应力区主要集中在涡轮叶片根部前缘和尾缘附近,进而预测静态裂纹产生的位置。Jianfu Hou等[4]对涡轮叶片的弹塑性静态应力进行全面的有限元分析,并考虑了静态应力对叶片振动应力的影响。Frauke[5]先运用有限元方法计算得到叶片的自振频率和振型,再利用实验方法测得叶片在非旋转状态下和旋转状态下的自振频率。
本文基于三维建模软件,对叶片的厚度和展弦比进行变化,利用有限元软件对其进行强度计算,研究叶片造型对强度性能的影响。目的是通过分析和计算,得出提高叶片工作可靠性的最优造型,进而得出普适性结论。
1 压气机叶片有限元计算 1.1 叶片强度分析有限元方程动力学的通用运动方程为:
| $ \left[ {{M}} \right]\left\{ {{\ddot u}} \right\} + \left[ {{C}} \right]\left\{ {{\dot u}} \right\} + \left[ {{K}} \right]\left\{ {{u}} \right\} = \left\{ {{{F}}\left( t \right)} \right\}{\text{。}} $ | (1) |
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度系数矩阵;{u}为位移矢量;
模态分析是动力学分析中的基础内容,主要寻求结构的自振频率和主振型。对于模态分析,振动方程为:
| $ \left[ {{M}} \right]\left\{ {{\ddot u}} \right\}\left[ {{K}} \right]\left\{ {{u}} \right\} = \left\{ 0 \right\}\text{,} $ | (2) |
任何弹性体的自由振动均可以看作由一系列简谐振动叠加而成。设方程(2)的简谐振动解为:
| $ \left\{ u \right\} = \left\{ {{\phi _i}} \right\}\sin \left( {{w_i}t} \right){\text{,}} $ | (3) |
式中:wi为第i阶固有圆周频率;ϕi为第i阶的特征向量。
将式(3)代入自由振动方程(2),得
| $ \left( {\left[ {{K}} \right] - {w_i}^2\left[ {{M}} \right]} \right)\left\{ {{\phi _i}} \right\} = \left\{ 0 \right\}{\text{。}} $ | (4) |
对于自由振动,结构中各节点的振幅不全为0,即
| $ \left| {\left[ {{K}} \right] - {w_i}^2\left[ {{M}} \right]} \right| = 0{\text{。}} $ | (5) |
式(5)是关于
由动力学得到自振频率:
| $ {f_i} = \frac{{{w_i}}}{{2{\text{π}} }}{\text{。}} $ | (6) |
以等截面叶片作为研究对象,叶片的材料特性:弹性模量为200 000 MPa,泊松比为0.3,密度为7.85 g/cm3。叶高初始值为200 mm,叶片厚度初始值为5 mm。
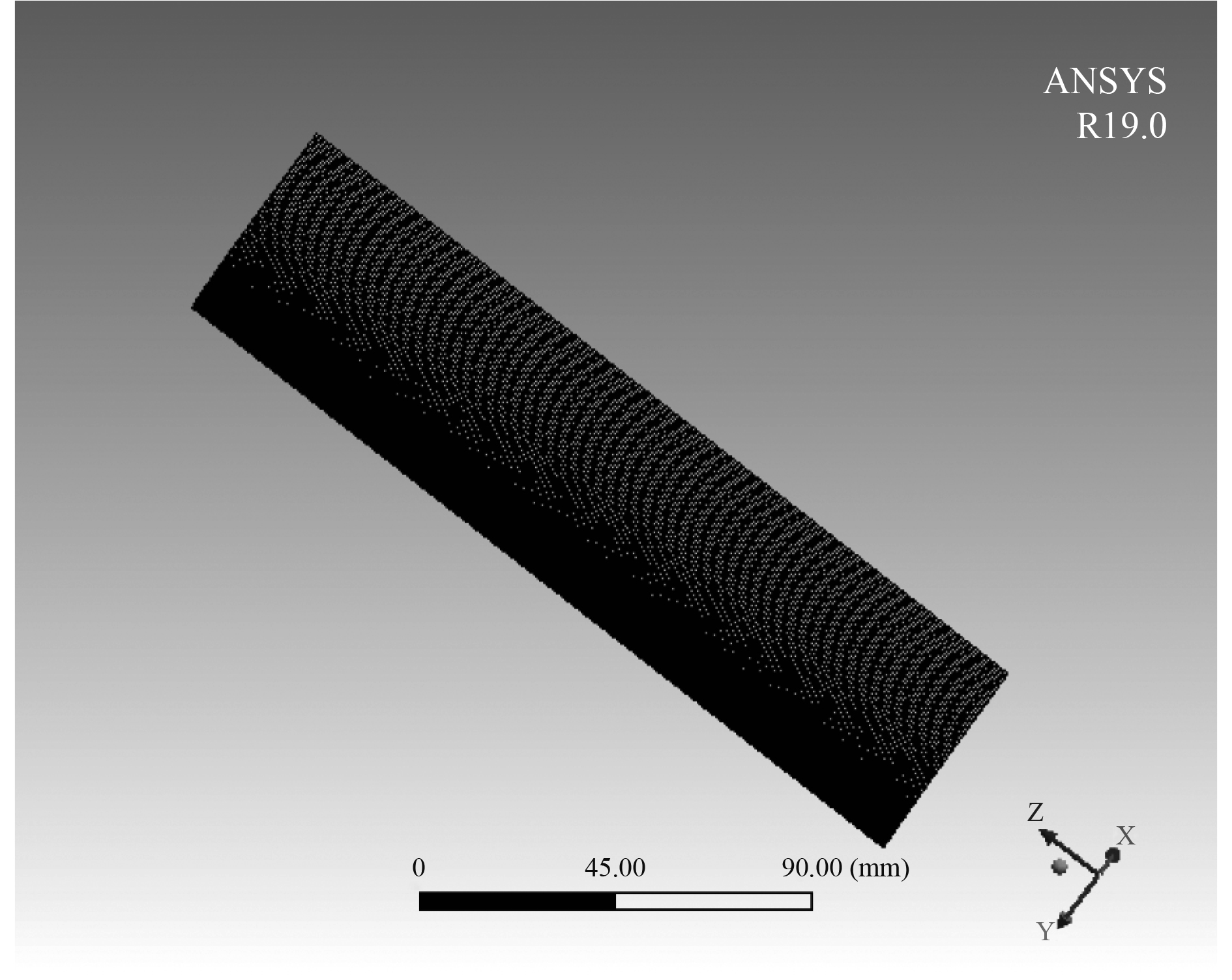
在Ansys结构力学分析的模态分析模块中,采用solid187单元,使用智能尺寸控制技术划分网格。共得到152 743个节点,21 600个单元,网格划分结果如图1所示。
|
图 1 压气机叶片有限元模型 Fig. 1 Finite element model of compressor blade |
因为动叶根部通过榫头固定于压气机轮盘上,所以在叶片根部截面采用固定约束,即根部截面上节点位移全约束。模拟设计工况下转子叶片的转动方向,叶片以785 rad/s的角速度绕X轴正向旋转。采用分块法进行模态分析。
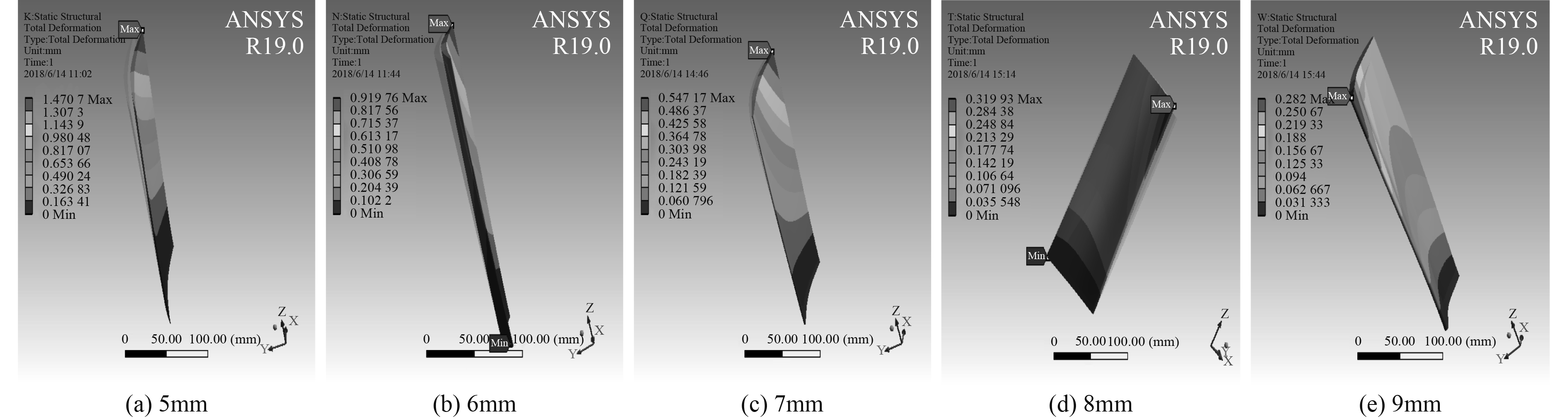
2 静强度性能分析 2.1 叶片厚度对静强度性能的影响叶片厚度初始值为5 mm,梯度为1 mm,设置5组叶片进行比较分析。
|
图 2 不同厚度叶片变形图 Fig. 2 Blade deformation with different thickness |

|
图 4 不同厚度叶片应力图 Fig. 4 Blade stress with different thickness |

|
图 3 不同厚度叶片应变图 Fig. 3 Blade strain with different thickness |
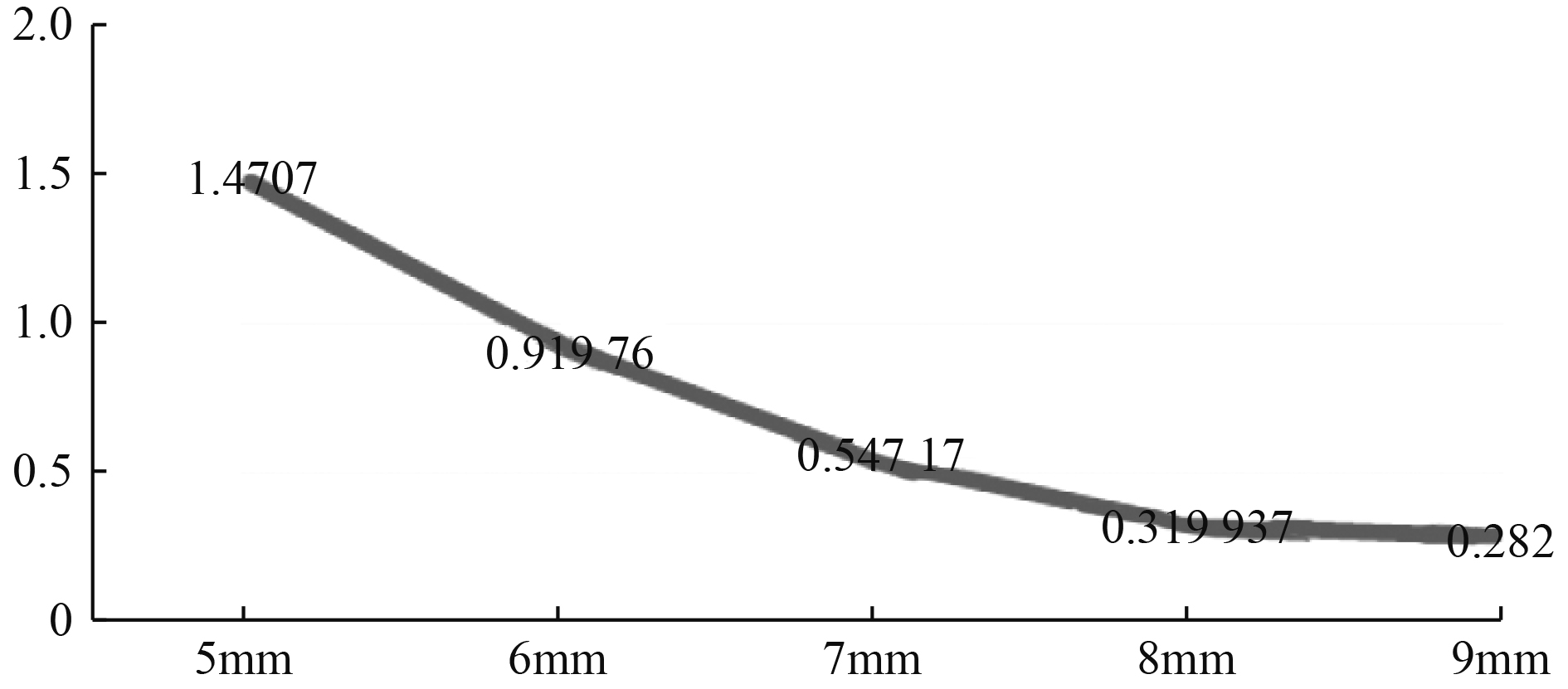
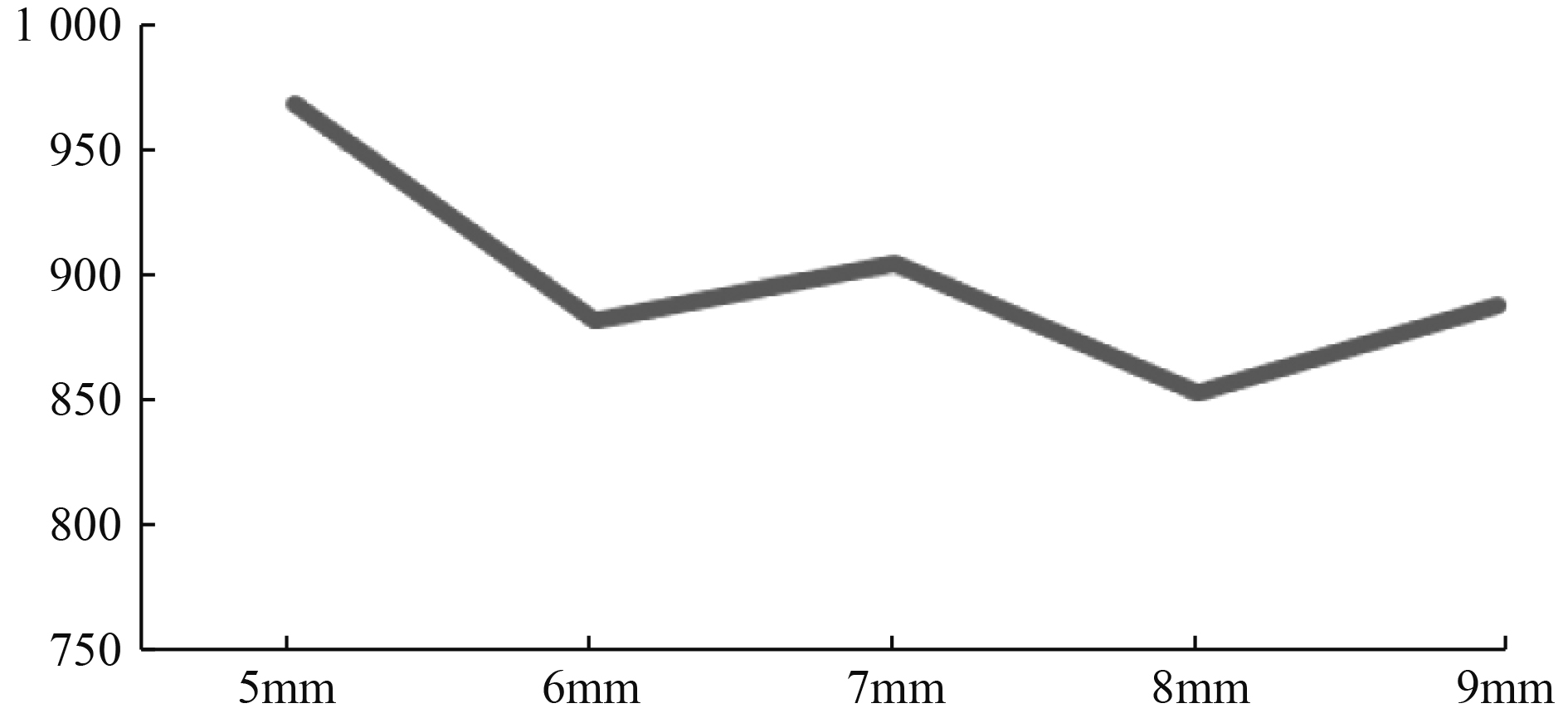
不同厚度叶片的静强度计算结果最大值与厚度的关系如图5~图7所示。
|
图 5 叶片最大变形值与厚度关系 Fig. 5 Relation between blade maximum deformation value and thickness |
|
图 7 叶片最大应力值与厚度关系 Fig. 7 Relation between blade maximum stress value and thickness |

|
图 6 叶片最大应变值与厚度关系 Fig. 6 Relation between blade maximum strain value and thickness |
由图可见,对于同一厚度的叶片,叶片顶部尖端处产生最大变形,应力和应变最大值出现在叶根处。叶片的变形量大小自叶根至叶顶呈增大趋势,应力和应变大小自叶根至叶顶呈减小趋势。
叶片的厚度越大,叶片在同样工况下发生的最大形变量越小,叶片的最大应变和最大应力值也相应减小。当叶片厚度由5 mm逐渐增大到9 mm时,叶片模型的最大形变量呈减小趋势;叶片的最大应力与最大应变大体上呈减小趋势,在7 mm厚度时和9 mm厚度时有增大的情况。
当叶片厚度由8 mm增大至9 mm时,其最大形变量的变化率为11.86%,其最大应力的变化率为4.1%,最大应变量的变化率为4.1%。可见,当叶片厚度由8 mm变化至9 mm时,叶片最大形变量的变化相对较大,叶片最大应变和最大应力的变化相对较小。所以在这5组叶片中,叶片最优厚度为8 mm。
2.2 叶片高度对静强度性能的影响选取厚度为5 mm的叶片模型,只改变叶片模型的叶高,研究叶高变化对于叶片强度的影响。取200 mm叶高的叶片为起始,5 mm为一个梯度,设置5组对照,叶高分别为200 mm,205 mm,210 mm,215 mm,220 mm。
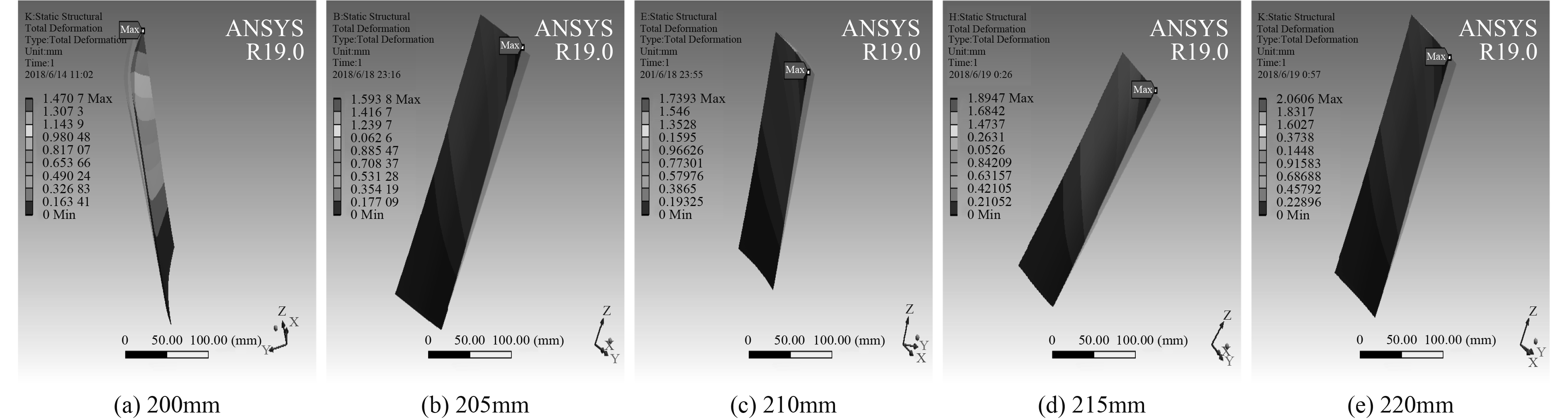
|
图 8 不同高度叶片变形图 Fig. 8 Blade deformation with different heights |
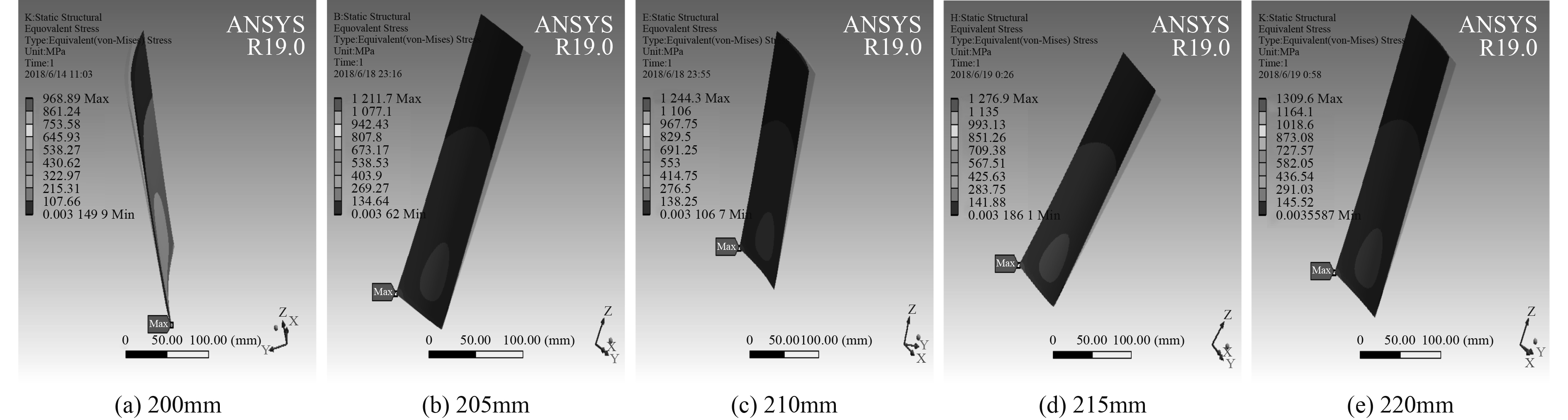
|
图 10 不同高度叶片应力图 Fig. 10 Blade stess with different heights |
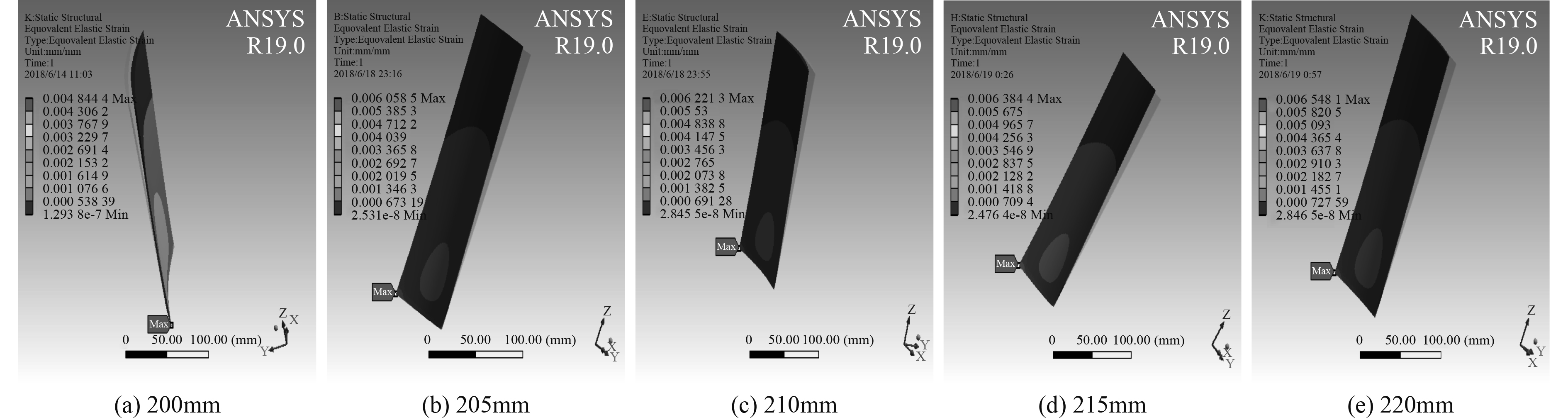
|
图 9 不同高度叶片应变图 Fig. 9 Blade strain with different heights |
不同高度叶片的静强度计算结果最大值与厚度的关系如图11~图13所示。
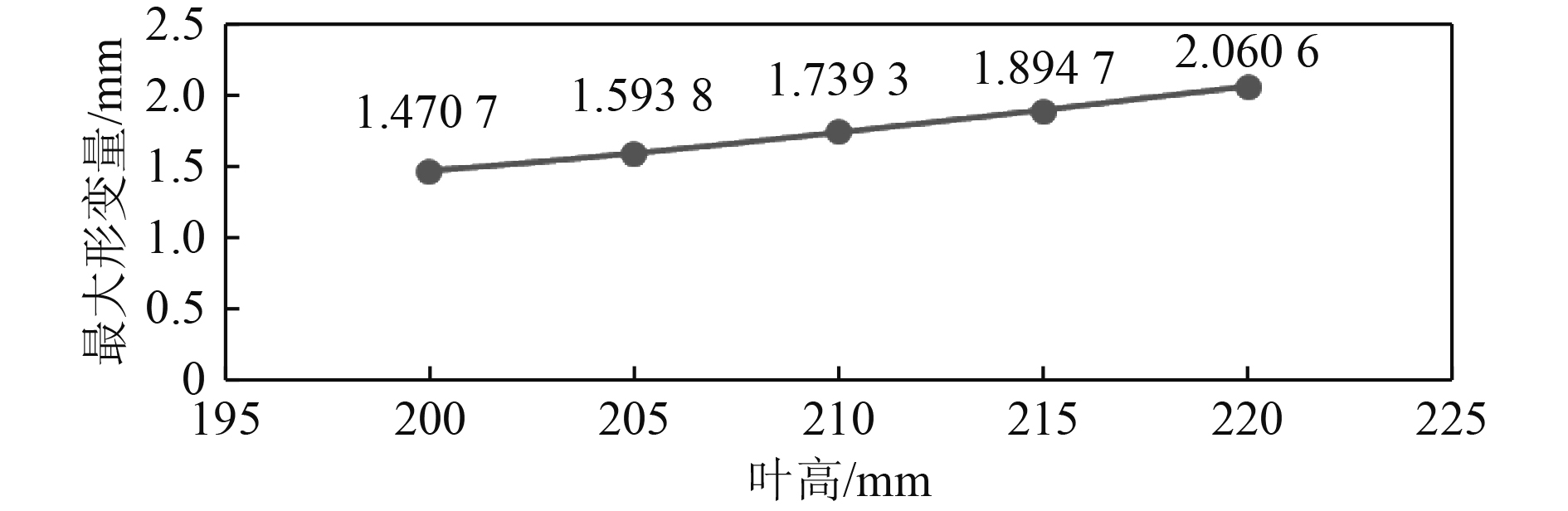
|
图 11 叶片最大变形值与叶高关系 Fig. 11 Relation between blade maximum deformation value and height |
|
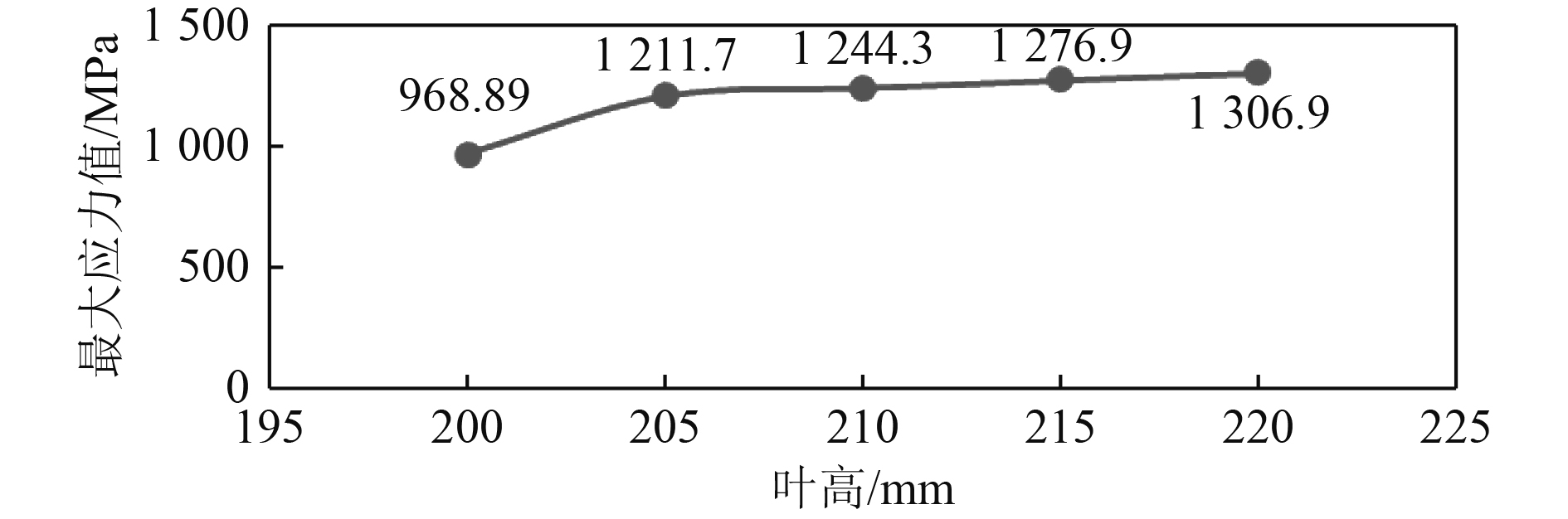
图 13 叶片最大应力值与叶高关系 Fig. 13 Relation between blade maximum stress value and blade height |

|
图 12 叶片最大应变值与叶高关系 Fig. 12 Relation between blade maximum strain value and blade height |
从图中可见,当叶高增加时,叶片的最大变形值、最大应变值及最大应力值均呈现增大的趋势。在相同的工况下运行时,叶高越大,其变形、应变值越大,所受应力越大。
3 动强度性能分析 3.1 叶片厚度对固有频率的影响对不同厚度的叶片进行模态分析,得到不同厚度叶片的前6阶固有频率,如表1所示。
|
|
表 1 不同厚度叶片的固有频率 Tab.1 Natural frequency of blades with different thickness |
由表1可知,随着叶片厚度的增大,前6阶固有频率均呈现增大的趋势。分析叶片模型的固有频率时,应当预防低频振动,也就是说叶片的固有频率越高时,在相同工况下其可靠性相对较好,不容易发生共振断裂的现象。
3.2 叶片高度对固有频率的影响对不同高度的叶片进行模态分析,得到不同高度叶片的前6阶固有频率,如表2所示。
|
|
表 2 不同高度叶片的固有频率 Tab.2 Natural frequency of blades with different heights |
由表2可知,叶高增大时,叶片模型各阶的固有频率均减小。由于在高速旋转的压气机中,主要预防低频振动,因此,从频率方面考量,叶高为200 mm的叶片模型为最佳方案。
4 结 语1)对叶片进行静强度计算,分析叶片只在离心力载荷作用下的变形和应力分布规律。结果显示,厚度越大的叶片受到的应力越小,其变形也越小;叶高越大的叶片,其发生的变形及受到的应力越大。最大变形量一般出现在叶尖部位,叶根的变形量很小,叶身的应力值普遍较低,由叶尖向叶根逐渐增大。
2)对不同厚度的叶片和不同叶高的叶片进行模态分析,从预防低频共振的角度得出一组最优叶片造型方案:叶片厚度为8 mm,叶片高度为200 mm。
| [1] |
李其汉, 王延荣. 航空发动机结构强度设计问题[M]. 上海: 上海交通大学出版社, 2014.
|
| [2] |
曲文浩. 航空发动机压气机叶片的静力学及模态分析[D]. 沈阳: 东北大学, 2012.
|
| [3] |
RALSTON F, SAMI E B, KHALED A, et, al. Static fracture and modal analysis simulation of a gas turbine compressor blade and bladed disk system[J]. Advanced Modeling and Simulation in Engineering and Science, 2016(3): 30-35. |
| [4] |
JIANFU H, BRYON J W, ROSS A. An investigation of fatigue failure of turbine blades in a gas turbine by mechanical analysis[J]. Engineering Failure Analysis, 2002(9): 201-211. |
| [5] |
FRAUKE H, RALF K, JOHNANNES R. Strucural modeling and validation of an active twist model rotor blade[J]. CEAS Aeronautical Journal, 2016(7): 43-45. |
 2019, Vol. 41
2019, Vol. 41
