曲轴是柴油机的核心部件,起着传递功率的关键作用。在柴油机运行过程中,曲轴不仅承受着由连杆传递过来的巨大燃气爆发压力,而且还承受曲柄连杆机构产生的往复惯性力和旋转惯性力,这些周期作用力在曲轴上引起周期性的交变载荷。这种交变载荷会引起曲轴疲劳破坏,曲轴疲劳破坏严重时会导致曲轴断裂,随之造成柴油机损坏等重大安全事故[1]。因此,对曲轴疲劳强度分析显得至关重要。通过试验方法进行疲劳强度分析涉及投入较大人力物力财力,研究对象是单个体,不具有普遍的意义,因而广泛采用有限元法进行理论分析。通过建立曲轴三维实体模型,对实体进行合适的体切割,面选定。然后施加尽量逼近实际情况的边界条件。通过有限元方法对曲轴进行受力分析,得出它的平均应力以及危险受力面的应力幅,在此基础上应用曲轴静强度校核公式以及软件分析,验证曲轴是否满足相关要求。
因此,准确地分析出曲轴的应力分布情况,合理校核曲轴的疲劳强度就成为了研究曲轴强度的主要问题。计算曲轴强度最新的理论是基于可靠性理论的疲劳强度理论[2],通过有限元软件Ansys对内燃机曲轴进行静态应力分析,研究了圆角部位的疲劳强度[3]。曲轴疲劳强度是曲轴强度的关键指标,而曲轴疲劳强度计算归结于曲轴的力计算和疲劳计算。通过多体运动学和Pro-E三维软件,构建曲轴动力学模型和三维实体模型,并对曲轴三维实体模型进行细致网格划分,加载受力模型,从而计算得出的曲轴应力分布、疲劳强度和疲劳破坏寿命数值。从而验证了柴油机曲轴疲劳强度和疲劳破坏寿命都满足设计要求,性能合乎标准,保证船舶的安全运行。
1 曲轴疲劳强度力学计算模型 1.1 受力模型1)气体作用力
最大气缸爆发压力可由通过使用测爆仪测量爆发压力得到,气体作用压力Fg的值可表示为:
| ${F_g} = \frac{{{\text{π}} {D^2}}}{4}\left( {{P_g}{\rm{ - }}{P^{\rm{'}}}} \right){\text{。}}$ | (1) |
式中:D为发火气缸的内径;Pg为气缸工作空间内的气体的绝对压力;P'为曲轴容积箱内气体的绝对压力。
2)动力机构的惯性力
①往复惯性力
往复惯性力与活塞运动方向相反,其方向沿气缸的中心线,和活塞加速度有着一样的运动规律,但两者方向相反:
| ${F_j} = {\rm{ - }}{m_j}{V^{\rm{'}}} = {\rm{ - }}{m_j}R{\omega ^2}\left( {\cos \alpha + \lambda \cos 2\alpha } \right){\text{。}}$ | (2) |
②离心惯性力
同样,与旋转质量mr相对应,旋转惯性力Fr可表示为:
| ${F_r} = {m_r}R{\omega ^2}{\text{。}}$ | (3) |
因为质量一定,如果旋转速度不变,那么旋转惯性力也不会发生变化,方向沿旋转圆半径向外。
3)活塞销处的受力[4]
活塞销是一个重要的部件,连接的是活塞与连杆,把气体力传递给连杆,所以受力应该是气体力以及自身质量引起的往复惯性力之和。
| $F = {F_g} + {F_j}{\text{。}}$ | (4) |
合成力可分解为2个分力Fh和Fc。
| ${F_h} = F{\rm{tg}}\beta = F\frac{{\sin \alpha }}{{\sqrt {1/{\lambda ^2}{\rm{ - }}{{\sin }^2}\alpha } }}{\text{,}}$ | (5) |
| ${F_c} = \frac{F}{{\cos \beta }} = \frac{F}{{\sqrt {1{\rm{ - }}{\lambda ^2}{{\sin }^2}\alpha } }}{\text{。}}$ | (6) |
式中:Fh垂直作用于活塞侧壁,也被称为侧推力;Fc为连杆轴颈推力,沿连杆中心线而下。
连杆轴颈推力Fc沿连杆中心线作用曲柄销的外表面,可分解为切向力F
| ${F_\tau } = {F_c}\sin \left( {\alpha + \beta } \right) = F\left( {\sin \alpha + \frac{{\lambda \sin 2\alpha }}{{2\sqrt {1{\rm{ - }}{\lambda ^{\rm{2}}}{{\sin }^2}\alpha } }}} \right){\text{,}}$ | (7) |
| ${F_n} = {F_c}\cos \left( {\alpha + \beta } \right) = F\left( {\cos \alpha + \frac{{\lambda {{\sin }^2}\alpha }}{{\sqrt {1{\rm{ - }}{\lambda ^{\rm{2}}}{{\sin }^2}\alpha } }}} \right){\text{。}}$ | (8) |
在Ansys软件中把重力通过物理荷载形式输入,在参数设置里设置加速度值大小为9.8×103 mm/s2,密度
确定力学模型后需要对曲轴施加特定的边界条件,由于轴颈上的力是通过油膜传递的,将压力分布分为2个方向:在轴向上,应力按照二次抛物线变化;在周向上,应力按照余弦变化,以轴颈垂直面为中心向两边延伸π/3角度。通过在有限元中设置后,轴颈压力分布到各个节点,从而能够求得各处的等效载荷。
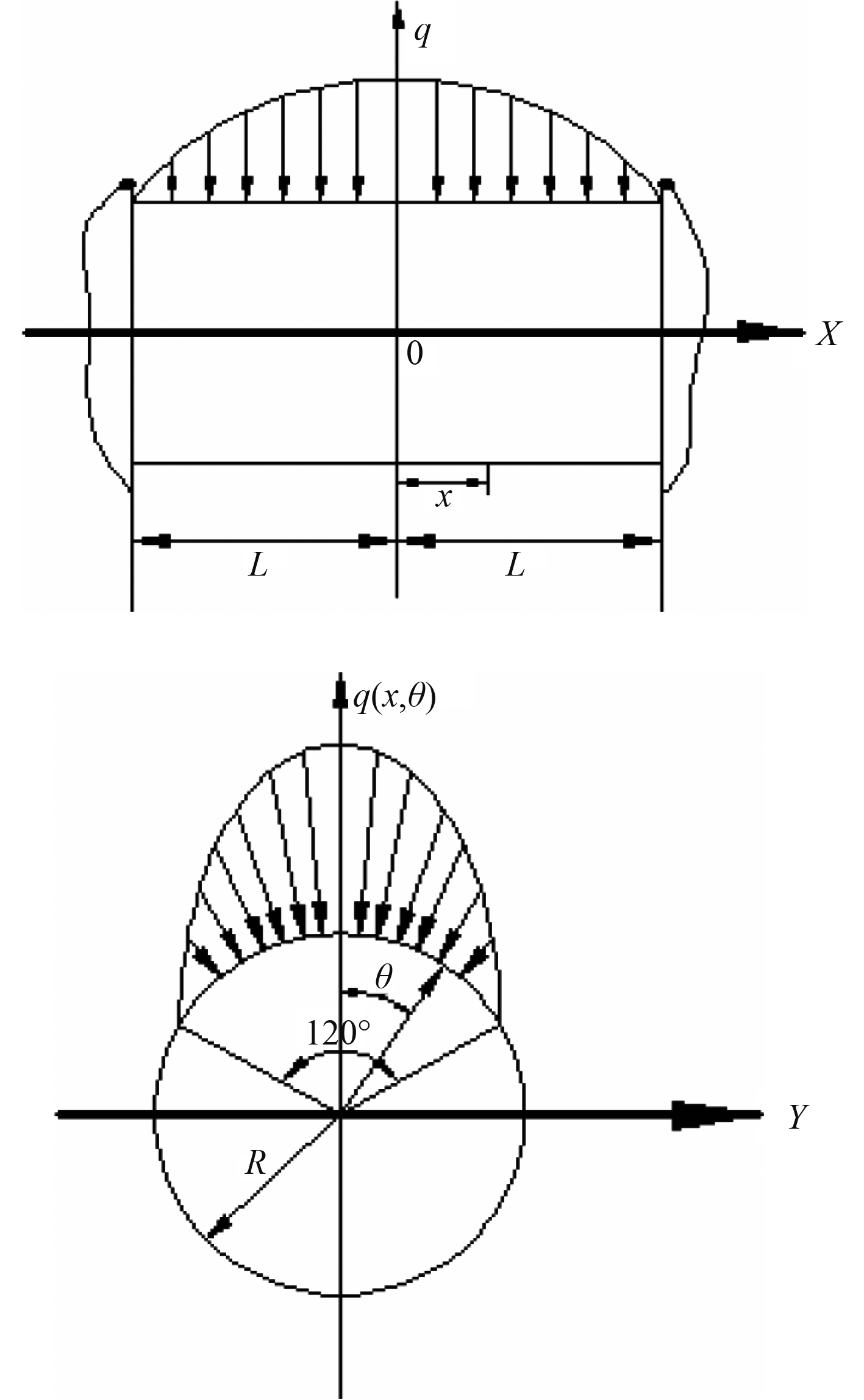
|
图 1 轴颈压力分布示意图 Fig. 1 Sketch of axial pressure distribution |
1)在轴颈轴向上
| ${q_x} = {q_{\max }}\left( {1{\rm{ - }}\frac{{{x^2}}}{{{L^2}}}} \right){\text{。}}$ | (9) |
式中:qmax为作用轴颈上的总载荷;L--单个轴承有效载荷长度的一半,
2)在轴颈周向上
| $q\left( {x{\rm{,}}\theta } \right) = \frac{9}{{16}} \times \frac{Z}{{RL}}\left( {1{\rm{ - }}\frac{{{x^2}}}{{{L^2}}}} \right) \times \cos \frac{3}{2}\theta{\text{。}} $ | (10) |
式中:L取轴颈一半的长度,
曲轴形状复杂,有很多圆角、倒角和油孔通道,为降低计算工作量,并提高计算结果的精度,暂不考虑这些细小的因素,适当对连杆轴颈和主轴颈过渡圆角连接处的网格进行加密。对曲轴建立三维实体模型后,将文件转为“.IGS”格式,再通过Ansys Workbench中进行预处理。通过Ansys Workbench中的Mesh,对曲轴实体模型进行网格的划分。网格划分采用六面体单元,共有82 580个单元,11 235个节点。曲轴材料为42CrMoA,弹性模量为210 GPa泊松比为0.32,密度为7.86×103 kg/m3。
图2所呈现的就是利用Ansys中Mesh这个功能得出的网格化模型图。

|
图 2 曲轴网格划分图 Fig. 2 Grid diagram of crankshaft |
本文仿真的对象是型发动机曲轴系统,结构方式为直列水冷6缸4冲程,缸径×行程:460 mm×530 mm,标定功率为8 400 kW/750 r·min–1,点火顺序:1–5–3–6–2–4。
根据柴油机的各种性能数据及其实际工作时的示功图,通过力学知识及仿真模拟得到气缸内燃烧气体的最大压力,再通过此最大压力可以算出连杆轴颈处径向载荷,其最大值为166 740 N,该力作用点与上止点相差6.5°。同样的计算方法,也可以得到当曲轴转过120°,240°,360°,480°,600°时连杆轴颈载荷。
2 曲轴疲劳强度计算结果分析 2.1 轴颈受力分析|
|
表 1 曲轴连杆轴颈载荷 Tab.1 Crankshaft connecting rod journal load |
对于四冲程柴油机,轴颈在活塞上止点的位置受应力最大,因此各缸发火时的受力状态均可用活塞在这个点的受力来替代。柴油机发火时,气缸按照一定的发火次序发火,即1–5–3–6–2–4。柴油机运作过程中,曲轴不仅受到气体力、惯性力,还承受着动力输出端传递过来的扭转应力和推力。扭转应力和推力使得曲轴扭转振动,形成激励力矩。柴油机轴系扭转振动的激励力矩分为输出扭矩和负荷扭矩。输出扭矩包括气体力产生的周期性交变扭矩、连杆往复惯性力产生的交变扭矩和活塞连杆重载荷产生的交变扭矩,负荷扭矩为螺旋桨传递的周期性扭矩。曲轴输出扭矩与轴系的负荷扭矩大小相等,方向相反,相互抵消。
曲轴对外输出功扭矩,其扭转力的作用方向与曲轴旋转方向相反,扭矩值根据动力学计算得出。在Ansys分析过程中,设定主轴颈的扭矩值演变成径向线性变化的切应力,大小与该圆周上切应力大小相等,且与该圆周相切。

|
图 3 扭矩切应力分布 Fig. 3 Distribution of torque shear stress |
根据材料力学,横截面扭转切应力计算:
| ${\tau _\rho } = \frac{T}{{{I_p}}} \cdot \rho{\text{,}} $ | (11) |
| $T = \frac{{9\;550 \cdot P}}{n}{\text{。}}$ | (12) |
其中:
考虑到船舶输出扭矩的作用,除上述的应力分析外,还应在曲轴的功率输出端加上一个驱动力矩
| $F = \frac{T}{R} = \frac{{{\rm{4}}{\rm{.78}} \times {{10}^{\rm{4}}}}}{{{\rm{25}} \times {{10}^{{\rm{ - }}3}}}} = {\rm{1}}{\rm{.91}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}{\rm{N}}{\text{。}}$ | (13) |
根据有限元计算结果,可以得出各缸的最大应力值,如表2所示。其中,在第 5 缸出现最大应力值。
|
|
表 2 各缸最大应力值 Tab.2 Maximum stress value of each cylinder |
可见,在负荷扭矩的作用下,在第4缸发火时,第4连杆轴颈过渡处的应力值为最大,达到44.86 MPa,(见图4),但远低于材料的屈服极限,具有足够的强度系数7.29。

|
图 4 第4缸发火曲轴应力云图 Fig. 4 Stress cloud diagram of firing crankshaft of fourth cylinder |
柴油机各缸发火时,曲轴受到应力以及本身的变形都是最大的。根据柴油机的性能参数和实际工作的示功图,通过计算公式和测爆压得到气缸燃烧的最大爆发压力,将这些参数代入,从而得到曲轴变形云图。

|
图 5 第5缸发火曲轴变形云图 Fig. 5 Deformation cloud diagram of fifth cylinder crankshaft |
根据有限元计算结果,可以得出各缸发火时曲轴变形量,如表3所示。其中,在第 5 缸出现最大应力值。
|
|
表 3 各缸最大变形量 Tab.3 Maximum deformation of each cylinder |
曲轴疲劳强度安全系数校核
| $ n_\sigma = \frac{{{\sigma _{ - 1}}}}{{\frac{{{K_\sigma }{k_\sigma }}}{{{\varepsilon _\sigma }\beta }}{\sigma _\alpha } + {\psi _\alpha }{\sigma _m}}}{\text{。}} $ | (14) |
其中:σ–1为材料对称弯曲循环疲劳极限;σα为曲轴弯曲时的名义应力幅,
基于安全系数方法进行疲劳强度分析,输入相关参数,从Ansys Workbench分析受力最大的第4缸的疲劳情况,可以得到曲轴安全系数最小值为2.333 7,如图6所示。若生产合金钢曲轴的工艺流程保持不变,则取n≥1.5,符合设计要求。

|
图 6 曲轴的安全系数显示图 Fig. 6 Safety factor display of crankshaft |
关于破坏寿命(Damage Life),计算结果显示,其值为1×109cycles。
3 结 语本文采用有限元法计算柴油机曲轴疲劳强度与寿命分析,对柴油机曲轴的进行建模,得到曲轴应力变形量与应力应变的分布情况。基于疲劳强度理论计算曲轴在交变载荷下的安全系数,利用有限元法计算曲轴疲劳寿命。结果表明,柴油机曲轴具有足够的安全保障,安全系数能够满足设计标准。按照Fatigue Wizard 模块提供的疲劳评价方法,柴油机具有较高的安全系数,安全系数高于5。
| [1] |
王银燕. 柴油机曲轴疲劳强度可靠性分析[J]. 舰船科学技术, 2004(1): 20-23. |
| [2] |
于洪亮. 船舶柴油机曲轴动态强度分析[J]. 船海工程, 2012. 10. 25
|
| [3] |
KIMURA J, SHIONO K, OKAMURA H. Experiments and analysis of crankshaft three-dimensional vibrations and bending stress in a V-Type Ten-Cylinder engine: influence of crankshaft gyroscopic motions[J]. SAE Technical Paper, 1995.
|
| [4] |
孙连科, 唐斌, 薛冬新, 等. 6110柴油机曲轴的三维有限元分析[J]. 车用发动机, 2007(2): 81-84. DOI:10.3969/j.issn.1001-2222.2007.02.022 |
| [5] |
SPITERI P V, Yung-li LEE, SEGAR R. An exploration of failwe modes in rolled, ductile, cast-iron crankshafts using a resonant bending testing rig[J].SAE Technical Paper 2005 (01).
|
| [6] |
V Yu, CHIEN W. Y., CHOI K. S., J. Pan, D. Close. Testing and Modeling of Frequency Drops in Resonant Bending Fatigue Tests of Notched Crankshaft Sections [J].SAE Technical Paper 2004 (01).
|
| [7] |
FENG Mei-bin, GE GAN, LI Man-liang. Development of a computerized electrodynamics resonant fatigue test machine and its applications to automotive components.[J]. SAE Technical Paper, 2003 (01).
|
| [8] |
冯国胜, 张幽彤, 张玉申. 柴油机曲轴静动特性的三维有限元分析[J]. 内燃机工程, 2003, 24(2). DOI:10.3969/j.issn.1000-0925.2003.02.016 |
| [9] |
何芝仙, 等. 基于动力学和摩擦学分析的曲轴疲劳强度分析[J]. 内燃机学报, 2008(5): 470-475. DOI:10.3321/j.issn:1000-0909.2008.05.014 |
 2019, Vol. 41
2019, Vol. 41
