2. 大连理工大学,辽宁 大连 116023
2. Dalian University of Technology,Dalian 116023, China
近年来,水动力载荷计算一直是业内的热门话题,理论方法方面也取得了不少的成就,从计算方法来说,可以分为线性方法和非线性方法;从计算域来说,可以分为时域和频域方法;从格林函数的选择上,又可以分为自由液面格林函数和Rankine源法;从计算维度上,可以分为二维方法、二维半方法以及三维方法等等。
吴介基[1]用Rankine源方法对某小水线面双体科考船在不同航速、不同海况与不同浪向下的耐波性进行了计算与分析;杨俊[2]对三维时域非线性波浪载荷计算方法进行了研究,并结合散货船、油船进行了实例验证;李学菊[3]对Rankine源法的计算原理进行了阐述,并分析了用于舰船计算时的难点;崔兵兵[4]对船体结构强度评估的非线性设计波法进行了研究,通过与线性设计波法进行比较验证了该方法的可行性。
海洋核动力平台属于一种特殊船型,国内对其波浪载荷特性的研究相对较少。本文以渤海海域某水上软钢臂单点系泊下的海洋核动力平台为研究对象,通过对比数值结果与规范计算,研究目标载荷随浪向、频率、船长的分布规律,并分析这些现象产生的原因。此外,通过线性和非线性分析方法的对比研究,分析了总纵载荷的非线性特性,并在设计波下完成全船结构强度校核计算。
1 计算方法和理论 1.1 计算流程本文采用DNV开发的水动力软件Sesam/Wasim,通过pln文件创建水动力模型,Patran创建质量棒模型和全船结构模型,基于时域Rankine源法,求解作用在船体上的波浪力,通过傅里叶变换得出目标载荷的幅值响应,再结合北大西洋风浪谱模型模拟核动力平台在海上遭受的实际海况进行长期预报,并将计算结果与CCS的规范计算值进行比较,研究目标载荷随浪向、频率、船长的分布规律,分析这些现象产生的原因,最后由设计波载荷完成全船结构强度校核计算。
1.2 理论基础三维时域Rankine源法基于三维时域势流理论,选择最基本的、不符合自由面以及远方控制面边界条件的拉普拉斯方程基本解1/r作为格林函数,在物面和自由面上分布奇点进行计算,是一种将时域自由面格林函数计算的复杂性转化成大的计算量的方法,并能计入非线性自由面条件的影响。Kring最早应用Rankine源法进行船舶耐波性的时域分析,后续有学者不断进行非线性以及对计算稳定性、收敛性的扩展研究。船舶在波浪中时域自由运动微分方程可写为:
| $ \begin{aligned} ({{M}} + {{a}})\{ {\rm{\ddot \eta }}(t)\} + {{b}}\{ {\rm{\dot \eta }}(t)\} + ({{C}} + {{c}})\{ \eta (t)\} = &\{ f(t)\} = \\ &\int_{ - \infty }^t K (t - \tau ){\rm{\dot \eta }}({\rm{\tau }}){\rm{d\tau }} {\text{。}}\end{aligned} $ |
式中:C为复原力矩阵;M为质量矩阵;a,b,c,为水动力系数;
求解过程中,需要满足以下边界条件:
1)总速度势Ψ要满足质量连续方程,即Laplace方程
| $ {\nabla ^2}\varPsi ({\vec r},t) = 0 {\text{。}}$ |
2)自由液面不可穿透,即满足运动学条件
| $ \left( {\frac{\rm d}{{{\rm {d}}t}} + \nabla \varPsi .\nabla } \right)(z - \zeta (x,y,t)) = 0\text{。} $ |
3)自由液面上任意一点的压力均满足大气压力,即满足动力学条件
| $ {p} - {p_0} = \frac{{{\rm d}\varPsi }}{{{\rm d}t}} + g\zeta + \frac{1}{2}|\nabla \varPsi {|^2} = 0\text{。} $ |
选取最基本的Rankine源作为格林函数,对基本势、局部势和记忆势的调和方程进行求解,速度势求出来后再代入运动微分方程,即可得出位移。进一步根据达朗贝尔原理便可求解出各剖面波浪载荷。
2 海洋核动力平台计算模型本文通过Wasim软件进行波浪载荷预报,需要湿表面模型、质量模型和自由液面模型。
由核动力平台的型值表建立pln文件生成湿表面模型,并根据实际吃水切分水线,充分考虑计算的精确性、稳定性、收敛性以及对应海浪谱99%的能量范围,对其进行划分网格(见图1),其能满足计算波浪频率为0.2~2.3 rad/s的海况。

|
图 1 平台湿表面模型 Fig. 1 Wet surface model of platform |
根据核动力平台的实际质量分布,通过patran利用质量棒的方法来模拟。

|
图 2 平台质量模型 Fig. 2 The quality model of platform |
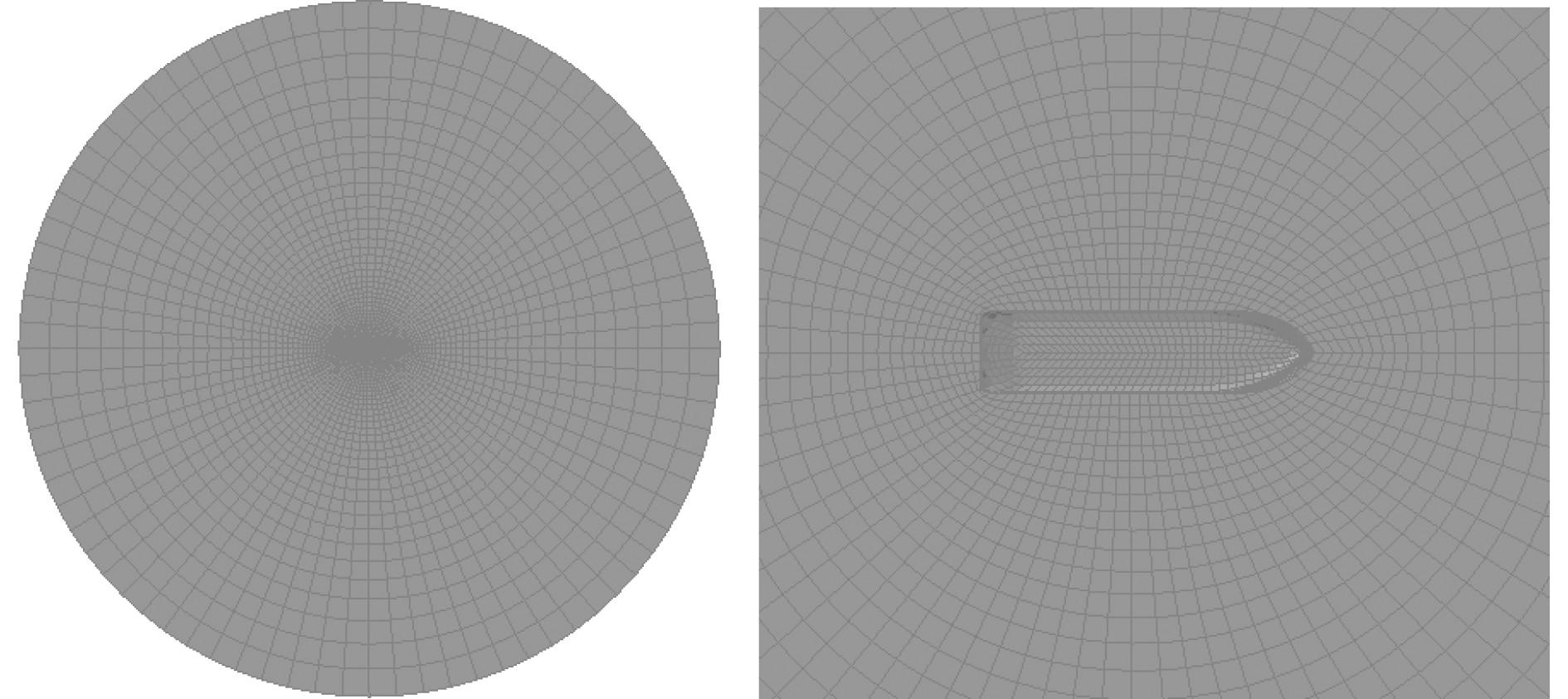
由于Rankine源法时域计算时需要在自由液面上布置点源(见图3),由船体湿表面模型处向外延伸至5倍船长处截断,对该区域自由液面进行离散,划分网格,网格尺寸由泊松函数确定,自船体中心处至自由液面边界逐步变大,得到自由液面模型。
|
图 3 平台自由液面模型 Fig. 3 Free liquid surface model of platform |
由于本文研究的核动力平台L/B=3.78≤5,属于《钢制海船入级规范》(以下简称《规范》)2.2.1.2(4)节规定的非常规船型,需要利用水动力直接计算波浪载荷。
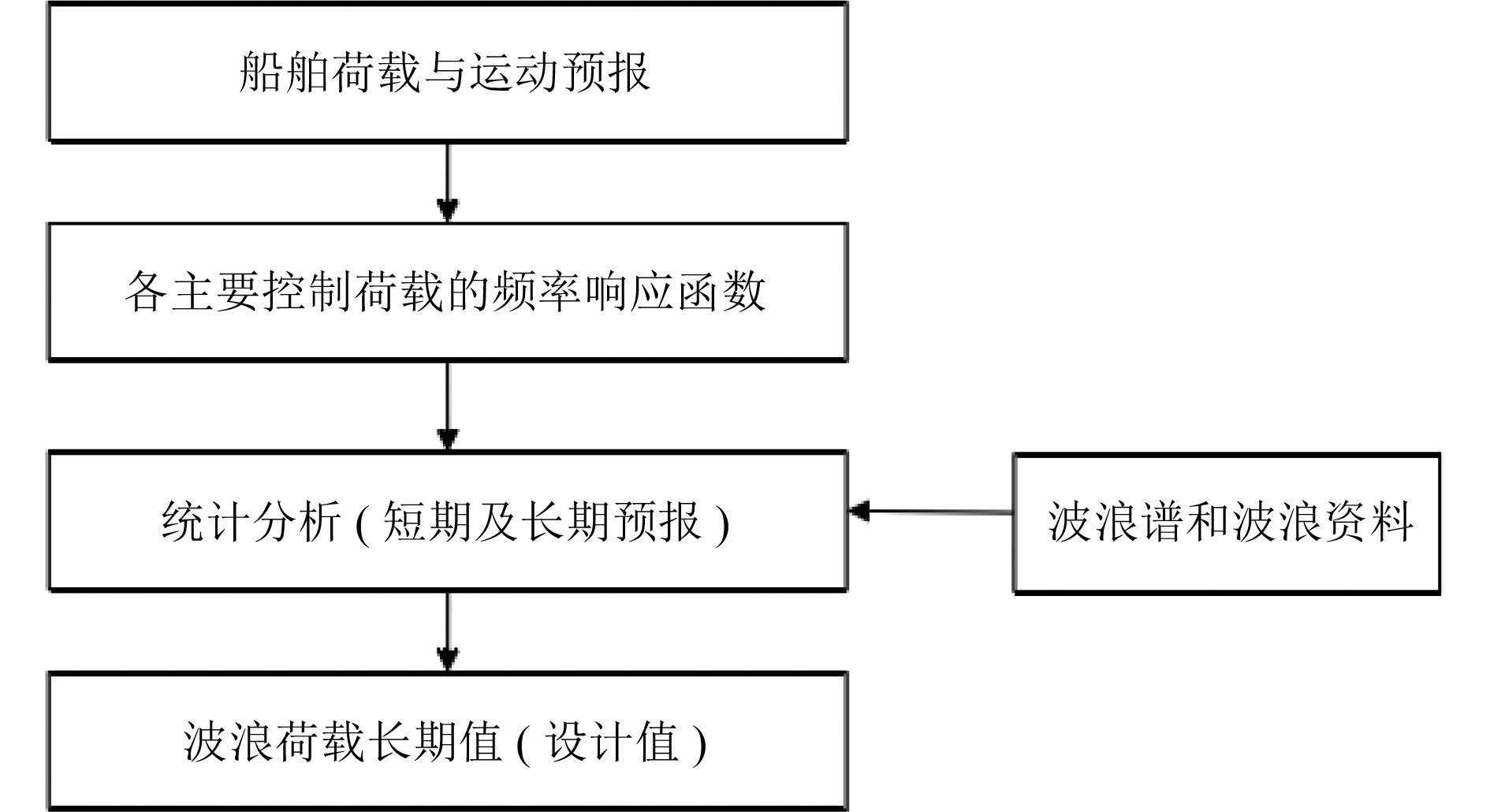
因此,按照《规范》给出的标准流程(见图4)确定设计波各要素。首先,分析待评估船舶的受力特点,确定运动或载荷控制参数。本船为单体船,所以本文重点关注它的总纵强度;然后通过数值计算获得选定的控制参数的幅频响应;再结合海浪谱和海况资料计算目标载荷参数的长期分布,得到对应一定概率水平的长期值;最后,确定设计波参数(波幅、波浪频率、浪向角、相位角等),使待评估船舶产生的目标载荷的最大值与该载荷的长期预报值相当。
|
图 4 波浪载荷设计波法计算流程 Fig. 4 Design wave method for wave loads |
具体计算参数选取如下:
1)波浪频率。根据所处海域,选取0.2~2.2 rad/s为波浪频率计算范围,步长0.1 rad/s,共21个频率,保证波浪频率涵盖99%的能量范围。
2)波浪浪向。考虑到船舶的对称性,选取0°~180°为波浪浪向计算范围,步长30°,共7个浪向。
3)航速。考虑到平台在海上永久系泊,选取航速为0 kn。
4)海浪资料。选取选取1998年IACS海浪资料组推荐的北大西洋海浪长期统计资料NA-1C为计算海况,海浪谱选择PM谱。
5)概率水平。选取10~8为长期预报概率水平,相当于船舶的生命周期为20年。
6)波浪扩散函数。考虑短峰波的影响,选取cos2为波浪扩散函数。
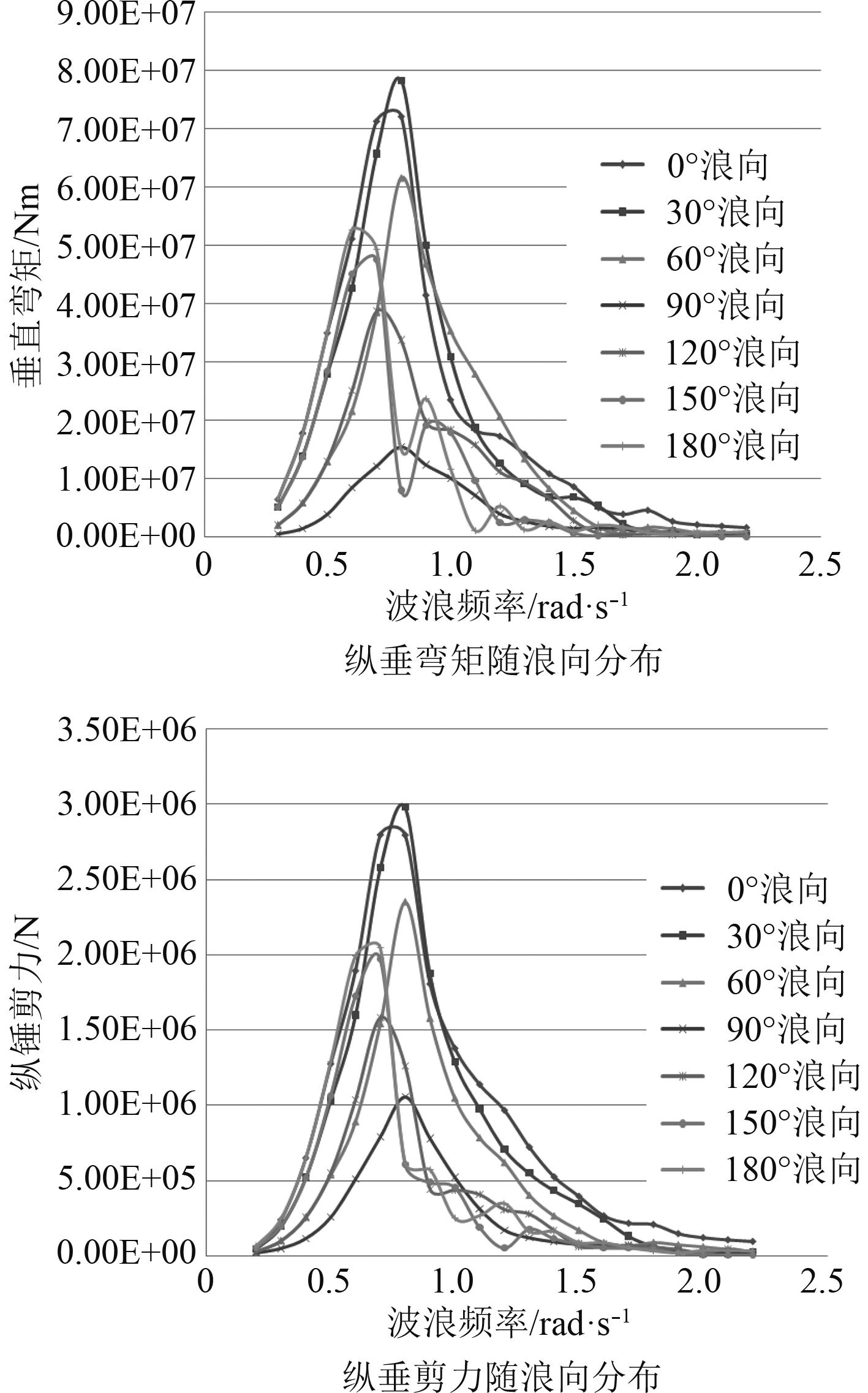
3.1 总纵载荷随浪向的分布特性根据核动力平台在单位波幅正弦波下的载荷频响计算结果,总纵载荷(纵垂弯矩、纵垂剪力)的数值计算均在尾斜浪30º浪向下出现了最大值,横浪90º下出现了最小值,并且纵垂弯矩和纵垂剪力有着相似的随浪向的分布规律,30º>0º>60º>180º>其他入射浪向角(见图5)。同时,由图中可知,对应的峰值频率为0.8 rad/s,该频率下对应的波长96.28 m和船舶在该方向下的特征长度非常接近。
|
图 5 总纵载荷随浪向的分布特性 Fig. 5 Distribution characteristics of longitudinal load with wave direction |
总纵载荷的最危险浪向出现在尾斜浪(30º浪向)下,而并非常见的迎浪(180º浪向)或者顺浪(0º浪向)下,主要是因为:
1)通过纵摇运动RAO可以发现,海洋核动力平台在30º浪向下的纵摇运动最大,纵摇运动对总纵载荷具有较大的贡献作用。同时,纵摇运动固有频率为1.0 rad/s,该纵摇频率与总纵载荷的峰值频率0.8 rad/s较为接近,进一步说明总纵载荷和纵摇运动存在着正相关联系。
2)本平台的船长船宽比L/B=3.89<5,比绝大多数的船舶都肥大。因此,在斜浪下的纵向扭矩更为突出,弯矩和扭矩耦合作用使得该平台在尾斜浪(30º浪向)下的总纵载荷更为突出。
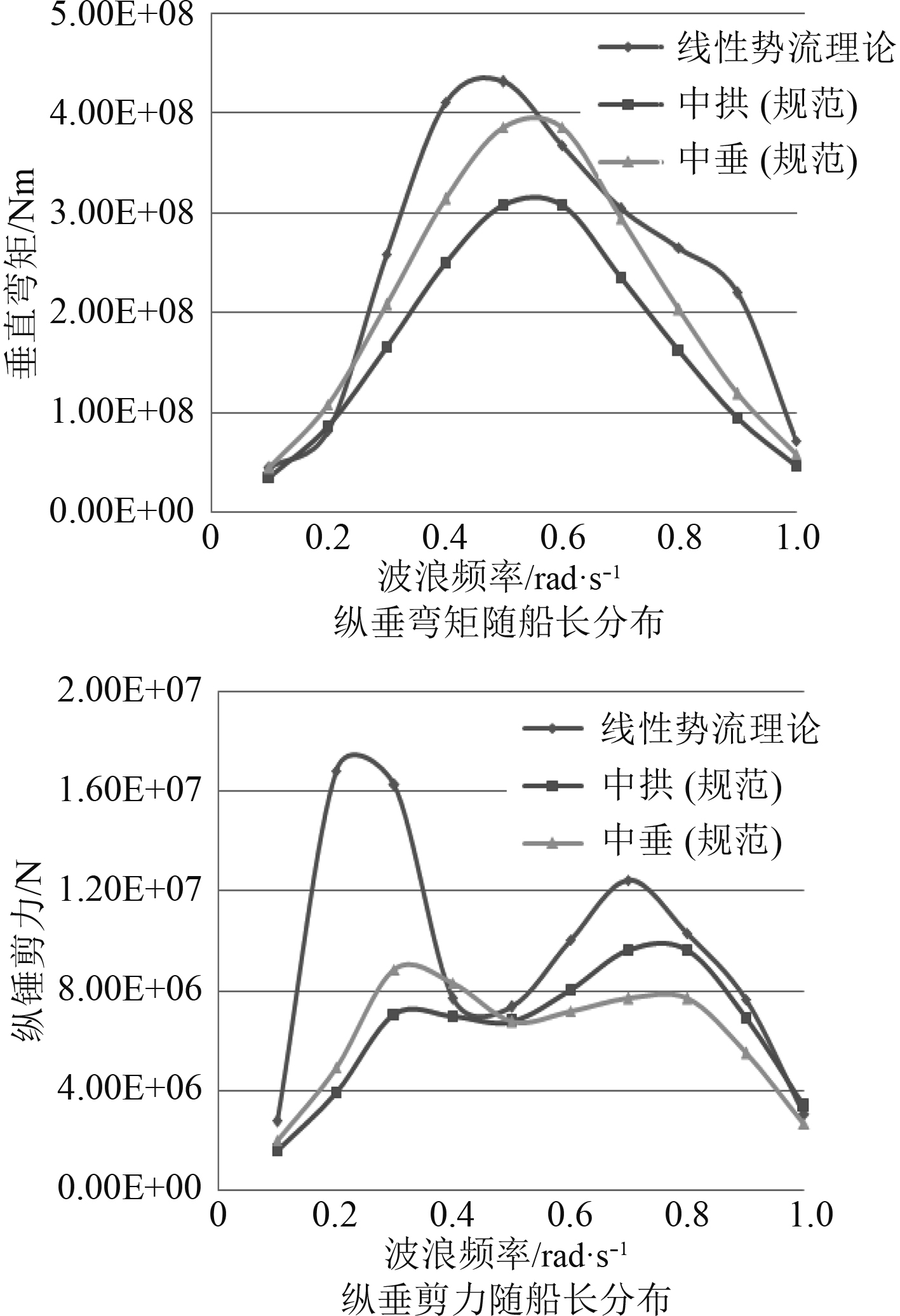
3.2 总纵载荷随船长的分布特性分别将纵垂弯矩、剪力载荷的数值结果和规范计算值沿船长分布进行对比分析,如图6所示。
|
图 6 总纵载荷随船长的分布特性 Fig. 6 Distribution characteristics of longitudinal load with the captain |
根据核动力平台在长期预报下的计算结果发现,总纵载荷数值计算与规范计算沿船长的分布规律几乎一致,纵垂弯矩在船中附近出现最大值,首尾两端趋近于0,纵垂剪力在距离首尾1/4处出现最大值;数值大小方面,纵垂弯矩的数值预报值和规范计算值较为接近,但是纵垂剪力的预报值比规范值大很多。主要是因为:
1)海洋核动力平台和一般的民用船舶存在着较大不同,在平台中后部布置有重要设备,且重量较大,使得纵垂剪力在船尾部出现明显的峰值,而规范计算是基于大量实船资料统计,忽略了这些偶然载荷因素;
2)主流的民用船舶(散货船、油船、集装箱船)均具有一定的航速,航速的存在会使得在迎浪下的遭遇频率降低,波浪力作用点前移动,而本文计算的核动力平台为海上固定平台,不具有自我航行能力。
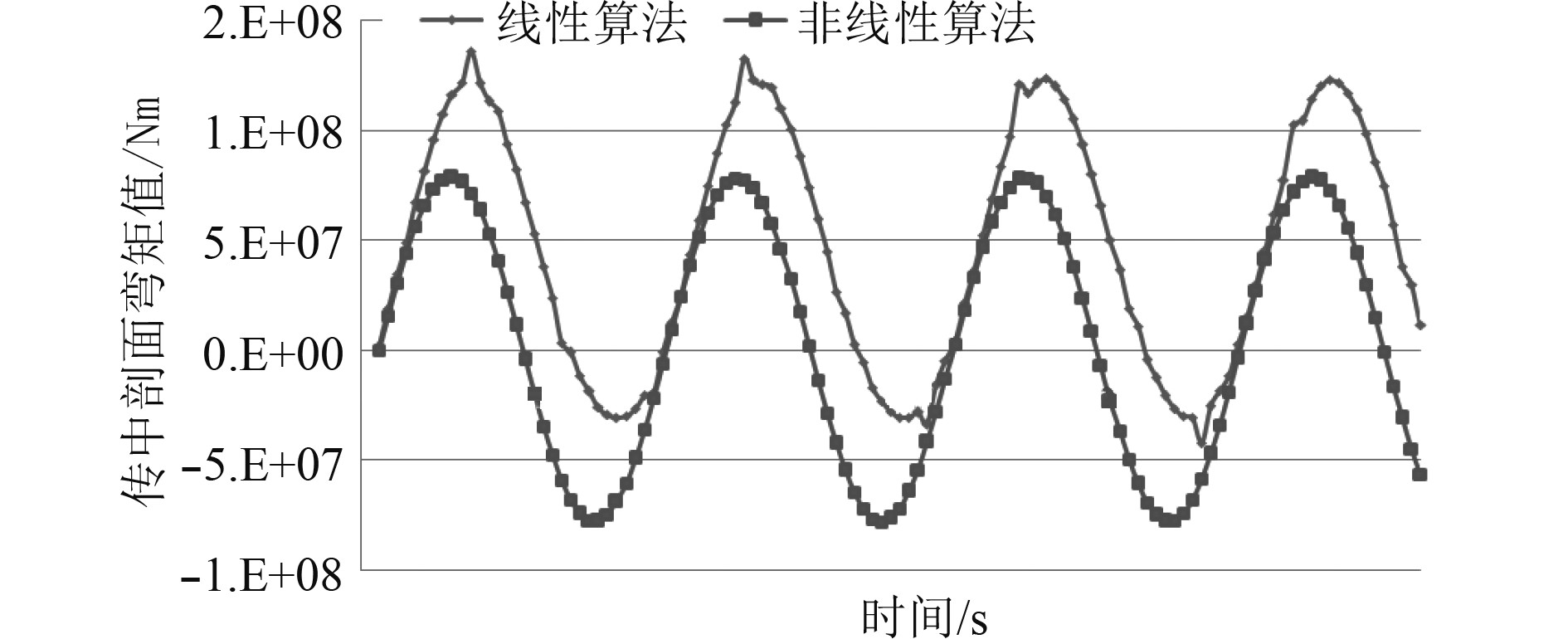
3.3 总纵载荷的非线性特性将上述总纵载荷长期预报得出的结果确定的设计波(浪向30°,波浪频率0.8rad/s)作为入射波浪,可以在频域线性和时域非线性条件下分别对波浪载荷进行计算,探究波浪载荷的非线性特性。
|
图 7 线性算法和非线性算法的结果对比 Fig. 7 Comparison of results between linear algorithm and nonlinear algorithm |
使用线性方法得出的中剖面波浪载荷是与激励波浪同频率的简谐量,船中剖面处的垂向弯矩载荷幅值等于设计弯矩值7.83 × 107 N·m。
使用非线性算法得出的中剖面弯矩则较为复杂,由于船体在波浪中运动时外飘力,船底出水等非线性现象,使得中剖面波浪弯矩的计算结果中出现了非简谐现象。此外,非线性设计波法可以考虑船体外表面的真实形状和波浪自由表面起伏引起的湿表面变化,能够更好地反映出中拱、中垂下实际的波浪载荷,使得计算结果更有针对性。
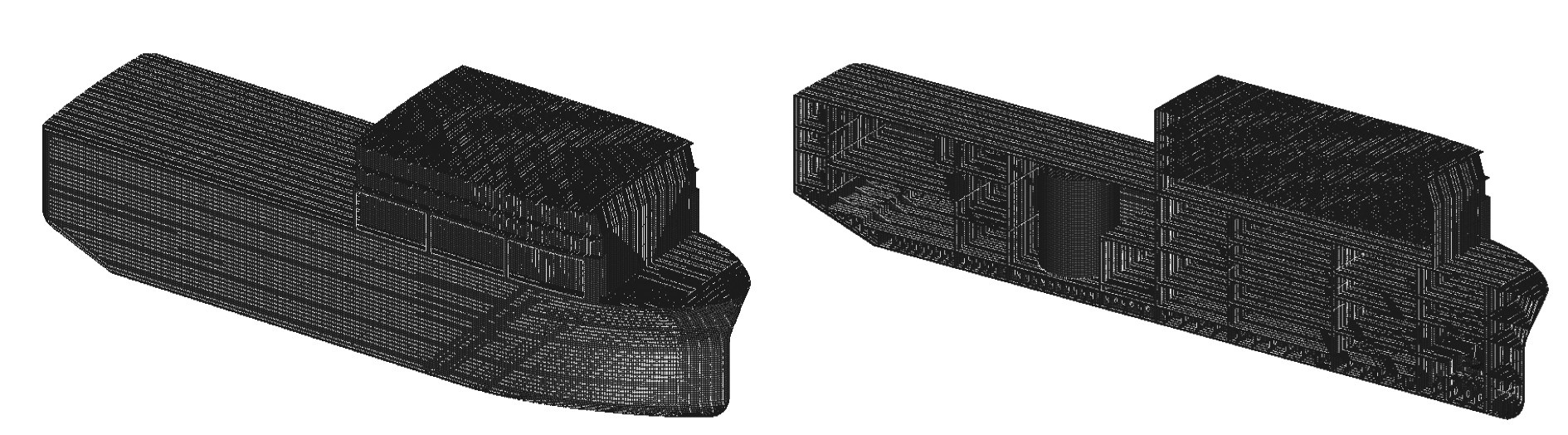
4 实船结构强度计算参照CCS《船体结构强度直接计算指南》建立全船结构有限元模型。通过线性插值的办法将湿表面的水动压力映射到结构模型的节点上,重力和船舶运动产生的加速度通过惯性力施加在船体结构上。通过这种方式加载,浮力、重力、波浪力和惯性力基本平衡,仅有微小的计算误差。误差通过约束点的反力来平衡。
|
图 8 平台有限元模型 Fig. 8 Finite element model of platform |

|
图 9 计算结果应力云图(Pa) Fig. 9 Stress diagram of calculation results |
通过应力云图可以发现,船舶中后部区域应力出现了较大值,主要是因为在这些区域波浪载荷值较大,并且存在一定重物的原因,在进行结构设计的时候需要关注这些区域。
5 结 语基于时域Rankine源法求解作用在船体上的波浪力,并结合北大西洋风浪谱模型进行核动力平台的载荷预报可以发现:
1)船长船宽比较小的肥大型船舶,纵向扭矩表现比较突出,更容易出现弯扭耦合,因此,在斜浪下其总纵载荷(纵垂弯矩、纵垂剪力)更危险。
2)核动力平台总纵载荷随船长的分布特性与普通单体船具有一定的相似规律,纵垂弯矩在船中区域最大,纵垂剪力在首尾1/4L区域内较大,但是考虑到目标船舶的特殊性,其出现峰值的载荷剖面偏于船尾。
3)通过波浪载荷线性算法和非线性算法的对比,发现非线性算法能够更好地反映出中拱、中垂下实际的波浪载荷,如果更好地将设计波法和非线性算法结合,具有一定的研究价值。
4)通过全船有限元计算,发现该船舶在船中区域具有较大应力,为结构设计重点考虑的区域。
| [1] |
吴介, 谷家扬, 管义锋, 等. 基于Rankine源法的小水线面双体科考船耐波性预报[J]. 江苏科技大学学报(自然科学版), 2015(2): 103-107. DOI:10.3969/j.issn.1673-4807.2015.02.001 |
| [2] |
杨骏. 三维时域非线性波浪载荷计算方法研究[D]. 北京: 中国舰船研究院, 2016.
|
| [3] |
李学菊. 基于Rankine源的舰船波浪载荷时域计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [4] |
中国船级社. 钢制海船入级规范[S]. 北京: 人民交通出版社, 2015.
|
| [5] |
高骏. 船体结构强度评估的非线性设计波法研究[J]. 全文版: 工程技术: 299–299.
|
| [6] |
汪雪良, 顾学康, 等. 船舶波浪载荷预报方法和模型试验研究综述[J]. 舰船科学技术, 2008. DOI:10.3404/j.issn.1672-7649,2008.01.004 |
| [7] |
秦洪德. 船舶运动与波浪载荷计算的非线性方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2003.
|
| [8] |
KRING D C. Time domain ship motion by a three-dimensional rankine panel method[D]. MTT, Cambridge, 1994.
|
| [9] |
MANSOUR, A.E, WASSON, J. P. Charts for estimating nonlinear hogging and sagging bending moments. Journal of Ship Research, 1995, 39(3): 240–249.
|
 2019, Vol. 41
2019, Vol. 41
