浮式堆平台采用小堆发电型式,将船舶与核电有机结合,能够漂浮于海上如同一座海上核电站,可以为钻井平台、岛礁、沿海居民等提供电力与热水。这是一项具有开拓性意义的工程,为海核领域开辟了一条大道[1]。但浮式堆平台自身没有动力设施,其独自漂浮于海上不具备抵御极端海况的能力,此时需要单点系泊装置将其固定于海上,才能在任意位置完全发挥其独特的功能。单点系泊装置在世界范围内由几家公司技术垄断,所以每次进口都需要支付大额费用,且在系泊装置故障诊断和维修过程中国外单点系泊公司积累了大量工程案例经验,进一步促进了其技术发展及垄断[2 – 4]。因此,开展单点系泊装置的自主研发,实现单点系泊装置的国产化,建立一条完整的单点系泊装置生产链,在填补技术空白,打破国外垄断,促进经济增长,增强国家影响力等方面具有巨大的积极作用。
分析浮动平台定位系统固有特性,对平台船体、软刚臂系统、固定塔架整体建模,考虑风、浪、流环境载荷,以水动力计算得到船体位移,基于LS-dyna显示动力学建立整体刚柔耦合模型,以船体位移作为输入对结构进行动力学耦合计算,分析各分系统模块、运动副的受力,得到关键部位和运动副的应力时程曲线以及关键节点的位移时程曲线,并给出各运动副最大受力时的运动姿态。

|
图 1 平台定位系统 Fig. 1 Platform positioning system |
平台定位系统采用软刚臂单点系泊型式,其设计输入由船体运动决定,而船体位移来自于风浪流的作用,基于不规则波下船体运动理论,利用Ansys-AQWA水动力软件,设置波浪谱、波浪周期、波高、浪向、风速、流速等环境参数,计算平台所受到的时域环境载荷,包括海浪载荷(1阶波浪力、2阶波浪漂移力等,得到船体的位移时程曲线。把平台、固定塔架作为刚体,将软刚臂系统中结构件系泊支架、系泊腿和系泊刚臂作为变形体,建立整体力学耦合的有限元模型,基于动力学基础理论,采用LS-dyna进行时域动态计算,确定最不利载荷组合;得到构件内力时间历程曲线以及关键部位位移时程曲线,再进行局部构件的力学分析,得到每一部件在极端载荷工况下的应力时程曲线,一方面得到结构极值应力,另一方面将应力时程结果作为疲劳设计输入,得到结构的疲劳寿命,流程图如图2和图3所示。
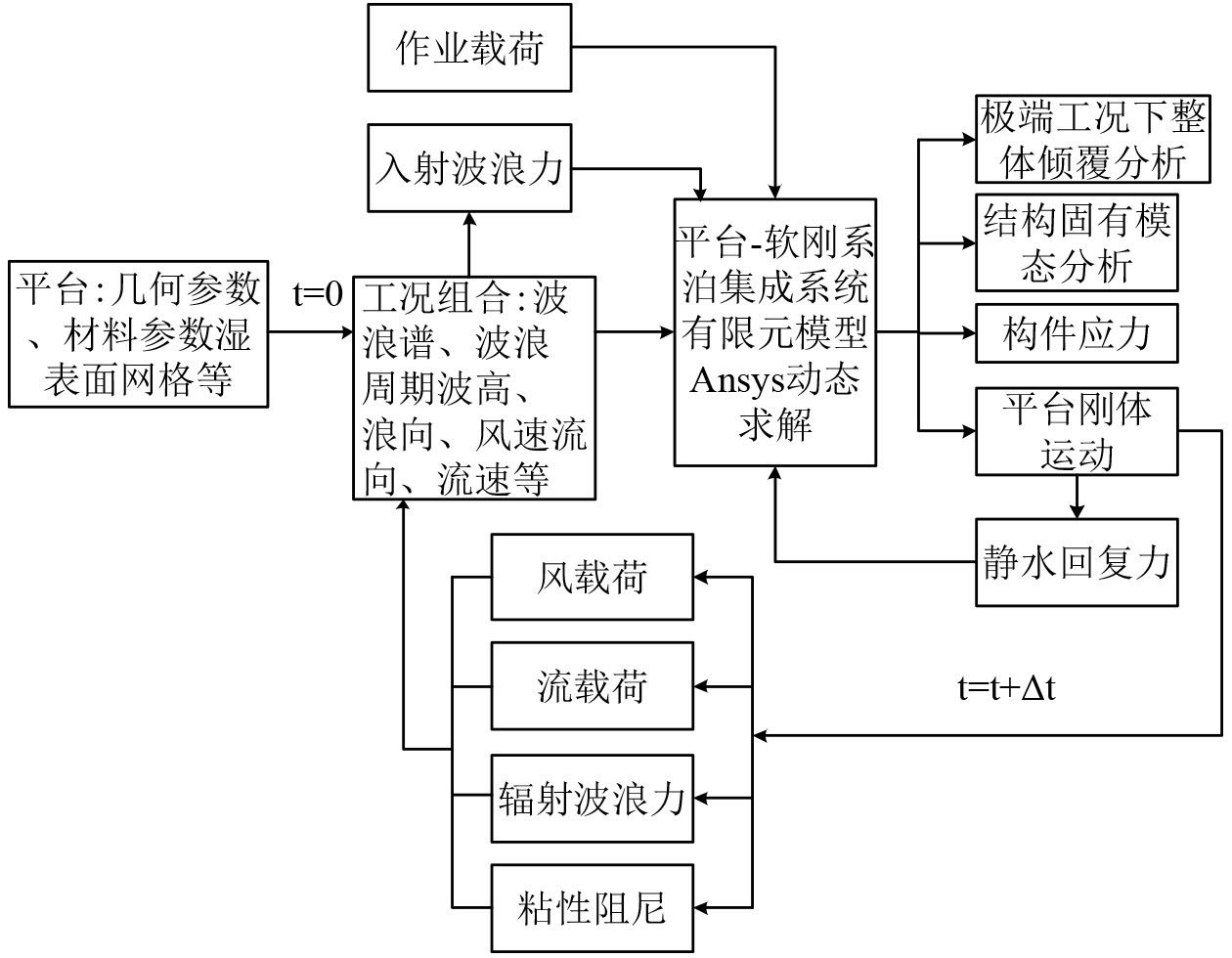
|
图 2 平台位移计算流程 Fig. 2 Process of platform displacement calculation |
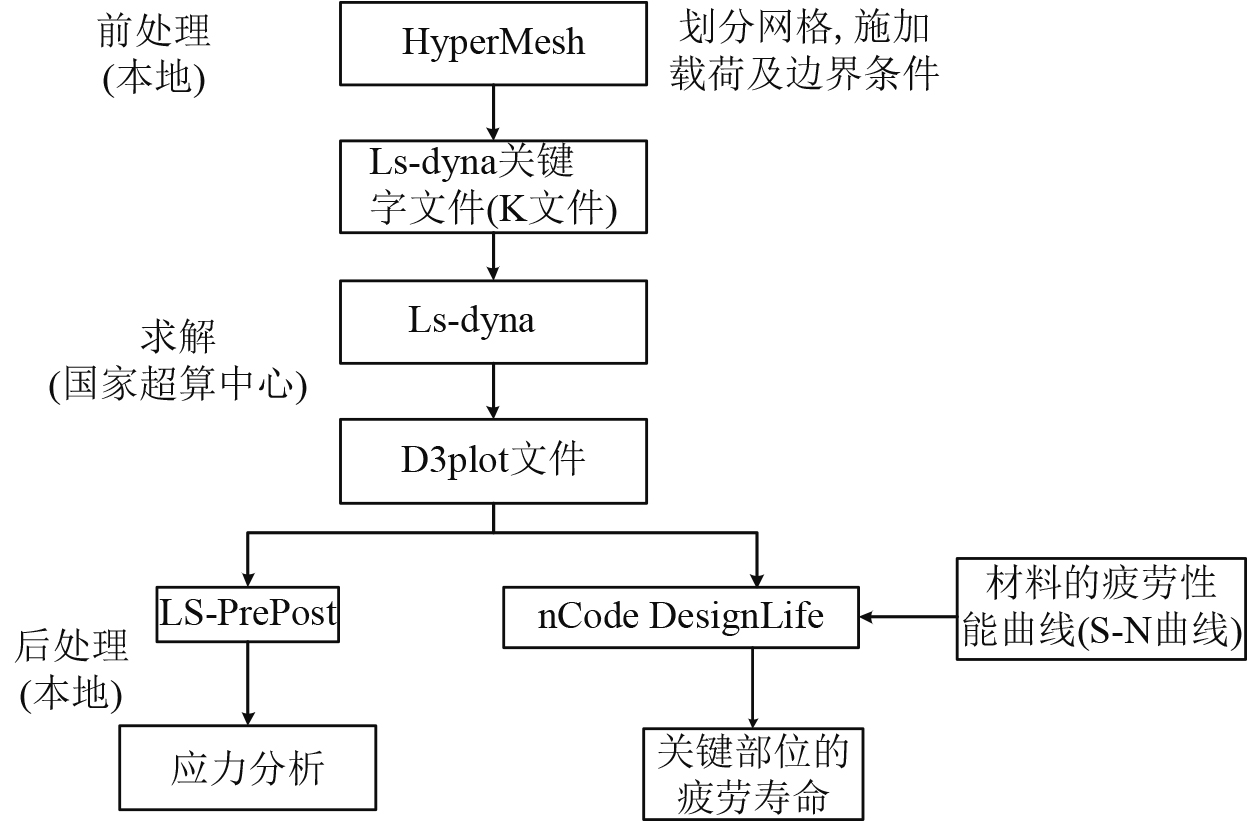
|
图 3 整体动力学计算流程 Fig. 3 Process of overall dynamics calculation |
单点系泊浮式堆平台在迎浪不规则波中的运动主要包括1阶波频运动和2阶低频纵荡运动,对于1阶波浪力,其谱密度函数可直接根据波浪谱密度函数S(ω)和波频运动传递函数|H_x(ω)|计算得到。
对于1阶波浪力,其谱密度函数可直接根据波浪谱密度函数S(ω)和波频运动传递函数|H_x(ω)|计算得到:
| $ {S_x}\left( \omega \right) = {\left| {{H_x}\left( \omega \right)} \right|^2}S\left( \omega \right)\text{,} $ | (1) |
对于2阶波浪力,其谱密度函数计算公式为:
| $ {S_F}\left( \mu \right) = 8\int_0^\infty {S\left( {\omega + \mu } \right)} S\left( \omega \right){T^2}\left( {\omega + \mu ,\omega } \right){\rm d}\omega \text{。} $ | (2) |
式中:
平均波漂力可由波浪谱密度函数
| $ {{\bar F}_{WD}} = 2\int_0^\infty {S\left( \omega \right)T\left( {\omega ,\omega } \right)} {\rm d}\omega \text{,} $ | (3) |
系泊船低频纵荡运动的最大值可按下式计算:
| $ \sigma _{xl}^2 = \frac{{\text{π}} }{{2b{C_{11}}}}{S_F}\left( {{\mu _c}} \right)\text{,} $ | (4) |
| $ {X_{max,lf}} = \sqrt 2 {\sigma _{xl}}\sqrt {lnN} \text{。} $ | (5) |
式中:

|
图 4 平台位移分析模型 Fig. 4 Model of platform displacement analysis |
考虑风浪流,在AQWA中建立系泊系统的整体模型,平台与系泊腿之间采用2个万向节和2个回转装置连接,释放3个转动自由度,系泊刚臂与系泊腿之间采用2个万向节连接,释放横摇和纵摇2个自由度,系泊刚臂与旋转塔台之间采用球铰接,具有3个自由度。建立耦合分析模型之后划分网格,设置相关参数,耦合分析模型计算网格。由于水面以上部分网格对水动力计算没有影响,故只对平台水面以下部分进行网格划分[5 – 7]。最终得到船体位移运动曲线,如图5所示。
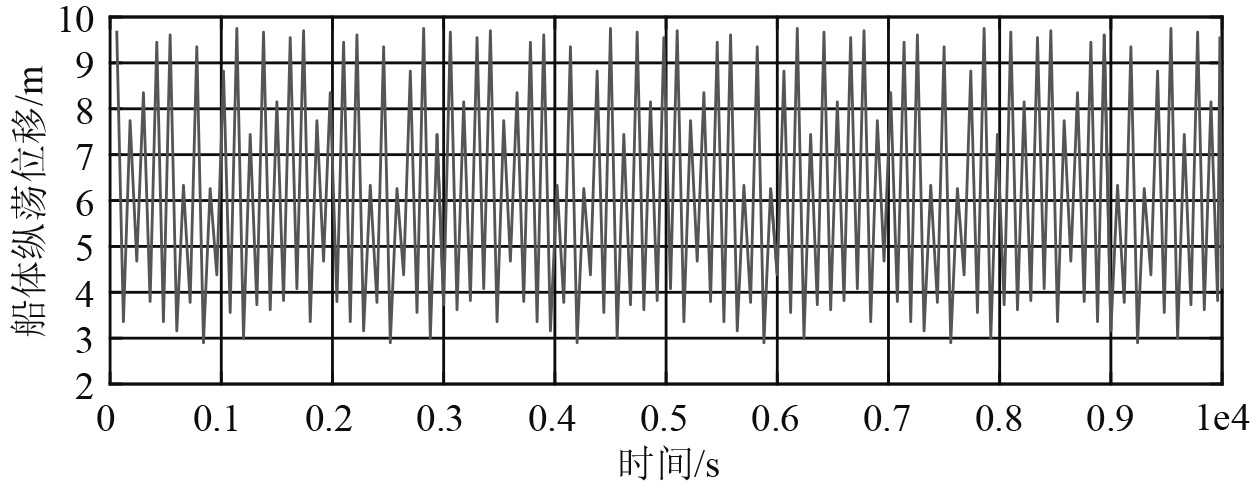
|
图 5 平台纵荡位移 Fig. 5 Turbulent displacement of platform |
考虑水动力计算中所有结构均设置为刚体,且结构模型均作简化处理,所得节点力并不能作为结构强度计算准确的输入,故提出了将船体位移作为设计输入,建立包含系泊支架、系泊腿和系泊刚臂的软刚臂系统与船体、固定塔架之间的刚柔耦合整体模型,将动力学分析得到的节点位移作为局部构件强度计算的输入,计算可得应力时域值,结果更加准确且能反映构件的运动规律,为后续监测提供参考。
动力学的通用运动方程为,
| $ [{ M}]\left\{ {\ddot u} \right\} + [{ C}]\left\{ {\dot u} \right\} + [{ K}]\left\{ { u} \right\} = \left\{ {F\left( t \right)} \right\}\text{。} $ | (6) |
其中:[M]=结构质量矩阵;[C]=结构阻尼矩阵;[K]=结构刚度矩阵;{F}=随时间变化的载荷函数;{u}=节点位移矢量;
LS-dyna是著名的通用显示动力分析程序,以拉格朗日算法为主,具有强大的非线性处理功能,结合软刚臂系统运动的多结构耦合非线性问题,采用此软件能较好的处理模型计算问题[8 – 10]。如上述流程所示,前处理采用hypermesh建模,系泊支架采用管单元与梁单元,系泊腿采用管单元,两端设置球铰接转动副,系泊刚臂采用壳单元及梁单元,旋转塔台采用板单元,平台与固定塔架设置为刚体,建立整体有限元动力学模型。
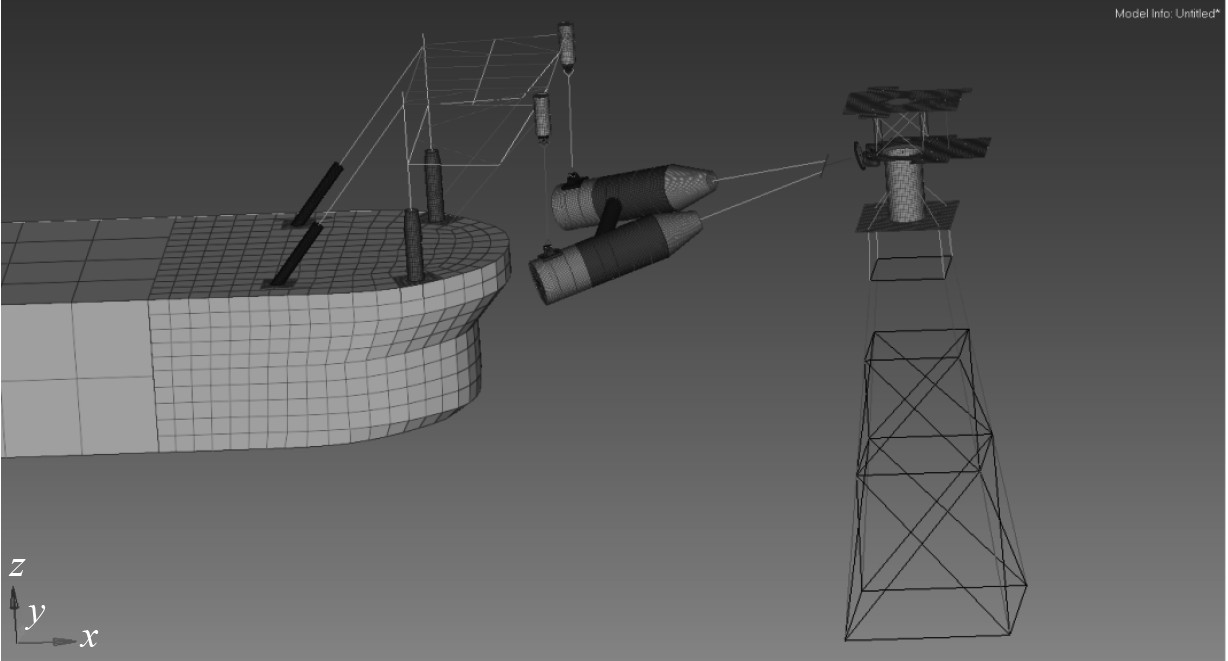
|
图 6 整体动力学模型 Fig. 6 Overall dynamics model |
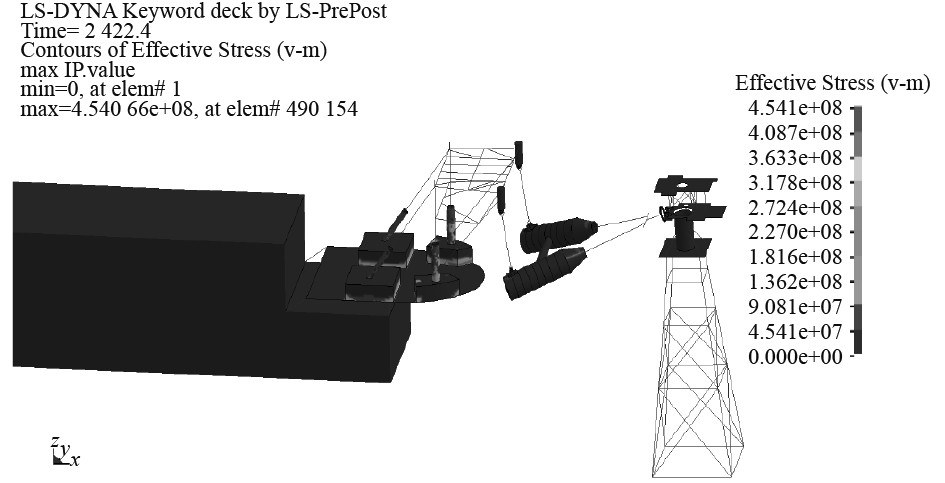
|
图 7 整体动力学计算结果 Fig. 7 Result of overall dynamics model |
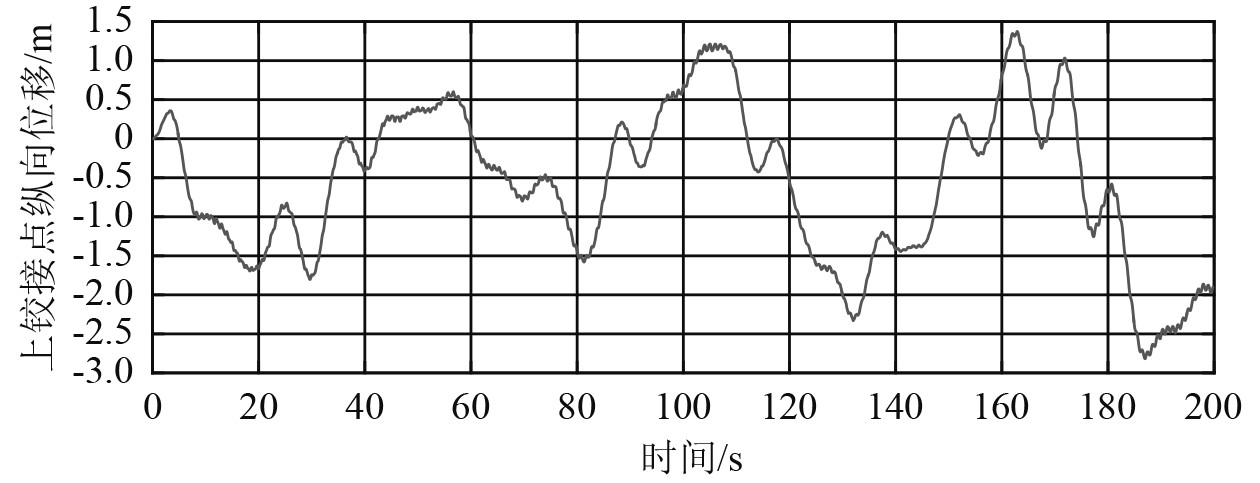
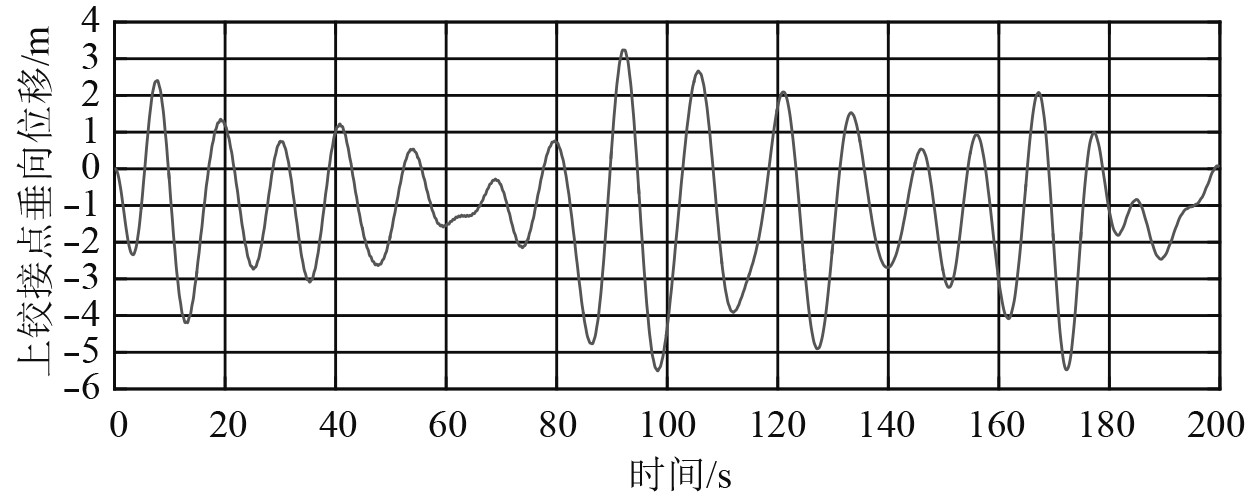
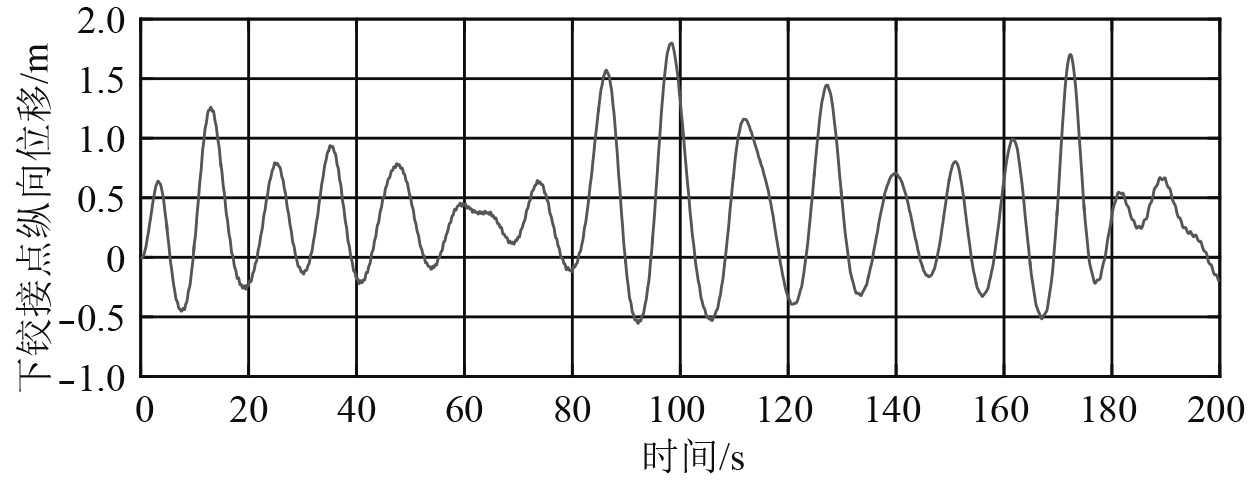
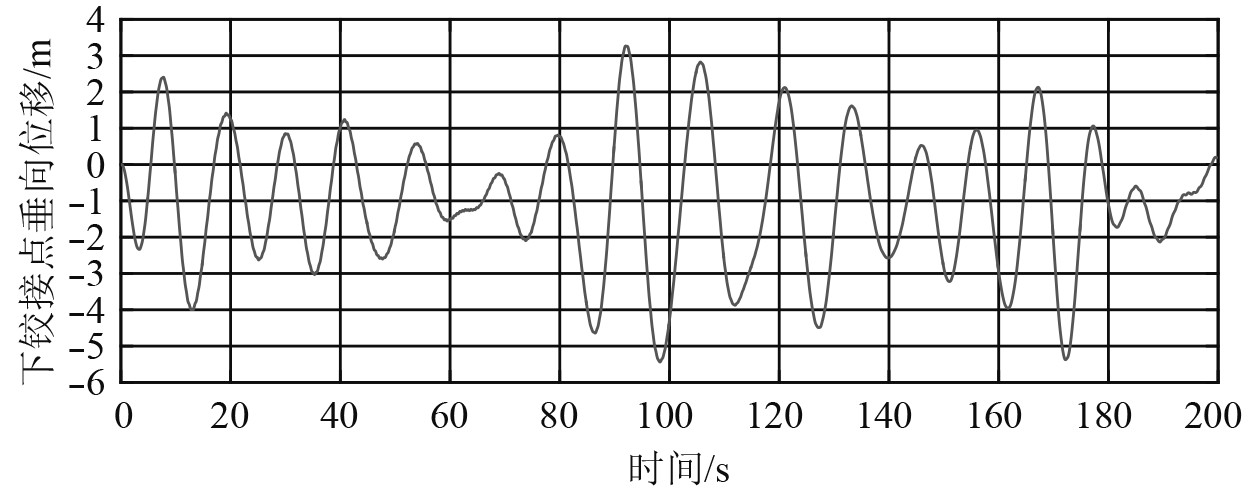
提取K文件,输入船体位移,经过计算可得节点位移。以系泊腿为例,截取前200 s数据,上下两端万向节铰接点处位移如图8~图11所示。将上下铰接点的纵向、垂向位移作为输入,在局部结构模型中建模计算,得到结构应力时程数据,可进行应力极值分析和疲劳强度分析。
|
图 8 上铰接点纵向位移 Fig. 8 Longitudinal displacement of the upper hinge point |
|
图 9 上铰接点垂向位移 Fig. 9 Vertical displacement of the upper hinge point |
|
图 10 下铰接点纵向位移 Fig. 10 Longitudinal displacement of the lower hinge point |
|
图 11 下铰接点垂向位移 Fig. 11 Vertical displacement of the lower hinge point |
由于整体仿真中将平台(船),旋转塔台甲板等作为刚体计算,系泊支架、系泊腿、系泊刚臂虽作为变形体建立了有限元模型,但是进行了一些简化处理,没有考虑构件特别是构件连接处(万向节,系泊头轴承)的局部细节。对于需要进行强度和疲劳分析的构件,进一步建立其详细的有限元模型,进行详细的局部应力计算分析。
以软刚臂系统系泊腿为例,采用hypermesh前处理软件进行建模,系泊腿由上部万向节、系泊腿钢管、下部万向节组成,上部万向节分为万向接头、回转装置、吊耳座,下部万向节分为万向接头、法兰盘。系泊腿钢管由钢板卷制焊接而成。建模中系泊腿孔等结构简化处理,回转装置部位以及万向接头回转部位采用刚柔体接触设置,法兰连接考虑螺栓连接及预紧力,除系泊腿钢管采用壳单元,其余结构均采用实体单元,且采用六面体网格划分,材料选用材料库中的MATL24[11 – 12],与常用钢材对应,模型如图12所示。

|
图 12 系泊腿有限元模型 Fig. 12 Finite element model of mooring leg |
两端吊耳座为刚体,将上下铰接点位移数据加载其上,进行系泊腿整体运动计算,可得结构应力,部分数据如图13~图16所示。

|
图 13 t=2 s系泊腿应力云图 Fig. 13 Mooring leg stress cloud of t=2 s |

|
图 14 t=20 s系泊腿应力云图 Fig. 14 Mooring leg stress cloud of t=20 s |

|
图 15 t=100 s系泊腿应力云图 Fig. 15 Mooring leg stress cloud of t=100 s |
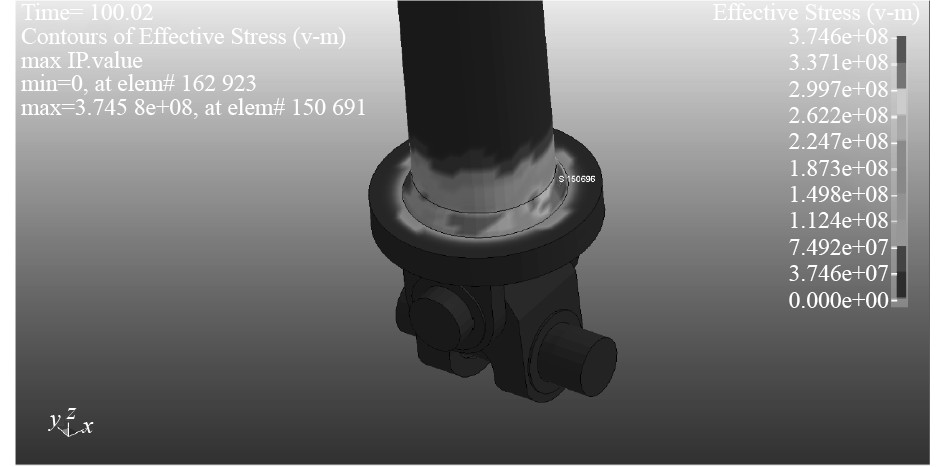
|
图 16 单元1应力云图 Fig. 16 Stress cloud of unit 1 |

|
图 18 单元2应力云图 Fig. 18 Stress cloud of unit 2 |
综上,可得系泊腿各部件应力时程曲线,图17~图19所示。通过分析可校核结构薄弱环节的极值应力与疲劳强度。
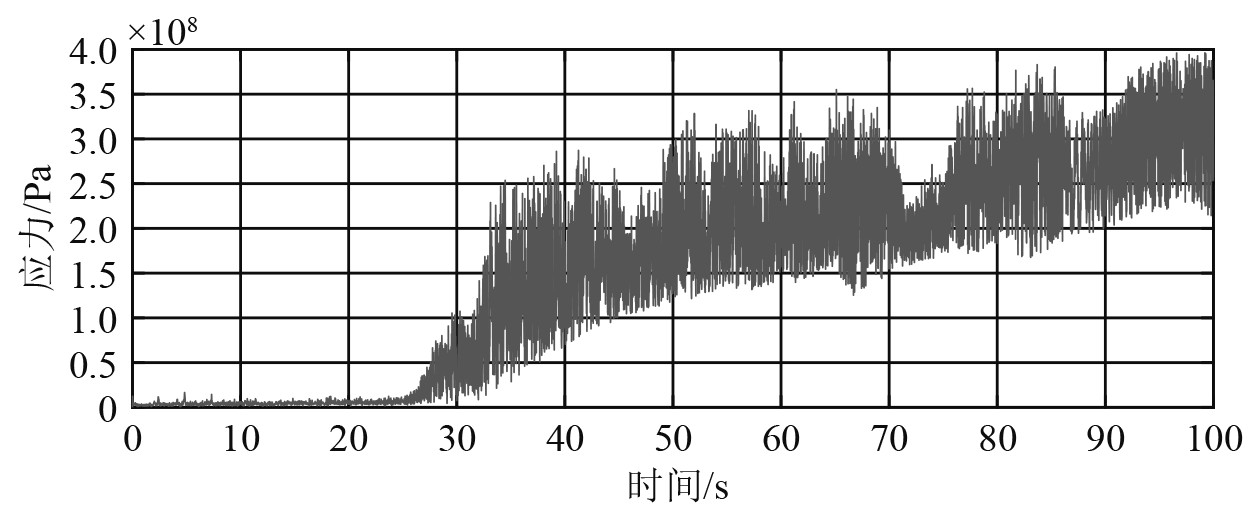
|
图 17 单元1应力曲线 Fig. 17 Stress curve of unit 1 |
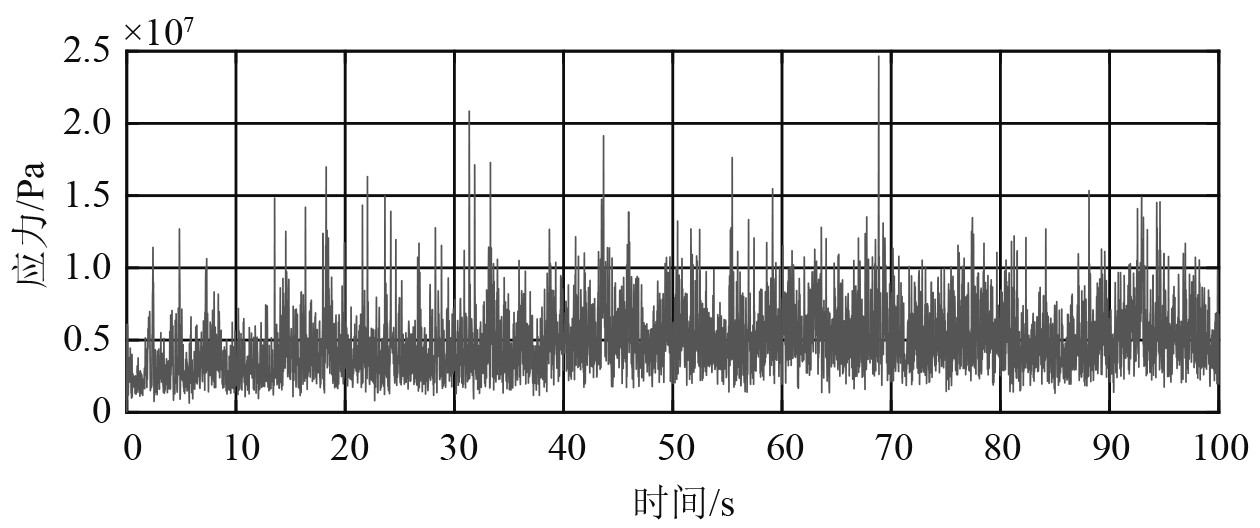
|
图 19 单元2应力曲线 Fig. 19 Stress curve of unit 2 |
基于LS-dyna,通过对浮动堆平台定位系统固有特性进行分析,得到如下结论:
1)结合浮动平台定位系统的固有特性,提出了一种以水动力计算得到船体位移,将船体位移作为输入对结构进行动力学耦合计算,分析各分系统模块、运动副的受力,求得关键部位和运动副的应力时程曲线以及关键节点的位移时程曲线的方法。
2)基于LS-dyna显示动力学,建立了平台船体、软刚臂系统、固定塔架整体刚柔模型,计算得到节点位移,并以节点位移建立局部模型,得到了结构应力时程曲线,验证了建模思路的可行性。
3)通过分析节点位移曲线,结构应力时程曲线,可得软刚臂系统系泊腿运动规律,以及其结构薄弱环节,并后续可将应力结果作为输入进行结构疲劳强度校核,具有一定的工程应用价值。
4)建立的整体刚柔耦合模型计算速度较为缓慢,模型网格、构件简化等方面还有改善空间,后续针对这方面会进行相关优化,提高模型计算效率。
| [1] |
《海洋石油工程设计指南》编委会. 海洋石油工程FPSO与单点系泊系统设计[M]. 北京: 石油工业出版社, 2007.
|
| [2] |
XIAO L, YANG J and LI X. Shallow water effects on surge motion and load of Soft Yoke Moored FPSO[J]. Ocean Eng, 2007, 21: 187-196. |
| [3] |
API. Design and analysis of station keeping systems for floating structures[S]. API RP 2SK, 2005.
|
| [4] |
许海东. 软钢臂单点系泊系统系泊腿损坏故障分析及改进措施[J]. 企业技术开发, 2013(3): 32-9. XU Haidong. Fault Analysis and Improvement Measures for Mooring Leg Damage of Soft Boom Single Point Mooring System[J]. Enterprise technology development, 2013(3): 32-9. DOI:10.3969/j.issn.1006-8937.2013.07.016 |
| [5] |
国家石油和化学工业局. 海上单点系泊装置入级与建造规范: SY/T10032-2000[S]. 北京: 中国标准出版社, 2000, 01.
|
| [6] |
刘涛. FPSO软刚臂单点系泊系统监测技术研究[D]. 大连: 大连理工大学. 2013. 05. LIU Tao. Research of Monitoring Technology for FPSO soft yoke single mooring system[D]. Dalian: Dalian University of Technology, 2013. 05 |
| [7] |
李欣, 杨建民, 肖龙飞. FPSO软刚臂单点系泊动力分析[J]. 中国造船增刊, 2005, 11: 141-148. LIXin, YANG Jian-min, XIAOLong-fei. Dynamic analysis on the tower-yoke mooring system of FPSO[J]. Shanghai: Shipbuilding of china, 2005, 11: 141-148. |
| [8] |
刘生法. 单点系泊系统关键技术探讨[J]. 中国海洋平台, 2012, 27(1): 39-43. LIU Sheng-fa. The Critical Technology of Single Point Mooring System[J]. CHINA OFFSHORE PLATFORM, 2012, 27(1): 39-43. DOI:10.3969/j.issn.1001-4500.2012.01.009 |
| [9] |
李英辉, 李喜斌, 戴杰, 等. 拖曳系统计算中拖缆与拖体的耦合计算[J]. 海洋工程, 2002, 20(4): 37-42. LI Yinghui, LI Xibin, DAI Jie, et al. Calculation of coupling between the cable and the towed-body in the towed system[J]. The Ocean Engineering, 2002, 20(4): 37-42. DOI:10.3969/j.issn.1005-9865.2002.04.007 |
| [10] |
FONSECA N, PESSOA J, MAVRAKOS S, et al. Experimental and numerical investigation of the slowly varying wave exciting drift forces on a restrained body in bi-chromatic waves[J]. Ocean Engineering, 2011, 38(17): 2000-2014. |
| [11] |
INSTITUTE N M T R. SIMO-theory manual[G]. Norway: 2004.
|
| [12] |
CONG P W, GOU Y, TENG B. A new approach to low-frequency QTF and its application in predicting slow drift force[J]. Ocean Engineering, 2012, 53: 25-37. DOI:10.1016/j.oceaneng.2012.06.005 |
 2019, Vol. 41
2019, Vol. 41
