2. 太原(天津)重型机械有限公司,天津 300450
2. Taiyuan (Tianjin) Heavy Machinery Group Company, Tianjin 300450, China
随机波浪是具有各态历经性的平稳随机过程,许多学者根据某些特定海域的长期观测资料提出了多个波浪谱公式用于描述随机波浪。这些理论波浪谱的能量成分主要集中在0.2~2.0 rad/s的波浪频率范围内,至于0~0.2 rad/s的低频范围,一般没有波浪能量成分。然而,在近岸浅水海域,伴随着大幅度振荡的波浪时历,总会出现较明显的低频波浪成分,这即是在浅水非线性波浪中出现的低频能量成分[1]。该低频能量成分及其诱导的1阶低频波浪力会导致总的低频波浪力大幅增加,从而导致单点系泊船体的低频运动响应以及由此产生的系泊力相比于数值计算有明显的增大。因此,为保证船体在浅水中低频响应预报的准确性,在总体设计流程中必须要考虑浅水波中低频能量成分的影响。
关于浅水中低频能量成分的存在及其形成机理,已被许多理论研究和实际观测所证实[2]。为分析其对船体纵荡、垂荡和纵摇低频响应的影响,主要包括低频波浪力和低频运动响应,许多学者都采用数值计算与水池试验相结合的方法。肖龙飞等[3]通过频域数值计算和模型试验研究,分析了浅水不规则波浪谱中低频成分对低频纵荡运动的影响,结果表明浅水低频纵荡运动响应主要是1阶的,2阶成分几乎可以忽略。李欣等[4]在线性三维势流理论的基础上,采用时域计算方法分析了浅水软刚臂系泊FPSO的触底情况,并与模型试验进行了对比。郭彬[5]通过时域数值计算和模型试验分析了船体在浅水非共线风浪流海况作用下的运动性能与舷侧甲板上浪情况。
本文针对作业于渤海浅水海域的海洋核动力平台示范工程,通过数值计算和水池试验2种方法得到浅水波浪谱,通过结果对比,分析浅水中的低频能量成分对平台纵荡、垂荡和纵摇3个自由度上的低频波浪力和低频运动响应的影响。
1 理论基础 1.1 纵荡运动方程单点系泊平台在迎浪不规则波作用下的低频纵荡运动方程可表示为[6]:
| $\begin{split}& \left[ {m + {a_{11}}\left( {{\mu _1}} \right)} \right]{\ddot x_{1L}} + \left[ {{B_{11}}\left( {{\mu _1}} \right) + {B_{wdd}}} \right]{\dot x_{1L}} + \\ &\quad\quad{C_{11}}{x_{1L}} = {F_{1L}}\text{。}\end{split}$ | (1) |
其中:
以纵荡低频波浪力作为输入,以纵荡低频运动作为输出,二者的能量谱密度函数关系可通过线性幅值传递函数进行表示,如下式:
| ${S_{{x_{1L}}}}\left( \mu \right) = \frac{{{S_{{F_{1L}}}}\left( \mu \right)}}{{{{\left[ {{C_{11}} - \left( {m + {a_{11}}} \right){\mu ^2}} \right]}^2} + {{\left( {{B_{11}} + {B_{wdd}}} \right)}^2}{\mu ^2}}}\text{。}$ | (2) |
其中:
在小阻尼条件下,纵荡低频运动的标准差
| $\sigma _{{x_{1L}}}^2 = \int_0^\infty {{S_{{x_{1L}}}}\left( \mu \right)} {\rm{d}}\mu = \frac{{\text{π}} }{{2\left( {{B_{11}} + {B_{wdd}}} \right){C_{11}}}}{S_{{F_{1L}}}}\left( {{\mu _1}} \right)\text{。}$ | (3) |
由式(3)可知,纵荡低频运动不仅受纵荡低频波浪力影响,也与运动阻尼、回复力系数有关。其中回复力系数与单点系泊系统的设计有直接关系,在本文讨论平台低频响应时,假设其为常量。因此影响纵荡低频运动响应大小的因素主要有纵荡低频波浪力和运动阻尼,而后者又包含静水阻尼和波浪慢漂阻尼两部分。
在浅水波中,纵荡低频波浪力不仅包含2阶平均波浪力和2阶波浪慢漂力,还必须考虑1阶波浪力中的低频能量成分。对于1阶低频波浪力,其谱密度函数可直接根据波浪谱密度函数
| $S_{{F_{1L}}}^{\left( 1 \right)}\left( \omega \right) = S\left( \omega \right){\left| {{H_{{F_{1L}}}}\left( \omega \right)} \right|^2}\text{,}$ | (4) |
2阶平均波浪力决定了平台的平均位移,可以表示为:
| $F_{1L}^{\left( 2 \right)} = 2\int_0^\infty {S\left( \omega \right)T\left( {\omega ,\omega } \right)} {\rm{d}}\omega \text{,}$ | (5) |
其中,
2阶波浪慢漂力谱密度函数可以表示为:
| $S_{{F_{1L}}}^{\left( 2 \right)}\left( \mu \right) = 8\int_0^\infty {S\left( {\omega + \mu } \right)S\left( \omega \right){T^2}\left( {\omega + \mu ,\omega } \right){\rm{d}}\omega }\text{,} $ | (6) |
其中,
| ${S_{{F_{1L}}}}\left( \mu \right) = S_{{F_{1L}}}^{(1)}\left( \mu \right) + S_{{F_{1L}}}^{(2)}\left( \mu \right)\text{,}$ | (7) |
静水阻尼系数与粘性有关,一般根据静水衰减试验结果计算得到,如下式[8]:
| ${B_{11}}\left( {{\mu _1}} \right) = 2\delta \sqrt {{C_{11}}\left[ {m + {a_{11}}\left( {{\mu _1}} \right)} \right]} = \frac{{2\delta {C_{11}}}}{{{\mu _1}}}\text{,}$ | (8) |
其中,无因次变量
| $\delta = \frac{{\ln {x_1} - \ln {x_{n + 1}}}}{{2{\text{π}} n}}\text{。}$ | (9) |
其中,
纵荡波浪慢漂阻尼是由波浪引起的,可以通过平均波浪力的二次传递函数计算得到,如下式[9]:
| ${B_{wdd}} = 2\int_0^\infty {S\left( \omega \right){b_{wdd}}\left( \omega \right){\rm{d}}\omega } \text{,}$ | (10) |
| ${b_{wdd}}\left( \omega \right) = - \frac{\omega }{g}\left[ {\omega \frac{{{\rm{d}}T\left( {\omega ,\omega } \right)}}{{{\rm{d}}\omega }} + 4T\left( {\omega ,\omega } \right)} \right]\text{。}$ | (11) |
对于垂荡和纵摇运动,由于其固有频率处在波频范围内,所以主要表现为1阶运动,而且其自身静水回复力远大于系泊系统提供的回复力,因此一般在频域计算中不考虑系泊系统的影响。基于线性势流理论,自由漂浮的平台在频率
| $\begin{split}\!\!\!\!\!\! \sum\limits_{j = 1}^6 {\left\{ {\left[ {{m_{ij}} + {a_{ij}}\left( \omega \right)} \right]\ddot x_j^{\left( 1 \right)} + {\lambda _{ij}}\left( \omega \right)\dot x_j^{\left( 1 \right)} + {C_{ij}}x_j^{\left( 1 \right)}} \right\}} = F_i^{\left( 1 \right)}\text{,} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 3,5\text{。} \end{split} $ | (12) |
其中:
与纵荡低频响应相同,垂荡和纵摇1阶低频波浪力谱密度函数也可通过式(4)计算得到,而低频运动标准差可由下式计算得到。
| $\sigma _{{x_{iL}}}^2 = \int_0^\infty {{S_{{x_{iL}}}}\left( \omega \right)} {\rm{d}}\omega\text{,} \;\;i = 3,5\text{。}$ | (13) |
海洋核动力平台是我国核动力水面舰船示范工程,属浮动式核动力能源保障船式平台,由软刚臂单点系泊装置长期定位于渤海海域,主要解决渤海油气开采中的电力、淡水等能源需求。
平台整体有两部分组成:船体和软刚臂单点系泊系统,分别如图1和图2所示。平台作业场址平均海平面30.6 m,设计重现期为500年。基于国家海洋环境预报中心监测数据,相对于平均海平面重现期500年最低水位为–5.1 m,因此平台的最小作业水深为25.5 m,属于浅水海域。

|
图 1 船体网格划分示意图 Fig. 1 Sketch of ship meshing |
|
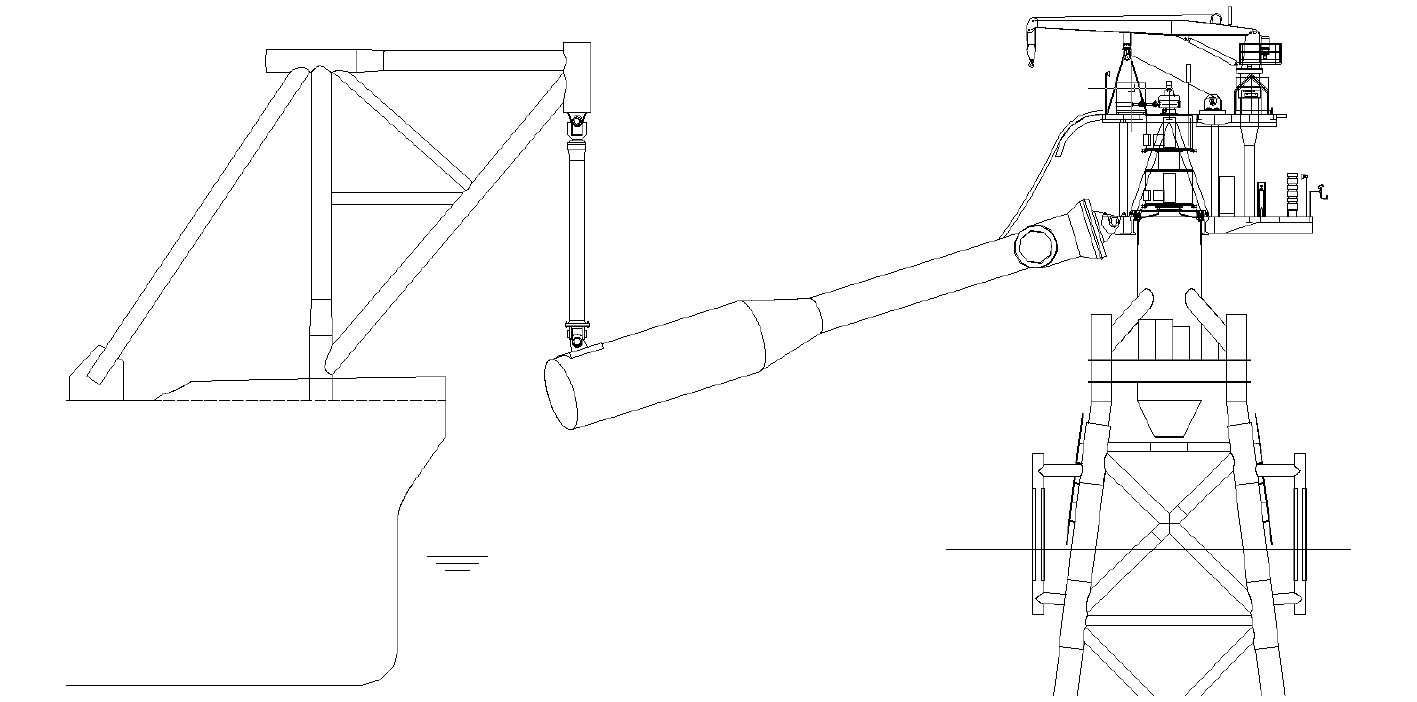
图 2 软刚臂系泊系统总体布置 Fig. 2 General arrangement of soft yoke mooring system |
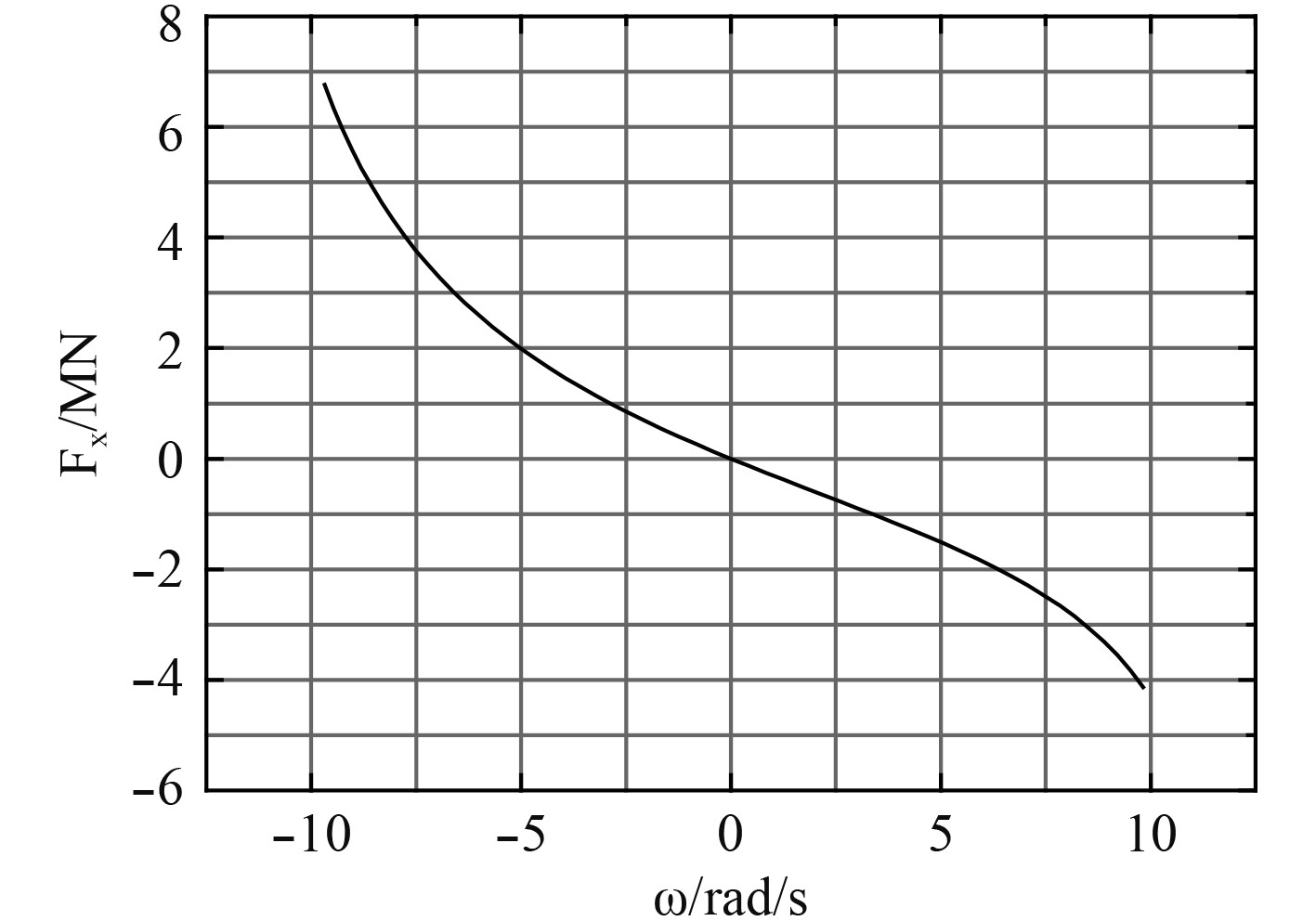
单点系泊系统的纵荡水平回复力曲线如图3所示。图中x为纵荡位移,
|
图 3 单点系泊系统纵荡水平回复力曲线 Fig. 3 Horizontal restoring force of soft yoke mooring system in surge direction |
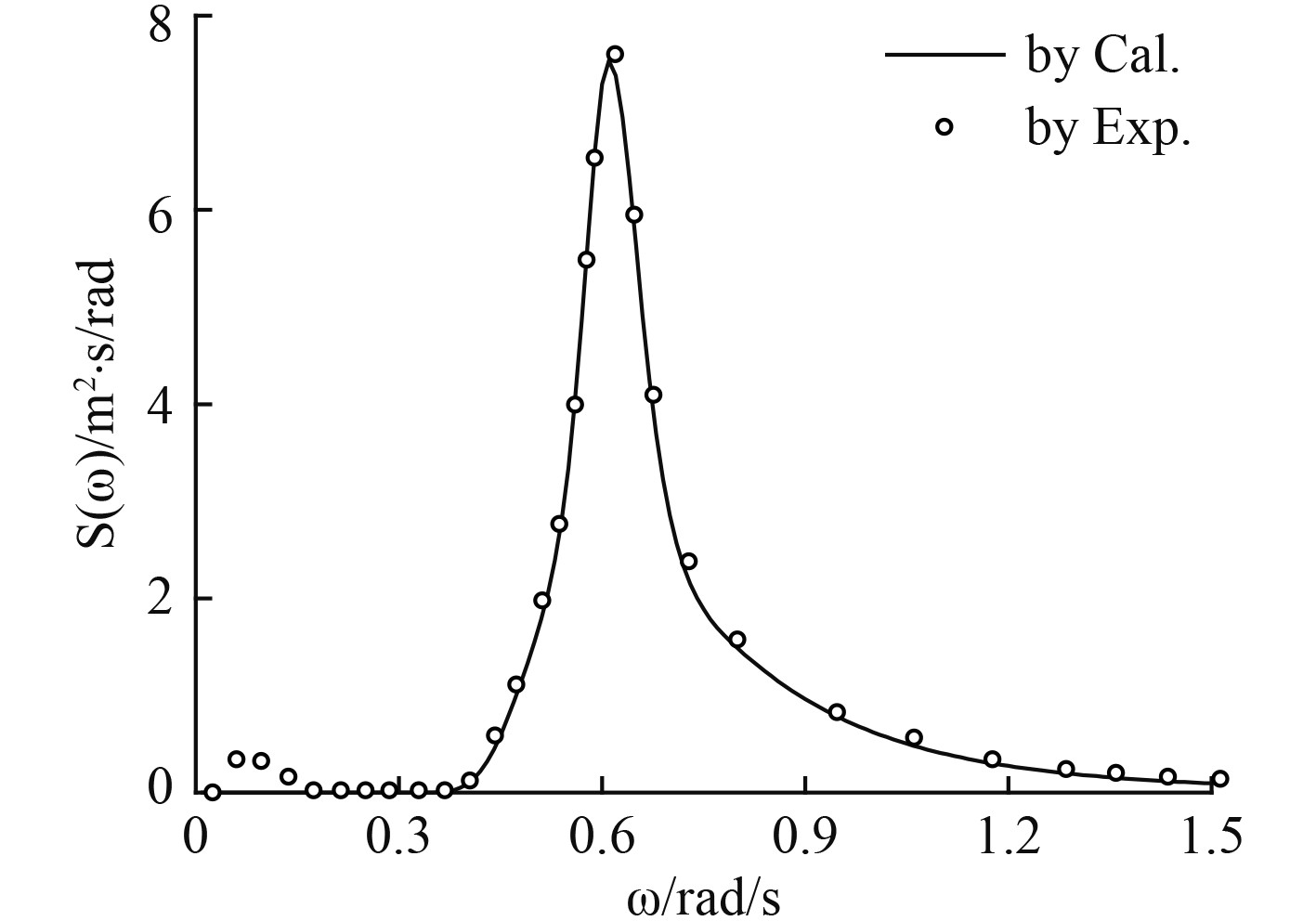
本文选取在上海交通大学海洋工程水池中模拟的一组不规则波,
|
图 4 波浪谱密度计算值与试验值对比结果 Fig. 4 Comparative results of calculating and experimental wave spectrums |
由图可知,计算值与试验值吻合良好。但波浪谱的试验值在0~0.2 rad/s的低频范围内出现了计算值所没有的能量成分,这即是在浅水中出现的低频能量成分。该浅水低频能量成分的存在,将对平台的运动响应和单点系泊系统的设计产生重要的影响,在实际工程设计中需要给予考虑。
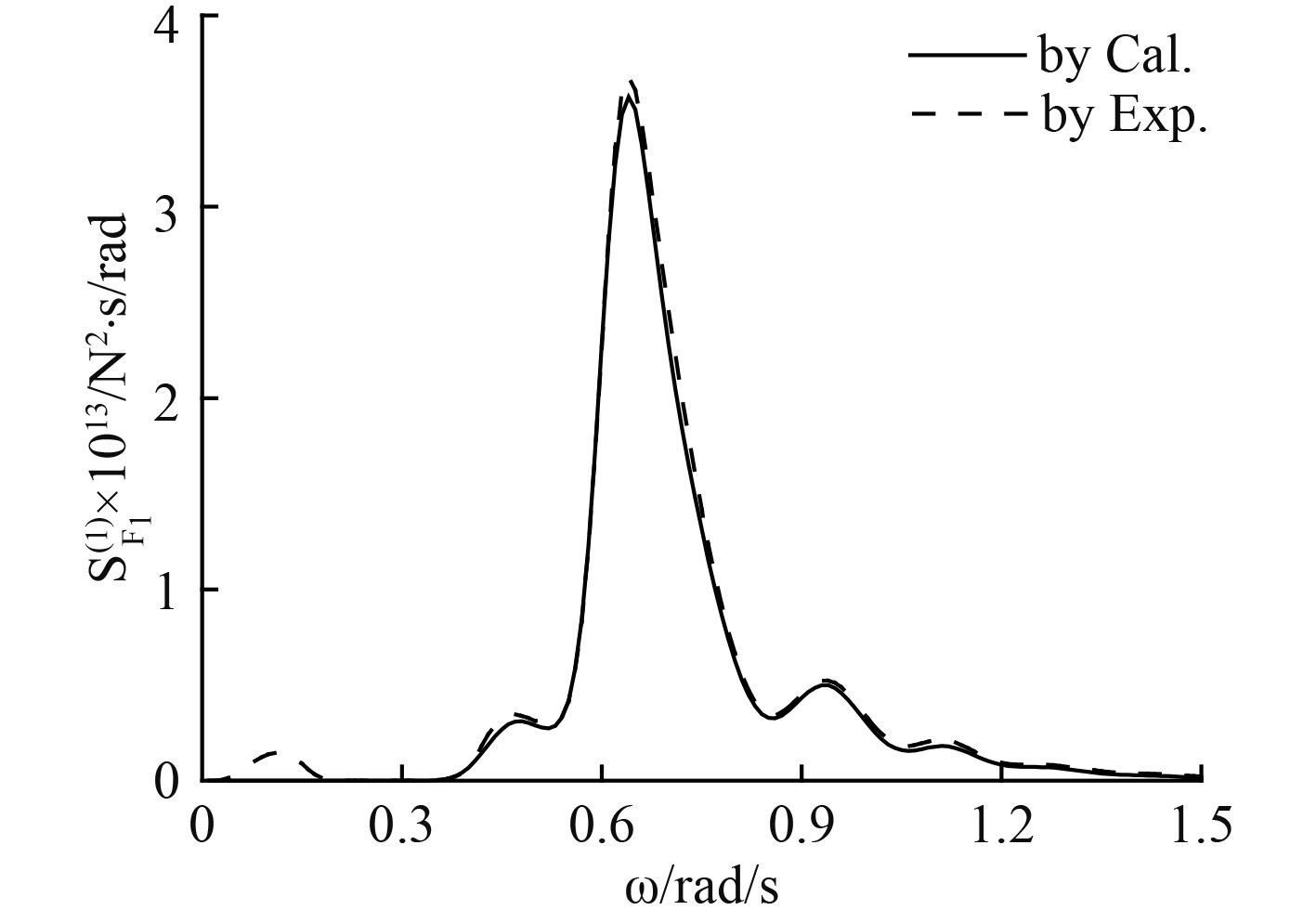
3.2 纵荡低频响应根据式(4)~式(6)可以计算得到纵荡1阶低频波浪力谱、2阶平均波浪力和2阶波浪慢漂力谱,分别如图5~图7所示。为分析浅水中的纵荡低频波浪力,以标准差为判断标准,波浪谱计算值和试验值2种情况下的纵荡1阶低频波浪力和波浪漂移标准差无因次比值以及平均波浪力大小的无因次比值如图8所示。
|
图 5 纵荡1阶低频波浪力谱 Fig. 5 First order LF wave force spectrum in surge direction |
|
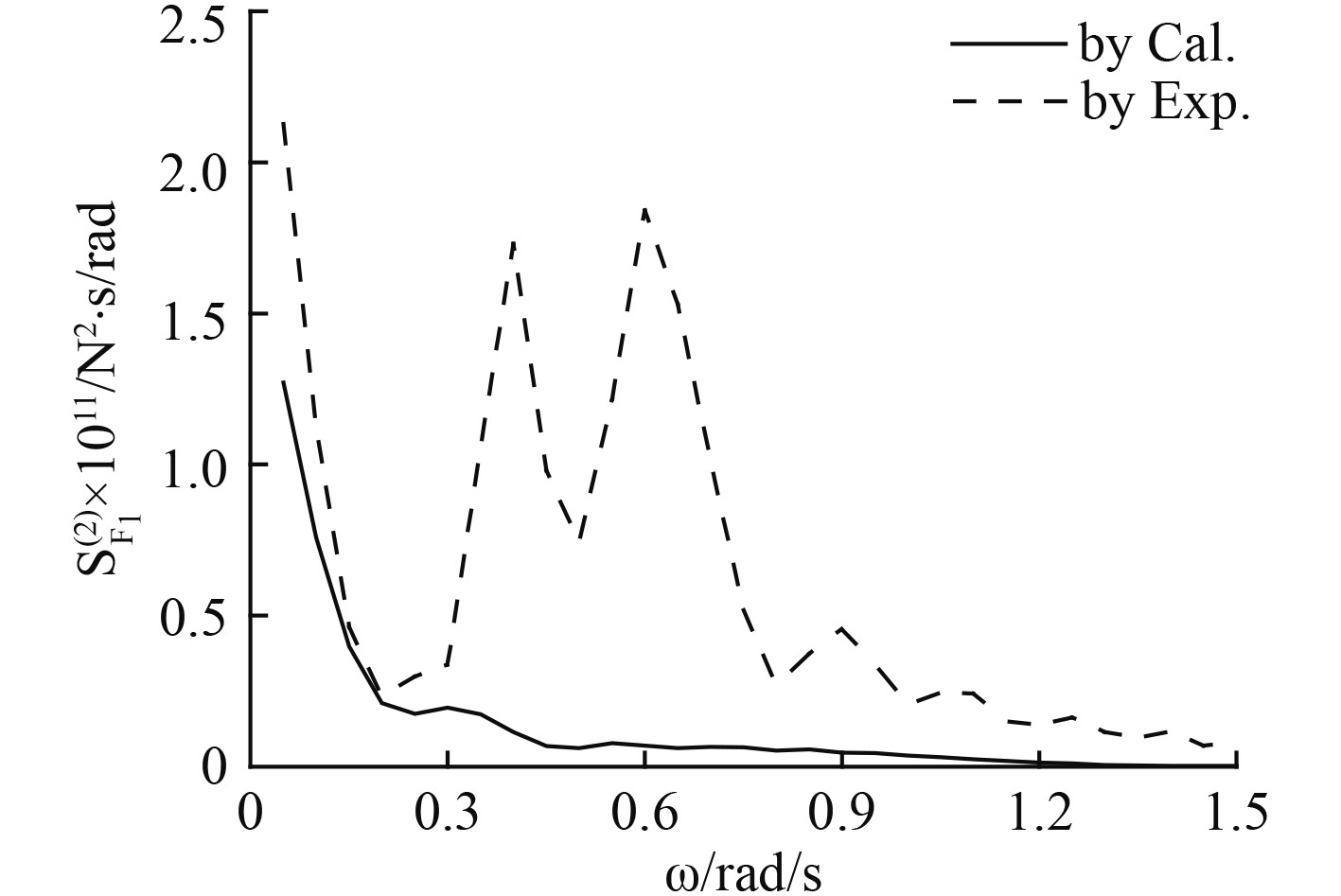
图 7 纵荡2阶波浪慢漂力 Fig. 7 Second order wave slow drift force in surge direction |
|
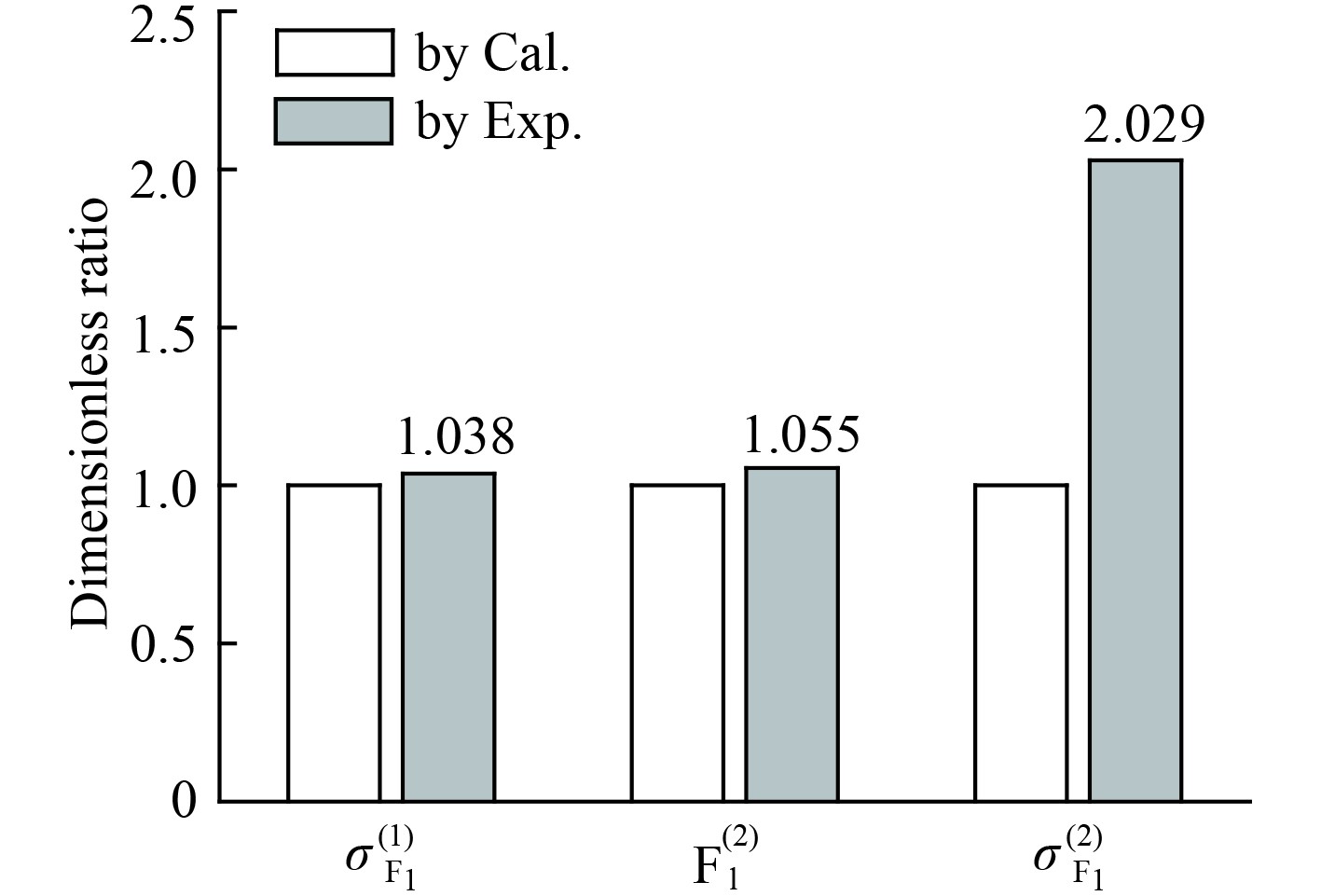
图 8 纵荡低频波浪力标准差对比 Fig. 8 Standard deviation comparison of LF wave force in surge direction |
|
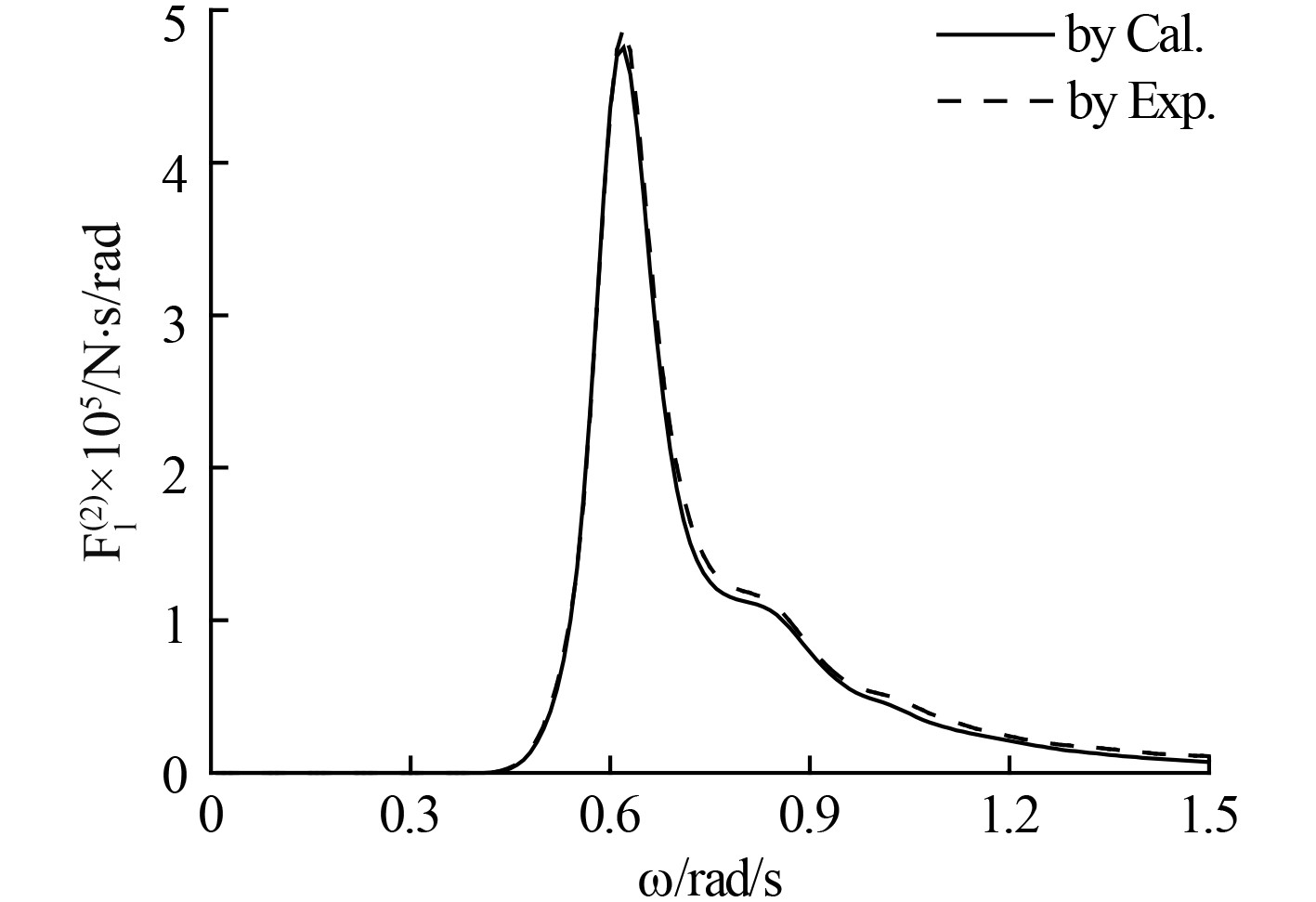
图 6 纵荡2阶平均波浪力 Fig. 6 Second order mean wave force in surge direction |
对比波浪谱计算值和测量值2种计算结果:
1)对比图5和图7,在0~0.2 rad/s的低频范围内,1阶低频波浪力为1012量级,2阶平均波浪力为1011量级,两者相差十倍至几十倍。这说明,在浅水海域,由于低频能量成分的存在,低频波浪力的主要贡献为1阶低频波浪力,这一点与深水海域截然不同。
2)由图8可知,浅水低频能量成分对纵荡1阶低频波浪力、2阶平均波浪力影响较小,而对2阶波浪慢漂力影响很大,考虑浅水低频能量成分相比于不考虑时2阶波浪慢漂力增大1倍左右。
由式(5)计算得到平均波浪力大小为186.8 kN,重现期500年对应迎风迎流条件下的风载荷为340.4 kN和流载荷33.8 kN,因此对应平均系泊力为561.0 kN。由图3可知,在该平均系泊力下,平台的平均位移为-1.70 m,此时系泊系统的纵荡水平回复力系数
| ${\mu _1} = \sqrt {{{{C_{11}}} / {\left[ {m + {a_{11}}\left( \infty \right)} \right]}}} \text{。}$ | (14) |
其中,
根据式(8)和式(10)分别计算得到
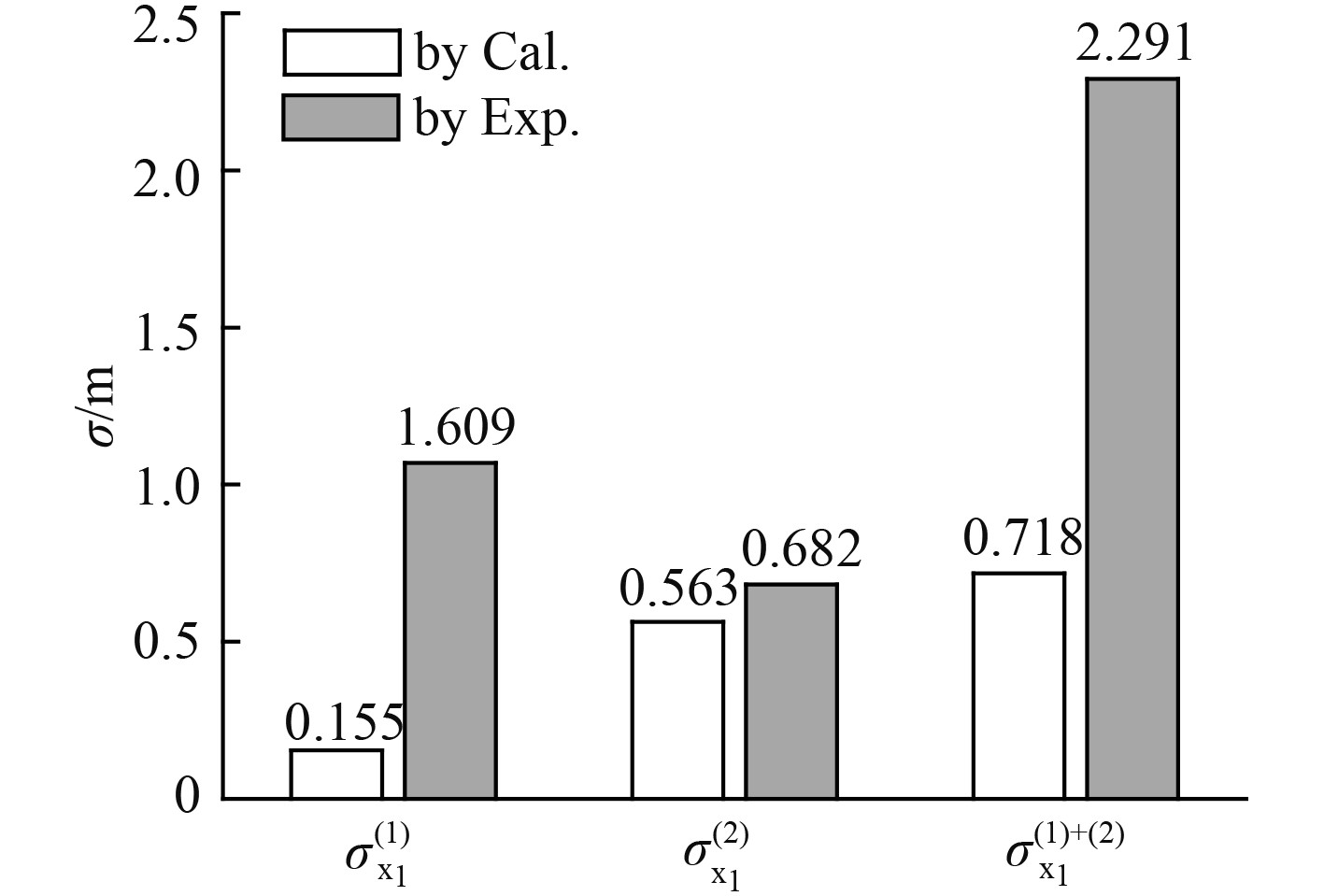
|
图 9 纵荡运动标准差对比 Fig. 9 Standard deviation comparison of motion response in surge direction |
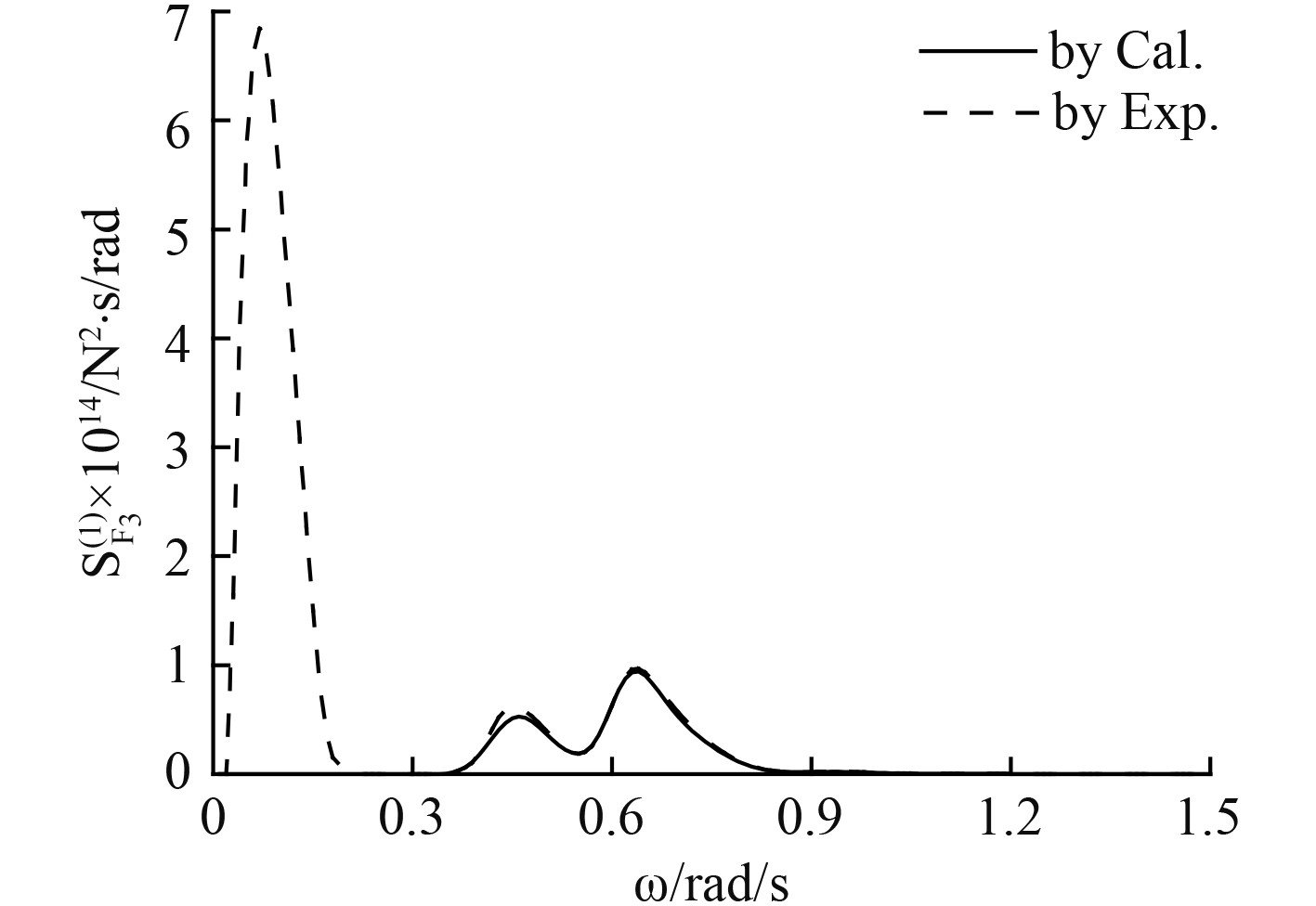
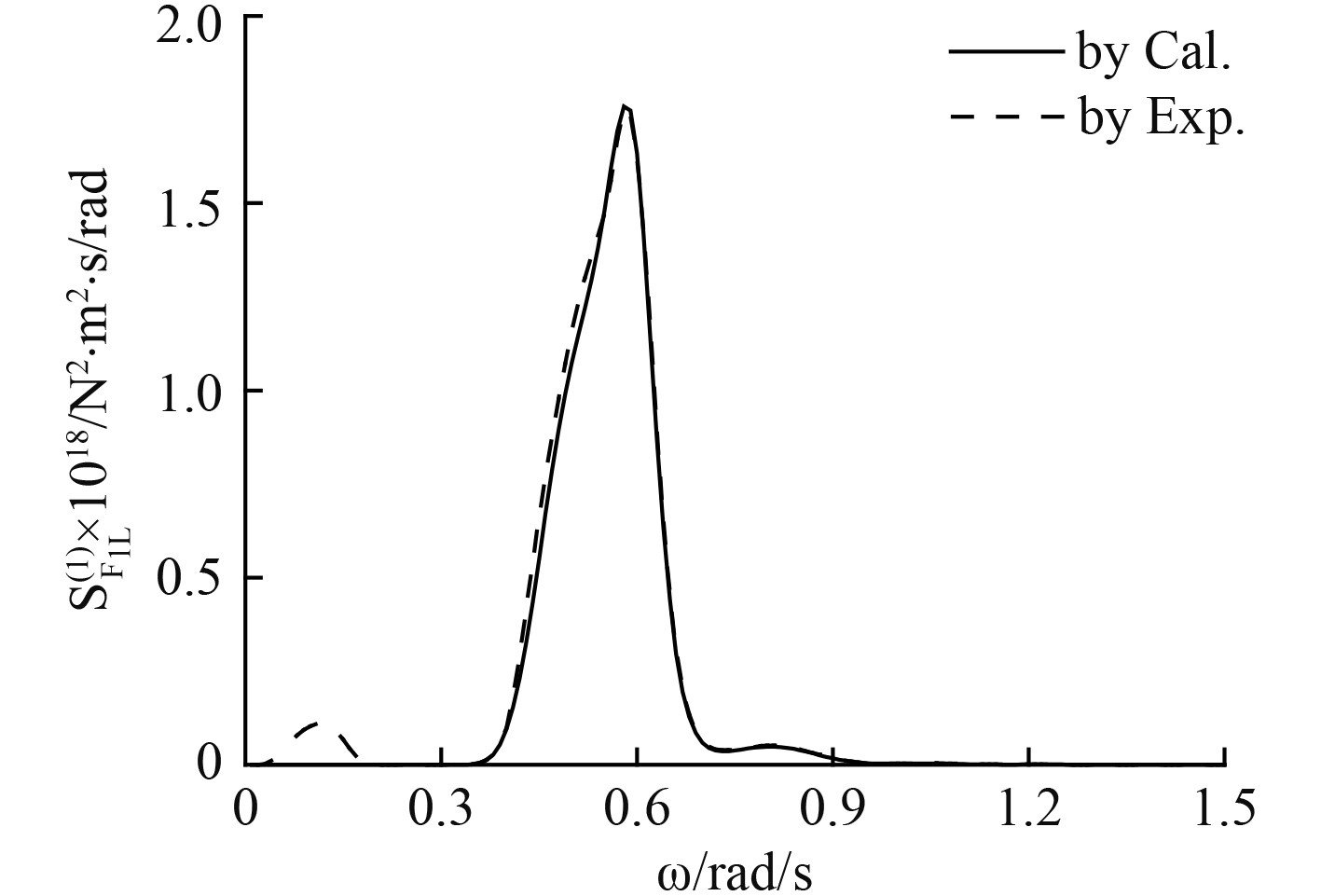
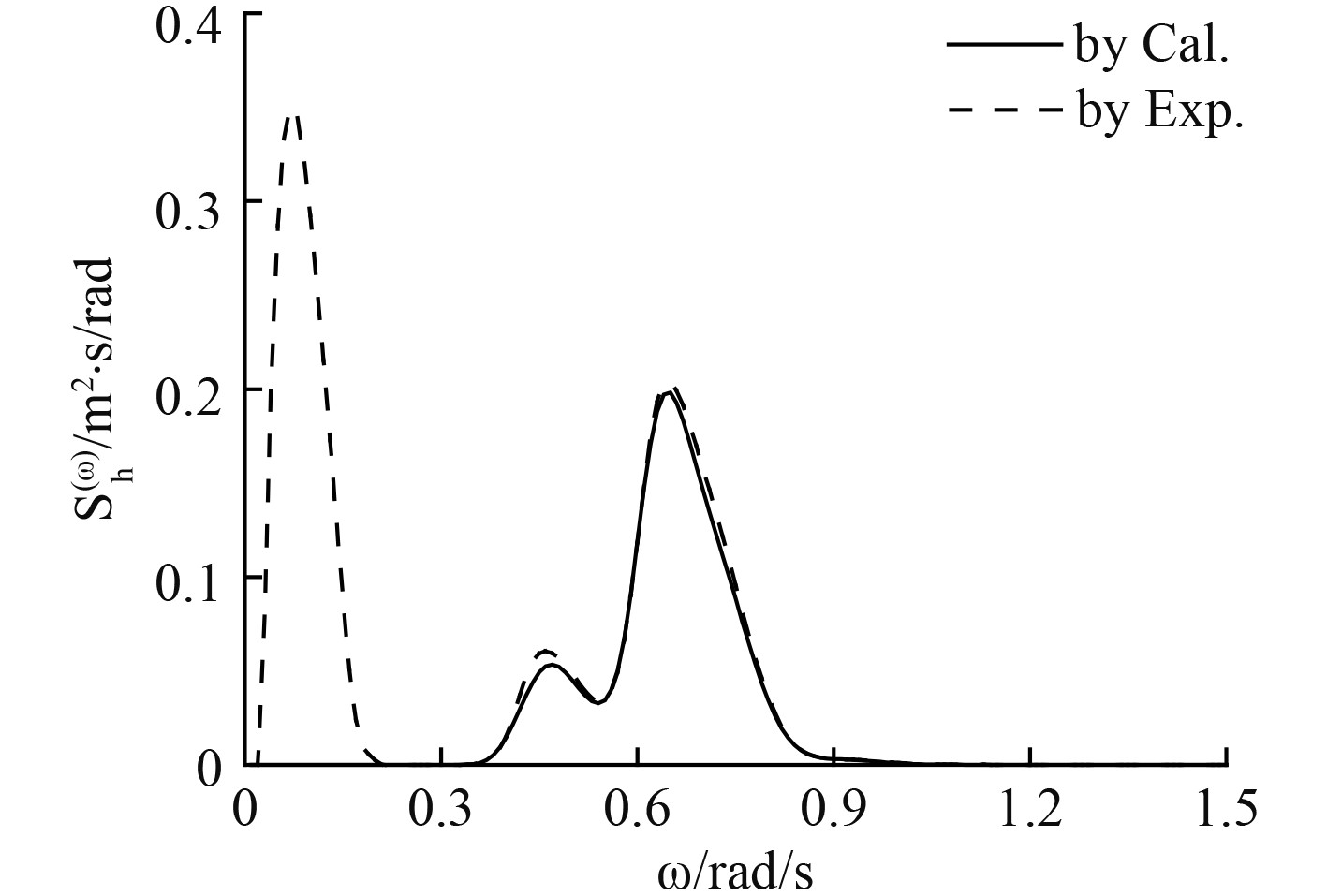
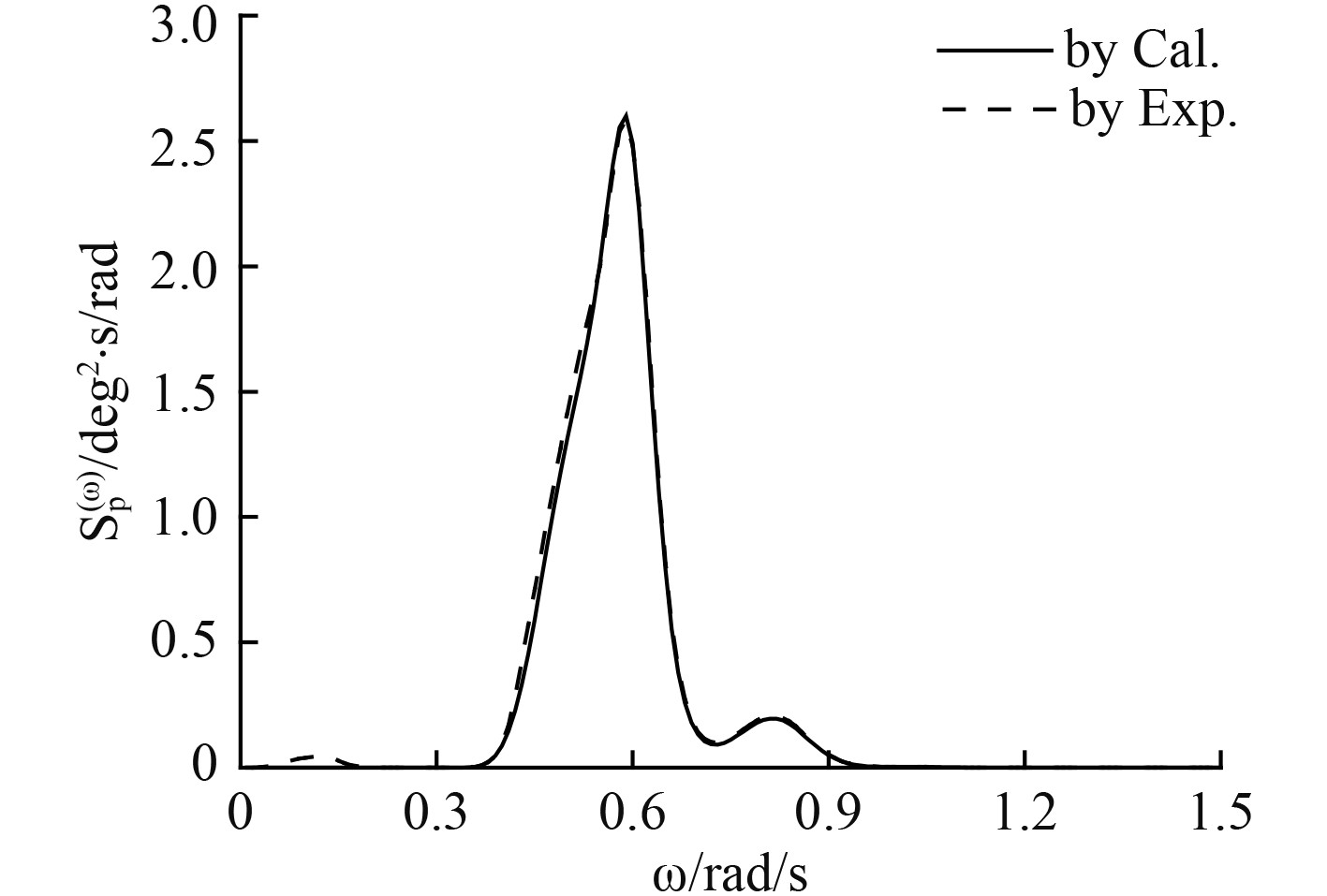
只考虑1阶低频响应,垂荡和纵摇1阶低频波浪力谱如图10和图11所示,1阶低频运动响应如图12和图13所示,而同样以各自的标准差研究浅水中的垂荡和纵摇低频响应,如图14所示。
|
图 10 垂荡1阶低频波浪力谱 Fig. 10 First order LF wave force spectrum in heave direction |
|
图 11 纵摇1阶低频波浪力谱 Fig. 11 First order LF wave force spectrum in pitch direction |
|
图 12 垂荡1阶低频运动响应谱 Fig. 12 First order LF motion response spectrum in heave direction |
|
图 13 纵摇1阶低频运动响应谱 Fig. 13 First order LF motion response spectrum in pitch direction |
|
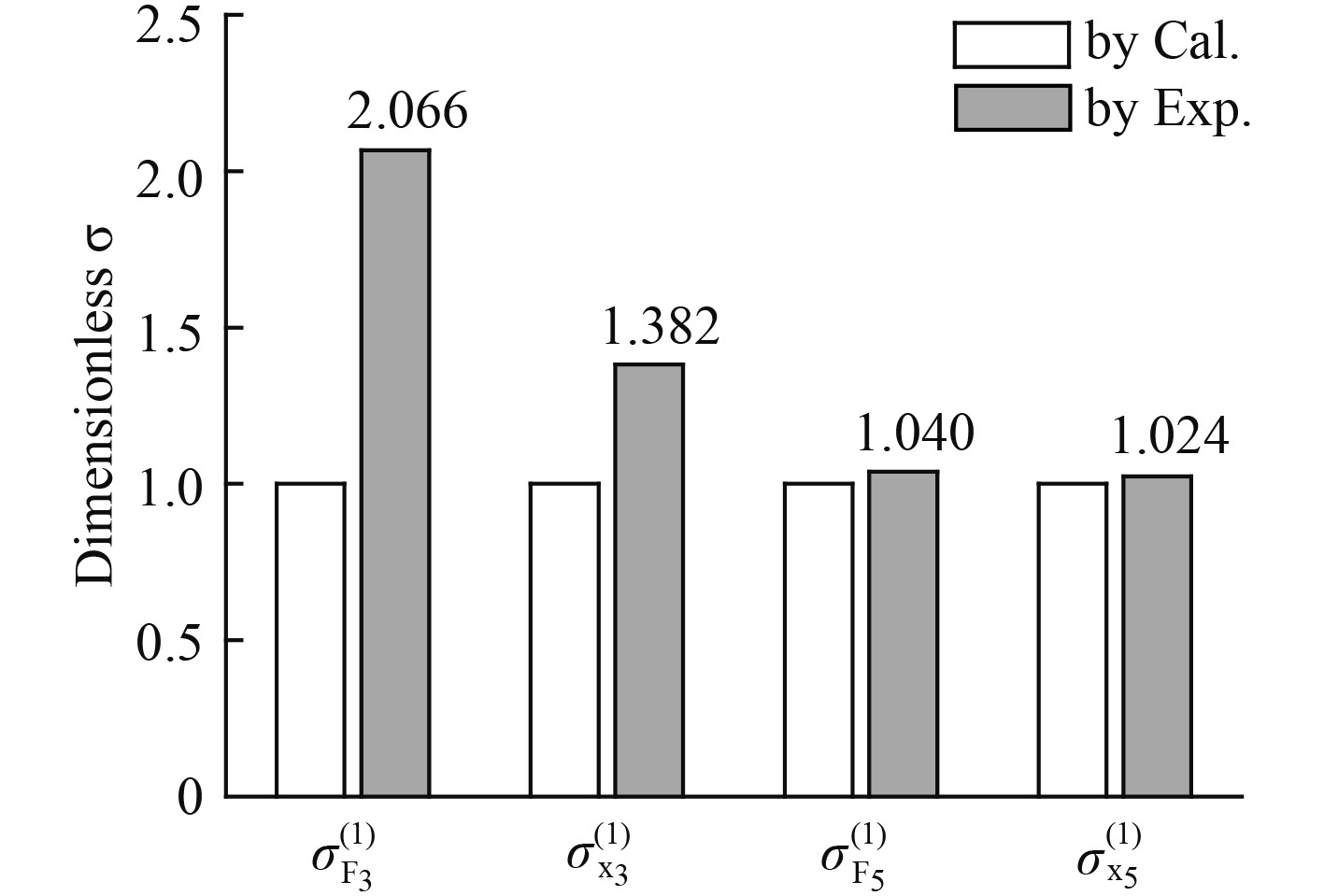
图 14 垂荡和纵摇1阶低频响应标准差对比 Fig. 14 Standard deviation comparison of first order LF response in heave and pitch direction |
对比波浪谱计算值和测量值2种计算结果:
1)由图10和图12可知,浅水波浪谱中的低频能量成分对垂荡1阶低频波浪力和1阶低频运动响应的影响非常大;
2)由图14可知,浅水低频能量成分使得垂荡1阶波浪力增大1倍左右,相应地使得垂荡1阶运动响应增大38.2%,而对纵摇低频波浪力和低频运动响应影响较小。
4 结 语本文针对作业于浅水海域的海洋核动力平台,采用数值模拟和水池试验2种方法得到波浪谱密度函数并结合频域势流理论,分析浅水中平台纵荡、垂荡和纵摇3个自由度上的低频响应,包括低频波浪力和低频运动响应的影响,经过结果对比可以得出如下结论:
1)浅水中的低频能量成分在通常数值计算中所应用的不规则波理论中是不存在的,由于其对平台的低频波浪力和低频运动响应十分重要,在理论预报时必须予以特别重视;
2)浅水低频能量成分对平台纵荡2阶波浪慢漂力和纵荡1阶低频运动响应影响很大;
3)浅水低频能量成分使得垂荡1阶低频波浪力和1阶低频运动响应出现了非常大的能量成分,说明其对垂荡低频响应影响很大。
| [1] |
肖龙飞. 浅水波及软刚臂系泊FPSO浅水效应研究[D]. 上海: 上海交通大学, 2007.
|
| [2] |
邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005.
|
| [3] |
肖龙飞, 杨建民, 胡志强. 极浅水单点系泊FPSO低频响应分析[J]. 船舶力学, 2010, 14(4): 372-378. XIAO Long-fei, YANG Jian-min, HU Zhi-qiang. Analysis on the low frequency response of a single point moored FPSO in ultra-shallow water[J]. Journal of Ship Mechanics, 2010, 14(4): 372-378. DOI:10.3969/j.issn.1007-7294.2010.04.007 |
| [4] |
李欣, 杨建民, 范模. 渤海油田浅水软刚臂系泊FPSO触底分析[J]. 海洋工程, 2004, 22(2): 51-57. DOI:10.3969/j.issn.1005-9962.2004.02.014 |
| [5] |
郭彬, 肖龙飞, 杨建民. 浅水非共线海况下FPSO运动与上浪分析[J]. 中国海洋平台, 2009, 24(6): 20-24. DOI:10.3969/j.issn.1001-4500.2009.06.004 |
| [6] |
WICHERS J E W. A simulation model for a single point moored tanker[D]. Delft: Delft University of Technology, 1988.
|
| [7] |
PINKSTER J A. Low-frequency phenomena associated with vessels moored at sea[J]. Society of Petroleum Engineers Journal, 1975, 15(6): 487-494. DOI:10.2118/4837-PA |
| [8] |
FALTINSEN O M. Sea loads on ships and offshore structures[M]. Cambridge: Cambridge University Press, 1990.
|
| [9] |
ARANHA J A P. Formula for ‘wave damping’ in the drift of a floating body[J]. Journal of Fluid Mechanics, 1994, 275: 147-155. DOI:10.1017/S0022112094002314 |
 2019, Vol. 41
2019, Vol. 41
