单点系泊系统(Single Point Mooring System,SPM)是一种特殊的海洋工程装备[1],主要作用是通过缆绳或特定结构将船舶系泊在一定的海域,同时使船舶可以绕系泊点作360°回转,并且可以将船舶上的油、水、气、电、信号等输出至海底管线,或将其输送至穿梭油轮。1958年,由美国IMODCO公司设计的第1套悬链浮筒式单点系泊(CALM)系统在瑞典制造成功,该浮筒直径4.5 m,由4根锚链对称固定,重60 t,可以系泊2 000 t左右的舰船,用于军舰的海上加油,揭开了单点系泊技术在海洋石油开采和海上原油中转等领域上的应用的序幕[2]。
塔架式软刚臂单点系泊系统是通过软刚臂系统和固定塔架将船舶系泊于预定海域,在各种风浪流作用下受力最小,从而保证船舶在海上能长期连续工作。按照软刚臂结构相对水面的位置分为水上软刚臂和水下软刚臂2种主要类型[3],其中水上软刚臂根据压载舱型式的不同又分为横向单压载舱式、双瓶型压载舱式、双箱型压载舱式。本文研究的软刚臂系泊系统是国家能源局批复的海洋核动力平台示范工程项目的重要组成部分。
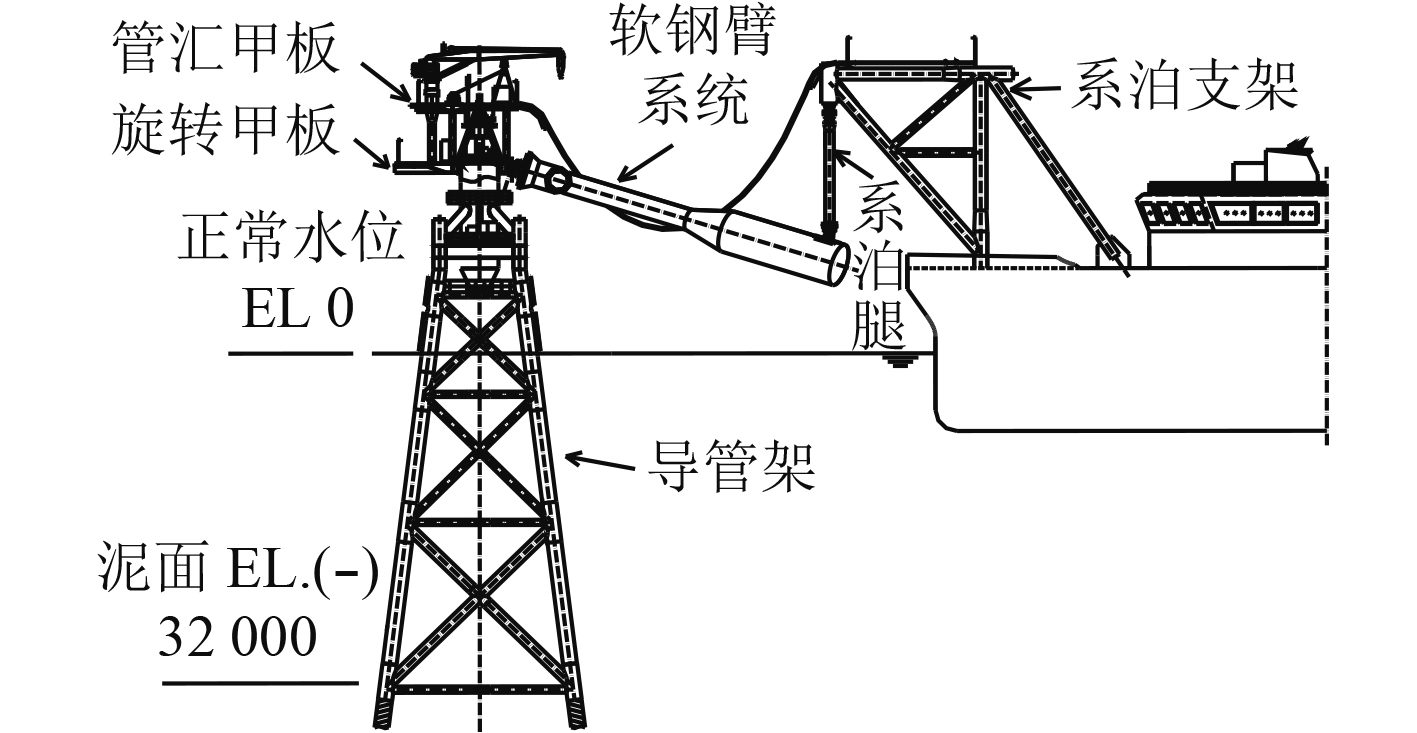
1 软刚臂系泊系统图1为软刚臂单点系泊系统示意图,其主要组成为软刚臂系统、旋转塔台系统和导管架系统等。
|
图 1 软刚臂单点系泊系统示意图 Fig. 1 Schematic diagram of the soft-arm single-point mooring system |
软刚臂YOKE通过系泊轴承挂钩与旋转甲板相连,当船体纵摇运动时,它能围绕挂钩轴线上下转动;当船体横摇运动时,YOKE通过自身发生扭转运动,另外船体能通过软刚臂系统实现风向标效应,绕着导管架转动。系泊腿下部通过万向节与软刚臂YOKE连接,上部也是通过万向节与系泊支架连接,上下两端均通过销轴能实现多自由度运动。
本文主要针对软刚臂系统、系泊腿与船体支架、导管架系统之间的多自由度运动进行分析,有学者已经针对船体纵向运动刚度曲线进行了研究,肖龙飞研究FPSO的水动力发展,通过理论推导,计算软刚臂系统的受力特性[4 – 5]。苏方磊研究水上软刚臂系统的水动力响应特性,进一步分析其纵向刚度特性[6]。软刚臂系统的横向运动刚度很少研究,本文通过船体纵向刚度曲线理论推导和试验,验证ADAMS模型分析正确性,重点分析船体横向运动时,软刚臂YOKE呈现空间扭转变化,系统的刚度随位移的变化以及各关节点的受力,同时也分析了船体与软刚臂在极限位置时的碰撞情况,为示范工程单点系泊系统的设计提供理论支撑。
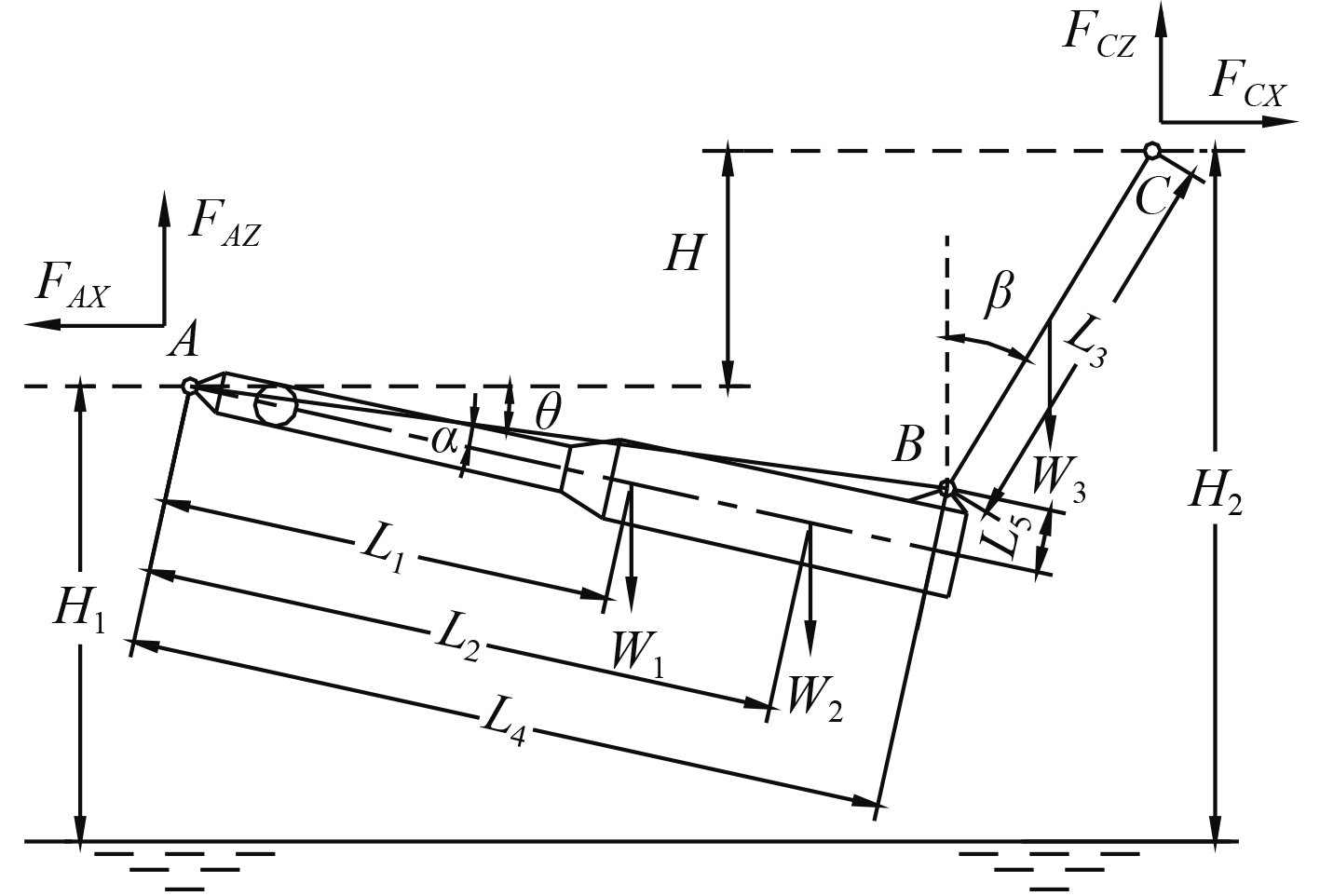
2 纵向运动时软刚臂系统刚度理论计算图2为软刚臂与系泊腿的几何关系与受力简化图,根据图中几何关系、力平衡和力矩平衡,可得到如下计算式:
|
图 2 软刚臂单点系泊系统的几何关系与受力 Fig. 2 Geometric relationship and force of the soft-arm single-point mooring system |
软刚臂系统水平X向受力平衡
| ${F_{AX}} = {F_{CX}}\text{,}$ | (1) |
系统Z方向受力平衡
| ${F_{AZ}} + {F_{CZ}} = {W_1} + {W_2} + {W_3}\text{,}$ | (2) |
系泊腿相对于B点的力矩平衡
| $\begin{gathered} {F_{CZ}} \times {L_3} \times \sin \beta = {F_{CX}} \times {L_3} \times \cos \beta+ \\ {W_3} \times \frac{{{L_3}}}{2} \times \sin \beta \text{,} \\ \end{gathered} $ | (3) |
软刚臂系统对于A点力矩平衡
| $\begin{split} {W_1} \times {L_1} \times \cos (\alpha + \beta ) + {W_2} \times {L_2} \times \cos (\alpha + \beta ) + \\ {W_3}\left(\sqrt {L_4^2 + L_5^2} cos\alpha + \frac{{{L_3}}}{2}sin\beta \right) =\quad\quad\\ {F_{CZ}}\left(\sqrt {L_4^2 + L_5^2} cos\alpha + {L_3} \times \sin \beta \right) - {F_{CX}}({H_2} - {H_1}) \text{。} \\ \end{split} $ | (4) |
由式(3)和式(4)式得出:
| ${F_{CX}} = \left({F_{CZ}} - \frac{{{W_3}}}{2}\right){\rm{tan}}\beta \text{,}$ | (5) |
平衡状态下:
| ${L_0} = \sqrt {L_4^2 + L_5^2 - {{({L_3} - H)}^2}} \text{,}$ | (6) |
软刚臂系统运动偏移距离:
| $X = \sqrt {L_4^2 + L_5^2} \cos \theta + {L_3}\sin \beta - {L_0}\text{。}$ | (7) |
通过上述关系等式,计算出C点的水平回复力为:
| ${F_{CX}} = \frac{{({W_1}{L_1} + {W_2}{L_2})cos(\beta + \theta ) + \frac{{{W_3}}}{2}\sqrt {L_4^2 + L_5^2} \cos \theta }}{{\frac{{\sqrt {L_4^2 + L_5^2} \cos \theta }}{{\tan \beta }} + {L_3}\cos \beta - H}}\text{。}$ | (8) |
系泊系统的刚度为特性曲线切线的斜率值,系统刚度随曲线的变化而变化。当曲线为直线时,其系统刚度如下:
| $K = \frac{{{F_{CX}}}}{X}\text{。}$ | (9) |
本文以ADAMS进行平台与系泊系统的三维建模,并进行一定的简化[7],如图3所示。
|
图 3 ADAMS三维分析模型 Fig. 3 Adams three-dimensional analysis model |
|
|
表 1 软刚臂系统主要构件参数 Tab.1 Main component parameters of soft rigid arm system |
导管架到旋转塔台之间采用固定约束,旋转甲板与管汇甲板添加绕导管架主轴中心线的转动副,软刚臂YOKE与旋转甲板挂钩处添加绕挂钩中心线的转动副,其系泊头同时添加自转的约束,系泊腿下部和上部万向节分别与软刚臂和系泊支架添加相应活动铰接转动副,能实现系泊腿多个方向的运动。通过仿真运动测试,整个系统能实现船体沿x,y,z方向上的多自由度运动。分析过程中,纵向运动以平衡位置靠近导管架为负方向,远离导管架为正方向;由于横向运动具有对称性,方向不影响分析结果。
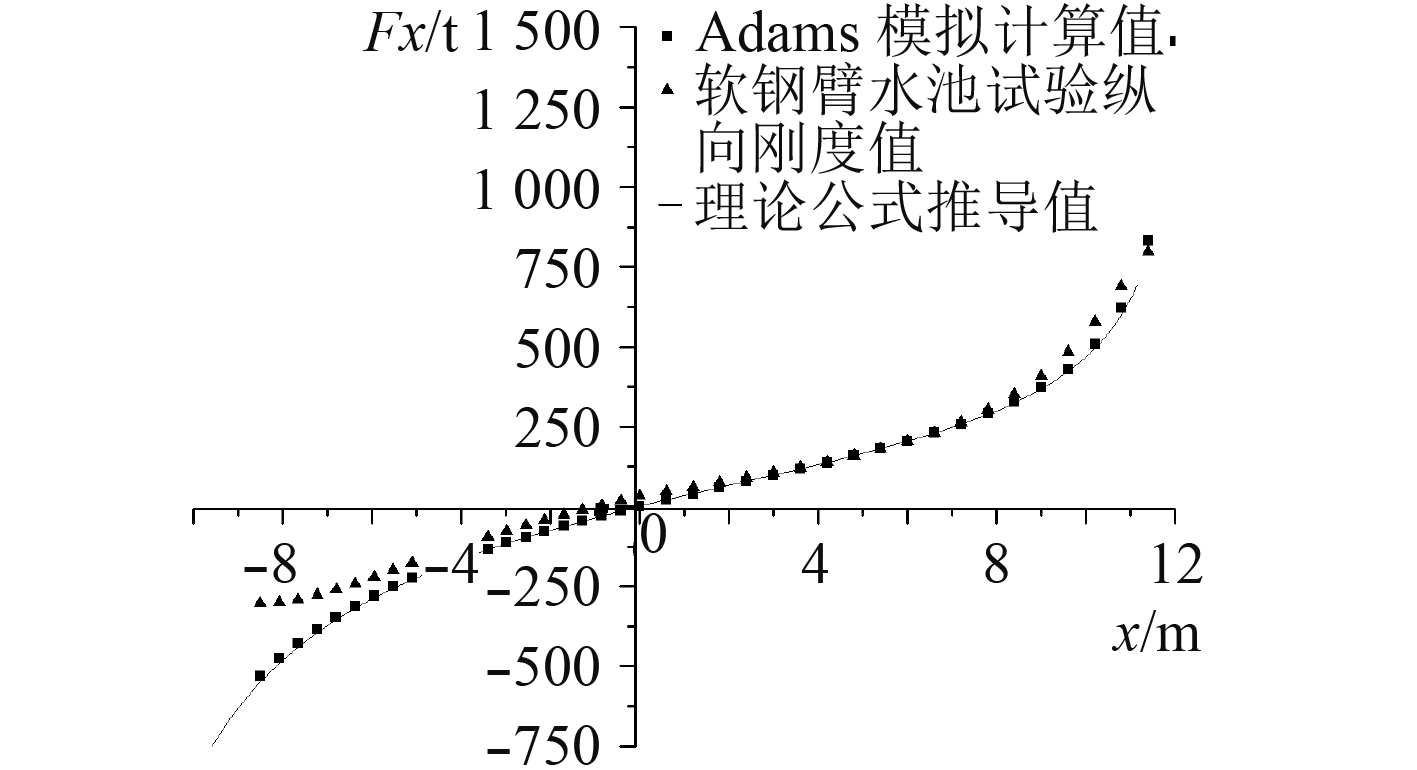
由图4可知,通过对比船体纵向运动,理论公式推导的刚度曲线和试验结果发现,在相同的质点坐标和质心重量下,ADAMS计算结果和理论公式推导结果是一样的,刚度随着平衡位置位移的增大,呈现增加趋势,在远离和靠近导管架8 m以上,刚度出现陡增,这是因为软刚臂分别处于水平拉直和竖向下垂的2种极端状态。这2种结果和试验结果存在一定的偏差,当船体靠近导管架6 m以上和远离10 m以上时,计算结果值大于试验值,在其他区域,两者几乎保持一致,这主要是由于水池试验模型是按比例缩放,质心和理论会存在一定偏差,随着纵向运动位移增大,这种偏差逐渐变得明显。
|
图 4 船体纵向运动刚度曲线 Fig. 4 Longitudinal motion stiffness curve of hull |
图5为ADAMS模拟船体纵向运动时,旋转塔台所受FZ(如图2中a点FAZ方向)方向力和系泊腿张力,由于2条系泊腿在船体纵向运动时,呈平行运动,关节角度变化一致,受力完全一样,从靠近导管架到平衡位置,张力从大变小;从平衡位置到远离导管架,张力从小变大,方向均为正值。在FZ方向上,靠近导管架,旋转塔台受拉,方向向上;在平衡位置受压,方向向下;远离导管架,塔台受拉,方向向上。
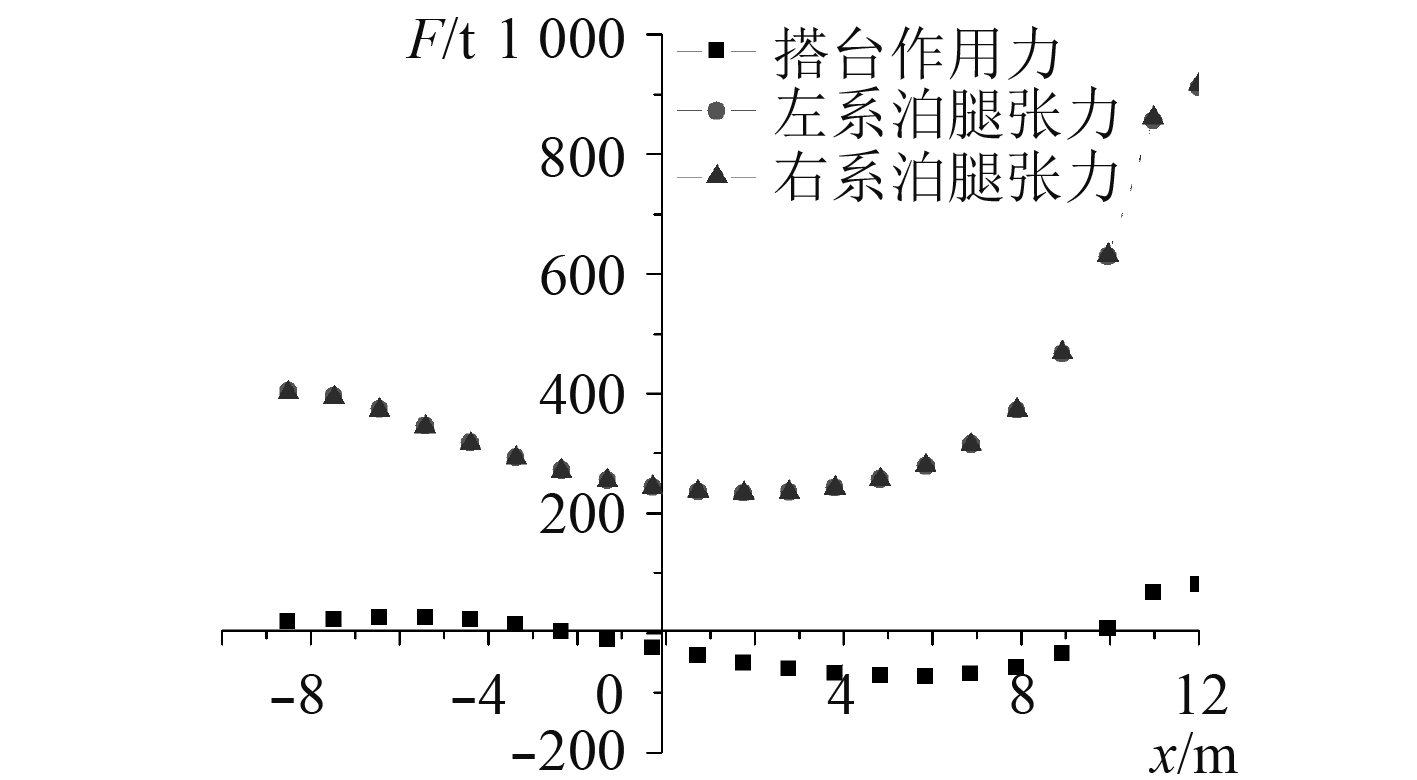
|
图 5 船体纵向运动时塔台作用力及系泊腿张力 Fig. 5 Tower force and mooring leg tension during longitudinal movement of the hull |
图6为船体横向运动时,系泊腿的恢复力和软刚臂系统的刚度曲线,由于软刚臂系统在横向运动时,依靠2条系泊腿来提供恢复力,所以软刚臂系统的刚度为2条系泊腿恢复力之和。软刚臂系统的刚度随着横向运动位移的增加而增加,变化趋势和纵向运动时一致。相同位移下,其幅值小于纵向时的刚度,横向运动10 m时,其刚度值为81.17 t的力,远小于纵向运动10 m时的刚度。另外2条系泊腿的刚度也不相同,沿正方向运动时,左系泊腿的恢复力接近为右系泊腿恢复力的2倍,变化趋势是一致的。
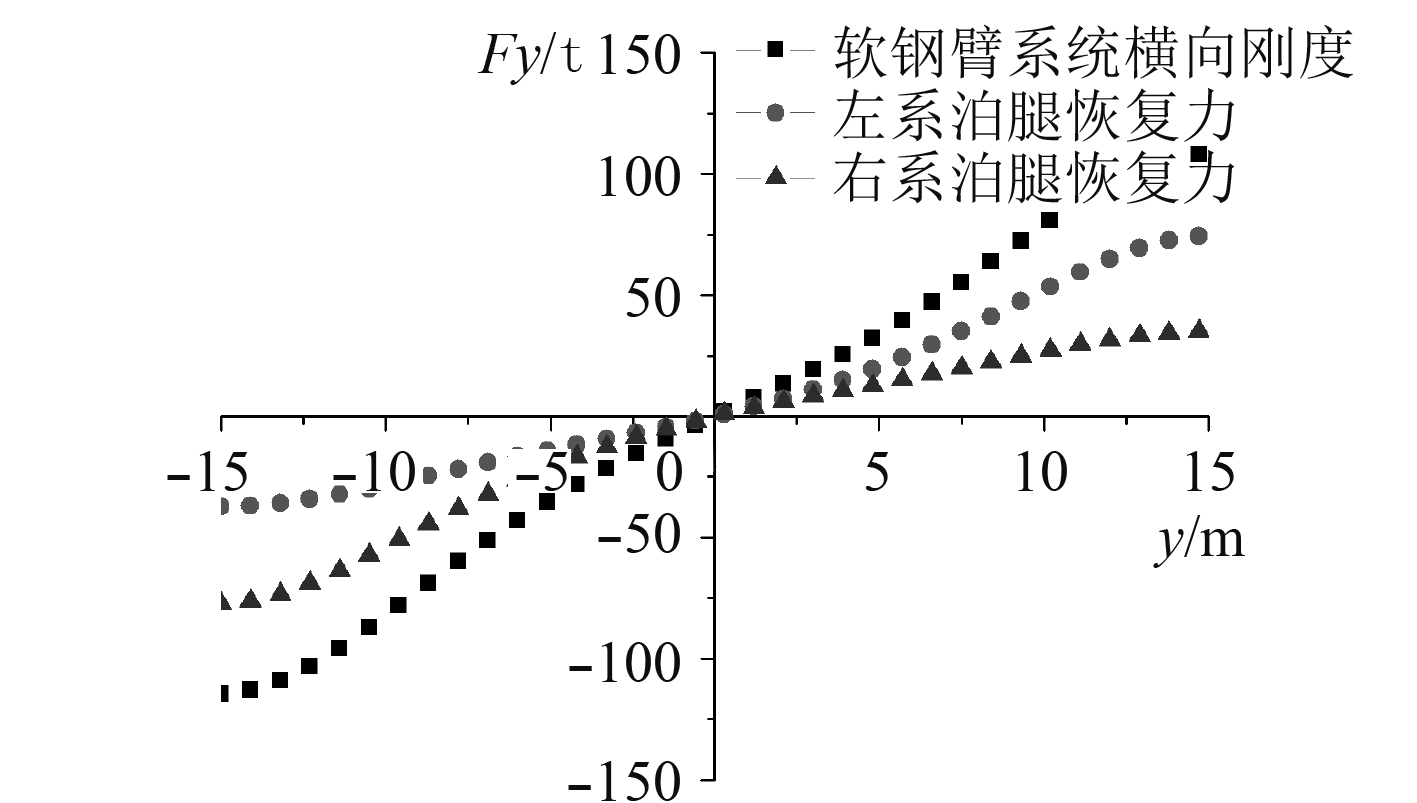
|
图 6 船体横向运动刚度曲线 Fig. 6 Hull lateral motion stiffness curve |
图7为船体横向运动时,旋转塔台承受的作用力和系泊腿的张力,从图中可以看出,曲线在平衡位置两端呈现对称分布。从横向运动正方向上看,左右2条系泊腿的张力并不相同,主要由于随着船体运动位移的增加,2条系泊腿的姿态也不相同,左系泊腿随着软刚臂自转,出现向上翘起,张力大于右系泊腿,反向运动时,右系泊腿张力大于左系泊腿。旋转塔台在FZ方向上始终是负值,方向向下,变化比较平稳,这是由于横向运动时,软刚臂一直处于下垂状态,不同于纵向运动时被拉直和下垂向上顶的极端状态。
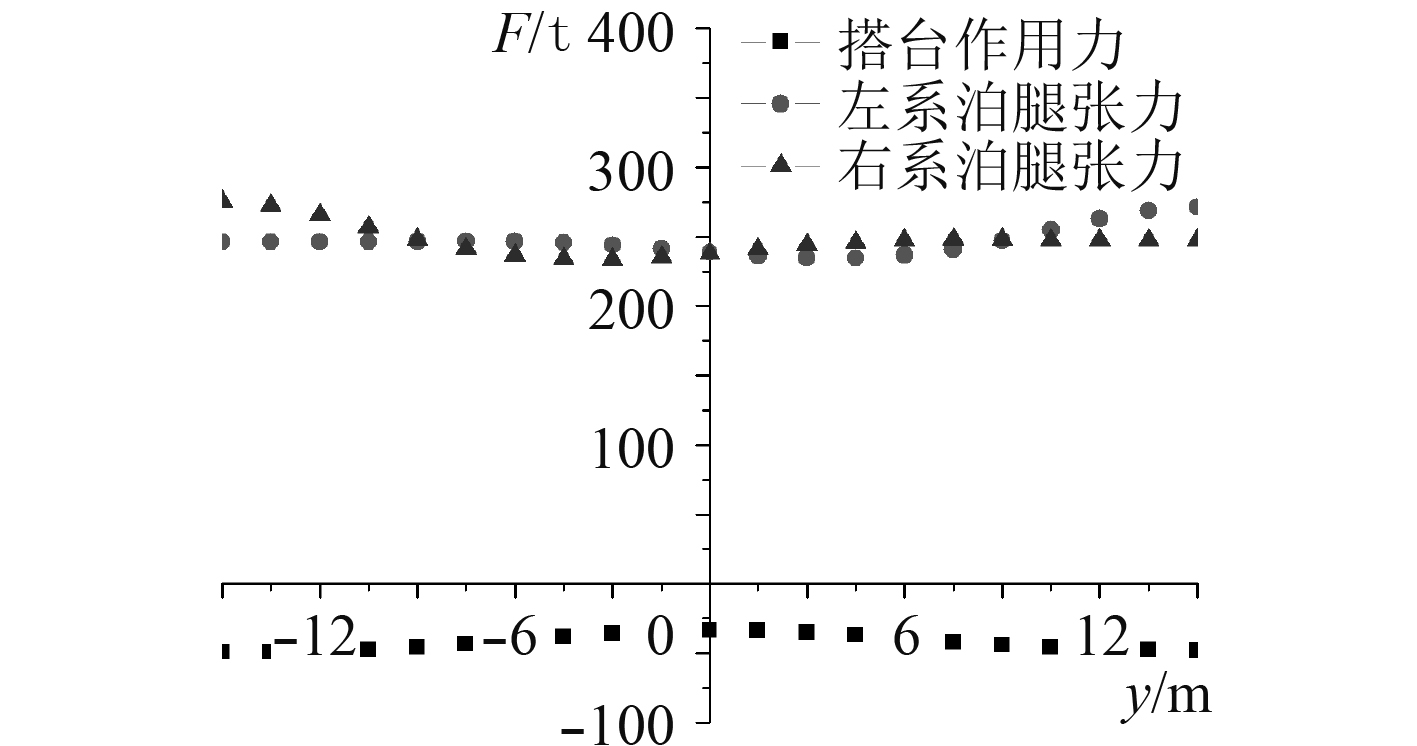
|
图 7 船体横向运动时塔台作用力及系泊腿张力 Fig. 7 Tower force and mooring leg tension when the hull is moving laterally |
图8为船体横向运动时,软刚臂系统绕导管架中心轴线的转角变化,系泊头处横摇角变化以及纵摇角变化(船体横摇和纵摇产生的角度,在船体横向平动时,这2个角度也发生相应变化)。可以看出,船体横向位移增加,软刚臂自转角度较大,增大至22.3°后趋于稳定,说明船体运动接近极限位置,纵摇角度值较小,最大为1.5°,横摇角度数值略微大于纵摇角度。
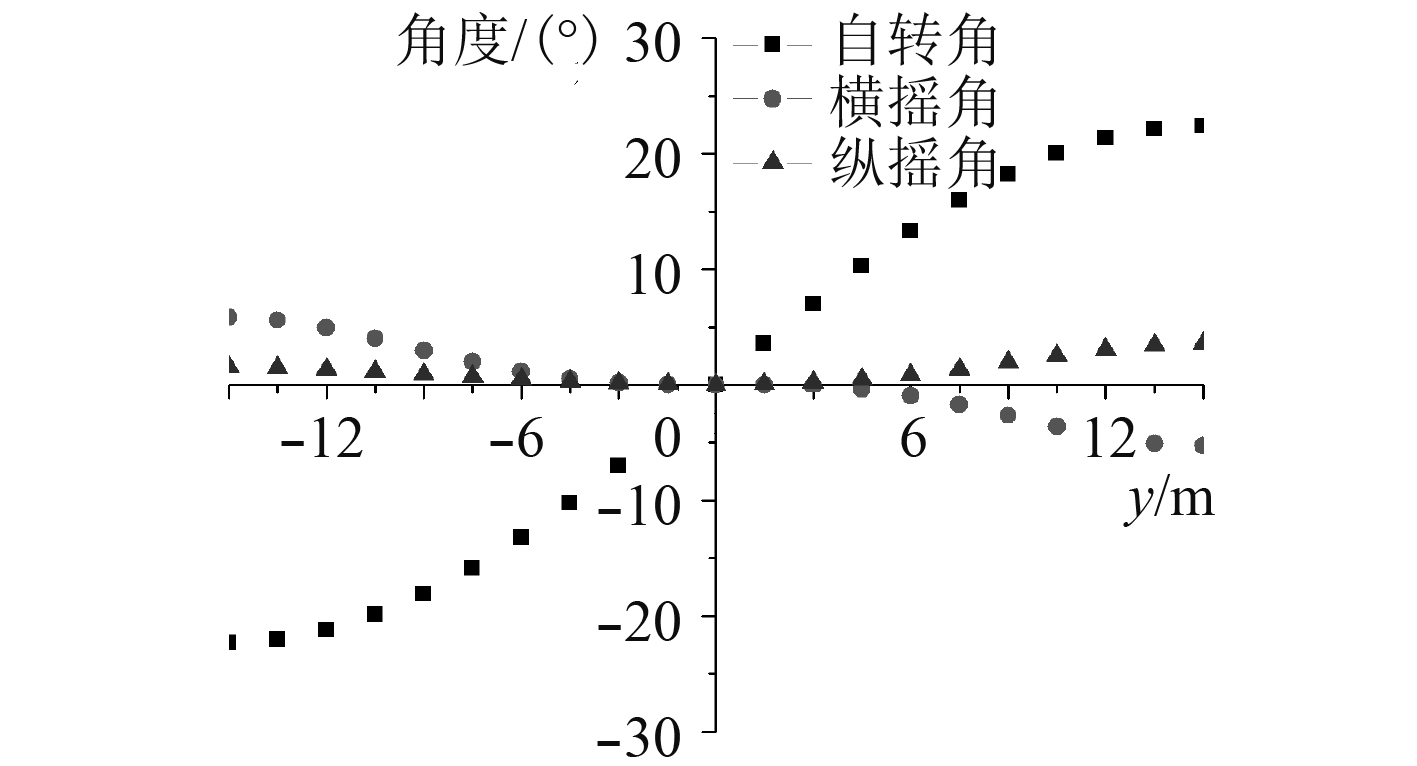
|
图 8 船体横向运动时软刚臂角度变化 Fig. 8 Angle change of soft rigid arm when the hull moves laterally |
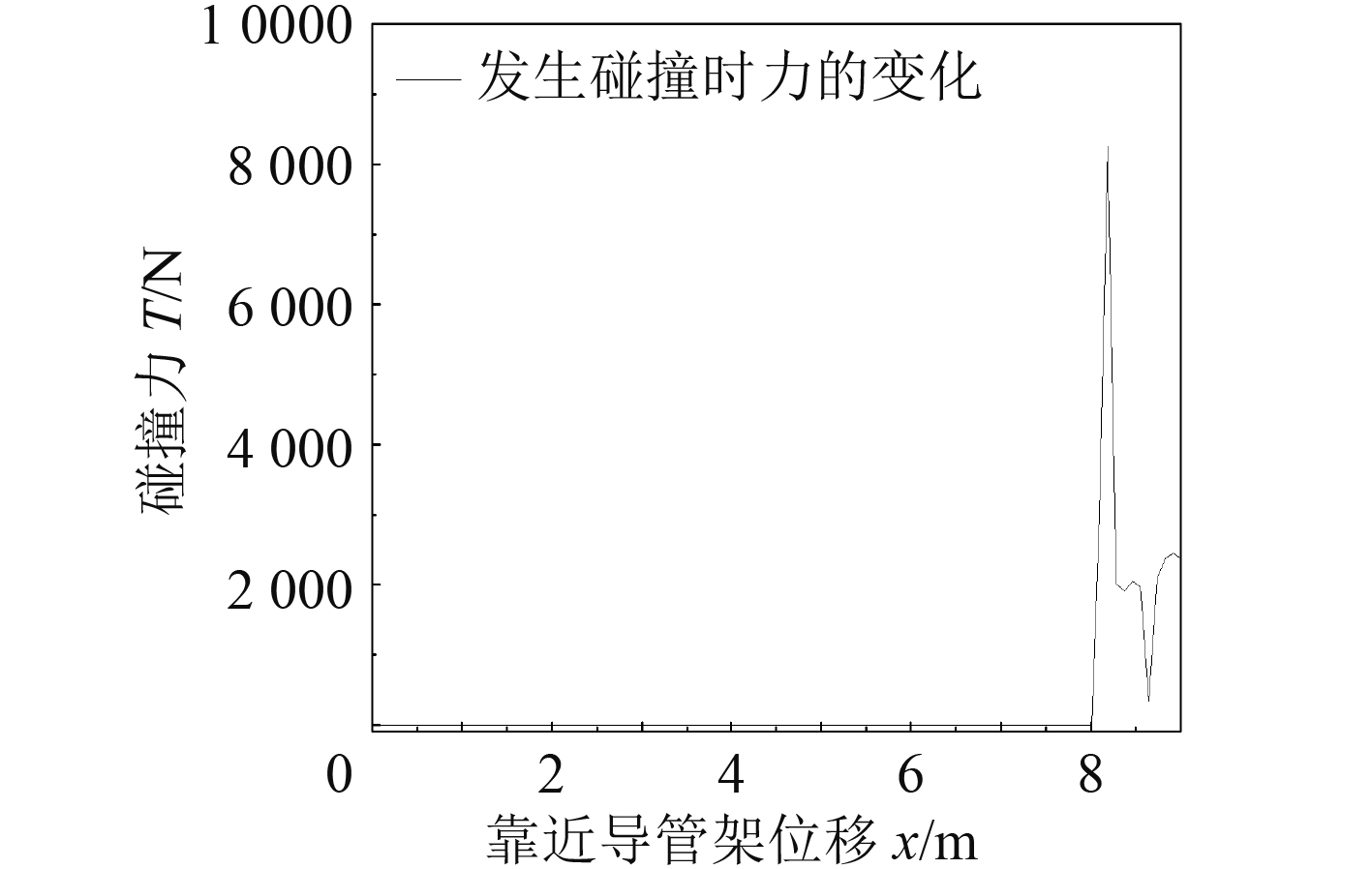
由图9可知,当船体靠近导管架时,随着距离的靠近,软刚臂与船体很容易发生碰撞,针对单点系统模型进行分析。
|
图 9 船体纵向运动靠近导管架时与软刚臂碰撞分析 Fig. 9 Collision analysis between the soft rigid arm and the jacket when the longitudinal movement of the hull |
船体纵向运动靠近距离为8.19 m时,软刚臂与船首甲板会发生碰撞[8,9],其碰撞力达到8 251 N,表2为接触碰撞参数设置。若船体存在一定的冲击速度,碰撞力也会相应变大;当碰撞造成材料塑性变形或者破坏时,其碰撞力会逐渐变小,逐渐趋于稳定。碰撞分析有利于前期设计的优化,通过模型参数的调整或者有效的措施来避免发生碰撞破坏。
|
|
表 2 接触碰撞参数设置 Tab.2 Contact collision parameter settings |
本文采用ADAMS对单点系泊软刚臂系统进行多自由度运动分析,船体纵向运动时,通过软刚臂系统刚度理论推导和水池试验值,验证软件计算模型和计算结果的准确性。进一步分析讨论船体横向运动,软刚臂系统的刚度、受力以及碰撞等运动分析,得出以下结论:
1)船体横向运动时,软刚臂系统的刚度呈递增的趋势,和纵向运动时一致,当横向运动Y=10 m时,FY=81.17 t,数值上小于相同位移的纵向运动刚度。2条系泊腿的恢复力也不相同,沿正方向运动时,左系泊腿的恢复力接近为右系泊腿恢复力的2倍。
2)横向运动系泊腿张力和塔台作用力与纵向运动时也不相同,主要由于随着船体正向运动位移的增加,2条系泊腿的姿态逐渐不相同,左系泊腿随着软刚臂自转,出现向上翘起,张力大于右系泊腿。
3)当船体横向运动时,软刚臂系统绕导管架中心轴线的转角变化、横摇角和纵摇角度也发生一定的变化,软刚臂自转角度变大,增大至22.3°后趋于稳定,说明船体运动接近极限位置,纵摇角度值较小,最大为1.5°。
4)通过碰撞分析发现,当船体靠近导管架8.19 m时,软刚臂与船首甲板发生碰撞,其碰撞力达到8 251 N,当碰撞造成材料塑性变形或者破坏时,其碰撞力会逐渐变小,这有利于单点系泊系统前期设计的优化。
| [1] |
周守为, 曾恒一, 范模. 我国浮式生产储油装置的研制与开发[J]. 中国海上油气, 2006, 18(2): 73-78. DOI:10.3969/j.issn.1673-1506.2006.02.001 |
| [2] |
XIE Y H, XU J S, LI R P. Wave- induced loads on very large FPSOs at restricted water depth[J]. China Ocean Engineering, 2005, 19(2): 215-224. |
| [3] |
张宝雷. FPSO水下软刚臂单点系泊系统刚度特性分析[J]. 资源节约与环保, 2012, 14(5): 113-116. DOI:10.3969/j.issn.1673-2251.2012.05.020 |
| [4] |
肖龙飞, 杨立军. FPSO水动力研究与进展[J]. 海洋工程, 2006, 24(4): 116-123. DOI:10.3969/j.issn.1005-9865.2006.04.021 |
| [5] |
肖龙飞, 杨立军, 杨建民. 软刚臂系泊系统水平恢复力特性数值预报[J]. 海洋工程, 2008, 26(1): 1-5. DOI:10.3969/j.issn.1005-9865.2008.01.001 |
| [6] |
苏方磊.水上软刚臂系泊FPSO水动力响应特性试验研究[D].大连: 大连理工大学, 2015.
|
| [7] |
刘银虎, 繆炳祺. 多体动力学仿真软件ADAMS理论[J]. 电子与封装, 2005, 5(4): 1681-1070. |
| [8] |
张映雪, 姚文莉. 基于连续接触力方法的接触碰撞问题研究[J]. 力学研究, 2017, 6(1): 17-23. |
| [9] |
安雪斌, 潘尚峰. 多体系统动力学仿真中的接触碰撞模型分析[J]. 计算机仿真, 2008, 25(10): 92-98. |
 2019, Vol. 41
2019, Vol. 41
