随着核能事业的发展,核动力的应用越来越广泛。船舶核动力装置是以原子核裂变能作为产生推进动力的能源。核裂变是重核分裂为2个或更多较轻原子核,同时放出自由中子和大量能量的过程。裂变产物会持续放出β粒子和γ射线,直到最后变成稳定的同位素。为了阻挡和减弱核反应堆释放的对工作人员和设备造成危害的中子和γ射线等,在反应堆外设置了一次屏蔽结构和生物屏蔽结构。围绕反应堆压力容器的屏蔽为一次屏蔽,设置在反应堆安全壳外的屏蔽体称为生物屏蔽。船用核动力装置生物屏蔽是核动力装置在舰船上应用的安全保障[1]。
目前,生物屏蔽材料通舱采用铅板作为主要的γ射线屏蔽材料,采用聚乙烯、含硼聚乙烯或铅硼聚乙烯[2]等聚乙烯基材料作为主要的中子屏蔽材料,在靠近反应堆方向通常采用铅板、聚乙烯基屏蔽材料通过不同形式组合的安装方式。当反应堆失水事故(LOCA,设计基准事故之一)时,冷却剂泄漏造成反应堆侧温度升高,可达190 ℃以上。纯铅的熔点为327 ℃,通常能够满足堆事故工况时的使用需求;但聚乙烯基的中子屏蔽材料维卡软化点在100 ℃左右,尽管可能有设备、结构材料以及γ射线屏蔽材料铅板等的隔离,聚乙烯基中子屏蔽材料承受的温度虽不会达到最高的温度,但也可能高于聚乙烯基材料的软化点。若该高温环境持续较长时间,聚乙烯基材料将发生软化,因变形而产生空隙,降低对中子的屏蔽效果,甚至可能导致对中子屏蔽局部失效,具有一定辐射安全隐患。总而言之,生物屏蔽结构及屏蔽材料在基准事故工况下耐高温技术研究将是需要关注的课题之一。
1 计算模型及边界条件 1.1 计算模型本计算模型基于现有生物屏蔽安装结构的基本布置设计,包含台架部分、铅板、含硼聚乙烯板、屏蔽安装辅材(角钢、钢盖板等)等几部分组成。其中,屏蔽材料安装的部位整体分为上、下、左、右、中共5个区域,边缘区域因热传导的条件与实物不一致,故而最终结果仅取中间区域方格的屏蔽材料为准。

|
图 1 计算模型结构示意图 Fig. 1 Calculation model structure |

|
图 2 算例热传导示意图 Fig. 2 Heat conduction diagram of calculation example |
热量的传递机理分为导热、对流换热、热辐射3种[3],在本算例中,包含了导热和对流换热2种方式。由图1和图2可知,热端通过与材料1的对流换热将热量导出,材料1、材料2、材料3、材料4、材料5、材料1之间为导热,人员活动区的材料1为对流换热。为使计算与实际屏蔽结构和屏蔽材料一致,在此算例中,材料1为钢材、材料2为铅板、材料3为含硼聚乙烯、材料4为空气(考虑最苛刻的情况,材料3填满空腔,此处可忽略)。
1.2 计算边界条件传热又分为稳定传热和不稳定传热,实际的LOCA工况,温度场随时间变化。
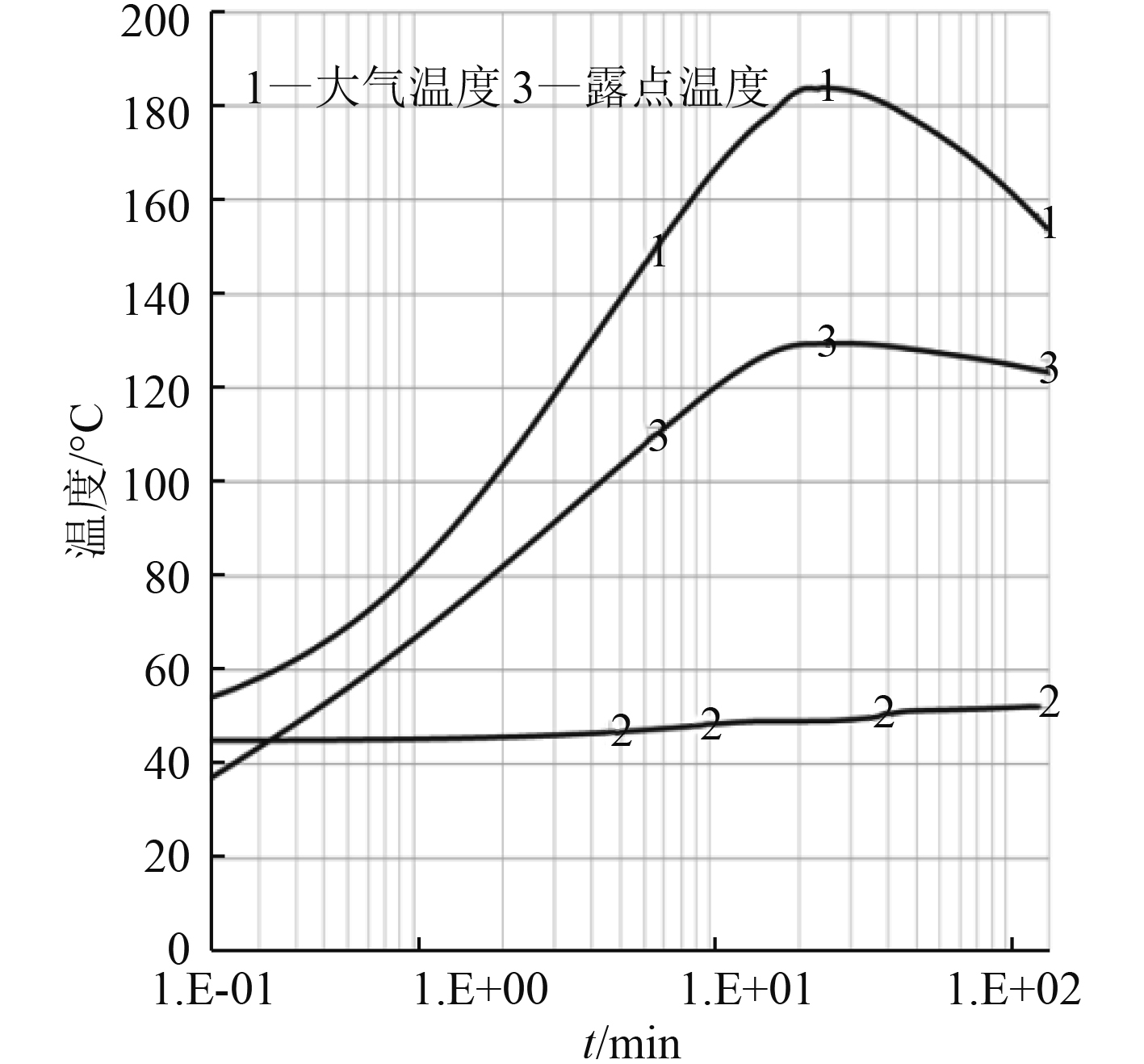
|
图 3 核电站某堆型设计基准工况(LOCA)环境条件露点温度及大气温度变化曲线 Fig. 3 Dew point temperature and atmospheric temperature change curve under environmental conditions of a reactor type design reference condition (LOCA) of nuclear power plant |
为确保屏蔽结构和屏蔽材料的有效性,并方便后续进行试验验证(试验模拟LOCA事故曲线的成本,要远高于材料样机生产的成本),在计算时,采用最苛刻的工况计算,亦即,将算例假定为稳定传热,采用最高温度和最长时间进行模拟。
计算本文所述模型的热传导问题,实际上材料的物性参数是随温度变化的,热传导方程是非线性的偏微分方程[4]。
一般来说,材料的导热系数是随温度变化的线性关系式[5]:
| $ \lambda {\rm{ = }}a + b\frac{{{t}_1}{\rm{ + }}{t_2}}{2}\text{。} $ | (1) |
式中:a为0 ℃时材料的导热系数,W/m·K;b为温度系数;t1,t2为材料的高温面和低温面温度。
实际计算时,为保留一定的计算余量,采用较苛刻的导热系数,查资料得,计算所用的材料参数如表1所示。
|
|
表 1 算例材料的基本参数 Tab.1 Basic parameters of calculation example materials |
通过以上分析及近似的参数化处理,将此算例简化为一个典型的多层平壁稳定传热的问题。
2 多层平壁热传导计算数学方程的建立多层平壁导热的导热量与壁两侧表面的温度差成正比;与壁的厚度成反比,通过经典公式推导,得到本算例数学表达式为:
| $ {Q} = \frac{1}{{\frac{{{{\rm{\delta }}_1}}}{{{{\rm{\lambda }}_1}}} + \frac{{{{\rm{\delta }}_2}}}{{{{\rm{\lambda }}_2}}} + \cdots \frac{{{{\rm{\delta }}_{\rm{n}}}}}{{{{\rm{\lambda }}_{\rm{n}}}}}}}\Delta {\rm{t}}\cdot{\rm{A}} = \frac{1}{{\mathop \sum \nolimits_{{\rm{i}} = 1}^{\rm{n}} {{\rm{R}}_{\rm{i}}}}}\Delta {\rm{t}}\cdot{\rm{A}}\text{。} $ | (2) |
式中:Q为单位时间内的平壁导热量,W;q为平壁导热的的热流密度,W/m2;λ为平壁材料的导热系数,W/m·K;λn为第n层屏蔽的导热系数,W/m·K;A为壁面积,m2;δ为壁厚,m;δn为第n层屏蔽的导热系数,W/m·K;∆t为壁两侧表面的温度差;R为单层平壁的导热阻,m2·K/W;Ri为第i层屏蔽的导热阻,m2·K/W。
另外,根据图2可知,在本算例中,存在肋壁传热的现象,因此在式(1)中的
| $ {{\bar R}} = \frac{{{{{A}}_{\rm{I}}} + {{{A}}_{{\rm{II}}}} + {{{A}}_{{\rm{III}}}} + \cdots }}{{\frac{{{{{A}}_{\rm{I}}}}}{{{{{R}}_{\rm{I}}}}} + \frac{{{{{A}}_{{\rm{II}}}}}}{{{{{R}}_{{\rm{II}}}}}} + \frac{{{{{A}}_{{\rm{III}}}}}}{{{{{R}}_{{\rm{III}}}}}} + \cdots }}\text{。} $ | (5) |
式中:RⅠ,RⅡ,RⅢ···为第Ⅰ,Ⅱ,Ⅲ···部分平壁导热阻(此处即为式(2)中的
根据图2可知,在此算例中有导热和对流换热2种传热现象。因此,需要根据算例的情况对计算公式进行最后的修正。对流换热的计算公式与导热公式类似,只不过对流换热的热阻与对流换热系数有关,在此可推导出此算例稳定传热算例的总计算公式:
| $ {{Q}} = \frac{1}{{{{{R}}_0}}}\left( {{{{t}}_{{i}}} - {{{t}}_0}} \right){{A}} = \frac{1}{{\frac{1}{{{{{\alpha }}_{{i}}}}} + {{\bar R}} + \frac{1}{{{{{\alpha }}_{{i}}}}}}}\left( {{{{t}}_{{i}}} - {{{t}}_0}} \right){{A}}\text{,} $ | (3) |
或
| $ {{q}} = \frac{1}{{{{{R}}_0}}}\left( {{{{t}}_{{i}}} - {{{t}}_0}} \right) = \frac{1}{{\frac{1}{{{{{\alpha }}_{{i}}}}} + {{\bar R}} + \frac{1}{{{{{\alpha }}_{{i}}}}}}}\left( {{{{t}}_{{i}}} - {{{t}}_0}} \right)\text{。} $ | (4) |
式中:αi为平壁内表面的对流换热系数,W/m2·K;α0为平壁外表面的对流换热系数,W/m2·K;ti为平壁内侧的流体温度,K;t0为平壁外侧的流体温度,K;R0为平壁稳定传热的总热阻。
通以上推导公式,计算出Q或者q后,就可以计算出算例中屏蔽结构和屏蔽材料任意一点的稳态温度。
3 使用有限元软件模拟瞬态和稳态温度场通过模型导热情况分析,计算时对算例选用solid185和shell两种单元建模,其中格子板钢结构和T型材采用shell单元,壁板、屏蔽材料采用solid185单元。建立模型如图4所示。

|
图 4 Ansys有限元计算模型 Fig. 4 ANSYS finite element calculation model |
稳态计算温度:热端为LOCA工况下的最高温度210 ℃(选取一定的计算裕量,下同),冷端人员活动区选用27 ℃,计算结果如图5所示。
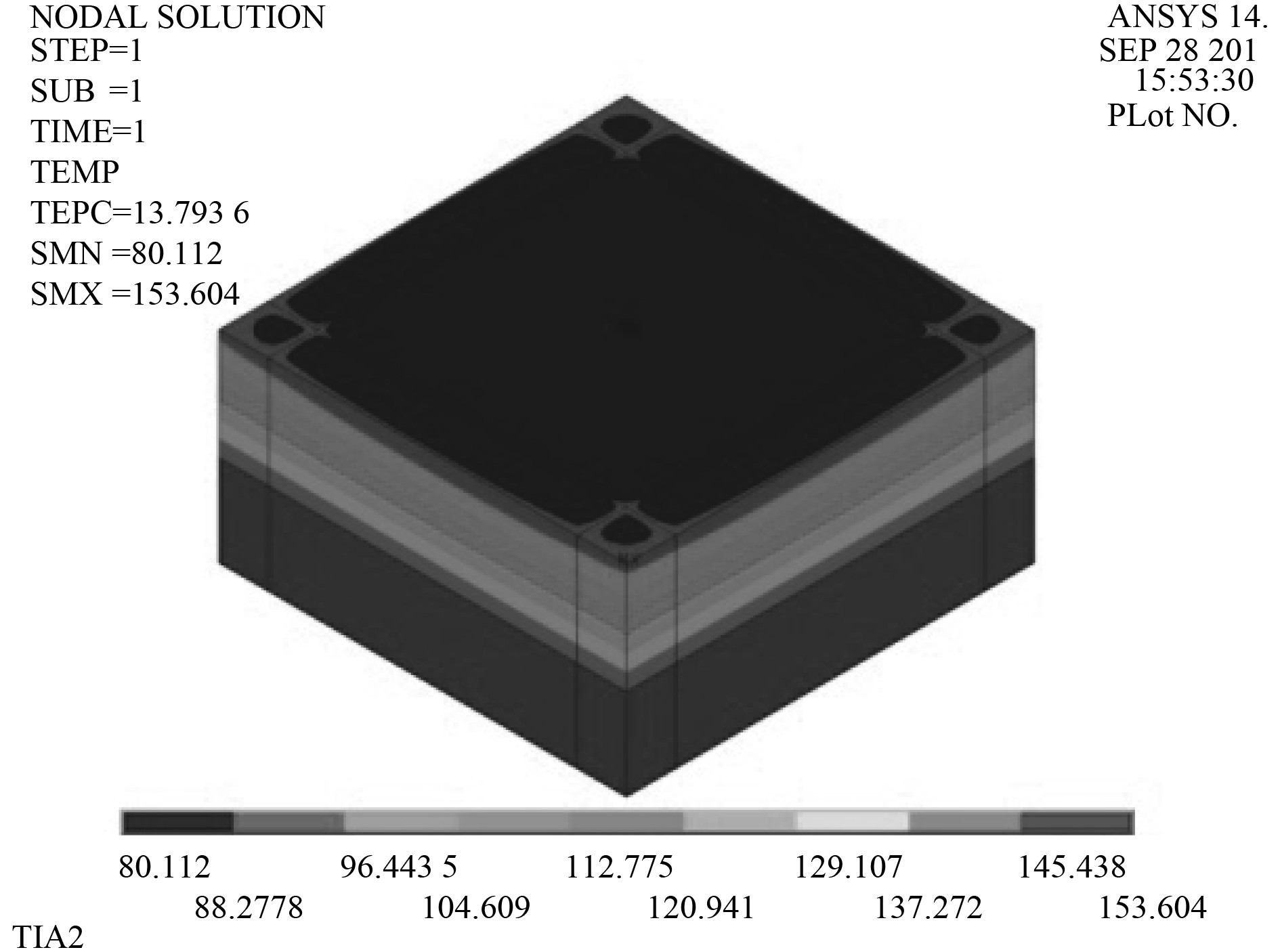
|
图 5 本算例的稳态计算结果 Fig. 5 Steady state calculation results |
选用一个典型的截面分析计算结果如图6所示。

|
图 6 X-Y平面计算结果 Fig. 6 Calculation results of X-Y plane |
定义10个典型坐标节点与其对应的稳态温度值如表2所示。
|
|
表 2 节点坐标及稳态温度 Tab.2 Node coordinates and steady state temperature |
计算结果表明:
1)铅板内部温差较小,第1层铅板的温度为148.67 ℃,最后1层铅板的温度为147.41 ℃;
2)含硼聚乙烯板的隔热效果较好,节点3为147.41 ℃,为第1层含硼聚乙烯板的温度;节点4为114.05 ℃,是中间1层含硼聚乙烯板的温度;节点5为80.11 ℃,是最后1层含硼聚乙烯板的温度;
3)最低温度80.112 °C,已经达到聚乙烯基材料的热变形温度,部分含硼聚乙烯板温度区域超过110 ℃,超过聚乙烯基材料的维卡软化点,因此现有屏蔽结构确实存在风险。
3.2 瞬态计算结果210 ℃的温度采用阶跃加载(包络LOCA曲线),计算时间9 000 s,温度云图如图7所示。

|
图 7 9 000 S的温度云图 Fig. 7 Temperature nephogram of 9 000 s |
计算典型节点的温度随时间的变化(节点坐标值见表2)。
计算结果表明:
1)9 000 s后,第1层铅板铅板处最高温度(node2)为44.6 ℃,第1层含硼聚乙烯板(node3)最高温度为42.27 ℃,温度值均较小;
2)图8表明,温度的传导并非线性关系,在温差较大时,温度传导较快,因此node1/node2的温度在开始的2000 s上升较快,后面渐渐平缓,而温度从node1/node2区域继续往后传递,后面节点的温升呈现大致的线性关系。
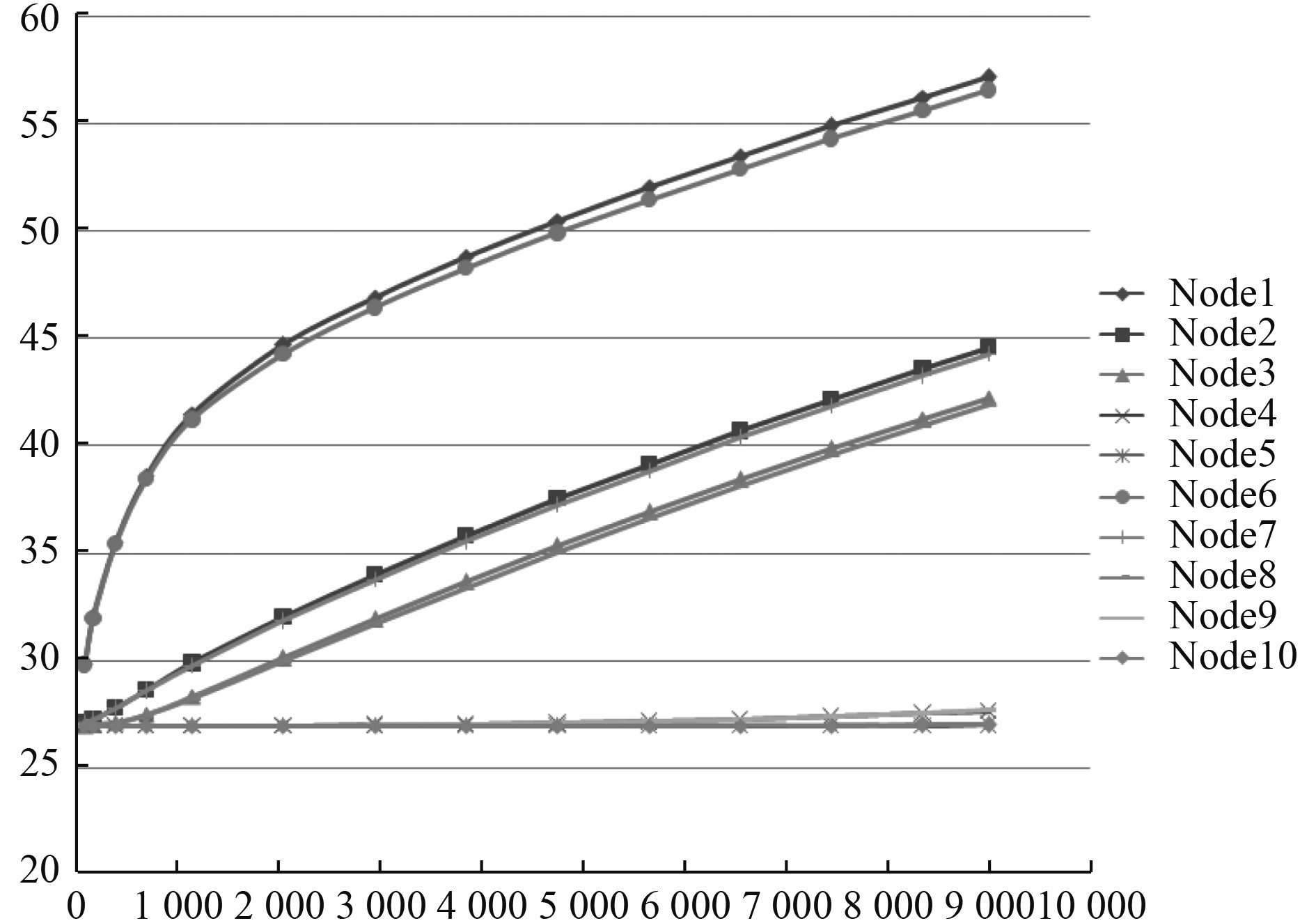
|
图 8 典型坐标温度随时间变化的曲线 Fig. 8 Typical coordinate temperature versus time curve |
3)瞬态计算结果表明,含硼聚乙烯板区域的温度并未达到聚乙烯基类材料的维卡软化点。
4 结 语本文通过对典型生物屏蔽结构和屏蔽材料的耐高温性能分析,提出了对该模型进行耐高温性能研究的要求。之后建立了典型生物屏蔽结构和屏蔽材料的三维数据模型,从理论上分析了如何建立该模型的热传导理论方程,并对模型中的对流传热、导热、组合材料层导热阻等因素综合考虑,最终导出模型热传导的计算公式。通过Ansys软件对该模型进行稳态和瞬态的热传导数值模拟,选取典型截面和典型节点进行温度变化的趋势分析,得出以下结论:
1)稳态计算结果表明,现有典型生物屏蔽结构无法满足LOCA工况下耐高温要求,铅屏蔽层的热阻小,无法起到隔热效果,故应考虑从结构上进行改进。
2)瞬态计算结果表明,9 000 s内典型生物屏蔽结构不会破坏。因此,此时间反应堆安全系统的响应时间,以控制工作区域人员所受的剂量限值。
3)聚乙烯基类的屏蔽材料受基材所限,耐高温性能无法进一步加强,后续工作可以考虑使用环氧树脂、铝合金等基材进行耐高温屏蔽材料的研究。
对典型生物屏蔽结构和屏蔽材料的耐高温性能分析研究还远远没有结束。本文所用的理论计算和数值模拟方法,可以推广到更复杂的屏蔽结构模型更多层的屏蔽材料搭配中。同时,本文的计算结果和计算方法也可为后续样机生产和试验模拟提供数据支持。
| [1] |
李春槐. 反应堆主回路设备间辐射屏蔽设计方法述评[J]. 核动力工程, 2003, 24(5): 846-489. |
| [2] |
李晓玲. 铅硼聚乙烯复合屏蔽材料成分配比优化设计[J]. 舰船科学技术, 2015, 37(12): 148-154. DOI:10.3404/j.issn.1672-7649.2015.12.031 |
| [3] |
扬世铭, 传热学[M]. 北京: 高等教育出版社, 1987.
|
| [4] |
钱炜祺. 非线性热传导逆问题的表面热流辨识方法[J]. 空气动力学学报, 2012, 30(2): 145-150. DOI:10.3969/j.issn.0258-1825.2012.02.002 |
| [5] |
孙庆利. Excel在稳态导热计算中的应用[J]. 山东陶瓷, 2010, 33(5): 30-31. DOI:10.3969/j.issn.1005-0639.2010.05.008 |
 2019, Vol. 41
2019, Vol. 41
