2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics (HUST), Wuhan 430074, China
随着人类经济活动不断向海洋拓展,浮式核电站作为一种高效的海上能源解决方案,越来越受到各个国家的重视。它可以灵活的布置在不同的海域,甚至是北极地区,为海上设施和海岸城市提供稳定的电力资源。此外,还可以满足供热、海水淡化等多种需求[1]。
目前,最成熟的浮式核电站是俄罗斯的“罗蒙诺索夫”号,它是在1艘大型的无动力驳船上搭载了2个“KLT-40”型号的核反应堆[2]。美国的麻省理工设计并开发了一款新型的近海圆筒式浮式核电站,它结合了先进的轻水反应堆和浮动平台,结构类似于海上油气设备[3]。韩国和法国分别提出了将浮式核电站沉入水底的安全设计的概念[4]。
浮式核电站的安全性是其结构设计中的核心因素。因为存在核反应堆舱,浮式核电站中心区域的温度远高于以运输人员物资为目的的传统船舶。因此,在堆舱安全壳舱段的设计阶段,需要进行温度场和温度应力的计算分析。本文基于封闭无源空腔的热流量守恒,计算出舱段内各个腔室的空气温度,并通过有限元仿真,得到舱段的温度场和温度应力分布。
1 研究对象 1.1 几何模型俄罗斯的“罗蒙诺索夫”号是1艘典型的浮式核电站,其主体为1艘无动力的大型驳船。长140 m,宽30 m,最大吃水为5.6 m,最大排水量21 500 t[1]。“罗蒙诺索夫”号搭载有2个“KLT-40S”型核反应堆,核反应堆被放置于长5.1 m,宽4 m,高7.5 m的堆舱安全壳中。2个堆舱安全壳被宽1.3 m的纵向箱形构件分隔开,舱室结构沿中纵剖面对称[5]。“罗蒙诺索夫”号的布置示意图如图1所示[1]。
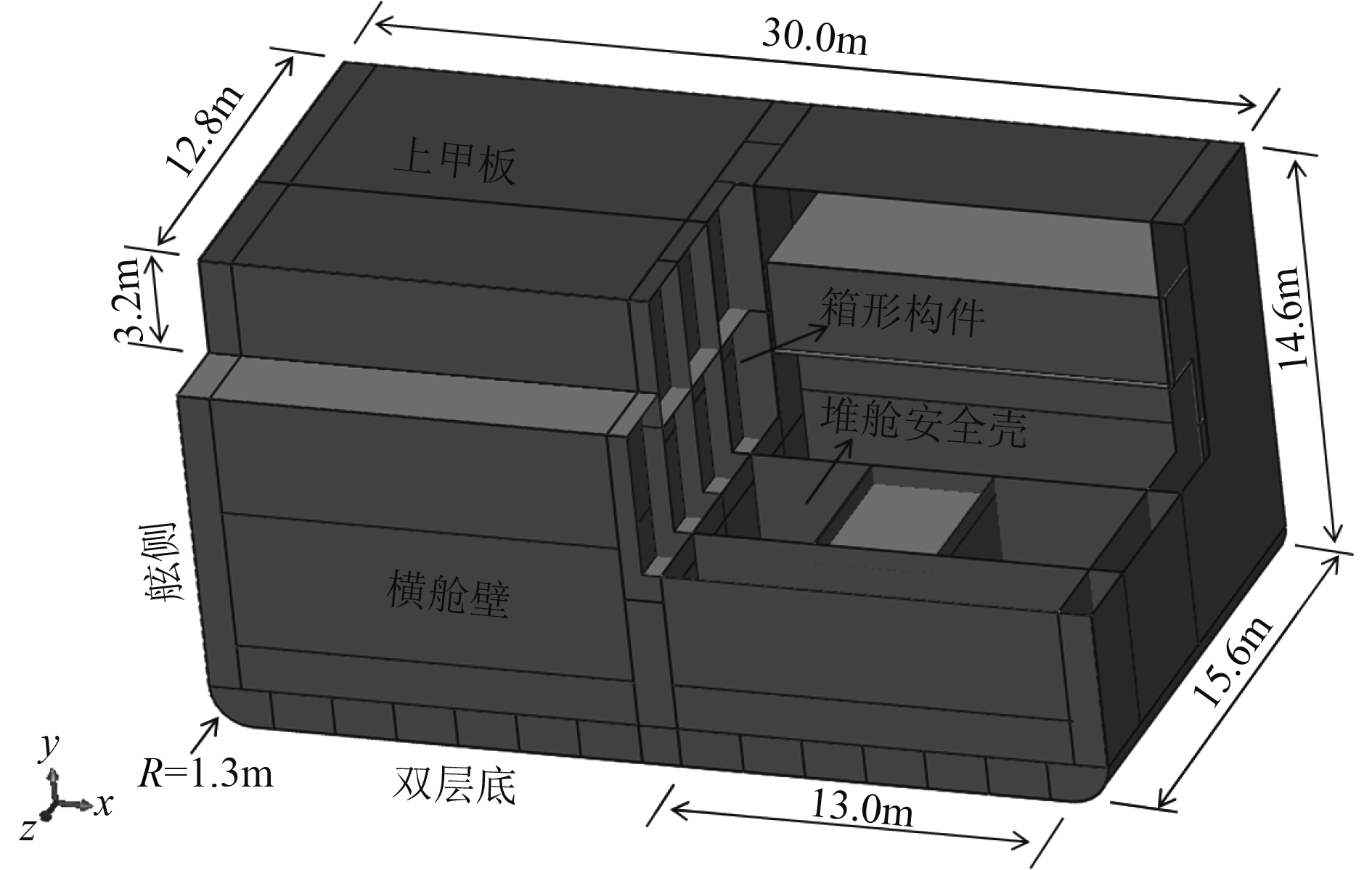
参照“罗蒙诺索夫”号的布置示意图和船体结构的相关信息。本文设计一个浮式核电站的堆舱安全壳舱段。因为舱段结构沿中纵剖面对称,因此在显示其几何模型时,将其左舷一部分剖开以方便显示内部结构,如图2所示。舱段的主要结构尺寸已在图中标出。
|
图 2 堆舱安全壳舱段几何模型图 Fig. 2 Geometric model of nuclear compartment tank |
为满足核反应堆舱的安全性,堆舱安全壳舱段钢板的材料不能采用传统的船舶钢材,而是高强度钢。本文采用美国军舰所采用的HY型高强度钢。其中堆舱安全壳结构采用HY-100钢,其余船体结构采用HY-80钢。2种钢材的材料属性如表 1所示[6]。
|
|
表 1 HY-80和HY-100型钢的材料属性 Tab.1 The material properties of HY-80, HY-100 steel |
本文采用Abaqus有限元分析软件,根据顺序耦合法,计算堆舱安全壳舱段的温度场和温度应力分布。因此,建立的舱段有限元模型包括传热模型和力学模型。
在传热模型中,钢板采用4节点传热单元(DS4),加强筋采用2节点传热单元(DC1D2)。在力学模型中,钢板采用4节点壳单元(S4),加强筋采用2节点梁单元(B31)。2个有限元模型的单元类型不同,但网格划分完全相同。堆舱安全壳舱段的有限元网格如图3所示,共有143 144个节点和166 184个单元。

|
图 3 堆舱安全壳舱段有限元模型图 Fig. 3 Finite element model of the nuclear compartment tank |
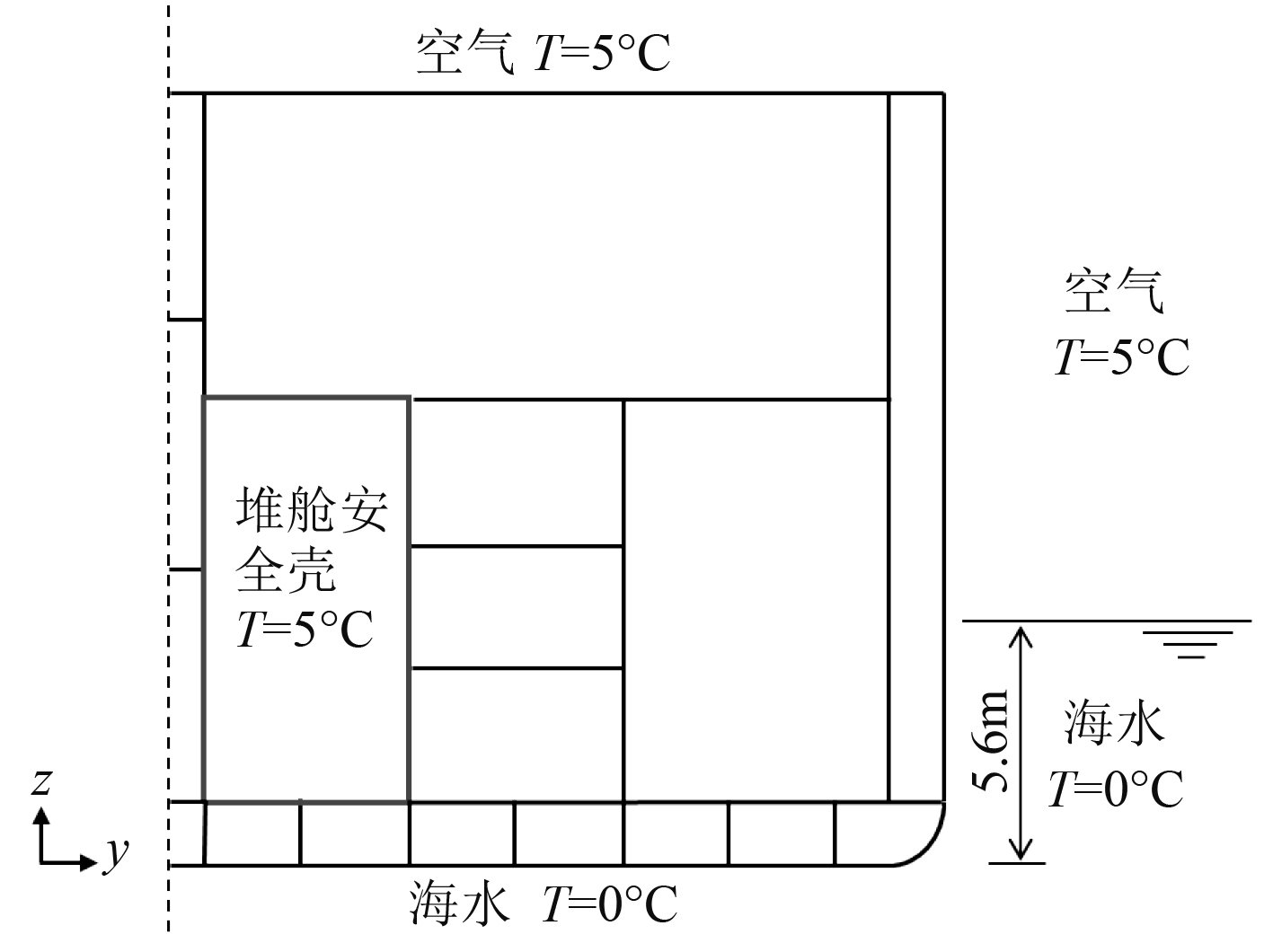
堆舱安全壳舱段的传热边界条件如图4所示,因为结构和边界条件关于中纵剖面对称,因此只显示舱段的右舷剖面。其水线以上的外部钢板和空气接触,水线以下的外部钢板和海水接触。舱段前后的横舱壁不与外界环境接触。
|
图 4 堆舱安全壳传热边界条件示意图 Fig. 4 Thermal boundary condition of nuclear compartment tank |
根据国际海事组织的IGC规范,外界空气温度为5 ℃,海水温度为0 ℃。本文取堆舱安全壳的温度为60 ℃[7]。在5级海风的海况下,钢板与外界空气之间的对流换热系数为16.27 W/m2K,钢板与海水之间的对流换热系数为139.5 W/m2K[8],钢板与舱段内各腔室空气之间的对流换热系数为4.65 W/m2K[9]。
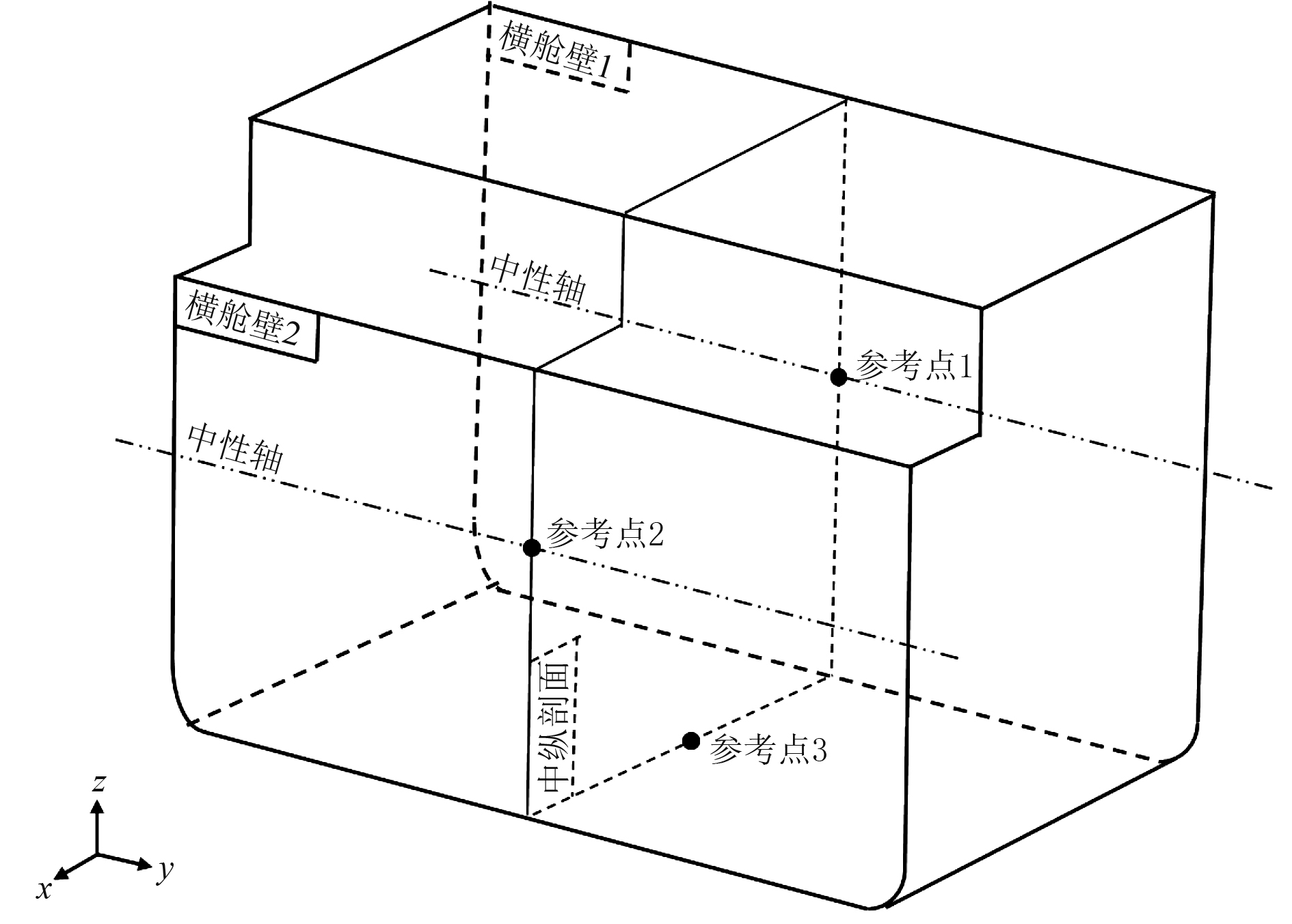
2.2 力学边界条件在计算堆舱安全壳舱段的温度应力时,需要对其设置力学边界条件。舱段结构简图如图5所示。图中横舱壁1和横舱壁2表示堆舱安全壳舱段前后两端的舱壁,参考点1表示舱段中纵剖面和横舱壁1的中性轴的交点,参考点2表示舱段中纵剖面和横舱壁2的中性轴的交点,参考点3 表示舱段下底板的几何中心。
|
图 5 堆舱安全壳舱段结构简图 Fig. 5 Structural schematic of nuclear compartment tank |
将横舱壁1上所有节点的平动自由度(dx,dy,dz)与参考点1进行耦合,将横舱壁2上的所有节点的平动自由度(dx,dy,dz)与参考节点2进行耦合。约束参考点1沿X、Z方向的平动自由度(dx,dz)以及绕X方向的转动自由度(Rx);约束参考点2沿Z方向的平动自由度(dz)以及绕X方向的转动自由度(Rx);约束参考点3沿Y方向的平动自由度(dy)。
堆舱安全壳舱段的力学边界条件详细说明见表 2。
|
|
表 2 堆舱安全壳舱段力学边界条件 Tab.2 Mechanical boundary condition of nuclearcompartment tank |
热能的传递有3种基本方式:热传导、热对流与热辐射[10]。因为堆舱安全壳(热源)的温度仅为60 ℃,热辐射效应较弱。因此,本文仅考虑热传导和热对流对温度分布的影响。
对流换热是指流体流经固体时流体与固体表面之间的热量传递现象。根据流体运动方式的不同,可以将其分为强制对流换热和自然对流换热2种。强制对流换热由于外界的强制流场所引起,自然对流换热由于流体本身的密度变化引起。在堆舱安全壳舱段中,不同厚度的钢板将舱段分隔为75个封闭腔室。舱段与外界环境(空气和海水)之间是强制对流换热;舱段内封闭腔室是自然对流换热。
在计算舱段内封闭腔室的对流换热时,需要预先得到腔室内空气的温度分布。但本文中舱段的腔室数量较多且形状复杂,采用CFD仿真方法精确计算出腔室内空气的温度分布难度巨大。本文参考LNG船封闭腔室温度的计算方法[11],假设任意封闭腔室内空气温度保持恒定,根据封闭无源空腔的热流量守恒以及环境温度的边界条件,可以计算得到舱段内所有腔室的空气温度。
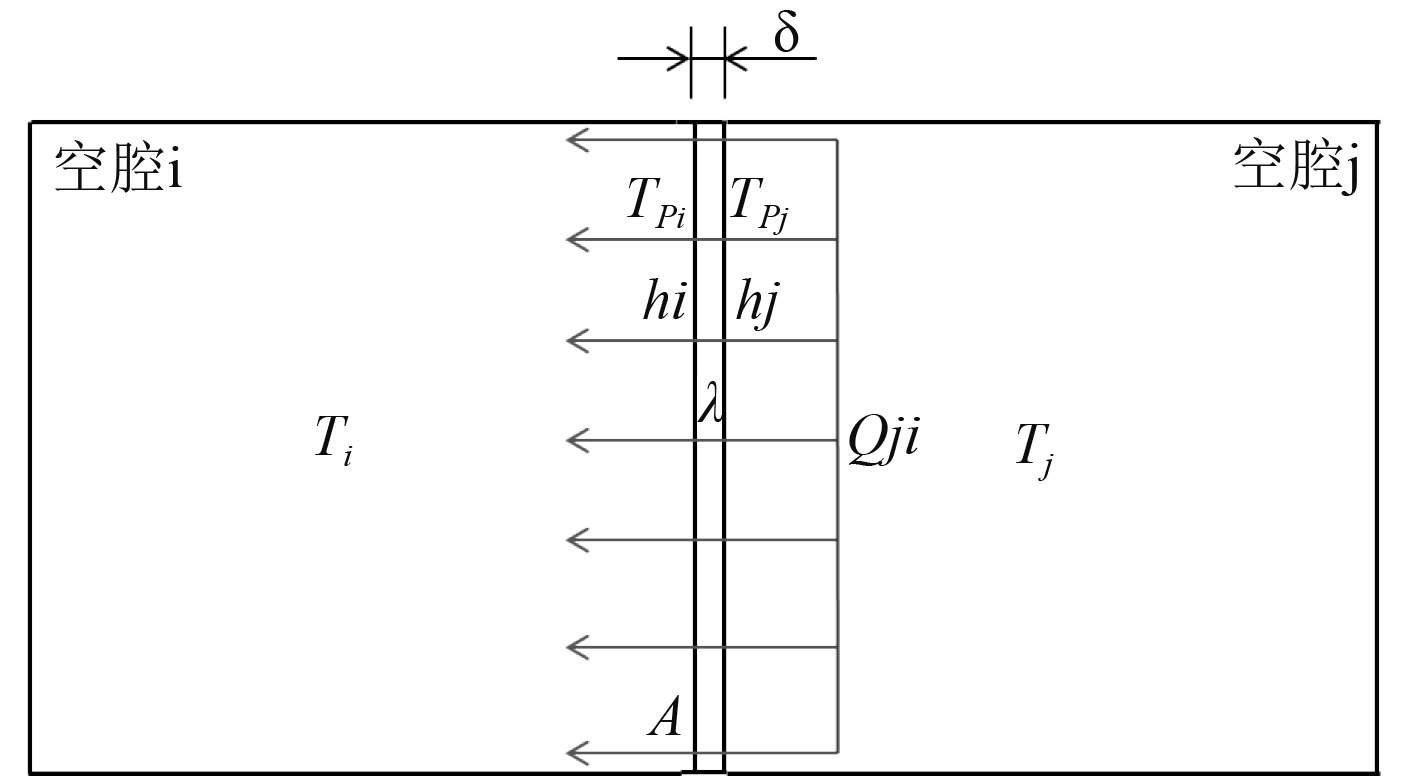
3.1 空腔热流量计算空腔j到空腔i的热流传递如图6所示。根据对流换热和热传导公式,空腔j到空腔i的热流量Qj,i可以用下式表示,其中式(1)表示空腔i与钢板之间的对流换热,式(2)表示钢板的两侧面的热传导,式(3)表示空腔j与钢板之间的对流换热。
|
图 6 空腔j到空腔i的热流传递示意图 Fig. 6 Heat flow from cavity j to cavity i |
| $A{h_i}({T_{pi}} - {T_i}) = {Q_{j,i}}\;{\text{,}}$ | (1) |
| $\frac{{A\lambda ({T_{pj}} - {T_{pi}})}}{\delta } = {Q_{j,i}}\;{\text{,}}$ | (2) |
| $A{h_j}({T_j} - {T_{pj}}) = {Q_{j,i}}\;{\text{。}}$ | (3) |
其中:A表示钢板侧面的表面积,δ表示钢板的厚度。Ti、Tj表示空腔i、空腔j的空气温度,TPi、TPj表示钢板在空腔i、空腔j侧的表面温度。hi、hj表示钢板在空腔i、空腔j侧的对流换热系数。λ表示钢板的导热系数。
根据式(1)~式(3),消去钢板两侧的温度Tpi和Tpj,则空腔j到空腔i的热流量Qj,i可以用下式表示:
| ${Q_{j,i}} = {U_{j,i}}{A_{j,i}}({T_j} - {T_i}){\text{,}}$ | (4) |
| $ {U_{j,i}} = \dfrac{1}{{\dfrac{1}{{{h_i}}} + \dfrac{1}{{{h_j}}} + \dfrac{\delta }{\lambda }}} {\text{。}}$ | (5) |
对于已知形状大小和钢板厚度的空腔i和空腔j,在式(4)中,其Uj,i和Aj,i均为常数,因此,其热流量Qj,i只与空腔i和空腔j的温度有关。将式(4)简化为下式:
| ${Q_{j,i}} = {m_{j,i}}({T_j} - {T_i}){\text{。}}$ | (6) |
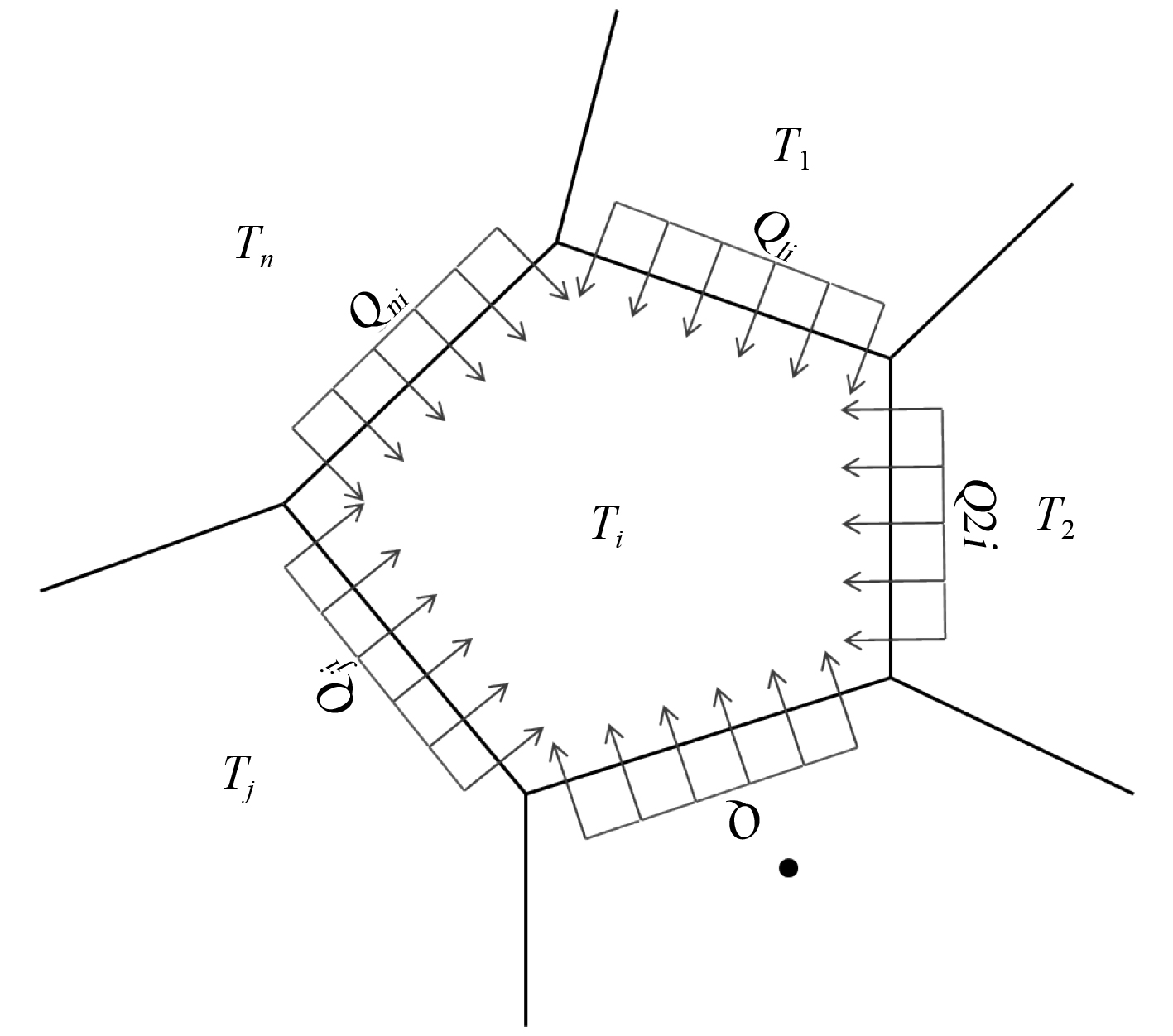
对于任一封闭无源空腔,根据能量守恒,流入该空腔的热量必然等于流出的热量。如图7所示,对于空腔i,必然存在如下关系式:
|
图 7 封闭无源空腔的热流量守恒 Fig. 7 Heat flow conservation of closed passive cavity |
| $\sum\limits_{j = 1}^n {{Q_{j,i}}} = 0{\text{。}}$ | (7) |
值得注意的是,对于外界环境,例如本文中的外界空气和海水,它不是一个封闭系统,因此不满足热流量守恒;对于存在内热源的封闭空腔,因为其内部的热源会自行产生热量,因此,该空腔也不满足热流量守恒。
本文中堆舱安全壳舱段结构,存在75个封闭腔室,其中2个为有源腔室(堆舱安全壳),73个为无源腔室。舱段外壳水线以上部分和外界空气接触,水线以下部分和海水接触。将外界空气和海水也分别视为系统中的腔室结构,它们与舱段进行热量交换,但自身不满足热流量守恒。由上所述,将堆舱安全壳舱段内的无源封闭腔室依次编号1~73,将堆舱安全壳编号74~75,外界空气编号为76,海水编号为77。
根据式(6)~式(7),1~73号腔室的热流量守恒可以表示为如下矩阵形式:
| $ \left[ {\begin{array}{*{20}{c}} {{S_1},}&{ - {m_{1,2}},}& \cdots &{ - {m_{1,73}}}\\ { - {m_{2,1}},}&{{S_2},}& \cdots &{ - {m_{2,73}}}\\ \vdots & \vdots &{}& \vdots \\ { - {m_{73,1}},}&{ - {m_{73,2}},}& \cdots &{{S_{73}}} \end{array}} \right]\left[ \begin{array}{l} {T_1}\\ {T_2}\\ \vdots \\ {T_{73}} \end{array} \right] = \left[ \begin{array}{l} {C_1}\\ {C_2}\\ \vdots \\ {C_{73}} \end{array} \right] {\text{,}}$ | (8) |
| ${S_i} = \sum\limits_{j = 1,j \ne i}^{77} {{m_{i,j}}} {\text{。}}$ | (9) |
式中,C1~C73为常数,式(9)中,i=1~73。根据式(8)~式(9)可知,求解腔室温度T1~ T73的系数矩阵为满秩矩阵,因此,堆舱安全壳舱段内1~73号舱室的空气温度必有唯一解。将系数矩阵求逆,即可得到堆舱安全壳舱段内各舱室的空气温度。
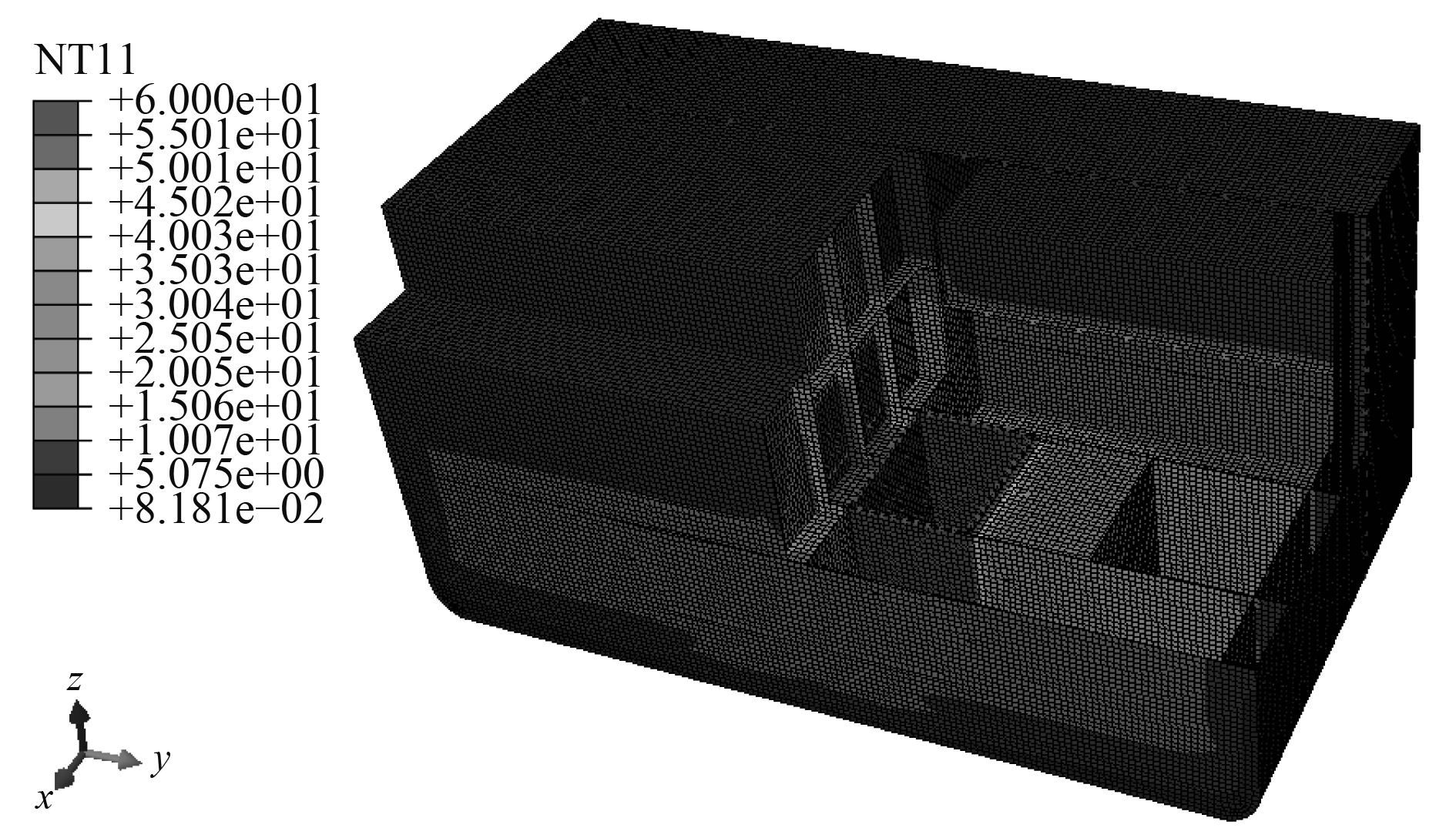
4 堆舱安全壳舱段温度场与温度应力计算 4.1 堆舱安全壳舱段温度场计算根据第3节的方法,得到舱段内各腔室的空气温度,将其带入有限元分析软件Abaqus中进行舱段的温度场计算。计算得到的舱段温度场云图如图8所示,参照舱段的几何模型图2,将舱段左舷一部分剖开以显示舱段内部结构的温度分布。
|
图 8 堆舱安全壳舱段温度分布云图 Fig. 8 Thermal distribution of nuclear compartment tank |
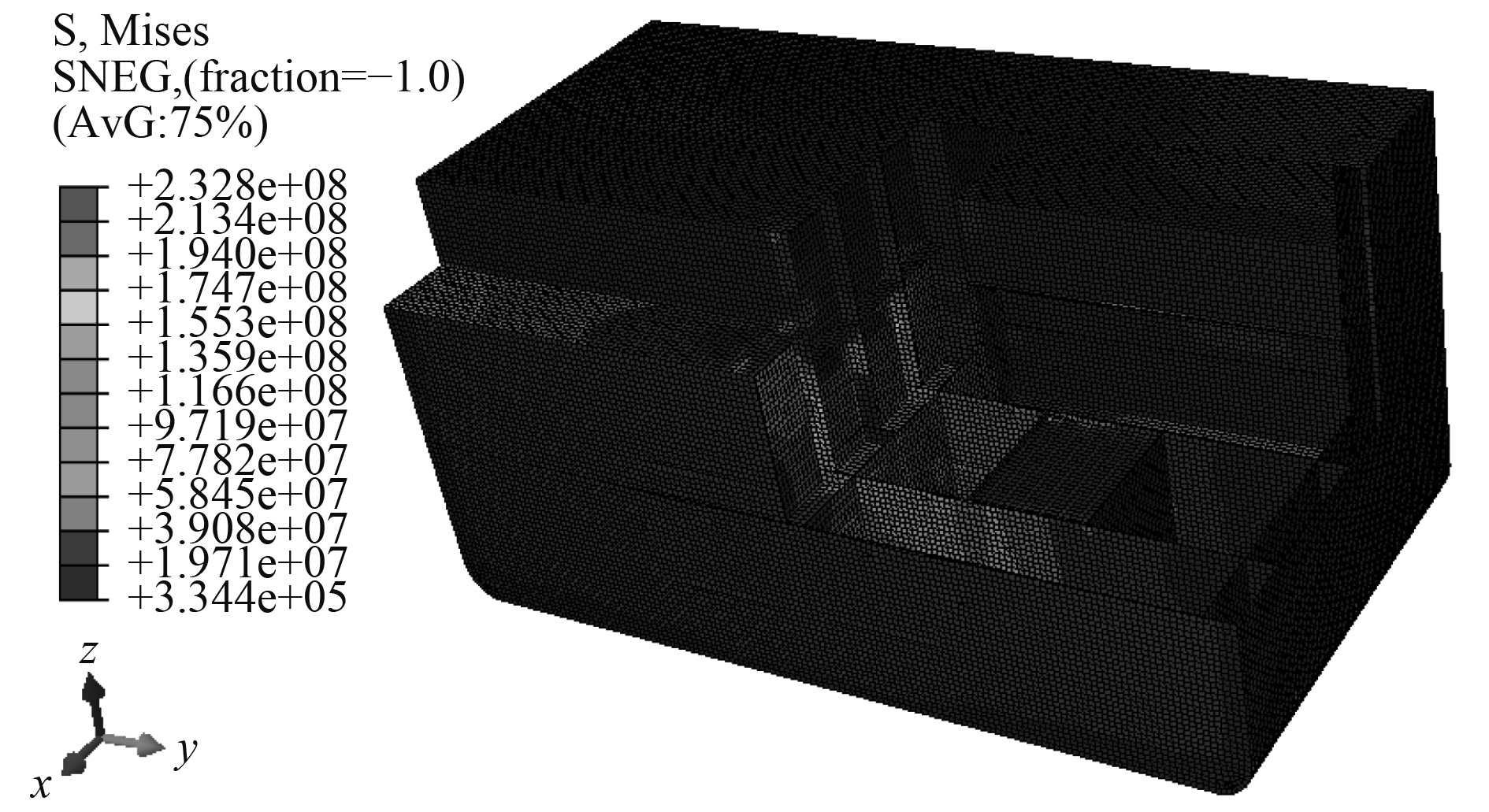
本文采用顺序耦合法计算堆舱安全壳舱段的温度应力,即忽略舱段的应力场对温度场的影响。首先计算处出舱段的温度场,然后将其作为预设场施加在舱段的力学有限元模型上,最后计算出舱段在力学边界条件下的应力分布。通过Abaqus软件计算,舱段的温度应力(Mises应力)分布如图9所示,图中应力单位为Pa。最大应力为232.8 MPa,位于2个堆舱安全壳之间的箱形构件处。
|
图 9 堆舱安全壳舱段温度应力(Mises)分布云图 Fig. 9 Thermal stress(Mises)distribution of nuclearcompartment tank |
通过本文的计算与分析,可以发现:
1)浮式核电站在正常工况下(堆舱安全壳温度为60 ℃),其整体温度应力水平较低,但是在堆舱安全壳周围的结构不连续处,因为温度梯度较大,易产生应力集中。
2)本文通过合理的传热过程简化,基于封闭无源空腔的热流量守恒,能够快速有效地计算出堆舱安全壳舱段内腔室的空气温度,结合有限元分析软件,能够计算出舱段的温度场和温度应力分布。针对复杂的三维结构,该方法具有很好的适用性。
| [1] |
VUJIĆ J, BERGMANN R M, ŠKODA R, et al. Small modular reactors: Simpler, safer[J]. Energy, 2012, 45(1): 288-295. DOI:10.1016/j.energy.2012.01.078 |
| [2] |
DOWDALL M, STANDRING W. Floating nuclear power plants and associated technologies in the northern areas[J]. Norwegian Radiation Protection Authority, 2008. |
| [3] |
KINDFULLER V, TODREAS N, BUONGIORNO J, et al. Overview of Security Plan for Offshore Floating Nuclear Plant[C]// International Conference on Nuclear Engineering. 2016: V005T15A076.
|
| [4] |
IAEA. Nuclear Technology Review. Section B, ADVANCED FISSION AND FUSION. 2014.
|
| [5] |
IAEA. Status of advanced light water reactor designs. 2004, IAEA-TECDOC-1391
|
| [6] |
HOLMQUIST T J. Strength and Fracture Characteristics of HY-80, HY-100, and HY-130 Steels Subjected to Various Strains, Strain Rates, Temperatures, and Pressures[J]. Naval Surface Warfare Center Research and Technology Department, 1987(Report No. AD-A233-061). |
| [7] |
陈玉清, 杨磊, 刘俊腾. 船用堆失水事故下堆舱模型敏感性分析[J]. 原子能科学技术, 2014, 48(s1): 376-380. CHEN Yu-qing, YANG Lei, LIU Jun-teng. Sensitivity analysis of ship reactor compartment model during LOCA[J]. Atomic Energy Science and Technology, 2014, 48(s1): 376-380. |
| [8] |
IMO. International Code for the Construction and Equipment of Ship Carrying Liquefied Gases in Bulk. 1993.
|
| [9] |
丁仕风, 唐文勇, 张圣坤. 大型液化天然气船温度场及温度应力研究[J]. 船舶工程, 2008, 30(5): 16-19. DING Shi-feng, TANG Wen-yong, ZHANG Sheng-kun. A research on temperature field and stress field of large-scale LNG ship[J]. Ship Engineering, 2008, 30(5): 16-19. DOI:10.3969/j.issn.1000-6982.2008.05.005 |
| [10] |
杨世铭, 陶文栓. 传热学(第四版)[M]. 北京: 高等教育出版社, 2006: 4-12.
|
| [11] |
WANG B, CHEN Y, SHIN Y S, et al. Thermal analysis and strength evaluation of cargo tanks in offshore FLNGs and LNG carriers[C]// ASME 2013, International Conference on Ocean, Offshore and Arctic Engineering. 2013: V003T03A050.
|
 2019, Vol. 41
2019, Vol. 41

