为了确定船体绕流场及其绕流发声问题,船模试验是一个非常重要的实验手段。但是与CFD方法比较,船模试验在时间和试验成本等消耗上是巨大的,且不能对船体周围流场及声场做出局部的特征估计和预报。在2000年召开的第四次国际船舶水动力学数值计算学术研讨会上,参加会议的学者讨论认为:采用计算流体动力学研究船舶绕流场已经达到很髙的精度要求,船舶各个部分的绕流情况基本可以利用CFD进行精确的模拟。对于物体的绕流问题,Zebib等[1]采用数值计算的方法研究了圆柱体的绕流扰动问题,结果表明圆柱体在对称情况下绕流扰动是稳定的,非对称情况下绕流不稳定。Y.Ahmed等[2]利用CFD数值模拟了VLCC船体周围的自由液面情况,为船舶阻力确定提供了很好的预报;之后又利用CFX模拟了不同弗劳德数下复杂船体绕流场的变化情况,模拟结果与实验数据非常接近[3]。物体绕流发声问题首先在航空和航海领域得到高度关注,航空方面它会造成航空乘员感官和心理上的不适,航海方面对海洋生物短期和长期造成严重负面影响,特别是对海洋哺乳动物的影响更大。对于物体绕流发声的研究,Lighthill[4-5]提出的声类比理论奠定了流致发声的理论基础,随后各国学者对绕流发声问题开展广泛的研究。Paula Kellett[6]等基于CFD研究了LNG船水动力性能预报问题,利用FW-H方程计算船舶水下辐射噪声,并与实船噪声测量数据进行了比较,验证了船舶水下噪声预报的可行性。曾文德[7]、魏英三[8]等针对SUBOFF潜艇开展CFD数值计算研究,获得了潜艇表面辐射声源的强度分布,指出水流动转捩区是主要的发声部位。
本文基于CFD数值模拟了某成品油船的绕流场分布,并对船体绕流发声进行了数值预报。首先研究了不同弗劳德数下不同球鼻首船型的绕流场变化情况,总结不同工况下不同球首船型的阻力与弗劳德数的变化规律;其次应用FW-H方程计算船体流噪声,研究不同球鼻首船型的船体流噪声指向性分布情况;最后针对船体绕流发声问题,分析不同球鼻首船型流噪声的声场分布规律。
1 数学计算模型 1.1 船舶绕流场模拟的湍流控制方程湍流运动基本控制方程为连续方程和Navier-Stokes方程[9]:
| $ \frac{\partial }{{\partial {{t}}}}\left( {\rm{\rho }} \right) + \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {{\rm{\rho }}{{{u}}_{{i}}}} \right) = 0 {\text{,}}$ | (1) |
| $ \begin{split} \frac{\partial }{{\partial {{t}}}}\left( {{\rm{\rho }}{{{u}}_{{i}}}} \right) + \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left( {{\rm{\rho }}{{{u}}_{{i}}}{{{u}}_{{j}}}} \right) =\;& - \frac{{\partial {\rm{p}}}}{{\partial {{{x}}_{{i}}}}} + \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left( { - {\rm{\rho }}\overline {{{u}}_i^{\rm{'}}{\rm{u}}_j^{\rm{'}}} } \right)+\\ & \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left[ {{\rm{\mu }}\left( {\frac{{\partial {{{u}}_{{i}}}}}{{\partial {{{x}}_{{j}}}}} + \frac{{\partial {{{u}}_{{j}}}}}{{\partial {{{x}}_{{i}}}}}} \right)} \right] {\text{。}}\end{split} $ | (2) |
湍流控制方程采用剪切应力输运(SSTκ-ω)模型,湍流动能κ方程及特殊耗散率ω方程如下[10]:
| $ \frac{\partial }{{\partial {{t}}}}\left( {{{\rm \rho } {\textit{κ}}}} \right) + \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {{\rm{\rho {\textit{κ}} }}{{{u}}_{{i}}}} \right) = \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left( {{{\rm{\varGamma }}_{{k}}}\frac{{\partial {{k}}}}{{\partial {{{x}}_{{j}}}}}} \right) + {{{G}}_{{k}}} - {{{Y}}_{{k}}} + {{{S}}_{{\textit{κ}}}} {\text{,}}$ | (3) |
| $ \frac{\partial }{{\partial {{t}}}}\left( {{\rm{\rho \omega }}} \right) + \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {{\rm{\rho {\textit{ω}} }}{{{u}}_{{i}}}} \right) = \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left( {{{\rm{\varGamma }}_{\rm{\omega }}}\frac{{\partial {\rm{\omega }}}}{{\partial {{{x}}_{{j}}}}}} \right) + {{{G}}_{\rm{\omega }}} - {{{Y}}_{\rm{\omega }}} + {{{D}}_{\rm{\omega }}} + {{{S}}_{\rm{\omega }}} {\text{。}}$ | (4) |
其中,κ和ω分别为湍流动能和湍流耗散率;有效扩散率
| $ {{\rm{\sigma }}_{{k}}} = \frac{1}{{{{{F}}_1}/{{{\textit{σ}}}_{{{\textit{κ}}}1}} + \left( {1 - {{{F}}_1}} \right)/{{{\textit{σ}}}_{{{\textit{κ}}}2}}}} {\text{,}}$ | (5) |
| $ {{\rm{\sigma }}_{\rm{\omega }}} = \frac{1}{{{{{F}}_1}/{{{\textit{σ}}}_{{\rm{\omega }}1}} + \left( {1 - {{{F}}_1}} \right)/{{{\textit{σ}}}_{{\rm{\omega }}2}}}} {\text{。}}$ | (6) |
式中,混合函数F1=tanh(ϕ14)。
| $ {{\rm{\phi}} _1} = {\rm{min}}\left[ {\max \left( {\frac{{\sqrt {\rm{\kappa }} }}{{{{\rm{\beta }}^{\rm{*}}}{{\omega y}}}},\frac{{500{\rm{\nu }}}}{{{{{y}}^2}{\rm{\omega }}}}} \right),\frac{{4{\rm{\rho \kappa }}{{\rm{\sigma }}_{{\rm{\omega }}2}}}}{{{{D}}_{\rm{\omega }}^ + {{{y}}^2}}}} \right] {\text{,}}$ | (7) |
| $ {{D}}_{\rm{\omega }}^ + = \max \left[ {2{\rm{\rho }}{{\rm{\sigma }}_{{\rm{\omega }}2}}\frac{1}{{\rm{\omega }}}\frac{{\partial {\rm{\kappa }}}}{{\partial {{{x}}_{{j}}}}}\frac{{\partial {\rm{\omega }}}}{{\partial {{{x}}_{{j}}}}},{{10}^{ - 10}}} \right] {\text{。}}$ | (8) |
式中:β*=0.09,σκ1=0.85,σκ2=1,σω1=0.5,σω2=0.856。
1.2 声学方程以Lighthill理论为基础发展的FW-H方程[11]:
| $ \frac{1}{{{{a}}_0^2}}\frac{{{\partial ^2}{{p'}}}}{{\partial {{{t}}^2}}} - {\nabla ^2}{{p'}} = \frac{\partial }{{\partial {{t}}}}\left[ {{{\rm{p}}_0}{{\rm{u}}_{{n}}}{\rm{\delta }}\left( {{f}} \right)} \right] + \frac{{{\partial ^2}}}{{\partial {{{x}}_{{i}}}\partial {{{x}}_{{j}}}}}{{{T}}_{{{ij}}}} - \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left[ {{{{p}}_{{{ij}}}}{{{n}}_{{j}}}{\rm{\delta }}\left( {{f}} \right)} \right] {\text{,}}$ | (9) |
其中,Lighthill应力张量、压应力张量分别为
| $ {{{T}}_{{{ij}}}} = {{\rho }}{{{u}}_{{i}}}{{{u}}_{{j}}} + {{{p}}_{{{ij}}}} - {{a}}_0^2\left( {{{\rho }} - {{{\rho }}_0}} \right){{{\delta }}_{{{ij}}}} {\text{,}}$ | (10) |
| $ {{{p}}_{{{ij}}}} = {{p}}{{{\delta }}_{{{ij}}}} - {{\mu }}\left[ {\frac{{\partial {{{u}}_{{i}}}}}{{\partial {{{x}}_{{j}}}}} + \frac{{\partial {{{u}}_{{j}}}}}{{\partial {{{x}}_{{i}}}}} - \frac{2}{3}\frac{{\partial {{{u}}_{{k}}}}}{{\partial {{{x}}_{{k}}}}}{{\rm{\delta }}_{{{ij}}}}} \right] {\text{。}}$ | (11) |
式中:i,j=1,2,3;p′为远场声压(p′=p–p0);δ(f)为狄拉克函数;δij为克罗内克符号;f为壁面函数;ui,un为
某16 500DWT成品油船主尺度参数如表1所示,型线图如图1所示,船体三维模型如图2所示。
|
|
表 1 16500DWT成品油船主尺度 Tab.1 Main dimensions of 16500DWT oil product tanker |
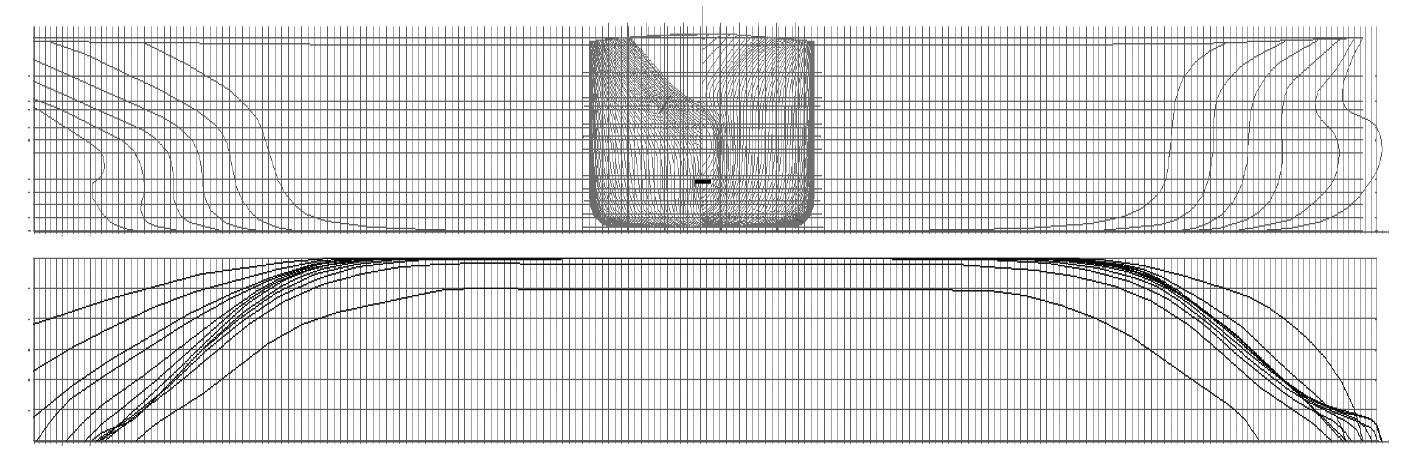
|
图 1 油船型线图 Fig. 1 Oil tanker lines |

|
图 2 船体模型示意图 Fig. 2 Schematic diagram of hull model |
创建船体外部流域即计算域,计算域尺寸示意图如图3所示。本文选取一个长方体作为计算域,在纵向上从船首向前延伸1倍船长,在船尾向后延伸4倍船长,在横向上从船舶的中纵剖面向两侧各延伸1倍船长,在水线面向下延伸1倍船长,向上延伸半个船长,因为计算流域是对称的,所以仅选取计算流域的一半作为计算区域。
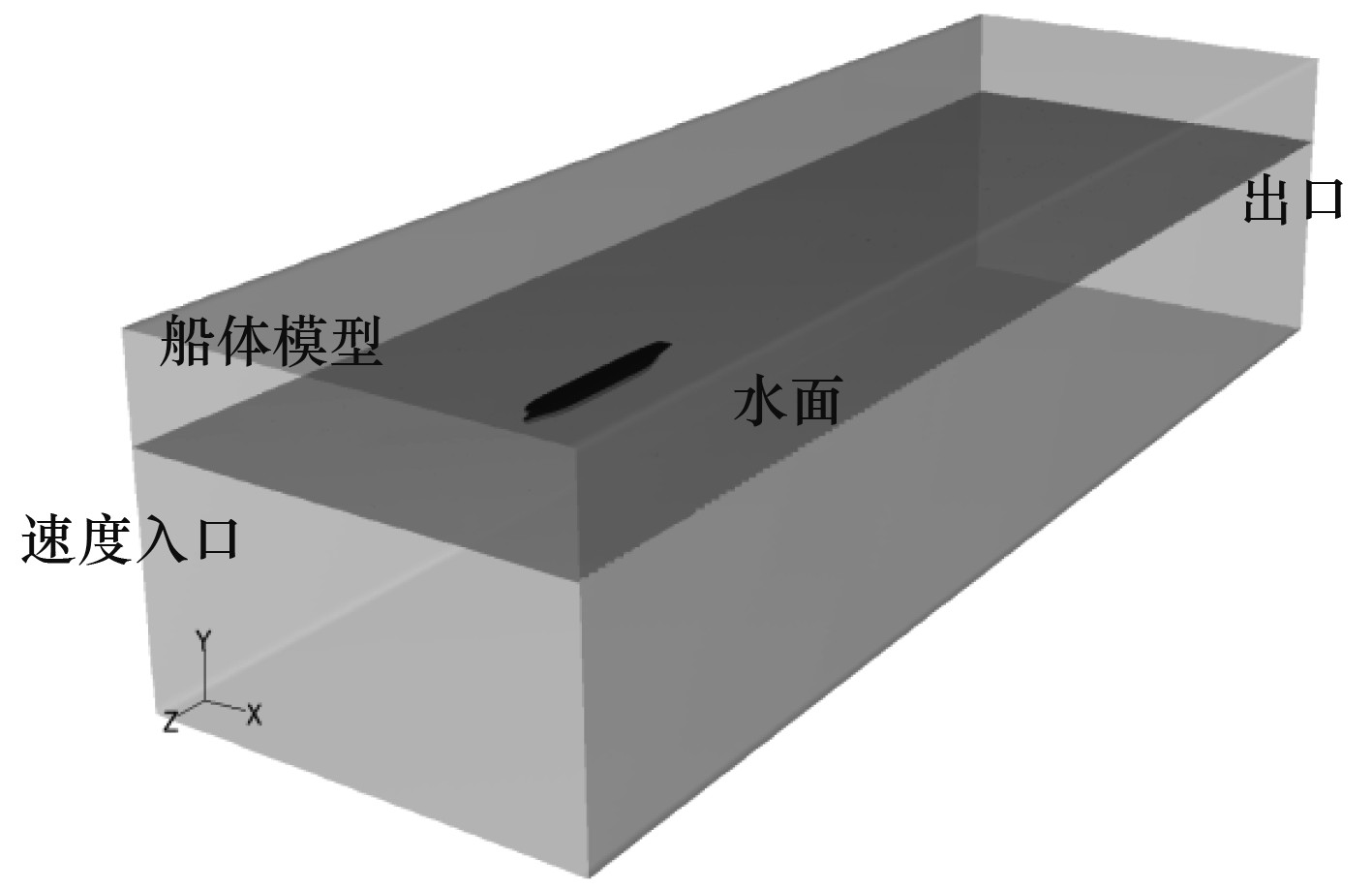
|
图 3 边界条件设置示意图 Fig. 3 Schematic diagram of boundary condition setting |
在CFD软件中完成对边界条件的设置。由于计算流域存在自由面,在软件中应将计算域的入口与出口分别设置成空气入口、水入口与空气出口、水出口。对来流入口设置为速度入口。把计算域出口设为自由出流(OUTFLOW)。但在大量计算发现定义OUTFLOW 边界条件时流体回流问题较为明显,即使网格细化后也难以解决此类问题,所以将出流边界设定为压强出口,压强通过UDF文件来控制。计算流域的对称面设置成对称的边界(SYMMETRY)。由于计算域范围选取的较大,因而把计算域的其他外边界包括船体表面均设为无滑移壁面。
3 船体绕流场和流噪声场的数值模拟 3.1 模型计算条件设置依据船舶主尺度参数构建船体模型,以缩尺系数为0.044899436进行缩比,不同球鼻首船型的船模如图4所示。

|
图 4 普通型(上)和上翘型(下)球艏的对比图 Fig. 4 Comparison of ordinary (Upper) and upwarping (Lower) bows |
船舶湍流方程经有限体积法离散后,应用SIMPLE算法进行求解。对于非稳态流场中迭代时间间隔的选取,要与声场的计算求解相统一。因为在一个时间序列上计算FFT的最大频率是1/(2Δt)(Δt为时间步长),而流致发声又是高频宽带噪声,并且关于水洞模型试验的噪声频率基本在10 kHz以上,所以本文以2.81E-5 s为时间步长进行计算,所研究的频率范围在10 Hz–20 kHz之间。
3.2 声接收点的选择大型船舶流噪声特性主要与流速、线型、附体分布、船体开孔大小等有关。为了确定船体流噪声的基本声场分布特性,本文需要在声接收点的选取上考虑能够测出船舶流噪声的空间指向性,首尾流噪声的纵向分布特性[12]。在数值计算中水听器接收点位置分布如图5所示。

|
图 5 船舶流噪声指向性示意图 Fig. 5 Directional diagram of ship flow noise |
船舶流噪声水平指向性位于船舶水平剖面,该平面平行于X-Z平面,在水平剖面内以点(0,0.187,4.692)为圆心(坐标值为Fluent中模型缩比后的数值),极轴方向垂直船舶首尾轴线,以半径为6 m在船舶水平剖面内做一个圆形,在圆上从船首开始每隔30°均匀设置了12个虚拟水听器;流噪声垂直指向性位于船舶的中横剖面上,以点(0,0.187,4.692)为中心,2 m为半径,在平行于X-Y平面上绘制一个圆形平面。在该平面内的船舶水线面以下设置7个虚拟水听器。
为确定船舶流噪声在首尾(即沿船体Z方向)的噪声分布,将在首部与尾部沿Z方向上取一系列的参考点,分别距离首部船体表面及尾封板垂线下参考点0.1 m,0.3 m,0.5 m,1 m,1.5 m,2 m,3 m,5 m,7 m,10 m处建立纵向特征参考点;在船体纵向正方向上距船尾205 m处外表面沿X轴取一系列的特征参考点,分别船体表面0.1 m,0.2 m,0.3 m,0.4 m,0.5 m,0.8 m,1 m,1.2 m,1.7 m,2.5 m。
4 计算结果分析 4.1 船体绕流场结果分析

|
图 6 上翘型球首船体静压力云图 Fig. 6 Static pressure contour of upwarping bow hull |

|
图 7 普通型球首船体静压力云图 Fig. 7 Static pressure contour of ordinary bow hull |
由图可知,在球首前端的流场驻点附近,压强最大,定性地符合船舶绕流场的规律。上翘型比普通型船首局部区域的静压力大。在球首部,沿着流线方向,流体的静压先减小,后增大,流场性质合理,而静压的极小值位于球首长度的中部位置处附近。若近似以球首长度的中部位置处作为球首前端与后端的分界线,在球首前端顺压梯度区,压力变化剧烈,在球首后端逆压梯度区,压力变化平缓。考虑到球鼻首的三维几何外形,其曲率在前端变化剧烈,后端变化平缓。所以,可以根据球首部压力分布合理优化首部线型。
上翘型与普通型球首的船舶首部流场速度云图比较情况,如图8和图9所示。

|
图 8 上翘型球首船首速度云图 Fig. 8 Head velocity contour of upwarping bow hull |

|
图 9 普通型球首船首速度云图 Fig. 9 Head velocity contour of ordinary bow hull |
上翘型与普通型球首的船舶尾部流场速度云图比较情况,如图10和图11所示。
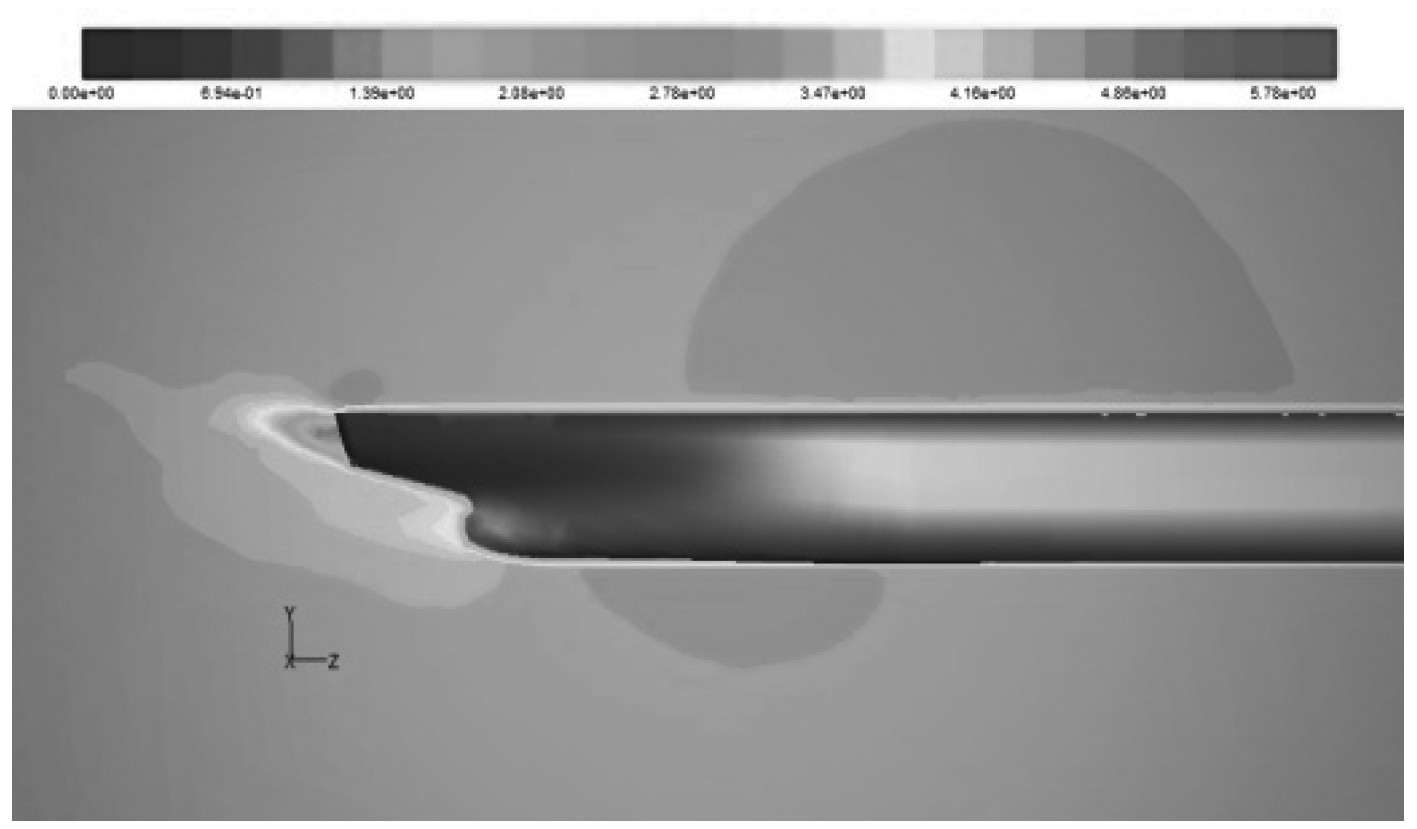
|
图 10 上翘型球首船尾速度云图 Fig. 10 Stern velocity contour of upwarping bow hull |
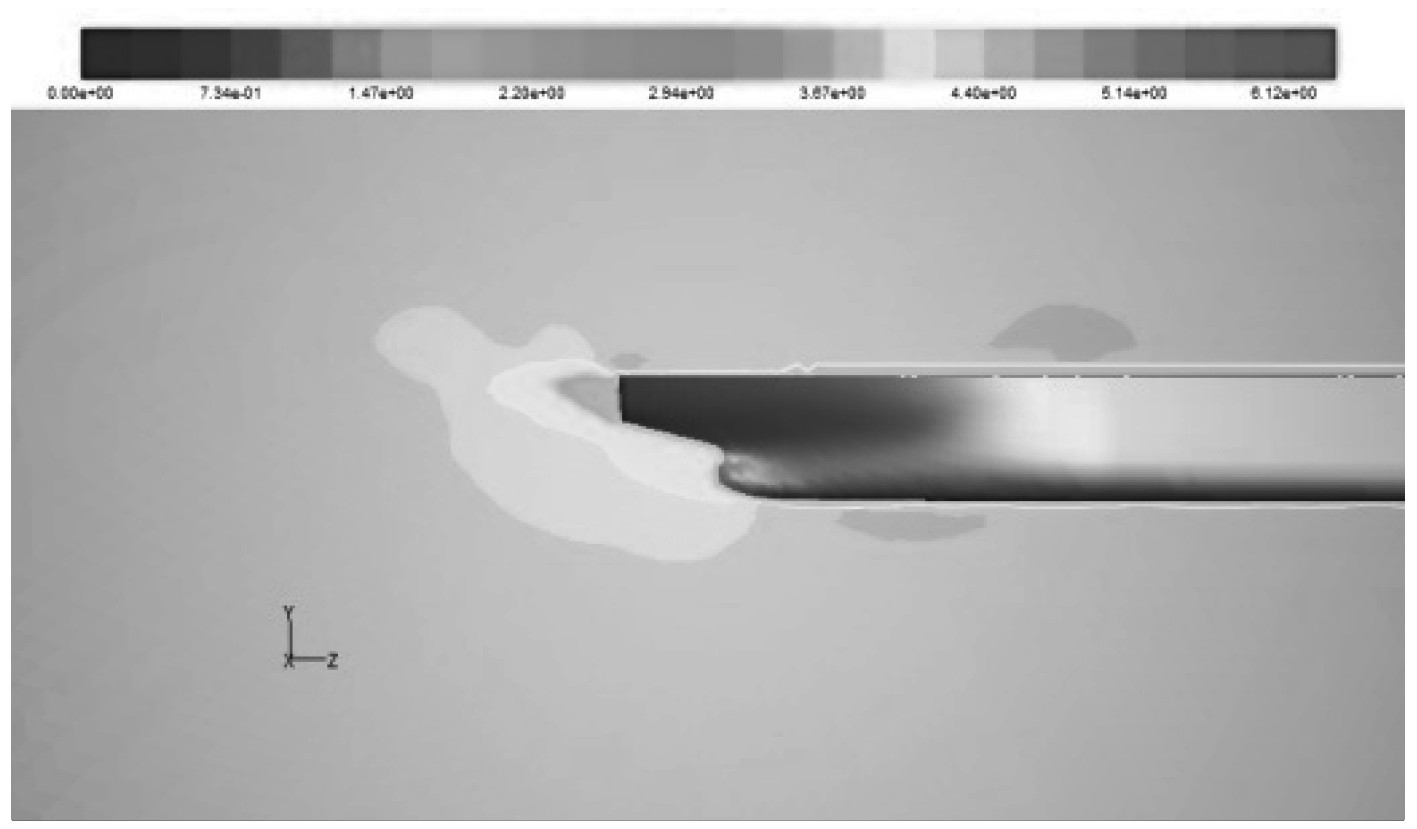
|
图 11 普通型球首船尾速度云图 Fig. 11 Stern velocity contour of ordinary bow hull |
船舶航行工况为5 m/s时,在设计水线处不同球鼻首船型的波形分布如图12和图13所示。船体绕流场自由液面波形图基本相似,上翘型球首船兴波比较明显。

|
图 12 上翘型球首船波形分布图 Fig. 12 Waveform distribution of of upwarping bow hull |

|
图 13 普通型球首船波形分布图 Fig. 13 Waveform distribution of of ordinary bow hull |

|
图 14 船首自由液面分布情况 Fig. 14 Free surface distribution of bow |

|
图 15 船尾自由液面分布情况 Fig. 15 Free surface distribution of stern |
在不同工况下,不同球首的船舶阻力与弗劳德数的关系如图16所示,船舶流噪声与弗劳德数的关系如图17所示。由图可知,因为弗劳德数增加,船舶的阻力亦增大,基本同船舶阻力和航速的规律关系相似。随着弗劳德数增加,船舶的流噪声亦增大,基本符合船舶流噪声和航速的变化关系。
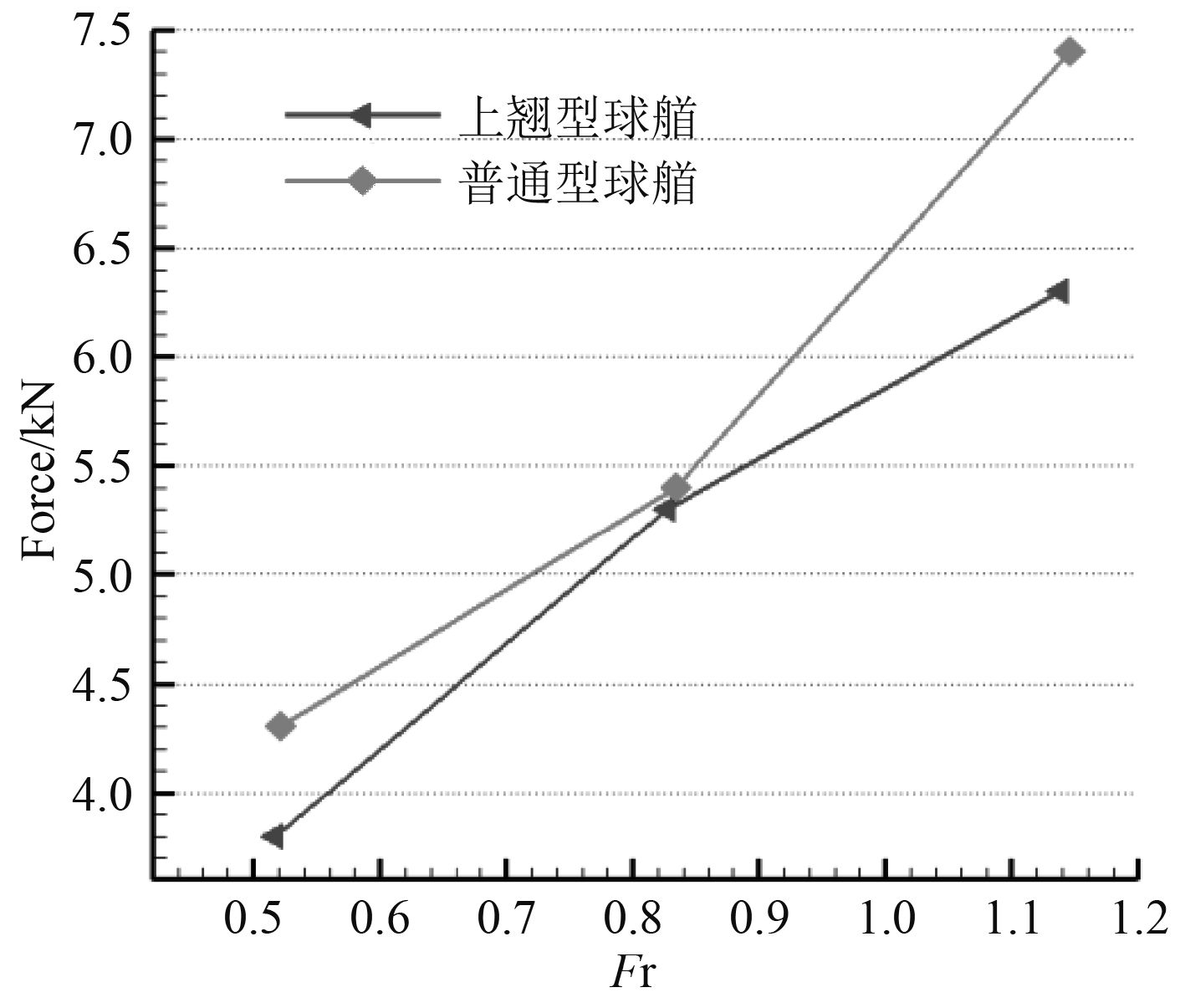
|
图 16 不同工况下阻力与弗劳德数的关系 Fig. 16 The relation between resistance and froude number under different working conditions |

|
图 17 不同工况下流噪声与弗劳德数的关系 Fig. 17 The relation between flow noise and froude number under different conditions |
图18和图19分别给出了船舶流噪声的水平指向性图和垂直指向性图。为直观地观察船舶指向性图,在声压数值的处理中,一般要用总声压级减去某个基数。在图中的横坐标表示了这一点,如“OSPL-100”代表图中每点的声压值均减小100 dB后得到图中的结果[13 – 14]。显然,由于船壳是左右对称的,故在船舶水平剖面内能够得到图中所示的结果。由图可以看出,船舶纵轴沿船首方向左右30°方位角处,船舶流噪声水平指向性最强,在首尾方向流噪声向外辐射较弱,在船首方向声源级较小是由于船壳首部左右30°方位角处承受的流体脉动压力较大,而船尾方向声源级下降则是由于船舶尾流对声波的掩蔽效应。在船舶流噪声垂直指向性图中,从船舶舭部向外辐射的量级较高,船底处声辐射较弱,船舷两侧的声辐射强度最弱。船舶舭部是船壳上连接船底和舷侧列板间的弯曲部分。在船舶航行时,由于船体舭部曲率大,水流过船体的阻尼增大,流速较高,从而导致舭部流噪声增高。船体舷侧列板较船底列板光顺规整,壁面平滑,因此舷侧处湍流脉动壁压较船底处小。此外,舷侧处对湍流边界层拟序结构的抑制和破坏能力更强,故而舷侧处的船舶流噪声大幅降低。

|
图 18 船舶流噪声水平指向性图 Fig. 18 Horizontal directivity diagram of ship flow noise |

|
图 19 船舶流噪声垂直指向性图 Fig. 19 Vertical directivity diagram of ship flow noise |
针对船舶舭部流噪声的降噪处理措施是,适当增加船体舭部列板高度,增大舭部圆弧半径。这样减小了船舶的涡旋阻力,抑制了湍流壁压脉动作用对舭部的影响,从而达到减阻降噪的效果。其不足之处是减小了船舶的舱容,影响了船舶的装载能力。
4.3 不同球鼻首船型基本声场特性分析图20和图21分别给出了不同球鼻首船型在首尾部某一特征点处的声压频响曲线对比情况。
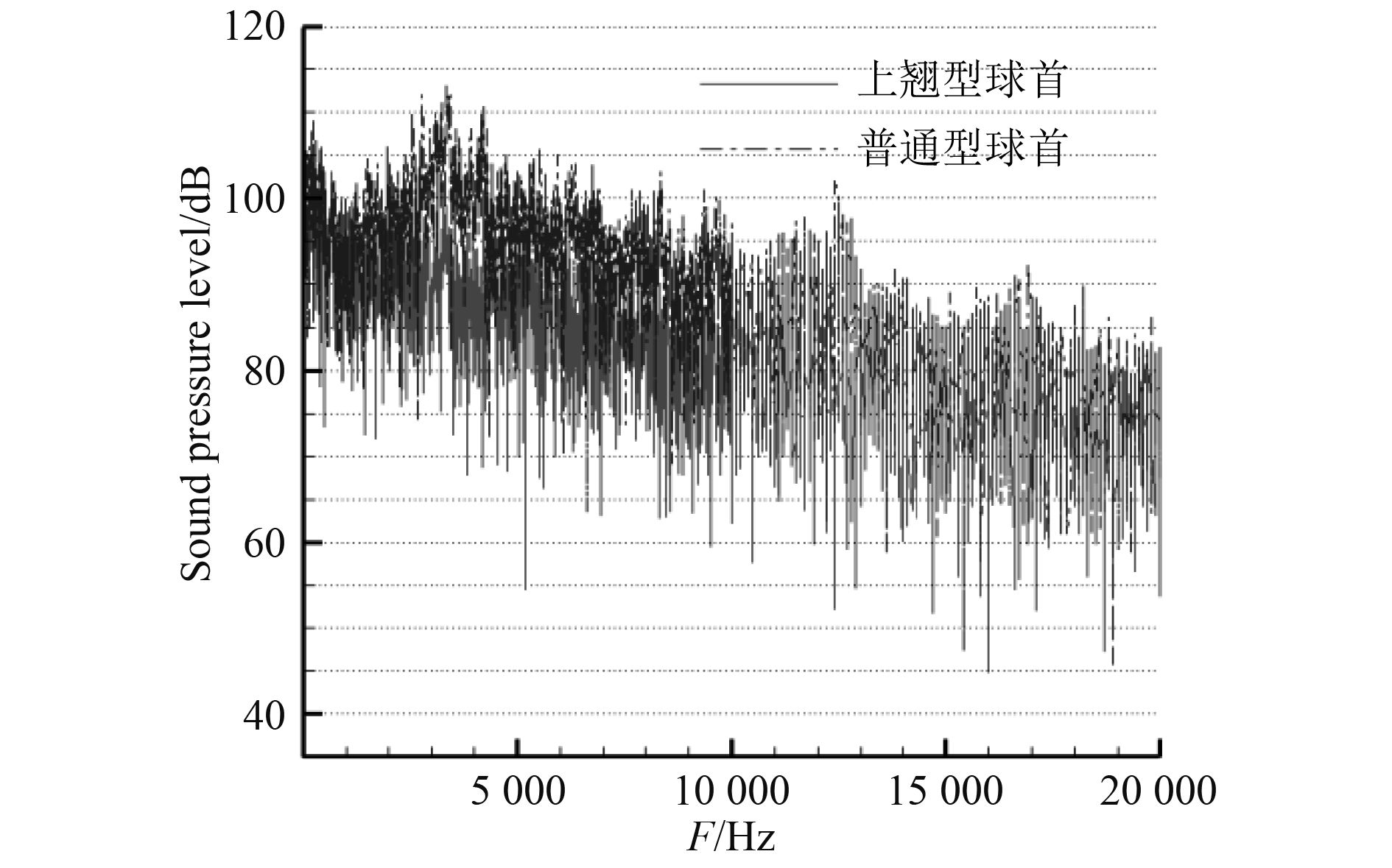
|
图 20 不同球首船型艏部特征点处的声压频响曲线对比 Fig. 20 Comparison of sound pressure frequency response curves at the bow characteristic points of different bows |
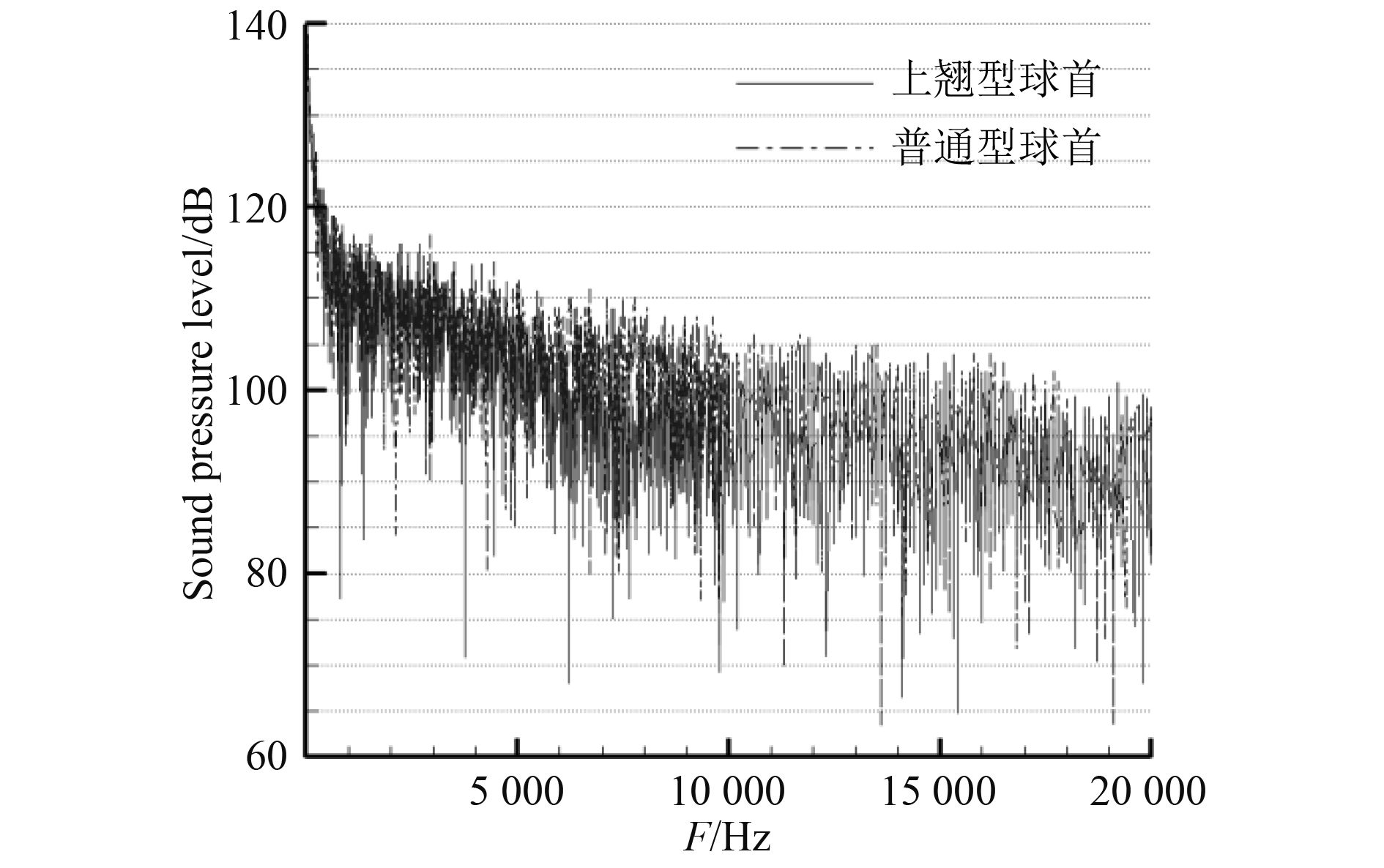
|
图 21 不同球首船型尾部特征点处的声压频响曲线对比 Fig. 21 Comparison of sound pressure frequency response curves at the stern characteristic points of different bows |
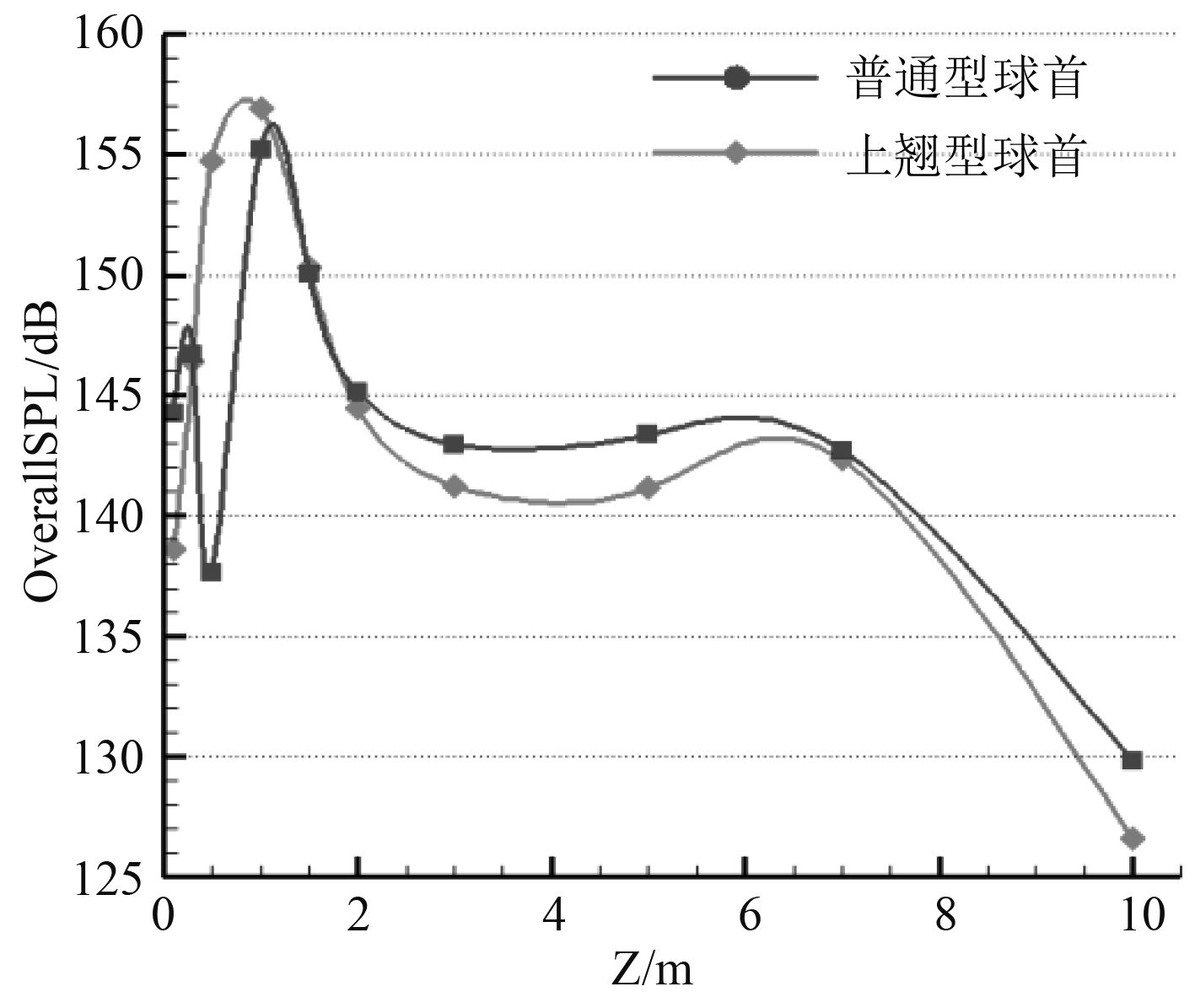
从总声压级的角度来分析不同球鼻首船型沿Z方向特征点声压值的变化情况。如图22所示,其横坐标为所取的10个特征点Z方向坐标值,纵坐标则为总声压级。从图中可以看到,在靠近船体壁面2 m内的区域,上翘型球首船的流噪声高于普通型球首船流噪声,但上翘型球首船声压下降的速度比较快。在离壁面2 m外比较远的地方不同船型声压变化相对平缓,二者变化趋势相似,上翘型球首船的计算结果小于普通型球首船的计算结果。
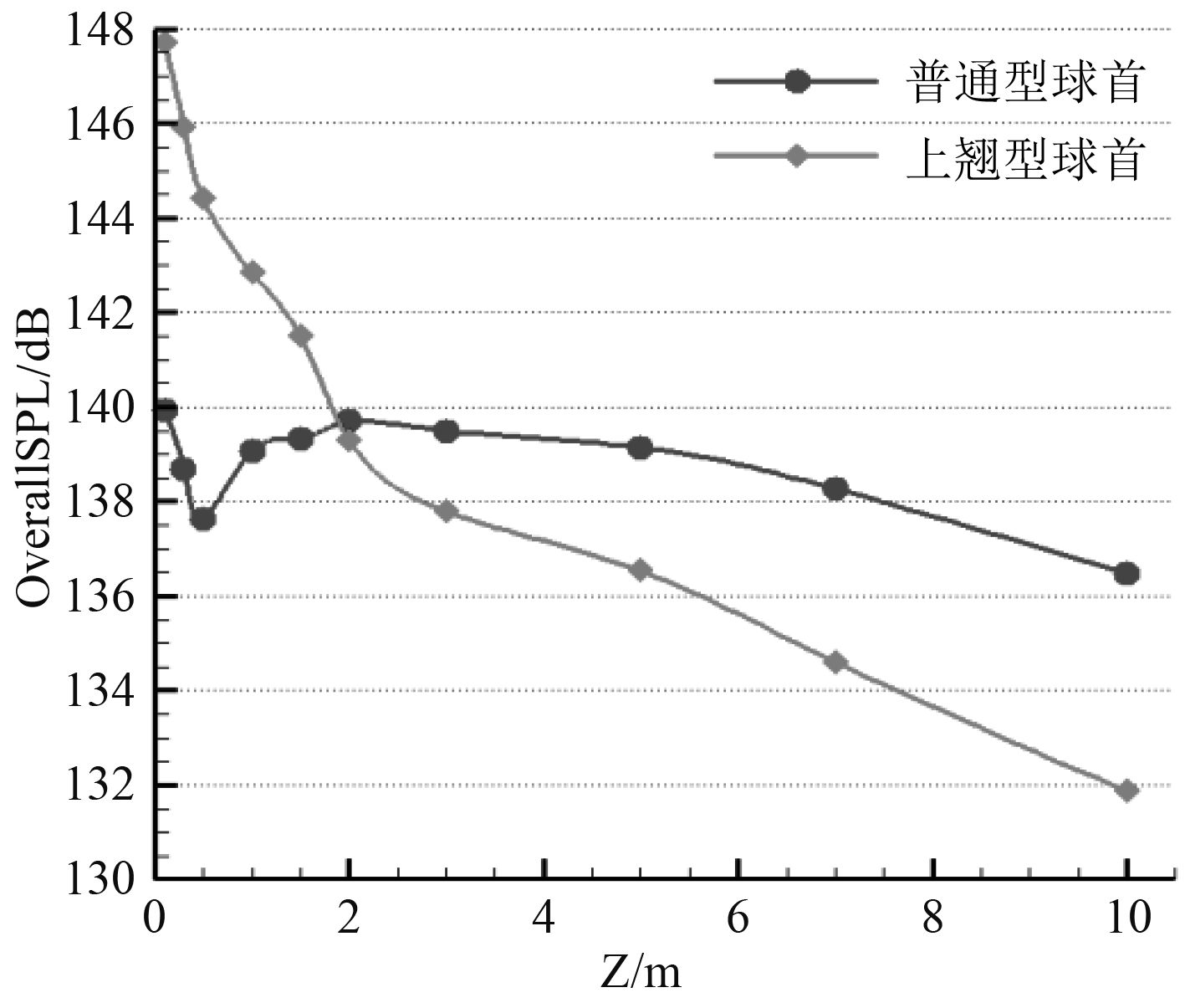
|
图 22 沿船舶首部Z方向特征点声压值变化曲线图 Fig. 22 Acoustic pressure curve of characteristic points along Z direction of ship bow |
图23给出了船尾Z方向特征点声压值的变化曲线。从图中看到,在靠近船体表面区域中,2种船型的流噪声声压波动较大,随着距船体壁面的远离,两者的差值逐渐减小,当壁面距离超过2 m后利用这2种方法计算的结果就相当接近了,这说明不同船舶球首线型对尾部影响较小。
|
图 23 沿船舶尾部Z方向特征点声压值变化曲线图 Fig. 23 Acoustic pressure curve of characteristic points along Z direction of ship stern |
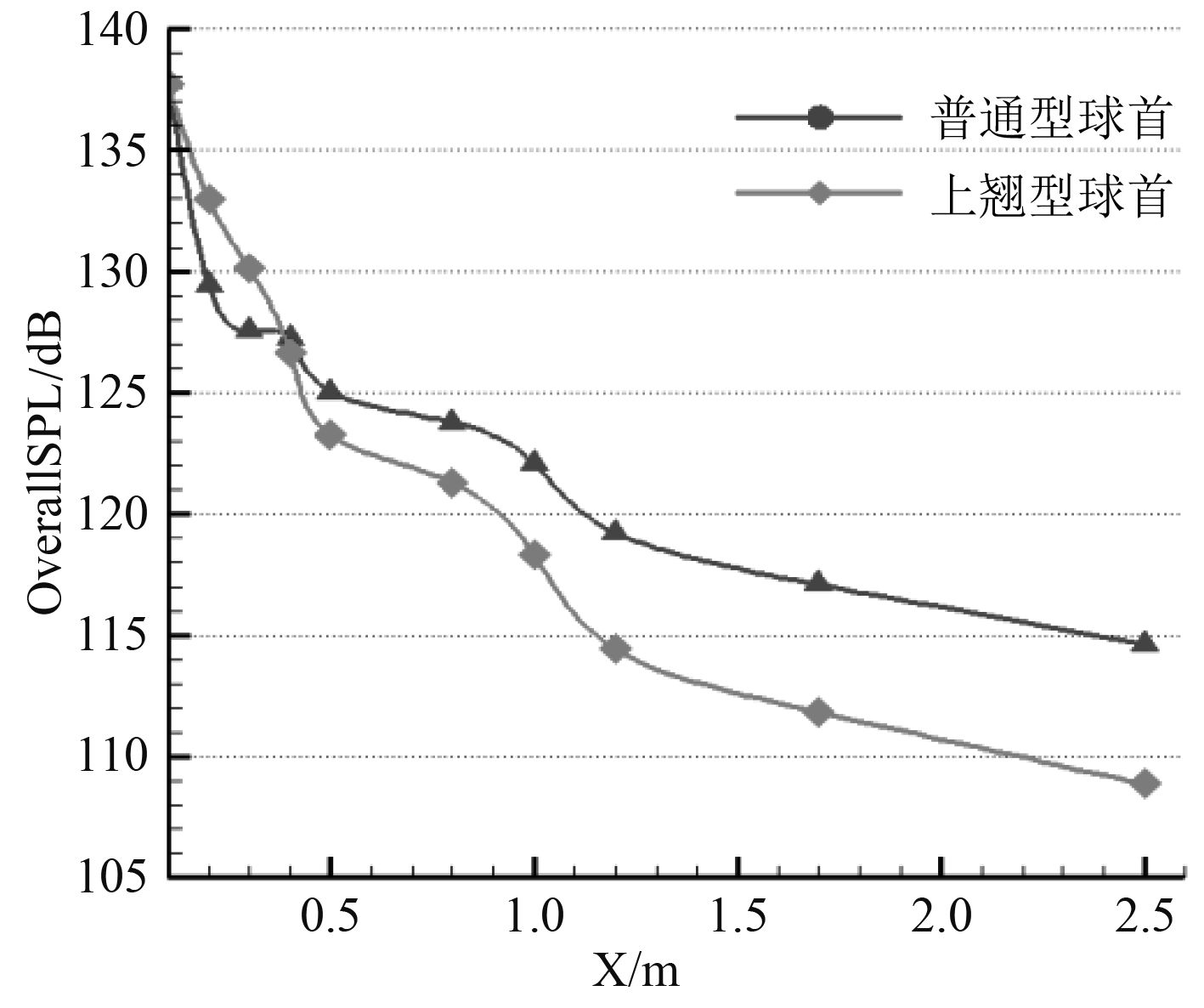
图24是船首X方向上声压值在特征点处的变化曲线。由图中可知,距船体表面0.1 m和0.4 m处,2种球首船的声压差值很小,随着距离的增大,上翘型球首船的声压计算结果要优于普通型船的计算结果。由该图亦可得出:在近壁面区域,声压下降速度较快;在远壁面区,声压变化相对缓慢。整体而言,2种球首船型的计算结果变化趋势相同,但上翘型船的计算结果比普通型船的计算结果小。
|
图 24 沿船舶首部X方向特征点声压值变化曲线图 Fig. 24 Acoustic pressure curve of characteristic points along X direction of ship bow |
通过对船舶绕流场以及绕流发声的研究可以得到如下结论:
1)在船舶首部区域,高压较集中,且集中点位于首部前缘;在船舶中线面处,船首部高速区域比较明显、船尾部出现较明显的低速带。
2)在相同工况下,上翘型球首船所受静压比普通型大,且上翘型球首因其形状特点,球鼻首最前端下方出现最大压力点,这样对延长球鼻首的使用寿命很有益处,并对内部结构起到保护作用。
3)不同工况下,上翘型球首船型比普通型所受船舶阻力略小,船舶流噪声总声级略低。
4)在船舶流噪声水平指向性图中,船舶纵轴沿船首方向左右30°方位角处,船舶流噪声水平指向性最强,在首尾方向流噪声向外辐射较弱;在船舶流噪声垂直指向性图中,从船舶舭部向外辐射的量级较高,船底处声辐射较弱,船舷两侧的声辐射强度最弱。由船舶的指向性分析能够很好地观察船舶的辐射噪声分布情况,并以此为船舶的型线优化设计提出改进措施。
5)在船舶流噪声分布特性方面,沿船舶首部Z方向上,上翘型球首船型在近壁区声压级高于普通型球首船,远场区则低于普通型球首船;沿船舶尾部Z方向上,上翘型球首船型在近壁区声压级先略低于普通型球首船,然后高于普通型球首船,之后缓慢下降低于普通型球首船;在沿船舶首部X方向上,上翘型球首船型在近壁区声压级高于普通型球首船,而在远场区则逐渐低于普通型球首船型。
综上所述,通过利用CFD方法提取典型船体水线下伴流场速度、压力特性、声场特性,研究船体型线对水动力噪声的影响,得出船舶流噪声在不同工况下的频响变化规律,从而可以利用水动力噪声评估方法优化分析船舶的型线,以起到减阻降噪之效果。
| [1] |
ZEBIB. Stability of viscous flow past a circular cylinder[J]. Journal of Chemistry, 2007(2): 21-22. |
| [2] |
AHMED Y, GUEDESSOARES C. Simulation of free surface flow around a VLCC hull using viscous and potential flow methods[J]. Ocean Engineering, 2009, 36: 691-696. DOI:10.1016/j.oceaneng.2009.03.010 |
| [3] |
AHMED Y. Numerical simulation for the free surface flow around a complex ship hull form at different Froude numbers[J]. Alexandria Engineering Journal, 2011(50): 229-253. |
| [4] |
LIGHTHILL M.J. On sound generated aerodynamically.Ⅰ. general theory[J]. Proceedings of the Royal Society of London(Series A), 1952, 211(1107): 564-587. DOI:10.1098/rspa.1952.0060 |
| [5] |
LIGHTHILL M.J. On sound generated aerodynamically. Ⅱ. turbulence as a source of sound[J]. Pcoceedings of the Royal Society of London(Series A), 1954, 222(1148): 1-32. DOI:10.1098/rspa.1954.0049 |
| [6] |
PAULA K, OSMAN T, ATILLAINCECIK. A study of numerical ship underwater noise prediction[J]. Ocean Engineering, 2013(66): 113-120. |
| [7] |
曾文德, 王永生, 杨琼方. 全附体潜艇流噪声数值计算[J]. 兵工学报, 2010, 31(9): 1204-1208. |
| [8] |
WEI Ying-san, WANG Yong-sheng, DING Ke, et al. Submarine underwater structure-borne noise and flow noise due to propeller excitation[J]. Acoustics Australia, 2012, 40(2): 122-127. |
| [9] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004.
|
| [10] |
高霄鹏.舰艇水动力噪声的数值分析与拖曳模测试技术研究[D]. 上海: 上海交通大学, 2008.
|
| [11] |
孟生, 张宇文, 王艳峰. 潜艇流水孔流噪声特性研究[J]. 计算机仿真, 2011, 28(7): 57-62. DOI:10.3969/j.issn.1006-9348.2011.07.015 |
| [12] |
王之程, 等. 舰船噪声测量与分析[M]. 北京: 国防工业出版社, 2004.
|
| [13] |
孙权. 水下航行体流致噪声的数值研究[D]. 武汉: 武汉理工大学, 2014.
|
| [14] |
孟堃宇. 基于大涡模拟的潜艇脉动压力与流噪声性能数值计算[D]. 上海: 上海交通大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
