船舶破损始终是威胁船舶安全的严重事故之一。在船舶生命周期内,很可能因天气、人为操作或者设备故障造成如船舶搁浅、碰撞、触礁等突发事故,造成船舶外壳破损,进而威胁船舶安全,造成一定的生命财产损失,同时也可能因船舶破损造成的油污泄露对海洋生态环境造成严重破坏。船舶操作指挥人员在破舱发生的第一时间能对破口进行准确的损害评估和合适的应急处理将非常重要。
与传统试验相比,CFD数值仿真计算花费少,自由度较高,可以较为便捷的创造多种试验场景进行分析计算。随着计算机计算能力的大幅提高和算法的不断优化,CFD仿真结果越加准确,其用于船舶破口的水动力研究也以持续多年,但其位置大多位于船侧(也是破口更易发生的区域)。在实际事故中,船舶破口也有可能发生在船底,同时其形状也并非完全规则。
为此,本文采用VOF方法,使用Fluent针对船舶底部破口这一特殊情况进行仿真计算并检测进水量,从而得出基于瞬时的流量系数。在简化模型中,针对底部不同破口形状、大小及破口所处水深的瞬时流量系数进行分析,探究破口形状、大小及破口所处水深等因素对进水速度的影响,为船舶操作指挥人员可以更为快速准确地评估船舶破舱可能造成的损失提供一定的参考。
1 理论基础 1.1 VOF方法在Fluent当中,若采用VOF方法,2个或多个流体之间必须互不相容,所以水–空气、水–油、油–气等多相流体的模拟仿真可以采用该方法。如果a代表某个单元中某种流体占据的体积比例,那么在计算过程中a将有3种状态:
1)a=0:在该单元中目标流体不存在;
2)0<a<1:在该单元中有至少包括目标流体在内2种或以上流体类型存在,且该单元内存在不同流体间的交界面;
3)a=1:在该单元中充满了目标流体。
在采用VOF方法模拟计算时,采用如下连续方程检测多相流界面[1]:
| $ \frac{\rm{1}}{{{\rho }_{{q}}}}\left[ \frac{\partial }{{{\partial }_{t}}}\left( {{a}_{q}}{{\rho }_{q}} \right)+\nabla \left( {{a}_{q}}{{\rho }_{q}}\overset{\to }{\mathop{{{v}_{q}}}}\, \right)={{S}_{{{a}_{q}}}}+\sum\limits_{p=1}^{n}{\left( \overset{\bullet }{\mathop{{{m}_{pq}}}}\,–\overset{\bullet }{\mathop{{{m}_{qp}}}}\, \right)} \right]\text{。} $ |
式中:
本文对流体的基本假设是不可压缩且带粘性的流体,其密度和粘性系数为常数,仿真计算以三维不可压缩的粘性流体瞬态运动方程为理论基础。
质量守恒方程(连续性方程):
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\text{。} $ |
式中:u,v,w为速度矢量v沿着x,y,z轴3个方向上的速度分量。
动量守恒方程(运动方程):
| $ \rho \frac{{\rm d}v}{{\rm d}t}=\rho F-gradp+\mu {{\nabla }^{2}}v\text{。} $ |
式中:F为质量力;p为压强;
基于理想流体假设的伯尼利方程:
| $ {{p}_{1}}\cdot\rho g{{z}_{1\cdot}}\frac{1}{2}\rho v_{1}^{2}\ll {{p}_{2}}\cdot pg{{z}_{2}}\cdot\frac{1}{2}\rho v_{2}^{2}\text{。} $ |
假设稳流P1=P2=Pa及v1<<v2,可以得出底部破口进水的理想流速为:
| $\begin{align} BL=&First\_cell(1-growth\_rat{{e}^{\max imum\_layers)}})/\\ &(1-growth\_rate)\text{,} \end{align}$ |
理想进水流量为:
| $ {{Q}_{ideal}}=A{{v}_{2}}\text{。} $ |
式中:A为破口截面面积
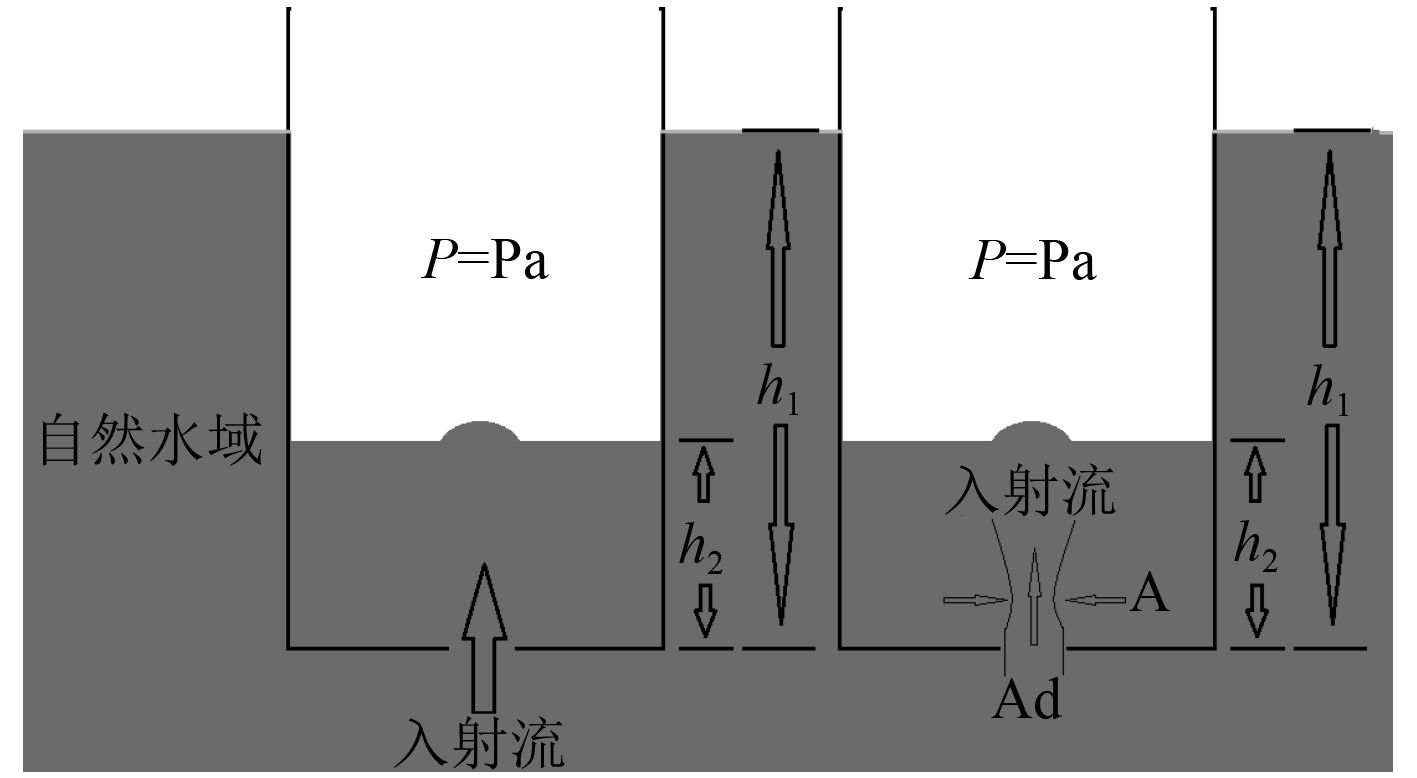
|
图 1 破口进水情况(左)与进水流量系数示意(右) Fig. 1 Sketch for coefficient of discharge |
但由于实际情况中不存在理想流体,流体均具有一定的粘性,通过这种方式估算的进水流量不准确。在底部进水事件中,进水流量通常受到2个方面的影响。一是受到水的粘性,导致实际进水速度低于估算值,二是进水射流截面通常会发生收缩,其截面面积小于破口面积。实际进水流量会小于理论进水流量,则在此引入进水流量系数Cd:
| $ {{C}_{d}}=\frac{{{Q}_{actual}}}{{{Q}_{ideal}}}\text{,} $ |
实际底部破口进水流量为:
| $ {{Q}_{actual}}={{C}_{d}}{{A}_{d}}\sqrt{2g({{h}_{1}}-{{h}_{2}})}\text{。} $ |
式中:h1为舱外水平面高;h2为舱内水平面高;Ad为破口截面面积。
2 模型与计算参数 2.1 模型尺寸本文主要探究的是不同形状、大小及破口所处水深对于破口进水速度的影响,因此需要对多组对比试验进行仿真计算,为了提高计算速度和效率,采用简化模型进行数值模拟。简化模型采用外径200 mm、壁厚1.5 mm、内径197 mm、高1 000 mm的圆柱代表舱室,圆柱底部中心设有不同大小及形状的开口代表破口,柱体上方不封闭。表1为不同试验组的主要参数:
|
|
表 1 试验编号及对应参数 Tab.1 Experiment serial number and model data |
在建立几何模型时建立一半,另一半由镜像产生。
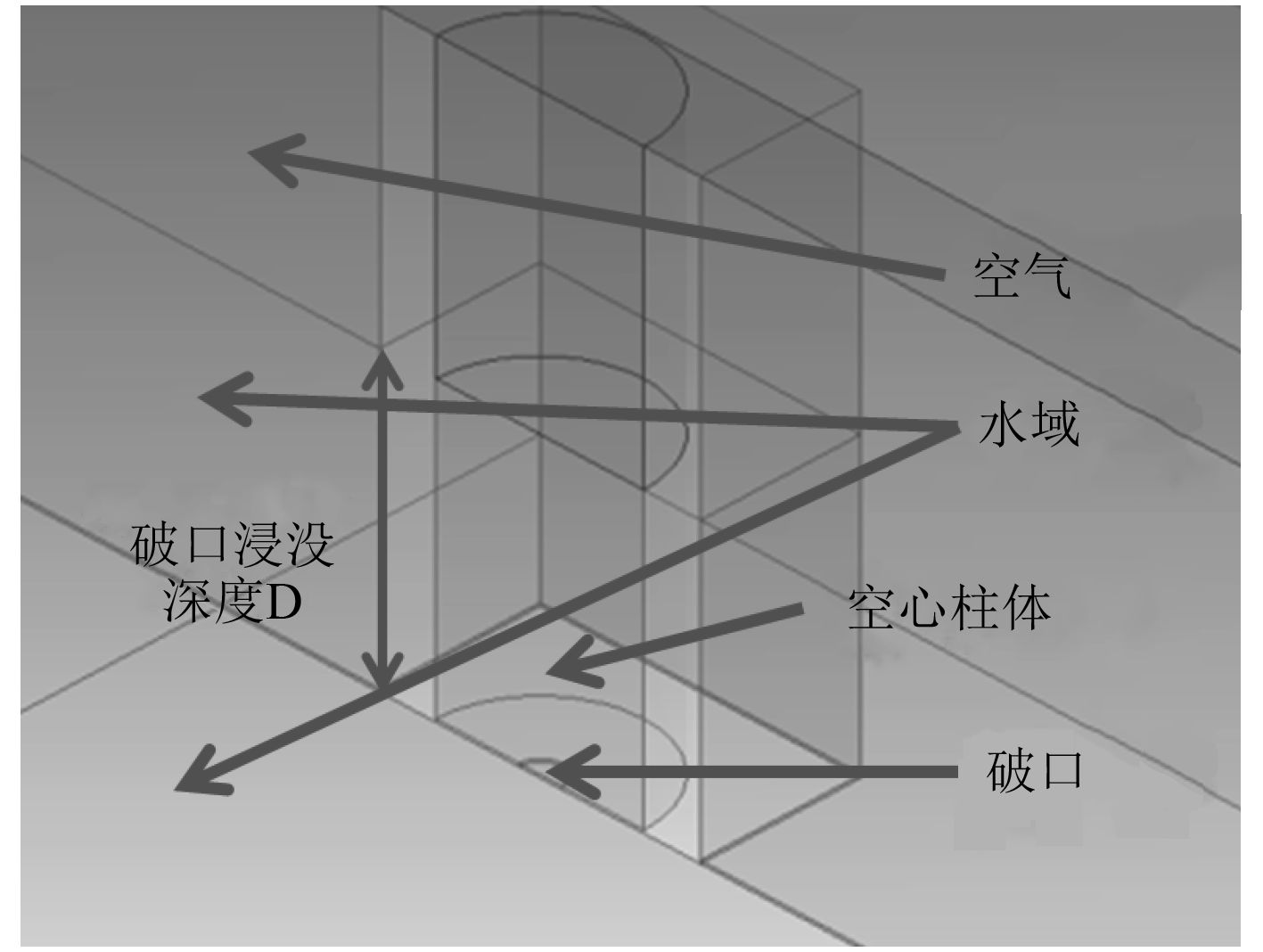
|
图 2 几何模型划分示例C1-300-3D Fig. 2 Model geometry example C1-300-3D |
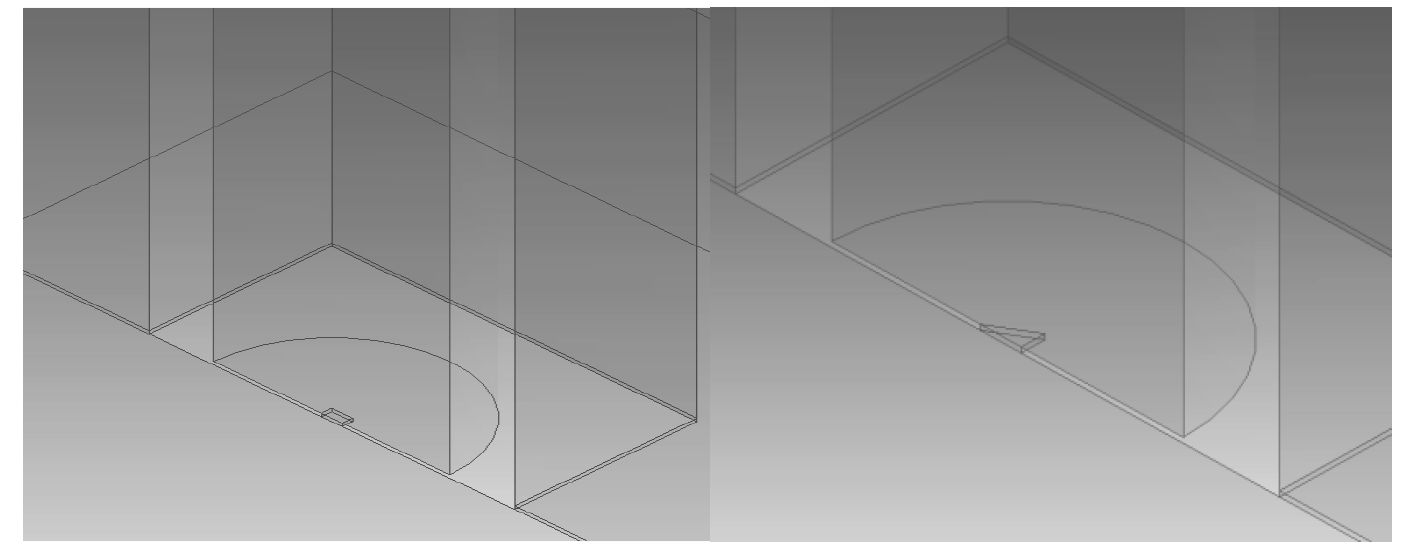
|
图 3 几何模型不同破口示例S1-500-3D(左),T1-500-3D(右) Fig. 3 Model geometry example with different shapes of breach S1-500-3D(left)T1-500-3D(right) |
在进行CFD仿真计算时,网格质量对仿真计算结果的准确性影响较大,精细的网格可以提升计算结果准确性但会显著增加计算负荷,为平衡计算速度和结果精度,在划分网格时,对于破口及柱体内水平面以下部分采用精细网格进行划分。由于流体粘性在边界处对水流的影响较大,破口边界处网格进行进一步细化,其他区域网格按距离进行放大,减少模型网格总数。
在示例C1-300-3D的破口处网格中,边界厚度为0.077 mm,最外沿处网格尺寸为1.511e–05 m,共分为30层,网格尺寸增长率为1.2。网格共计194 335个,其中破口及柱体水平面下部分及附近约13万个。
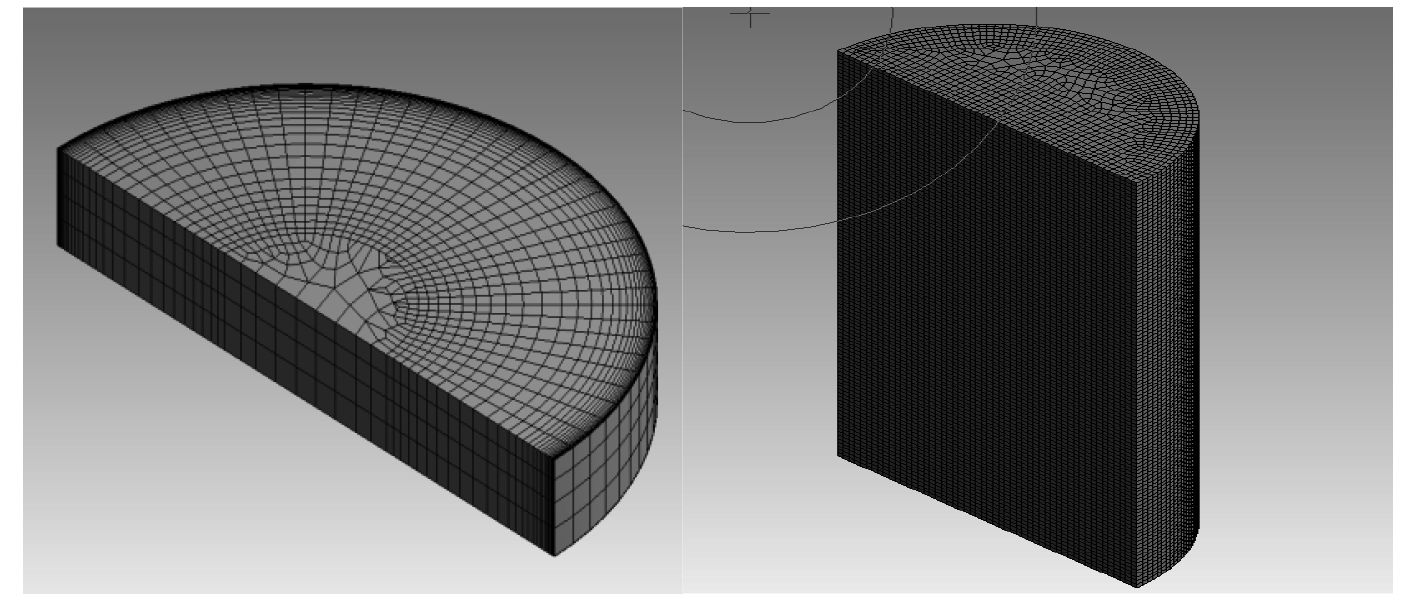
|
图 4 C1-300-3D破口处网格(左)和柱体内水平面以下部分网格(右)示意 Fig. 4 Mesh example of C1-300-3D breach(left)and cylinder below water line(right) |
设置流体a为空气,b为淡水。当t=0时,除柱体及破口外,模型水平面以下部分b的VOF参数为1,a为0,代表这些区域初始充满淡水,其他部分设置a的VOF参数为1,b为0,表示这些区域初始充满空气。柱体上方不封闭,计算过程中柱体空气部分始终维持一个标准大气压。
计算采用K-epsilon湍流模型,空气及淡水不可压缩,柱体在模拟中保持静止。考虑不同时期需要的计算精度不同,为提高计算效率,选用动态计算时间步长,时间步长变化范围从0.000 1~0.01 s,每歩计算都进行一次数据记录。
3 结果与分析 3.1 破口形状对进水流量系数的影响
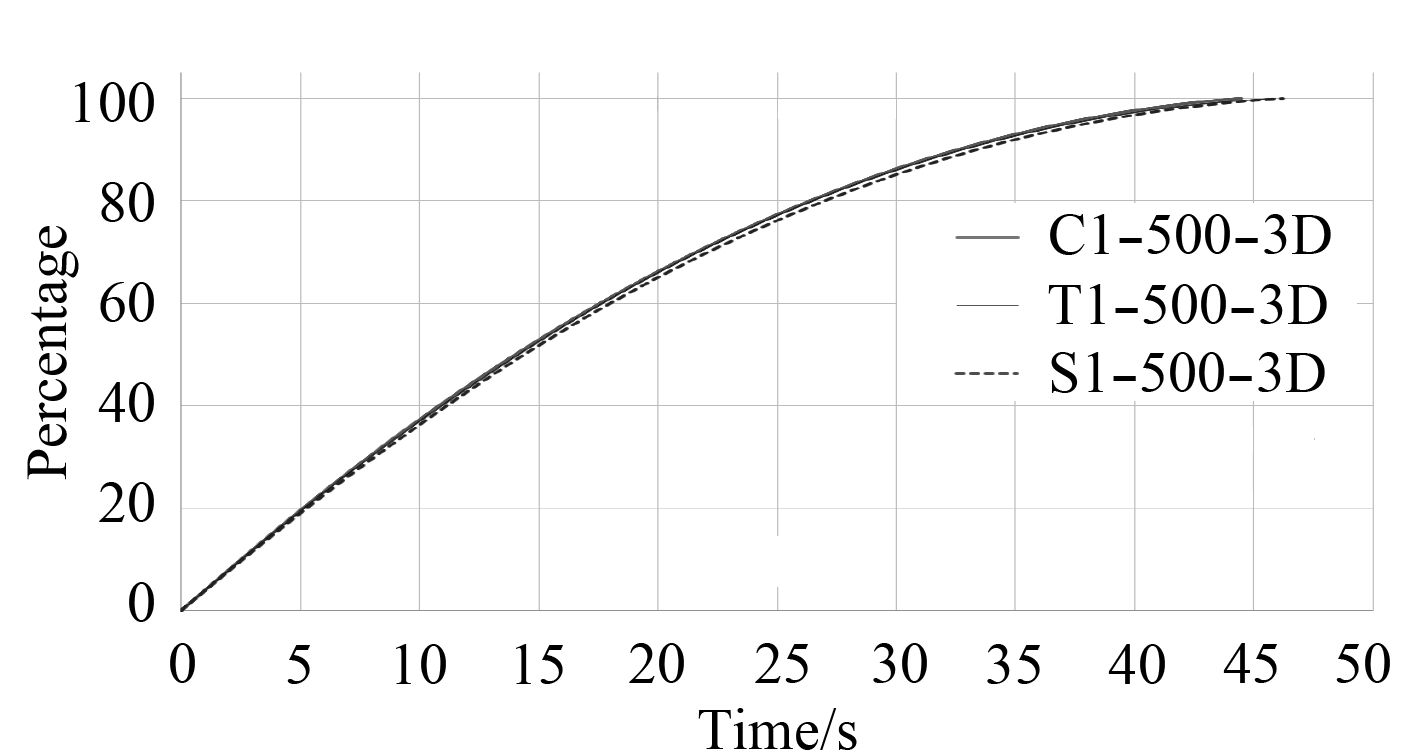
|
图 5 不同破口形状进水填充速率图 Fig. 5 Charge rate for different shapes of breach |
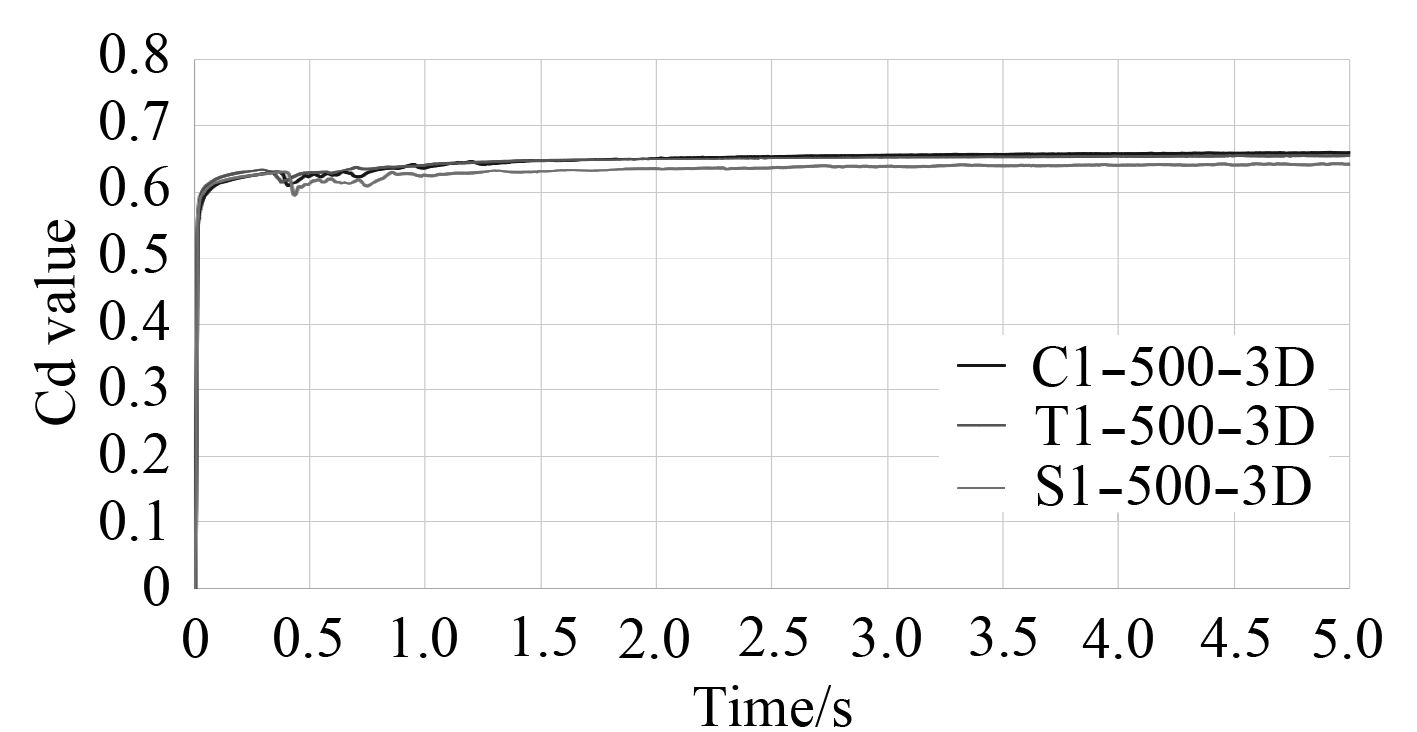
|
图 6 深度500 mm,1%破损,不同破口形状流量系数-时间曲线(前5 s) Fig. 6 Cd value-time curve for different shapes of breach with 500 mm depth and 1% damage(first 5 second) |
在不同深度下,圆形破口的筒体最先被水充满,三角形及方向其次,进一步观察前5 s的进水流量系数-时间曲线,经过最初1 s的震荡波动后,破口为三角形与方形时的进水流量系数均小于破口为圆形时的进水流量系数。同水深下带尖锐边角的破口造成进流相对不稳定,降低了进水速度。可以推断破口形状越不规则,进水流量系数越小。
3.2 破口尺寸对进水流量系数的影响
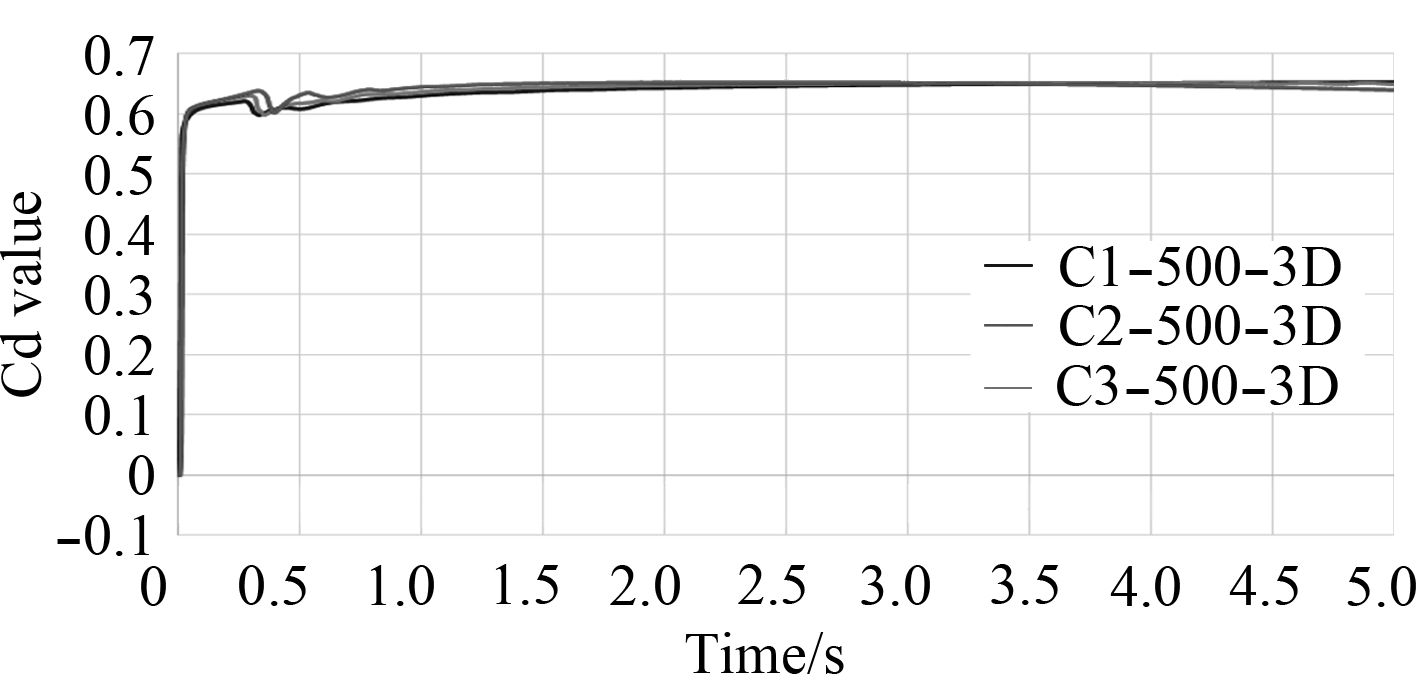
|
图 7 深度300 mm,圆孔,不同破口尺寸流量系数-时间曲线(前5 s) Fig. 7 Cd value-time curve for different sizes of breach with 300 mm depth and circle shape(first 5 second) |
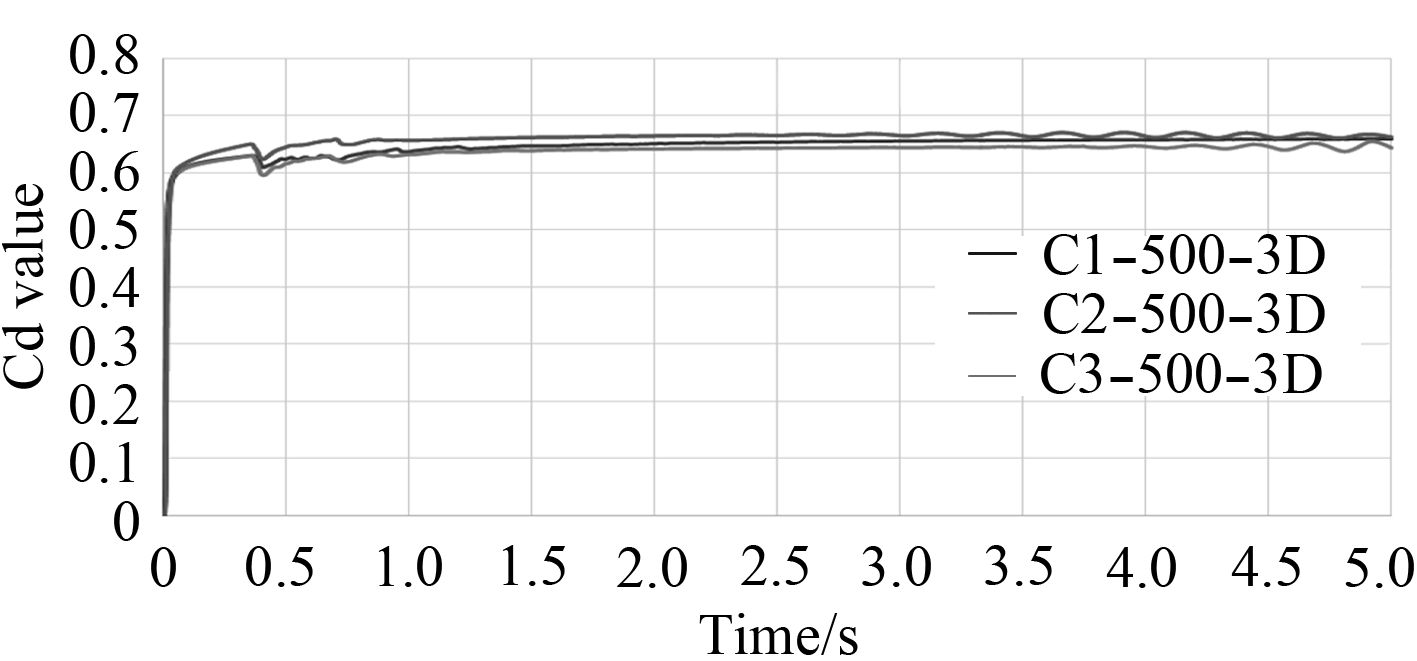
|
图 8 深度500 mm,圆孔,不同破口尺寸流量系数-时间曲线(前5 s) Fig. 8 Cd value-time curve for different sizes of breach with 500 mm depth and circle shape(first 5 second) |
破口尺寸增加会略微增加进水流量系数的大小。随着水深的提高,这种变化越明显。在300 mm水深对比组中,不同破口尺寸的进水流量系数之间相差不大,但在500 mm水深对比组中,破口尺寸最大的C4-500-3D进水流量系数明显高于另2个同组实验。在初始波动后,进水流量系数大多稳定在0.6~0.7之间,这与Wood等[5]在之前的研究结果相同。
3.3 破口水深对进水流量系数的影响
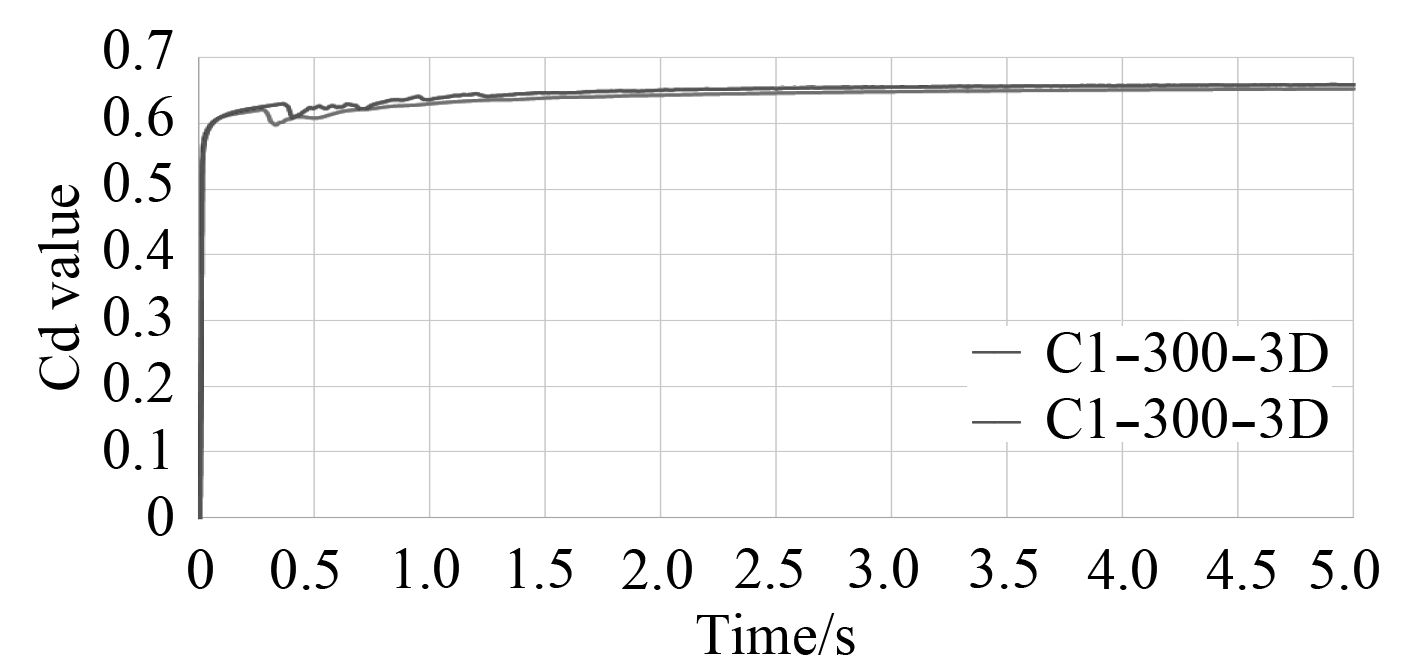
|
图 9 圆孔,1%柱底面积,300 mm和500 mm水深流量系数-时间曲线(前5 s) Fig. 9 Cd value-time curve for 300 mm and 500 mm depth with circle shape and 1% damage(first 5 second) |
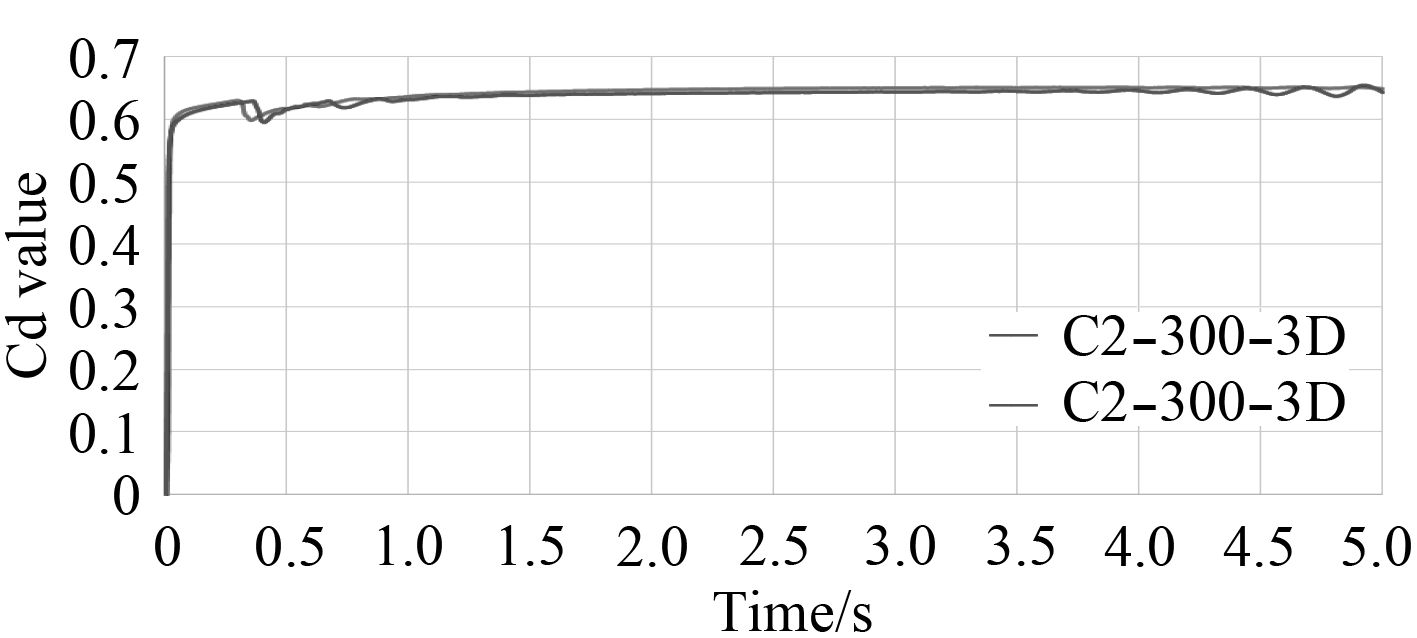
|
图 10 圆孔,2%柱底面积,300 mm和500 mm水深流量系数-时间曲线(前5 s) Fig. 10 Cd value-time curve for 300 mm and 500 mm depth with circle shape and 2% damage(first 5 second) |
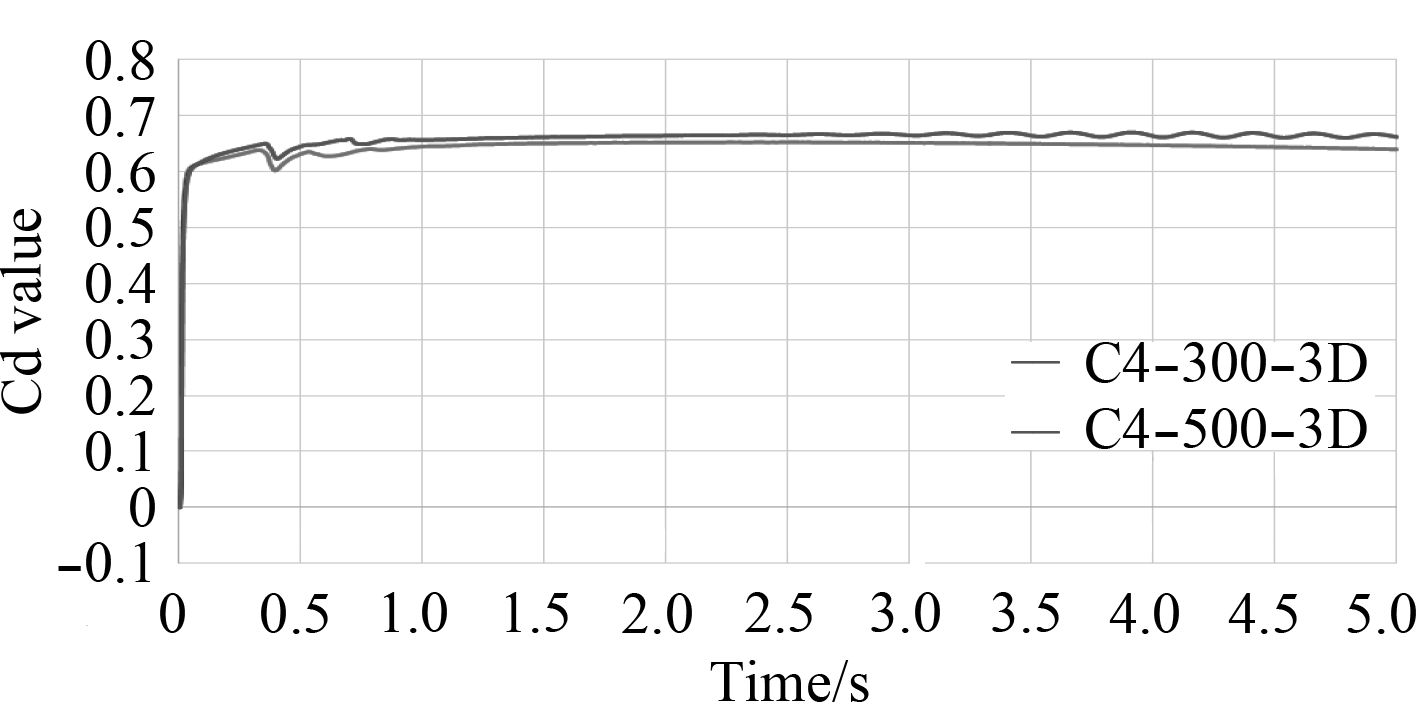
|
图 11 圆孔,4%柱底面积,300 mm和500 mm水深流量系数-时间曲线(前5 s) Fig. 11 Cd value-time curve for 300 mm and 500 mm depth with circle shape and 4% damage(first 5 second) |
破口所处水下深度的增加将提高破口处水压,随着水深增加,不同破口尺寸的进水流量系数出现了不同的变化趋势。1%和4%两种破口面积情况下,水深增加会造成进水流量系数增加,但在2%破口面积情况下,水深增加反而造成进水流量系数降低。不同深度下,1%破口的进水流量系数-时间曲线在3~5 s并未出现明显波动,稳定性明显好于另2组。
4 结 语本文采用Fluent,使用简化模型对船舶底部破口进水情况进行模拟计算。计算结果显示不规则边缘会减缓进水速度,在一定程度上降低进水流量系数Cd的值,增大破口尺寸会略微增加进水流量系数,且会对进水流量系数的稳定性带来不利影响,而水深对进水流量系数的影响暂不明朗。
多种情形的模拟计算均显示出底部破口实际进水速率达不到理论值计算值,在本文模拟场景中,两者差额在35%左右,即进水流量系数Cd的值在0.65左右。本研究结果可为船舶发生底部破损时进行损害评估和制定应急方案提供参考,也为后续船舶破舱问题在真实尺度和二维简化模拟上打下基础。
| [1] |
Ansys, Ansys Fluent, Ansys Fluent Theory Guide[Z], ANSYS inc, 2013.
|
| [2] |
LI J, RENARDY Y. Numerical study of flows of two immiscible liquids at low reynolds number[J]. SIAM Review, 2000, 42(3): 417–439.
|
| [3] |
LI Y, SOBEY A J, TAN M. Investigation in to the effects of petalling on coefficient of discharge during compartment flooding[J], Journal of Fluids ans Structures, 2013, 45: 66–78.
|
| [4] |
TAVAKOLI M T, AMDAHL J, LEIRA B J. Experimental investigation of oil leakage from damaged ships due to collision and grounding[J], Journal of Fluids ans Structures, 2011, 38: 1894–1907.
|
| [5] |
WOOD C D, HUDSON D A, TAN M, et al. Experimental investigation into factors affecting the transient flow of fluid through an orifice in realistic conditions[Z], Fluid Structure Interactions Group, University of Southampton, 2014.
|
| [6] |
李月萌, 段文洋, 金允龙, 等. 基于CFD模拟的船舶破舱进水过程研究[J]. 中国造船, 2016(2): 149-142. DOI:10.3969/j.issn.1000-4882.2016.02.017 |
| [7] |
郑宇, 马宁, 顾解忡. 基于CFD的船舶破舱进水时域模拟[J]. 舰船科学技术, 2017(10): 29-33. DOI:10.3404/j.issn.1672-7649.2017.10.005 |
| [8] |
李昂, 金良安, 田奥, 等. 舰船破口流量系数的仿真研究[J]. 舰船科学技术, 2010(4): 105-108. DOI:10.3404/j.issn.1672-7649.2010.04.026 |
 2019, Vol. 41
2019, Vol. 41
