2. 海军工程大学 动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
全垫升气垫船阻力特性的研究,是为了对其动力系统进行仿真,进而为机桨匹配和控制优化提供基础。但是,由于全垫升式气垫船运行于水、气2种介质的界面上,在航行中受到静水稳态阻力和风、浪引起的动态阻力影响,其阻力来源非常复杂,计算相对复杂。全国船舶标准化技术委员会1983年提出了气垫船静水阻力估算方法[1]。1991年邓佑生[2]提出了气垫船动态阻力的估算方法,并给出了相关的数学模型及阻力系数。李林根和孙永权[3,4]对气垫船的动量阻力、喷射阻力以及气垫船兴波及兴波阻力进行了细致的分析与计算。李青[5]利用数值计算分析阻力,提出了数值计算方法,计算出兴波阻力以及阻力系数,并利用瑞典SSPA系列阻力回归计算分析估算方法和船模试验进行对比评估。
可以看出,国内学者在大型气垫船阻力特性仿真研究中没有很好地反映出气垫船阻力的整体特性,同时并未将海洋环境以及装载等因素考虑到阻力计算当中。针对这些问题,本文以某大型全垫升气垫船为研究对象,全面分析了气垫船的各阻力分量,建立了仿真模型。通过仿真实验,研究全垫升气垫船在不同航速下阻力的变化规律,获取了在不同环境因素和装载条件下的阻力特性曲线,分析了外部环境对其阻力的影响和各因素的影响权重。
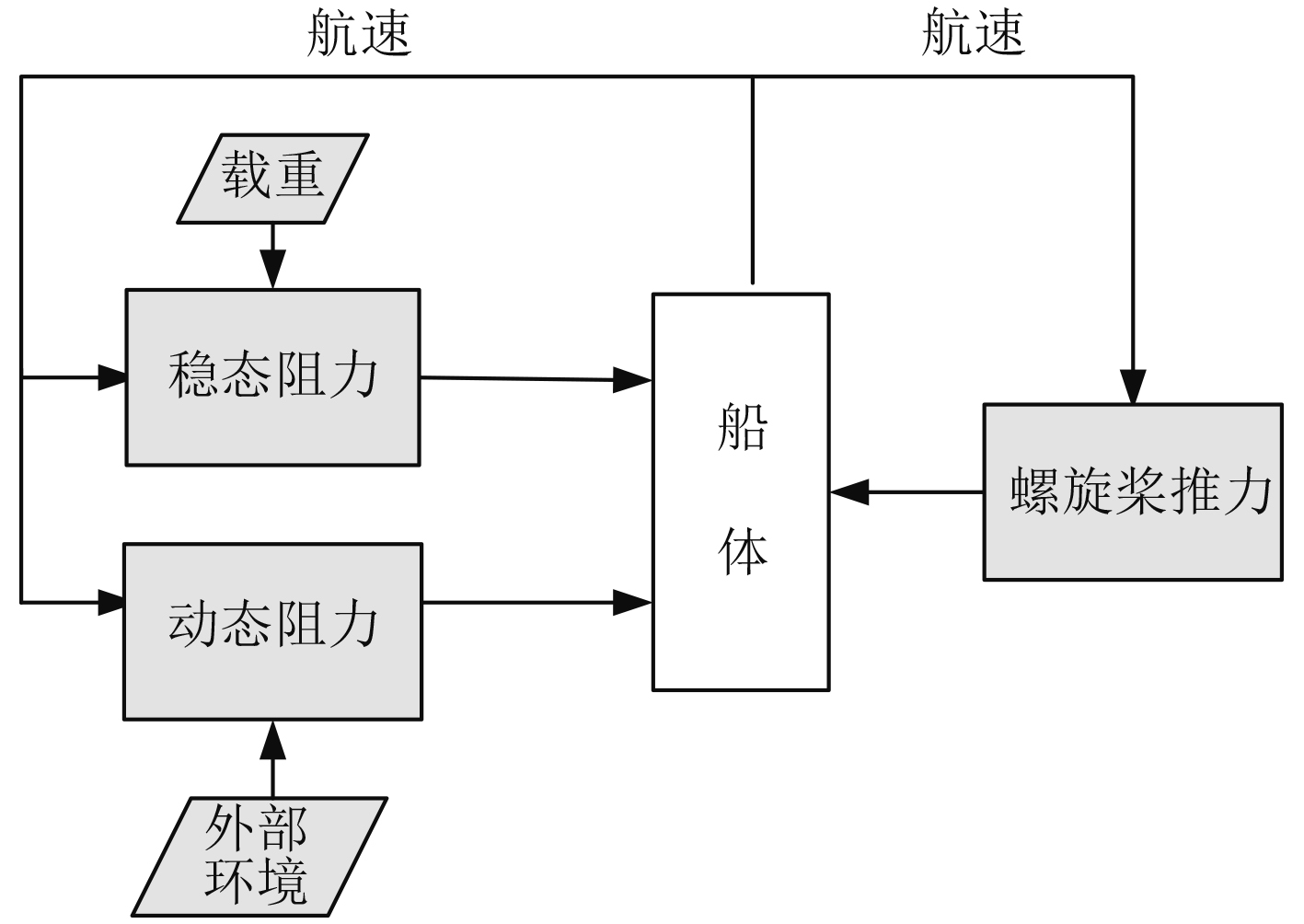
1 阻力系统仿真原理 1.1 大型气垫船阻力系统物理模型气垫船阻力由稳态阻力与动态阻力组成,其中外部环境主要影响动态阻力,载重则主要影响稳态阻力。物理模型如图1所示。
|
图 1 阻力系统模型 Fig. 1 Resistance system model |
气垫船是利用空气螺旋桨产生推力,克服船体阻力进行推进。气垫船在变速过程中的速度变化率与推力和阻力的矢量和成正比:
| $ \frac{{\rm d }v}{{\rm d }t} = \frac{1}{m}(F - R){\text{。}} $ | (1) |
对上式积分可得船速计算公式为:
| $ v = \int {\frac{{F - R}}{m}{\rm d}t}{\text{,}} $ | (2) |
式中:
龙格库塔算法是对微分方程的数值解法,该方法的思想是在积分区间内进行插值,优化总的斜率得到更新结果,其精度应高于直接积分[6]
因此,本文从气垫船阻力系统的原理性微分方程出发,采用4阶5级龙格库塔算法,在计算过程中修正步长,保证计算精度。从而在每次循环中直接取得总阻力
气垫船水面垫态航行总阻力
| $R = {R_a} \!+\! {R_m} \!+\! R_w^{} \!+ \!{R_z} \!+ \!{R_{se}}\! + \!{R_{sw}} \!+\! \Delta {R_a} \!+ \!\Delta {R_m} \!+\! \Delta {R_{se}} {\text{,}} $ | (3) |
| $ {R_a} = {C_a} \cdot \frac{{{\rho _a} \cdot {V^2}}}{2} \cdot {S_a}{\text{。}} $ | (4) |
式中:
| $ {R_m} = {\rho _a} \cdot {Q_f} \cdot V {\text{,}} $ | (5) |
式中:
| $ \mathop R\nolimits_w = \mathop C\nolimits_w \cdot \frac{{\mathop P\nolimits_c^2 \cdot \mathop B\nolimits_c }}{{\mathop {g \cdot \rho }\nolimits_w }} {\text{,}} $ | (6) |
式中:
| $ {R_z} = W \cdot \alpha {\text{,}} $ | (7) |
式中:
| $ {R_{se}} = {K_1} \cdot {10^{ - 6}} \cdot {\left( {\frac{h}{{{C_l}}}} \right)^{ - 0.34}} \cdot {C_l} \cdot \sqrt {{S_c}} \cdot {q_w} {\text{。}} $ | (8) |
式中:
| $ {R_{SW}} = \left[ {2.816\;7 \cdot {{\left( {\frac{{{P_c}}}{{g{L_c}}}} \right)}^{ - 0.259}} - 1} \right] \cdot {R_w}{\text{,}} $ | (9) |
| $ \Delta {R_a} = {C_a} \cdot \frac{{{\rho _a} \cdot {{(V + {V_b})}^2}}}{2}{S_a} - {R_a}{\text{,}} $ | (10) |
式中:
| $ \Delta {R_m} = {\rho _a} \cdot {Q_f} \cdot {V_b} {\text{,}} $ | (11) |
| $\Delta {R_{se}} = {q_w} \cdot {C_l} \cdot \sqrt {{S_c}} \cdot 20 \times 1{0^{ - 5}} \cdot {\left[ {\frac{{2{H_w}}}{{({H_c} + {H_f}) \cdot 1.604}}} \right]^{5 / 3}}{\text{。}} $ | (12) |
式中:
为仿真计算气垫船航速,本文螺旋桨推力模型采用参考文献[7]的经验公式进行仿真。
3 仿真计算及结果分析本文利用模块化建模思想在Matlab/Sim-ulink仿真平台上搭建了包括稳态阻力、动态阻力、推力、船体等组成的气垫船阻力系统仿真模型。同时在仿真计算过程中做如下基本假定:
假定1 表1所示数据即为海况等级与风速、有义波高的对应数据。
|
|
表 1 海况等级与风速、有义波高对应表 Tab.1 Corresponding table of sea state level, wind speed and significant wave height |
假定2 螺旋桨推力是在燃机0.8工况,额定转速,最大螺距角条件下产生的。
假定3 风机流量及气垫压力的取值均在垫升风机额定工作点处。
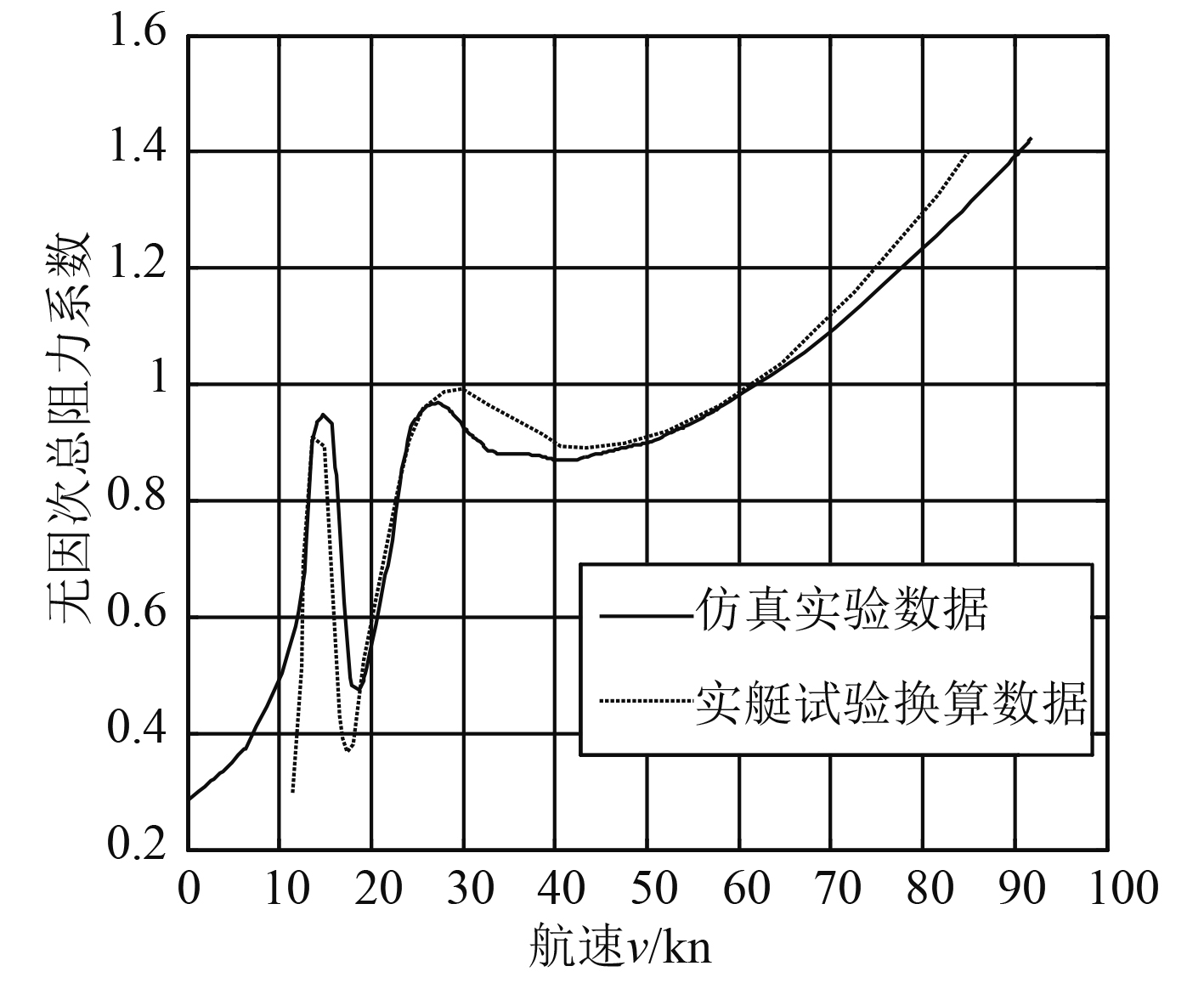
3.1 阻力仿真结果及分析根据大型艇气垫船数据,在排水量554 t,海况2时,仿真得出的气垫船无因次阻力的变化曲线,并与实艇试验换算数据进行对比,如图2所示。
|
图 2 仿真阻力数据与实艇试验换算数据对比曲线 Fig. 2 Comparison curve between simulated resistance data and converted data of real boat test |
图2表明,总阻力在航速较低的情况下会迅速升高,在15 kn时会达到第一个峰值,随后迅速降低,在19 kn时总阻力为最低值,而在28 kn时则会达到第2个峰值,随后会略微降低,当航速达到40 kn后阻力会随着航速的增加而不断升高。这是由于当航速低于40 kn时,兴波阻力起主导因素,总阻力变化趋势随着兴波阻力系数曲线变化而变化。但其他阻力会随着航速的增加而不断升高,因而当航速超过40 kn时,其他阻力成为了影响总阻力的主导因素。
本文方法得出的阻力值与实艇试验换算数据结果基本一致,整个加速过程中最大误差为4.5%,说明本文所阐述的阻力值计算方法能够较好反映该艇阻力特性。在计算过程中,阻力计算存在偏差的原因:
1)本文对海况和风速的对应关系只是根据简单的海况风速表进行赋值,和实际情况存在一定出入,并不能很好地反应实际情况;
2)本文所使用的兴波阻力系数曲线由Newman图谱插值得到,且其海水密度、空气密度取值均与实际情况存在误差,故在阻力变化过程中存在偏差;
3)推力值公式是由经验公式得来,计算值与实际情况有差别。
3.2 气垫船阻力影响因素分析1)海况对气垫船阻力的影响
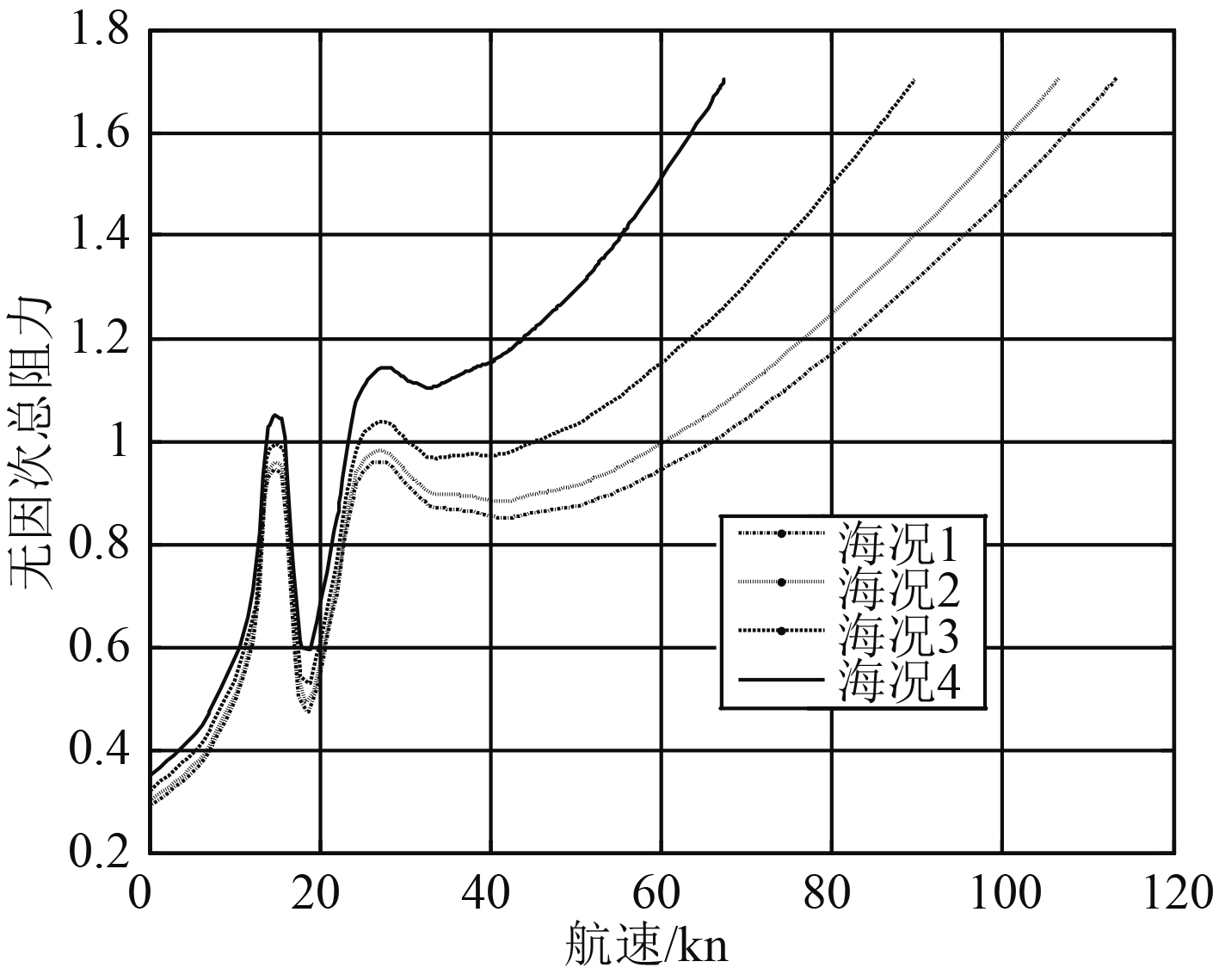
假定在空气密度为1.29 kg/m3、逆风且其他参数不变的情况下,气垫船阻力在不同海况等级下的曲线如图3所示。
|
图 3 气垫船总阻力随海况变化特性曲线 Fig. 3 Characteristic curve of total resistance of hovercraft changing with sea condition |
由图3的阻力计算结果可知,在逆风、其他参数不变的情况下,气垫船阻力随着海况的升高即风速越强、有义波越高,阻力值越大,在航速较低的情况下阻力值变化不大。当航速在20 kn时,海况4阻力值是海况1阻力值的1.30倍;当航速在40 kn时海况4阻力值是海况1阻力值的1.42倍;当航速在60 kn时,海况4阻力值是海况1阻力值的1.7倍。因此,在海况不好的情况下为确保舰艇续航力,应控制航速在20~30 kn之间;同理,在海况良好的情况下,可尽快跨过阻力峰值。
2)风向对阻力值的影响
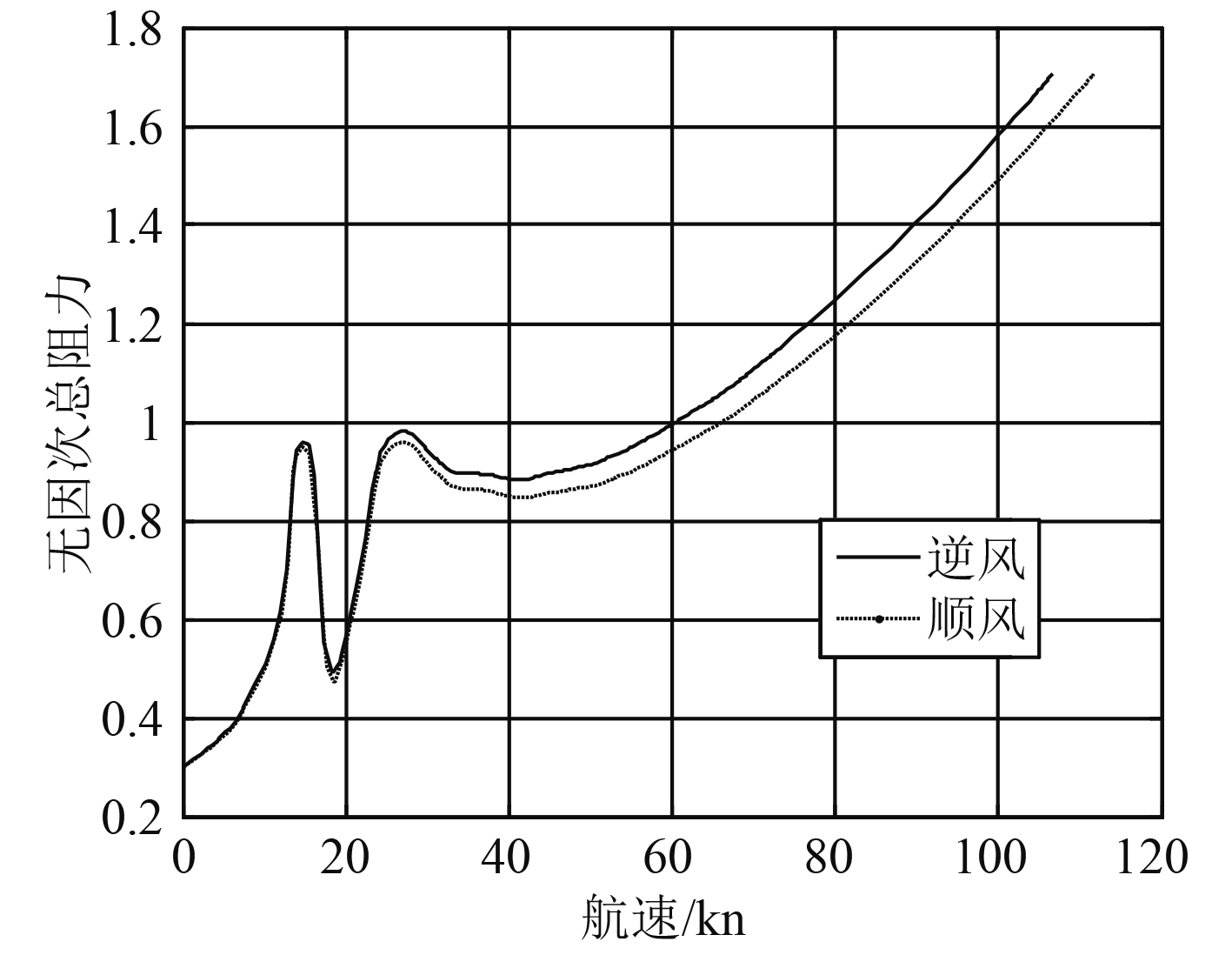
假定在海况2且其他参数不变的条件下,气垫船在顺风与逆风情况下阻力值曲线如图4所示。假定在海况4且其他参数不变的条件下,气垫船在顺风与逆风情况下阻力值曲线如图5所示。
|
图 4 海况2气垫船总阻力随风向变化特性曲线 Fig. 4 Characteristic curve of total resistance of hovercraft changing with wind direction under sea condition two |
|
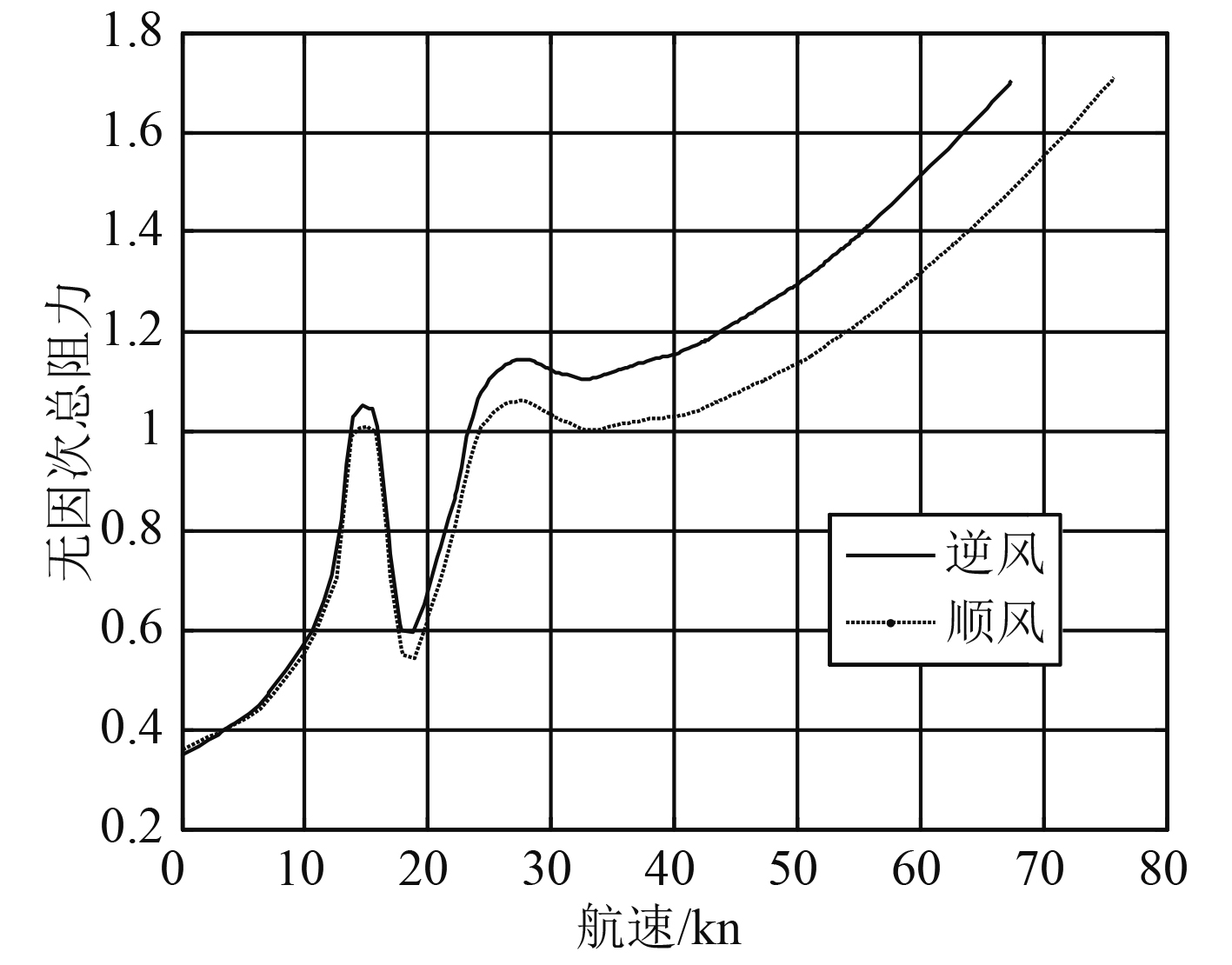
图 5 海况4气垫船总阻力随风向变化特性曲线 Fig. 5 Characteristic curve of total resistance of hovercraft changing with wind direction under sea condition four |
通过图4和图5对比不难发现,相同航速下顺风的阻力值较小;在航速较低的情况下,顺风阻力与逆风阻力相差不大;当航速达到28 kn后,相同航速下,逆风阻力比顺风阻力大,但二者差值基本保持一致;当航速在60 kn时,海况2的逆风阻力是顺风阻力的1.06倍;海况4的逆风阻力是顺风阻力的1.15倍,即海况越恶劣,顺风阻力与逆风阻力差值越大,风向对阻力值的影响越大。
3)空气温度、装载对气垫船阻力的影响
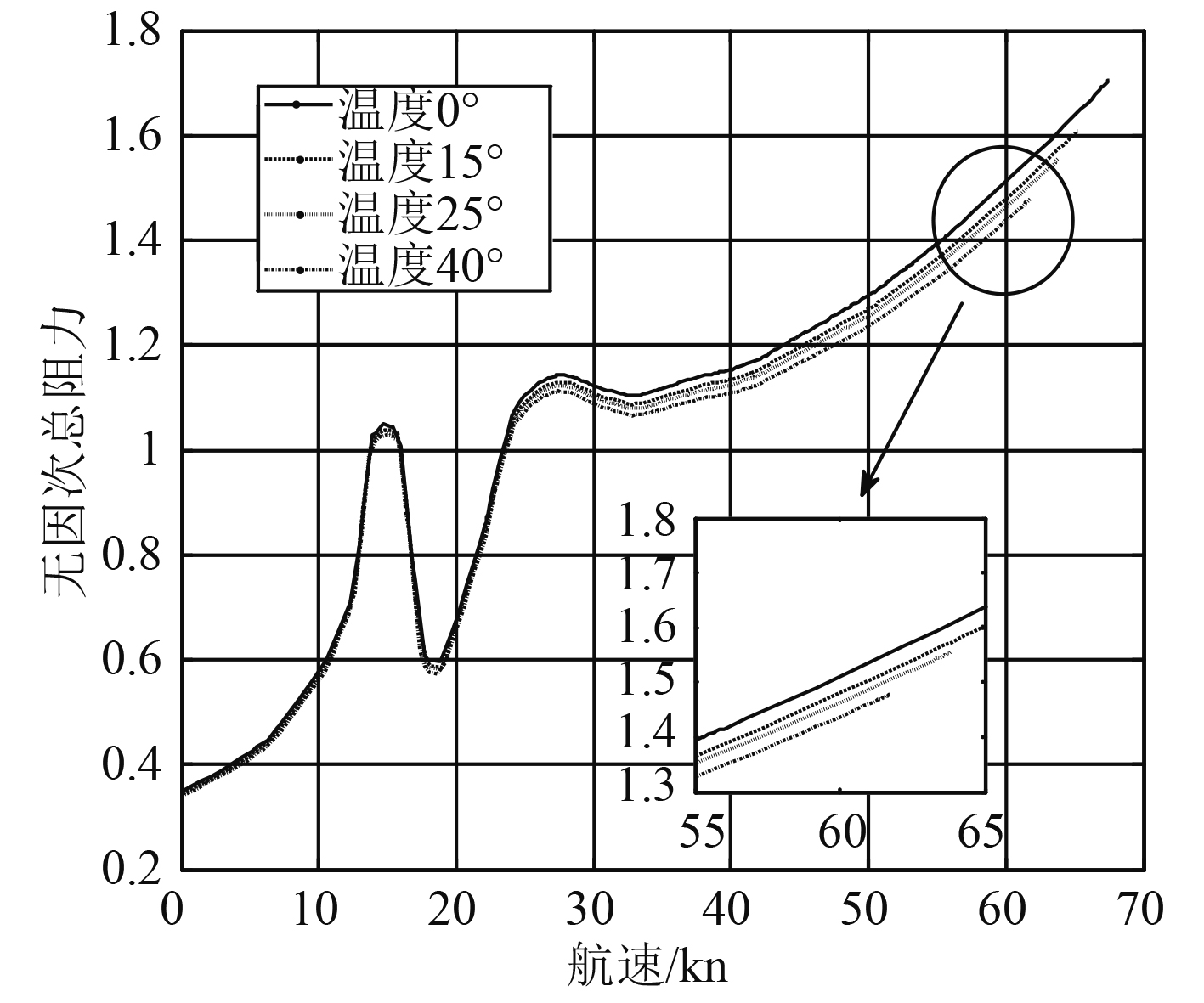
假定在海况4、逆风,其他参数不变的情况下,气垫船在不同外部温度下阻力曲线如图6所示;而图7表示在海况4、逆风,其他参数不变的情况下,气垫船在不同装载下的阻力曲线。通过图6和图7不难发现,空气温度越高,空气密度越低,装载越少,气垫船阻力越低。当在低速的情况下,空气温度阻力几乎没有影响,装载对气垫船阻力有一定的影响。当达到一定的速度时,空气温度对阻力的影响随着航速的增加而逐渐增大,但总体上影响并不明显。而船速在7~27kn之间时,装载对阻力值影响不大,但在其他航速时,满载时阻力是空载时阻力的1.1倍左右。
|
图 6 气垫船总阻力随空气温度变化特性曲线 Fig. 6 Characteristic curve of total resistance of hovercraft changing with air temperature |

|
图 7 气垫船总阻力随装载变化特性曲线 Fig. 7 Characteristic curve of total resistance of hovercraft changing with loading |
本文基于Matlab/Simulink软件,建立了气垫船的总体阻力仿真模型,同时验证了仿真模型的有效性和正确性,通过仿真实验分析了气垫船在不同外部环境条件下阻力值的变化规律。
1)总体而言,气垫船在低航速下会达到阻力峰值,随着航速的不断增加,跨过峰值后阻力会有一定程度的下降,而后随着航速不断的增加而增大;
2)在其他外部环境不变的情况下,海况越恶劣,阻力值越大,越不利于气垫船航行,且海况变化对阻力值的变化影响明显,航速越高,影响越大。因此,在海况不好的情况下,应控制航速在20~30 kn之间;同理,在海况良好的情况下,可尽快跨过阻力峰值;
3)在其他外部环境不变的情况下,顺风比逆风的阻力值低,海况越差,风向对阻力值的影响越大;
4)总体上来看,外部气温对阻力的影响并不明显,航速在7~27kn时,气垫船装载对阻力值影响有限,但在其他航速下满载时阻力会比空载时阻力大1.1倍左右。
| [1] |
全国船舶标准化技术委员会.气垫船静水阻力估算方法[S]. CB*/Z 329-83.
|
| [2] |
邓佑生.气垫船原理与设计[M]. 北京: 国防科技图书出版, 1991.
|
| [3] |
李根林, 孙永权. 气垫船的兴波和兴波阻力(续)[J]. 船舶, 1999(2): 58-62. |
| [4] |
李根林, 孙永权. 气垫船的动量阻力和喷射阻(推)力(续)[J]. 船舶, 1999(5): 52-60. |
| [5] |
李青. 利用数值计算分析阻力性能方法初探[J]. 船舶, 2003(6): 15-18. |
| [6] |
王励扬, 翟昆朋, 何文涛, 等. 四阶龙格库塔算法在捷联惯性导航中的应用[J]. 计算机仿真, 2014(11): 56-59. DOI:10.3969/j.issn.1006-9348.2014.11.013 |
| [7] |
安卫, 敖晨阳, 刘强. 气垫船垫升推进系统控制仿真[J]. , 2005, 46(4): 104–107.
|
 2019, Vol. 41
2019, Vol. 41
