2. 武汉理工大学,湖北 武汉 430063
2. Wuhan University of Technology, Wuhan 430063, China
环肋圆柱壳是水下航行器等主要的结构形式,其振动与声辐射问题一直是研究的重点。文献[1-3]分别用解析法和数值法计算了单层圆柱壳的振动和声辐射性能。文献[4-5]分别对不同边界条件下的环肋柱壳在流场中的振动特性进行了理论方面的研究,讨论了不同参数改变下对壳体结构固有频率的影响。文献[6-8]主要研究了单一激励下圆柱壳的模态、振动与声辐射特性。本文在上述文献基础上对单层圆柱壳在不同激励下的振动及水下声辐射进行试验测试,得到单层圆柱壳的振动及水下声辐射特性,将试验结果与结合有限元与边界元的计算结果进行比较分析,为模型结构振动声学性能测试评估提供参考。
1 试验模型试验模型为单层环肋圆柱壳,结构的主体尺寸为长
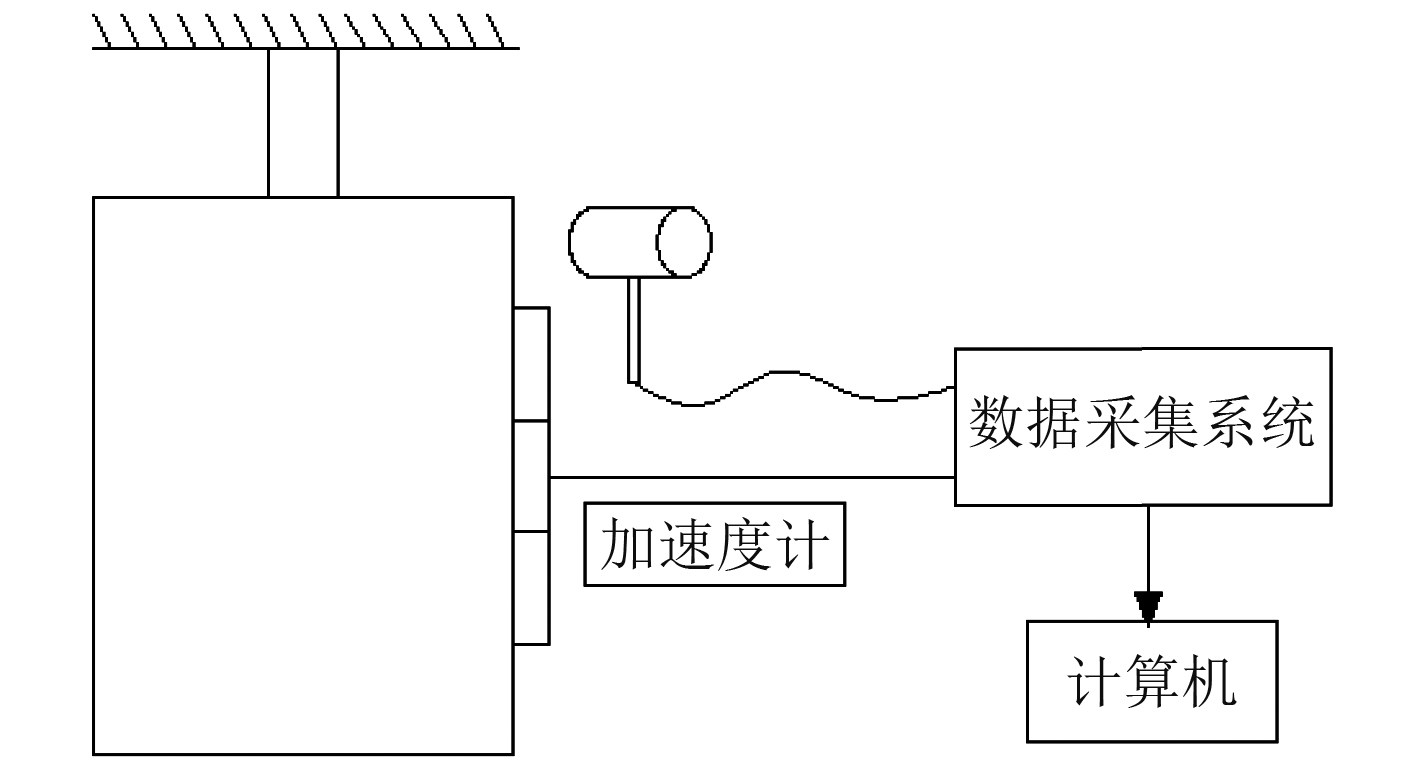
如图1所示,试验振动测试系统主要由消声水池、激振器、信号发生器、数据采集器和加速度传感器等部分组成。消声水池长10 m、宽5 m、深4 m,采用楔形吸声尖劈间隔排列在水池四周。采用柔性绳将吊耳与水池上方航车连接,在模型上端盖放置重物,固定试验模型,以保证试验模型的振动为弹性振动。模型结构与两端端盖处采用螺栓进行固定,并在端盖上开设线缆孔,通过线缆连接激励器和信号放大器,并注意防水密封。

|
图 1 试验模型与测试系统 Fig. 1 Test model and system |
由于圆柱壳为轴对称结构,本试验将圆柱壳沿周向16等分、沿轴向10等分,在轴向和周向上均匀布置测点。
壳体模型自由振动试验通过航车用柔性绳将模型吊起,将加速度传感器布置在圆柱壳的测点上,与数据采集系统连接。通过力锤敲击结构模型,得到其振动响应,在系统的后处理模块中进行分析,得到结构的固有频率及模态,自由振动试验如图2所示。
|
图 2 自由振动试验示意图 Fig. 2 Schematic diagram of free vibration test |
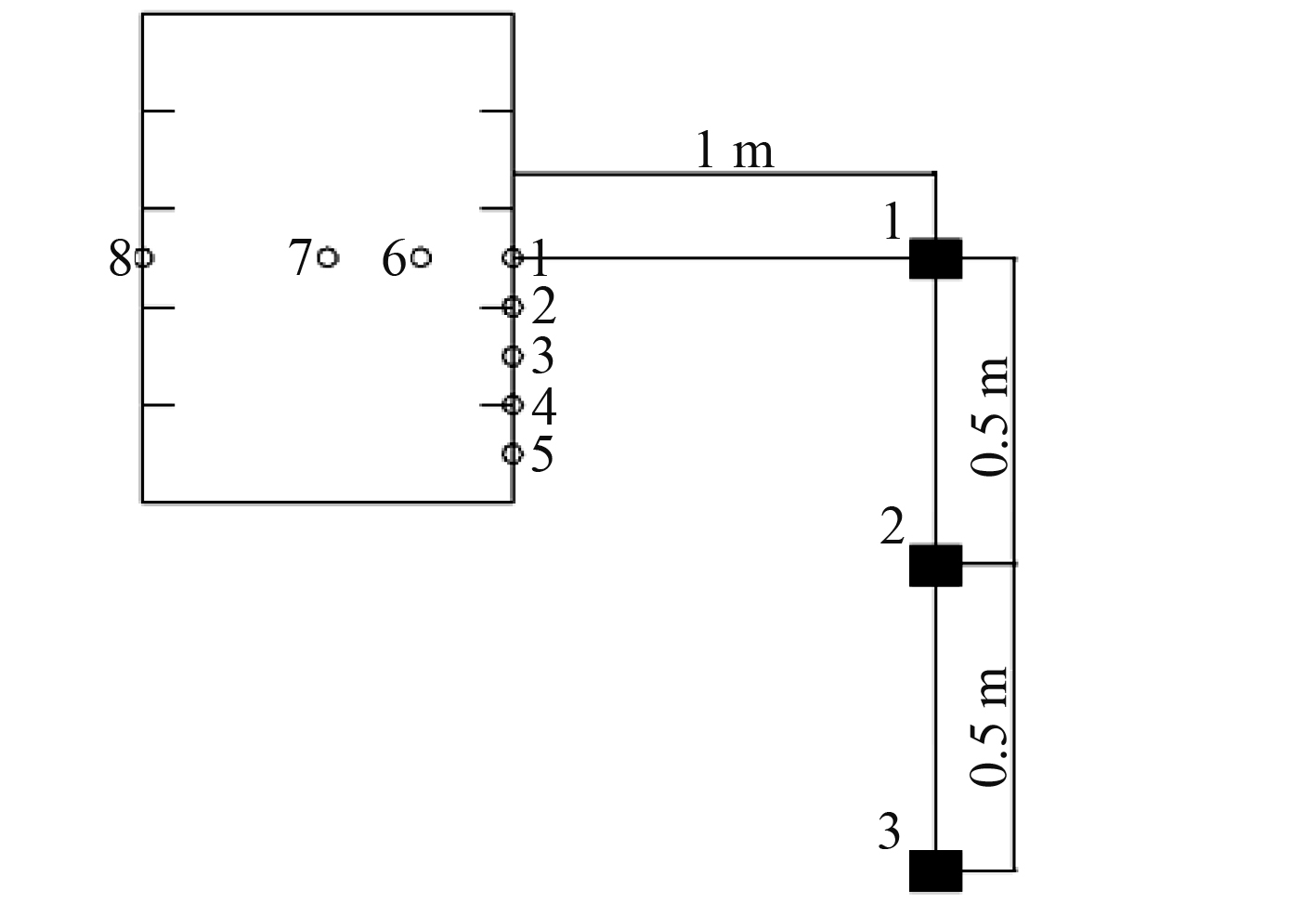
强迫振动测点布置以激振点1为起点沿周向45°,90°,180°水平布置6,7,8号加速度传感器,以激振点1为起点沿轴向向下每间隔0.08 m布置2,3,4,5号加速度传感器,用以记录模型结构的振动情况,测点布置如图3所示。
|
图 3 圆柱壳测点布置示意图 Fig. 3 Schematic diagram of measuring point arrangement of cylindrical shell |
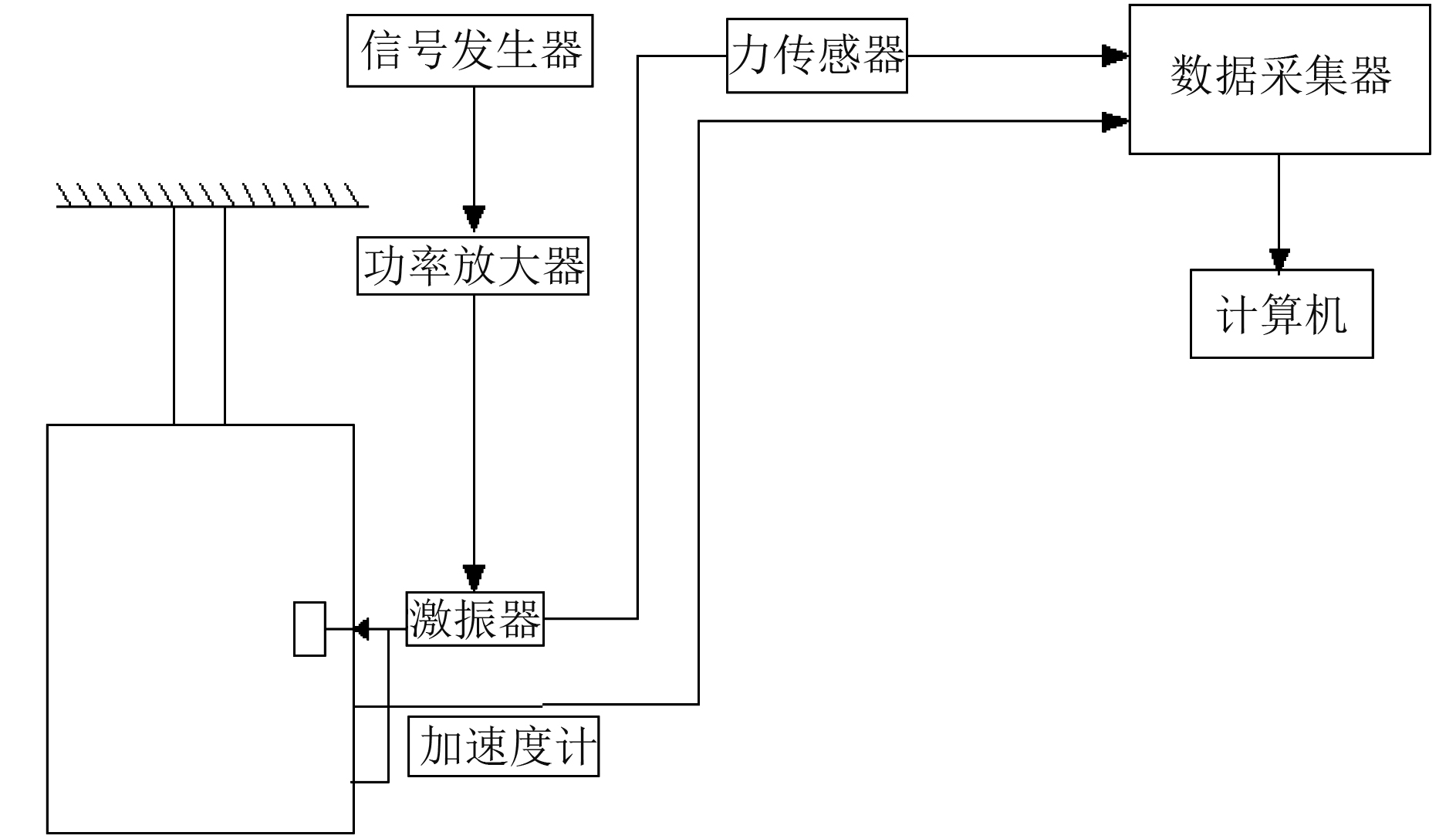
强迫振动试验将激振器和无指向性声源安装于结构内部,如图4所示。
|
图 4 强迫振动试验示意图 Fig. 4 Schematic diagram of forced vibration test |
试验过程中,对于力激励工况下,由信号发生器产生单频正弦信号作为输入信号,经功率放大器放大后驱动激振器工作,对圆柱壳模型进行激励,使结构振动,测得其各测点处的加速度级。在声加力激励工况下,壳体内再加一十二面体无指向性声源,由信号发生器产生输入信号,对圆柱壳进行激励。激励形式为线性扫频(100~4 000 Hz),测其各测点处的加速度级,然后用式(1)将加速度传感器所测得的数据换算成振动加速度级。
| ${L_a} = 20\lg (\frac{a}{{{a_0}}}){\text{。}}$ | (1) |
式中:
声辐射试验各加速度传感器测点布置和空气中强迫振动测点布置相同,由于消声水池的尺度限制,试验在圆柱壳模型结构周围径向1 m处采用水听器固定支架布置3个水听器,水听器在同一平面内垂向等间距布置(见图3),用于测量水下模型结构的水下声辐射。
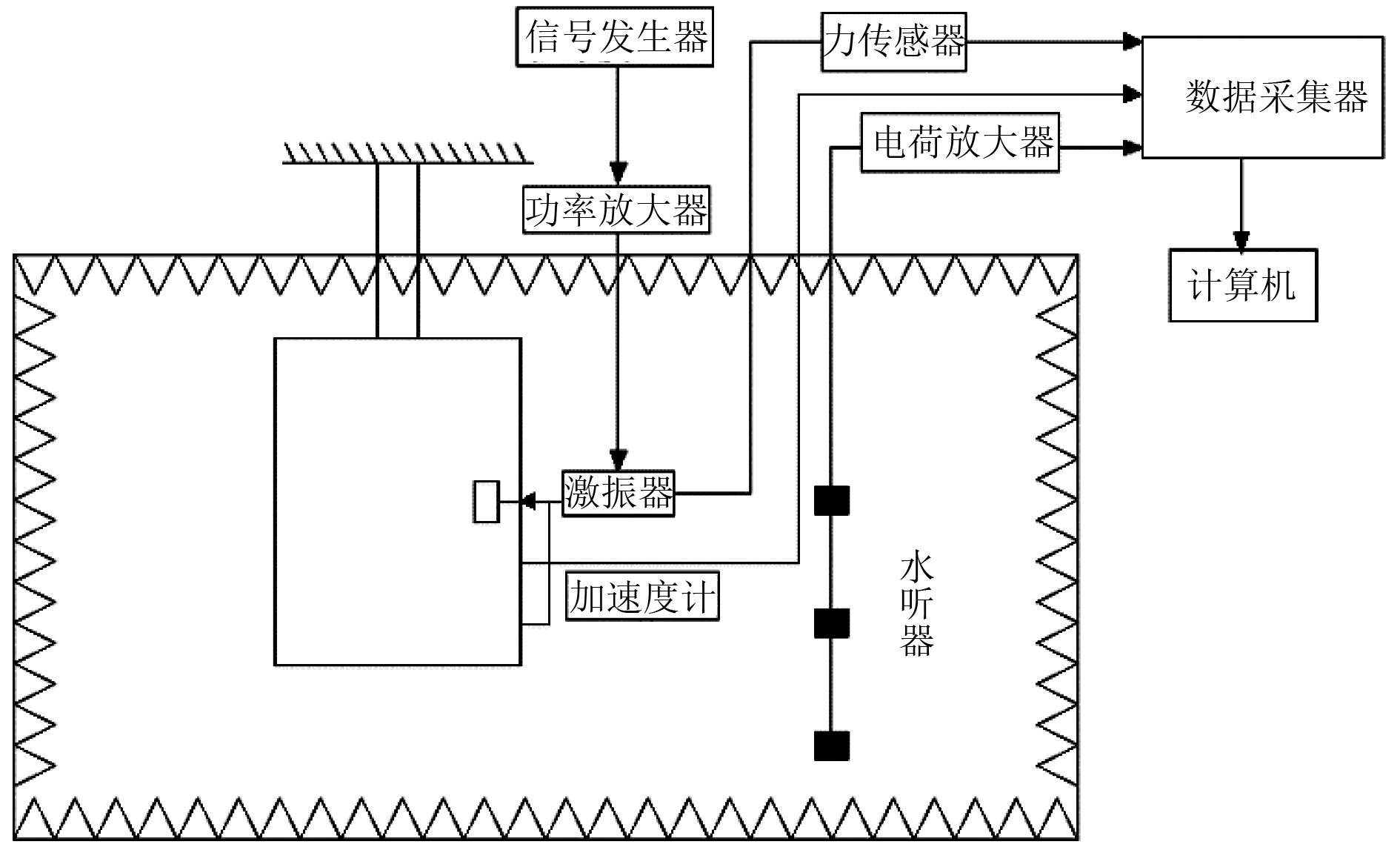
水下声辐射试验如图5所示。将圆柱壳两端盖进行封装,用水密封胶将其密封,用柔性绳将其吊入消声水池中,圆柱壳结构内部设一激振器和十二面体无指向性声源,声源型号为AWA5510,最大声功率级为110 dB。由信号发生器产生输入信号,驱动激振器及无指向性声源工作,对圆柱壳进行激励,使模型在水中向外辐射声压。激励形式为线性扫频(100~4 000 Hz),包括激振器线性扫频、声源线性扫频、激振器和声源线性扫频。然后用式(2)换算得到水听器测得的辐射声场的声压级。
|
图 5 水下声辐射试验示意图 Fig. 5 Schematic diagram of underwater acoustic radiation test |
| ${L_p} = 20\lg (p/{p_0}){\text{,}}$ | (2) |
式中,
根据试验模型的特点和结构参数,采用HyperMesh前处理软件进行建模,得到计算模型结构。本文应用有限元软件Abaqus6.14-4和边界元软件LMS Virtual.Lab Acoustics 12来计算结构的振动和声辐射。以结构表面振速作为结构振动和声辐射的边界条件,将Abaqus计算得到的振动响应文件导入Virtual.Lab中,与声学模型网格耦合,计算处理得到结构的声学物理量。
3.1 自由振动试验数据与数值计算分析为保证振动响应及声辐射数值计算的准确性,如表1所示。将试验结构与有限元建立的壳体结构计算模型的固有频率进行对比。对比分析可知,有限元数值计算结果的误差较小,最大误差在5%以内,为之后的强迫振动及声辐射计算提供了基础。
|
|
表 1 试验与数值计算固有频率比较 Tab.1 Comparison of natural frequencies between experimental and numerical calculations |
将单层圆柱壳各测点得到的加速度进行处理,得到各测点的在测试频段内加速度响应幅值,对采集到的数据进行频谱分析。利用Abaqus软件对试验模型的振动响应进行有限元仿真计算。在空气中,圆柱壳两端面沿圆周边自由,激励力作用在圆柱壳中心位置,测量激励为1 N正弦激励。在试验过程中发现,声激励对于振动的影响较小,故仅将力激励振动加速度级计算结果与试验对比,由于圆柱壳结构具有高度的对称性,为不失一般性,这里仅给出部分具有代表性的测点响应结果,如图6所示。

|
图 6 空气中强迫振动各测点频率响应对比图 Fig. 6 Frequency response comparison of forced vibration in air at different measuring points |
可知,在100~1 500 Hz频段,振动加速度响应在共振峰值处相差不大,计算值略低于试验值,试验测试峰值数较有限元计算值多。这主要是由于模型制造误差和缺陷引起的结构局部振动较多,导致局部模态增加,而有限元计算模型忽略了初始缺陷等因素,较为理想化;在实际工况中,实际边界条件与有限元计算不能完全相似。在1 500~4 000 Hz频段,计算值与试验值误差增大,可能原因是激振器在高频时易导致信号失真。从整体上看,在环频段内计算值和试验值振动响应趋势吻合较好,说明模型振动响应计算方法可靠,计算结果可信。
图7选取了响应较强的1,2,3测点处的数值计算振动响应。从图中可看出,在环频段内,壳体的振动响应都随着频率的增加而增高,单层壳2,3测点较激励点(1测点)峰值平缓,是因为激振点处的振动远高于2,3测点,2测点处的响应较低于3测点,这是因为2测点在环肋处,环肋增大了壳体刚度,降低了振动响应。图中A,B,C三处峰值为别在340 Hz、680 Hz和840 Hz处,这与模态响应结果一一对应。从侧面反映了结构模态振型对比较好,计算结果与试验结果误差不大。
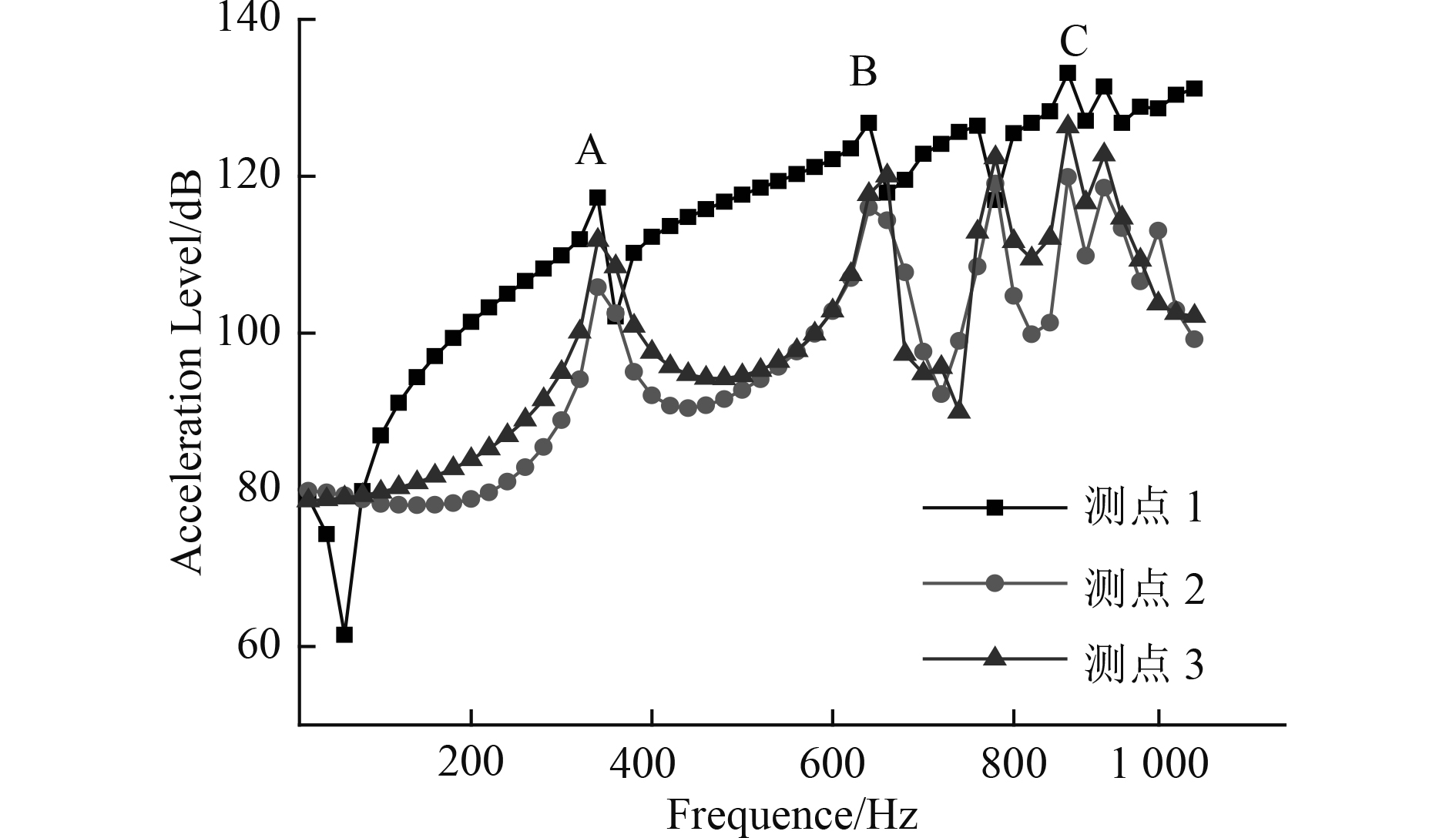
|
图 7 各测点振动响应对比图 Fig. 7 Vibration response contrast diagram of each measuring point |
对于水中的谐响应振动,为降低软件计算规模,需控制流场大小,流场规模的控制需要保证有限域流场大小应该确保流体与所要计算结构的耦合效应,并且声波到达流场边界处不反射声压。基于以上条件,流场域最小半径由下式计算确定[9]:
| $ {R_f} \geqslant \max \left(\frac{D}{2} + 0.2\lambda ,2D \right) {\text{。}} $ | (3) |
式中:D为结构的最大直径;
为能满足上述条件,流场边界取距离结构6倍的结构长度,即4.8 m。结合前述,本文流场半径取8 m,流固耦合声场模型结构图如图8所示。
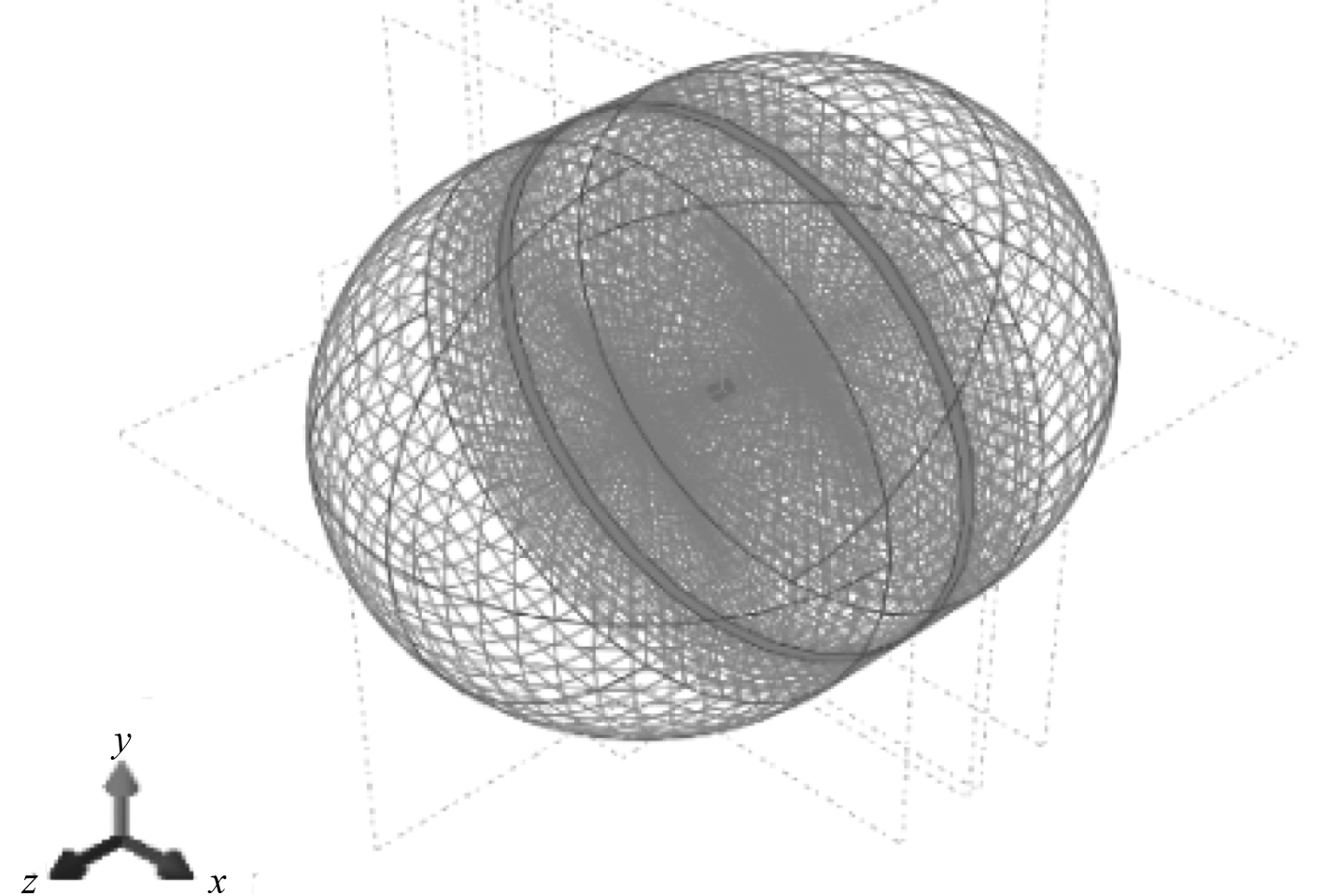
|
图 8 流固耦合模型结构图 Fig. 8 Structural diagram of fluid-solid coupling model |
水中强迫振动各测点频率响应对比图和水中与空气中激振点处频率响应比较图,分别如图9和图10所示。
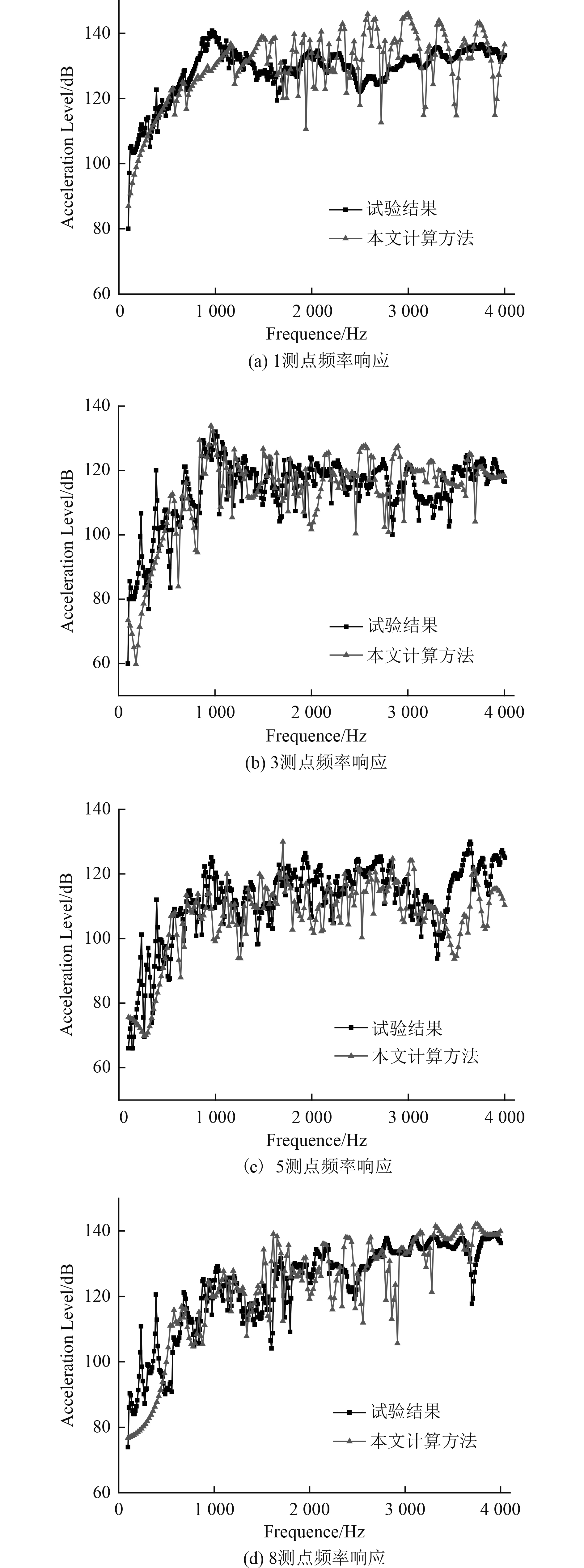
|
图 9 水中强迫振动各测点频率响应对比 Fig. 9 Frequency response comparison of forced vibration in water |
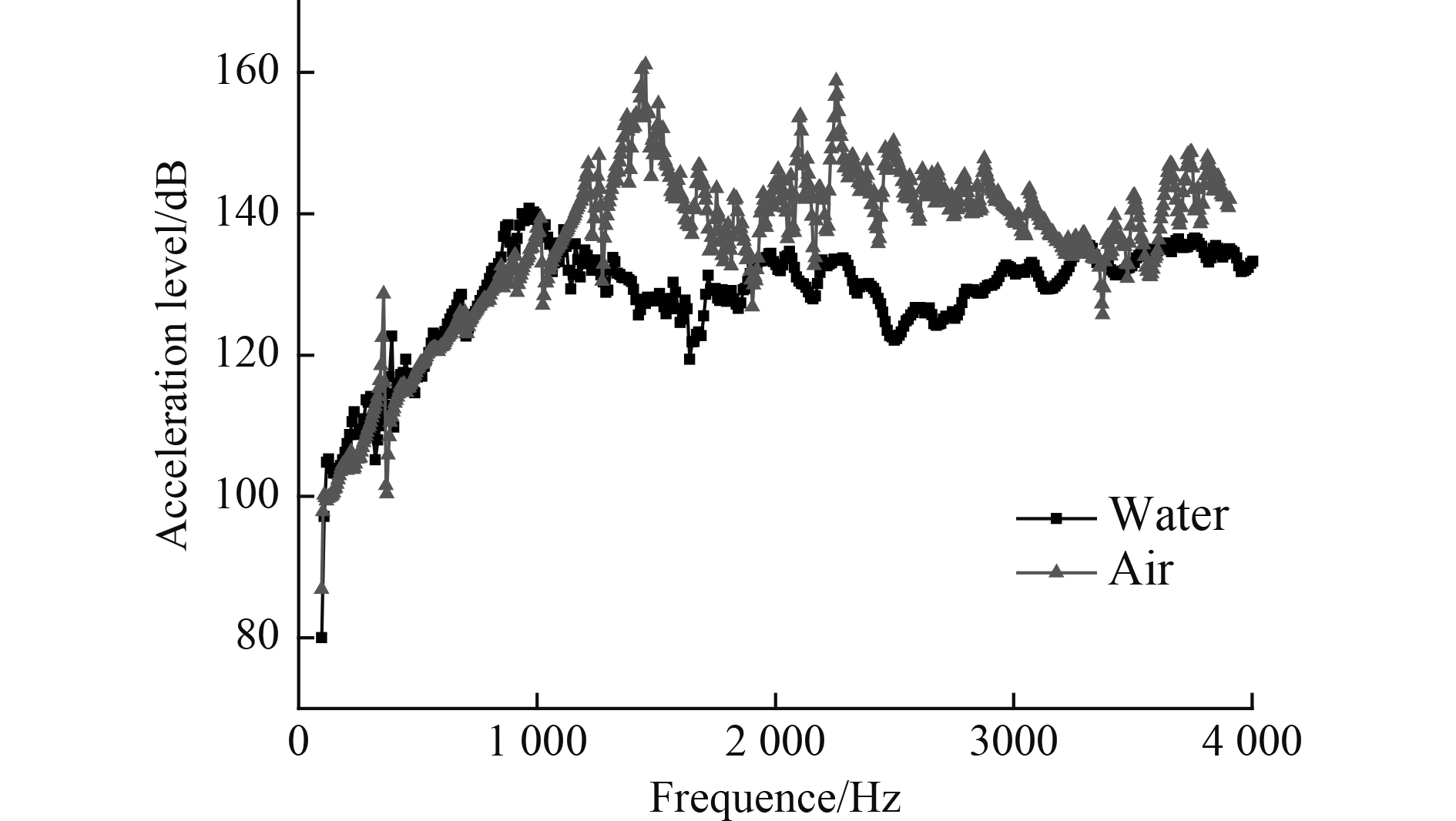
|
图 10 水中与空气中激振点处频率响应比较 Fig. 10 Comparison of frequency responses at excitation points in water and air |
由图9可知,在中低频段可对结构在重流体中的振动特性进行较准确的预报,随着频率的增高,流固耦合模态急剧增加,因此在3 000~4 000 Hz频段数值计算结构与试验值有一定偏差,总体看来本文计算方法与试验结果吻合较好。
对比结合图6、图9和图10可知,在激励处,水中的强迫振动响应比空气中的响应更快地达到峰值,且峰值向低频方向移动,水中的振动加速度响应峰值远低于空气中的峰值;在中低频段(100 ~1 000 Hz),结构在水中与空气中的响应基本吻合,频谱特征及峰值特征较为相似;在中高频段(1 000 ~4 000 Hz),结构在空气中与水中的振动特性差别较大,在空气中的响应出现多个峰值,而结构在水中的响应相较于平缓,且整体低于空气中的响应。以上特性表明:在流场中,圆柱壳的振动受到耦合效应的影响,导致振动频率响应发生改变,而这种变化反映在圆柱壳各阶振动模态上,圆柱壳的振动模态越低,则受流场作用越明显。
3.3 水下声辐射试验数据与数值计算分析基于Virtual.Lab软件对单层圆柱壳结构的水下声辐射特性进行数值计算。在力激励工况下,力作用在圆柱壳中心位置,激励幅值为1 N。场点取为矩形平面,设在结构周围径向1 m处,辐射介质为水,水密度为
1,2,3测点力激励实验值与数值计算值的对比情况如图11所示,可知在中低频内,三测点处所测声压级均无明显突出峰值,高频处的响应略高于中低频响应。如图11(d)所示为1测点处力激励、声激励和力加声激励3种工况下的实验值,其中声激励与力激励响应在频段中差异较大,力激励与力加声激励的声压级响应在100~2000 Hz频段中极为相似,总的趋势表明在力与声同时激励时,力激励为圆柱壳声辐射的主要影响因素。
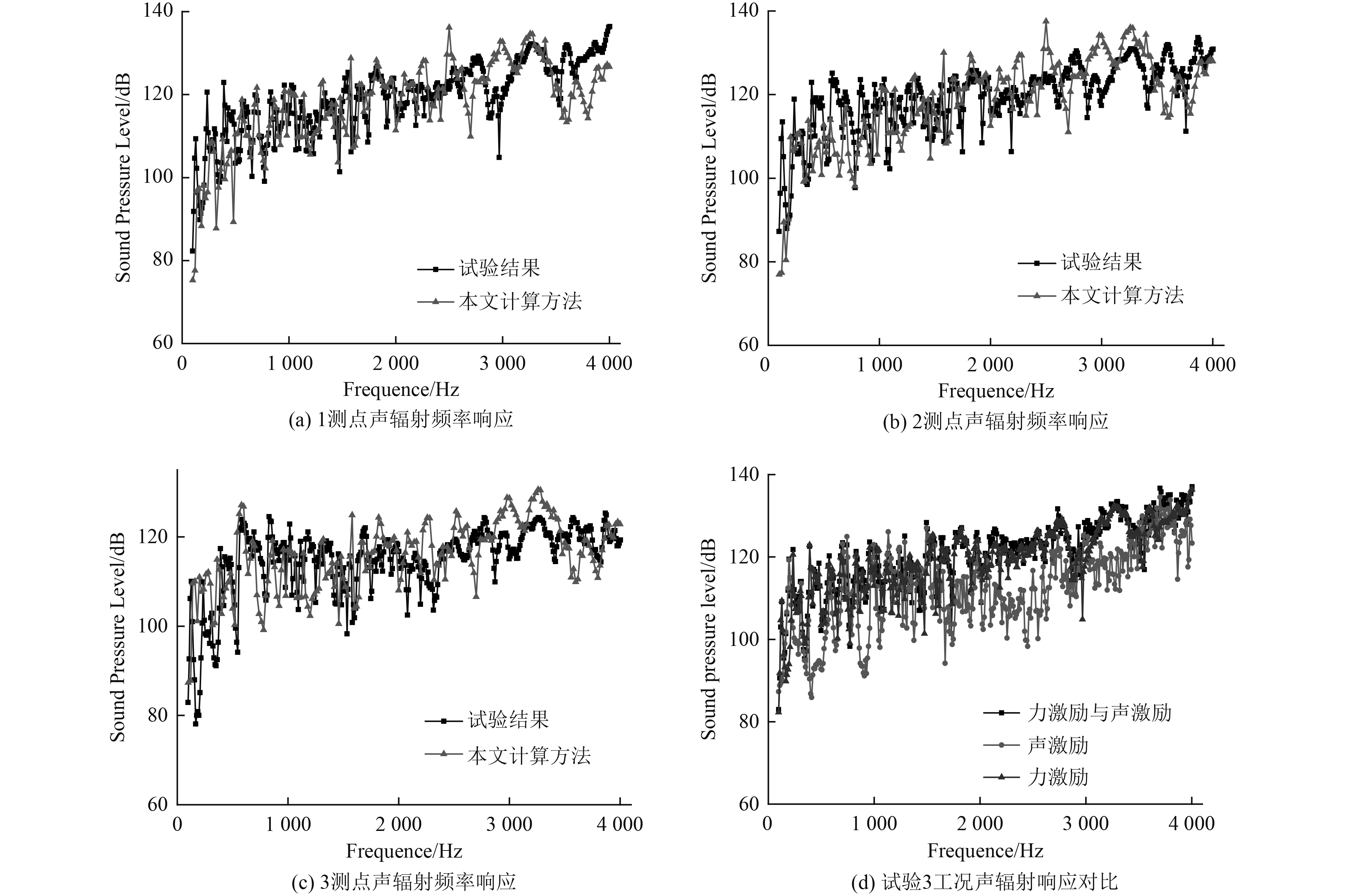
|
图 11 声辐射各测点频率响应 Fig. 11 Frequency response of acoustic radiation |
本文通过对单层环肋圆柱壳在不同激励下的振动与声辐射试验研究,并基于有限元分析和边界元求解相结合,利用Abaqus与Virtual.Lab软件,分别对圆柱壳在空气中与水中的振动及结构声辐射特性进行了数值计算,得出以下结论:
1)通过计算值与实验值对比表明:利用FEM/BEM结合本文所用2种软件,对结构在中低频段的振动和声辐射的预报准确可行。
2)结构在空气中和水中的振动特性有较大差别,通过实验与数值分析发现:在100~1000 Hz频段两者振动响应相差无几,但随着频率增高,空气中振动响应逐渐升高,而水中结构的振动响应衰减较快,逐渐成为有效辐射体。
3)结构在水中的辐射声压响应曲线较为复杂,呈多峰值状,这是因为水中的模型模态密集且规律性差,声激励对结构的影响微弱。
| [1] |
WANG C, LAI J C S. Sound radiation efficiency of finite length acoustically thick circular cylindrical shells under mechanical excitation I:theoretical analysis[J]. J Sound Vib, 2000, 232(2): 431-447. DOI:10.1006/jsvi.1999.2749 |
| [2] |
WANG C, LAI J C S. Sound radiation efficiency of finite length acoustically thick circular cylindrical shells under mechanical excitation II:limitations of the infinite length model[J]. J Sound Vib, 2001, 241(5): 825-838. DOI:10.1006/jsvi.2000.3338 |
| [3] |
KO SUNG Hwan, SEONG Woojae, PYO Sangwoo. Structure-borne noise reduction for an infinite, elastic cylindrical shell[J]. J Acoust Soc Am, 2001, 109(4): 1483-1495. DOI:10.1121/1.1349540 |
| [4] |
骆东平, 徐治平. 环肋柱壳在流场中振动特性分析[J]. 中国造船, 1990(02): 69-81. |
| [5] |
汤渭霖, 何兵蓉. 水中有限长加肋圆柱壳体振动和声辐射近似解析解[J]. 声学学报, 2001, 6(1): 1-5. DOI:10.3321/j.issn:0371-0025.2001.01.001 |
| [6] |
彭旭, 关珊珊, 骆东平, 等. 内部声激励下加筋圆柱壳的声辐射特性分析[J]. 固体力学学报, 2007, 28(4): 355-361. DOI:10.3969/j.issn.0254-7805.2007.04.005 |
| [7] |
杨德森, 张睿, 时胜国. 内部声激励下圆柱壳低阶模态声振特性研究[J]. 哈尔滨工程大学学报, 2017, 38(8): 1210-1215. |
| [8] |
罗琦, 陈美霞, 关姗姗. 内部声激励下单层圆柱壳声振性能的影响规律分析[C]// 船舶水下噪声学术讨论会. 2013.
|
| [9] |
庞福振. 船舶结构噪声截断模型数值预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
 2019, Vol. 41
2019, Vol. 41
