0 引　言

当船舶在极地航行时，船体与海冰将发生频繁、剧烈的碰撞，此时船体将遭受动态效应显著且具有明显非线性特性的冰载荷的作用，对船体结构的安全性将造成较大的威胁。因此，对于各类极地船型，如何准确的预报其在极地航行期间可能遭受的冰载荷是船体结构设计的关键。目前，随着北极航道的开发以及极地资源开发逐步进入实际行动阶段，海冰与结构的相互作用问题已成为目前学术界的一个研究热点。国内外很多学者都在此领域开展了十分深入、广泛的研究。他们采用通常有3类方法，包括（半）解析法、模型或实船实验方法以及数值仿真方法^{[1 – 5]}。基于冰力学和结构动力学理论，解析法虽然理论上比较严谨，但通常只能适用于解决简单的问题。模型或实船实验法的结果最为准确，但是试验条件要求高，实施难度大，限制了其应用范围。相比较而言，数值仿真方法简单易行。随着结构动力学理论的不断发展以及计算能力的不断提高，数值仿真方法已成为研究船冰相互作用问题的一种有效的手段。

本文在现有研究成果的基础上^{[6 – 10]}，以极地多用途集装箱船首部的关注区域为研究对象，参考IACS冰级规范有关内容，应用动态数值仿真方法模拟该船在设计工况下破冰过程。将得到的结构最大应力响应等效目标，提出一种能达到相同动态响应的局部脉冲载荷计算方法。将脉冲载荷极值与规范计算的设计冰载荷之间的比值定义为动力缩放系数，使动态载荷转化为等效静载荷，应用于船体局部结构静力分析。本文提出的动/静态冰载荷计算方法可为极地船设计冰载荷的合理确定提供参考。

1 数值模拟 1.1 碰撞方程的建立和求解

极地船破冰过程是一个动力特性显著、非线性特性明显的过程。对于这个过程中的动态响应求解一般使用显示时间积分方法^[11]。若设当前系统已知时刻为 $t_n$ ，那么 $t_{n + 1}$ 时刻系统的各项参数应该满足运动微分方程式：

${ M}{a'_{n + 1}} + { C}{v'_{n + 1}} + { K}{d'_{n + 1}} = { F}_{n + 1}^{ext}{\text{。}}$

(1)

式中： ${ M}$ ， ${ C}$ 和 ${ K}$ 分别为系统质量矩阵，阻尼矩阵和刚度矩阵； ${ F}_{n + 1}^{ext}$ 为外载荷矢量矩阵； $a'_{n + 1}$ ， $v'_{n + 1}$ 和 $d'_{n + 1}$ 分别为加速度，速度和变形在 $t_{n + 1}$ 时刻的近似值。

显示时间积分法将运动微分方程（1）转化为：

${ M}{a'_{n + 1}} = F_{n + 1}^{ext} - F_{n + 1}^{\operatorname{int} }{\text{，}}$

(2)

${a_n} = {{ M}^{ - 1}}(F_{n + 1}^{ext} - F_{n + 1}^{\operatorname{int} }){\text{。}}$

(3)

式中： $F_{n + 1}^{ext} - F_{n + 1}^{\operatorname{int} }$ 为剩余力矢量。加速度为质量矩阵的逆与剩余力矢量的乘积。

若 ${ M}$ 为一对角阵，则线性方程组为一系列关于各自由度的独立的一元一次方程，从而求得加速度：

${a_{ni}} = { M}_i^{ - 1}(F_{n + 1}^{ext} - F_{n + 1}^{\operatorname{int} }){\text{，}}$

(4)

在时间历程上采用中心差分法，即假设在一个时间步长内加速度是一个定值：

${v_{n + {1 / 2}}} = {v_{n - {1 / 2}}} + {a_n}(\Delta {t_{n + {1 / 2}}} + \Delta {t_{n - {1 / 2}}})/2{\text{，}}$

(5)

${d_{n + 1}} = {d_n} + {v_{n + {1 / 2}}}\Delta {t_{n + {1 / 2}}}{\text{。}}$

(6)

由于显式时间积分法省去了矩阵分解，节省了时间资源，但是考虑到要保证计算的稳定性，需要积分时间步长满足小于网格的最小固有周期的要求，即时间步的取值要小于应力波跨越结构模型最小单元的时间。因此，运用显示时间积分计算应该注意时间步长的大小以保证计算结果的收敛性。在LS-DYNA中，ALE方法的时间步长 $\Delta t$ 是与材料声速、节点速度以及单元特征长度的相关函数：

$\Delta t < \frac{{\Delta l}}{{v + x}}{\text{，}}$

(7)

并应该满足Courant稳定性条件：

$\Delta t < \frac{{\Delta x}}{{Q + \sqrt {{Q^2} + {v^2}} }}{\text{。}}$

(8)

式中： $\Delta l$ 为单元特征长度； $Q$ 为冲击波年度导出参数，对于受压材料取0； $v$ 为材料声速： $v = \dfrac{{0.75G + k}}{\rho }$ ， $G$ 为剪切模量， $\rho $ 为材料密度， $k = \dfrac{P}{\rho }\tfrac{{\partial P}}{{\partial e}} + \rho \dfrac{{\partial P}}{{\partial \rho }}$ ；P为压力。

1.2 模型建立及工况设置

将上述冰载荷数值计算方法应用于1艘极地甲板运输船，该船主要参数见表1。

图1为计算过程中生成的船冰碰撞模型图，包括船首破冰与船尾破冰2种形式；表2为计算工况。

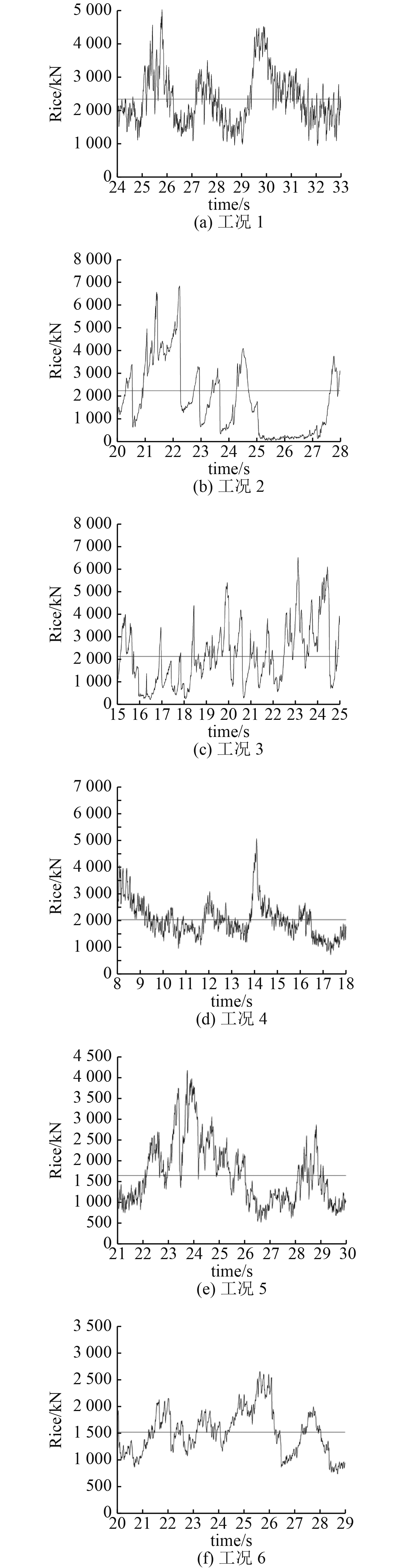
图2为目标船破冰过程中的冰阻力的时历计算结果。该曲线是由多个脉冲曲线组合而成，反映了破冰过程中船体与海冰接触、挤压、弯曲破坏和卸载的过程。冰阻力时历曲线呈现了显著的非线性特性，在船体长周期运动的基础上叠加了船冰作用过程中的局部振动响应。在同一冰厚下，破冰速度越高冰载荷的非线性特性越为明显，冰阻力平均值越大。

2 冰载荷模型试验 2.1 试验模型

海冰模型试验的目的是确定船舶在各种冰情下的性能，主要针对水平冰层，该船在1.5 m冰面上的性能要求为航速达到2 kn。模型缩尺比为1：27；模型的表面按照AARC标准方法处理，表面与冰之间的目标摩擦系数为0.050 ± 0.01，图3显示了研究模型的首尾侧视图。在测试系列开始时，所有传感器都进行了校准，根据AARC标准对阻力、推进参数和冰性质进行了测量，并且保证了在机动测试过程中船只的自由航行特性。

2.2 数值计算结果与试验结果对比

在所有测试中，目标弯曲强度为18.5 kPa（满量程为500 kPa）。层冰试验的测试以船只自推试验为主，首破冰以及尾破冰在2种全尺度冰厚1.0 m和1.5 m下进行试验。所定义的冰阻力通常与船速之间的函数关系是线性的，在指定的冰情条件下船舶达到的航速由净推力曲线和冰阻力曲线的交点确定，当确定不同冰厚下的船舶最大航速，就会生成冰厚对速度曲线（称为h-v曲线）。

在本研究中，关于冰载荷的计算进行了数值模拟和有限元计算，2种结果与实验结果的对比见表3。通过数值模拟、数值仿真计算计算以及船模试验得出了连续式破冰6种工况下冰阻力大小，2种数值计算结果与模型试验结果吻合较好。

3 直接计算值与规范值对比

船冰碰撞是一个动力学问题，但是结构动力分析难度大、耗时长，难以在实际工程中应用。相对而言，静力分析的时效性更好，在工程应用更加广泛，并且与船级社规范结合更加紧密。因此，将基于动力分析算得的冰载准确等效为静态载荷，建立冰载荷作用下的结构静力分析方法对于极地船的结构分析与设计具有重要的意义。

本文以1艘极地多用途集装箱船为研究对象，重点关注其首部冰带区。如图4所示。

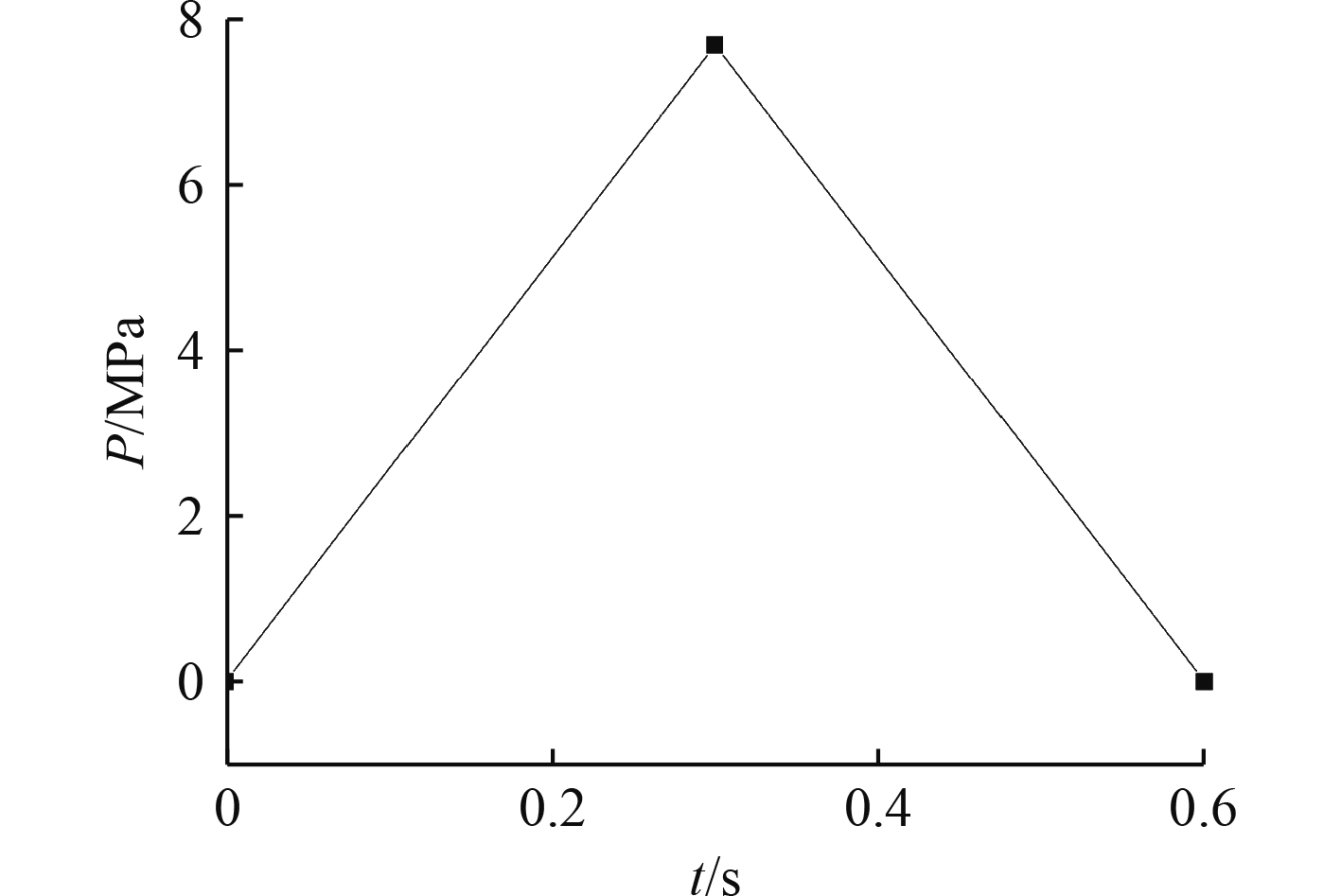
为使船体结构局部效应等同，该位置与IACS规范中计算位置一为同一位置，加载区域面积为规范计算得到的设计作用区域面积。依据国际船级社极地船规范IACS-Polar Class有关内容，确定其设计工况。应用动态仿真方法对该船在设计工况下的破冰过程进行仿真计算，将得到的结构最大等效应力响应等效指标，提出一种能够式船体结构达到同等动态响应的脉冲载荷。如图5所示，等效冰载荷脉冲曲线的响应周期为载荷时历响应的峰值周期（0.6 s），脉冲幅值为使结构响应与动力响应结构一致的载荷值（7.7 MPa）。

在等效冰载荷作用下的结构最大等效应力运动见图6，图中响应最大值为401.162 MPa，与动态响应结果（393.196 MPa）十分接近（相对偏差为2%）。进而，将等效脉冲载荷峰值与规范设计冰载荷的比值定义为动力缩放系数 $\lambda $ ，通过引入该系数，使动态载荷等效转化为静态载荷。表3为该极地多用途集装箱船的规范设计静载荷与规范设计工况下动态等效载荷的对比结果，通过计算可得船首结构动力放大系数 $\lambda $ 为1.542。

4 冰载荷简化模拟方法

冲撞式破冰是具有自破冰能力的极地船的极限工况，船体结构设计冰载荷可通过冲撞式破冰工况计算得到。本文通过数值模拟极地多用途集装箱船冲撞式破冰，借助动力放大系数获得船体结构设计冰载荷（见表4）。

表5为通过该极地多用途集装箱船的准静态方法下的动力缩放系数计算得到的冲撞式破冰工况下的船体首部结构的设计载荷。

在一定程度上达到了简化模拟设计冰载荷的目的，具有一定的研究意义；对于不同的极地船型，动力缩放系数 $\lambda $ 往往不同，虽然需要重新计算，相比传统的设计载荷评估方法，在保证可行性的前提下仍具有很大优势，实现了简化模拟冰载荷的初步构想。

5 结　语

本文给出了一种模型船舶与海冰发生相互作用时，考虑流固耦合作用的影响的数值仿真方法。通过将数值计算结果与模型试验结果进行对比，二者吻合良好，验证了该方有效性和准确性。碰撞过程中海冰的破坏主要发生在接触区域，海冰单元在达到其截断压力或最大塑性应变时，发生失效被移除并形成裂纹。由于船体的侵蚀形成大量的横向和纵向裂纹，被移除后的海冰单元形成与船体水线面一致的边界形状。

为了将动态冰载荷简化，首先提出了一种等效脉冲冰载荷计算方法，该脉冲载荷的周期取为动态冰载荷的峰值周期，其峰值取为时船体产生相同应力响应的量值。将等效脉冲载荷峰值与规范冰载荷设计值比值定义为动力放大系数，从而将动态载荷等效转化为静载荷。