极地船舶在冰区水域航行时,破碎冰块会沿船底滑动进入船尾螺旋桨,与螺旋桨发生冰桨干扰相互作用,影响桨盘面入流和螺旋桨水动力性能。同时,船舶在冰区航行的冰水作用阻力增大,使得螺旋桨多处于低进速重载负荷运行工况,再加上冰水介质中冰块的阻塞逼近作用,极易造成桨叶表面压力陡降而产生空泡两相流动现象。冰水混合环境的螺旋桨空泡激振力对螺旋桨及整个推进系统的水动力、结构强度和振动等综合性能产生影响,与常规无冰水域的作用过程存在显著差异,因此,开展此类力学问题研究具有重要意义。
Sampson等[1]采用模型试验手段,在具有压力可调节功能的ETC空泡水筒模拟了冰桨干扰螺旋桨工作环境,进行不同运行和空泡环境的冰桨作用螺旋桨模型水动力性能试验测试。研究表明冰桨流作用程度受到螺旋桨和冰块几何、运动等多参数影响,提出螺旋桨在冰阻塞低进速运行时的空泡压力环境是重要影响因素。武珅等[2-3]在中国船舶科学研究中心的空泡水筒开展了冰桨轴垂向距离、进速和空泡数等冰阻塞几何和运动参数对螺旋桨水动力性能影响试验,给出了各参数与螺旋桨水动力之间的量化影响关系,并指出冰阻塞环境下空泡效应加剧了螺旋桨水动力的非定常特性。
对冰区螺旋桨水动力性能的数值模拟,前期多是基于势流理论方法。如Walker等[4-5]采用面元法模拟冰阻塞流,计算了冰阻塞状态下的螺旋桨水动力性能变化,并且与Luznik[6]的试验结果进行了验证对比。Liu等[7]开发了非定常面元法模型对加拿大海警R级破冰船吊舱推进器螺旋桨水动力性能进行了数值分析,实现了冰与螺旋桨变间隙工况的干扰水动力载荷预报。但由于势流理论在计算过程忽略了粘性的影响,对冰区螺旋桨空泡与粘性流的非线性作用问题无法给出量化计算结果。采用粘流方法对冰水混合环境下的螺旋桨非定常空泡和水动力性能的模拟计算工作还开展不多。WANG等[8]基于CFD利用重叠网格处理方法,数值计算了冰阻塞状态下的螺旋桨水动力,而且获取了单片桨叶随旋转周向位置的水动力和桨叶表面压力分布的变化情况。但由于计算为常压状态,未考虑到空泡压力环境对螺旋桨性能的影响,与冰区螺旋桨的实际运行环境还存在一定差异。
因此,本文利用RANS方法考虑不同冰块阻塞状态和压力环境的影响作用,对螺旋桨非定常空泡和水动力性能进行了数值模拟,从流场结构与空泡激振力的相关性角度出发,结合时频域处理分析冰块阻塞状态的螺旋桨空泡激振力特性,揭示冰块阻塞对螺旋桨空泡激振力的影响变化规律。
1 计算方案 1.1 计算方法空泡流动的连续性方程和动量方程,分别如下式:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {{U}}} \right) = 0 {\text{,}}$ | (1) |
| $ \frac{{\partial \left( {\rho {{U}}} \right)}}{{\partial t}}{\rm{ + }}\nabla \cdot \left( {\rho {{UU}}} \right){\rm{ = }} - \nabla p + \nabla \cdot \left( {\left( {\mu + {\mu _{\rm{t}}}} \right)\nabla {{U}}} \right) + \sigma \kappa {{n}} {\text{。}}$ | (2) |
式中:U为汽液两相流速度;ρ和μ为汽液两相流的密度和粘性系数;σ和κ为表面张力系数和表面曲率;n为汽液界面法向矢量。式(2)右端依次表示动量方程中的压力梯度、粘性剪切力和汽液界面表面张力。
采用VOF方法,通过描述液相体积分数γ的输运方程来捕捉汽液界面,如式(3)所示。γ=0表示汽相,γ=1表示液相,0<γ<1表示汽液界面。
| $ \frac{{D\gamma }}{{Dt}} = \frac{{\partial \gamma }}{{\partial t}} + \nabla \cdot \left( {\gamma U} \right) = \frac{{\dot m}}{{{\rho _l}}} {\text{,}}$ | (3) |
式中,
| $ \dot m = {\rm sign}({p_v} - p)\frac{{{n_0}}}{{1 + {n_0}\frac{4}{3}{\text{π}} {R^3}}}4{\text{π}}{R^2}\sqrt {\frac{2}{3}\frac{{\left| {{p_v} - p} \right|}}{{{\rho _l}}}} {\text{。}}$ | (4) |
式中:sign为符号函数;n0为单位体积内汽核密度;R为汽核半径。
式(2)中的μt是湍流运动引起的涡粘性系数,需要使用湍流模型计算,在本文中采用SST k-ω湍流模型。
本文首先采用多参考系MRF方法进行定常计算,得到近似稳定流场。然后采用非定常滑移网格方法模拟螺旋桨的真实旋转,其中压力速度的求解采用SIMPLE分离算法,最后导入空泡模型进行螺旋桨非定常空泡计算。
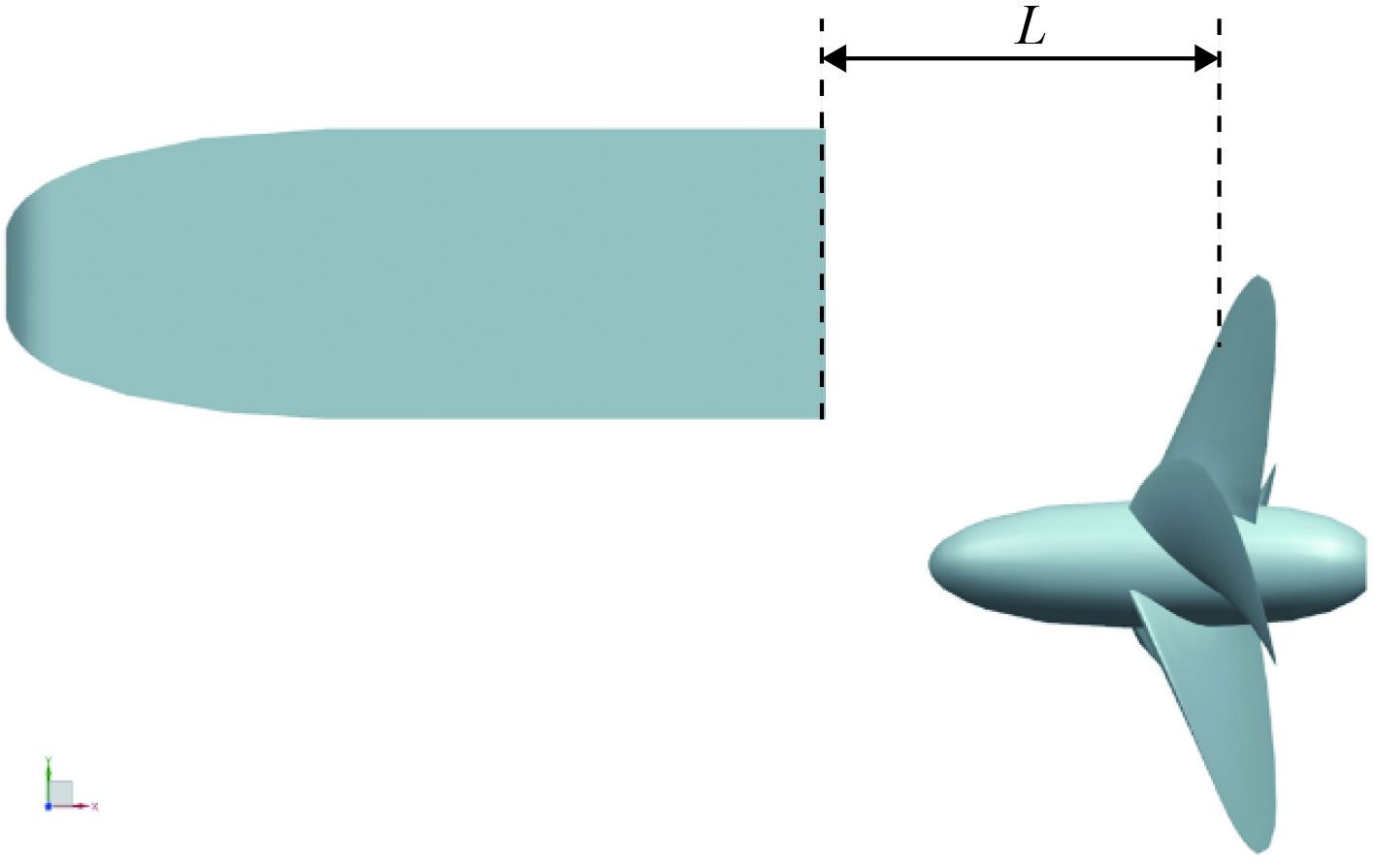
1.2 计算模型选用文献[2]中的冰阻塞螺旋桨试验模型,如图1所示。定义冰阻塞物右端面到桨盘面的轴向距离为L,螺旋桨模型直径为D,以无量纲参数L/D来表达冰桨轴向间距。
|
图 1 冰阻塞物与螺旋桨模型示意图 Fig. 1 Schematic of ice-propeller model |
为调节螺旋桨工作的压力环境,定义转速空泡数σn如下式:
| $ {\sigma _n} = \frac{{p - {p_v}}}{{\dfrac{1}{2}\rho {{\left( {nD} \right)}^2}}} {\text{。}}$ | (5) |
式中:p为桨轴中心压力;pv为饱和蒸汽压;ρ为水密度;n为螺旋桨转速。
定义螺旋桨无量纲进速、推力和扭矩系数分别为J,KT和KQ,如下式:
| $ J = \frac{V}{{nD}}{\text{,}} $ | (6) |
| $ {K_T} = \frac{T}{{{\rho ^{}}{n^2}{D^4}}}{\text{,}} $ | (7) |
| $ {K_Q} = \frac{Q}{{{\rho ^{}}{n^2}{D^5}}}{\text{。}} $ | (8) |
式中:V为螺旋桨远前方来流速度;T和Q分别为螺旋桨推力和扭矩。
整个计算域划分为旋转域和静止域两部分,采用滑移网格法处理旋转与静止区域交界面的数据传递。采用切割单元体网格对计算域进行划分,在螺旋桨及阻塞物附近进行网格加密,如图2所示。

|
图 2 计算网格 Fig. 2 Computational grids |
在计算中螺旋桨模型的进速系数和转速不变,选取了5个冰桨阻塞相对位置和4个空泡压力环境,共20个计算工况,如表1所示。
|
|
表 1 计算工况 Tab.1 Calculation condition |
文献[3]将冰阻塞典型工况的螺旋桨均值水动力和桨叶空泡形态的计算模拟结果与模型试验结果进行对比,验证了本文采用的空泡、湍流模型和粘流计算方法可对冰阻塞状态的螺旋桨非定常空泡和水动力进行有效模拟。
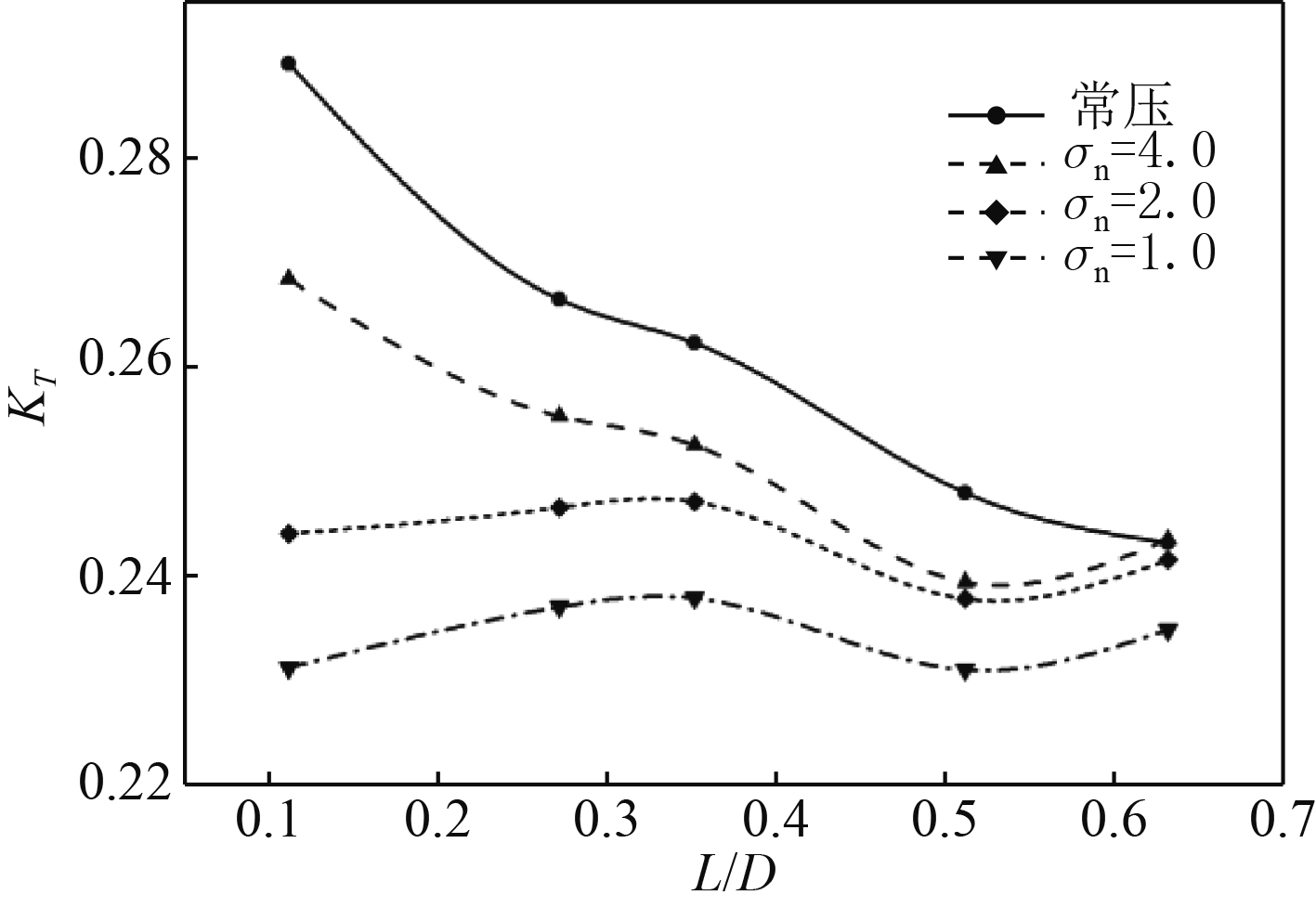
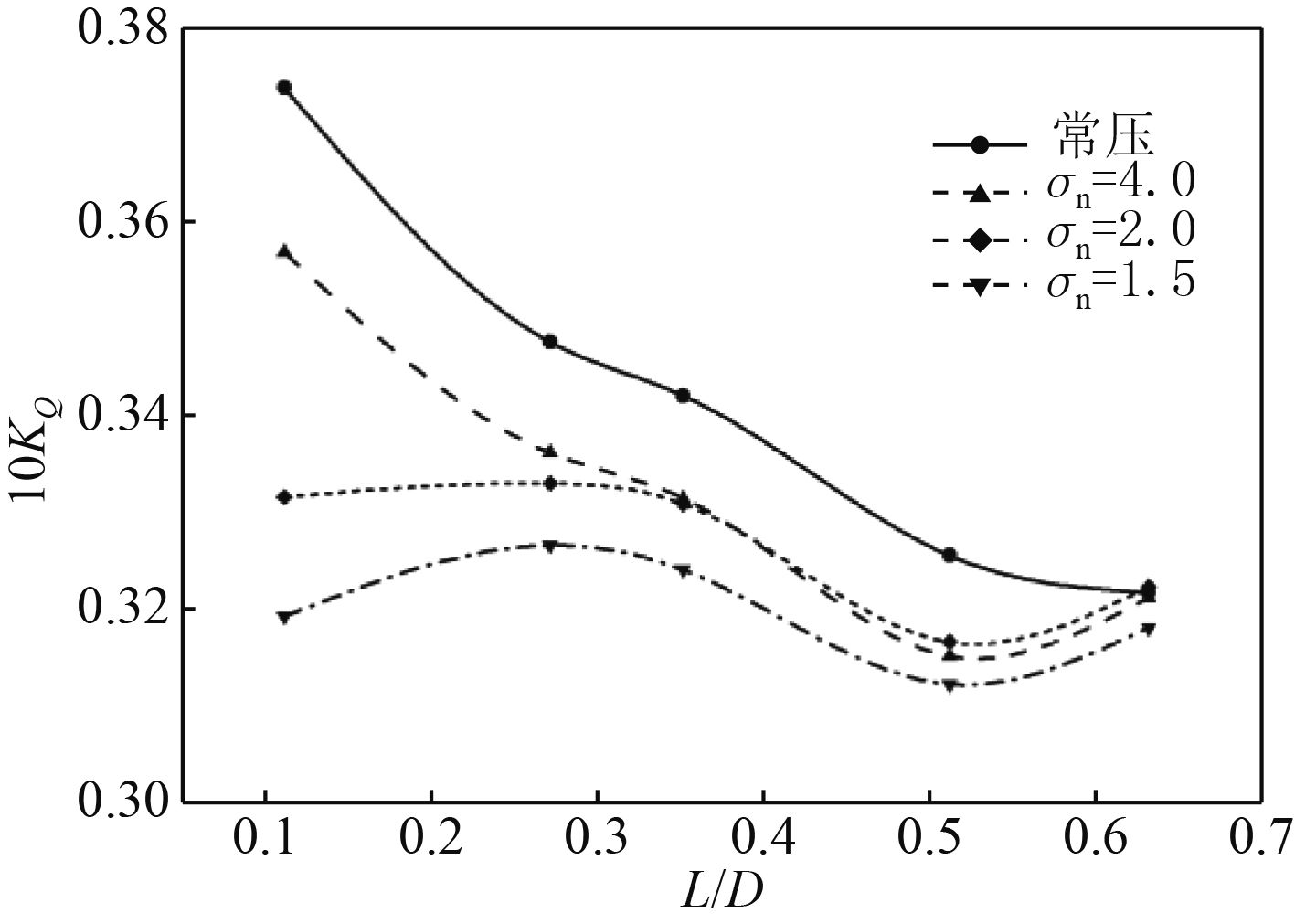
图3和图4分别给出了在表1冰桨阻塞状态,螺旋桨旋转1周的均值推力和扭矩系数随冰桨间距和空泡压力环境的变化对比。
|
图 3 推力系数随冰桨间距变化曲线 Fig. 3 Thrust coefficient versus ice-propeller distance curves |
|
图 4 扭矩系数随冰桨间距变化曲线 Fig. 4 Torque coefficient versus ice-propeller distance curves |
从图3和图4中的实线可以看出,在常压环境,螺旋桨推力和扭矩均值随冰桨轴向间距的减小而增大,且在阻塞物逼近螺旋桨时的变化幅度尤为显著。在σn=4.0时,受到桨叶空泡的影响,螺旋桨的均值水动力相比于常压状态下降,但基本维持螺旋桨无空泡状态均值水动力随冰桨间距减小而增大的变化趋势。而在σn=2.0和σn=1.5的压力状态,桨叶的严重空化使得螺旋桨水动力大幅下降,已基本抵消了流场阻塞造成的推扭力上升。可见,冰阻塞环境的螺旋桨水动力性能是由冰桨逼近的流场阻塞和桨叶的空泡效应所共同决定。
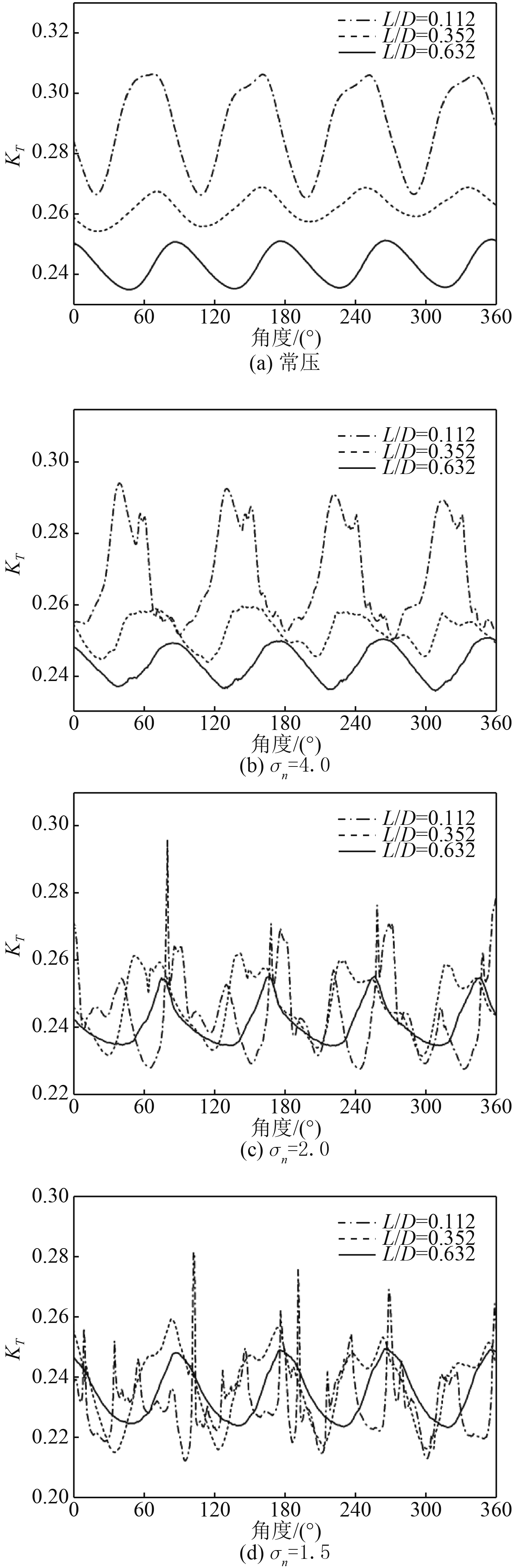
2.2 螺旋桨空泡激振力为进一步分析冰阻塞状态的螺旋桨非定常空泡水动力和激振特性,图5给出了上述冰阻塞状态,螺旋桨推力系数KT在一个旋转周期的时间历程变化曲线。
|
图 5 不同冰阻塞状态的推力系数时历曲线 Fig. 5 Time history curves of thrust coefficient indifferent ice-block condition |
从图5可以看出,随着阻塞物逼近螺旋桨,推力系数KT在旋转周期内的绝对值和变化幅值均发生较大变化,而且幅值相位也发生一定程度改变。如图5(a)所示,在常压状态螺旋桨KT时历曲线的光滑度较好,其波峰波谷的形态较为规则;而随着阻塞物靠近螺旋桨,在推力系数KT绝对值增大的同时,波动幅值也有大幅提升。图5(b)空泡数σn=4.0时,KT随时间的周期性变化规律与无空化状态下基本相似,但曲线逐渐变得不光顺,在主波峰波谷上出现了2次甚至3次峰谷。图5(c)空泡数σn=2.0时,螺旋桨空化加剧,在阻塞物距螺旋桨较远时还可观察到特征较为明显的波峰波谷,但随着阻塞物进一步逼近螺旋桨,KT随时间变化波峰波谷周期性的重合度较差,此时的分布近似于由一种周期性桨叶运动信号与空化极度不稳定的随机信号叠加形成。而在图5(d)空泡数σn=1.5时,桨叶空化最为严重,KT的绝对值下降,在逼近桨叶(L/D=0.352,0.112)状态螺旋桨旋转周期内的非定常激励均开始增多,且幅度增强。
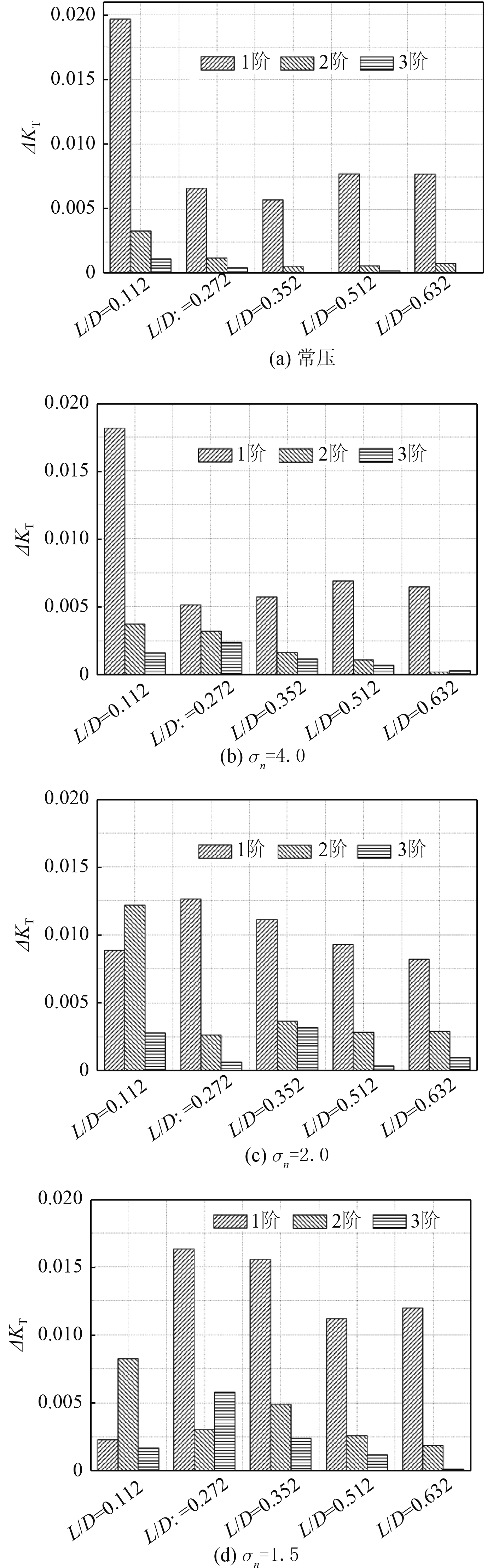
从频域角度对不同冰阻塞状态的螺旋桨推力系数KT进行傅里叶分析,得到叶频整数倍下的各阶脉动量ΔKT变化,如图6所示。
|
图 6 推力系数各阶次的脉动幅值 Fig. 6 Fluctuation amplitude of each order for thrust coefficient |
从图6(a)可以看出,在常压无空化状态下,在阻塞物靠近螺旋桨过程中,ΔKT的1阶脉动量都远大于2阶和3阶量,在未达到逼近桨叶时(L/D=0.112)各阶次的变化量均不大。而在L/D=0.112状态的1阶量出现大幅上升,2阶和3阶量也有一定程度增加,与时域表现出的规律一致。如图6(b)所示,当空泡数σn=4.0时,各阶量随冰桨间距的变化规律与无空化状态基本相似,主要区别在于进入阻塞流场的桨叶开始不稳定空化,导致ΔKT的2阶和3阶量大幅提升。图6(c)中在空泡数σn=2.0时桨叶空化加剧,在阻塞物距螺旋桨L/D=0.272,0.352,0.512和0.632时,ΔKT的各阶脉动量均有一定程度升高,且随着阻塞物的逼近脉动幅值更大。可是,在阻塞物极度逼近螺旋桨状态(L/D=0.112),ΔKT的1阶脉动量不升反降,2阶量却出现了大幅度升高,甚至超过了1阶量,表明此时桨叶的不稳定空泡使得螺旋桨空泡激振频率向更高阶次移动,加剧了螺旋桨空泡激振力的非定常性。在图6(d)中空泡数极低的σn=1.5状态,桨叶空化最为严重,除L/D=0.112外不同冰桨间距的螺旋桨推力各阶脉动量相比σn=2.0进一步上升,尤其在L/D=0.272状态的3阶脉动量已经超过了2阶值。而在螺旋桨极度逼近螺旋桨时(L/D=0.112)的各阶脉动量均有所下降,此时在阻塞物逼近流场和桨叶大面积片空化作用下的螺旋桨空泡激振力却有一定程度的削弱。
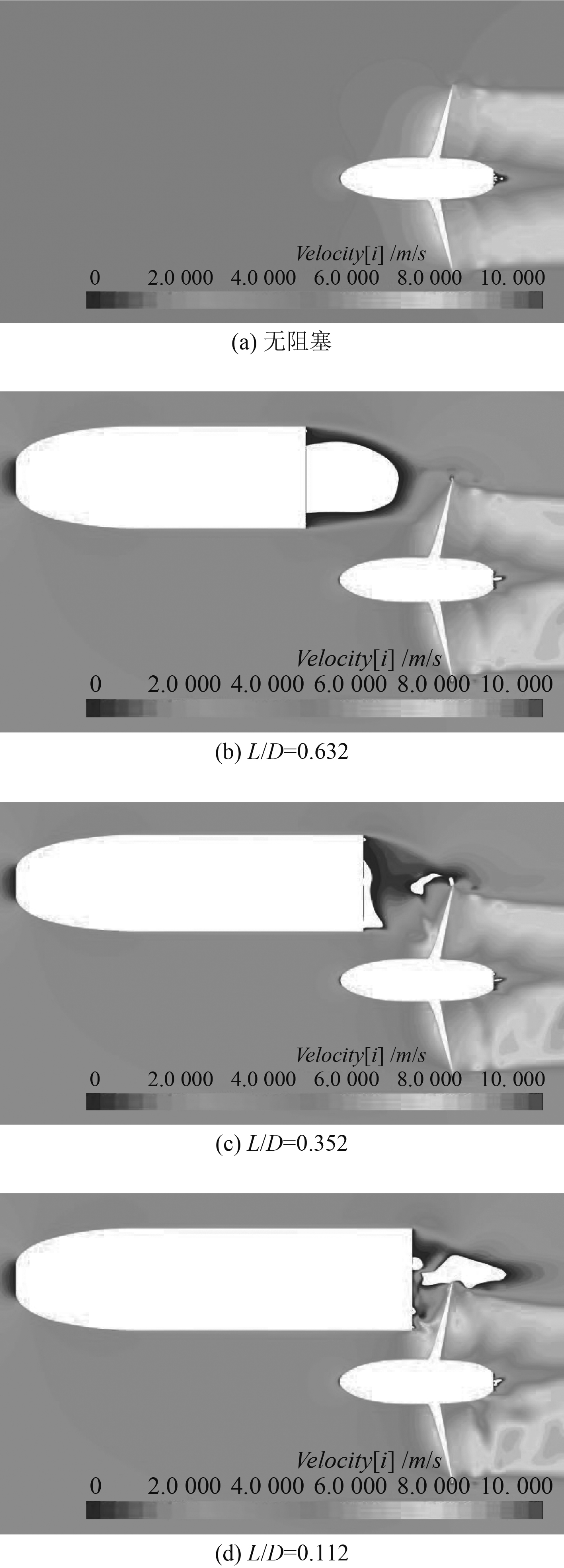
2.3 流场结构从流场结构出发,分析冰块阻塞对螺旋桨空泡激振力作用的影响成因。图7和图8分别给出了无阻塞物和冰阻塞状态不同冰桨间距时的流场压力分布和轴向速度分布对比。需要指出的是,图8中除阻塞物和螺旋桨所在的固体区域之外,将轴向速度小于0的区域也表示为白色,即轴向回流区。

|
图 7 压力分布对比 Fig. 7 Comparisons of pressure distribution |
|
图 8 轴向速度分布对比 Fig. 8 Comparisons of axial velocity distribution |
从图7可以看出,阻塞物的存在使得下游压力有所降低,靠近螺旋桨叶背区域的压力降低程度较大,且在叶背梢部区域压力降低最为显著,并随着阻塞物的逼近,各区域压力进一步降低。在阻塞物极度逼近螺旋桨时,螺旋桨叶背梢部区域压力降低的同时叶面梢部区域的压力却有所升高,这是由于阻塞物使螺旋桨进流攻角的改变引起,导致叶梢附近回流压差增加,进而使螺旋桨叶梢附近的回流现象加剧,压力变化再影响到速度场的变化分布。
从图8可以看出,相比于敞水无阻塞状态,在阻塞物的下游存在一个低速低压回流区,随着阻塞物靠近螺旋桨,低速低压回流区对螺旋桨的影响作用逐渐增大。由于阻塞物下游的流速急剧降低,使得螺旋桨的来流攻角发生变化,在桨叶梢部附近产生严重的流动分离,如图8(c)和图8(d)所示。这一方面是由于螺旋桨叶面和叶背的压差升高所致,另一方面是由阻塞物下游本身回流区的叠加造成,甚至在阻塞物和桨叶之间的回流区产生连体涡的空化现象,连续的流动分离使得桨叶空泡形态的不规则性和空泡激振力的非定常性增强,这与常规水域船后螺旋桨的空泡水动力特性存在很大差别。
3 结 语本文采用RANS方法模拟分析了冰阻塞状态的螺旋桨非定常空泡激振力和流场结构特性,得到结论如下:
1)冰阻塞状态的螺旋桨水动力性能是由冰桨逼近的流场阻塞和桨叶的空泡效应共同决定。冰桨阻塞间距的减小会带来螺旋桨均值水动力的增加,而桨叶空化会起到一定的削弱作用。
2)流场阻塞和桨叶空泡不稳定作用下的螺旋桨水动力在旋转周期内近似于周期旋转信号和随机激励信号的叠加,非定常水动力的变化幅度随着阻塞和空化程度的加剧而增强。而从频域角度看,冰阻塞会造成螺旋桨空泡激振力的高阶量显著上升,使空泡激振频率向高阶次移动。
3)冰阻塞物下游产生低速低压的回流区,改变螺旋桨附近的流场结构和压力场分布,加剧螺旋桨叶梢附近的流动分离,使得冰阻塞环境下的螺旋桨空泡形态不规则,甚至在桨叶与阻塞物之间产生连体涡空化现象。
| [1] |
SAMPSON R, ATLAR M, SASAKI N. Propeller ice interaction- effect of blockage proximity[C]// Proceedings of First International Symposium on Marine Propulsors, Trondheim, Norway, 2009.
|
| [2] |
武珅, 曾志波, 张国平. 冰阻塞参数对螺旋桨水动力性能影响试验研究[J]. 船舶力学, 2018, 22(2): 156-164. WU Shen, ZENG Zhi-bo, ZHANG Guo-ping. Experimental research on the influence of ice block parameters on propeller hydrodynamic performance[J]. Journal of Ship Mechanics, 2018, 22(2): 156-164. DOI:10.3969/j.issn.1007-7294.2018.02.004 |
| [3] |
武珅, 刘亚非, 曾志波, 等. 空泡效应对冰阻塞环境下的螺旋桨性能影响研究[J]. 中国造船, 2018, 59(1): 110-121. WU Shen, LIU Ya-fei, ZENG Zhi-bo. Research on the influence of cavitation effect to propeller performance in ice block environment[J]. Shipbuilding of China, 2018, 59(1): 110-121. DOI:10.3969/j.issn.1000-4882.2018.01.011 |
| [4] |
WALKER D, BOSE N, et al. Influence of cavitation on Canadian R-Class propellers[J]. Journal of Offshore Mechanics and Arctic Engineering, 1995. |
| [5] |
WALKER D, BOSE N, et al. Hydrodynamic performance and cavitation of an open propeller in a simulated ice blocked flow[J]. Journal of Offshore Mechanics and Arctic Engineering, 1994, 116. |
| [6] |
LUZNIK L, WALKER D, et al. Effects of ice blockage size and proximity on propeller performance during non-contact propeller-ice interaction[C]// Proceedings of Offshore Mechanics and Arctic Engineering, Denmark, 1995.
|
| [7] |
LIU P, DOUCET J M, et al. Numerical prediction of ice induced hydrodynamic loads on propellers due to blockage[J]. Oceanic Engineering International, 2000, 4(1): 31-38. |
| [8] |
WANG Chao, SUN Sheng-xia, et al. Numerical simulation of hydrodynamic performance of ice class propeller in blocked flow-using overlapping grid method[J]. Ocean Engineering, 2017, 141: 418-426. DOI:10.1016/j.oceaneng.2017.07.028 |
 2019, Vol. 41
2019, Vol. 41
