水下非接触爆炸冲击载荷是舰、艇载设备设计时必须要考虑的载荷环境。高压气瓶连接有管路系统,并与管道刚性连接,因而高压气瓶及管道系统减震系统设计时,不仅要为高压气瓶配备减振器,也要为管道系统配备减振器,从而实现整个系统的缓冲隔振保护。管道一般较长,其减振器刚度及布置位置十分关键,过小的刚度将不能有效约束冲击载荷下管道的运动,导致管道弯曲变形过大,但过大的刚度也将会导致冲击载荷下管道位移小,高压气瓶位移大时很容易导致高压气瓶与管道连接处受损。高压气瓶减振器设计也面临类似问题。所以,在设计前期,通过仿真及相应的优化算法对高压气瓶及其管道系统减振器刚度进行组合优化,使得冲击载荷下高压气瓶及管道系统尽可能在一定范围内整体平动就变得十分重要。
目前,优化算法在工程优化设计中已逐步成熟。Marcus等[1]利用神经网络法建立响应面,实现了对吸能盒外形尺寸的优化设计。姜衡等[2]结合了响应面法、遗传算法等,以某设备的质量及固有频率为优化目标,开展多目标优化设计,在保证设备的动、静态性能不降的前提下,大幅减轻了设备质量。为实现汽车碰撞性能的优化设计,姜哲[3]探索性地进行桁架式Spar平台的概念设计和结构设计研究,通过设计初始阶段的多学科优化设计,实现了Spar平台系统的集成优化设计。
本文以某型高压气瓶及其管道减振系统为对象,研究高压气瓶及其管道系统缩聚梁动力学建模方法、冲击动响应计算方法、基于二次序列规划算法的高压气瓶及其管道优化设计方法,降低了冲击过程管道的变形,提高了高压气瓶及其管道系统的抗冲击能力。
1 高压气瓶及其管道减振系统动力学建模高压气瓶及其管道系统如图1所示。高压气瓶为金属材料,结构刚度较大,可以不用考虑冲击过程高压气瓶的变形。管道与高压气瓶同种材料,并与高压气瓶法兰螺栓连接,管道末端配有自密封装置。为减小传递到高压气瓶及其管道系统的冲击载荷,拟为高压气瓶及其管道系统布置3个减振器,减振器主要承担高压气瓶及管路系统横向缓冲减振功能。
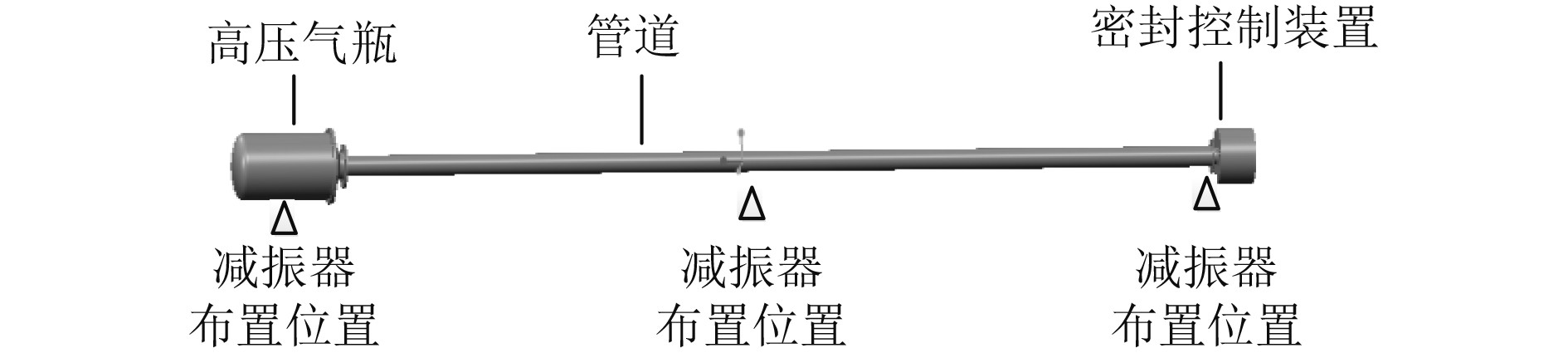
|
图 1 高压气瓶及其管道减振系统 Fig. 1 Shock absorption system for high pressure cylinders and pipelines |
可以采用实体建模方法建立高压气瓶及其管道系统动力学模型,但实体模型冲击动力学计算量大,不适用于减震系统优化计算(优化计算需要多轮多工况计算),因而本文采用缩聚梁建模方法建立高压气瓶及其管道系统动力学模型。
本文使用Ansys软件建立该高压气瓶及其管道系统动力学计算模型。相较于管道,高压气瓶、自密封装置结构刚度较大,冲击过程基本不变形,因而可以使用质量点模拟。管道弯曲变形较大,表现出典型的梁特征,采用三维Beam188梁模型,减振器使用三向弹簧combin14单元模拟。建立后的高压气瓶及其管道系统动力学计算缩聚梁模型如图2所示。
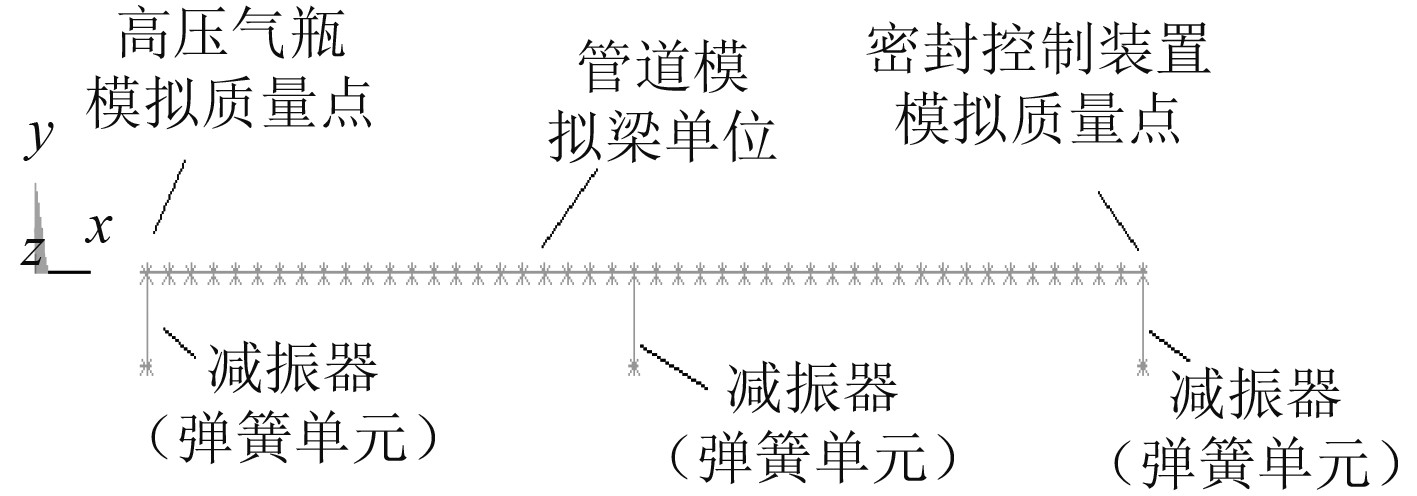
|
图 2 高压气瓶及其管道系统动力学计算模型 Fig. 2 The dynamics calculation model of high pressure cylinder and pipelines system |
首先根据工程设计经验确定高压气瓶及管道减振系统初始设计:第1个减振器刚度为1E7 N/m、第2个减振器刚度5E6 N/m、第3个减振器刚度5E6 N/m(减振器从高压气瓶到密封控制装置依次编号)。
为避免冲击过程高压气瓶及管道系统与舱壁碰撞,减小管道弯曲幅度,高压气瓶及管道系统的缓冲减振系要求为:
1)横向冲击过程减振器最大压缩量不大于30 mm;
2)管路各部分最大横向位移差不大于25 m。
2.2 冲击输入与计算方法冲击计算方法主要有静态G法、时域动力学分析和谱分析方法[4],每种冲击计算方法对应不同的冲击输入。
静载荷法是将动载荷等价为一定倍数的静载荷,用静态的方法进行强度校核。在具体应用中,根据结构设备质量及抗冲击等级,查图得出冲击设计因数,将基座及设备的总重量乘以冲击设计因数,得到1个作用于基座和设备重心的垂向(或横向、纵向)力。此力即为静态计算的冲击力F,然后根据刚度系数即可得到结构的响应。由于该方法没有考虑设备的高频响应与1阶低频响应的差异,实际上只校核了1阶低频响应的强度[5]。
时域动力学分析法是规定系统承受某一冲击的时间信号,将其作为冲击输入,以计算系统的冲击响应。该时间信号由压力、速度或加速度作为时间函数定义。在时间域求解冲击响应的方法主要是直接积分法,即通过振动方程将全时间域内连续位移函数的问题,转化为由时间分段点平衡方程求时间分段点处未知位移的问题。振动方程所描述的是在时间分段点所处的时刻,空间各点所受的惯性力、阻尼力、弹性恢复力和外力处于瞬时平衡状态,然后假设时间单元内位移、速度和加速度随时间的变化规律,并找出时间段始末时刻位移、速度和加速度之间的关系式,该方法主要缺点是计算量过大,并且结果过分依赖于输入加速度时程数据。
GJB 1060.1-1991规定的动力学分析方法是谱分析方法[6],其主要内容是:动力学分析一般在设备和(或)基座的设计阶段进行,动力学分析将近似为弹性的分析系统简化为承受给定冲击输入的质量-弹簧系统,即数学模型(对于复杂结构可用有限元方法),通过建立和求解平衡方程组求出与分析系统中每一质量和弹簧有关的力和变形,然后应用这些力和(或)变形计算危险区域的应力和(或)变形,最后将这些力、应力和(或)变形与规定的许用值相比较,确定所分析的设备或基座是否符合抗冲击要求。
GJB 1060.1-1991规定的潜艇设备冲击设计值(基准加速度、基准速度)为:
| ${A_0} = 102.02\frac{{217.73 + {m_a}}}{{9.07 + {m_a}}}\text{,}$ | (1) |
| ${V_0} = 0.51\frac{{217.73 + {m_a}}}{{45.36 + {m_a}}}\text{。}$ | (2) |
其中
设备冲击设计加速为
我国冲击动力学分析标准GJB 1060.1-91来源于美国相关标准,美军标规定使用的动力学设计分析方法(DDAM)已内置到了Ansys软件中,由于国军标与美军标本质相同,二者计算方法通用,可采用Ansys内置的动态设计分析方法(DDAM)。动态设计分析方法(DDAM)源于美军对爆炸冲击的研究,以机械振动的自然模态理论为基础,以一系列水下爆炸试验结果为参考,考虑谱跌效应,根据舰艇类型、设备安装位置以及设备模态质量选取而对加速度和速度进行限定,进而选择不同设计冲击谱值。DDAM方法首先对设备进行模态分析,并根据冲击方向,依据模态质量选取相应的模态阶次,然后对设备进行谱分析,通过对模态解的合成得出设备的位移或应力响应。模态合成的方法有多种,常用的有3种:绝对值求和(Absolute sum,ABS)、平方和之平方根(Square-root-sum-of-squares,SRSS)和美国海军研究实验室求和(Naval research laboratory sum,NRL)。DDAM计算一般采用的是美国海军研究实验室求和(NRL),其计算公式为:
| ${x_i} = {x_{ib}} + \sqrt {\sum\limits_a {{x_{ia}}^2 - {x_{ib}}^2} }\text{。} $ | (3) |
其中
Ansys内置的DDAM分析模块是基于美军研究报告而实现的,由于美军研究报告是以英制单位编制而成的,故而Ansys的DDAM算法亦采用英制单位,然而国内大部分用户习惯采用国际单位制进行建模分析,因此需要进行单位制转换,如表1所示。
|
|
表 1 单位制转换表 Tab.1 Unit conversion table |
本文直接使用恒定阻尼比定义系统阻尼,恒定阻尼比设置为0.1。
2.3 计算结果分析提取横向冲击过程高压气瓶设管路系统的位移云图,如图3所示。横向冲击过程高压气瓶及管路系统最大位移量为42 mm,出现在第1道减振器与第2道减振器中间部位。高压气瓶及管路系统各部位最大位移最大相差29.7 mm。可以看出,根据工程经验设置的减振器初始刚度并不能满足设计要求,需要对3个减振器的刚度进行组合优化设计。
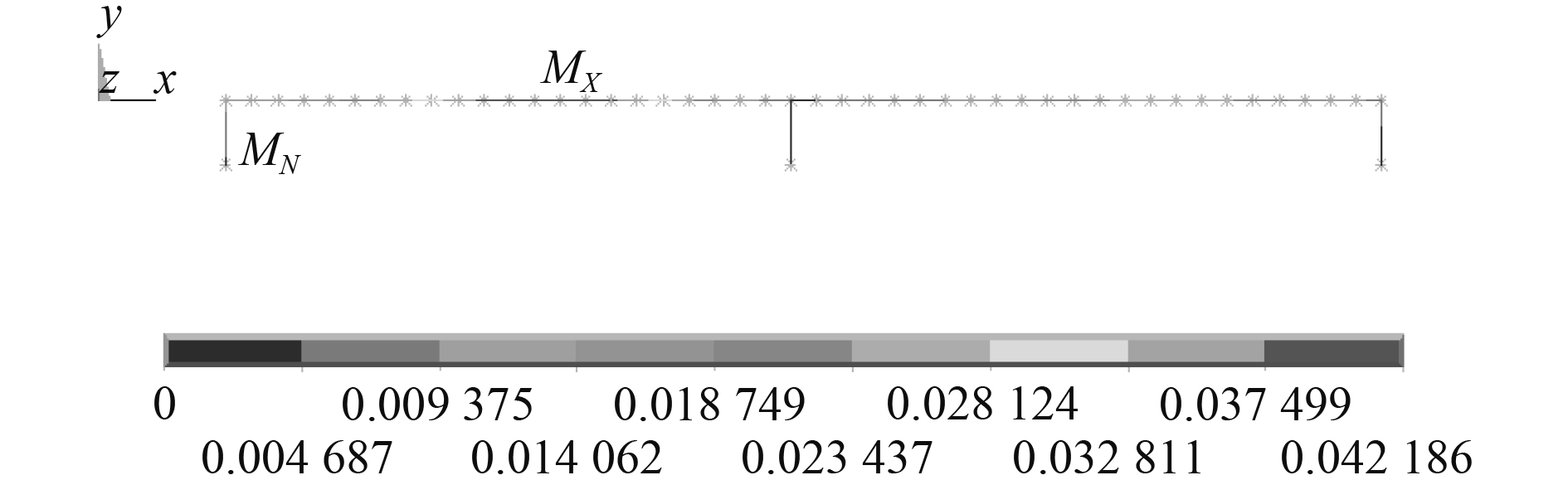
|
图 3 冲击载荷下高压气瓶及管路系统位移响应 Fig. 3 Displacement response of high pressure cylinders and pipelines system under impact load |
为减小横向冲击载荷下管道系统的弯曲变形,同时控制高压气瓶及管路系统的运动幅度,避免冲击过程高压气瓶及其管路系统与舱壁碰撞,需要对高压气瓶及其管路系统进行优化设计。根据工程设计实际需要,设定相关条件。
高压气瓶及管路减振系统优化的设计变量、约束条件、优化目标归纳如下:
1)设计变量:
减振器刚度组合
2)约束条件:
高压气瓶及管道系统最大横向位移不大于30 mm,
3)优化目标:
高压气瓶及管道系统各部位最大位移相差最小。
3.2 优化算法对于本文问题,可采用的优化算法较多,如多目标遗传优化算法、二次连续规划算法等。本文拟采用二次连续规划算法实现高压气瓶及管道系统3个减振器刚度的组合优化设计。二次连续规划法[7]常用来求解带有约束的非线性数学规划问题。二次连续规划法假定目标函数和约束条件是连续可微的,将目标函数以2阶泰勒级数展开,将原非线性求解问题转化为二次规划问题,通过求解二次规划得到下一个设计点,然后根据优化函数执行一次线性搜索。
本文优化模型如下所示:
1)减振器刚度
2)冲击过程管道的压缩量
| ${g_j}(x) - 30 \leqslant 0{\text{,}}j = 1,...,{m_e};$ |
3)优化目标函数
管道最大相对位移
二次序列规划算法一般可以通过一个类牛顿矩阵
| $ {\left( {\frac{1}{2}{d^{\rm T}}{B_k}d + \nabla f{{({x_k})}^{\rm T}}d} \right)_{\min }}, d \in {R^n}\text{,} $ | (4) |
| $\nabla {g_j}{({x_k})^{\rm T}}d + {g_j}({x_k}) = 0,j = 1,...,{m_e}\text{,}$ | (5) |
| $\nabla {g_j}{({x_k})^{\rm T}}d + {g_j}({x_k}) \geqslant 0,j = 1,...,{m_e}\text{,}$ | (6) |
| ${x_l} - {x_k} \leqslant d \leqslant {x_u} - {x_k}\text{。}$ | (7) |
二次序列规划算法优化求解的高压气瓶及其管道系统最优的减振器刚度组合为:
| ${K_1} = 1.9 \times {10^7}\ {\rm{N/m}}\text{,}$ | (8) |
| ${K_2} = 2.0 \times {10^6}\ {\rm{N/m}}\text{,}$ | (9) |
| ${K_3} = 5.0 \times {10^6}\ {\rm{N/m}}\text{。}$ | (10) |
同样使用DDAM方法求解优化后高压气瓶设管路系统横向冲击载荷下的动响应。优化后管路最大位移29.7 mm,各部位最大位移最大相差22.4 mm。
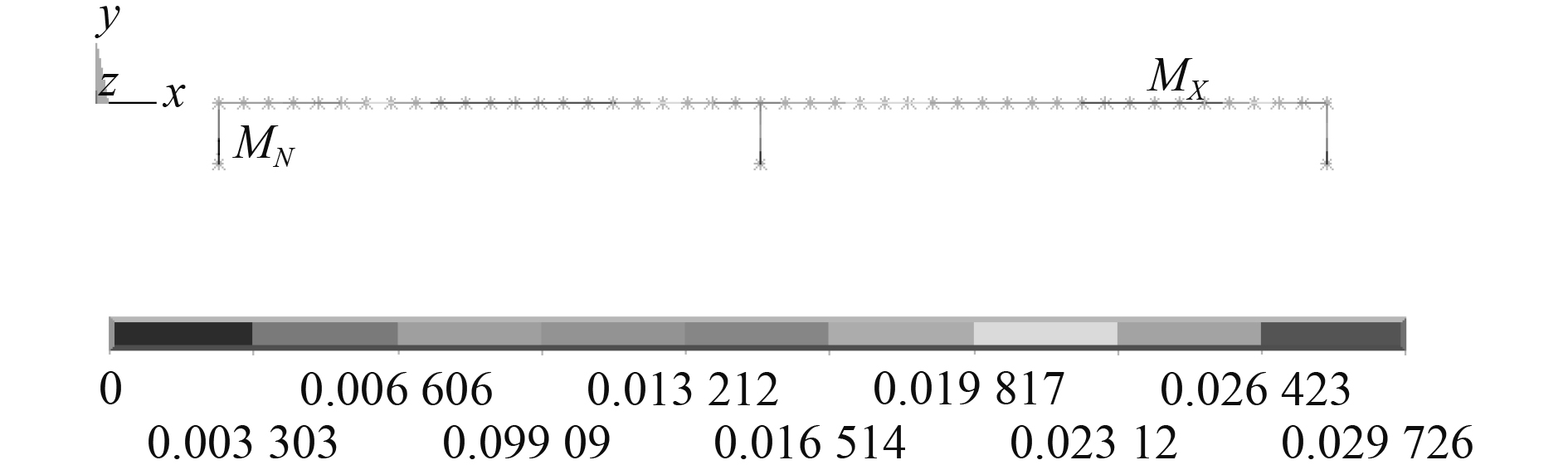
|
图 4 优化减振后冲击载荷下高压气瓶及管路系统位移响应 Fig. 4 Optimized displacement response of high pressure cylinders and pipelines system under impact load |
优化前后的减振系统缓冲减振能力对比如表2所示。可以看出,优化后横向冲击载荷下高压气瓶及管路系统的最大横向位移为29.7 mm,比优化前40.6 mm下降约27%,高压气瓶及管路系统各部位最大横向位移最大相差22.4 mm,比优化前37.1下降了约39.6%,即优化后的减振器刚度组合方案可以更有效的抑制横向冲击载荷下管道的弯曲变形。
|
|
表 2 减振系统优化前后缓冲减振效果对比 Tab.2 Effects comparison of the damping system |
1)本文采用缩聚梁建模的方法建立了某高压气瓶及管路系统动力学模型,可大幅减少冲击动力学计算量,为后续优化计算奠定了基础;
2)本文基于动态设计方法(DDAM),计算分析了高压气瓶及管路系统在水下爆炸载荷下的冲击动响应;
3)本文将高压气瓶及管道系统几个减振器的刚度组合作为设计变量,将高压气瓶及管道系统最大横向移动量作为约束条件,将高压气瓶及管道系统各部位最大位移相差最小化为目标,基于二次序列规划算法,实现了高压气瓶及其管路系统减振器刚度的组合优化设计。优化后减振系统可以有效抑制高压气瓶及其管路系统的横向移动及管道系统的弯曲变形,提高了高压气瓶及管道系统在水下爆炸冲击载荷下的安全性。
| [1] |
MARCUS Redhe, LARSGUNNAR Nilsson, FREDRIK Bergman. Shape optimization of a vehicle crash-box using LS-OPT[C]. 5th European LS-DYNA User conference. Sweden: Engineering Research Nordic, 2005: 27–31.
|
| [2] |
姜衡, 管贻生, 邱志成. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125-133. |
| [3] |
姜哲. 多学科设计优化在桁架式Spar平台概念设计中的应用研究[D]. 上海: 上海交通大学, 2010.
|
| [4] |
汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005.
|
| [5] |
冯麟涵, 汪玉, 杜俭业, 等. 舰船设备冲击响应计算方法等效性研究[J]. 船舶工程, 2011, 33: 210-214. |
| [6] |
张晓阳, 刘建湖, 潘建强, 等. 各主要海军国家设备抗冲击标准之评述[J]. 船舶力学, 2011, 15(11): 1322-1334. DOI:10.3969/j.issn.1007-7294.2011.11.018 |
| [7] |
郑总准, 吴浩, 王永骥, 等. 基于序列二次规划算法的再入轨迹优化研究[J]. 航天控制, 2009, 27(6). |
 2019, Vol. 41
2019, Vol. 41
