2. 常州工程职业技术学院,江苏 常州 213164
2. Changzhou Vocational Institute of Engineering, Changzhou 213164, China
在我国“十三五”规划中,海洋开发已成为前沿技术研发布局的重点领域。潜水器作为海洋观测与作业的重要技术装备,是探查深海资源、开展深海科学研究、进行深海工程作业的重要一环。耐压壳是潜水器的核心结构部件,其重量占潜水器总重的1/4~1/2,是潜水器浮力的主要提供者[1]。耐压壳主要承受深水压力,需要足够的强度和可靠的密封性,为内部的仪器设备、电子元器件装置等提供正常运作的环境,保护它们不会因海水压力和腐蚀而受到损害[2],在载人潜水器中,耐压舱为工作人员提供生活环境与工作空间,确保舱内人员设备的安全性,耐压壳体结构的安全性和可靠性至关重要。
耐压壳结构的设计和制造是潜水器的关键技术,其强度和稳定性是需要重点关注的问题。本文结合国内外潜水器的发展概况,介绍潜水器耐压壳的结构形式特点,材料选用以及设计计算方法的研究现状,展望未来的研究和技术应用方向。
1 国内外潜水器发展现状概述潜水器主要分为载人潜水器(HOV)和无人潜水器(UUV)两大类。
1.1 国内外载人潜水器概况作业型载人潜水器是由人员驾驶操作的,具备水下观察和作业能力的潜水装备。作业型载人潜水器工作于水深1 000 m以下,可以执行海底地质勘探、海底开发和打捞、海洋生物标本采集等多种复杂科学任务。大深度作业型载人潜水器技术是海洋开发和海洋技术发展的最前沿和制高点之一,目前,仅中国、美国、法国、俄罗斯、日本具备该领域自主研发的能力,表1为各国在役的大深度作业型载人潜水器的对比情况[3]。
|
|
表 1 各国在役的大深度作业型载人潜水器对比 Tab.1 Comparison between manned deep submersible of every countries |
观光型载人潜水器在海洋旅游中得到了广泛应用。小型观光潜水器通常用于科学考察和探险,如美国Triton深潜公司的Triton系列、SEAmagine Hydrospace公司开发的Ocean Pear和Triumph两个型号产品、Ocean Gate公司的Cyclops1和Cyclops 2潜水器、荷兰U-Boat Worx公司的C-Quester和C-Explorer两大系列产品等[4 – 5],这类潜水器具有工作深度大、乘员数量少(通常为1~5名)的特点。大型观光潜水器主要用于携带普通乘客观光旅游,工作深度一般小于100 m。1985年,世界上第1台大型观光潜水器美国的28客位的观光潜水器AtlantisⅠ投入使用,现在的AtlantisⅤ已升级至64客位,最大潜深38 m[6];芬兰、加拿大、韩国、西班牙、俄罗斯也建造了大型观光潜水器,我国于2015年由中船重工七〇二所研制成功世界最大全通透载客潜水器—“寰岛蛟龙”,最大下潜深度40 m,可搭载12名乘员。
1.2 国内外无人潜水器概况无人潜水器分为遥控无人潜水器(ROV)、自治式无人潜水器(AUV)以及水下滑翔机(UG)。
ROV由人员在母船上通过主缆和系缆对潜水器进行操作,在海洋研究、近海油气开发、矿物资源调查取样、打捞和军事等方面都有广泛的应用。1960年,美国研制成功世界上第1台ROV-CURV1,曾与载人潜水器ALVIN号协同打捞起西班牙外海856 m水深的1颗氢弹;1995年,日本海洋技术研究所研制的“海沟”号ROV(KAIKO),下潜到了马里亚纳海沟的最深处(11 022 m),创造了世界纪录[7]。目前,在ROV技术研究方面,美国、加拿大、英国、法国、德国、意大利、俄罗斯、日本等国处于领先地位[8]。我国从20世纪70年代末起,先后研制成观察型、作业型、大深度拖曳型ROV,2004年,由上海交通大学水下工程研究所研制成功“海龙”号ROV,2018年11月“海龙11000”完成了6 000米级试验,最大潜深5 630 m,创造了国产ROV最大潜深。
AUV无人无缆,自主作业范围广、机动性强、是发达国家海军和海洋技术研究发展的热点之一。美国拥有众多的AUV研究机构,如WHOI,MBARI,MIT等,应用在军事上的AUV数量在不断增多[9],欧洲各国、俄罗斯、加拿大、日本、韩国等也在AUV的研究方面取得巨大成就[10]。2011—2018年,我国自主研发了“潜龙”系列1~3号作业型AUV,其中“潜龙3号”创造了深海AUV单潜次航程最远的深海航行纪录,并首次实现AUV与船载地质取样同时作业的新模式。
UG是一种新型AUV,它依靠浮力调节实现升沉,借助滑翔翼姿态角调整获得推进力来实现水中长距离滑翔。国外UG技术的发展与应用主要集中于美国、法国、英国和澳大利亚等海洋强国,美国曾于20世纪90年代开发成功第1代水下滑翔机Spray Glider,Slocum,SeaGlider,日本和法国也都相继研制出了名为ALBAC和STERNE的水下滑翔机[11]。我国UG的研究始于本世纪初,2017年3月,由中科院沈阳自动化研究所自主研发的“海翼”号水下滑翔机,在马里亚纳海沟完成了6 329 m大深度下潜观测任务;2018年4月,由天津大学自主研发的采用最新混合推进技术的水下滑翔机—“海燕”号,创造了8 213 m的潜深世界纪录,刷新了国产水下滑翔机连续工作时间最长、测量坡面最多,续航里程最远等纪录。
2 潜水器耐压壳的结构形式和应用潜水器耐压壳的设计目标是在满足结构强度和稳定性要求的前提下,在减少壳体重量的同时增大内部容积,耐压壳的重量−排水量比越小,潜水器能提供的有效载荷越大,决定重排比的主要因素是结构的形式和材料。
2.1 常规耐压壳结构形式耐压壳常规的结构形式包括球形、圆柱形、椭球形、锥形、倒楔形以及它们的组合形状等。
在容积相等的条件下,球壳可获得最小的重排比值;球壳受载时内力分布均匀,薄膜应力只有圆柱壳结构的一半,下潜深度越大,优势越明显。大深度载人潜水器,由于舱室空间要求、材料限制、安全性、深水压力等因素,球形耐压壳是最佳选择,现有的大深度作业形载人潜水器(见表1),均采用球形耐压壳结构,球壳直径范围2~2.1 m,可容纳3人。在用于科学考察和探险的小型载人潜水器中,也多采用球形耐压壳结构,如美国的Triton系列潜水艇,荷兰的c-explorer3探索式潜水艇等都采用了球形载人舱。美国的Deep Flight Dragon具有2个球形载人舱(见图1),可下潜到120 m。

|
图 1 小型载人潜水器的球形耐压壳 Fig. 1 Spherical pressure hull in small manned submersibles |
在潜深较小时,球壳需要增大厚度来提高稳定性,导致重排比变大,故对于潜深小于800 m的潜水器耐压壳,大多采用带封头的圆柱形耐压壳[12],圆柱壳易加工制造,内部空间利用率高,可与半球形、椭球形、圆锥形组合成耐压壳结构。大型观光潜水器多采用圆柱形耐压壳,载人舱通常由圆柱形壳体和半球封头组成,内径在1.8~2.6 m之间,如我国的“寰岛蛟龙”载客型潜水器、Atlantis观光潜水器、MarkII观光潜水器[6](见图2)。一些小型私人潜水器中也有球柱组合结构耐压壳,Aurora-5潜艇,C-Explorer5的载人舱均采用了圆柱壳和球壳组合的结构,这种结构比单球形载人舱可载人数更多(见图3)。

|
图 2 大型观光潜水器的球柱组合型耐压壳 Fig. 2 Spherical-cylindrical combined pressure hull in large tourist submersibles |

|
图 3 小型私人潜水器的球柱组合耐压壳 Fig. 3 Spherical-cylindrical combined pressure hull in small private submersibles |
无人潜水器的耐压舱主要用来放置计算机、电子元器件和电池组等重要装备,环形肋骨加强的耐压圆柱壳有着内部舱室布置便利、加工简单、水中运动阻力小等特点,在现有的UUV以及水下滑翔机UG中应用广泛。耐压壳的形状需要考虑潜水器的外形,AUV的外形大多设计成类似于鱼雷的回转体,其耐压壳形状主要为带半球形封盖的圆柱体。ROV分为流线型壳体和开架式壳体(见图4),大多数ROV的耐压壳形状为球壳或球壳和圆柱壳的组合结构。UG的艇体外形主要有2种:带平行中体的水滴形和低阻层流形(见图5)。水滴形UG的耐压壳为组合形式,如头部椭圆形封头,中间段圆筒结构,尾部圆筒加球形封头,低阻层流形UG如美国的Seaglider滑翔机器人,其耐压壳体采用波纹管式套筒结构[13]。

|
图 4 ROV壳体结构 Fig. 4 Shell structure of ROV |

|
图 5 UG壳体结构 Fig. 5 Shell structure of UG |
随着壳体设计方法的完善和计算机技术的发展,在传统球柱锥组合型潜水器耐压壳结构的基础上,提出了新型耐压壳结构形式。
结合球壳的最佳重排比与圆柱壳较高空间利用率的优点,提出了藕节形耐压壳结构形式[14-15]。这种耐压壳由一系列球壳交接而成,交接球壳的个数可以分为双球型、三球型、四球型以至多球型,球壳之间的连接方式是该结构设计的关键点之一,目前有环向加强肋连接、切弧连接等几种设计方案[16-20]。藕节形耐压壳结构在载人潜水器和无人水下航行器中均可应用,2016年SH公司发布的私人潜水艇AURORA-6,即采用藕节形结构,载人舱共分4节(见图6),可载6人。

|
图 6 AURORA-6潜艇 Fig. 6 AURORA-6 submarine |
基于仿生学原理,以鹅蛋壳为原型,提出[21-22]蛋形及多蛋交接形耐压壳。研究表明,蛋形耐压壳水动力学特性较好,两端所受应力较低,便于开孔、开窗,具有良好的综合性能。多蛋交接形耐压壳包括若干个蛋形仿生壳,相邻蛋形壳的钝端和尖端通过环形肋骨顺次连接,可进一步扩大舱室空间,提高人机环特性,同时也便于分段制造[23-26]。目前蛋形耐压壳还处于概念设计性阶段,尚未有应用实例。
3 潜水器耐压壳材料的应用海洋的特殊环境对潜水器的耐压壳材料提出了特殊要求,耐压壳应采用高比强度、耐腐蚀、耐疲劳、物理性能稳定、成型工艺好的高性能材料。潜水器耐压壳材料一般分为金属和非金属两大类,金属材料主要有各种钢材料、铝合金、钛合金等,非金属材料主要有结构陶瓷、复合材料、有机玻璃等。
3.1 金属材料在潜艇和深潜器上的应用钢具有较高的比强度,良好的造船工艺性,在制造耐压容器和潜艇耐压壳方面,实用经验丰富,现阶段仍是潜水器耐压壳的主要材料。高强度合金钢具有高屈服强度、高韧性和高抗爆性、良好的焊接性、良好的耐海水腐蚀性能和抗低周疲劳等性能,常用于潜艇耐压壳。潜水器耐压壳体与潜艇相比较,结构较简单、所用材料量较少,目前各国潜水器中,以中等强度钢到超高强度钢作为潜水器耐压壳体材料的占绝大多数,美、法、日等国曾用钢材建造了不少潜水器,且这些国家的潜艇耐压壳体用钢与潜水器耐压壳体用钢一致。如美国潜艇用HY-80型、HY-100型和HY-130型钢,日本的NS30,NS46和NS90钢均作为深潜器耐压壳体材料。美海军用Hy-l30钢建造深海救援艇DSRV-I号,DSRV- Ⅱ号和核动力深潜器NR-l号,其先进蛙人输送系统(ASDS)前2艘艇ASDS Ⅰ和ASDS Ⅱ的耐压壳材料使用的是Hy-80钢;日本的NS-90钢则用于潜深达2 000 m的深海调查船[27]。
铝合金作为一种高比强度的材料,可以用来制造大深度潜水器耐压壳,但其成本造价远高于钢质壳体,且高强度铝合金焊接性能差,大大限制了其应用,美国在20世纪60年代建造的2 000米级“海鳗”号潜水器和4 500米级“阿卢米诺特”号潜水器的耐压壳使用了高强度铝合金材料[28]。在中小型水下无人潜水器方面,耐压壳采用高强度铝合金材料较为广泛,如美国水下滑翔机Spray Glider,Seaglider和Slocum,天津大学水下滑翔机PETREL和沈阳自动化研究所研制的滑翔机耐压壳体也采用了铝合金材料[29]。
钛合金的强度高于钢铁,重量却只有同体积钢铁的一半,断裂韧性优于钢和铝,具有良好的机械性能,材料性能稳定,在海水中抗腐蚀性能极好,无磁性、耐高温。使用钛合金耐压壳的潜艇,潜深是钢铁耐压壳潜艇的2~3倍,且可以大大提高隐蔽性能,进一步提高艇的水下航速,延长潜艇的使用寿命。俄罗斯是世界上第1个用钛合金建造潜艇耐压壳的国家,先后制造了4级钛合金做耐压壳的潜艇。钛合金比强度高,能够承受大深度水压,非常适合用于建造潜深3 000 m以上的载人潜水器球壳,各国的潜水器用材都经历了从高强度钢到钛合金的发展过程[30]。目前世界上现役的工作型大深度载人潜水器,除俄罗斯的MIRⅠ&Ⅱ的耐压壳采用马氏体镍钢外,其余各国的耐压壳均采用钛合金材料,其中最常用的是Ti-6AL-4VELI和Ti-6AI-2Nb-lTa-0.8Mo钛合金。
3.2 非金属材料在潜水器上的应用随着材料研究的进步与制造技术难点的攻克,新型材料在潜水器耐压壳上得到了应用。
结构陶瓷具有高强度、高韧性、高硬度、耐高温、耐磨损、化学稳定性好等特性,近几年来已逐步开始研究并应用为水下耐压材料的基材。最为典型的应用是美国“海神”号HROV深海运载器,耐压壳体选用氧化铝陶瓷作为主要基材,于2009年5月下潜至马里亚纳海沟10 902 m的海底,证实了其满足力学强度要求[31]。2018年10月,我国海斗深渊考察队在万米深渊综合科考任务中,对全海深陶瓷耐压舱内的高清摄像系统进行试验,最大工作水深10 910 m,实现了国际上将陶瓷材料作为摄像机耐压舱体的最大工作水深。
先进树脂基复合材料是指用碳纤维、陶瓷纤维、芳纶纤维等增强的聚合物复合材料,它的比强度可达钢和铝的6倍,而比模量则超过钢和铝的3倍,更具备材料可设计性的优点,结构减重效果显著,国外论证研究和模型试验都表明,复合材料建造潜艇耐压壳比钢壳下潜深度提高了3~4倍[32]。美国海军1996年用石墨纤维增强环氧树脂材料成功地制造出无人深潜器AUSSMOD2的耐压壳体,该艇的下潜深度为6 096 m,耐压壳筒体由缠绕成型工艺制作。华盛顿大学研制出的用于监测深海环境的大深度UG—Deep Glider号,采用碳纤维复合材料耐压壳体,实现了工作深度近6 000 m的实际应用。2006年,英国BAE系统公司下水了新型Talisman多功能自主式无人水下航行器,该航行器由碳纤维复合材料制成壳体,内部装有包含电子系统和有效载荷的碳纤维复合材料耐压壳。2015年3月,美国Ocean Gate公司公布全新的载人潜水器Cyclops1,它采用一种厚实的碳复合材料外壳,极大提高了载人舱的舒适度和耐久度,并且具有很高的可靠性,显著轻于其他水下载人潜水器。复合材料外壳制造过程采用自动铺丝技术(AFP),使船体能够承受更高的压缩载荷。2017年,Ocean Gate启动Cyclops 2研制,它的外壳主要由碳纤维和钛制成,可载5人,潜深4 000 m。我国在2015年由中国海洋大学研制成功轻型高分子复合材料深海耐压舱—“海大一号”与“海大二号”,达到了国外同类耐压舱的水平,可作为通用耐压容器用于ROV、AUV、水下滑翔机等多种海洋观测平台。2016年,“海翼”-7000水下滑翔机,实现了基于碳纤维复合材料的大深度耐压结构的核心技术突破。
有机玻璃(透明丙烯酸树脂)材料具有密度小、机械强度高、易于加工等优势,极高的透明度可以给观察员提供优越的水下视野,在观光和探险型潜水器上,大多使用全透明有机玻璃载人舱。我国的“寰岛蛟龙”号观光潜水器,即采用了1段球形有机玻璃和和3段圆柱形有机玻璃作为载人舱。日本计划未来新一代“深海12000”载人潜水器的载人球壳采用强化玻璃制造,可以极大提升海底作业的视景作业效率。
4 潜水器耐压壳的设计计算潜水器耐压壳的设计主要是其强度和稳定性的计算问题,一般的设计方法主要有理论公式设计、基于规范的设计方法和基于有限元方法的直接设计方法,本节介绍各种结构形式的潜水器耐压壳的设计计算方法。
4.1 圆柱耐压壳设计计算方法概述[33-35]环肋圆柱壳是潜水器耐压壳结构的基本形式,对均匀外压作用下的环肋加强圆柱耐压壳,可以简化为两端刚性固定在弹性支座上的复杂弯曲弹性基础梁来研究。
表征环肋圆柱形耐压壳结构强度的特征量主要有:相邻肋骨跨中壳板应力、肋骨根部壳板应力、肋骨应力,文献[34]对各国规范中圆柱耐压壳的设计计算方法行了研究比较,将表征强度的3个量的表达式归纳如下:
| $\left\{ {\begin{split} & {{{\rm{\sigma}} _1} = {{{K}}_1}\frac{{{{{p}}_{{j}}}{{R}}}}{t}}{\text{,}} \\ & {{{\rm{\sigma}} _2} = {{{K}}_2}\frac{{{{{p}}_{{j}}}{{R}}}}{t}} {\text{,}}\\ & {{{\rm{\sigma}} _{{l}}} = {{{K}}_{{l}}}\frac{{{{{p}}_{{j}}}{{R}}}}{t}} {\text{。}} \end{split}} \right.$ | (1) |
式中:pj为计算压力;K1,K2,Kl的表达式及确定方法见参考文献[34]。
在均匀外压力的作用下,环肋耐压壳体的失稳方式一般有肋间壳板失稳和总体失稳2种方式,表征圆柱形耐压壳结构稳性的特征量有肋间壳板失稳压力、柱壳总体失稳压力。
1)局部失稳计算方法
肋间壳板弹性理论临界失稳压力计算基于Mises公式:
| $ \begin{split} {{{P}}_{{E}}} = & \frac{{{E}}}{{0.5{{\rm{\alpha}} ^2} + {{{n}}^2} - 1}}{\times} \\ & \left[ {\frac{{{t^3}}}{{12(1 - {{\rm{\mu}} ^2}){{{R}}^3}}}({{{n}}^2} - 1 +{{{{\rm{\alpha}} ^2})}^2} + \frac{{{t}}}{{{R}}}\frac{{{{\rm{\alpha}} ^4}}}{{{{({{{n}}^2} + {{\rm{\alpha}} ^2})}^2}}}} \right]{\text{。}} \end{split} $ | (2) |
其中:E为材料的弹性模量;μ为泊松比;
CCS规范中将上式简化,得到PE的表达式为:
| ${{{P}}_{{E}}} = {{E}}{\left( {\frac{{{t}}}{{{R}}}} \right)^2}\frac{{0.6}}{{{{u}} - 0.37}}{\text{。}}$ | (3) |
式中:
对理论临界压力PE进行折减得到肋间壳板实际临界压力Pcr的表达式为:
| ${{{P}}_{{{cr}}}} = 0.75{{{C}}_{{s}}}{{{P}}_{{E}}}{\text{。}}$ | (4) |
式中:Cs根据参数
2)总体失稳计算方法
相邻舱壁之间舱段的总体弹性失稳压力
| $ \begin{split} & {{P}}_{{E}}' = \frac{{{E}}}{{0.5{{\rm{\alpha}} ^2} + {{{n}}^2} - 1}} {\times}\\ & \left[ {\frac{{{{{t}}^3}}}{{12(1 \!-\! {{\rm{\mu}} ^2}){{{R}}^3}}}{{({{{n}}^2} \!-\! 1\! +\! {{\rm{\alpha}} ^2})}^2} + \frac{t}{{{R}}}\frac{{{{\rm{\alpha}} ^4}}}{{{{({{{n}}^2} + {{\rm{\alpha}} ^2})}^2}}}{\rm{ + }}\frac{{{{I}}{{({{{n}}^2} \!-\! 1)}^2}}}{{{{{R}}^3}{{l}}}}} \right]{\text{。}} \end{split} $ | (5) |
其中:I为肋骨的截面惯性距;l为肋骨间距。
CCS规范中对理论临界压力
| ${{P}}_{{{cr}}}' = 0.{\rm{83}}{{{C}}_{{s}}}{{{P}}'}_{{E}}{\text{。}}$ | (6) |
式中:Cs由参数
1)薄球壳理论
球壳承受均匀外压时,保持球形状态均匀压缩变形,产生的面内压应力为:
| ${\rm{\sigma}} = \frac{{{{PR}}}}{{2{{t}}}}{\text{。}}$ | (7) |
2)CCS规范中球壳强度设计
球壳体壳板应力按下式计算:
| ${{\sigma}} = \frac{{{{{P}}_{{j}}}{{R}}}}{{2{{t}}}}{\text{。}}$ | (8) |
1)理论公式和钱学森公式
薄球壳在均匀外压下屈曲的理论公式是1915年R.Zoelly[36]用小变形假设导出的,经典解的表达式如下:
| ${{{P}}_{{{cr}}}} = \frac{{2{{E}}}}{{\sqrt {3(1 - {{{\mu}} ^2})} }}{\left( {\frac{{{t}}}{{{R}}}} \right)^2}{\text{。}}$ | (9) |
式中:E为材料弹性模量;μ为泊松比,当μ=0.3时,
根据实验得到的受压球壳失稳压力远小于上式的计算值,且失稳破坏是突然发生,对于大深度潜水器耐压球壳,上述理论临界值将远远高于实际破坏压力。
1939年,Karman和钱学森[37]指出球壳的受压变形是一种大挠度非线性变形,该理论得到的受压球壳最小屈曲载荷可归纳为简化公式:
| ${{{P}}_{{{cr}}}} \approx 0.365{{E}}{\left( {\frac{{{t}}}{{{R}}}} \right)^2}{\text{。}}$ | (10) |
钱学森理论的结果与E.E.Sechler和W.Bollay的半径18in薄铜半球壳实验结果吻合较好。
2)CCS规范整球壳体屈曲计算
CCS规范潜水器规范整球屈曲压力按下式计算
| ${{{P}}_{{{cr}}}} = {{{C}}_{{s}}}{{{C}}_{{z}}}{{{P}}_{{e}}}{\text{。}}$ | (11) |
式中:
3)2013版CCS规范中承受外压的钛合金耐压壳体的极限承载压力计算
2013版CCS规范中“第16章潜深大于500 m的潜水器的补充规定”,给出了初步设计阶段,承受外压的钛合金耐压球壳的极限承载压力的计算公式:
| $ {{{P}}_{{u}}} = (1 - {{k}})\left(\frac{{{{{R}}_{{m}}}{{t}}}}{{{{{R}}_{{i}}}}} + \frac{{{{{R}}_{{m}}}{{t}}}}{{{{{R}}_{{{mid}}}}}}\right){\text{。}} $ | (12) |
式中:Rm为材料抗拉强度;k为制造偏差修正系数,按下式计算:
| $\begin{split} k = & {a_0} + {a_1}x + {a_2}y + {a_3}{x^2} + {a_4}xy + {a_5}{y^2} + {a_6}{x^2}y + \\ & {a_{^7}}x{y^2} + {a_8}{y^3} + {a_9}{x^2}{y^2} + {a_{10}}x{y^3}+ {a_{11}}{y^4} + \\ & {a_{12}}{x^2}{y^3} + {a_{13}}x{y^4} + a14{y^5} {\text{。}} \end{split} $ | (13) |
其中:
对于各种新型的耐压壳结构,至今还没有成熟的理论计算方法,学者们根据自己的研究成果建立相应的模型,得到了一些结论,提出了相应的设计计算方法。
4.3.1 藕节形耐压壳设计计算方法文献[16]研究了交接处采用环肋加强的藕节形耐压壳(见图7)的设计计算方法。

|
图 7 环肋加强的藕节形耐压壳局部截面图 Fig. 7 Local of ring stiffened corrugated hull wall construction. |
该结构的强度计算基于薄壳理论,计算公式同球壳强度式(7),稳定性分析近似圆柱壳理论公式,局部稳定的临界压力公式如下:
| ${{{P}}_{{{cr}}}} = \left[ {1\! -\! 0.175\left( {\frac{{{{70}^{\rm{0}}}{\rm{ - }}{\rm{\alpha}} }}{{{{20}^{\rm{0}}}}}} \right)} \right]\! \times\! \left[ {1 \!-\! 0.07\left( {\frac{{{R}}}{{400{{t}}}}} \right)} \right]\left( {0.3{{E}}\frac{{{{{t}}^2}}}{{{{{R}}^2}}}} \right){\text{。}}$ | (14) |
式中:α为切弧角。
整体稳定的临界压力公式如下:
| ${{{P}}'}_{{{cr}}} \!=\! \frac{{{{Et}}}}{{{{{R}}_{{{eff}}}}}}\left[ {\frac{{{{{m}}^4}}}{{({{n}}_{{m}}^2 \!+\! \left( {{{{m}}^2}/2} \right) \!-\! 1){{({{n}}_{{m}}^2 \!+\! {{{m}}^2})}^2}}}} \right] \!+\! \frac{{({{n}}_{{m}}^2 - 1){{EI}}}}{{{{R}}_{{{eff}}}^3{{{L}}_{{s}}}}}{\text{。}}$ | (15) |
式中:
文献[19]提出了三藕节切弧连接耐压壳体(见图8)结构形式,采用有限元方法,在考虑几何、材料非线性和初始缺陷的条件下,参考球壳和圆柱壳的稳定性公式,给出三藕节切弧连接耐压壳体强度公式和稳定性公式。
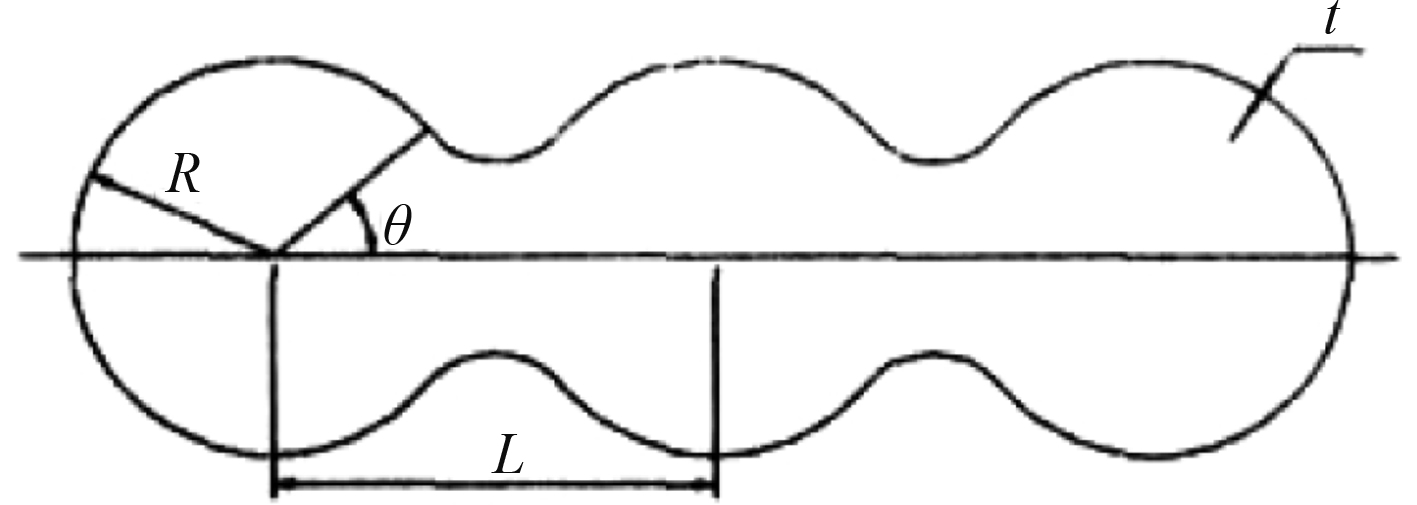
|
图 8 三藕节切弧连接耐压壳体 Fig. 8 Three intersecting spheres tangent arc connective pressure hull |
线性材料的三藕节切弧连接耐压壳体强度计算式如下:
| ${\rm{\sigma = }}{{P}} \cdot {{{f}}_1}({{{t}}_{{R}}}) \cdot {{{f}}_2}({{{L}}_{{R}}},{{sin}}(\theta )){\text{,}}$ | (16) |
| ${{{f}}_1}({{{t}}_{{R}}}){\rm{ = }}{{{a}}_1} \cdot {{t}}_{{R}}^2 + {{{a}}_2} \cdot {{{t}}_{{R}}} + {{{a}}_3}{^{{\rm{ - 1}}}}{\text{,}}$ | (17) |
| $ \begin{split} &{{{f}}_2}({{{L}}_{{R}}},{{sin}}(\theta )){\rm{ = }} \\ & {{sin}}(\theta ) \cdot ({{{b}}_1} \cdot {{L}}_{{R}}^4 + {{{b}}_2} \cdot {{L}}_{{R}}^3 + {{{b}}_3} \cdot {{L}}_{{R}}^2 + {{{b}}_4} \cdot {{{L}}_{{R}}} + {{{b}}_5}) + \\ & ({{{b}}_6} \cdot {{L}}_{{R}}^4 + {{{b}}_7} \cdot {{L}}_{{R}}^3 + {{{b}}_8} \cdot {{L}}_{{R}}^2 + {{{b}}_9} \cdot {{{L}}_{{R}}} + {{{b}}_{10}}){\text{。}} \end{split} $ | (18) |
式中:tR为厚度半径比t/R;LR为球壳间距半径比L/R;a,b参数的取值见参考文献[19]。
线性材料的三藕节切弧连接耐压壳体稳定性计算式如下:
| ${{{P}}_{{{cr}}}} = {{F}}'({{{f}}_{{R}}}) \cdot \frac{{{E}}}{{\sqrt {1 - {{\rm{\mu }}^2}} }} \cdot {{f}}{'_1}({{{t}}_{{R}}}) \cdot {{f}}{'_2}({{{L}}_{{R}}},{{sin}}(\theta )) \cdot {10^{ - 3}}{\text{,}}$ | (19) |
| ${{F}}'({{{f}}_{{R}}}){\rm{ = 6718}}{{f}}_{{R}}^2 - 73{{f}}_{{R}}^2 + 1{\text{,}}$ | (20) |
| ${{f}}{'_1}({{{t}}_{{R}}}){\rm{ = (}}{{{a}}_1}' \cdot {{t}}_{{R}}^2 + {{{a}}_2}' \cdot {{{t}}_{{R}}} + {{{a}}_3}'){\text{,}}$ | (21) |
| $\begin{split} {{f}}{'_2}({{{L}}_{{R}}},{{sin}}(\theta )){\rm{ = }}&{{si}}{{{n}}^{\rm{3}}}(\theta ) \cdot ({{{b}}_1}' \cdot {{L}}_{{R}}^2 + {{{b}}_2}' \cdot {{{L}}_{{R}}} + {{{b}}_3}') + \\ & {{si}}{{{n}}^2}(\theta ) \cdot ({{{b}}_4}' \cdot {{L}}_{{R}}^2 + {{{b}}_5}' \cdot {{{L}}_{{R}}} + {{{b}}_6}') +\\ & {{sin}}(\theta ) \cdot ({{{b}}_7}' \cdot {{L}}_{{R}}^2 + {{{b}}_8}' \cdot {{{L}}_{{R}}} + {{{b}}_9}') +\\ & ({{{b}}_{10}}' \cdot {{L}}_{{R}}^2 + {{{b}}_{11}}' \cdot {{{L}}_{{R}}} + {{{b}}_{12}}'){\text{。}} \end{split}$ | (22) |
式中:fR为缺陷幅值与半径比;a,b参数的取值见参考文献[19]。
4.3.2 蛋形耐压壳设计计算方法文献[39]研究了蛋形耐压壳设计计算方法,建立了蛋形耐压壳母线方程及解析法力学模型,得到了该结构的极限强度载荷、屈曲临界载荷的公式。
由薄壳理论确定蛋形耐压壳的径向应力
| ${{\rm{\sigma }}_\varphi }\left( {{x}} \right) = - \frac{{{{P}}{{{R}}_2}\left( {{x}} \right)}}{{2{{t}}}},{{\rm{\sigma }}_\theta }\left( {{x}} \right){\rm{ = }}{{\rm{\sigma }}_\varphi }\left( {{x}} \right) \cdot \left( {2 - \frac{{{{{R}}_2}\left( {{x}} \right)}}{{{{{R}}_1}\left( {{x}} \right)}}} \right){\text{。}}$ | (23) |
式中:
| ${{{R}}_1}\left( {{x}} \right){\rm{ = }}\left| {{{\frac{{\left( {{\rm{1 + }}{{\left( {{{R}}'\left( {{x}} \right)} \right)}^2}} \right)}}{{{{R}}''\left( {{x}} \right)}}}^{3/2}}} \right|,\;{{{R}}_{\rm{2}}}\left( {{x}} \right){\rm{ = }}{{R}}\left( {{x}} \right) \cdot \sqrt {1 + {{\left( {{{R}}'\left( {{x}} \right)} \right)}^2}}\;{\text{。}}$ | (24) |
蛋形耐压壳的屈曲临界载荷公式如下:
| ${{{P}}_{{{cr}}}} = \frac{{2{{E}}{{{t}}^2}}}{{\left( {2\overline {{{{R}}_1}} - \overline {{{{R}}_2}} } \right)\overline {{{{R}}_2}} }} \cdot \sqrt {\frac{1}{{3\left( {1 - {{\rm{\mu}} ^2}} \right)}}}\; {\text{。}}$ | (25) |
式中,
伴随着海洋装备的不断升级,未来的潜水器耐压壳结构可以从以下几个方面深化研究与应用:
1)海斗深渊科学成为海洋科学的最新前沿。在国际深海竞争中,用于海斗深渊科学研究的深海探测装备正成为各国关注的焦点,各国开始研发更轻、更小且拥有自航和作业能力的全海深潜水器[40]。随着下潜深度的不断提升,对耐压壳体的材料性能、制造工艺研究提出了新的要求,需要进一步提高耐压球壳临界压力计算的准确性,为潜水器的结构优化设计提供参考。
2)新材料耐压壳的安全性和可靠性研究。随着玻璃钢复合材料、碳纤维复合材料和陶瓷材料等的发展,新材料潜水器耐压壳已有多个应用实例,陶瓷材料,碳纤维复合材料都在无人潜水器上有所应用。“海神”号的丢失暴露出陶瓷耐压结构的安全性问题,已直接影响到其他潜水器的设计;对于大深度载人潜水器的耐压壳,国外在使用有机玻璃和新型复合材料时均遭遇过不少困难,使用时需特别谨慎;耐压壳在水下承受压应力,而抗压是纤维复合材料的弱点,其失效模式的研究应作为重点关注点。因此,新材料耐压壳的设计计算方法、制备工艺等的都是未来的研究方向。
3)全透明载人舱的设计和制造。半球或整球透明玻璃舱的应用是当下的热门课题,我国尚未能制造大深度的全透明球形丙烯酸树脂耐压壳,关于高透明度和大直径球状有机玻璃的研制、材料性能的研究、壳体强度及稳定性计算、制造加工工艺等方面研究在国内尚属起步阶段,未来在万米潜水器和一些小型载人潜水器均可以考虑应用。
6 结 语中国深潜“三龙”的研制成功,标志着我国深海技术的飞跃性发展,体现了我国深海技术装备发展的总体水平,进一步关心海洋、认识海洋、经略海洋已经成为的我国海洋事业发展的目标。本文对国内外潜水器的发展现状和潜水器耐压壳的研究情况进行概述,旨在为我国潜水器的研发提供参考。
| [1] |
ZHANG J, ZUO X L, WANG W B, et al. Overviews of investigation on submersible pressure hulls[J]. Advances in Natural Science, 2014, 7(4): 54-61. |
| [2] |
袁亚, 张木, 李翔, 等. 国外水下预置无人作战装备研究[J]. 战术导弹技术, 2018(1): 51-55. YUAN Ya, ZHANG Mu, LI Xiang, et al. Research on underwater pre-installed unmanned combat equipment[J]. Tactical Missile Technology, 2018(1): 51-55. |
| [3] |
李文跃, 王帅, 等. 大深度载人潜水器耐压壳结构研究现状与最新进展[J]. 中国造船, 2016, 57(1): 210-221. LI Wen-yue, WANG Shuai, et al. Current status and progress on pressure hull structure of manned deep submersible[J]. Shipbuilding of China, 2016, 57(1): 210-221. DOI:10.3969/j.issn.1000-4882.2016.01.023 |
| [4] |
沈允生, 刘涛, 张文忠. 小型观察型载人潜水器技术现状[J]. 江苏船舶, 2008, 25(4): 13-17. SHEN Yun-sheng, LIU Tao, ZHANG Wen-zhong. Technology Status of small manned submersibles[J]. Jiangsu ship, 2008, 25(4): 13-17. DOI:10.3969/j.issn.1001-5388.2008.04.005 |
| [5] |
李志伟, 马岭, 崔维成. 小型载人潜水器发展现状与展望[J]. 中国造船, 2012, 53(3): 244-254. LI Zhi-wei, MA Ling, CUI Wei-cheng. Status and prospects of small manned submersibles[J]. Shipbuilding of China, 2012, 53(3): 244-254. |
| [6] |
刘帅, 叶聪, 等. 观光潜水器发展现状与展望[J]. 中国造船, 2013, 54(3): 190-198. LIU Shuai, YE Cong, et al. Status and prospects of tourist submersibles[J]. Shipbuilding of China, 2013, 54(3): 190-198. DOI:10.3969/j.issn.1000-4882.2013.03.024 |
| [7] |
谢小龙. 深海ROV及组合结构设计与分析关键技术[M]. 上海交通大学, 2011.
|
| [8] |
许竞克, 王佑君, 侯宝科, 等. ROV的研发现状及发展趋势[J]. 四川兵工学报, 2011, 32(4): 71-74. XU Jing-ke, WANG You-jun, HOU Bao-ke, et al. Status and prospects of ROV[J]. Sichuan Ordnance Journal, 2011, 32(4): 71-74. |
| [9] |
钟宏伟. 国外无人水下航行器装备与技术现状与展望[J]. 水下无人系统学报, 2017, 25(3): 215-225. ZHONG Hong-wei. Review and prospect of equipment and techniques for unmanned undersea vehicle in foreign countries[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 215-225. |
| [10] |
马伟锋, 胡震. AUV的研究现状与发展趋势[J]. 火力指挥与控制, 2008, 33(6): 10-13. MA Wei-feng, HU Zhen. Current researches and development trend on AUV[J]. Fire Control and Command Control, 2008, 33(6): 10-13. |
| [11] |
沈新蕊, 王延辉, 等. 水下滑翔机技术发展现状与展望[J]. 水下无人系统学报, 2018, 26(2): 89-106. SHEN Xin-rui, WANG Yan-hui, et al. Development of Underwater Gliders: An Overview and Prospect[J]. Journal of Unmanned Undersea Systems, 2018, 26(2): 89-106. |
| [12] |
俞铭华, 王自力, 李良碧, 等. 大深度载人潜水器耐压壳结构研究进展[J]. 华东船舶工业学院学报, 2004, 18(4): 1-6. YU Ming-hua, WANG Zi-li, LI Liang-bi, et al. Development of research on the pressure shell structure of deep manned submersible[J]. Journal of East China Shipbuilding Institute (Natural Science Edition), 2004, 18(4): 1-6. DOI:10.3969/j.issn.1673-0453.2004.04.001 |
| [13] |
ERIKSEN C. C, OSSE T. J, LIGHT R.D.. Seaglider: a long-range autonomous underwater vehicle for oceanographic research[J]. IEEE Journal of Oceanic Engineering, 2001, 126(4): 424-436. |
| [14] |
GARLAND C. Design and fabrication of deep-diving submersible pressure hulls[J]. SNAME Transactions, 1968, 76: 161-179. |
| [15] |
LIANG Cho-chung, TENG Tso-liang, LAI Wen-hao. A study of diving depth on deep-diving submersible vehicle[J]. Pressure Vessels and Piping, 1998, 75: 447-457. DOI:10.1016/S0308-0161(98)00041-6 |
| [16] |
LIANG Cho-chung, SHIAH Sheau-wen, JEN Chan-yung, et al. Optimum design of multiple intersecting spheres deep-submerged pressure hull[J]. Ocean Engineering, 2004, 31: 177-199. DOI:10.1016/S0029-8018(03)00120-3 |
| [17] |
苟鹏, 刘涛, 崔维成. 深潜器多球交接耐压壳结构性能研究[J]. 舰船科学技术, 2008, 30(3): 55-59. GOU Peng, LIU Tao, CUI Wei-chen. A study on structural performance of the multiple intersecting spherical pressure hull[J]. Ship Science and Technology, 2008, 30(3): 55-59. |
| [18] |
苟鹏, 崔维成. 基于Kriging模型的深潜器多球交接耐压壳结构优化[J]. 船舶力学, 2009, 13(1): 100-106. GOU Peng, CUI Wei-cheng. Structural optimization of multiple intersecting spherical pressure hull based on Kriging model[J]. Journal of Ship Mechanics, 2009, 13(1): 100-106. DOI:10.3969/j.issn.1007-7294.2009.01.013 |
| [19] |
伍莉, 陈爱志, 陈小宁, 等. 藕节形大深度潜水器耐压壳体强度与稳定性研究[J]. 船舶力学, 2010, 14(1-2): 351-362. WU Li, CHEN Ai-zhi, CHEN Xiao-ning, et al. Strength and stability study of multiple intersecting spheres for great deep-submerged pressure hull[J]. Journal of Ship Mechanics, 2010, 14(1-2): 351-362. |
| [20] |
伍莉, 孟凡明, 陈小宁, 等. 藕节形大深度潜水器耐压壳体优化设计[J]. 船舶力学, 2008, 12(1): 100-109. WU Li, MENG Fan-ming, CHEN Xiao-ning, et al. Optimum design of multiple intersecting spheres great deep-submerged pressure hull[J]. Journal of Ship Mechanics, 2008, 12(1): 100-109. DOI:10.3969/j.issn.1007-7294.2008.01.015 |
| [21] |
ZHANG J, WANG M L, WANG W B, et al. Biological characteristics of eggshell and its bionic application[J]. Advance in Natural Science, 2015, 8(1): 41-50. |
| [22] |
王明禄. 基于蛋壳生物学特性的深海耐压壳仿生研究[M]. 镇江: 江苏科技大学, 2017.
|
| [23] |
张建, 王纬波, 高杰, 等. 深水耐压壳仿生设计与分析[J]. 船舶力学, 2015, 19(10): 1360-1367. ZHANG J, WANG W B, GAO J, el at. Bionic design and analysis of deep water pressure hull[J]. Journal of Ship Mechanics, 2015, 19(10): 1360-1367. |
| [24] |
张建, 朱俊臣, 王明禄, 等. 蛋形耐压壳设计与分析[J]. 机械工程学报, 2016, 52(15): 155-161. ZHANG J, ZHU J C, WANG M L, et al. Design and analysis of egg-shaped pressure hulls[J]. Journal of Mechanical Engineering, 2016, 52(15): 155-161. |
| [25] |
张建, 左新龙, 王纬波, 等. 多蛋交接耐压壳仿生研究[J]. 中国机械工程, 2016, 27(10): 2668-2674. ZHANG J, ZUO X L, WANG W B, et al. Bionic investigation on multiple intersecting egg-shaped pressure hull[J]. Journal of Mechanical Engineering, 2016, 27(10): 2668-2674. |
| [26] |
左新龙. 多蛋形交接耐压壳仿生设计及试验研究[M]. 镇江: 江苏科技大学, 2017.
|
| [27] |
王元. 深海装备材料防护技术最新研究进展[J]. 腐蚀防护之友, 2017(01). WANG Yuan. Latest research on material protection techniques of deep sea equipment[J]. Corrosion & Protection Fan, 2017(01). |
| [28] |
耐压与轻质结合潜水器的材料选择 [DB/OL]. https://qkzz.net/article/309064c3-f5e0-4f59-af31-caf9ab973da4.htm
|
| [29] |
刘进. 计及海洋参数水下滑翔机耐压壳体优化[M]. 天津: 天津大学, 2014.
|
| [30] |
曹福辛. 载人潜水器材料技术发展现状[J]. 中国材料进展, 2011, 30(6): 33-36. CAO Fu-xin. Development of materials for manned deep-ocean submersible[J]. Materials China, 2011, 30(6): 33-36. |
| [31] |
冯立超, 乔斌, 贺毅, 等. 深海装备材料之陶瓷基复合材料的研究进展[J]. 材料热处理技术, 2012, 41(22): 131-136. FENG Li-chao, QIAO Bin, HE Yi, el at. Development of ceramic matrix composite used in deep-sea equipment[J]. Material & Heat Treatment, 2012, 41(22): 131-136. |
| [32] |
朱孝信. 舰船用高技术新材料的发展[J]. 材料开发与应用, 1999, 14(1): 24-30. ZHU Xiao-xin. Development of hi-tech and new materials for shipbuilding[J]. Development and Application of Materials, 1999, 14(1): 24-30. DOI:10.3969/j.issn.1003-1545.1999.01.007 |
| [33] |
黎庆芬, 曾广武, 肖伟. 潜器圆柱形耐压壳体强度和稳性计算及衡准方法研究[J]. 中国舰船研究, 2006, 1(2): 45-49. LI Qing-fen, ZENG Guang-wu, XIAO Wei. Research on calculation and criteria of strength and stability of submersible cylindrical shell[J]. Chinese Journal of Ship Research, 2006, 1(2): 45-49. DOI:10.3969/j.issn.1673-3185.2006.02.011 |
| [34] |
黄进浩, 邱昌贤, 等. 主要潜水器规范圆柱形耐压壳体设计计算方法比较分析[J]. 船舶力学, 2017(Z1): 351-362. HUANG Jin-hao, QIU Chang-xian, et al. Comparative analysis on cylindrical structure design calculation method by main submersible rules[J]. Journal of Ship Mechanics, 2017(Z1): 351-362. DOI:10.3969/j.issn.1007-7294.2017.z1.046 |
| [35] |
朱信尧, 宋保维, 等. UUV内、外环肋加强耐压壳体强度与稳定性分析[J]. 系统仿真学报, 2013, 25(2): 371-376. ZHU Xin-yao, SONG Bao-wei, et al. Strength and stability analysis of UUV'S cylindrical shell stiffened by inside and outside rings[J]. Journal of System Simulation, 2013, 25(2): 371-376. |
| [36] |
中国船级社. 潜水系统和潜水器入级规范2013综合文本[S]. 北京, 2013. Rules for the construction and classification of diving system and submersible[S]. Beijing, 2013. |
| [37] |
李长春, 施德培. 潜水器结构强度[M]. 上海: 上海交通大学出版社, 1991.
|
| [38] |
KARMAN TV, TSIEN HS. The buckling of spherical shells by external pressure[J]. Journal of the Aeronautical Sciences, 1939, 7(2): 43-50. DOI:10.2514/8.1019 |
| [39] |
张建, 王明禄, 王纬波, 等. 蛋形耐压壳力学特性研究[J]. 船舶力学, 2016, 20(1-2): 99-109. ZHANG J, WANG M L, WANG W B, et al. Research on mechanical properties of the eggshell-shaped pressure hull[J]. Journal of Ship Mechanics, 2016, 20(1-2): 99-109. |
| [40] |
徐伟哲, 张庆勇. 全海深潜水器的技术现状和发展综述[J]. 中国造船, 2016, 57(2): 207-221. XU Wei-zhe, ZHANG Qing-yong. Overview of present status and development trend of full ocean depth submersibles[J]. Shipbuilding of China, 2016, 57(2): 207-221. |
 2019, Vol. 41
2019, Vol. 41
