电磁轨道炮是近几年来发展较快的一种以脉冲功率电源提供能源的武器[1],同传统以火药能源发射的火炮相比,具有发射初速高、速度可调、响应快等优点,可用于防空、反导、反装甲、超远程打击等领域,具有明显的军事应用价值[2]。弹丸在洛伦兹力的作用下加速运动,使高压气体从膛内喷出,在膛口形成非定常流场对膛口附近的测试装置等可能造成冲击作用,并对后续一体化弹丸的脱壳造成影响,故需要研究分析膛口前部流场的分布情况。对于火炮膛口流场的仿真研究,许多学者已经做过了大量的理论研究和仿真试验,理论和手段较为成熟。姜孝海等采用基于ALE方程的动网格和嵌入式网格法及二阶精度Roe方法对膛口进行了数值模拟,再现了流场形成与发展以及与弹丸耦合和相互作用过程[3];郭则庆等基于Navier-Stokes方程和k-ε湍流模型,采用Roe格式分别对不同飞行速度下的菱形机翼中内埋航炮膛口流场发展过程进行了模拟对比[4];焦志刚等采用三维Navier-Stokes方程及S-A模型建立了流场计算模型,对带稳定装置的弹丸发射时形成的膛口流场进行数值模拟[5];王美懿等基于有限元体积法,采用二维轴对称标准k-ε湍流模型并结合动网格分层技术对某平衡炮膛口进行了模拟,再现了膛口马赫盘、冲击波的形成过程[6]。
区别于传统封闭式炮膛的火炮,电磁轨道炮发射时不存在膛压而采用开放式炮膛,为此本文建立三维电磁轨道炮发射非定常流场模型,采用AUSM+格式求解N-S方程,k-ε湍流模型,通过UDF控制弹丸运动规律,动网格(铺层)技术更新运动区域对发射过程中膛内流场进行数值模拟计算,为后续试验设计提供参考依据。
1 理论基础与计算模型建立 1.1 流场控制方程与湍流模型弹丸在膛内运动过程中在极端的时间内速度达到超音速状态,弹前气体被压缩,理想气体二维无量纲可压缩非定常方程[7]如下:
| $\frac{{\partial { U}}}{{\partial t}} + \frac{{\partial { F}}}{{\partial u}} + \frac{{\partial { G}}}{{\partial v}} = J\text{。}$ | (1) |
式中:
| $ E = \frac{p}{{r - 1}} + \frac{1}{2}\rho ({u^2} + {v^2})\text{。} $ | (2) |
式中,
| $p = \rho RT\text{,}$ | (3) |
式中,
| $\rho \frac{{{\rm d}k}}{{{\rm d}t}} = \frac{\partial }{{\partial {x_i}}}\left[\left(\mu + \frac{{{\mu _i}}}{{\sigma {}_k}}\right)\frac{{\partial k}}{{\partial {x_i}}}\right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}\text{,}$ | (4) |
| $ \begin{array}{l} \rho \displaystyle\frac{{{\rm d}\varepsilon }}{{{\rm d}t}} = \displaystyle\frac{\partial }{{\partial {x_i}}}\left[\left(\mu + \displaystyle\frac{{{\mu _i}}}{{{\sigma _\varepsilon }}}\right)\displaystyle\frac{{\partial \varepsilon }}{{\partial {x_i}}}\right] + \rho {C_1}S\varepsilon - \rho {C_2}\displaystyle\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }}+\\ {C_{1\varepsilon }}\displaystyle\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b}\text{。} \end{array} $ | (5) |
式中:
轨道炮发射弹丸在极短的时间内完成,炮膛内的物理变化过程复杂,峰值加速度可达到40 000 g[8],电枢与导轨接触摩擦,炮膛内空气参数急剧变化,电磁轨道炮炮尾馈电装置结构复杂,炮口有消弧装置,如果在仿真计算的过程将模型完全考虑,会使得计算后复杂,网格划分难度加大,网格数很多,求解时间很长,难以收敛甚至计算得不到结果。因此,在仿真时只关心膛内和膛口流场的变化,对于不影响或者影响不大的因素将不予考虑,做以下简化和假设:
1)忽略炮尾复杂的结构,不考虑炮口消弧装置,即将整个发射机构简化为一个长形轨道,将内膛截面简化为四边形;
2)将弹丸简化为同一尺寸的长方体,以便在整个计算流场区域内划分结构化网格;
3)忽略一弹丸与内膛的间隙,认为两者完全贴合;
4)不考虑膛内运动时,电枢由于高速摩擦和转捩而温度升高对内膛空气域参数的影响;
5)不考虑电枢出炮口后电源回路断开产生的高电压对周围空气电离的影响,即认为整个计算流体域的空气为理想气体。
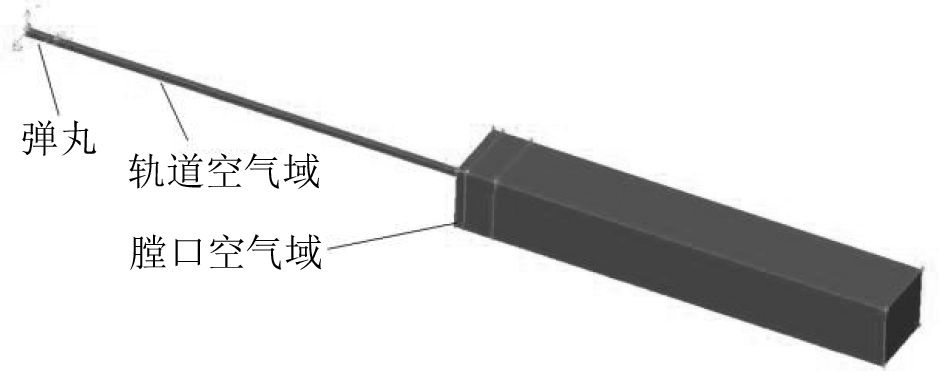
简化后的三维模型,轨道空气域长10 315 mm,外流场选8 970 mm×2 400 mm×2 400 mm的长方体空气域内,导轨伸进空气域210 mm的长度,如图1所示。
|
图 1 三维流场模型 Fig. 1 Model of 3-D flow field |
轨道内流体空间在发射时发生变动,在仿真计算时需要应用到动网格技术,其边界运动的任意一个控制体内,广义标量
| $\begin{array}{l} \displaystyle\frac{{\rm d}}{{{\rm d}t}}\int_V {\rho \varPhi } {\rm d}V + \int_{\partial V} {\rho \varPhi } \left( {\vec { u} - {{\vec { u}}_g}} \right) \cdot {\rm d}\vec A = \\ \displaystyle\int_{\partial V} {\Gamma \nabla \varPhi \cdot {\rm d}\vec A + \displaystyle\int_V {{S_\varPhi }} } {\rm d}V\text{。} \end{array}$ | (6) |
其中:
|
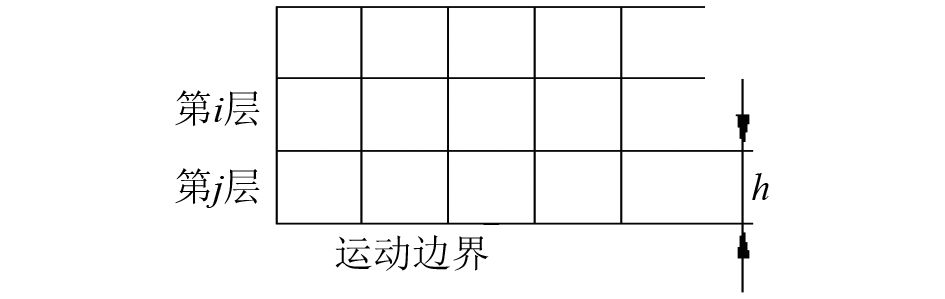
图 2 动态层模型 Fig. 2 Model of dynamic layer |
邻近边界的网格单元层j根据的单元层高度h来分裂出新的单元层或与邻近的层i合并成一个新层。
当网格层j扩大,单元高度的变化有一临界值:
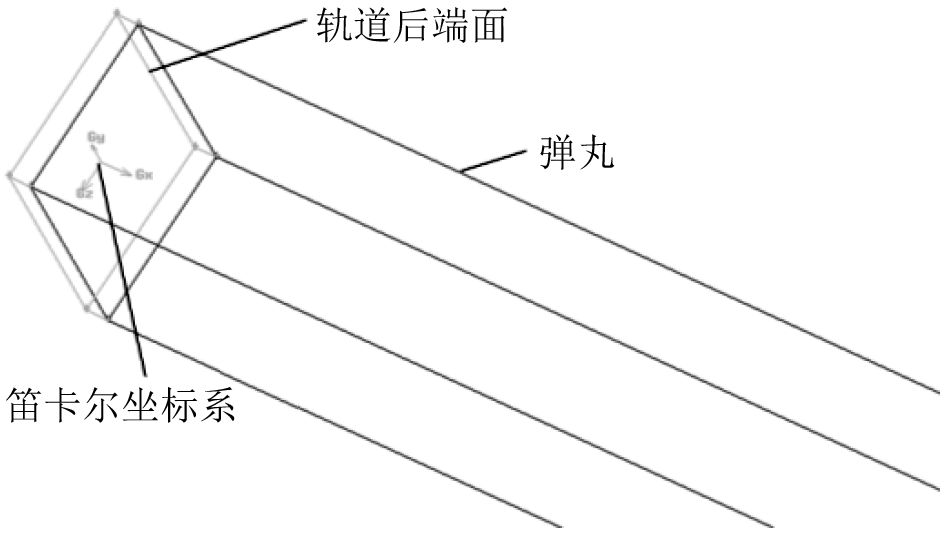
考虑弹丸运动的方向性,要确定坐标系的位置,选取炮膛起始点截面中心作为静止坐标系的原点,运动方向作为X轴正向,如图3所示。
|
图 3 坐标方向示意图 Fig. 3 Sketch of coordinate system direction |
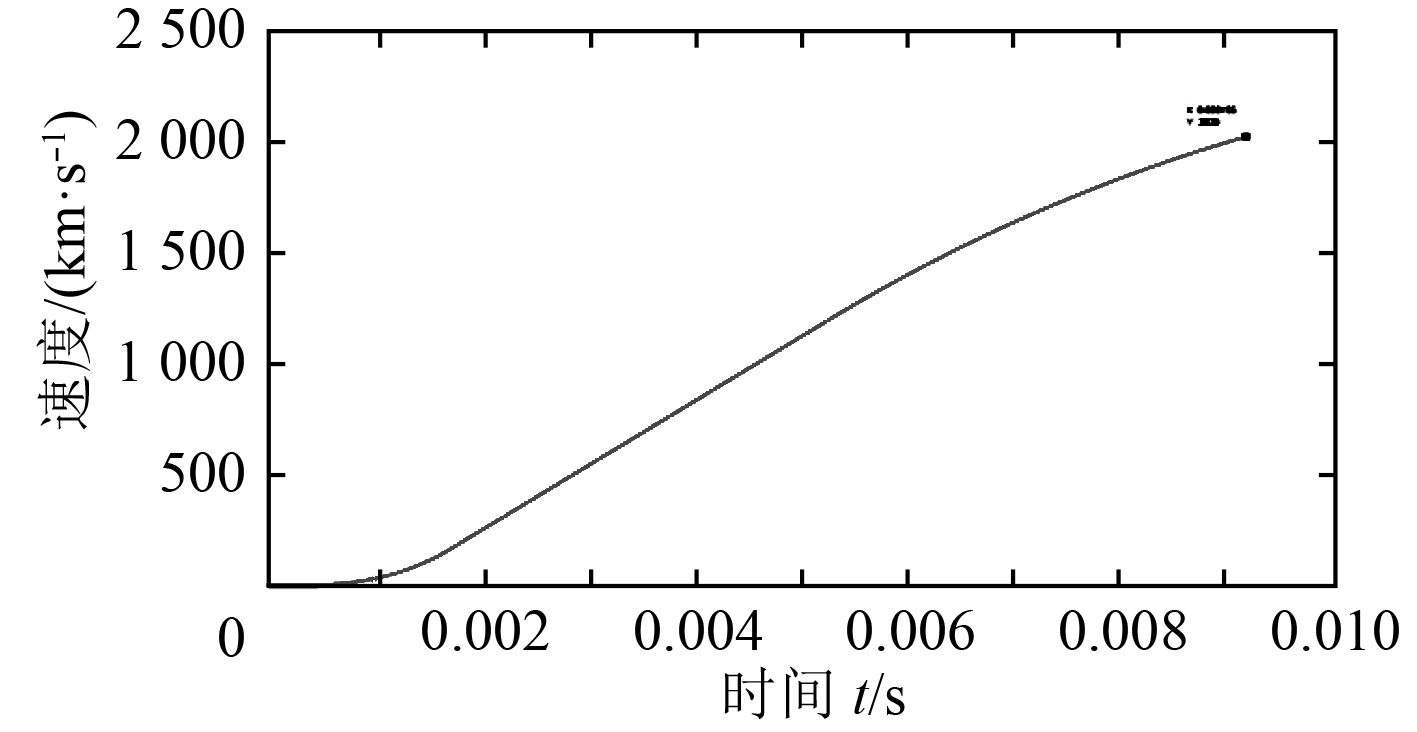
炮膛与外流场空气域的结合面分开划分并设置interface面用于仿真数据的传递。炮膛内部网格为动网格运动区域,弹丸在空气域中的网格一起运动形式,运动的规律由洛伦兹力推导得来的v-t曲线写入UDF进行控制,该v-t曲线图如图4所示。
|
图 4 弹丸膛内运动v-t曲线 Fig. 4 V-t curve of projectile moving in muzzle |
动网格设置采用铺层方式更新动网格,炮尾端面为网格生成边,炮口前端为网格消失面。所有流体域空气设置为理想气体(ideal-gas),整个外流场所有面为压力出口边界,最左端面为压力进口面,两者均为1个标准大气压值(101 325 Pa),采用基于压力的耦合求解器以便于加速收敛,显示求解以尽量降低消耗更多的计算机资源。整个模型流体域采用六面体结构化网格划分,以尽量提高网格的质量,膛内网格均匀划分,膛外靠近膛口流场网格较密,远离膛口的空气域网格稀疏,最终得到网格数量约为120万个。
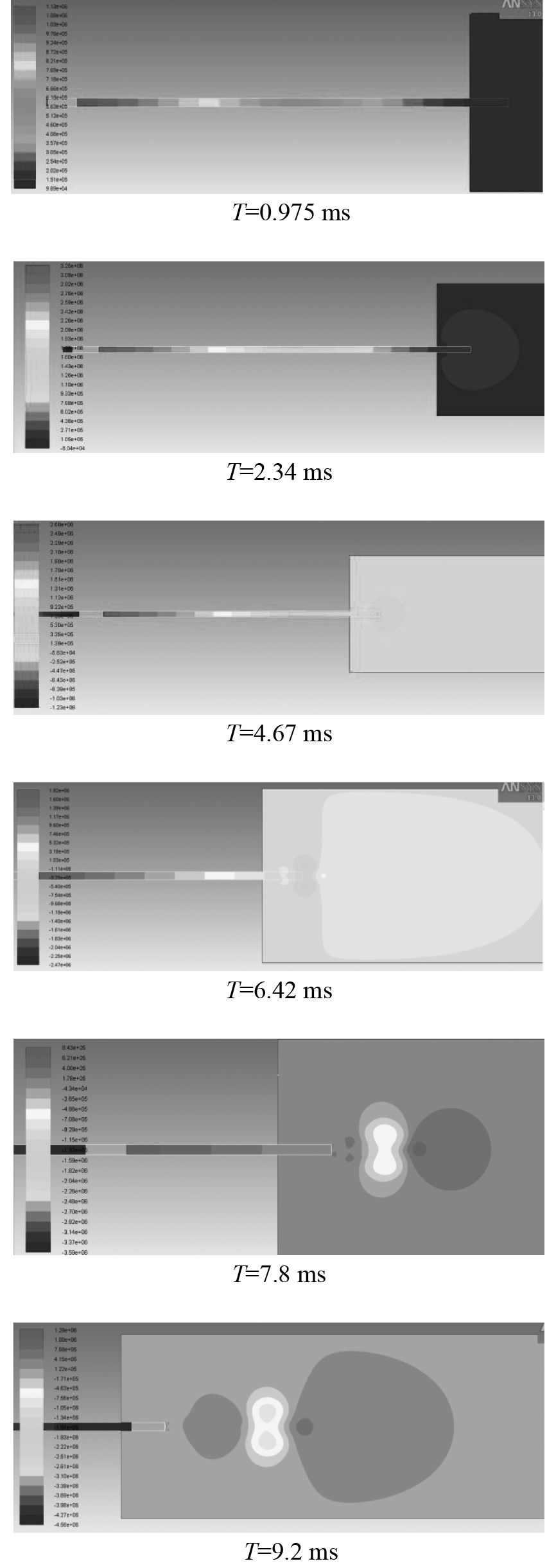
3 仿真结果与分析整个计算时间为9.2 ms,考虑到运动最大速度以及网格边尺寸为13.73 mm,以及在运动过程中网格更新出现负体积的情况,选取时间步长为6.5E-6 s,计算时间步为1 415步,以Z=0平面做切面,得到在不同时刻场内压力场分布图如图5所示。
|
图 5 不同时刻Z=0平面流场压力云图 Fig. 5 Pressure nephogram of flow field on Z=0 plane at different time |
可以看出,弹丸加速运动时膛内空气被挤压形成压力波使得在轴向方向上压力、密度、速度都成线性递减的分布形式,弹后气体参数为相同线性分布,为负低压区。开始运动初期,弹丸速度不高,达到一定的速度后,外场气体压力湍流足够明显,气流从膛口喷出,形成膨胀波,迅速向四周扩散,包裹轨道,随着弹丸速度的不断提高,膨胀高压区逐渐朝着X轴正向前移,到T=6.25 ms左右时刻高压区呈现蘑菇状扩展至流场边际,之后高压区随着涡流不断的形成扩大,低压涡流区域形成,同高压涡流团形成出现由耦合到分离的现象,在弹丸膛内运动结束时刻两者完全分离。
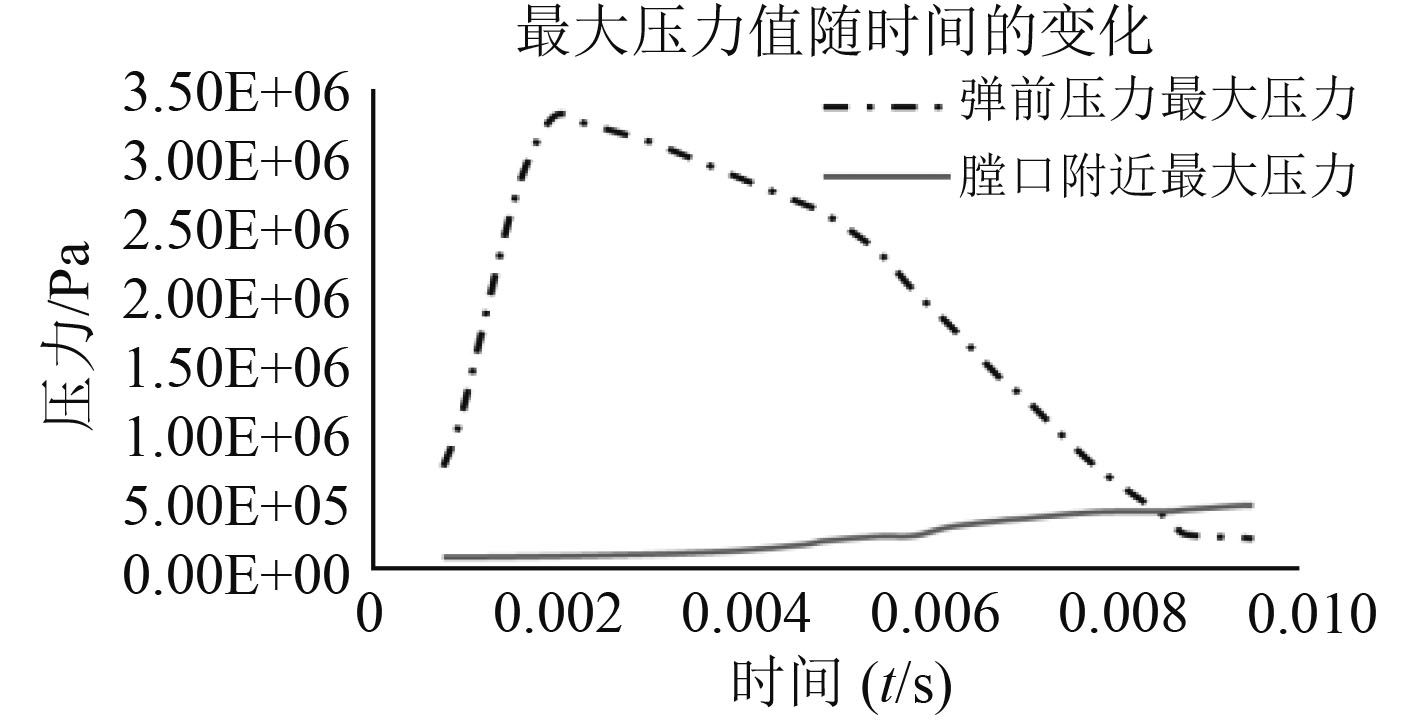
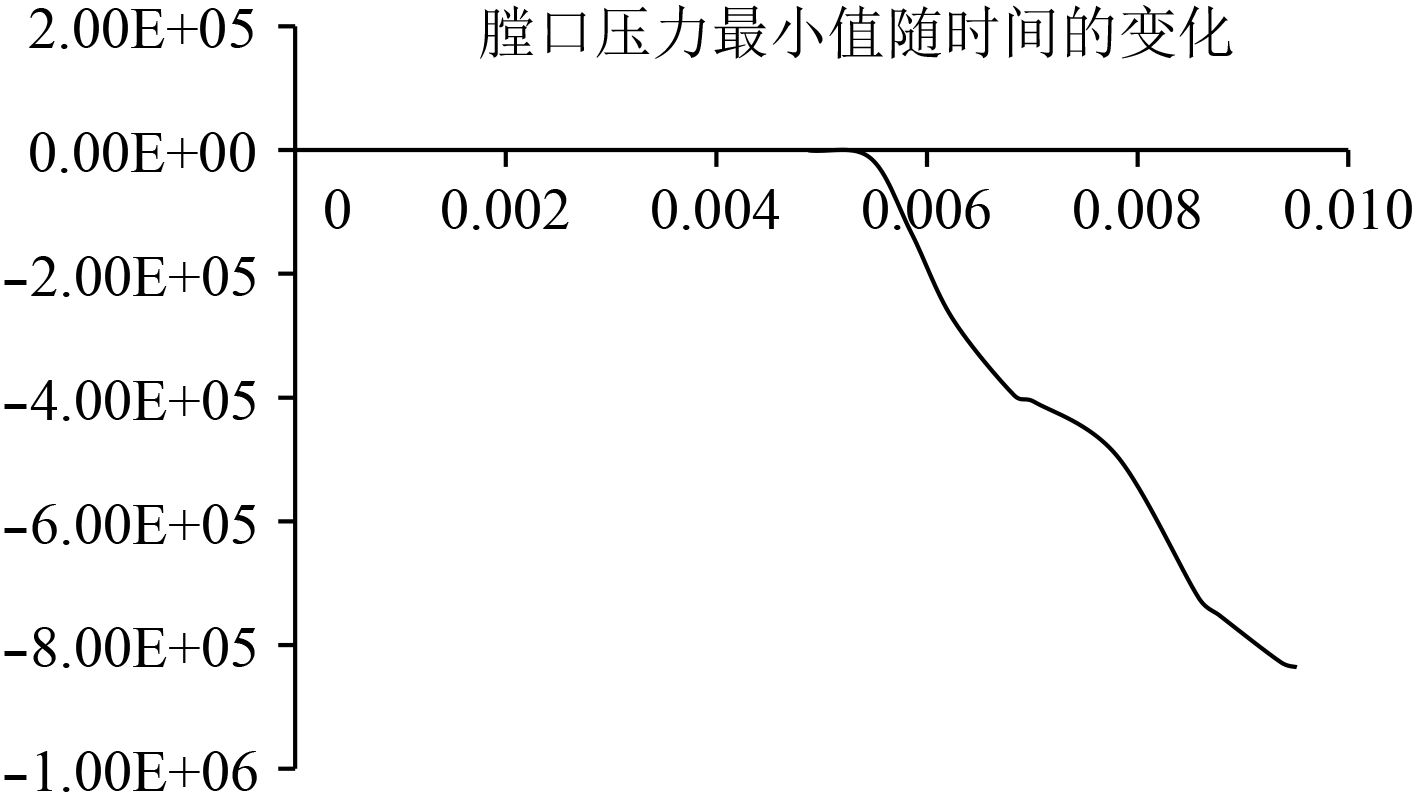
弹体前端为膛内最大压力区,该压力值在整个发射时间段内现急剧增大,然后缓慢下降,最后快速下降,整个变化趋势同弹丸的加速度变化趋势相近,最大在T=2.12 ms出现,为33个大气压值,最低值即为膛口出压力为2.3个大气压值,如图6所示。通过设置监控得到在时间T=9.56 ms前膛口始终处于标准大气压力值,说明在此时间以前膛内空气流场的流动还不足以引起膛口流场参数的变化。随着膛内高压气体的不断喷出膛口高压区和涡流低压区不断加强。结束时两者均达到峰值,相对高压为4.8个大气压值,相对低压为–7.8个大气压值,如图6和图7所示。
|
图 6 最大压力值随时间的变化情况 Fig. 6 The situation of maximum pressure changing with time |
|
图 7 膛口最小压力值随时间的变化情况 Fig. 7 The situation of minimum pressure changing with time on muzzle |
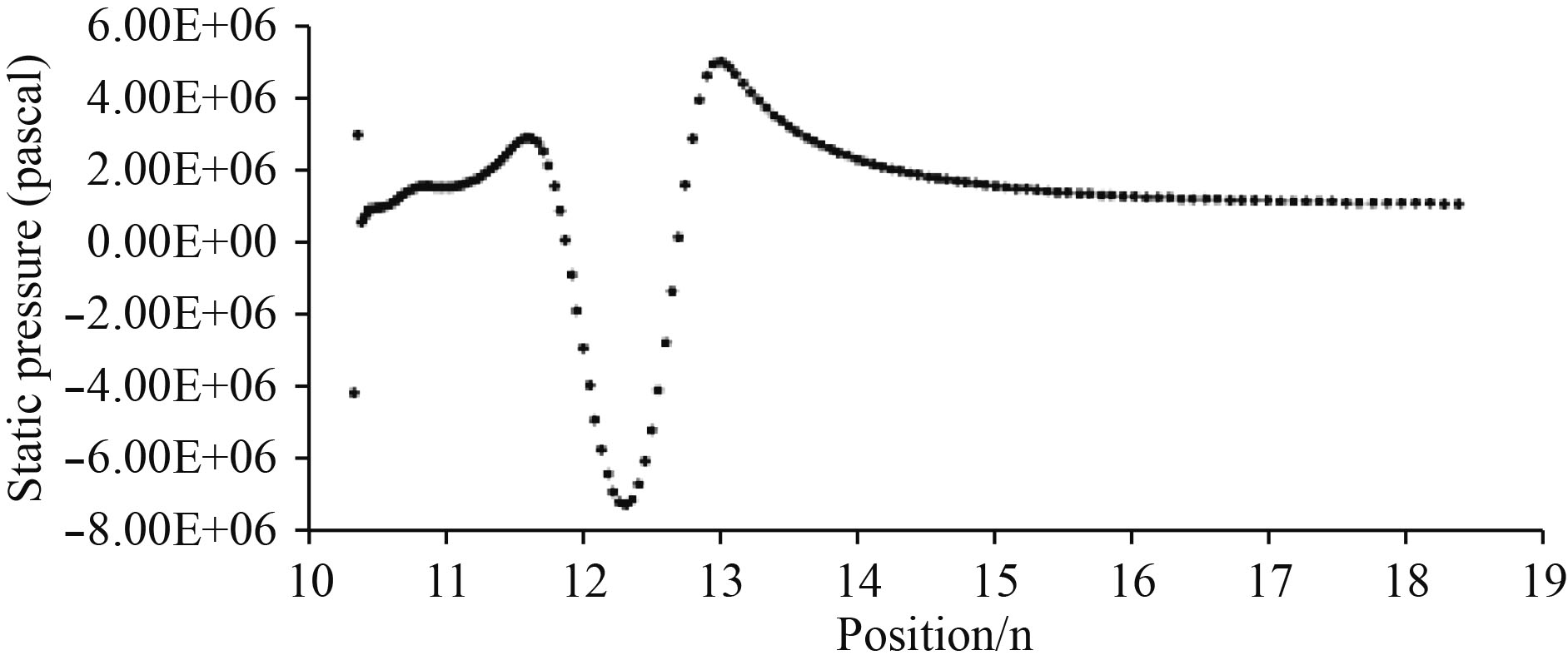
弹丸在膛内运动结束后,在膛口区域最终形成了2个高压区和1个阶梯状的负低压区(T=9.2 ms时刻),其中心方向上的压力值数如图8所示。弹丸出膛后进入该流场区域,其脱壳状态和初始外弹道飞行参数将受到影响。
|
图 8 T=9.2 ms时刻膛口中心轴向压力分布 Fig. 8 Pressure distribution of centre on muzzle from axial direction at T=9.2 ms |
本文通过建立轨道炮弹丸发射膛口流场模型,运用CFD仿真手段,对发射时膛内及膛口流场的动态变化过程进行了数值模拟,仿真结果表明:
1)发射时,膛内弹前空气域压力为线性递减分布,弹头部位始终为最大压力值区,该压力值随时间的变化情况与一体化弹丸运动的a-t曲线相近,反映出仿真结果与实际相符,且弹前阻力较大,在轨道炮模型推导时该因素需要考虑;
2)发射时膛口流场在不同时刻呈现出不同的状态,并随着时间不断前移,发射完成时刻膛外形成高压和负压的复杂流场区域将弹丸初始外弹道飞行参数有影响,需要进一步研究。
| [1] |
蔡喜元, 鲁军勇, 谭赛, 等. 基于双层梁模型的电磁轨道发射身管动力学研究[J]. 舰船科学技术, 2019, 43(3): 101-107. CAI Xi-yuan, LU Jun-yong, TAN Sai, et al. Transient resonance in electromagnetic launchers on double-deck rail[J]. Ship Science and Technology, 2019, 43(3): 101-107. |
| [2] |
王航宇, 卢发兴, 许俊飞, 等. 舰载电磁轨道炮作战使用问题的思考[J]. 海军工程大学学报, 2016, 28(3): 1-6. |
| [3] |
姜孝海, 李鸿志, 范宝春, 等. 基于ALE方程及嵌入式网格法的膛口流场数值模拟[J]. 兵工学报, 2007, 28(12): 1512-1515. DOI:10.3321/j.issn:1000-1093.2007.12.022 |
| [4] |
郭则庆, 乔海涛, 姜孝海. 内埋式航炮膛口流场特性数值模拟研究[J]. 兵工学报, 2017, 38(12): 2373-2378. DOI:10.3969/j.issn.1000-1093.2017.12.010 |
| [5] |
焦志刚, 孙冲, 邱浩. 带尾翼弹丸的膛口流场三维数值模拟[J]. 沈阳理工大学学报, 2017, 36(1): 38-41. DOI:10.3969/j.issn.1003-1251.2017.01.010 |
| [6] |
王美懿, 王浩. 超大口径平衡炮膛口流场数值仿真与流动特性分析[J]. 火炮发射与控制学报, 2017, 38(2): 16-19. |
| [7] |
ANDERSON J. D. (著), 吴颂平, 刘赵淼(译). 计算流体力学基础及其应用[M]. 北京: 机械工业出版社2003北京.
|
| [8] |
MCNAB IR. Progress on hypervelocity railgun research for launch to space[J]. IEEE Transactions on Magnetics, 2009, 45(1): 381-388. DOI:10.1109/TMAG.2008.2008601 |
 2019, Vol. 41
2019, Vol. 41
