由于被动探测器仅能获得目标的方位信息而不能检测目标的距离,利用单平台单基阵测量定位时,在本舰不进行机动的情况下,仅使用该探测平台的方位角测量值,目标运动状态不可观测[1 – 3]。被动声呐跟踪水中目标是典型的目标运动分析(TMA)问题,探测平台机动是目标运动可观测的必要条件,通过非线性滤波方法以及探测平台机动提高纯方位TMA问题中目标状态可观测性。目前常用的目标跟踪定位方法有直角坐标系下的扩展卡尔曼滤波、伪线性滤波及修正极坐标下的扩展卡尔曼滤波等[4 – 5]。随着军事技术的不断发展,敌我双方的对抗性显著提高,在双方平台对抗博弈的条件下,被跟踪目标会通过采取必要的机动提高生存能力,因此,机动目标运动要素估计的研究成为军事上的迫切需求。
本文在修正极坐标系下研究了单平台被动目标跟踪定位问题,提出一种距离参数化滤波器设计方法,降低滤波器初始参数对目标运动状态估计的不利影响,提高估计算法收敛速度和精度。给出基于目标运动状态滤波器的目标机动检测算法,实现对水中机动逃逸目标运动要素迅速、准确的估计,解决水中机动目标检测与跟踪问题。
1 修正极坐标系下目标运动分析 1.1 修正极坐标系在不同的坐标系中目标运动估计滤波系统方程有不同的特点,本文采用修正极坐标将系统状态变量分成了可观测和不可观测两部分。目标与探测平台的几何关系如图1所示。
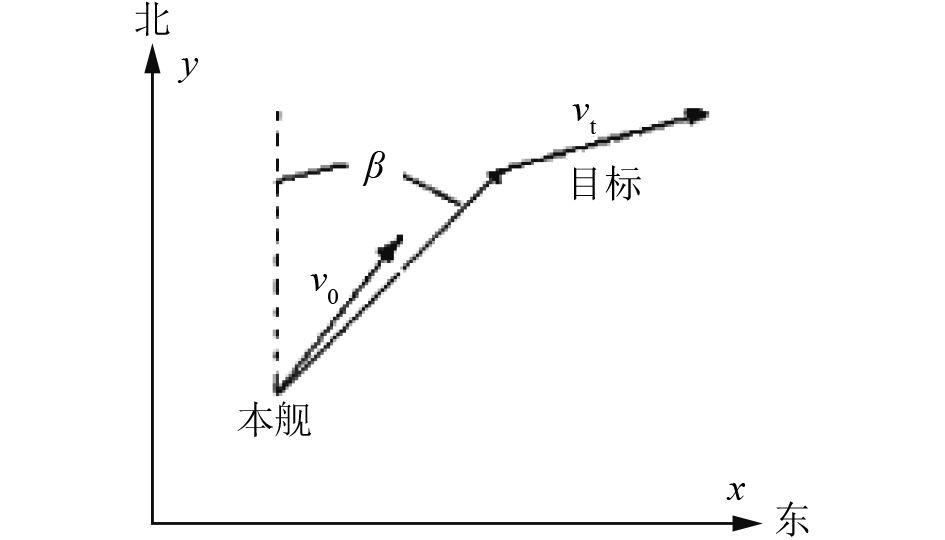
|
图 1 目标与探测平台的几何关系 Fig. 1 Relative geometric graph of target and detective platform |
直角坐标系的状态向量定义为:
| $x(t) = \left[ \begin{array}{l} {x_1}(t) \\ {x_2}(t) \\ {x_3}(t) \\ {x_4}(t) \\ \end{array} \right] = \left[ \begin{array}{l} {v_x}(t) \\ {v_y}(t) \\ {r_x}(t) \\ {r_y}(t) \\ \end{array} \right]\text{,}$ |
其中,
修正极坐标系下的系统状态向量定义为:
| $y(t) = \left[ \begin{array}{l} {y_1}(t) \\ {y_2}(t) \\ {y_3}(t) \\ {y_4}(t) \\ \end{array} \right] = \left[ \begin{array}{l} \dot \beta (t) \\ \dot r(t)/{\rm{r}}(t) \\ \beta (t) \\ 1/r(t) \\ \end{array} \right]\text{。}$ | (1) |
其中,
令目标和探测平台在x,y方向上的加速度分别为
| $\left[ \begin{array}{l} {a_x}(t) \\ {a_y}(t) \\ \end{array} \right] = \left[ \begin{array}{l} {a_{tx}}(t) - {a_{ox}}(t) \\ {a_{ty}}(t) - {a_{oy}}(t) \\ \end{array} \right]\text{。}$ |
令
| $w(t,{t_0}) \triangleq \left[ \begin{array}{l} {w_1}(t,{t_0}) \\ {w_2}(t,{t_0}) \\ {w_3}(t,{t_0}) \\ {w_4}(t,{t_0}) \\ \end{array} \right] = \left[ \begin{array}{l} \displaystyle\int_{{t_0}}^t {{a_x}(\lambda )d\lambda } \\ \displaystyle\int_{{t_0}}^t {{a_y}(\lambda )d\lambda } \\ \displaystyle\int_{{t_0}}^t {(t - \lambda ){a_x}(\lambda )d\lambda } \\ \displaystyle\int_{{t_0}}^t {(t - \lambda ){a_y}(\lambda )d\lambda } \\ \end{array} \right]\text{,}$ |
得
| $\begin{split} &x(t) = {f_x}\left[ {y(t)} \right] = \frac{1}{{{y_4}(t)}}\times\\ &\quad \left[ \begin{array}{l} {y_2}(t)\sin {y_3}(t) + {y_1}(t)\cos {y_3}(t) \\ {y_2}(t)\cos {y_3}(t) - {y_1}(t)\sin {y_3}(t) \\ \sin {y_3}(t) \\ \cos {y_3}(t) \\ \end{array} \right] + \left[ \begin{array}{l} {w_1} \\ {w_2} \\ {w_3} \\ {w_4} \\ \end{array} \right]\text{。} \end{split}$ | (2) |
令
| ${S_1}(t,{t_0}) \!=\! {y_1}({t_0}) \!+\! {y_4}({t_0})[{w_1}(t,{t_0})\cos {y_3}({t_0}) \!-\! {w_2}(t,{t_0})\sin {y_3}({t_0})]\text{,}$ |
| ${S_2}(t,{t_0}) \!=\! {y_2}({t_0}) \!+\! {y_4}({t_0})[{w_1}(t,{t_0})\sin {y_3}({t_0}) \!+\! {w_2}(t,{t_0})\cos {y_3}({t_0})]\text{,}$ |
| $ \begin{split}{S_3}(t,{t_0}) =& (t - {t_0}){y_1}({t_0})\! +\! {y_4}({t_0})[{w_3}(t,{t_0})\cos {y_3}({t_0}) -\\ &{w_4}(t,{t_0})\sin {y_3}({t_0})]\text{,} \end{split}$ |
| $\begin{split} {S_4}(t,{t_0}) \!=\!& 1\! +\! (t\! - \!{t_0}){y_2}({t_0})\! +\! {y_4}({t_0})[{w_3}(t,{t_0})\sin {y_3}({t_0}) +\\ &{w_4}(t,{t_0})\cos {y_3}({t_0})]\text{,}\end{split}$ |
可得到修正极坐标系下的状态方程为:
| $\begin{aligned} y(t) = \left[ {\begin{array}{*{20}{l}} {[{S_1}(t,{t_0}){S_4}(t,{t_0}) - {S_2}(t,{t_0}){S_3}(t,{t_0})]}\\ {/[{S^2_3}(t,{t_0}) + {S^2_4}(t,{t_0})]}\\ {[{S_1}(t,{t_0}){S_3}(t,{t_0}) - {S_2}(t,{t_0}){S_4}(t,{t_0})]}\\\ {/[{S^2_3}(t,{t_0}) + {S^2_4}(t,{t_0})]}\\ {{y_3}({t_0}) + {{\tan }^{ - 1}}[{S_3}(t,{t_0})/{S_4}(t,{t_0})]}\\ {{y_4}({t_0})/\sqrt {{S^2_3}(t,{t_0}) + {S^2_4}(t,{t_0})} } \end{array}} \right]\text{。} \end{aligned}$ | (3) |
由于在修正极坐标系中,目标方位角
| $\tilde \beta (t) = {h_y}[y(t)] + n(t) = [0,0,1,0]y(t) + n(t)\text{。}$ | (4) |
其中,
修正极坐标系下目标运动要素解算表达式如下:
| $\theta = {\tan ^{ - 1}}({v_x}/{v_y})\text{,}$ | (5) |
| $v = \sqrt {v_x^2 + v_y^2}\text{,} $ | (6) |
| $r = \sqrt {r_x^2 + r_y^2}\text{。} $ | (7) |
其中:
采用扩展Kalman滤波(EKF)算法求解纯方位TMA问题,该算法采用递推方式,计算量较小,能够对系统进行实时定位,且估计精度较高,利于实际工程的应用。纯方位TMA问题中系统状态方程(3)和测量方程(4)为连续形式,适当选取
| $ \begin{array}{l} {{y}}(k|k - 1) = f[{{y}}(k - 1|k - 1);kT,(k - 1)T]\text{,}\\ {{{A}}_{{y}}}(k,k - 1) = \displaystyle\frac{{\partial f[{{y}}(k - 1|k - 1);kT,(k - 1)T]}}{{\partial {{y}}(k - 1|k - 1)}}\text{,}\\ {{P}}(k|k - 1) = {{{A}}_{{y}}}(k,k - 1){{P}}(k - 1|k - 1){{A}}_{{y}}^{\rm T}(k,k - 1)\text{,}\\ {{K}}(k) = {{P}}(k|k - 1){{H}}{(k,k - 1)^{\rm T}}\text{,}\\ {[{{H}}(k,k - 1){{P}}(k|k - 1){{H}}{(k,k - 1)^{\rm T}} + {\sigma ^2}(k)]^{ - 1}}\text{,}\\ {{y}}(k|k) = {{y}}(k|k - 1) + {{K}}(k)[\tilde \beta (k) - {{H}}(k,k - 1){{y}}(k|k - 1)]\text{,}\\ {{P}}(k|k) = [{{I}} - {{K}}(k){{H}}(k,k - 1)]{{P}}(k|k - 1)\text{。}\\[-65pt] \end{array} $ | (8) |
其中:
在纯方位TMA问题中,探测平台与目标相对距离是不可观测变量,当目标与探测平台相对距离先验分布信息比较模糊时,直接使用EKF滤波算法容易导致状态协方差矩阵过早收敛,从而使得滤波发散。距离参数化(RP)方法将初始距离按照相对距离估计值的变异系数分成若干个独立区间,每个独立区间使用独立的EKF滤波器进行状态估计计算,初始时刻每个滤波器将赋予均匀的权值。当系统获得下一时刻观测值时,系统的状态向量和协方差矩阵要升级一次,与此同时,在RPEKF中各个独立区间的权重也需要重新计算并归一化处理。假定目标方位角的估计值和测量值服从高斯分布,利用贝叶斯理论,给出子区间权重递推计算公式,如式(9)。如果子区间内目标方位角的估计值与测量值有较大的差别,那么对应的子区间权重就会降低。反之,权重就会升高。
| ${W_{nk}} = {W_{nk - 1}}\frac{1}{{\sigma \sqrt {2{\text{π}} } }}\exp \left[ { - \frac{1}{2}{{\left( {\frac{{{{\tilde \theta }_n} - {\theta _m}}}{\sigma }} \right)}^2}} \right]\text{。}$ | (9) |
式中:
纯方位TMA问题针对静止目标或匀速直线运动目标开展研究,当目标出现机动时,目标运动要素估计算法无法实现对目标的无偏估计,系统状态无法收敛至真实状态值。为克服此缺陷,设计机动检测环节,在检测到目标机动时重新初始化目标运动状态滤波器。
由于RPEKF是几个独立EKF共同工作的滤波系统,所以其目标机动检测算法应在各EKF目标机动检测算法的基础上进行修正,算法中使用系统状态综合值和系统协方差矩阵综合值实现目标机动检测,表达式如下:
| ${e_k} = {\beta _k} - {{H}}^*{{\rm{y}}_{syn}}(k|k - 1)\text{,}$ | (10) |
| ${g_k} = {e_k}{({{H}}*{{{P}}_{syn}}(k|k - 1)*{{\rm{H}}^{\rm T}} + {\sigma ^2})^{ - 1}}{e_k}\text{,}$ | (11) |
| ${U_k} = a^*{g_{k - 1}} + (1 - a){g_k}\text{。}$ | (12) |
其中:
| ${{\rm{y}}_{syn}}(k|k - 1) = \sum\limits_{i = 1}^n {{W_{ik}}} {{\rm{y}}_i}(k|k - 1)\text{,}$ | (13) |
| ${{{P}}_{syn}}(k|k - 1) = \sum\limits_{i = 1}^n {{W_{ik}}} {{{P}}_i}(k|k - 1)\text{。}$ | (14) |
式中:
探测平台与目标相对距离34 000 m,目标舷角30°。
本文中探测平台采用“Z”字形机动方式,机动过程由匀速直线运动与匀速圆周运动交替进行。其中,探测平台移动速度为5 m/s,转弯角速率为1°s。该运动方式由3个参数决定,分别是一周期内匀速直线运动的时间
探测平台测量量为叠加了白噪声的目标方位角,噪声均值为0,标准差为1°。
4.1.2 滤波器初始参数探测平台采用被动声呐测量目标方位角,由于对目标初始位置缺乏先验信息,这里给出目标初始相对距离分布区间为[10 000 m,35 000 m],采用RPEKF滤波器对目标运动要素进行估计。
根据距离分布区间大小决定了EKF滤波器数量,本文选择滤波器个数为4。假定每个独立距离分布区间中距离误差服从均匀分布,对应于4组EKF滤波器的初始距离可以分为4个独立区间[10 000 m,14 000 m],[14 000 m,19 600 m],[19 600 m,27 400 m],[27 400 m,35 000 m],每个独立区间都对应一个独立的EKF滤波器,每个独立区间分配的权重为0.25。
4组独立的EKF滤波器初值如下:
| ${y_0} = \left[ \begin{array}{l} {\dot \beta } \\ \dot R/R \\ \beta \\ 1/R \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\beta (0)} \\ {1/{R_n}} \end{array}} \right]\text{,}$ |
| ${P_0} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{{\dot \theta }_n}}^2}&0&0&0 \\ 0&{\sigma _{\dot R/{R_n}}^2}&0&0 \\ 0&0&{\sigma _\theta ^2}&0 \\ 0&0&0&{\sigma _{1/{R_n}}^2} \end{array}} \right]\text{,}$ |
| ${R_n} = \left[ {\begin{array}{*{20}{c}} {12\;000}&{16\;800}&{23\;500}&{31\;200} \end{array}} \right]\text{,}$ |
| ${\sigma _{{R_n}}} = \left[ {\begin{array}{*{20}{c}} {2\;000/\sqrt {12} }&{2\;800/\sqrt {12} }&\\ {3\;900/\sqrt {12} }&{3\;900/\sqrt {12} } \end{array}} \right]\text{。}$ |
式中:
定义目标运动要素估计误差百分比如式(15)所示,估计误差比例反映了目标运动要素估计值的相对误差水平。
| $ e = \frac{{\left| {{y_{{\text{实际}}}} - {y_{{\text{估计}}}}} \right|}}{{{y_{{\text{实际}}}}}}*100\% \text{。} $ | (15) |
基于前述仿真条件,采用如式(3)所示EKF滤波器状态方程,如式(4)所示测量方程,如式(8)所示滤波方程,如式(9)所示各EKF滤波器权重升级方程,进行数字仿真分析。图2为探测平台与目标相对运动轨迹。图3~图5为目标距离、速度、航向估计误差百分比。
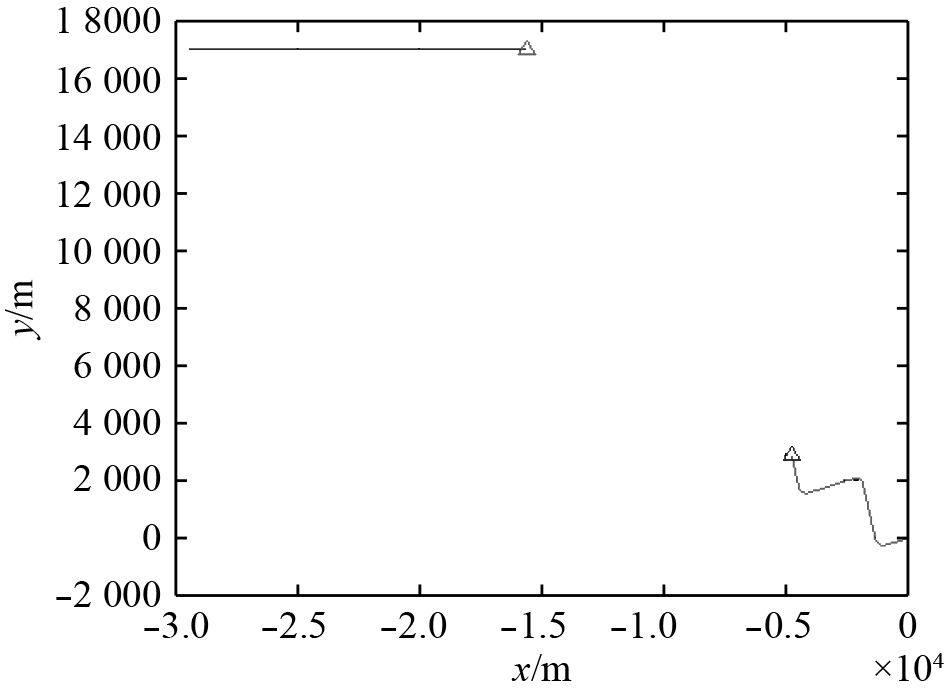
|
图 2 本舰-目标相对运动轨迹 Fig. 2 Trajectory of target and detective platform |
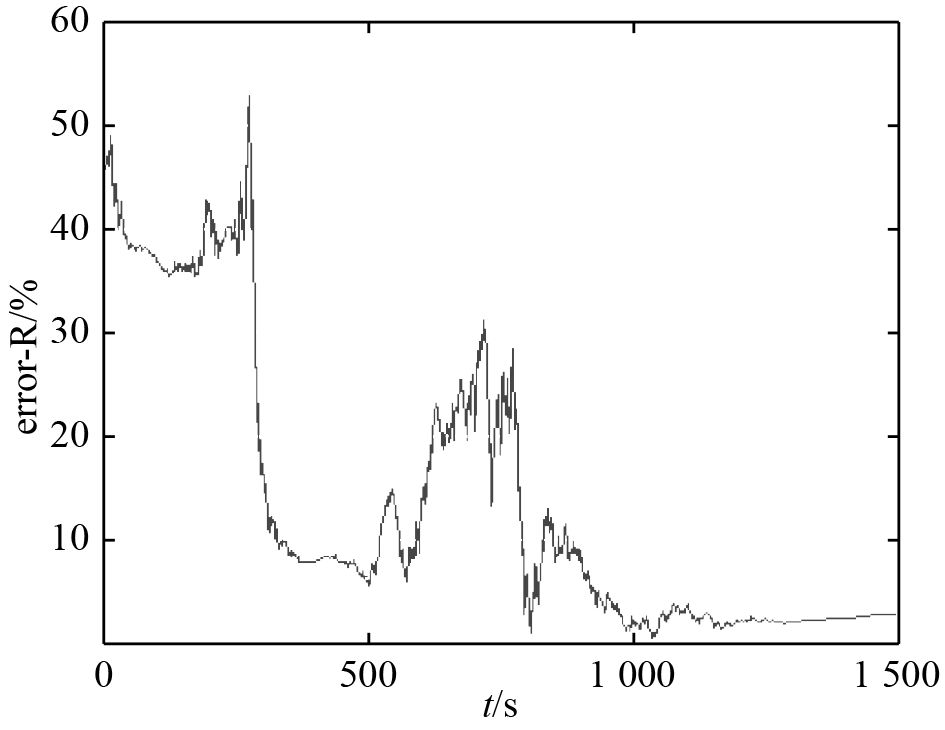
|
图 3 目标距离估计误差百分比 Fig. 3 Evaluated error percentage of target distance |
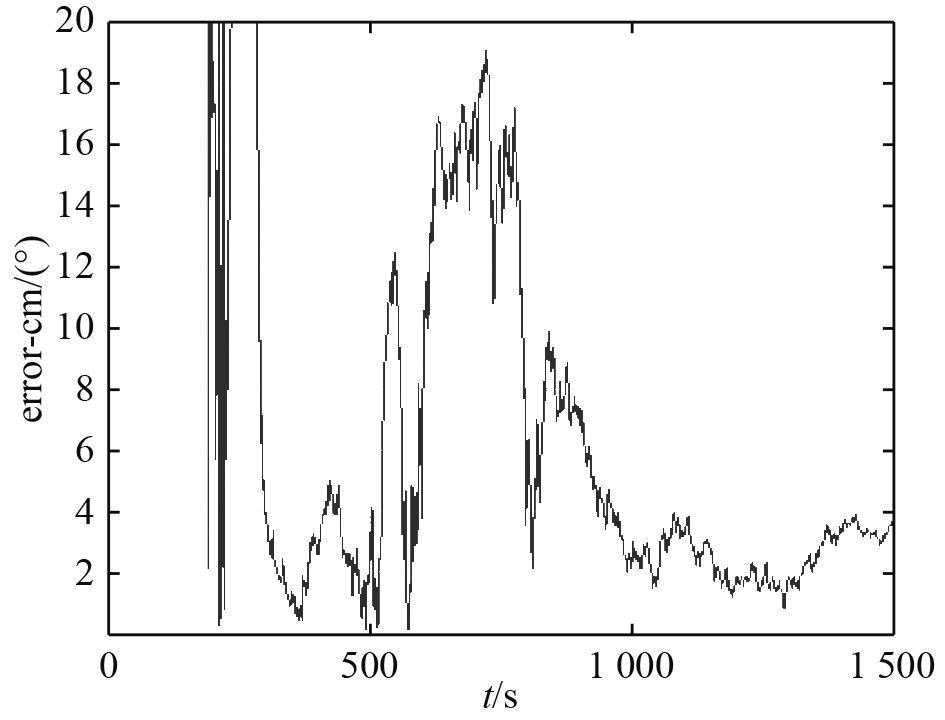
|
图 5 目标航向估计误差百分比 Fig. 5 Evaluated error percentage of target heading angle |
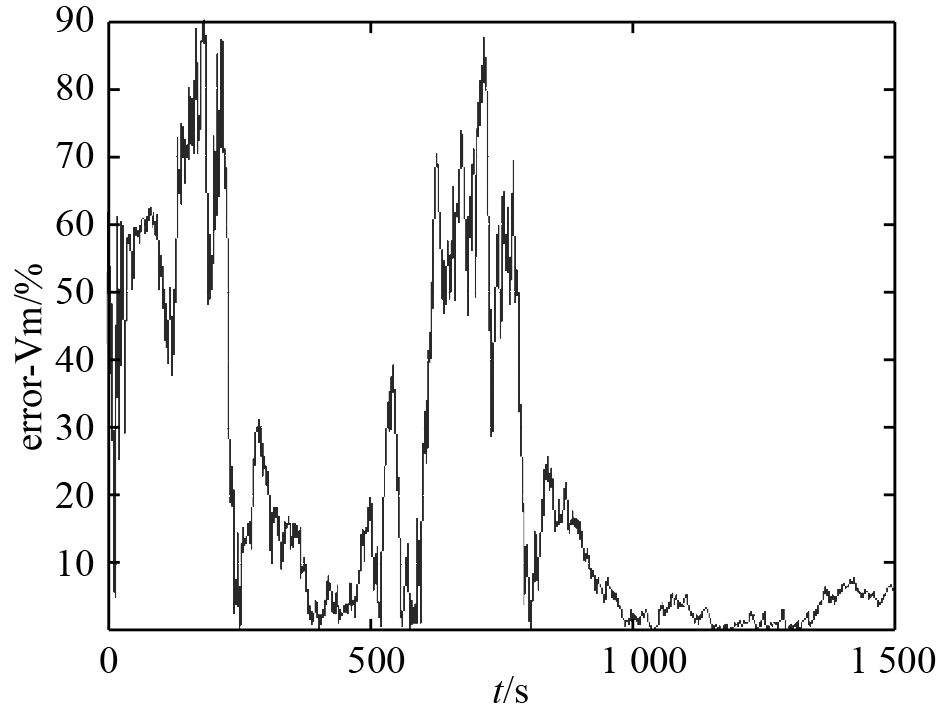
|
图 4 目标速度估计误差百分比 Fig. 4 Evaluated error percentage of target velocity |
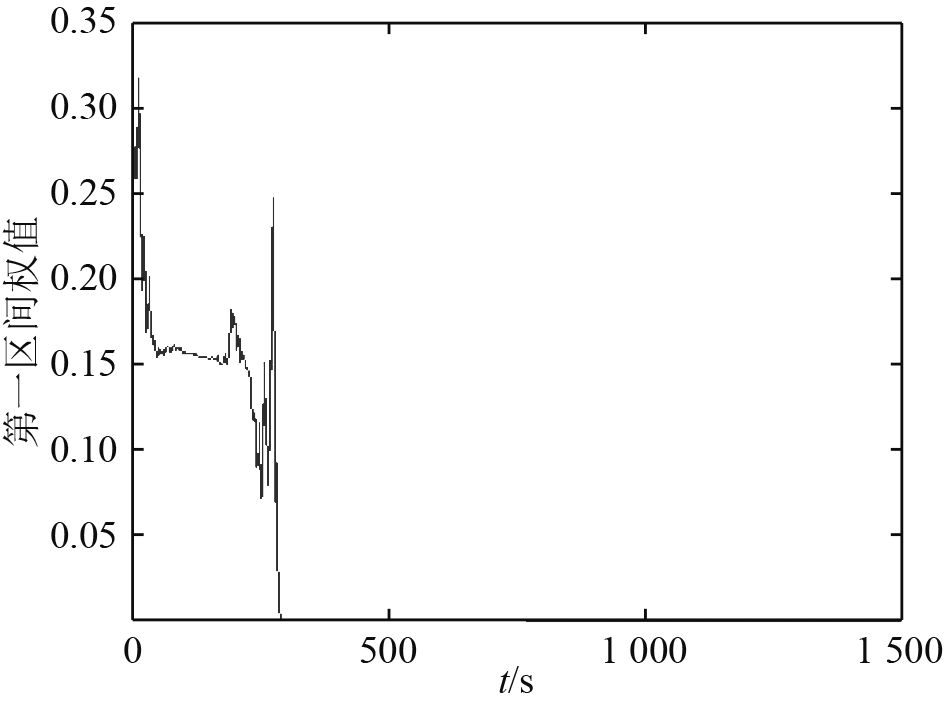
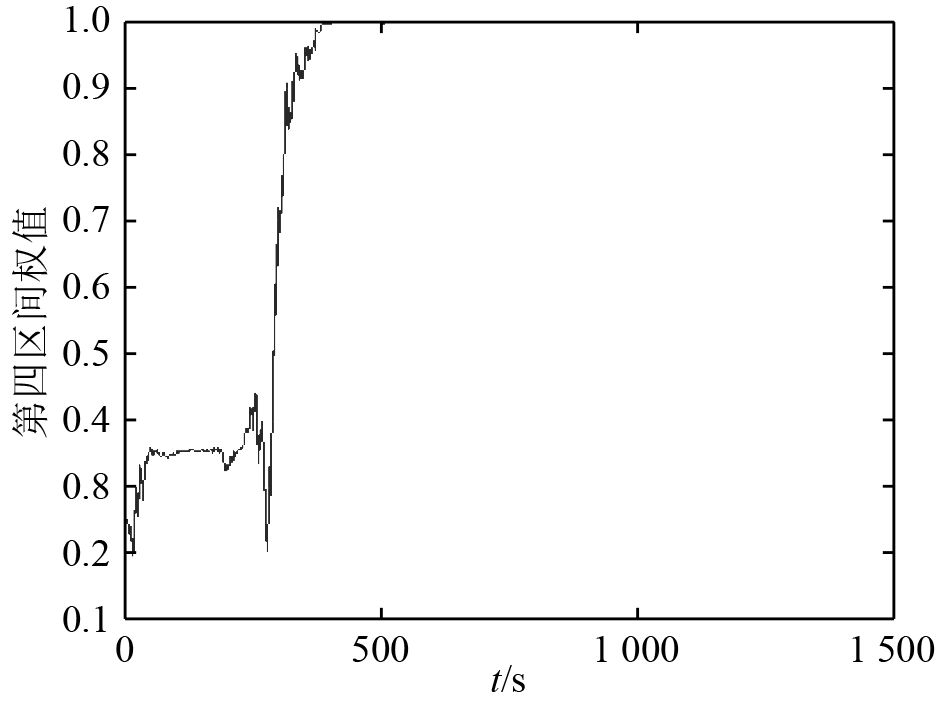
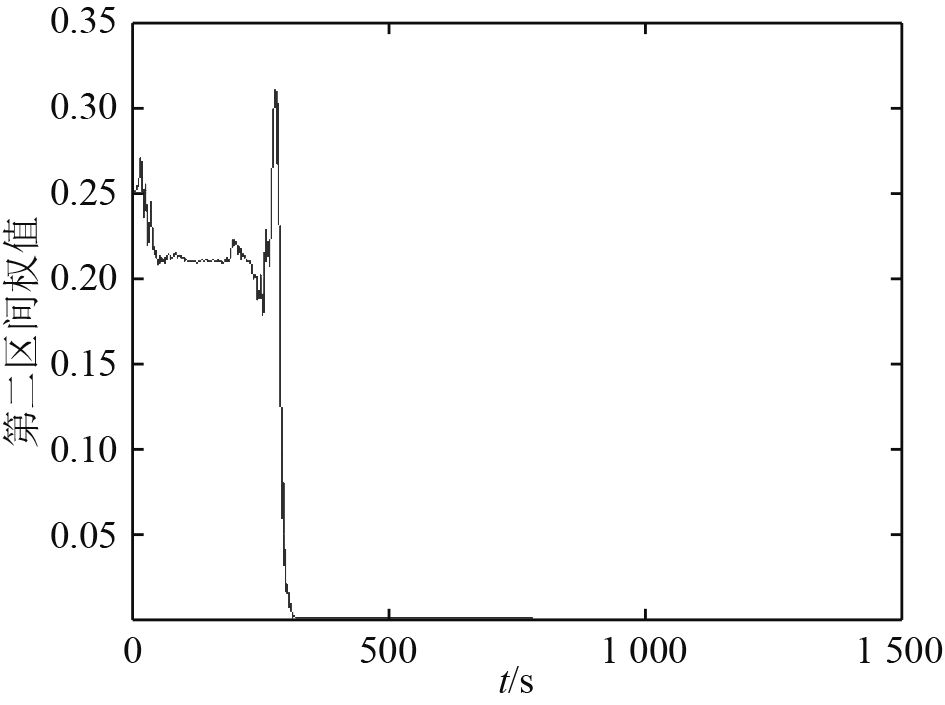
图6~图9为RPEKF滤波器中4组独立的EKF滤波器权值变化曲线。
|
图 6 第1区间权值变化曲线 Fig. 6 Weight coefficient curve of the first section |
|
图 9 第4区间权值变化曲线 Fig. 9 Weight coefficient curve of the fourth section |
|
图 7 第2区间权值变化曲线 Fig. 7 Weight coefficient curve of the second section |
|
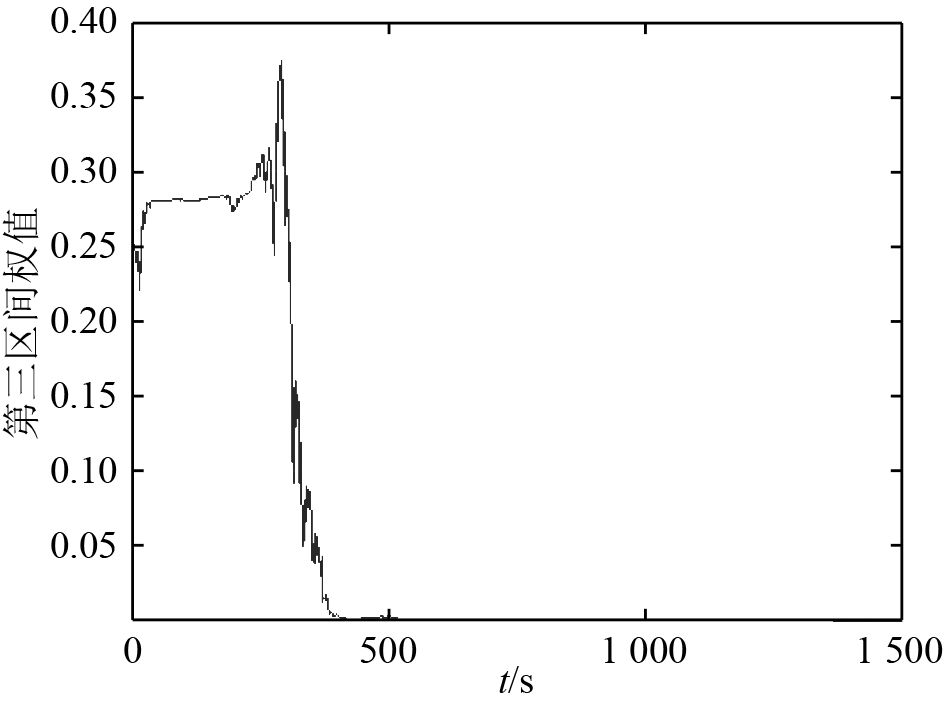
图 8 第3区间权值变化曲线 Fig. 8 Weight coefficient curve of the third section |
由图可知,目标距离,目标速度和目标航向均能收敛于真值。由于初始相对距离为34 000 m在第4区间内,第1、2、3区间权重值变为0,第4区间权重值为1,表明本文中提出的距离参数化方法是有效的。
4.2 机动目标运动要素估计仿真分析 4.2.1 仿真初始条件在实际水上目标机动场景中,最常见的运动形式是分段匀速直线运动,目标机动方式描述如下:
若
若
其中:
检测目标机动后,本舰机动形式如4.1节所述,轨迹参数
其余仿真初始条件同4.1.3节相关参数。
4.2.2 滤波器初始参数当检测到目标机动后,滤波器重置,其初始状态如下:
| ${y_0} = \left[ \begin{array}{l} {\dot \beta } \\ \dot R/R \\ \beta \\ 1/R \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{\beta _{reset}}} \\ {1/{R_{n\_reset}}} \end{array}} \right]\text{,}$ |
| ${P_0} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{{\dot \theta }_{n\_reset}}}^2}&0&0&0 \\ 0&{\sigma _{\dot R/{R_{n\_reset}}}^2}&0&0 \\ 0&0&{\sigma _\theta ^2}&0 \\ 0&0&0&{\sigma _{1/{R_{n\_reset}}}^2} \end{array}} \right]\text{,}$ |
| $\begin{split} \begin{array}{l} {R_{n\_reset}}=\left[\!\! {\begin{array}{*{20}{c}} {{R_{reset}} + 2\;250}\!\!\!&\!\!\!\!{{R_{reset}} + 750}\\ {{R_{reset}} - 750}\!\!\!&\!\!\!{{R_{reset}} - 2\;250} \end{array}} \right],{R_{reset}} < 2\!\times\! 10^4 \text{,}\\ {R_{n\_reset}} =\\ \quad \left[ \!\!\!{\begin{array}{*{20}{c}} {{R_{reset}} + 3\;750}\!\!\!&\!\!\!{{R_{reset}} + 1\;250}\\ {{R_{reset}} - 1\;250}\!\!\!&\!\!\!{{R_{reset}} - 3\;750} \end{array}}\!\!\! \right],2\!\times\! 10^4 \!\leqslant\! {R_{reset}} \!<\! 3\times 10^4 \text{,} \\ {R_{n\_reset}} = \left[ \!\!\!{\begin{array}{*{20}{c}} {{R_{reset}} + 4\;500}\!\!\!&\!\!\!{{R_{reset}} + 1\;500}\\ {{R_{reset}} - 1\;500}\!\!\!&\!\!\!{{R_{reset}} - 4\;500} \end{array}} \!\!\right],{R_{reset}} \geqslant 3\times 10^4 \text{,}\\ \end{array} \end{split}$ |
| $ \begin{array}{l} {\sigma _{{R_{n\_reset}}}} = \left[ {\begin{array}{*{20}{c}} {750/\sqrt {12} }\!\!\!&\!\!\!{750/\sqrt {12} }\\ {750/\sqrt {12} }\!\!\!&\!\!\!{750/\sqrt {12} } \end{array}} \right],{R_{reset}} < 2\times 10^4 \text{,}\\ {\sigma _{{R_{n\_reset}}}} =\\ \quad\left[ {\begin{array}{*{20}{c}} {1\;250/\sqrt {12} }\!\!\!&\!\!\!{1\;250/\sqrt {12} }\\ {1\;250/\sqrt {12} }\!\!\!&\!\!\!{1\;250/\sqrt {12} } \end{array}} \right],2\times 10^4 \leqslant {R_{reset}} < 3\times 10^4 \text{,} \\ {\sigma _{{R_{n\_reset}}}} = \left[ {\begin{array}{*{20}{c}} {1\;500/\sqrt {12} }\!\!\!&\!\!\!{1\;500/\sqrt {12} }\\ {1\;500/\sqrt {12} }\!\!\!&\!\!\!{1\;500/\sqrt {12} } \end{array}} \right],{R_{reset}} \geqslant 3\times 10^4\text{。} \\ \end{array} $ |
式中:
其余滤波器初始参数同4.1.2节相关参数。
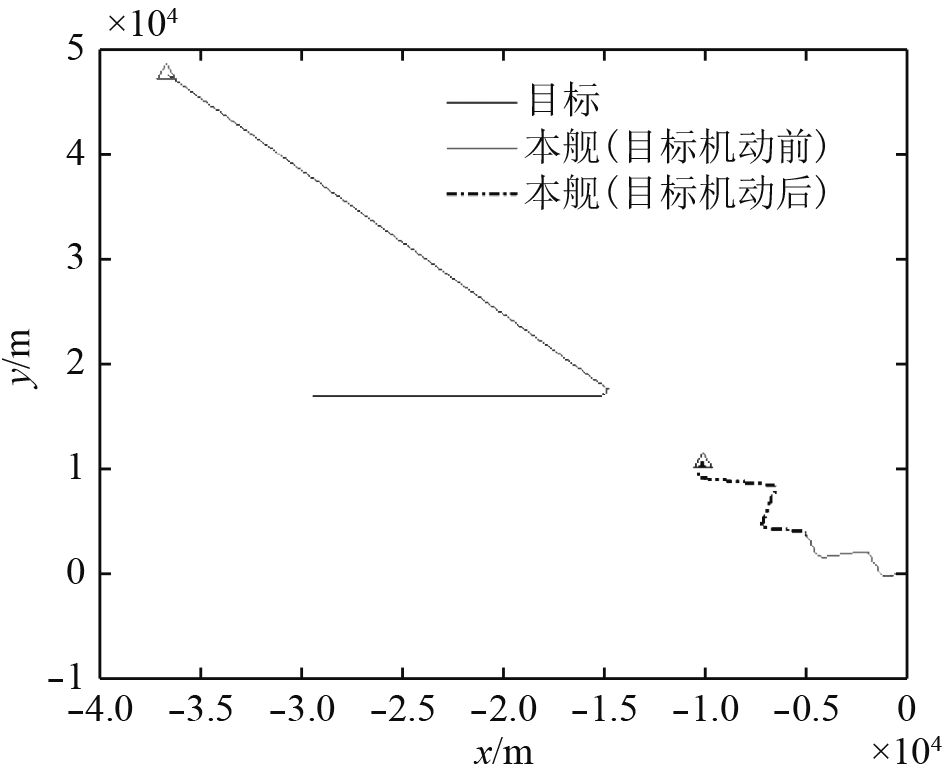
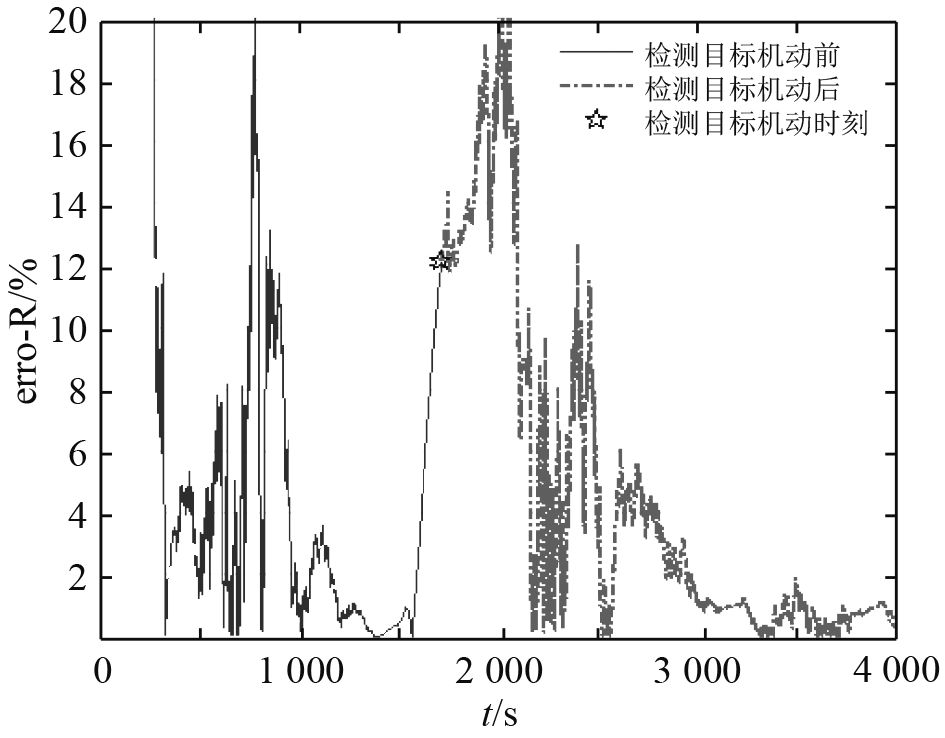
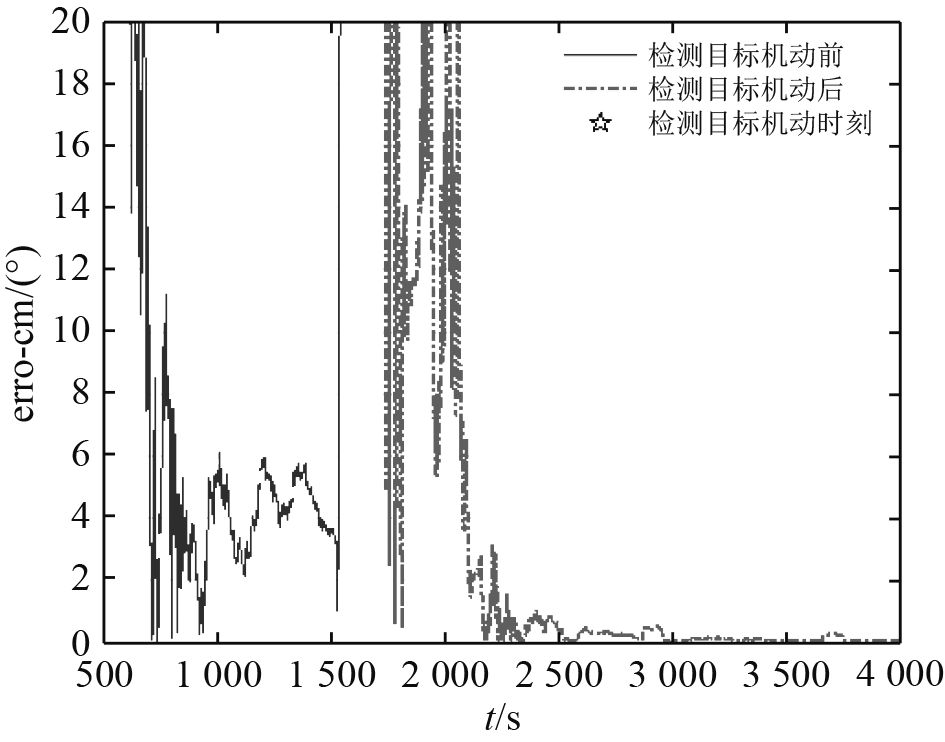
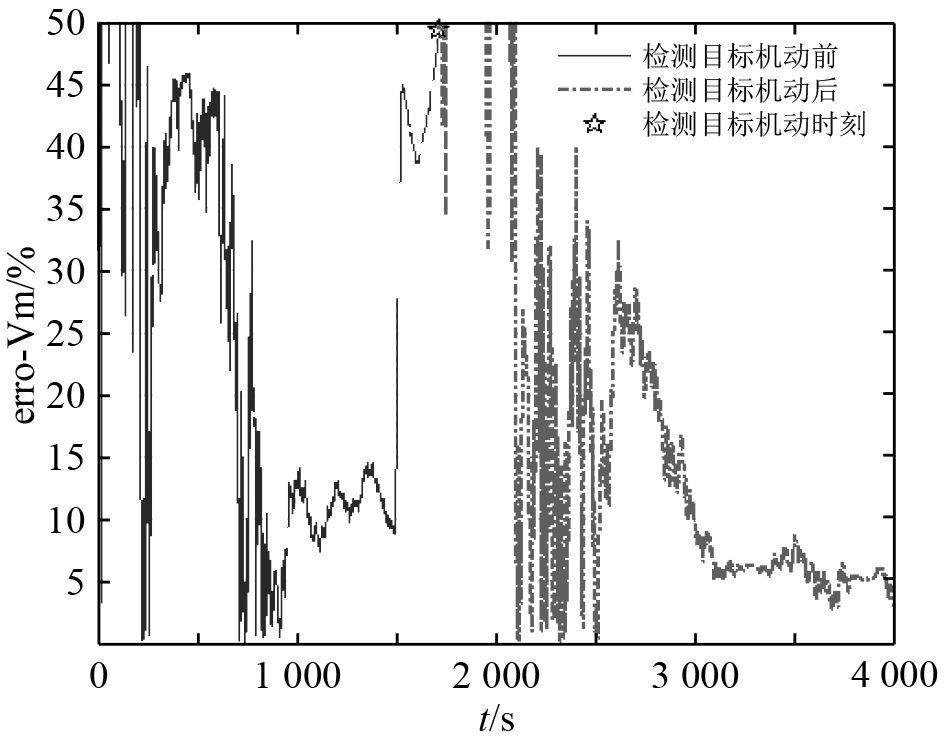
4.2.3 仿真分析基于前述仿真条件,采用如式(3)所示EKF滤波器状态方程,如式(4)所示测量方程,如(8)所示滤波方程,如式(9)所示各EKF滤波器权重升级方程,如式(10)~式(12)所示目标机动检测算法,进行数字仿真分析。图10为探测平台与目标相对运动轨迹,图11~图13为目标距离、速度、航向估计误差百分比。
|
图 10 本舰-目标相对运动轨迹 Fig. 10 Trajectory of target and detective platform |
|
图 11 目标距离估计误差百分比 Fig. 11 Evaluated error percentage of target distance |
|
图 13 目标航向估计误差百分比 Fig. 13 Evaluated error percentage of target heading angle |
|
图 12 目标速度估计误差百分比 Fig. 12 Evaluated error percentage of target velocity |
可知,该条件下检测到目标机动的时刻为1 721 s,目标机动检测算法可行。滤波器重置后,目标距离估计值于2 475 s收敛于10%误差范围内;目标速度估计值于3 004 s收敛于10%误差范围内;目标航向估计值于2 071 s收敛于10°误差范围内。
5 结 语1)针对纯方位TMA问题,本文给出非线性RPEKF滤波方法,通过引入多组EKF滤波器和滤波器权重调节,能够有效降低滤波器性能对于初值偏差的敏感性,改善其目标运动状态量的收敛特性。
2)针对水面目标常用的分段匀速直线机动形式,本文提出的基于RPEKF滤波器的目标机动检测方法能够有效检测目标机动,并通过重置滤波器参数抑制目标运动状态滤波发散。
| [1] |
CHEN Fei, JING Zhong-liang, LI Feng. Analysis and simulation of passive target tacking algorithm under polar coordinates[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation, 2002: 2682-2686.
|
| [2] |
张安民. 纯方位目标运动分析与鱼雷智能导引律研究[D]. 西安: 西北工业大学, 2002.
|
| [3] |
VINCENT J. AIDALA, SHERRY E. HAMMEL. Utilization of aodified polar coordinates for bearings-only tacking[J]. IEEE Transactions on Automatic Control, 1983(3): 283-294. |
| [4] |
杨新刚, 刘以安, 刘静. 水下目标的无源定位和融合技术研究[J]. 弹箭与制导学报, 2007, 27(5): 319-321. DOI:10.3969/j.issn.1673-9728.2007.05.098 |
| [5] |
李强, 李志舜, 穆海燕. 分布式目标方位估计新方法[J]. 弹箭与制导学报, 2005, 25(4): 975-977. DOI:10.3969/j.issn.1673-9728.2005.04.313 |
| [6] |
詹艳梅. 纯方位目标运动分析方法研究[D]. 西安: 西北工业大学, 2001.
|
| [7] |
徐景硕, 秦永元, 彭蓉. 自适应卡尔曼滤波器渐消因子选取方法研究[J]. 系统工程与电子技术, 2004, 26(11): 1552-1554. DOI:10.3321/j.issn:1001-506X.2004.11.006 |
| [8] |
刘忠, 邓聚龙. 多传感器系统纯方位定位与可观测性分析[J]. 火力与指挥控制, 2004, 29(5): 79-83. DOI:10.3969/j.issn.1002-0640.2004.05.024 |
| [9] |
刘健, 刘忠, 玄兆林. 纯方位TMA的变增益扩展卡尔曼滤波算法[J]. 火力与指挥控制, 2004, 32(1): 67-69. |
| [10] |
石章松. 水下纯方位目标跟踪中观测器机动航路对定位精度影响分析[J]. 电光与控制, 2009, 16(6): 5-8. DOI:10.3969/j.issn.1671-637X.2009.06.002 |
| [11] |
詹艳梅, 孙进才, 胡友峰. 纯方位目标运动分析的自适应算法[J]. 西北工业大学学报, 2002, 20(4): 648-650. |
| [12] |
PEACH N. Bearings-only tracking using a set of range-parameterised extended Kalman filters[J]. IEEE Control Theory Application, 1995, 142(1): 73-80. DOI:10.1049/ip-cta:19951614 |
 2019, Vol. 41
2019, Vol. 41
