舰船科学技术  2019, Vol. 41 Issue (9): 125-127, 141   PDF    
引用本文
芈小龙, 向敏. 多惯性导航系统信息融合方法研究. 舰船科学技术, 2019, 41(9): 125-127, 141  
MI Xiao-long, XIANG Min. Research on information fusion method of multi-inertial navigation system. Ship Science and Technology, 2019, 41(9): 125-127, 141  
多惯性导航系统信息融合方法研究
芈小龙, 向敏     
海军装备部，北京 100076
收稿日期: 2019-07-11.
作者简介: 芈小龙(1977 – )，男，工程师，主要从事信息系统研究
摘要: 舰船导航领域通常采用多传感器组合的方式保证导航精度，但对于水下舰船而言，由于其传感器种类少、精度低，导航精度水平有待提升。本文结合舰船配置特点，提出一种多惯性导航系统信息融合方法，通过设计Kalman滤波器实现多套惯导设备的信息融合，模拟仿真实验和半实物仿真试验结果表明，相较于单套惯导系统而言，所提方法可以将定位精度提升30%，为水下舰船的长航时高精度导航提供了保障。
关键词: 惯性导航系统     信息融合     Kalman滤波     半实物仿真    
Research on information fusion method of multi-inertial navigation system
MI Xiao-long, XIANG Min     
Naval Equipment Department, Beijing 100076, China
Abstract: In the field of shipping navigation, multi-sensors combination are usually adopted to ensure the navigation accuracy. But for underwater ships, the navigation accuracy needs to be improved due to its few types of sensors and low accuracy. In this paper, a multiple information fusion method of inertial navigation system is presented combining with the characteristics of ship configuration and the information fusion of multiple inertial navigation devices is realized through a Kalman filter. The simulation experiment and semi-physical simulation test show that the positioning accuracy of the proposed method is 30% higher than the single inertial navigation system, which provides a great guarantee in high precision navigation for underwater ships.
Key words: inertial navigation system     information fusion     kalman filter     semi-physical simulation test    
0 引　言

对于船舶导航领域，多传感器组合导航已成为最主要的导航方法，通过多传感间的信息融合，能够有效利用和处理来自多传感器的数据，克服单一导航模式的不足，达到提高导航精度、增强船舶导航系统自主性和可靠性的目的[1 – 4]。

由于不同船舶配备的导航传感器形式和数量各有不同，形成了不同的导航方案，其中最为常用的是惯性导航系统（Inertial navigation system，INS）和卫星导航系统（Global positioning system，GPS）组合的方案[5 – 6]。任民魁等将提出了基于Rodrigues参数的INS/GPS组合导航鲁棒滤波方法，通过增加抗差因子提高了组合系统的稳定性和可靠性，但算法未经过试验检验，精度有待验证；Qin 通过改善GPS环路，提高了INS/GPS的精度水平，但其对GPS的器件精度要求较高，较难实现应用。另外采用船上计程仪辅助惯性导航系统的方案也广泛应用于水下组合导航系统[7 – 8]，赵俊波等对计程仪/INS组合导航方法进行了总结，Liu等针对计程仪信息有限条件下的组合导航进行研究，提出了一种紧组合导航方法，但该方法计算量较大，难以保证算法的实时性。上述方案中主要以INS作为导航核心，辅以其他设备改善INS长航时下精度发散的问题，实现较高精度的导航。而对于水下导航来说，由于计程仪的精度水平有待提高，造成了长周期条件下导航精度无法满足使用要求的问题，所以如何结合船上现有装备实现长周期条件下的高精度导航是目前船舶导航领域面临的一个巨大问题[9 – 12]。通常来说，为保证船舶导航系统的可靠性，船上一般会配备2套惯导系统，所以开展多惯导系统信息融合研究是实现水下船舶导航的一种新思路，对提高长航时下的导航精度水平有重要意义。

1 多惯性导航系统融合方法 1.1 多惯性导航系统融合方案

对于静电惯导系统、激光惯导系统等高精度惯导系统而言，为提高其导航精度，一般会将惯性器件误差进行估计和补偿，以消减误差发散趋势，但惯导固有的随时间发散的特性仍然存在，使得惯导系统的振荡误差逐渐凸显出来[13 – 14]，因此，对于本方案来说，重点在于消除地球振荡误差，从而提升船舶导航系统长航时下的导航定位精度。

通过对长航时惯导误差模型进行分析，经度、纬度、航向的地球振荡误差幅值主要受航向初始角误差和陀螺漂移影响，起始振荡方向受航向初始角方向、北向和天向陀螺漂移的正负影响。基于此，设计多惯性导航系统融合方案如图1所示。结合惯导系统基本原理，2套惯导系统（以下简称惯导1、惯导2）相隔0.25个地球周期（即6 h）分别启动，并以惯导系统位置、速度、姿态和陀螺加表误差作为观测量，以两惯导系统互为导航基准，利用对方输出的经纬度信息作为量测信息进行卡尔曼滤波，在估出陀螺加表误差后对两惯导系统进行补偿，之后输出组合导航下的导航信息。

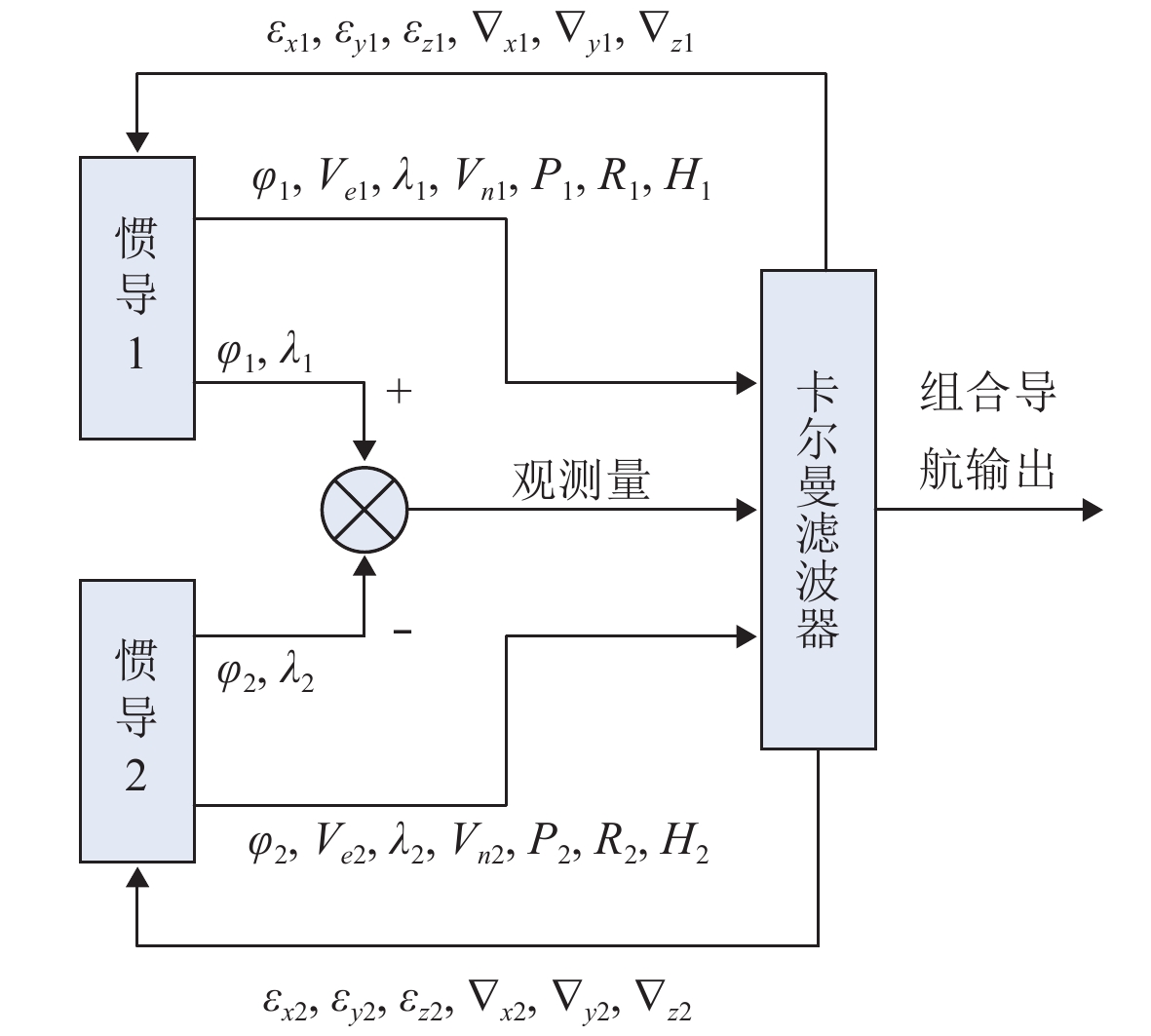
图 1 多惯性导航系统融合方案 Fig. 1 Multi-inertial navigation system integration scheme
1.2 多惯性导航系统融合模型

根据系统方案，建立多惯性导航系统（分别以下标1，2表示）量测方程，如下式：

$ \dot X = FX + GW{\text{。}} $ (1)

其中：

$ \begin{array}{l} X = \left[ {\delta {v_{e1}},\delta {v_{n1}},\delta {\lambda _1},\delta {\varphi _1},} \right.\\ \;\;\;\;\;\;\;\;\delta {R_1},\delta {P_1},\delta {H_1},{\varepsilon _{x1}},\\ \;\;\;\;\;\;\;{\varepsilon _{y1}},{\varepsilon _{z1}},{\nabla _{x1}},{\nabla _{y1}},{\nabla _{z1}},\\ \;\;\;\;\;\;\;\delta {v_{e2}},\delta {v_{n2}},\delta {\lambda _2},\delta {\varphi _2},\\ \;\;\;\;\;\;\;\delta {R_2},\delta {P_2},\delta {H_2},{\varepsilon _{x2}},\\ \;\;\;\;\;\;\;\left. {{\varepsilon _{y2}},{\varepsilon _{z2}},{\nabla _{x2}},{\nabla _{y2}},{\nabla _{z2}}} \right], \end{array} $
$ W = \left[ {{\varepsilon _{x1}},{\varepsilon _{y1}},{\varepsilon _{z1}},{\nabla _{x1}},{\nabla _{y1}},{\nabla _{z1}}} \right], $
$ F = \left[ {\begin{array}{*{20}{c}} {{{\left( {{F_1}} \right)}_{10 \times 10}},{{\left( 0 \right)}_{10 \times 10}}}\\ {{{\left( 0 \right)}_{10 \times 10}},{{\left( {{F_2}} \right)}_{10 \times 10}}} \end{array}} \right], $
$\scriptsize {\begin{array}{*{20}{c}} {{ F}_1} = [ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 2\varOmega \sin {\varphi _1}, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! - g, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0 \\ \!\!\!\!&\!\!\!\! - 2\varOmega \sin {\varphi _1}, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! {\rm{sec}}{\varphi _1}/R, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 1/R, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! - 1/R, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 1, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! {\rm{1/}}R, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! {\rm{ - }}\varOmega \sin {\varphi _1}, \!\!\!\!&\!\!\!\! {\rm{ - }}\varOmega \sin {\varphi _1}, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 1, \!\!\!\!&\!\!\!\! 0,\\ \!\!\!\!&\!\!\!\! {\rm{tan}}{\varphi _1}{{/R,}} \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! \varOmega \cos {\varphi _1}, \!\!\!\!&\!\!\!\! \varOmega \cos {\varphi _1}, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 1\\ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0\\ \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0, \!\!\!\!&\!\!\!\! 0] \end{array}} $
$\scriptsize{ \begin{array}{*{20}{c}} {{ F}_2} =\!\!\!&\!\!\![ 0, \!\!\!&\!\!\! 2\varOmega \sin {\varphi _2}, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! - g, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0 \\ \!\!\!&\!\!\!-2\varOmega \sin {\varphi _2}, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\!{\rm{sec}}{\varphi _2}/R, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\!0, \!\!\!&\!\!\! 1/R,\!\!\!&\!\!\!0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\!0, \!\!\!&\!\!\! - 1/R,\!\!\!&\!\!\!0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 1, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\!1/R, \!\!\!&\!\!\! 0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!{\rm{ - }}\varOmega \sin {\varphi _2},\!\!\!&\!\!\!{\rm{ - }}\varOmega \sin {\varphi _2}, \!\!\!&\!\!\! 0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!1,\!\!\!&\!\!\!0\\ \!\!\!&\!\!\! \tan{\varphi _2}{{/R,}} \!\!\!&\!\!\! 0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!\varOmega \cos {\varphi _2},\!\!\!&\!\!\!\varOmega \cos {\varphi _2}, \!\!\!&\!\!\! 0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!0,\!\!\!&\!\!\!0, \!\!\!&\!\!\! 1\\ \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0\\ \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0, \!\!\!&\!\!\! 0 ], \end{array}} $
$ \begin{align} G =& \left[ {{\rm{ }}1,{\rm{ }}0,{\rm{ }}0,0} \right.\\ & \ 0, 1, 0,0\\ &{\rm{ }}{\left( {\rm{0}} \right)_{4 \times 8}}\\ &{\rm{ cos}}\theta {\rm{, - sin}}\theta {\rm{,\qquad 0,0}}\\ &{\rm{ sin}}\theta ,\cos \theta ,\qquad\ \ 0,0\\ &{\rm{ }}\left. {{{\left( {\rm{0}} \right)}_{4 \times 8}}} \right]{\text{。}} \end{align} $

以两惯导的经纬度误差作为观测量得到观测方程如下式：

$\begin{gathered} Z = \left[ {\begin{array}{*{20}{c}} {{\lambda _1} - {\lambda _2}} \\ {{\varphi _1} - {\varphi _2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\delta {\lambda _1} - \delta {\lambda _2}} \\ {\delta {\varphi _1} - \delta {\varphi _2}} \end{array}} \right]= \\ {\rm{ }}\left[ {\begin{array}{*{20}{c}} {{0_{1 \times 2}}}&1&{{0_{1 \times 9}}}&{ - 1}&{{0_{1 \times 7}}} \\ {{0_{1 \times 3}}}&1&{{0_{1 \times 9}}}&{ - 1}&{{0_{1 \times 6}}} \end{array}} \right]X {\text{。}} \end{gathered} $ (2)

通过式（1）和式（2）构建多惯性导航系统融合Kalman滤波方程，实现多惯性导航系统的信息融合。

2 试验验证

为验证所提融合方法的有效性，分别采用仿真试验和半实物仿真试验进行验证。

2.1 模拟仿真试验

仿真条件及参数设置为：惯导1、惯导2加表零位 $5 \times {10^{ - 5}}\;{\rm{g}}$ ，陀螺漂移 $0.02^\circ /{\rm{h}}$ ，采样频率10 Hz，仿真时间24 h。单惯导仿真误差曲线如图2所示，基于融合算法的仿真结果如图3所示。

图 2 单惯导仿真误差曲线 Fig. 2 Simulation error curve of single inertial navigation

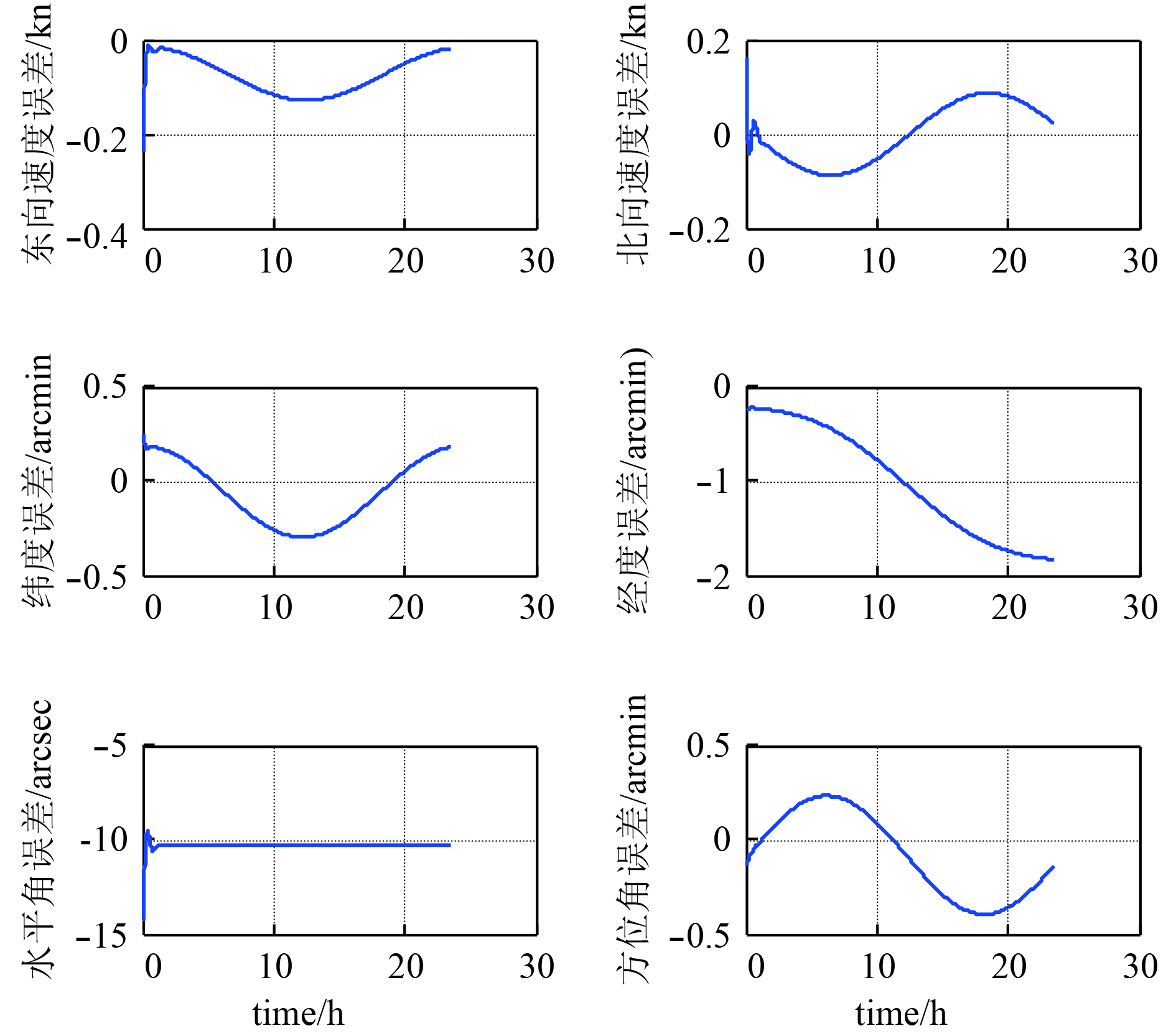
图 3 两套惯导融合后误差曲线 Fig. 3 Simulation error curves after inertial navigation fusion

为便于比较，统计了惯导1、惯导2在24 h的定位精度为1.7 n mail，速度误差波动小于0.2 kn，从图2可知，当采用多惯导系统信息融合方案时，24 h定位精度为1.5 n mail，速度误差波动小于0.15 kn，可以从理论上验证所提方法的有效性。

2.2 半实物仿真试验

以2套某型激光惯导系统静基座条件下工作5 d的试验数据进行分析，2台惯导系统和采用本文所提方案对两惯导系统信息进行融合的经度、纬度及位置误差曲线如图4所示。

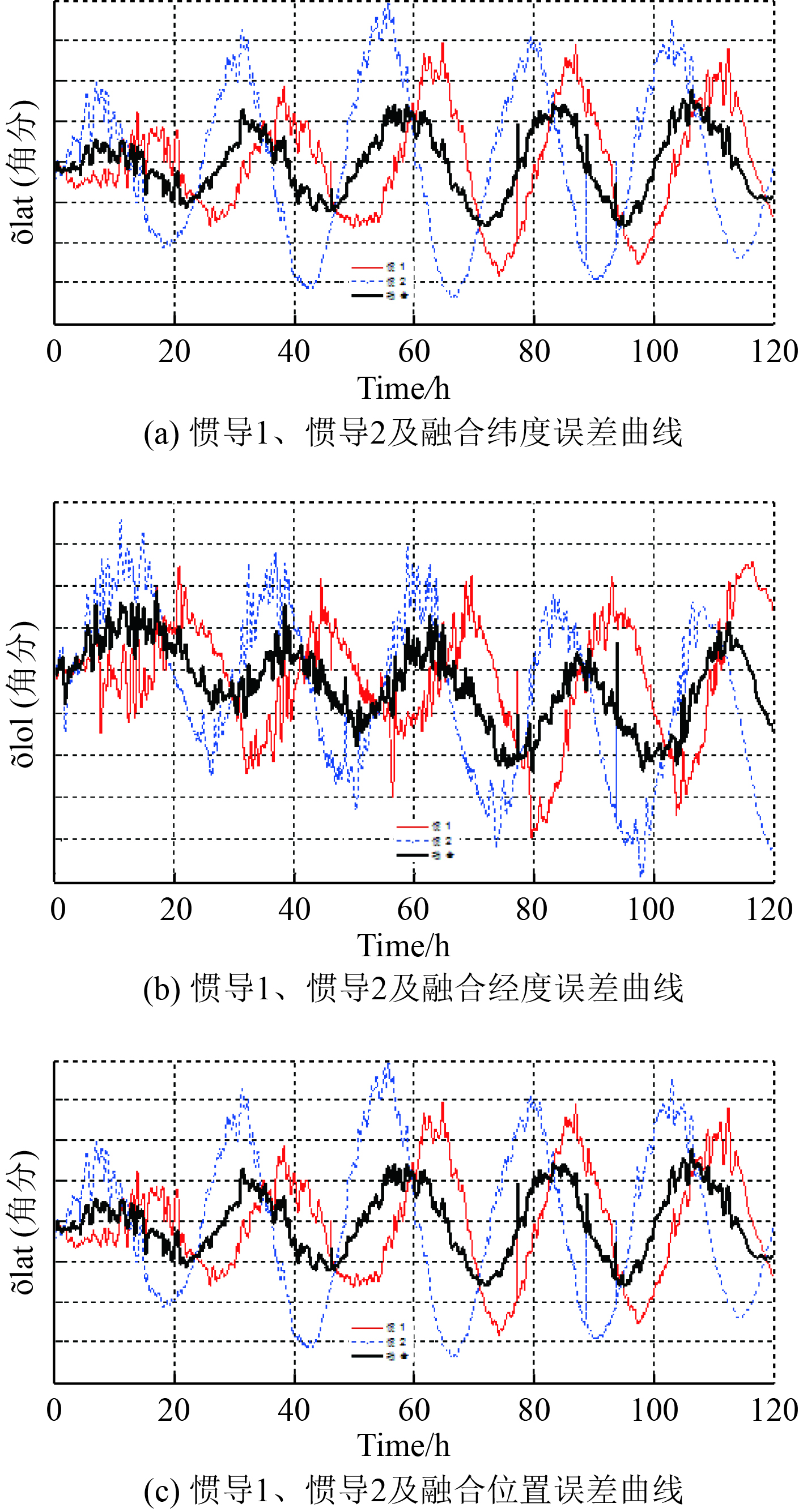
图 4 误差曲线 Fig. 4 Simulation error curves

由于2套惯导系统精度相当，启动时间相差了6 h，导致地球振荡曲线相位相差1/4，在进行融合后，精度水平得以提升。可以看出，采用所提方法，导航系统定位精度可提升30%，可以很好解决导航系统定位精度低的问题。

3 结　语

为解决水下舰船导航信息来源少、精度低的问题，本文结合惯导系统自身原理，提出一种多惯性导航系统信息融合方法，模拟仿真结果和半实物仿真试验表明相较于传统的单惯导导航条件，所提方法可以使导航精度提升30%，提高了水下舰船综合导航能力，保障了其长航时条件下的导航精度水平。

参考文献
[1]
张闯, 郭晨, 张大恒. 船舶组合导航自适应迭代粒子滤波方法及应用[J]. 系统工程与电子技术, 2019, 41(4): 884-889.
[2]
梅玲玉, 马磊, 张涛. 基于INS/GPS/磁力计的全组合导航[J]. 传感器与微系统, 2019, 38(3): 39-41.
[3]
XIONG Y, ZHANG Y, GUO X, et al. Seamless global positioning system/inertial navigation system navigation method based on square-root cubature Kalman filter and random forest regression[J]. Review of Scientific Instruments, 2019, 90(1): 015101. DOI:10.1063/1.5079889
[4]
ZHANG C, CHEN G, ZHANG D. Ship navigation via GPS/IMU/LOG integration using adaptive fission particle filter[J]. Ocean Engineering, 2018, 156: 435-445. DOI:10.1016/j.oceaneng.2018.03.012
[5]
任民魁, 蒋国萍, 姜宇琛. 基于修正Rodrigues参数的鲁棒滤波算法在组合导航中的应用[J]. 电光与控制, 2019, 26(03): 43-47.
[6]
QIN H, YUE S, CONG L, et al. A state-constrained tracking approach for Kalman filter-based ultra-tightly coupled GPS/INS integration[J]. GPS Solutions, 2019, 23(2).
[7]
赵俊波, 葛锡云, 冯雪磊, 等. 水下SINS/DVL组合导航技术综述[J]. 水下无人系统学报, 2018, 26(1). DOI:10.11993/j.issn.2096-3920.2018.01.001
[8]
LIU P, BO W, DENG Z, et al. INS/DVL/PS tightly coupled underwater navigation method with limited DVL measurements[J]. IEEE Sensors Journal, 2018, 18(7): 2994-3002. DOI:10.1109/JSEN.2018.2800165
[9]
EMAMI M, TABAN M R. A novel intelligent adaptive Kalman filter for estimating the submarine's velocity: With experimental evaluation[J]. Ocean Engineering, 2018, S0029801818304530.
[10]
GROVES P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[J]. Industrial Robot, 2013, 67(3): 191-192.
[11]
GROVES P D. Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd edition [Book review][J]. IEEE Aerospace & Electronic Systems Magazine, 2015, 30(2): 26-27.
[12]
NGUYEN T, MANN G K I, VARDY A, et al. Developing a cubature multi-state constraint kalman filter for visual-inertial navigation system[C]// Canadian Conference on Computer and Robot Vision. 2017.
[13]
冷传营, 刘锡敬. 自适应算法在单轴激光惯导初始对准中的应用[J]. 舰船电子工程, 2012, 32(10): 44-46. DOI:10.3969/j.issn.1627-9730.2012.10.017
[14]
查月. 舰艇惯性导航技术应用与展望[J]. 现代导航, 2017, 8(2): 147-151.