2. 哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
随着海洋资源开发的加剧和环境的复杂化,舰船被动声呐目标识别技术更显得重要。而从舰船辐射噪声信号中对目标进行识别的关键一步就是找到目标的特征。为对水面和水下目标进行分类,这需要从水声物理层面分析水面和水下目标的差异性,并应用信号处理的方法提取出辐射噪声的特征,进而解决对水面和水下目标分类的难题。然而,舰船辐射噪声非常复杂,它不仅随着海洋环境的变化而更加复杂,而且随着舰船本身运动状态的改变而多样化,仅仅依靠单一的特征来识别目标还远远不能满足实际的需求,因此研究反映目标特性的新特征仍然是一项迫切的工作。
近年来,对被动声呐目标特征提取的研究已成为一个热点,文献[1]通过分析浅海波导声源传播中声场幅度和相位起伏与海面波动的关系,探究相同海面波动不同海洋深度声场起伏的差异性。文献[2]分析了舰船辐射噪声的起伏特性,提出一种利用线谱幅度、相位随时间的低起伏性进行线谱提取的新方法。文献[3]通过分析浅海波导声源传播中声场幅度和相位起伏对海面的依赖关系,探究相同海面波动不同海洋深度声场起伏的差异性。文献[4]对海洋环境噪声的时间平稳与起伏特性进行研究,揭示了海洋环境噪声在时间维度上的特性,为后续信号处理提供平稳性处理依据。本文从水声物理层面上模拟海面情况进行特征提取,文献[5]为了研究随机起伏海面的散射对水声信道特性的影响,利用Monte Carlo方法模拟基于PM海浪谱的二维随机起伏海面,提取了与风向不同夹角的一维随机起伏海面。文献[6]在文献[5]的基础上采用积分方程方法对随机起伏界面的散射强度进行计算,得到不同风向、不同海面风速、不同频率时的前向和反向声散射特性。
现实中,舰船航行受到风浪等海况的影响会出现不同情况的起伏。为了避免舰船起伏对接收信号特征提取的影响,在信号处理时都会考虑到舰船起伏的因素并对其进行抑制,但舰船的起伏也可以是水面和水下目标分类的一个特征,因此本文从舰船起伏特性的角度出发对目标进行特征提取。用PM海浪谱对随机起伏界面进行建模,近似模拟海面的波动,并用积分方程方法对随机起伏界面的散射强度进行计算,得到声信号不同入射角进行散射的散射强度,进而模拟实际海面的起伏情况。然后提取信号幅度包络的特征,并基于信号的物理特征和幅度包络特征设计相关器,根据对相关系数的判断实现对水面和水下目标的分类。最后通过对不同深度的信号进行仿真,验证该算法的有效性。用海上实测数据验证该方法的实用性,结果表明,该方法对水面和水下目标的分类有良好的效果。
1 海面声起伏的特性建模 1.1 海面随机起伏的建模20世纪50年代以来,科学家们对真实海浪的波动进行了精细的统计,结果表明,海面波浪是由若干个独立高斯随机变量的谐波叠加而成的,同时海面横纵波动主要是受风速的影响,并且根据风向夹角的不同,海面的起伏也呈现差异性。在1964年,Pierson和Moscowitz对北大西洋海浪统计数据进行理论推导,得到了PM海浪谱,其适用的风速为1~20 m/s,其表达式为:
| $ S\left( {{k_n}} \right) = \frac{\alpha }{{4\left| {{{\left. {{k_n}} \right|}^3}} \right.}}{\rm {exp}}\left( { - \frac{{\beta {g_c}^2}}{{{k^2}{U_{19.5}}^4}}} \right)\text{。} $ | (1) |
其中:α和β为无纲经验系数,α=8.10×10-3;β=0.74;U19.5为海面19.5 m标准高度上的风速;gc为重力加速度,gc=9.8 m/s;kn为离散波束,kn=2πn/L,L为海面长度。
海面高度分布函数为:
| $ f\left( {{x}_{m}},t \right)\!=\!\frac{1}{L}\!\sum\nolimits_{n=-{}^{N}\!\!\diagup\!\!{}_{2}\;\ \!+\!1}^{{}^{N}\!\!\diagup\!\!{}_{2}\;}{F\left( {{k}_{n}} \right)}{\rm {exp}}\left( i{{k}_{n}}{{x}_{m}} \right){\rm {exp}}\left( i{{\omega }_{{{k}_{n}}}}t \right)\text{。}\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (2) |
其中:
| $ {{\omega }_{{{k}_{n}}}}={{\left\{ {{g}_{c}}\left| {{k}_{n}} \right|\left[ 1+{{\left( \frac{{{k}_{n}}}{363.2} \right)}^{2}} \right] \right\}}^{{}^{1}\!\!\diagup\!\!{}_{2}\;}}\text{,} $ | (3) |
| $ F\left( {{k}_{n}} \right)\!\!=\!\!\frac{2{\text{π}} }{\sqrt{2\Delta k}}\!\sqrt{S\left( {{k}_{n}} \right)}\!\times \!\left\{ \begin{matrix} N\left( 0,1 \right)+iN\left( 0,1 \right),\;\;n\ne 0,N/2 \text{;} \\ ~N\left( 0,1 \right),\qquad\qquad n= 0,N/2 \text{。} \\ \end{matrix} \right.\!\!\!\!\!\!\! $ | (4) |
其中:∆k为相邻谐波的波束差;
模拟一维随机起伏表面的几何模型,如图1所示。其中θin为入射角,θs为散射角,

|
图 1 随机起伏表面的几何模型 Fig. 1 Geometric Model of Random Fluctuating Surface |
对于一维随机起伏表面的声散射问题,可以利用Helmholtz积分表达式来求解散射声场,得到总散射声场
| $ {P_s}\left( r \right) = - {\left( {\frac{2}{{{\text{π}} k}}} \right)^{0.5}}{e^{ - i{\text{π}} /4}}\frac{{{e^{ikr}}}}{{\sqrt r }}\mathop \sum \nolimits_{n = 1}^N {e^{ - i{k_s}r}}{b_n}\text{。} $ | (5) |
对于表面长度为L的一维随机起伏界面,利用Thorsos在文献[8]中的推导可以得到一维随机起伏界面的散射截面表达式为:
| $ \sigma \left( {{\theta }_{in}},{{\theta }_{s}} \right)=\frac{\left\langle {{P}_{s}}{{\left( r \right)}^{2}} \right\rangle }{\sqrt{\displaystyle\frac{{\text{π}} }{2}}g\left[ 1-\displaystyle\frac{0.5\times \left( 1+2ta{{n}^{2}}{{\theta }_{in}} \right)}{2\times {{\left( kg cos {{\theta }_{in}} \right)}^{2}}} \right]}\text{,} $ | (6) |
其中g=L/4。
由此可以得到散射强度的散射强度:
| $ {S_b} = 10 \times lg\sigma \left( {{\theta _{in}},{\theta _s}} \right)\text{。} $ | (7) |
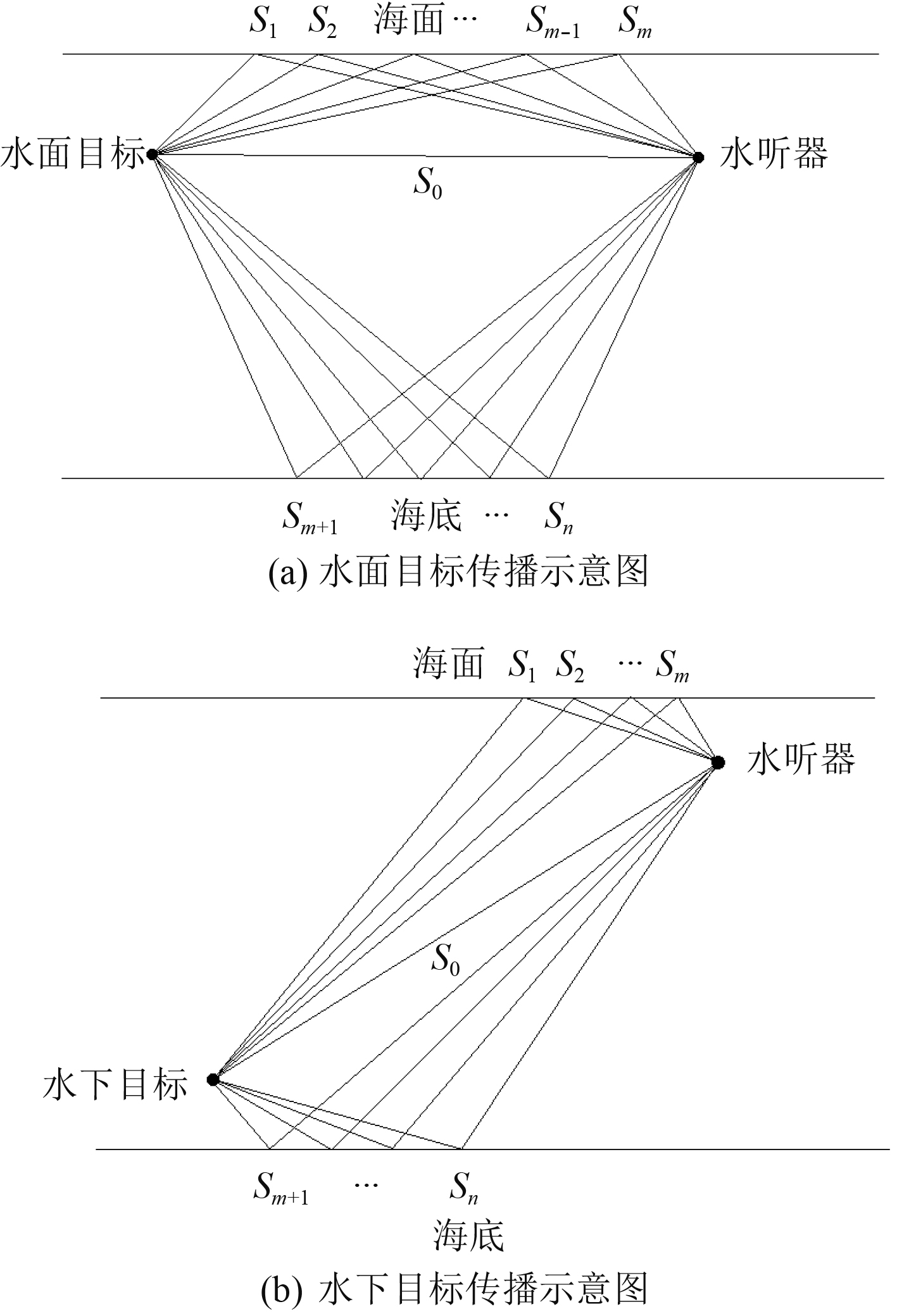
相关调查研究表明,声音在海水中传播时会遵循折射定律,总是朝着声速极小值的位置弯曲。因此舰船辐射噪声信号会通过不同的传播路径到达水声器,其中有直达信号也有海面和海底散射信号等[9],模拟声信号传播如图2所示。
|
图 2 水面目标传播示意图 Fig. 2 Schema of surface target propagation |
则水面目标信号经过多途到达水听器接收到的信号为:
| $ {{\rm{S}}_t}\left( t \right) = {A_1}{x_1}\left( t \right) + {A_2}{x_2}\left( t \right) + \cdots + {A_n}{x_n}\left( t \right),\;\;n = 1,2, \cdots ,n\text{。} $ | (8) |
水下目标信号经过多途到达水听器接收到的信号为:
| $ {{\rm{S}}_d}\left( t \right) = {A_1}{x_1}\left( t \right) + {A_2}{x_2}\left( t \right) + \cdots + {A_m}{x_m}\left( t \right),\;\;m = 1,2, \cdots ,m\text{。} $ | (9) |
被动声呐方程为:
| $ {{SL}} - {{TL}} - \left( {{{NL}} - {{D{ I}}}} \right) = D{\rm T}\text{。} $ | (10) |
其中:SL为辐射声源级,DI为接收阵的接收指向性指数,DT为时空处理器的检测阀,NL为背景噪声在设备工作带宽内的声级,TL为由声源到目标的传播损失,其公式为:
| $ {{TL}} = 20{\rm{lg}}{\log _{10}}r\text{。} $ | (11) |
相比于水下目标,水面目标经过海面起伏界面后到达水听器的距离比较近,传播损失较少。水下目标经过海面起伏界面后到达水听器的距离比较远,传播损失较大。因此,在接收到的信号中,水面目标经过海面反射传播到水听器的信号所占比例较多,水下目标经过海面反射传播到水听器的信号所占比例较少。
2.2 幅度包络的特征提取研究为了实现对水面水下目标的分类,从海面的物理特性出发,根据上述所求到的海面散射强度公式得到散射强度差异性的主要影响因素就是信号深度的不同,文本用微元法将模拟海面分成N个区间,根据各个区间的入射角计算散射强度,进而得到不同深度信号传播的总散射强度。
| $ SS\left( t \right) =\mathop \int \nolimits^N_{0} {S_b}\left( t \right){\rm d}l\text{,} $ | (12) |
由此可以提取出信号的幅度包络:
| $ X\left( t \right) = SS\left( t \right)x\left( t \right)\text{,} $ | (13) |
为了验证该算法的有效性,首先需要解析出声信号的包络曲线,然后通过相关器提取相关系数作为特征进行水面水下目标分类。目前,关于包络检测的方法主要有相关函数法、高斯-牛顿算法、多阶包络曲线拟合和小波变换分析算法等。本文采用相关函数法对包络进行检测,相关函数法要求先构造一个与信号相似的函数,对于不同的测量目标就会有不同的函数,然后用相关函数解析出稳定的包络曲线,得到相关系数。
将生成的信号
| $\begin{split} {S_1}\left( t \right) \!=\!& X\left( t \right){\rm {cos}} \omega t \!=\! SS\!\left( t \right)x\left( t \right){\rm {cos}} \omega t\! = \\ &SS\!\left( t \right)\left( {\left( {{\rm {cos}} 2\omega t \!+\! 1} \right)/2} \right) \!=\! SS\left( t \right)\left( {{\rm {cos}} 2\omega t + } 1 \right) + SS\left( t \right)\text{。} \end{split}$ | (14) |
本文在仿真实验中已知声信号为单频信号,因此可以直接对仿真信号进行调制解调。而在对海试数据处理中,由于舰船辐射噪声的未知性,且海试数据为宽带信号,本文对选取能量最强处线谱所对应的时域幅度包络进行调制解调处理。
根据《水声学》可知,在不同风速下的最大频率不同,但最大频率主要集中在0.1 Hz左右,由此可见,提取出包络的频率很低。而目标信号的频率一般远大于0.1 Hz,因此式(4)中第1项
经过上述分析,由于水面水下目标信号经过海面反射到达水听器所占比例的差异,本文对信号解调出的幅度包络进行相关处理。
水面水下目标相关系数为:
| $ {R_s}\left\langle {SS\left( t \right),{S_b}\left( t \right)} \right\rangle = \frac{{COV\left( {SS\left( t \right),{S_b}\left( t \right)} \right)}}{{\sqrt {Var\left[ {SS\left( t \right)} \right]Var\left[ {{S_b}\left( t \right)} \right]} }}\text{。} $ | (15) |
因为对于水面目标,经过海面反射到达水听器的距离较近,所以信号在传播过程中造成的损失较少,进而最终接收到的信号中舰船辐射噪声的所占比例多,因此在进一步用相关函数解析时相关系数更大,而水下目标解析出的相关系数较小,进而实现对水面和水下目标的分类。
3 仿真实验从《水声学》[10]中P-M观测谱可知,当风速为12 m/s时的最大频率为0.11 Hz,因此采用仿真信号的频率为0.11 Hz,为验证该算法对水面水下目标的分类效果,针对不同深度的信号分别进行包络提取和相关处理。
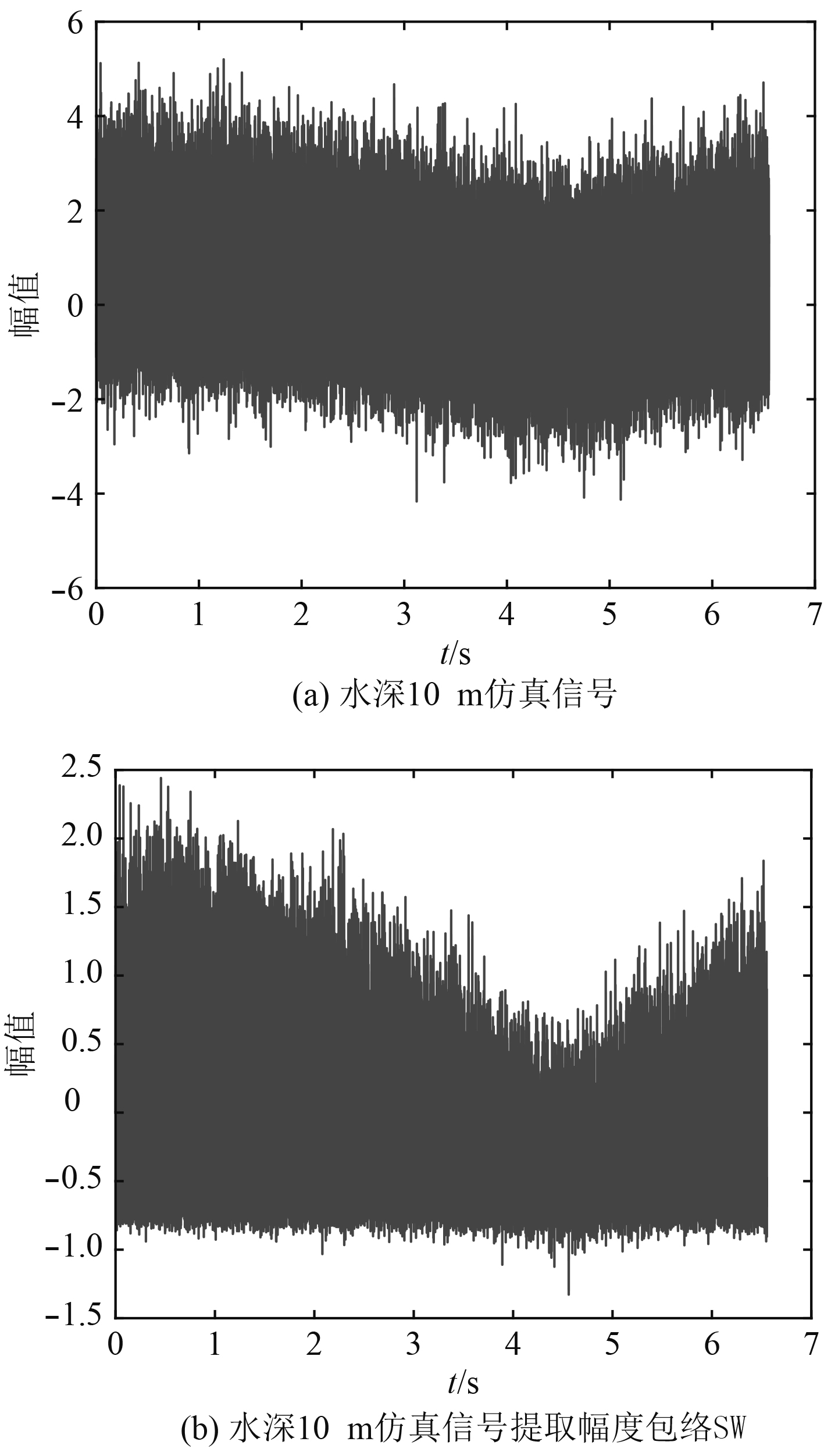
3.1 幅度包络提取本文采用的仿真信号为余弦函数,并分别仿真深度为4 m,10 m,50 m,100 m,200 m和300 m的6个信号,并用上述算法分别进行包络检波和低通滤波器处理,其中深度为4 m的仿真信号和处理后的仿真结果如图3所示。
|
图 3 水下目标传播示意图 Fig. 3 Water depth 10 m simulation signal and water depth 10 m simulation signal extracts amplitude envelope |
通过仿真结果的对比可以看出,本文对信号的解调、幅度包络的提取及处理有明显的效果。
3.2 相关处理结果为了提取舰船辐射噪声的特征,将提取到的不同深度的幅度包络通过相关处理并计算得到相关系数,其结果如表1所示。
|
|
表 1 相关系数 Tab.1 Coefficient of correlation calculated for differentdepth targets |
由表1可知,不同深度的目标和接收信号的相关系数不同,随着目标深度的增加,相关系数就越小,这一点就证明了水面和水下目标的声信号通过海面波浪的散射传播到水听器的信号有所不同,从这一点出发对水面和水下目标进行分类。
4 海上实测数据仿真由于海上实测数据是宽带信号,因此选取能量最强的线谱所对应的时域幅度变化作为信号的包络变化规律,并对幅度包络进行调制解调。
| $ {S_2}\left( t \right) = \mathop \int \nolimits {SS}\left( t \right){\rm {cos}} \omega t{\rm d}t\text{。} $ | (16) |
由《水声学》[10]中P-M观测谱可知,海面在不同风速下的最大频率主要集中在0.11~0.15 Hz。在一个快拍之内,

|
图 4 水深10 m仿真信号 Fig. 4 Water depth 10 m simulation signal |
将海上水面和水下目标的实测数据提取出幅度包络通过相关器处理并计算得到相关系数,其结果如表2和表3所示。
|
|
表 2 水面目标相关处理结果 Tab.2 Relevant processing results of measured data ofsurface targets at sea |
|
|
表 3 水下目标相关处理结果 Tab.3 Relevant processing results of measured data ofunderwater targets at sea |
通过大量海上实测数据表明,水面目标和水下目标的相关系数具有明显的差异性,由于实际海面情况的未知性和多变性,本文采用《水声学》[10]中的P-M观测谱,当风速为12 m/s时的最大频率为0.11 Hz的散射强度进行相关处理。考虑到海面起伏的复杂化,在实测数据处理中存在一些特殊情况,但通过对大量的海试数据处理结果分析研究得到,水面目标相关处理的相关系数比水下目标相关处理的相关系数普遍较大,因因此证明利用水面和水下目标的声信号通过海面波浪的散射传播到水听器的差异性进行特征提取的方法具有良好的效果。
5 结 语本文从真实海面波浪起伏的角度出发,建立了基于PM海浪谱的一维随机起伏界面,并利用积分方程方法计算海面起伏界面的散射强度。分析提取信号的物理特性和信号幅度包络特征,并通过相关函数法提取信号的包络。将相关函数解析出稳定的包络曲线与海面散射强度做相关处理,进而将得到的相关系数作为信号特征对水面和水下目标进行分类。最后仿真实验测试了4~300 m不同深度下的声源,结果表明,该算法可以稳健对水面水下目标进行判别。用大量海上实测数据对该算法进行验证,结果表明,水面目标相关处理的相关系数比水下目标相关处理的相关系数普遍较大,通过相关系数能够有效的判别水下目标和水面目标。
| [1] |
谢志诚, 葛辉良. 水面和水下目标起伏声场差异性研究[J]. 声学与电子工程, 2015(1): 24-29. |
| [2] |
张大伟, 章新华. 一种基于舰船辐射噪声起伏特性的线谱提取方法[J]. 舰船科学技术, 2015(10): 85-88. DOI:10.3404/j.issn.1672-7649.2015.10.018 |
| [3] |
王振, 马晓民. 海面波动引起的声场起伏特性研究[J]. 声学与电子工程, 2018(1): 22-25. |
| [4] |
蒋东阁, 林建恒. 浅海海洋环境噪声时间平稳性与起伏特性分析[J]. 声学技术, 2014(12): 52-55. |
| [5] |
陈文剑, 郎鹏远. 起伏海面环境下水声信道特性及估计方法[J]. 应用声学, 2018(9): 722-731. |
| [6] |
王永棒, 尹爽. 基于PM谱的随机起伏界面声散射特性研究[J]. 声学技术, 2017(8): 131-133. |
| [7] |
孟昭然, 孙辉. 随机起伏界面声散射的实验与理论研究[J]. 声学技术, 2014, 33(4): 299-303. |
| [8] |
E. I. THORSOS. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J]. J. Acoust. Soc. Am, 2003, 114(2): 726-736. DOI:10.1121/1.1591774 |
| [9] |
刘若芸, 李整林. 随机起伏海面对浅海声传播的影响[J]. 声学技术, 2018, 37(6): 151-152. |
| [10] |
汪德昭, 尚尔昌. 水声学[M]. 科学出版社. 2013, 7: 42-44.
|
 2019, Vol. 41
2019, Vol. 41
