0 引　言

随着现代工业的不断发展，管路被广泛应用于船舶、大型重装设备及石油、天然气等输送系统。管道的振动不仅对管道的寿命和安全造成一定影响，而且还会破坏与其相连接的仪表、阀口、机械等设备。研究表明，在船舶管系中，润滑油管路压力波动是引起润滑油管道及附属设备振动的主要原因。管内流体在泵的作用下压力、速度、密度等参数随时间呈周期性的脉动^[1]。当脉动的流体遇到阀门、法兰、弯头等阻抗管路部件时，将产生一定随时间周期变化的激振力，在激振力的作用下会引起振动和噪声问题^[2]。在我国每年因管道压力波动而导致管道破坏造成的损失难以估量，因此对管道压力波动研究具有广泛的工程背景与经济意义。

为了控制压力波动带来的危害，国内外学者不断探究管道流体压力波动的产生机理，寻找解决降低压力波动的方法，并取得了一定的成果。党锡淇^[3]介绍了气流脉动和振动的背景，研究内容和基本方法，并对流体的压力脉动给出了理论分析。周红等^[4]通过分析了管道内流体的连续方程和运动方程，推导了脉动压力的二阶偏微分方程，通过对弯管处的激振力分析，揭示了压力脉动引起管路系统振动的机理。祁仁俊^[5]对液压系统中压力产生脉动的机理进行分析，总结出脉动压力的基本种类与特征,并对压力脉动的频率成分进行了分析。Kanyanta^[6]进行了流体数值模型的验证试验研究，模型用于预测管内流体脉动。从目前的研究现状来看对输液流体压力脉动的研究较少且只停留在理论分析。

本文以细长复杂弯管为研究对象，采用计算流体动力学软件Fluent对管路内流场压力脉动特性进行数值模拟，分析管道不同位置压力脉动特性。采用快速傅里叶变换对监测点的压力进行分析，阐明管道布置及运行工况对管道内流体压力脉动特性的影响。并通过试验验证仿真结果的真实性，为减少管道压力波动、合理的管道布局和工况设置提供理论依据。

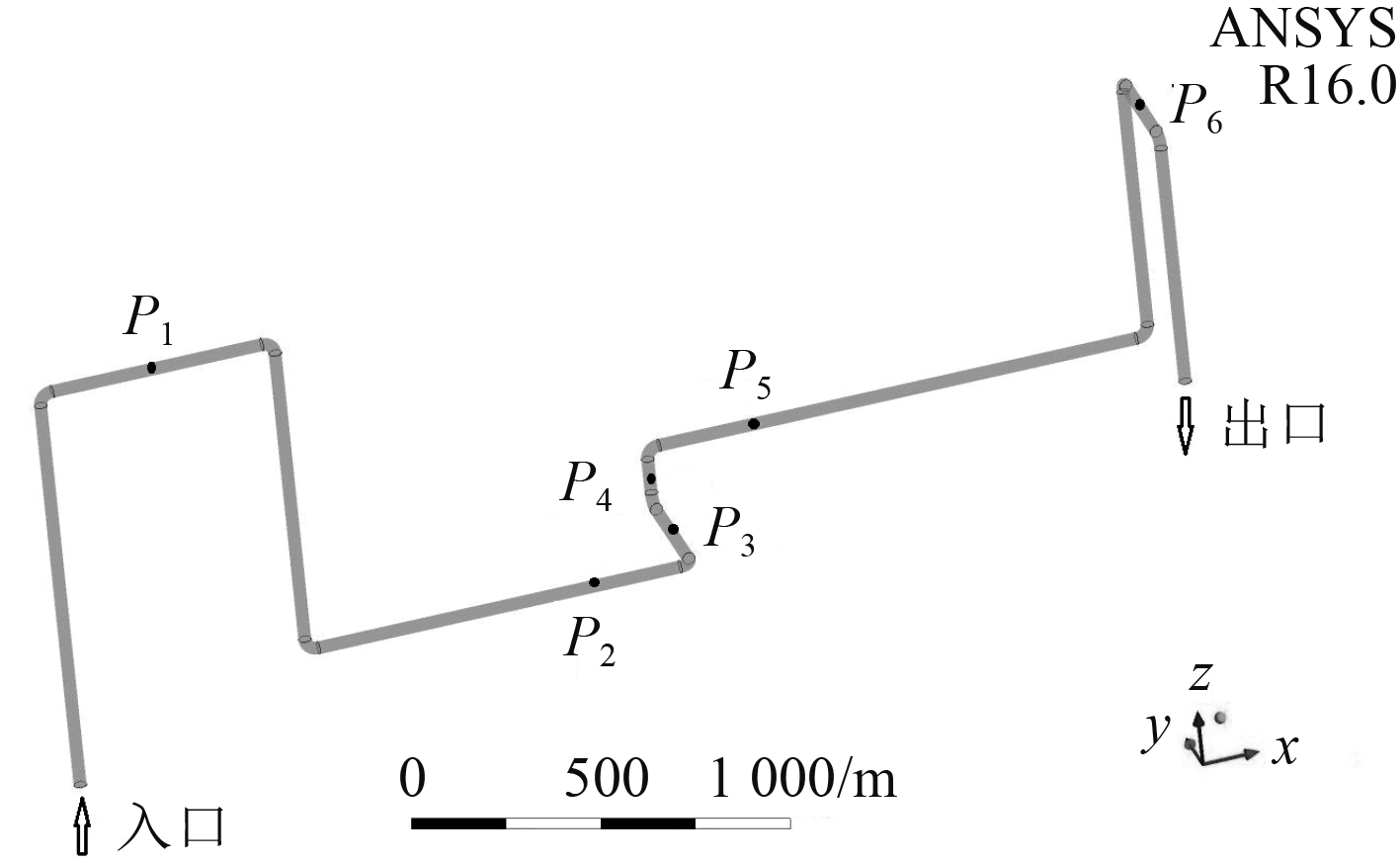
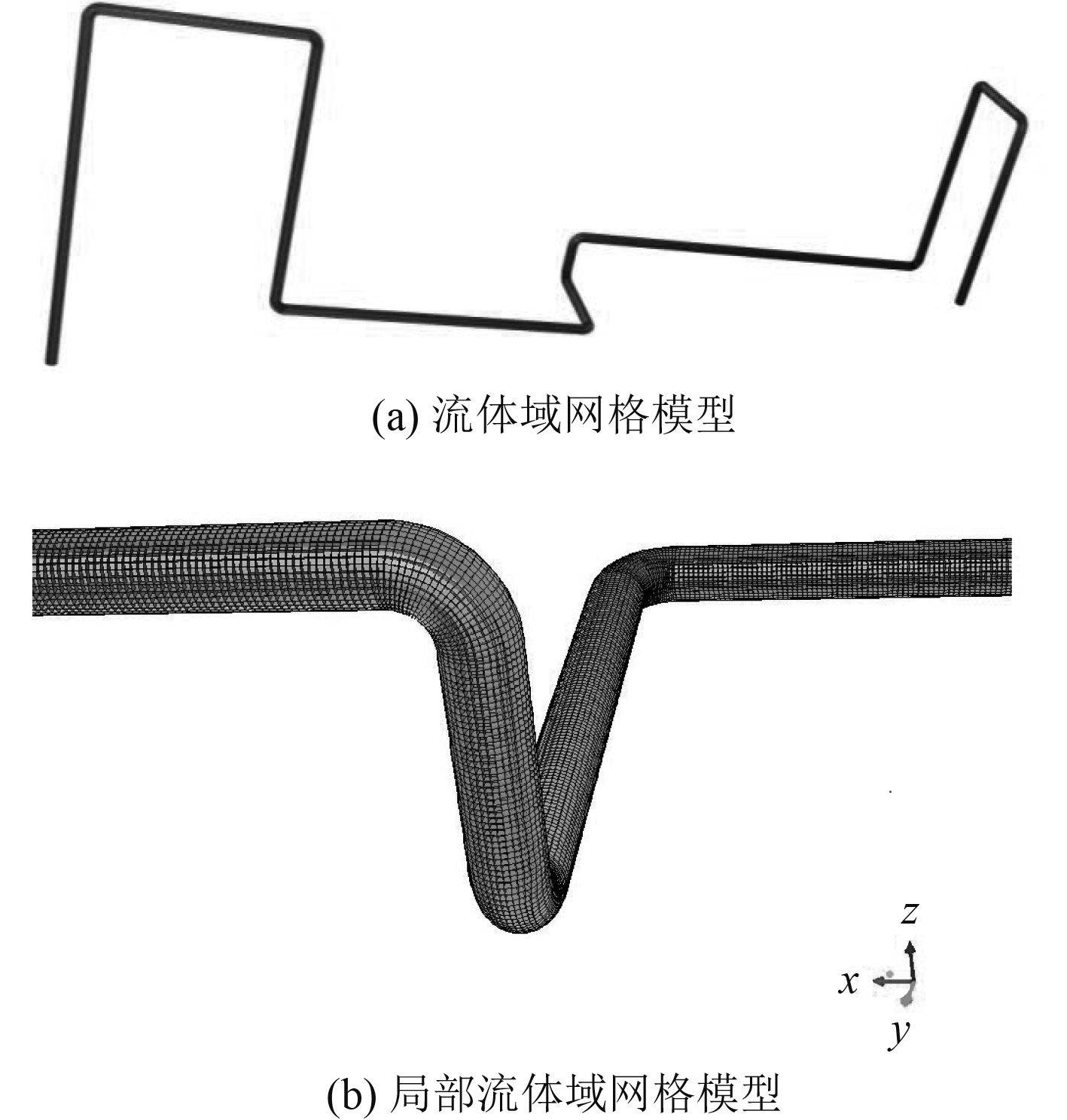
1 建立模型 1.1 几何建模与网格划分

该研究模型是由某船柴油机润滑油系统简化而来，该系统由双头三螺杆泵、管路及其附属设备组成，几何模型简化如图1所示，它由9个弯头和10个直管构成三维复杂弯管。管道的内径D为34 mm，壁厚e为4 mm，90°弯头的曲率半径Rc为34 mm，管道的总长约9.5 m。流体从入口垂直管流入管道后垂直流出。利用前处理软件ICEM来绘制管道流体图形并划分网格，网格生成图如图2所示。由于该管道是一个整体性比较好的封闭管道，故采用六面体结构化网格。考虑到网格尺寸过大会降低模拟精度，无法精确仿真流体的流动过程；网格过密时后期导入Fluent时因为网格数量过多迭代速度慢，对计算机配置有很高的要求，计算成本较高。综合以上因素选取网格总数为755 282。

1.2 计算模型的建立

流体在流经管道的过程中必须满足连续性方程。本文主要研究润滑油流经复杂弯管时内部流体的压力波动特性，因为所研究流体的初速度远小于声速，因此假设润滑油的流动是不可压缩流动。本次模拟的是不可压缩的粘性流体在管道内做湍流运动，考虑收敛性和计算精度及工程实际情况，湍流模型采用standard k-ε双方程模型，润滑油在管道流动过程中还要遵守质量守恒定律。具体微分公式如下^[7]：

连续性方程

$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_x})}}{{\partial x}} + \frac{{\partial (\rho {u_y})}}{{\partial y}} + \frac{{\partial (\rho {u_z})}}{{\partial z}} = 0{\text{，}} $

(1)

粘性流体动量方程

$\rho \frac{{\partial{{u}}}}{{\partial t}} = \rho {{f}} - gradp + \frac{\mu }{3}grad(\nabla {{u}}) + \mu {\nabla ^2}{{u}}{\text{，}} $

(2)

湍动能 $k$ 和湍流耗散 $\varepsilon $ 方程：

$\begin{array}{l} \displaystyle\frac{\partial }{{dt}}(\rho k) + \displaystyle\frac{\partial }{{\partial {x_i}}}(\rho {u_j}k) = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \displaystyle\frac{{{\mu _t}}}{{{\sigma _k}}}\right)\frac{{\partial k}}{{\partial {x_j}}}\right] + \\ {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_K}{\text{，}} \end{array} $

(3)

$\begin{array}{l} \displaystyle\frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i}) = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}\right]+\\ {C_{1\varepsilon }}\displaystyle\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) - \rho {C_{2\varepsilon }}\displaystyle\frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon }{\text{。}} \end{array}$

(4)

其中： $\rho $ 为流体密度； ${{{u}}_x}$ ， ${{ u}_y}$ ， ${{ u}_z}$ 为速度矢量在 $x,y$ 和 $z$ 方向上的速度矢量； $\mu $ 为流体动力学粘度； ${\mu _t}$ 为湍流粘性； ${{f}}$ 为切体力； ${G_K}$ ， ${G_b}$ 为湍动能项； $C_1$ ， $C_2$ ， $C_3$ 为经验常量，取值分别为1.44，1.92，0.99； ${\sigma _k}$ ， ${\sigma _\varepsilon }$ 为湍流prandtl数，取值为1.0和1.3^[8]。

双头螺杆泵出口压力波动频率是螺杆泵转频的2倍^[9]。润滑油速度和压力随时间呈周期性变化，但是管道内压力波动主要是压力的脉动所引起的，速度的脉动所占的比例很小。 $\delta $ 表示管内压力波动率， $\delta $ 值反映管内压力波动的大小。管内流体的瞬时压力可以看成在平均压力的基础上叠加若干脉动分量，所以输油管进口压力可以表述成：

$ {P_t} = {P_0}\left( {1 + \sum\limits_{i = 1}^m {\frac{{{\delta _i}}}{2}\sin (2{\text{π}} {f_i}t)} } \right){\text{，}} $

(5)

$ {f_i} = \frac{{n{Z_1}}}{{60}}{\text{，}} $

(6)

$ \delta = \frac{{\left( {{P_{\max }} - {P_{\min }}} \right)}}{{\mathop P\limits^ - }}{\text{。}} $

(7)

式中： ${P_0}$ 为管道进口的平均压力，不随时间的变化而变化； ${f_i}$ 为流体脉动频率； $n$ 为螺杆泵转速； ${Z_1}$ 为主动螺杆主的螺旋头数； ${P_{\max }}$ 为波动压力的最大值； ${P_{\min }}$ 为波动压力的最小值； $\mathop P\limits^ - $ 为平均圧力。

当m=1时，则

$ {P_t} = {P_0}\left( {1 + {\delta _1}\sin (2{\text{π}} {f_1}t)} \right){\text{。}} $

(8)

在工程的实际计算中，流体流经管道时流体流动的壁面沿程不变或微小变化时产生的阻力为沿程阻力。由沿程阻力引起的能量损失称为沿程损失 ${P_f}$ ；当固体边界急剧变化时，如管道弯头、扩缩、闸阀，在很短的距离流体为了克服边界发生的剧变而引起的阻力称为局部阻力；克服局部阻力的能量损失称为局部损失 ${P_m}$ 。

${P_f} = \lambda \frac{l}{d} \cdot \frac{{\rho {\nu ^2}}}{2}{\text{，}} $

(9)

${P_m} = \xi \frac{{\rho {\nu ^2}}}{2}{\text{。}} $

(10)

式中： $l$ 为管长； $d$ 为管径； $\nu $ 为断面平均流速； $g$ 为重力加速度； $\lambda $ 为沿程阻力系数； $\xi $ 为局部阻力系数。

整个管道的能量损失等于各管段沿程损失和局部损失的总和^[10]。

${P_l} = \sum {{P_f}} + \sum {{P_m}}{\text{。}} $

(11)

1.3 边界条件的设定与监测点的布置

选取流体介质为4520合成润滑油，初始温度为40 ℃，密度860 kg/m³，运动粘度46 mm²/s。流体入口设定为pressure-inlet，流体出口设定为pressure-out，通过用户自定义函数（UDF）的编写控制管道的出入口压力。在Fluent中选择基于压力分离式的求解器，离散格式采用2阶离散格式，采用SIMPLE算法。在计算过程中，根据收敛情况，可以将松弛因子进行适当调整，收敛残差标准均设为10^–3。为了充分获取管道内不同位置处的压力波动情况，在管道流体计算区域内布置了6个监测点，分别为P₁～P₆，这6个点布置在管道入口、出口及管道直管处，进而捕获各个监测点瞬态压力变化值，监测点的位置如图1所示。

2 计算结果与分析

根据柴油机实际工况，在不同转速下润滑油管道出口压力 ${p_b}$ 范围0.2～0.8 MPa，输油泵的转速范围 $n$ 为1 500～2 400 r/min。经实验测得不同转速下的能量损失如表1所示。由于管道入口平均压力 ${P_0}$ 由背压和能量损失共同决定，在仿真分析时选取入口平均压力为：

${P_0} = {P_b} + {P_l}{\text{。}} $

(12)

选取 ${P_t}$ 和 ${P_b}$ 作为压力入口和压力出口的边界条件进行仿真，分析不同工况下监测点处压力波动率系数 $\delta $ 值，进而分析背压，输油泵的转速及管道布置对管道流体压力波动的影响。

转速为1 500 r/min，1 800 r/min，2 100 r/min和2 400 r/min时，分别选取4个工况点作为边界条件，如表2~表5所示。

2.1 压力波动频率

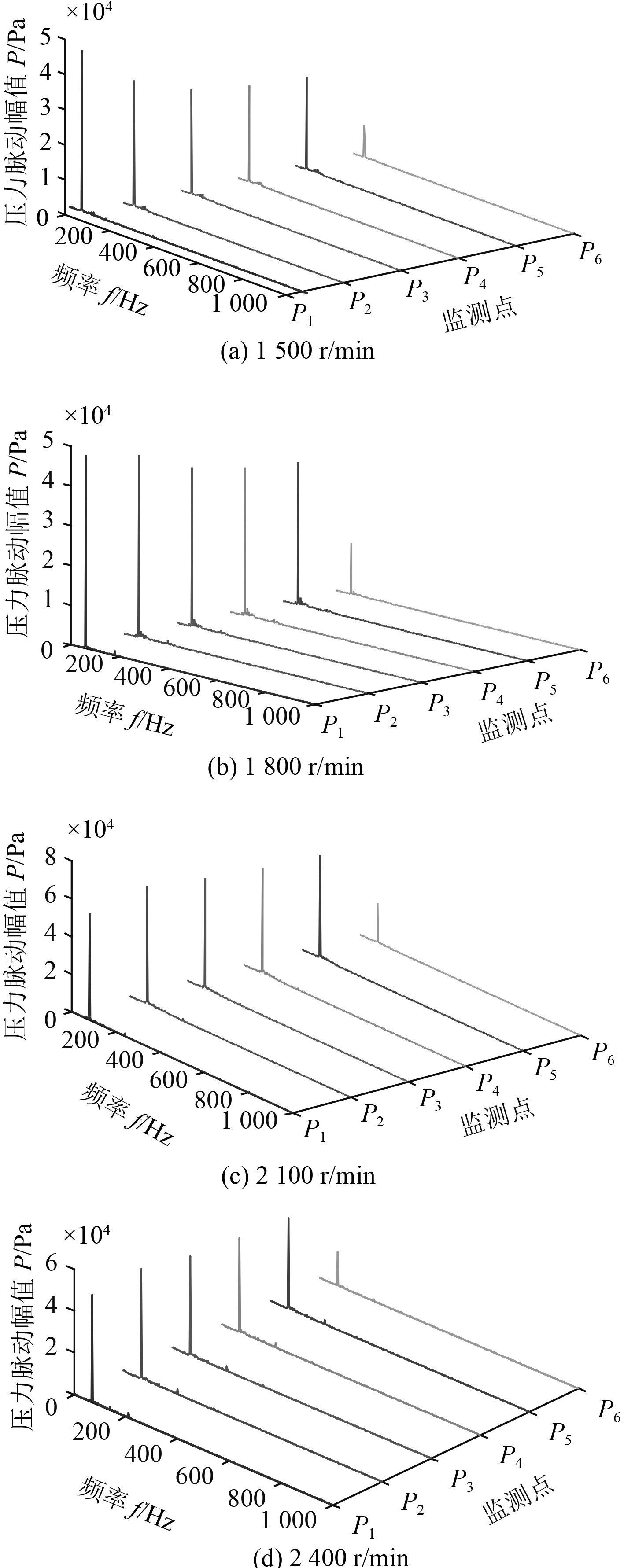
图3为选取背压0.8 MPa时，对不同压力监测点测试的压力信号进行傅里叶变换（FFT），得到不同压力监测点压力脉动幅值 $P$ 和频率 $f$ 。当转速是1 500 r/min，1 800 r/min，2 100 r/min和2 400 r/min时，管道内流体的脉动主频率分别50 Hz，60 Hz，70 Hz和80 Hz。虽然在4倍转频和6倍转频处也出现了压力波动幅值，但幅值相对于波动主频幅值较小。管道流体的压力波动主频率是转频的2倍，即管路液体压力波动频率就是泵的出口压力波动频率，它是由泵对流体的周期性吸排作用引起。

2.2 背压和泵转速对管道压力波动影响

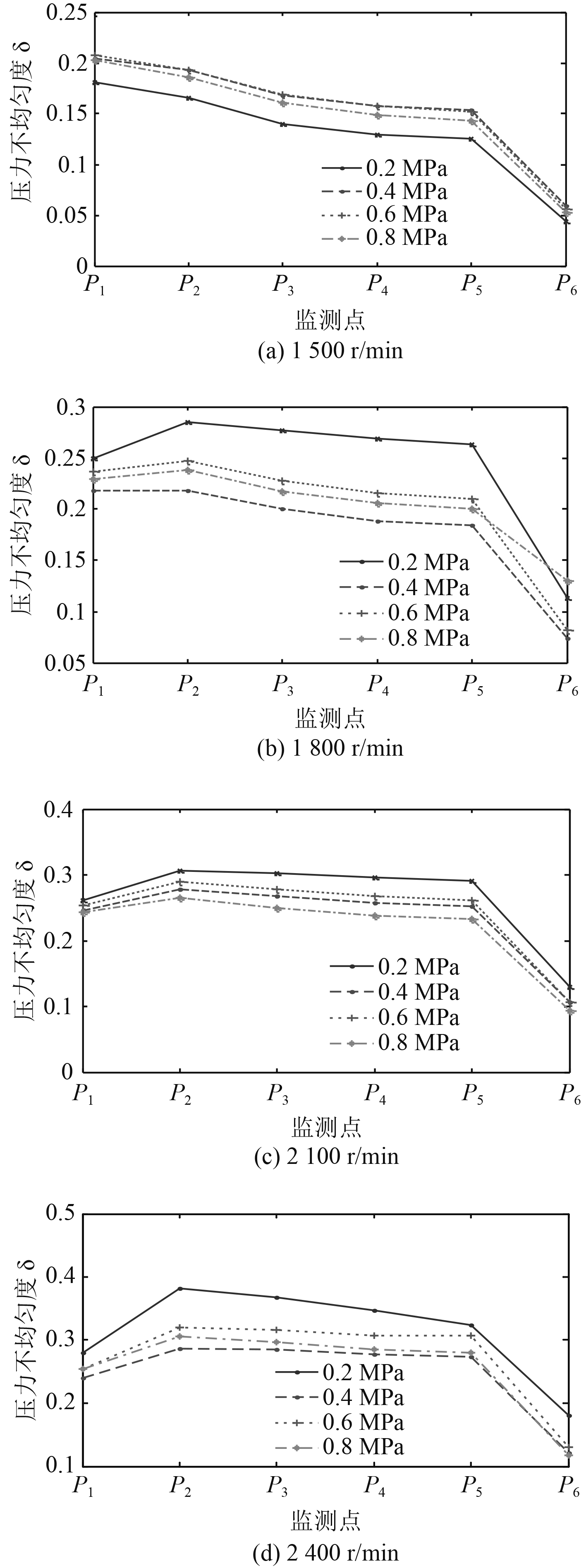
图4为不同背压下各监测点压力波动率 $\delta $ 大小分布。由图分析可得管道各监测点的压力波动大小不同，转速为1 500 r/min时，压力波动率最大值在p₁点，沿管路压力逐渐减小，当背压为0.2 MPa是压力波动相对其他工况较小；转速为1 800 r/min，2 100 r/min和2 400 r/min时，点P₂处压力波动率最大，当背压为0.2 MPa是压力波动相对其他工况较大。由于管道或液压元件的刚度大，振动阻力大且不存在缺陷时，压力波动将逐渐衰减趋于稳定，因此流体沿流动方向监测点压力波动率逐渐减小，在点P₃～P₅处减小的幅度较小，由于背压为恒压，监测点P₆靠近出口方向，所以P₆点的压力波动率减小显著。整体来看背压对压力波动的影响比较复杂，它受到背压和转速的耦合作用。在实际工程中，若要减少压力波动，不能只单一的调节背压来降低压力波动，需要综合考虑转速和背压的影响。

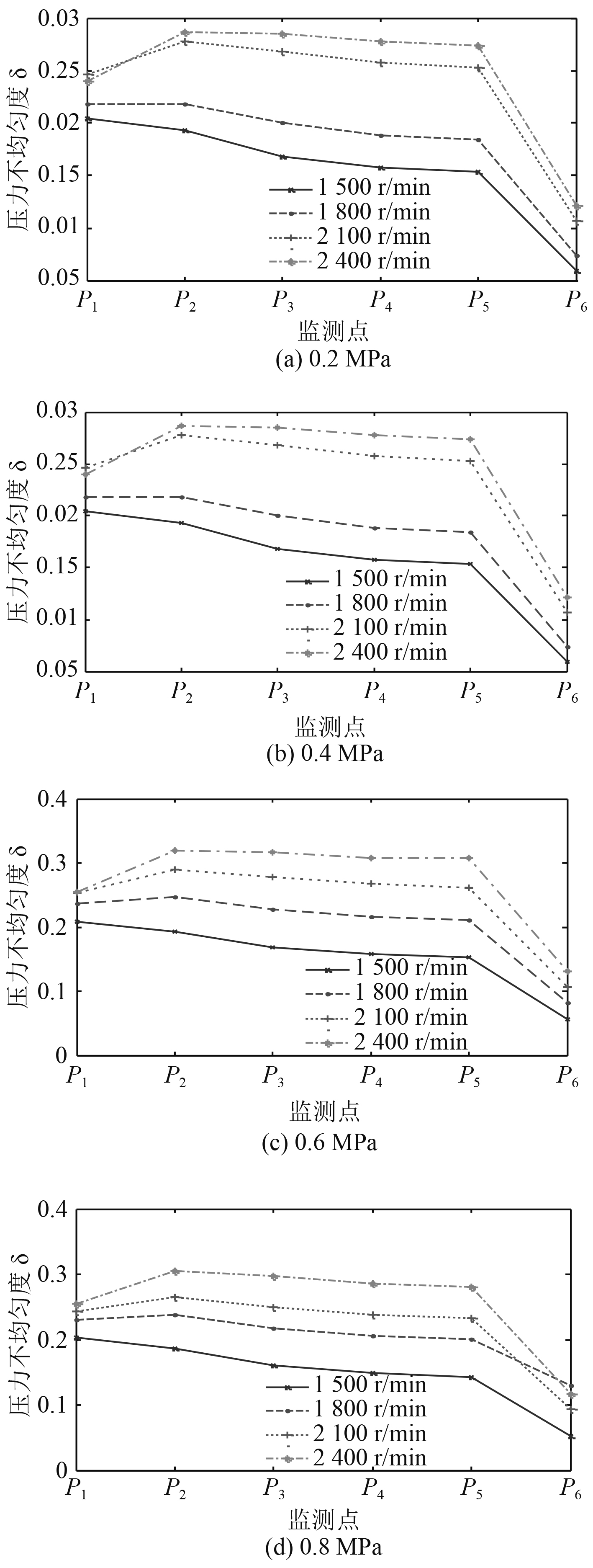
图5为相同被压不同转速下各监测点压力波动率 $\delta $ 的分布。管内各点压力波动率随转速增加而增加。当转速增加时，管内的润滑油脉动频率和流动速度增加，流体在管道弯头处撞击更加强烈，激振力增大使得管内压力波动率增加。由于该管道弯头集中在点P₂～P₅之间，波动的流体遇到弯管后产生反射波，导致P₂点的压力波动最大，流体压力波动率最大。

通过上述对不同工况下管内压力特性的分析，发现不同转速下随着背压改变，压力波动呈不同的变化趋势；背压相同时，随着转速的升高管内各监测点压力波动增大。

3 试验验证

为了验证所建仿真模型的可行性，搭建试验台架对部分试验进行验证，通过已验证仿真结果的正确性，判断其他仿真结果的正确性。

在试验台架润滑油管道的入口、出口及点P₁处安装压力传感器，采集各点的压力信号。把采集的入口和出口压力信号的时间序列，通过写入profile文件作为仿真的出入口边界条件。通过监控记录P₁点压力信号数据，与实验数据相对比判断仿真模型的可行性。如图6是对2 400 r/min背压0.8 MPa的工况下仿真曲线和试验曲线。

通过对比，试验得到的流体在P₁处的压力变化趋势及数值与仿真得到的相近，计算结果和试验结果吻合较好。可以看出试验和仿真得到的曲线存在误差，实验过程中背压的不稳定也会导致实验值略大于仿真值。计算误差在可接受范围内，表明仿真模拟与试验结果反映的规律基本一致，计算结果是可靠的。

4 结　论

1）利用计算流体力学软件Fluent，对润滑油管道内部流场压力波动规律进行了探索，通过对各监测点数据的傅里叶变换，发现管道流体脉动的频率和输液泵的激励频率相同，输液泵周期性吸排作用是导致管内压力波动的主要原因。

2）对不同工况下管内压力特性的分析，发现相同转速下随着背压的改变，压力波动呈不同的变化趋势，即背压是影响管路压力波动的重要因素；背压相同时，随着转速的升高管内压力波动增大。

3）流体在流经管道弯头密集区域时，产生的激振力增大较为明显；流体速度越大遇到弯管时所产生的激振力越大。因此在管道设计的过程中应尽量减小弯头的数量。

以上结论将有助于在工程实际中更好地进行液压系统管道的结构设计和管线的布局设计，为液压系统减振降噪的实现提供参考。