2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key laboratory on Ship Vibration and Noise, Wuhan 430033, China
永磁轴承是利用永磁体产生的磁力,将转子悬空,使得转子与定子无润滑和摩擦,具有高转速,低噪声,低功耗,无污染等优点。随着钕铁硼等高性能永磁材料的研究和制造工艺的改善,已造出高韧性,可直接成型的薄壁结构部件,为永磁轴承的工程实用打下了基础[1 – 4]。文献[1 – 2]对双环同心永磁轴承的轴向承载能力进行了研究。文献[3 – 4]对多个双环同心永磁轴承的轴向承载能力进行了研究。尽管上述文献已经对永磁轴承的简单结构和受力,以及复杂结构和受力进行了有价值的研究,但是,已有研究主要针对轴向位移和承载力较小的永磁轴承。船用轴承承载的推力在200 kN左右,为了使永磁轴承的应用更为广泛,本文针对船用推进系统用的一种径向磁化永磁推力轴承新结构,在基于和虚位移与线性叠加原理,结合船用永磁推力轴承结构特点和线性叠加原理,建立了径向磁化永磁推力轴承轴向磁力解析模型,并通过有限元计算验证解析模型,对于船用永磁轴承的设计与优化具有理论指导意义。
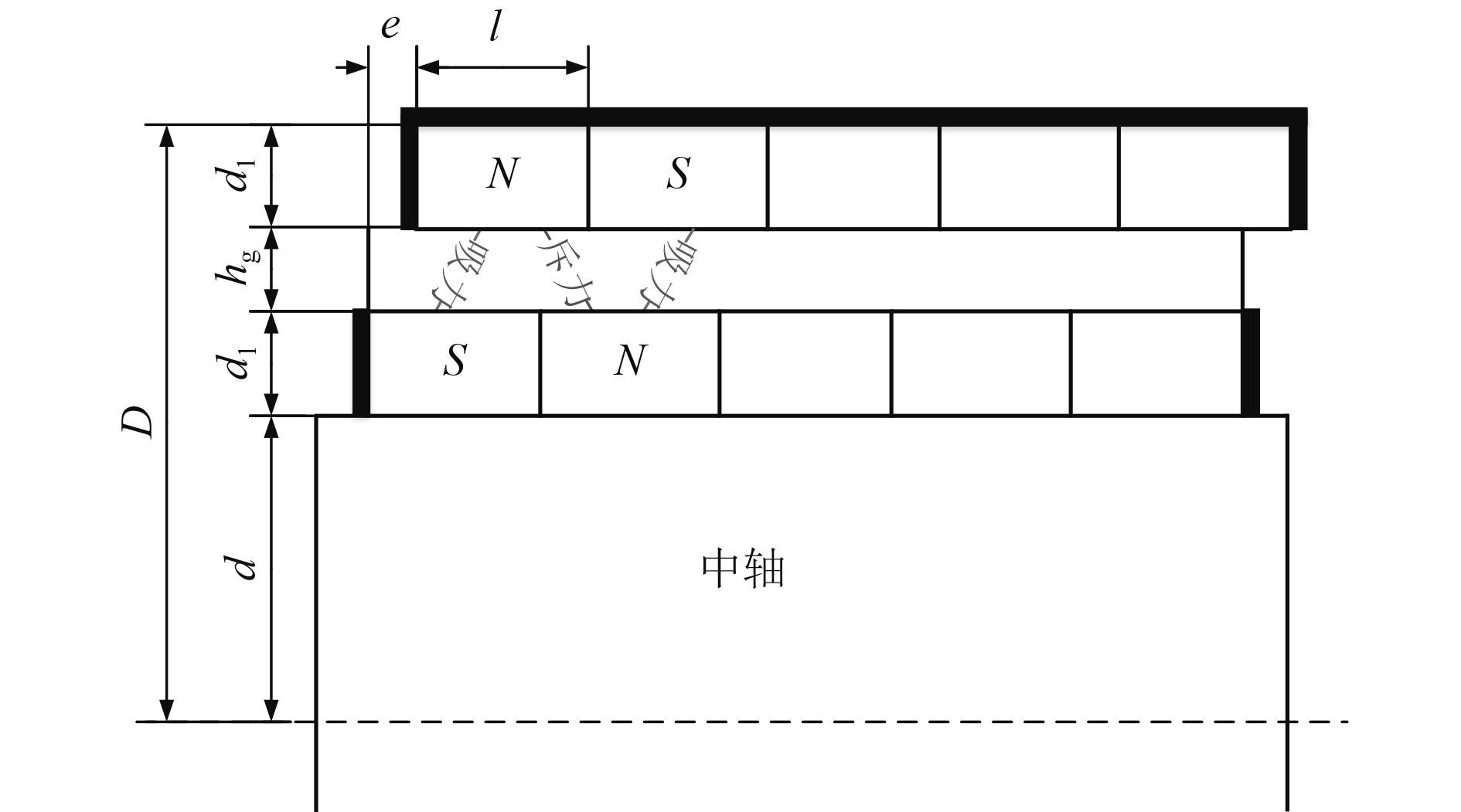
1 结构及工作原理永磁推力轴承结构如图1所示。图中以平行永磁环数N=5为例,中轴半径为d;径向磁化永磁圆环的厚度为d1,定磁环无间隙排布于外圈壳体,同心的动定磁环磁化方向相反。轴向长度为l,永磁环间径向气隙为hg,永磁环最小内径为d,最大外径为D。动磁环在轴向上不加约束,可以随中轴进行双向位移;对定磁环施加约束,保持固定。深色部分为内磁环与外磁环包裹的绝缘材料,用于控制漏磁。
|
图 1 永磁推力轴承结构及轴向位移受力图 Fig. 1 Configuration and displacement stress of PMTB |
永磁内环随中轴发生轴向偏移时,磁环间受力如图1所示。由于永磁轴承结构为N个平行永磁环,当磁环发生轴向偏移e时,同时受到永磁环的吸力外,其轴向回复力大大提高,在一定的轴向载荷下,可缩小永磁轴承体积,节省空间。图1中的永磁轴承结构在轴向自稳定,在径向需要其他方式来稳定。
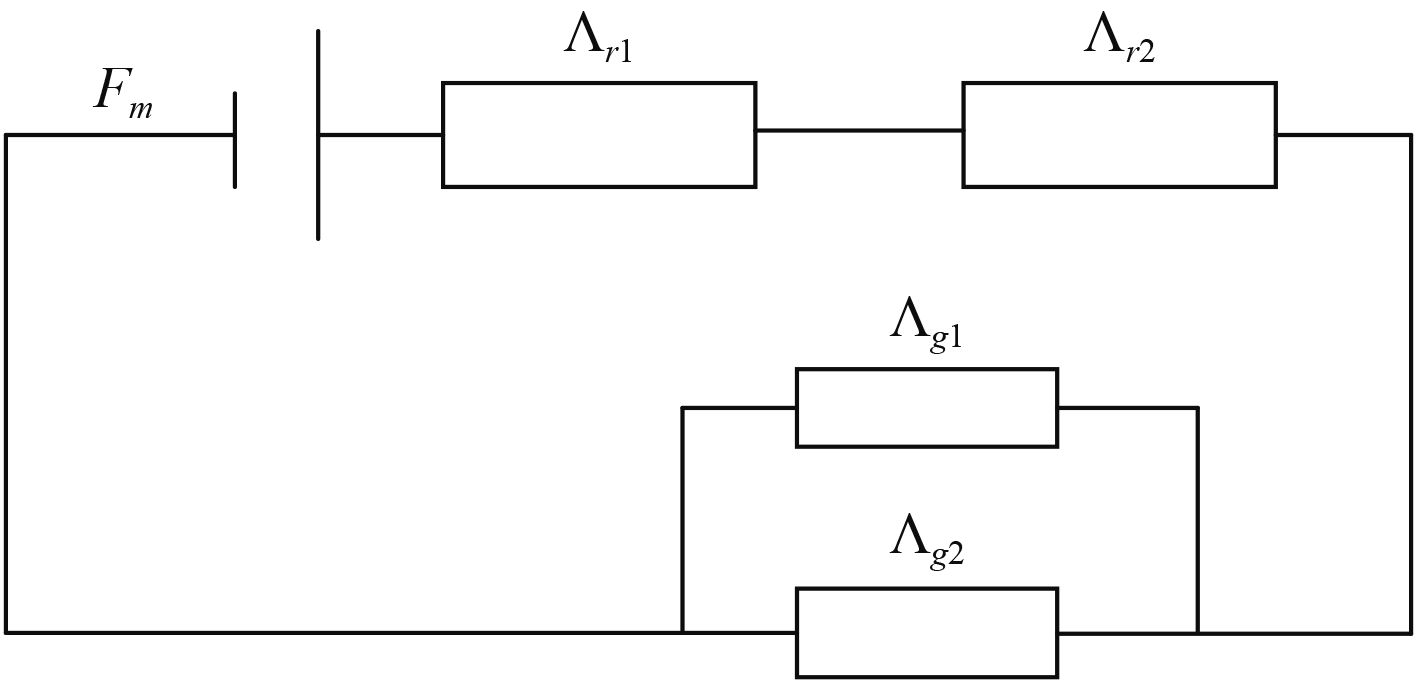
2 解析模型 2.1 磁路模型及磁导计算根据永磁推力轴承结构,建立磁路结构时,做出如下假设:1)忽略永磁环两端磁极侧面及其他部分的漏磁;2)永磁环两侧与空气接触的间隙部分,其漏磁忽略;3)将中轴部分作为良磁导材料,忽略其磁阻。图2为经过假设后的等效磁路,由磁路结构示意图中的磁导串并联关系得到磁路总磁导Λt为:
|
图 2 永磁推力轴承等效磁路 Fig. 2 Equivalent magnetic circuit of PMTB |
| $ \frac{1}{{{\varLambda _t}}} = \frac{1}{{{\varLambda _{r1}}}} + \frac{1}{{{\varLambda _{r2}}}} + \frac{1}{{{\varLambda _{g1}} + {\varLambda _{g2}}}} $ | (1) |
式中:Λr1同心永磁环外环磁导,Λr2同心永磁环内环磁导,Λg1为永磁环间吸力气隙磁导,Λg2为永磁环间斥力气隙磁导。
图中磁环内磁路与同心磁环间隙磁路相似。根据同心永磁环间隙磁导公式
| ${\varLambda _{r1}} = \frac{{2\mu {\text{π}} {L_n}}}{{\ln \left[ {D/\left( {D - {d_1}} \right)} \right]}}{\text{,}}$ | (2) |
永磁环内环磁导
| ${\varLambda _{r2}} = \frac{{2\mu {\text{π}} {L_n}}}{{\ln \left[ {(d + {d_1})/d} \right]}}{\text{。}}$ | (3) |
式中:
采用虚位移法,令磁环产生轴向为 e的偏移量,间隙磁力线长为
| $ {\varLambda _{g1}} = \frac{{2{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2){L_n}{h_g}}}{{{h_g}^2 + {e^2}}}{\text{,}} $ | (4) |
| $ {\varLambda _{g2}} = \frac{{2{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2){L_{n - 1}}{h_g}}}{{{h_g}^2 + {e^2}}}{\text{。}} $ | (5) |
磁路总磁阻为:
| $ \begin{array}{l} \displaystyle\frac{1}{{{\varLambda _a}}} = \displaystyle\frac{1}{{{\varLambda _r}}} + \displaystyle\frac{1}{{{\varLambda _{g1}} + {\varLambda _{g2}}}}= \\ \;\;\;\;\;\;\; \displaystyle\frac{{\ln \left[ {D/\left( {D - {d_1}} \right)} \right] + \ln \left[ {\left( {d + {d_1}} \right)/d} \right]}}{{2\mu {\text{π}} nl}}+\\ \;\;\;\;\;\;\;\; \displaystyle\frac{{{h_g}^2 + {e^2}}}{{2{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2)\left( {2n - 1} \right)l{h_g}}}{\text{。}} \end{array} $ | (6) |
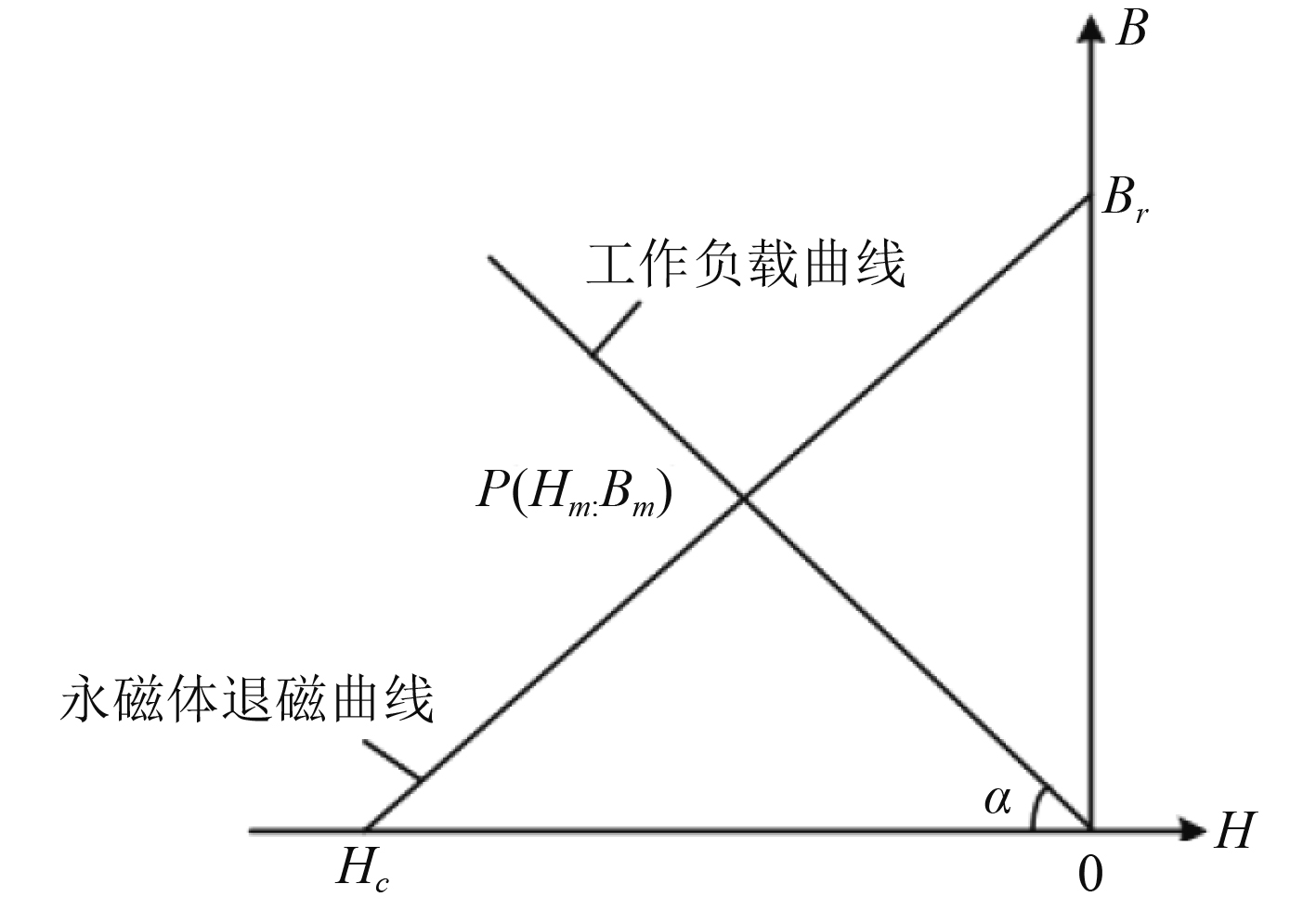
NdFeB等永磁材料的退磁曲线为直线,如图4所示。
|
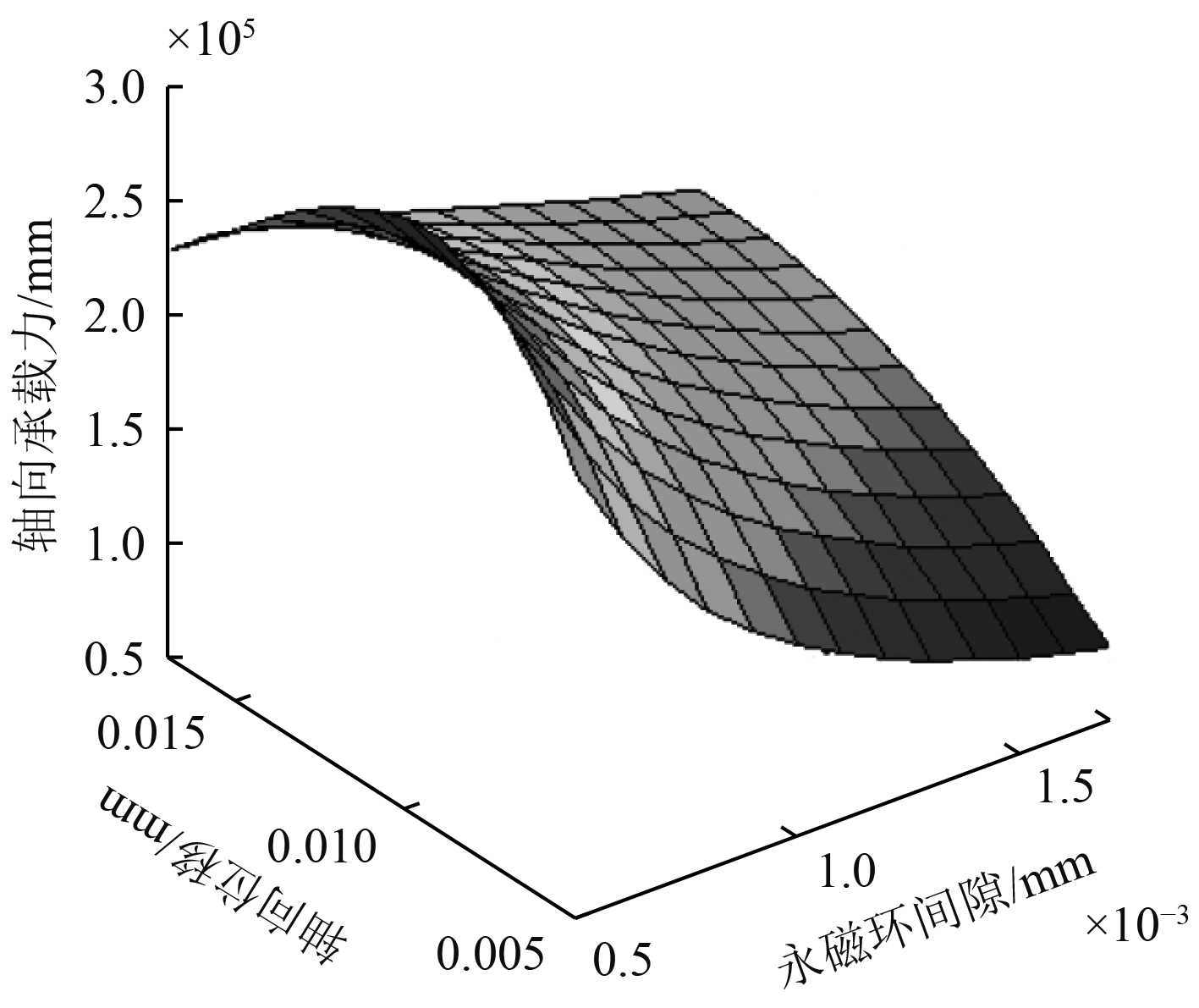
图 4 轴向承载力与永磁环间隙、轴向位移的关系 Fig. 4 Relationship between axial bearing capacity, axial air gap, and axial displacement |
永磁体工作点的磁通密度Bm[6]为
| $ {B_m} = \frac{{{B_r}{H_c}L\varLambda }}{{{B_r}S + {H_c}L\varLambda }}{\text{。}} $ | (7) |
式中:Br为永磁体的剩磁感应强度,Hc为永磁体矫顽力,S为永磁体中磁路的横截面积,L为永磁体在磁化方向的有效长度。
|
图 3 NdFeB永磁体退磁曲线和磁路工作负载曲线 Fig. 3 NdFeB demagnetization curve and magnetic circuit load cure |
根据磁通连续原理[7],磁环间隙径向磁通为:
| $ \begin{array}{l} {\varPhi _g} = {B_m}S = 2{\text{π}} RL{B_m} = \\ \mathop {}\limits_{} \mathop {}\limits_{} \displaystyle\frac{{2{\text{π}} RL{B_r}{H_c}{L_m}\varLambda }}{{2{\text{π}} RL{B_r} + {H_c}{L_m}\varLambda }} {\text{。}} \end{array} $ | (8) |
式中:R为永磁环等效平均半径;L为永磁环轴向长度;Lm为永磁体磁化方向有效长度。
根据电磁场理论,磁环间隙磁能
| $ {F_z} = \frac{{\partial {W_g}}}{{\partial e}} = - \frac{{\varPhi _g^2}}{{2\varLambda _g^2}} \times \frac{{\partial {\varLambda _g}}}{{\partial e}}{\text{,}} $ | (9) |
则磁环吸力产生的轴向磁力为:
| $\begin{array}{l} {F_{e1}} = {\left( {\displaystyle\frac{{2{\text{π}} Rnl{B_r}{H_c}{d_1}{\varLambda _a}}}{{2{\text{π}} Rnl{B_r} + {H_c}{d_1}{\varLambda _a}}}} \right)^2} \times \\ \mathop {}\nolimits_{\mathop {}\limits_{} } \mathop {}\limits_{} \displaystyle\frac{{{e^2}}}{{{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2)nl{h_g}\sqrt {{e^2} + h_g^2} }} {\text{。}} \\ \end{array} $ | (10) |
磁环斥力产生的轴向磁力为:
| $\begin{array}{l} {F_{e2}} = {\left( {\displaystyle\frac{{2{\text{π}} Rnl{B_r}{H_c}{d_1}{\varLambda _a}}}{{2{\text{π}} Rnl{B_r} + {H_c}{d_1}{\varLambda _a}}}} \right)^2} \times \\ \displaystyle\frac{{{e^2}}}{{{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2)\left( {n - 1} \right)l{h_g}\sqrt {{e^2} + h_g^2} }} {\text{,}} \\ \end{array} $ | (11) |
则轴向力的合力Fe为:
| $\begin{array}{l} {F_e} = {F_{e1}} + {F_{e2}} = \\ {\left( {\displaystyle\frac{{2{\text{π}} Rnl{B_r}{H_c}{d_1}{\varLambda _a}}}{{2{\text{π}} Rnl{B_r} + {H_c}{d_1}{\varLambda _a}}}} \right)^2} \times \\ \displaystyle\frac{{{e^2}}}{{{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2)nl{h_g}\sqrt {{e^2} + h_g^2} }} + \\ {\left( {\displaystyle\frac{{2{\text{π}} Rnl{B_r}{H_c}{d_1}{\Lambda _a}}}{{2{\text{π}} Rnl{B_r} + {H_c}{d_1}{\Lambda _a}}}} \right)^2}\times \\ \displaystyle\frac{{{e^2}}}{{{\mu _0}{\text{π}} (d + {d_1} + {h_g}/2)(n - 1)l{h_g}\sqrt {{e^2} + h_g^2} }} {\text{。}} \end{array} $ | (12) |
解析模型。
3 轴向承载力解析与仿真验证永磁轴承采用的永磁环材料为NdFeB,应用解析模型和有限元分别计算轴向承载力,其中轴向位移选取轴向最大位移作为计算位移,永磁轴泵计算参数如表1所示。
|
|
表 1 永磁推力轴承参数 Tab.1 Design parameters of PMTB |
由式(12)可知,轴向承载力是永磁环间隙hg和轴向位移e的复杂函数,将表1中的永磁环材料参数和结构参数代入式(12),轴向承载力Fe与hg的关系如图4所示。可以看出,轴向承载力随永磁环间隙增大而减小。在间隙为0.5~1.0 mm时,轴向承载力随轴向位移的增加先增加后减少,存在最大承载力;间隙大于1.0 mm时,轴向承载力随轴向位移的增加而增加。轴向承载力在永磁环间隙为1.0 mm左右时,并未出现最大承载力。
利用磁场仿真软件,对永磁推力轴承模型进行有限元分析,图5为根据表1参数建立的有限元模型结构图。
|
图 5 永磁推力轴承仿真结构图 Fig. 5 Simulation model of PMTB in Maxwell software |
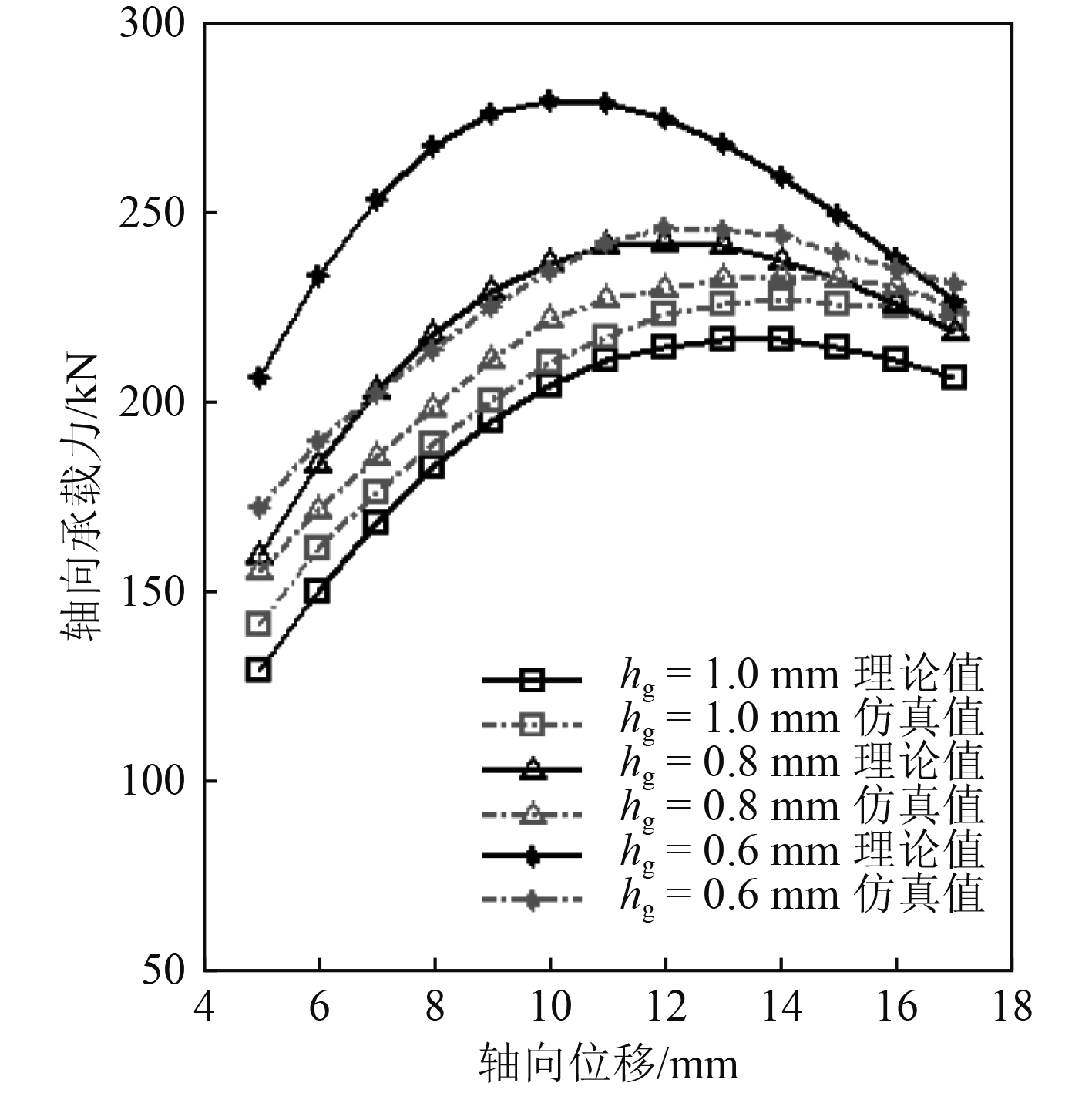
有限元计算在永磁环间隙分别为1.0 mm,0.8 mm,0.6 mm时进行解析模型与有限元计算的对比验证。解析模型计算结果Fe与有限元计算结果Fef见表2,对应曲线如图6所示。在永磁环固定间隙1.0 mm时,Fe与Fef基本吻合,平均误差为4.5%,最小误差为2.5%,最大误差为8.5%;永磁环固定间隙0.8 mm时,Fe与Fef基本吻合,平均误差为2.9%,最小误差为1.8%,最大误差为9.2%;永磁环固定间隙0.6 mm时,Fe与Fef的结果趋势基本吻合,但两者的误差较大。误差主要来自永磁材料的参数取值,中轴的磁阻以及轴承位移过大时两侧与空气部分的漏磁。
|
|
表 2 轴向磁力模型与有限元计算结果 Tab.2 Axial magnetic force model and FEM calculated results |
|
图 6 轴向承载力与轴向位移曲线 Fig. 6 Relationship between axial recovery force and axial displacement of PMTB |
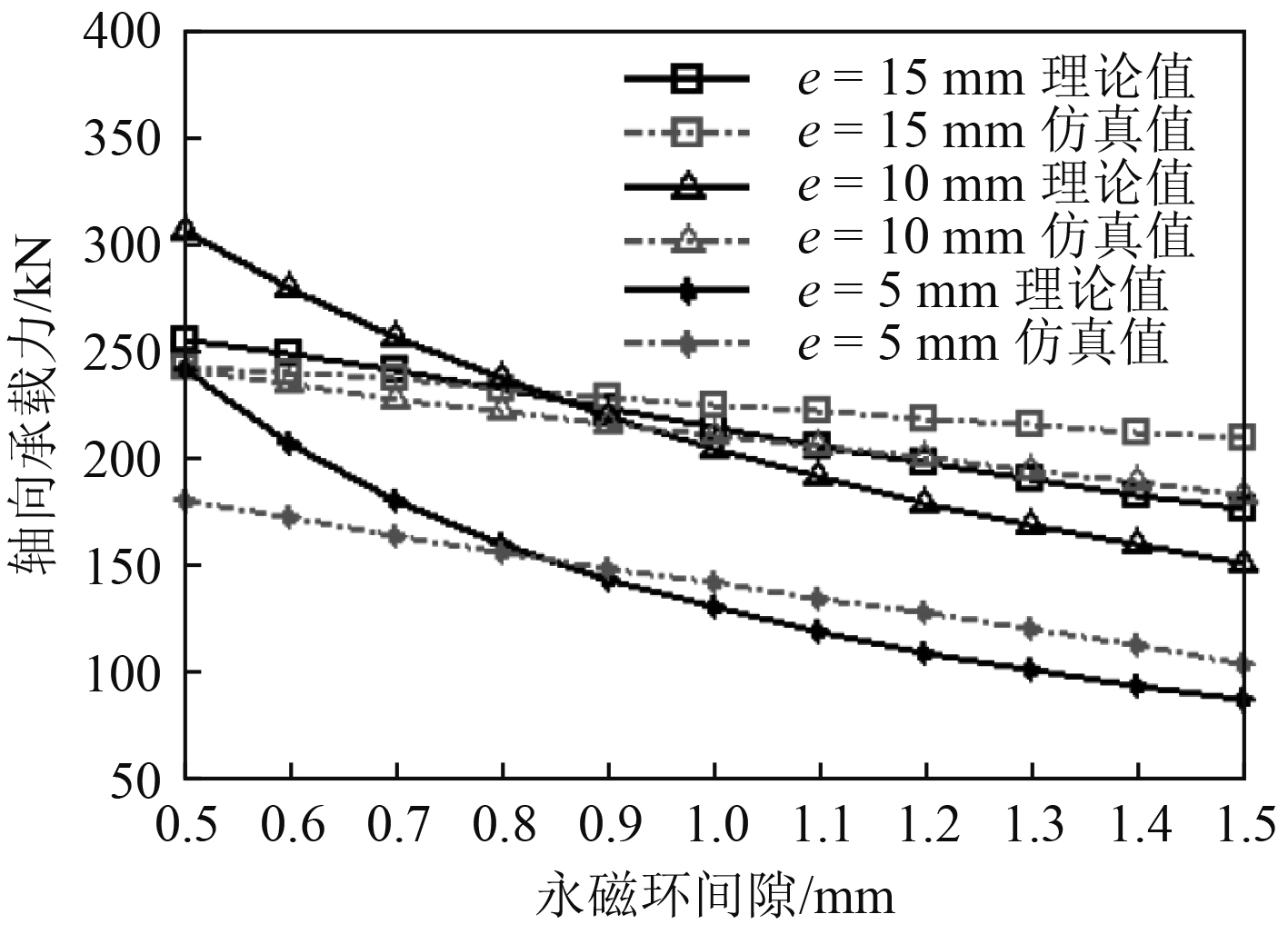
为确定解析模型在永磁环间隙的适用范围,在有限元模型计算时,轴向位移分别选取15 mm,10 mm,5 mm,计算结果Fef见表3,对应曲线如图7所示。模型计算结果与有限元计算结果在0.7~1.2 mm时两者的结果基本吻合,平均误差为6.3%,最小误差为0.4%,最大误差为11.7%。误差主要来自磁极间相互作用方式的改变,磁环之间采用线性叠加以及有限元仿真中求解域设定,磁路中间隙漏磁增加,使得解析模型计算结果与仿真结果相差较大。
|
|
表 3 轴向磁力模型与有限元计算结果 Tab.3 Axial magnetic force model and FEM calculated results |
|
图 7 轴向承载力与永磁环间隙曲线 Fig. 7 Relationship between axial recovery force and gap of PMTB |
比较图6理论值和仿真值曲线可知,轴向承载力随轴向位移的增加先增大后减小,两者在上升及下降部分都比较吻合。比较图7理论值曲线和仿真值曲线可知,轴向承载力随间隙的增加而减少,在间隙较小时,两者的结果基本吻合。
4 结 语1)针对一种新型大承载力的船用永磁推力轴承,建立轴向承载力的解析模型,在小间隙工况下,模型计算结果与有限元计算结果基本相符。解析模型为简单的数学表达式,方便了轴承的设计。
2)永磁推力轴承充分利用了永磁体的工作特性,产生的轴向回复力远大于由这些磁环所构成的若干个同心永磁环轴承产生的轴向磁力之和。
3)永磁轴承在间隙扩大后,需考虑其他部分的磁阻以及间隙的漏磁,本文提出的解析模型在小间隙工况下与有限元仿真较为吻合,适用于小间隙永磁推力轴承。
| [1] |
田录林, 李言, 杨国清, 等. 径向磁化的双筒永磁轴承轴向磁力研究[J]. 机械科学与技术, 2007, 26(9): 1216-1219. DOI:10.3321/j.issn:1003-8728.2007.09.030 |
| [2] |
田录林, 李言, 田琦, 等. 轴向磁化双环永磁轴承轴向磁力研究[J]. 中国电机工程学报, 2007, 27(36): 41-45. DOI:10.3321/j.issn:0258-8013.2007.36.008 |
| [3] |
田录林, 安源, 李言, 等. 轴向放置轴向磁化的多个永磁环轴承轴向磁力研究[J]. 机械科学与技术, 2008, 27(4): 549-553. DOI:10.3321/j.issn:1003-8728.2008.04.030 |
| [4] |
田录林, 李言, 田琦, 等. 径向磁化的多环嵌套永磁轴承轴向磁力解析模型[J]. 计算力学学报, 2010, 27(2): 379-384. DOI:10.7511/jslx20102034 |
| [5] |
宋后定, 陈培林. 永磁材料及其应用[M]. 北京: 机械工业出版社, 1984.
|
| [6] |
张云鹏, 刘淑琴, 李红伟, 等. 基于磁路分析的轴向混合磁轴承径向承载力解析计算[J]. 电工技术学报, 2012, 27(5): 137-142. |
| [7] |
林其壬, 赵佑民. 磁路设计原理[M]. 北京: 机械工业出版社.
|
 2019, Vol. 41
2019, Vol. 41
