滚动轴承是机械的重要零件,也是舰船动力传动系统易损件之一,据不完全统计,旋转机械故障约有30%是因滚动轴承引起的[1]。为尽早识别滚动轴承的故障防止对整个系统的失效影响,对轴承故障进行仿真,研究其故障机理积累大量的故障样本十分必要。
当前,针对滚动轴承局部故障动力学建模方面,国内外学者开展了大量研究,但大多数研究没有考虑非均匀滚道表面对轴承振动规律的影响,本文以较为复杂的内圈裂纹滚动轴承为对象,运用动力学等综合考虑滚道的波纹度、裂纹缺陷对滚动体与滚道之间的接触刚度、位移以及振动特性的影响,建立故障的冲击激励以和振动传递模型,并对模型进行仿真计算,最后通过仿真和试验信号的对比分析验证模型的合理性和正确性。
1 滚动轴承裂纹故障动力学建模对滚动轴承建模方法的研究,实质是研究滚动体通过故障缺陷边缘的过程,当滚动体通过缺陷部位时球与局部缺陷之间的接触关系发生变化,产生时变的冲击激励,从而影响轴承振动响应的输出。
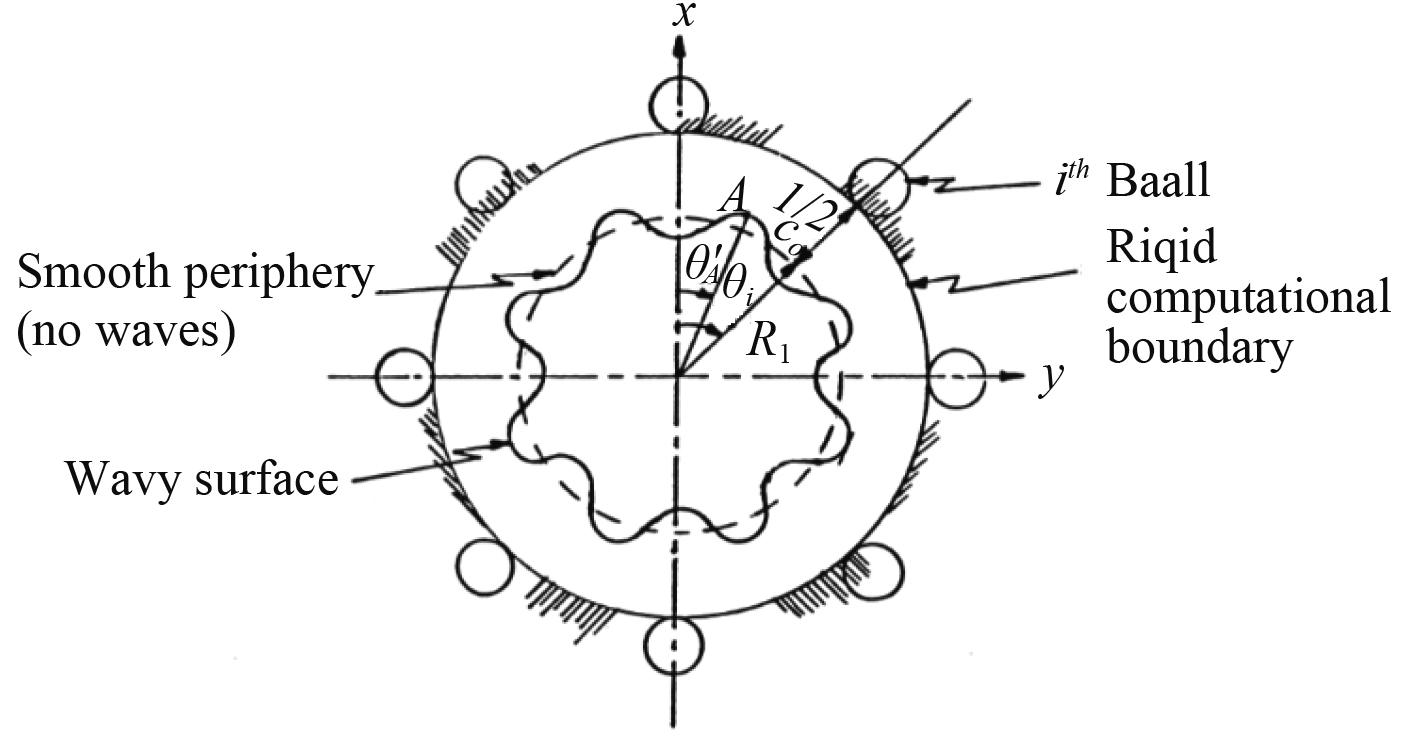
1.1 滚道正常处轴承接触刚度及位移本文基于滚道表面粗糙有裂纹的事实,建立滚道正常处的时变刚度及位移激励模型,当滚动体通过滚道的正常部位时,考虑滚道表面存在波纹如图1所示[2]。
|
图 1 滚动体与波纹滚道及平滑滚道接触示意图 Fig. 1 Schematic diagram of rolling element contact with corrugated raceway and smooth raceway |
裂纹的时变刚度及时变位移计算方式如下:
平滑表面时,滚动体有效刚度K是球与内圈和外圈接触的组合刚度[3 − 4]:
| $K = \frac{1}{{\frac{1}{{K_i^{3/2}}} + \frac{1}{{K_o^{3/2}}}}}\text{。}$ | (1) |
式中:Ki为内圈刚度,Ko为外圈刚度,其计算表达式为[4]:
| $K' = {\left( {\frac{{{{\text{π}} ^2}{k^2}{E^{*2}}\varSigma }}{{4.5{\varGamma ^3}\varSigma \rho }}} \right)^{0.5}}\text{。}$ | (2) |
其中:k,Γ,Σ分别为椭圆参数;E*为等效的弹性模量。根据赫兹理论,只要滚动体与滚道之间存在弹性接触变形,可把接触变形看成椭圆形(见图2),其表达式分别为[5]:

|
图 2 滚动体与滚道之间接触变形示意图 Fig. 2 Schematic diagram of contact deformation between rolling element and raceway |
| $k = 1.033\;9ln{\left( {\frac{{\varSigma {\rho _1}}}{{\varSigma {\rho _2}}}} \right)^{0.636}}\text{,}$ | (3) |
| $\varGamma = 1.527\;7 + 0.602\;3ln\left( {\frac{{\varSigma {\rho _1}}}{{\varSigma {\rho _2}}}} \right)\text{,}$ | (4) |
| $\varSigma = 1.000\;3 + 0.596\;8\left( {\frac{{\varSigma {\rho _1}}}{{\varSigma {\rho _2}}}} \right)\text{,}$ | (5) |
| $\frac{2}{{E*}} = \frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}\text{。}$ | (6) |
式中:为球与滚道之间的弹性模量,为球与滚道之间的泊松比,为球与滚道接触曲率,其表达式为[6]:
| ${\rho _{ws}} = \frac{{\left| {{\Pi_{ws}}{{\left( {\frac{{2{\text{π}}}}{{{\lambda _{ws}}}}} \right)}^2}{\rm {sin}}\left( {\frac{{2{\text{π}} {L_{ws}}}}{{{\lambda _{ws}}}}} \right)} \right|}}{{{{\left( {1 + \varPi _{ws}^2{{\left( {\frac{{2{\text{π}} }}{{{\lambda _{ws}}}}} \right)}^2}{\rm {cos}}^2\left( {\frac{{2{\text{π}} {L_{ws}}}}{{{\lambda _{ws}}}}} \right)} \right)}^{1.5}}}}\text{。}$ | (7) |
式中:λws,Lws分别为第S个波纹度的平均波长,Πws为第S个波纹的度的最大幅值。考虑实际滚动轴承存在一定径向间隙γ,滚道内圈及外圈存在纹波度为Πi,Πo的波纹,当第j个滚动体通过任意角位置θj时的变形量计算如下[6]:
| ${\delta _{jh}} = x \cos{\theta _j} + y \sin{\theta _j} - \gamma + {\varPi _j} + {\varPi _o}\text{。}$ | (8) |
式中:Πi,Πo分别为滚道内圈及外圈的纹波度。
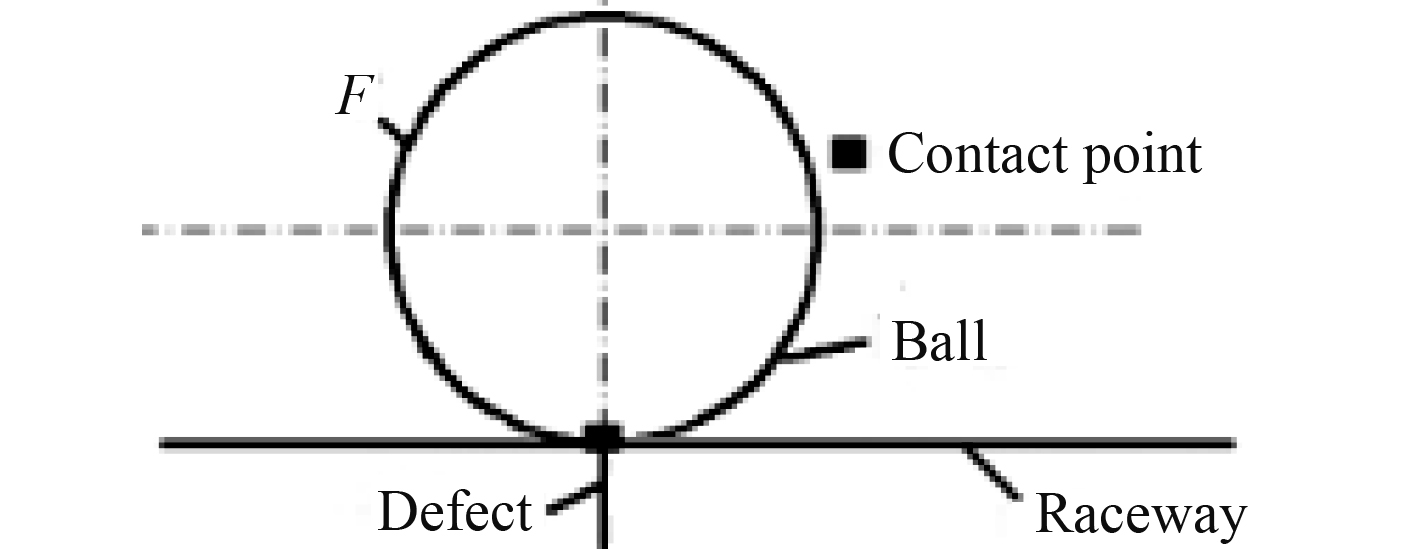
1.2 滚道故障处轴承接触刚度及位移根据实际的裂纹故障的轮廓特征,本文给出故障实际缺陷接触关系的表征模型[7],当滚动体与滚道接触关系发生了变化,实质是接触点的变化,滚动体通过裂纹缺陷时有一个接触点,简化模型如图3和图4所示。
|
图 3 滚动体与裂纹滚道接触示意图 Fig. 3 Schematic diagram of the contact between the rolling element and the crack raceway |
|
图 4 滚动体与裂纹滚道接触点示意图 Fig. 4 Schematic diagram of the contact point between the rolling element and the crack raceway |
当通过裂纹时刻,滚动体与正常滚道的时变接触刚度及形变量不再适用,原因在于球与滚道之间的接触形式变为球与缺陷点之间的接触形式,接触面小并忽略裂纹边缘扩展影响,通过故障部位时的形变量及变刚度计算方式如下:
考虑滚动轴承存在径向间隙γ,第j个球的总接触变形δj,表达式为:
| ${\delta _{jp}} = x \cos{\theta _j} + y \sin{\theta _j} - \gamma - H\text{,}$ | (9) |
为裂纹的深度。其分段函数表示为[8]:
| $H = \left\{ {\begin{array}{*{20}{c}} {{H_1}}\text{,}&{\left| {mod\left( {{\theta _{dj}},2{\text{π}} } \right) - {\theta _o} - {\theta _e}} \right| \leqslant {\theta _e}}\text{。}\\ 0 \text{,} &{{\rm {otherwise}}} \end{array}} \right.$ | (10) |
由于缺陷是尺寸非常小的裂纹或点,滚动体通过缺陷时接触刚度考虑为恒定值Kp,H总形变量与刚度之间关系如下:
| ${\delta _{jp}} = {\left( {\frac{{{{{F}}_r}}}{{{{{K}}_p}}}} \right)^{\frac{1}{{{n_p}}}}}$ | (11) |
式中:np为载荷-形变指数,用有限元方法求解[9],再根据式(11)数据拟合的方法求解[10]通过故障时的接触刚度Kp。
1.3 轴承内部激励球与滚道之间的时变接触刚度
| ${{{K}}_{{e}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {{{{K}}_{{b}}}} \text{,} &{\left| {mod\left( {{\theta _{dj}},2{\text{π}}} \right) - {\theta _o} - {\theta _e}} \right| \leqslant {\theta _e}}\text{,}\\ K \text{,} &{\rm{otherwise}} \text{,} \end{array}} \right.$ | (12) |
球与滚道之间的时变形变量
| $\delta = \left\{ {\begin{array}{*{20}{l}} {{\delta _j},}&{\rm{otherwise}}\text{,}\\ {\delta _j^e,}&{\left| {mod\left( {{\theta _{dj}},2{\text{π}} } \right) - {\theta _0} - {\theta _e}} \right| \leqslant {\theta _e}}\text{。} \end{array}} \right.$ | (13) |
滚动轴承裂纹故障的冲击激励表达式为:
| $F\left( t \right) = {K_e}\left( t \right){\delta ^{n\left( t \right)}}\text{,}$ | (14) |
| ${F_x} = \mathop \sum \limits_{j = 1}^z {k_e}{\varsigma _j}{\delta ^n}\cos{\theta _j}\text{,}$ | (15) |
| ${F_y} = \mathop \sum \limits_{j = 1}^z {k_e}{\varsigma _j}{\delta ^n}\sin{\theta _j}\text{。}$ | (16) |
其中,ςj为第j个球的载荷区系数,表达式为:
| ${\varsigma _j} = \left\{ {\begin{array}{*{20}{c}} 1\text{,}&{{\delta ^n} > 0}\text{;}\\ 0\text{,}&{{\delta ^n} \leqslant 0}\text{。} \end{array}} \right.$ | (17) |
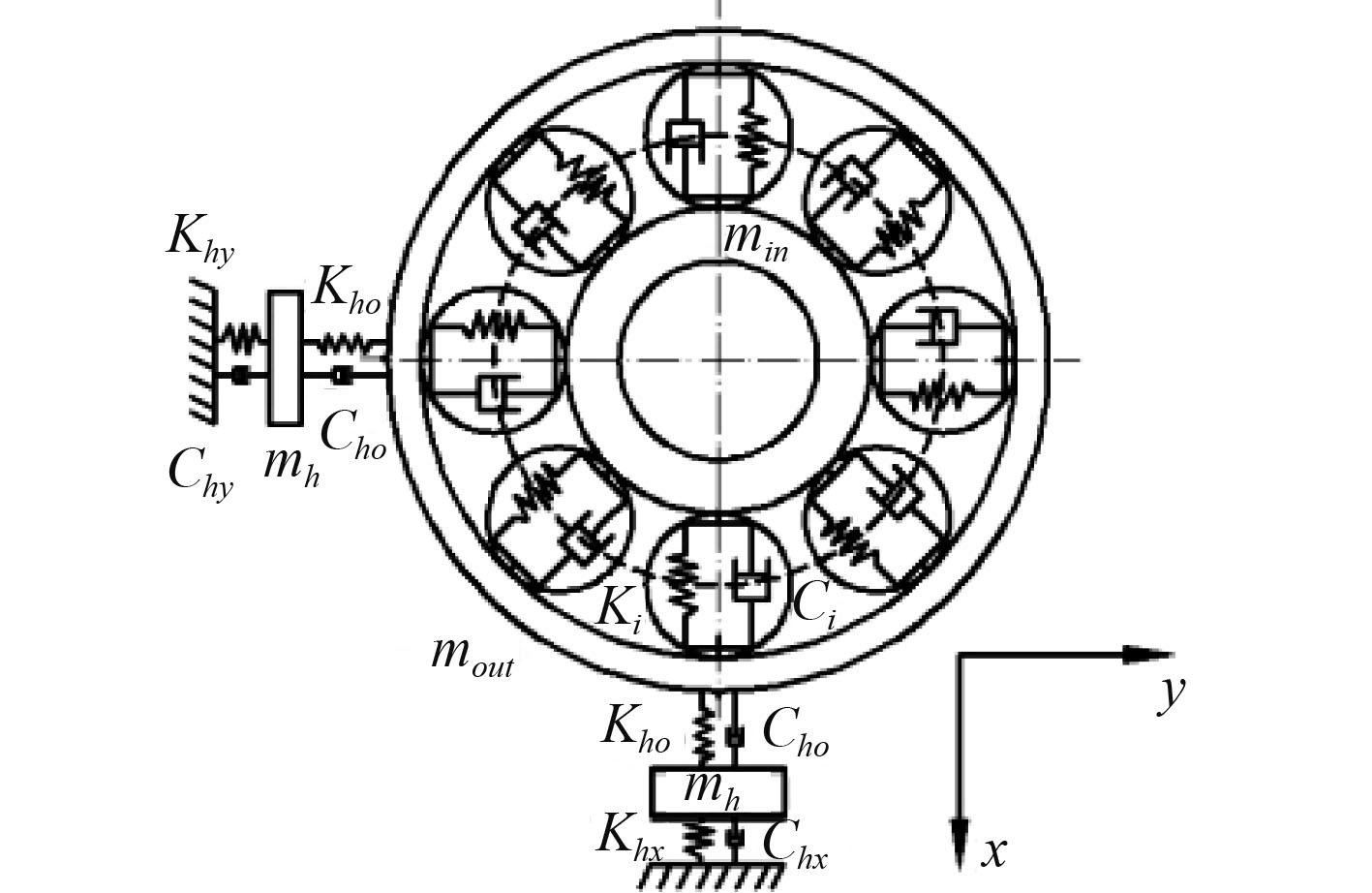
轴承-轴承座系统的振动模型看作六自由度的振动模型(见图5和图6),根据牛顿第二定理,列出系统的运动微分方程,并运用龙库塔法对下式求解[11 − 14]。
|
图 5 轴内圈-轴承外圈-轴承座振动传递 Fig. 5 Shaft inner ring - bearing outer ring - bearing housing vibration transmission |
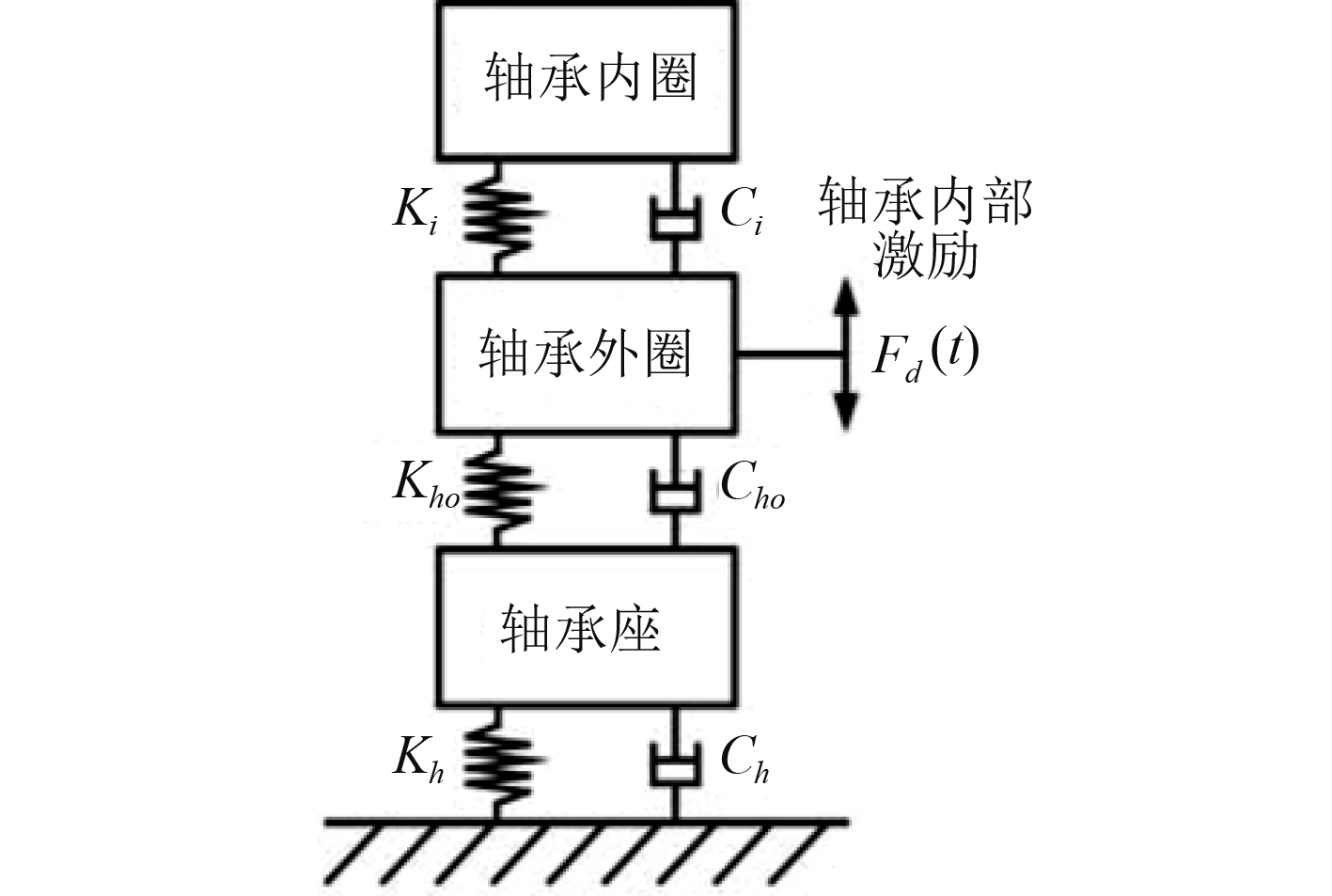
|
图 6 X轴方向上动力学模型 Fig. 6 Dynamics model in the X-axis direction |
轴承内圈运动学方程:
| $\left\{ {\begin{aligned} & {{m_{in}}{{\ddot X}_{in}} + {C_b}\left( {{{\dot X}_{in}} - {{\dot X}_{out}}} \right) + \mathop \sum \limits_{j = 1}^z {k_e}{\varsigma _j}{\delta ^n}\cos{\theta _j} = {F_{rx}}}\text{,}\\ & {{m_{in}}{{\ddot Y}_{in}} + {C_b}\left( {{{\dot Y}_{in}} - {{\dot Y}_{out}}} \right) + \mathop \sum \limits_{j = 1}^z {k_e}{\varsigma _j}{\delta ^n}\sin{\theta _j} = {F_{ry}}}\text{。} \end{aligned}} \right.$ | (18) |
轴承外圈运动学方程:
| $\left\{\begin{split} & {m}_{out}\ddot{{X}_{out}}+{K}_{ho}\left({X}_{out}-{X}_{h}\right)+{C}_{ho}\left({\dot{X}}_{out}-{\dot{X}}_{h}\right) -\\ & {C}_{b}\left({\dot{X}}_{in}-{\dot{X}}_{out}\right)-{\sum _{j=1}^{z}{k}_{e}{\varsigma }_{j}{\delta }^{n}\mathop {\cos }\limits_{j}\theta }=0\text{,}\\ & {m}_{out}\ddot{{Y}_{out}}+{K}_{ho}\left({Y}_{out}-{Y}_{h}\right)+{C}_{ho}\left({\dot{Y}}_{out}-{\dot{Y}}_{h}\right)-\\ & {C}_{b}\left({\dot{Y}}_{in}-{\dot{Y}}_{out}\right)-{\sum _{j=1}^{z}{k}_{e}{\varsigma }_{j}{\delta }^{n}\mathop {\sin }\limits_{j} \theta }=0\text{。}\end{split}\right.$ | (19) |
轴承座运动学方程:
| $ \left\{\begin{split} & {m}_{h}\ddot{{X}_{h}}+{K}_{hx}{X}_{h}+{C}_{h}{\dot{X}}_{h}-{C}_{ho}\left({\dot{X}}_{out}-{\dot{X}}_{h}\right)-\\ & {K}_{ho}\left({X}_{out}-{X}_{h}\right)=0\text{,}\\ & {m}_{h}\ddot{{Y}_{h}}+{K}_{hy}{Y}_{h}+{C}_{h}{\dot{Y}}_{h}-{C}_{ho}\left({\dot{Y}}_{out}-{\dot{Y}}_{h}\right)-\\ & {K}_{ho}\left({Y}_{out}-{Y}_{h}\right)=0\text{。} \end{split}\right. $ | (20) |
其中:min为内圈和轴的总质量,mout为外圈质量,mh为轴承座质量,Cb为轴承内部阻尼系数,Ke为滚动体与内、外圈的总接触刚度,Frx为在内圈X方向的径向力,Fry为Y方向上的径向力,δ为滚动体与滚道接触的总形变量,Ch为轴承座的阻尼系数,Khx为轴承座在X方向的刚度,Khy为轴承座在Y方向的刚度,Xout和Yout分别为外圈分别在X和Y方向的振动位移,Xin和Yin分别内圈在X和Y方向的振动位移,Xh和Yh分别为轴承座分别在X和Y方向的振动位移。
2 数值仿真分析以轴承内圈为例对裂纹故障进行仿真,仿真参数如表1所示,数值仿真结果如图7所示。
|
|
表 1 轴承外圈故障仿真 |
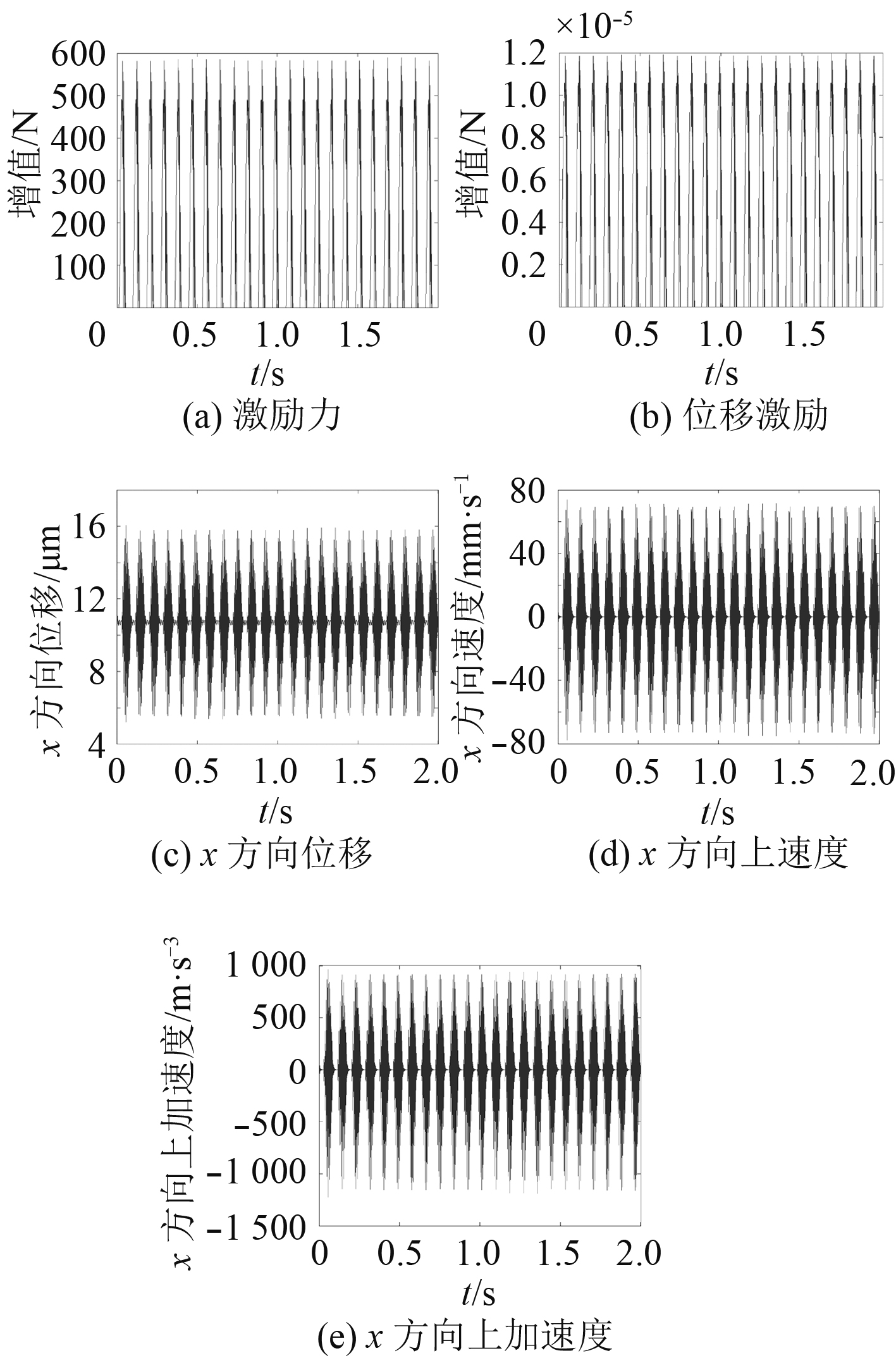
|
图 7 滚动轴承内圈故障振动信号图 Fig. 7 Faulty vibration signal diagram of the inner ring of the rolling bearing |
由图7可知,故障的激励力为在时域均匀分布的冲击信号,具有明显的周期性,根据统计激励力最大值为487.01 N,激励力平均值为135.36 N。故障的位移激励为在时域均匀分布的冲击信号,具有明显的周期性,根据统计位移激励最大值为1.12E−5 m,位移激励平均值为3.351E−6 m。故障的速度响应为冲击信号,且在时域均匀分布,具有明显的周期性。在x方向位移峰值为16.03 μm,平均位移为10.696 μm;速度峰值为73.71 mm/s,速度平均值为0 mm/s;加速度峰值为963.05 m/s2平均加速度值为−0.092 m/s2。可见,当轴承内圈存在裂纹故障时,滚动体通过裂纹部位时会产生冲击作用振动幅值增加,当冲击过后振动信号衰减,由于滚动体断续通过故障部位,自由衰减也被断续地被激起。
3 试验验证采用轴承模拟试验台对仿真模型的正确性与有效性进行验证。试验台由主轴系统、加载系统以及故障模拟系统组成,主轴系统由主轴驱动系统和变频器组成,为主轴回转提供动力、调节轴转速范围。加载系统可对故障模拟系统实现径向和轴向加载,通过施加一定的载荷来模拟实际负载情况。故障模拟系统通过电火花加工方式在轴承内圈割出局部凹坑后安装在主轴上实现轴承故障模拟,选用轴承模拟试验台如图8所示。验证所用轴承参数与表1仿真轴承参数相同。

|
图 8 轴承故障模拟试验台 Fig. 8 Bearing failure simulation test bench |
根据信号分析提取方法,对仿真信号及实测信号进行信号处理,得到仿真信号与实测信号对比,如图9所示。由图可知,信号存在明显调制现象,经信号解调后,仿真信号故障频率为151.06 Hz,实测信号故障频率为147.5 Hz,误差为2.4%,信号包络谱波形存在明显的周期现象,且周期与故障特征频率一致号。

|
图 9 仿真信号与实测信号对比 Fig. 9 Comparison of simulated signal and measured signal |
基于滚动体与裂纹缺陷之间接触关系的研究,结合滚道表面粗糙度、波纹度对滚动体通过滚道表面的振动影响,给出滚动体通过缺陷时接触位移、刚度以及冲击激励计算方法,并建立了轴系-轴承-轴承座六自由度的振动传递模型。通过数值仿真及试验验证,证明了本文模型的正确性,为轴承裂纹故障诊断的机理研究提供了理论依据。
| [1] |
RUBINI R. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearing[J]. Mechanical System and Signal Processing, 2001, 15(2): 287-302. DOI:10.1006/mssp.2000.1330 |
| [2] |
LYNAGH N, RAHNEJAT H, EBRAHIMI M, et al. Bearing induced vibration in precision high speed routing spindles[J]. International Journal of Machine Tools & Manufacture, 2000, 40: 561-577. |
| [3] |
HARRIS T. A, KOTZALAS M. N. Rolling bearing analysis-essential concepts of bearing technology, 5th[M]. Taylor and Francis, 2007.
|
| [4] |
LIU J, SHAO Y. M, LIM T. C. Vibration analysis of ball bearings with a localized defect applying piecewise response function[J]. Mechanism and Machine Theory, 2012, 56: 156-169. DOI:10.1016/j.mechmachtheory.2012.05.008 |
| [5] |
BREWE D, HAMROCK B. Simplified solution for elliptical-contact deformation between two elastic solids[J]. ASME Journal of Lubrication Technology, 1977, 101(2): 231-239. |
| [6] |
LIU J, SHAO Y. M, ZHOU J. J, et al. Vibration analysis of a cylindrical roller bearing considering multiple localized surface defects on races[J]. International Journal of COMADEM, 2014, 17(1): 25-32. |
| [7] |
PATEL V N, TANDON N, PANDEY R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races[J]. ASME Journal of Tribology, 2011, 133(1): 011102. DOI:10.1115/1.4003088 |
| [8] |
CAO M, XIAO J. A comprehensive dynamic model of double-row spherical roller bearing-modeling development and case studies on surface defects, preloads, and radial clearance[J]. Mechanical Systems and Signal Processing, 2007, 22(2): 467-489. |
| [9] |
LIU J, SHAO Y. M, ZUO M. J. The effects of the shape of localized defect in ball bearings on the vibration waveform[J]. Proc IMechE, Part K: Journal of Multi-body Dynamics, 2013, 227(1): 261-274. |
| [10] |
徐秉业. 应用弹塑性力学[M]. 北京: 清华大学出版社, 2005.
|
| [11] |
ZHONG Z. H. Finite element procedures for contact-impact problems [M]. Oxford University Press Inc. New York, 1993.
|
| [12] |
ARSLAN H, AKTURK N. An investigation of rolling element vibrations caused by local defects[J]. ASME Journal of Tribology, 2008, 130(4): 041101. DOI:10.1115/1.2958070 |
| [13] |
邵毅敏, 陈再刚, 周晓君, 等. 冲击振动能量通过" 齿轮-轴-轴承-轴承座”多界面传递损耗研究[J]. 振动与冲击, 2009, 28(6): 60-65. DOI:10.3969/j.issn.1000-3835.2009.06.013 |
| [14] |
关贞珍, 郑海起, 王彦刚, 等. 滚动轴承局部损伤故障动力学建模及仿真[J]. 振动、测试与诊断, 2012, 32(6): 985-955. |
 2019, Vol. 41
2019, Vol. 41
