海上人命安全公约(以下简称SOLAS)规定了“主操舵装置和舵杆能在船舶最大航海吃水和以最大营运前进航速时将舵自一舷35°转至另一舷35°,并在相同条件下在不超过28s内将舵自一舷35°转至另一舷30°。”对于绝大部分船舶而言,航行试验只能在压载状态下进行,无法满足最大航海吃水的操舵试验条件,这意味着SOLAS对舵机能力的要求无法通过航行试验直接验证。为此,国际船级社联合会(IACS)于2015年9月将解释SOLAS本条要求的UI SC246文件修正为Rev.1版本,提出了根据非满载试航的操舵试验结果对满载航行舵机能力进行验证的计算方法。该方法于2016年6月在第96届IMO海上安全委员会(IMO MSC)上获得通过,以通函的形式(MSC.1/Circ. 1536)发布,成为SOLAS公约的组成部分。
按照UI SC246 Rev.1(以下简称SC246)的要求,若试航时舵叶的浸没面积无法达到舵叶面积的95%及以上时,应根据试航舵机试验结果,采用式(1)、式(2)的方法换算最大航海吃水时的舵杆扭矩值以验证是否能满足SOLAS要求。
| $ {{{Q}}_{{F}}} = {{{Q}}_{{T}}}\alpha {\text{,}} $ | (1) |
| $ \alpha = 1.25 \cdot \left( {\frac{{{{{A}}_{{F}}}}}{{{{{A}}_{{T}}}}}} \right) \cdot {\left( {\frac{{{{{V}}_{{F}}}}}{{{{{V}}_{{T}}}}}} \right)^2} {\text{。}} $ | (2) |
式中:QF为最大航海吃水,最大主机转速情况下的舵杆扭矩,kN·m;QT为试航状态实测的舵杆扭矩,kN·m;α为换算系数;AF为最大航海吃水情况下浸没的舵叶可动部分面积,m2;AT为试航状态浸没的舵叶可动部分面积,m2;VF为最大航海吃水、最大主机转速情况下的合同航速,kn;VT为试航状态实测航速,kn。
SC246明确了采用定量泵的舵机在非最大航海吃水下的操舵试验结果换算到最大航海吃水下的方法,指出系统压力与转舵所需扭矩之间是线性关系,如下式:
| $ {{{P}}_{{F}}}{\rm{/}}{{{P}}_{{T}}}{\rm{ = }}{{{Q}}_{{F}}}{\rm{/}}{{{Q}}_{{T}}} {\text{。}} $ | (3) |
式中:PF为推算得到的最大航海吃水下的舵机系统压力,MPa;PT为非最大航海吃水下实测的舵机系统压力,MPa。
由式(1)和式(3)可得下式:
| $ {{{P}}_{{F}}}{{ = 1}}{\rm{.25 \times }}\left( {{{{A}}_{{F}}}{\rm{/}}{{{A}}_{{T}}}} \right){{ \times }}{\left( {{{{V}}_{{F}}}{\rm{/}}{{{V}}_{{T}}}} \right)^{\rm{2}}}{\rm{ \times }}{{{P}}_{{T}}} {\text{。}} $ | (4) |
SC246提供的舵机能力验证方法包含了一系列假设的简化方法,各个环节均留有一定余量,具有明显的保守倾向,客观上提高了对舵机能力的要求。大量实船试验数据表明,根据该方法,相当一部分船舶,尤其是采用半悬挂舵设计的船舶,难以通过验证[1]。以某型批量建造的散货船为例,该船舵机扭矩在规范计算值的基础上留有50%的余量,根据实船试航过程中实测系统压力换算的最大航海吃水下系统压力偏大,无法通过验证。
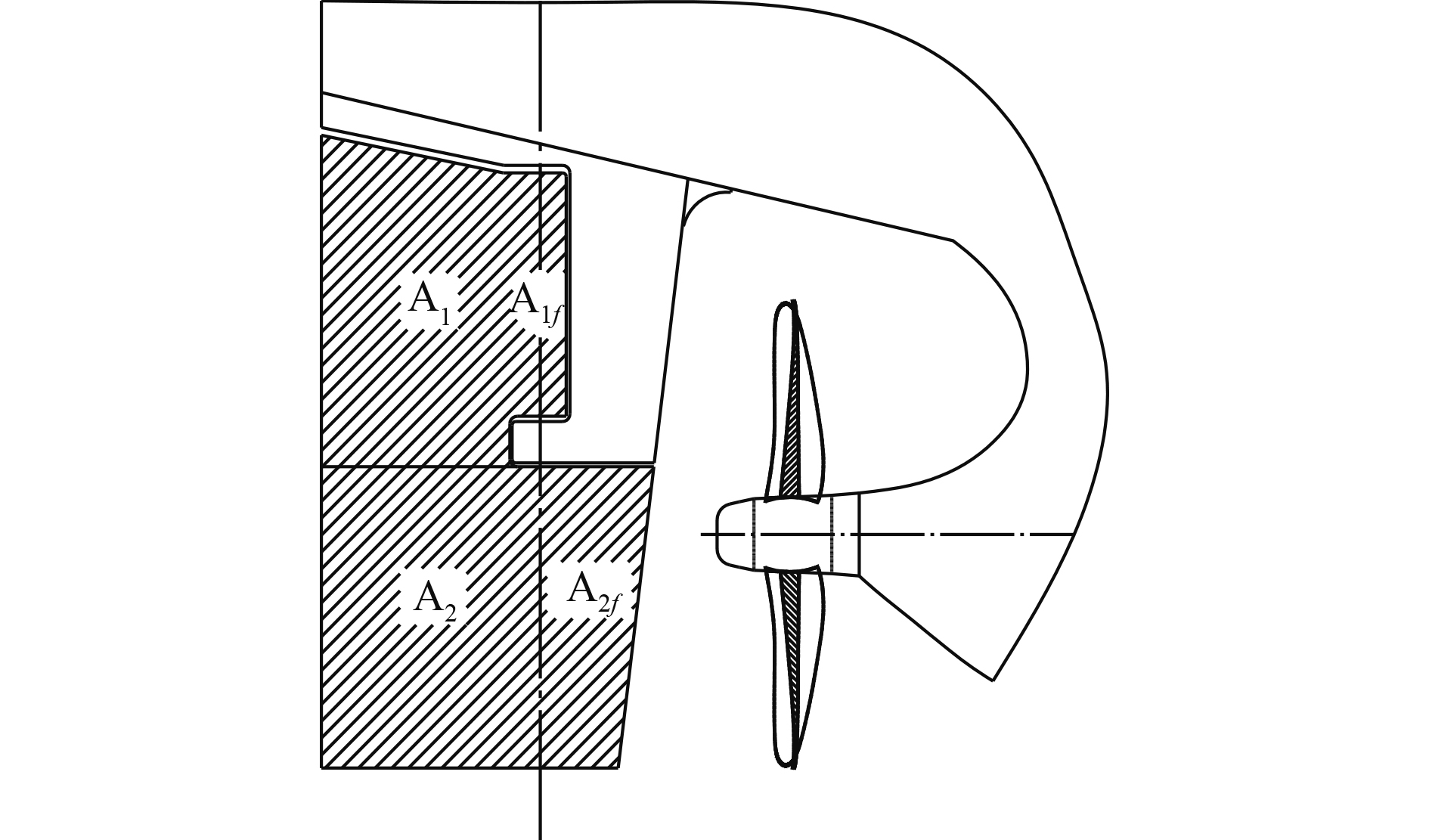
该船的舵叶采用HSVA0017翼型,平衡比为0.21,展弦比为1.898,舵叶面积为30.0 m2。舵叶外形如图1所示。
|
图 1 某系列散货船舵叶外形图 Fig. 1 The rudder blade outline of bulk ship |
按照规范方法进行舵系计算,得到该船舵杆扭矩的规范计算值约570 kN·m,实际选用的转叶式舵机最大工作扭矩为845 kN·m,舵机液压泵为定量泵,系统压力参数如下:最大工作压力170 Bar,设计压力(安全阀设定压力)213 Bar。
该船的试航结果如表1所示。
|
|
表 1 某散货船压载试航的操舵试验结果 Tab.1 Steering test results of ballast trial for a bulk carrier |
根据式(4),可对PF做如下推算:
PF=1.25×(30.0/23.0)×(15.5/14.1)2×140=276 Bar。
可以看出,推算出的最大航海吃水和以最大营运前进航速时将舵叶自一舷35°转至另一舷30°时舵机系统压力已经超过舵机允许的最大工作压力,甚至超过了安全阀设定的压力。
尽管这一问题可以通过设计前期大幅度提高舵机扭矩余量予以解决,但代价是船东、船厂将为此付出更多的成本。如何在现有的规范框架之下,通过对舵系的合理优化设计,降低舵杆水动力扭矩,是更具实际意义的解决思路。这也是目前舵系优化设计的方向之一。
随着计算流体力学(CFD)的发展,数值仿真模拟手段越来越多应用到舵设计之中,文献[2 – 5]表明CFD在舵性能预报方面有较高的可靠性。得益于硬件技术的不断发展,实尺度的舵系计算也能够在工程中得到广泛应用。本文利用CFD计算方法从理论上研究其主要几何参数对舵杆扭矩的影响,为舵系的优化设计提供理论依据。
2 半悬挂舵舵杆扭矩CFD分析 2.1 布置方案在给定舵面积的情况下,常规船型半悬挂舵可形成3种典型的布置方案。
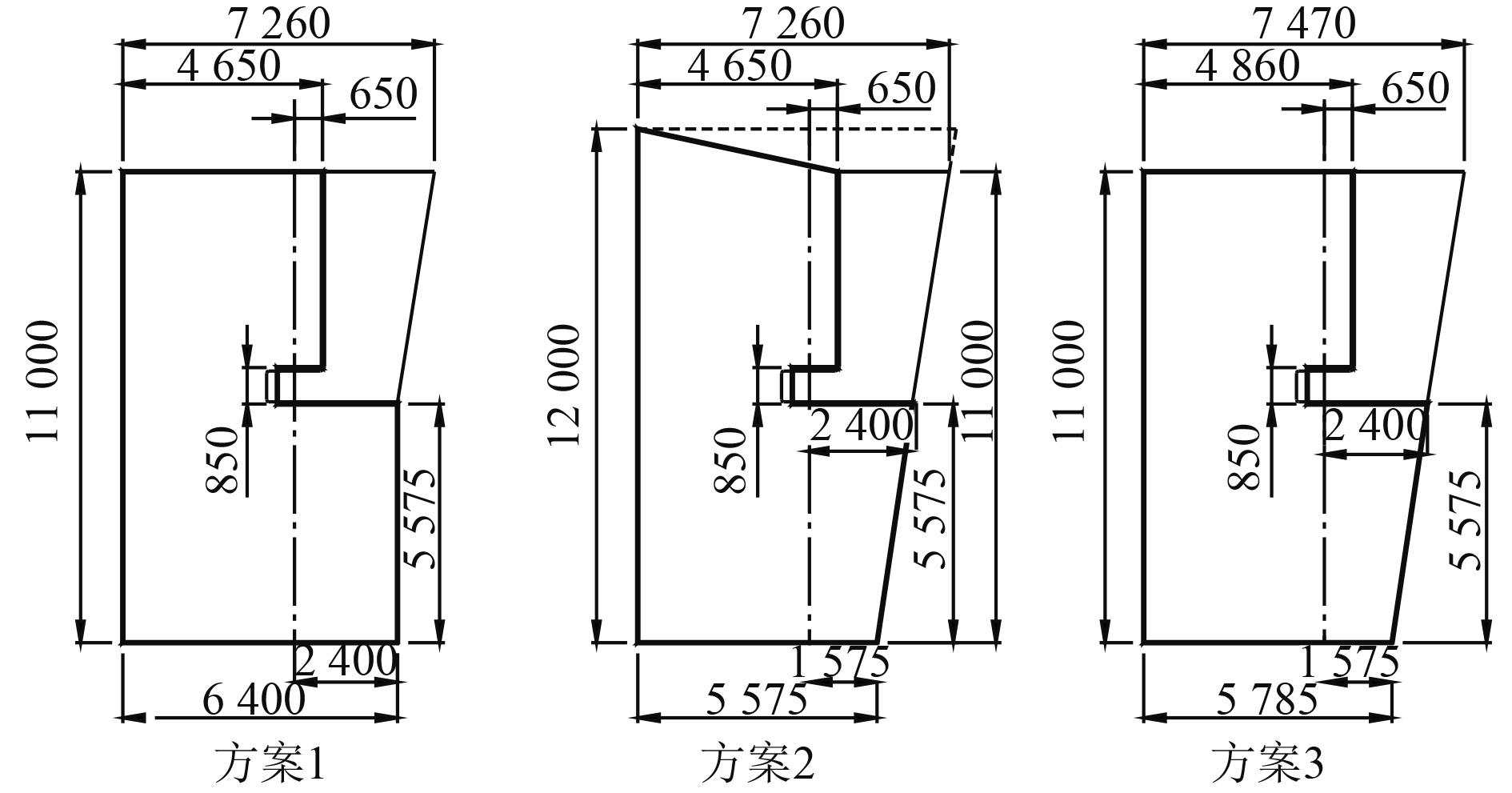
方案1(原型方案):舵叶下部导边无后掠角,舵叶顶部平直。
方案2:在方案1的基础上,舵叶下部导边具有后掠角,角度与挂舵臂后掠角一致;舵叶顶部向斜后方抬升,斜率通常与船体尾部中纵线型一致。
方案3:在方案1的基础上,舵叶下部导边具有后掠角,角度与挂舵臂后掠角一致;舵叶顶部保持平直;舵叶随边后移。
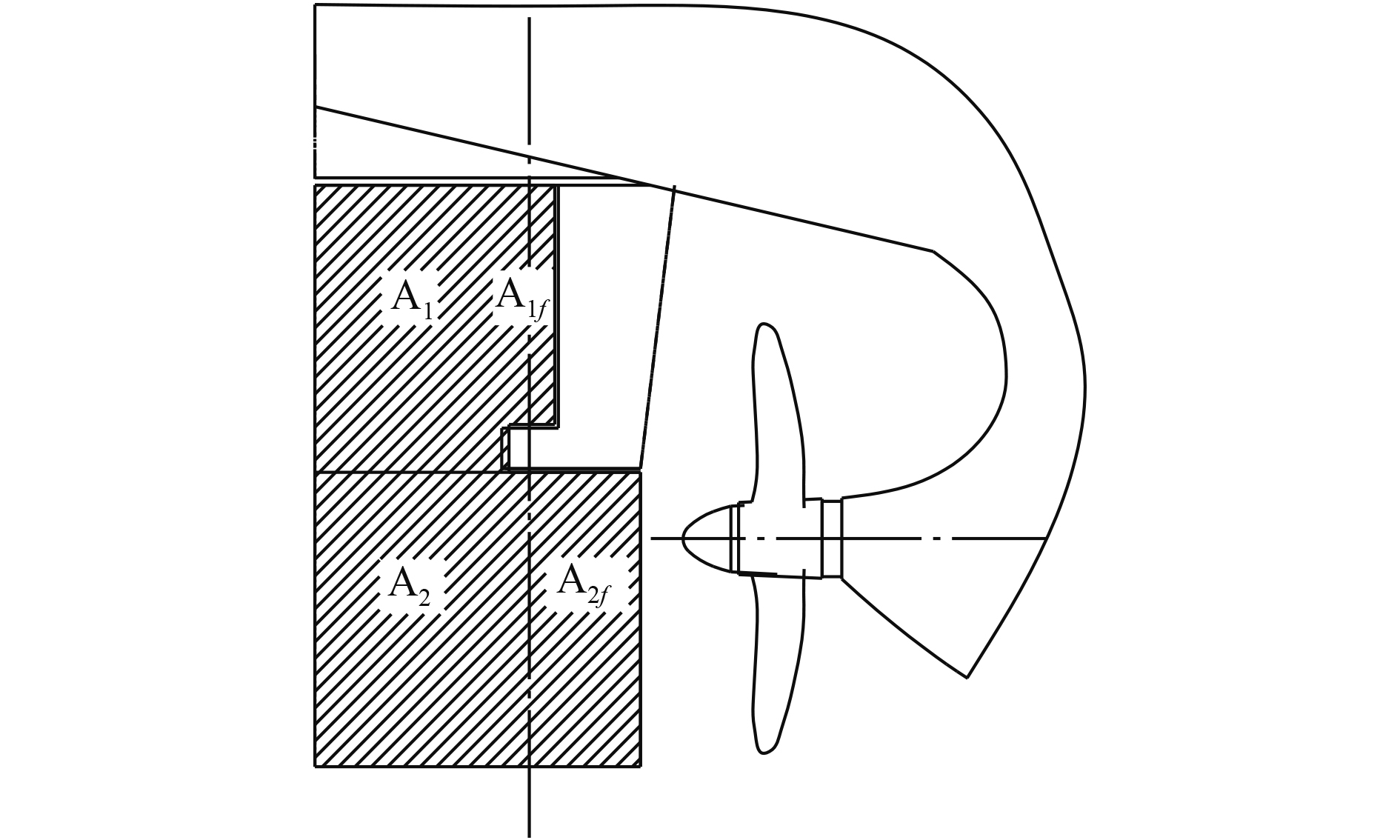
以可动部分面积为60 m2的舵叶为例,方案1~方案3的基本布置如图2所示。
|
图 2 三种典型的半悬挂舵布置方案 Fig. 2 Three typical semi-balanced rudder arrangement |
各方案均采用HSVA0020翼型,舵面积均为60 m2,主要几何参数如表2所示。
|
|
表 2 三种典型的半悬挂舵布置方案几何参数 Tab.2 The geometric parameters of three typical semi-balanced rudder |
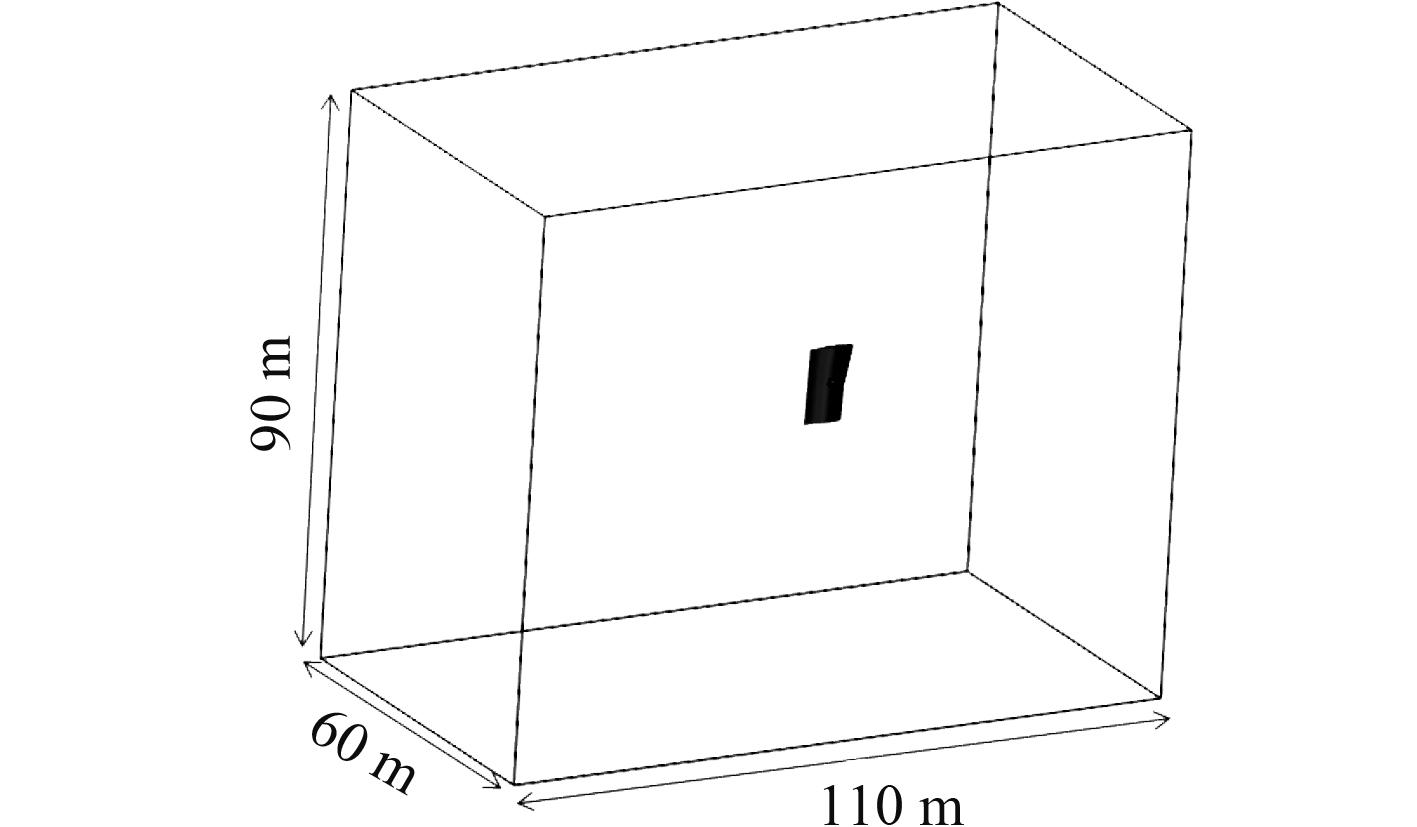
利用Star CCM+软件计算各方案在不同舵角下舵杆所受水动力扭矩的大小,每个方案计算从5°~35°范围内的7个舵角,水流速度15 kn,计算域及模型如图3所示。网格划分如图4所示。
|
图 3 全浸没状态计算域及模型 Fig. 3 Calculation domain and model for full immersion |

|
图 4 全浸没状态计算域网格划分 Fig. 4 Computational domain meshing for full immersion |
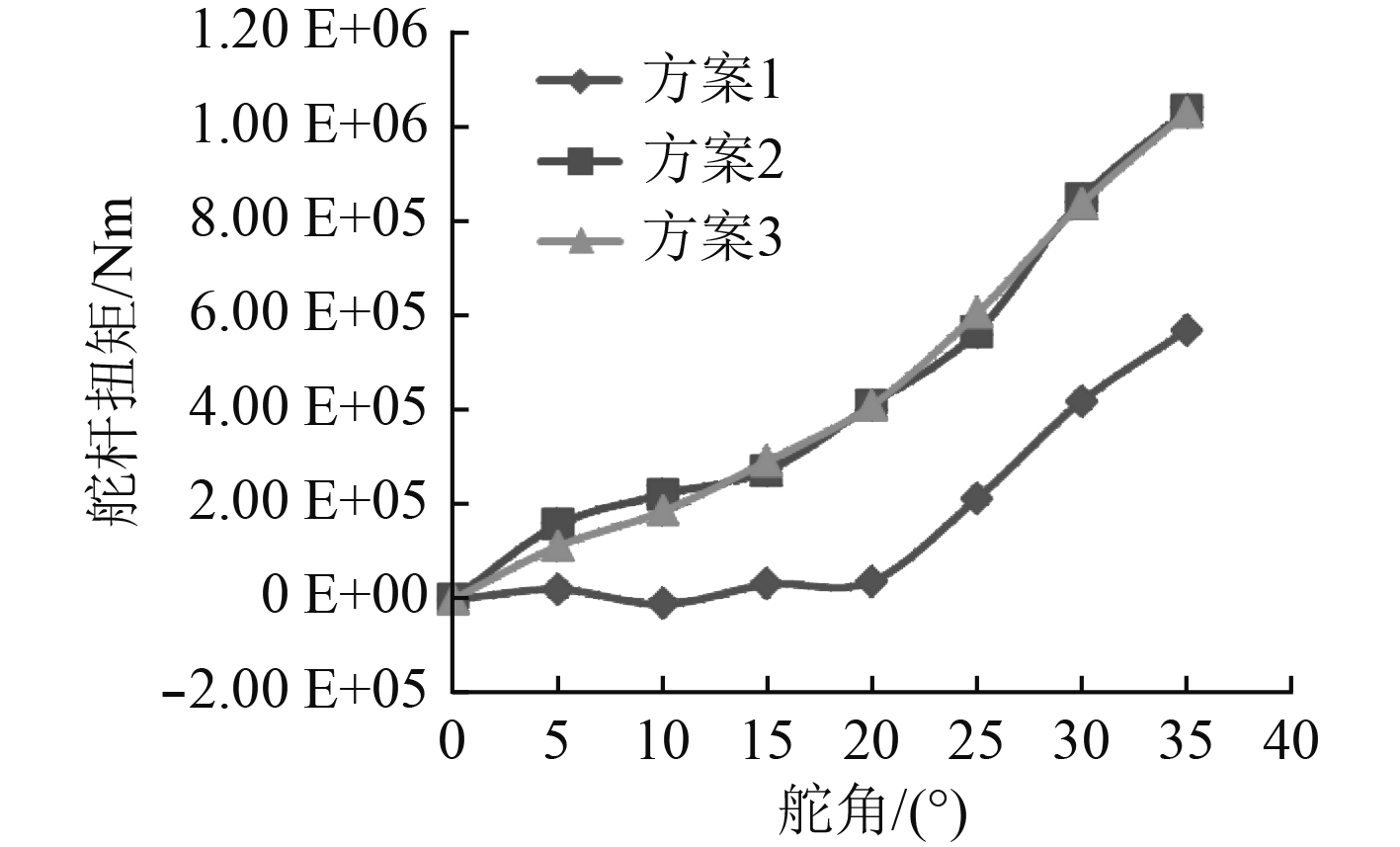
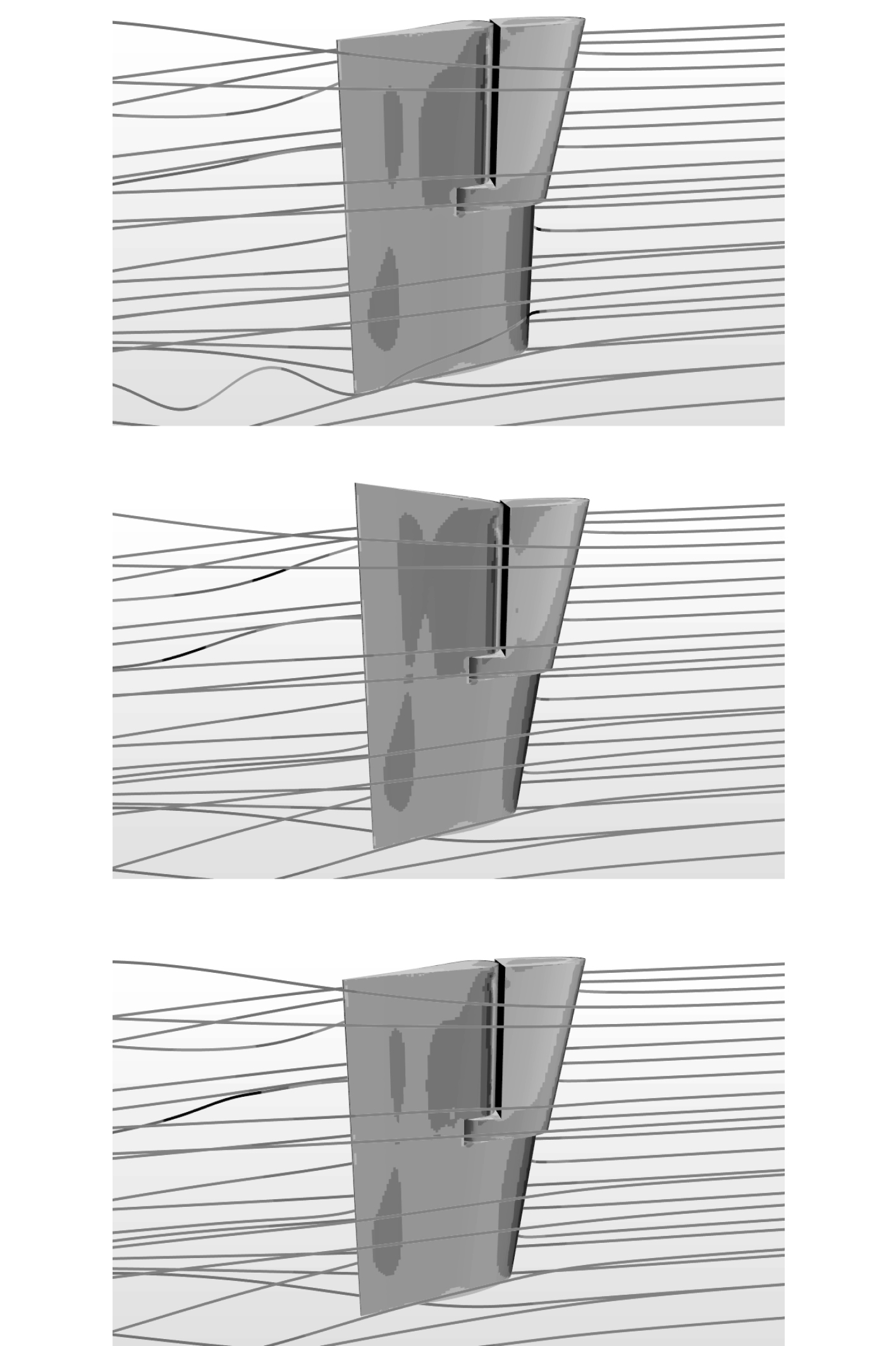
3种方案的舵杆扭矩计算结果如图5所示。舵杆扭矩负值表示舵叶作用于舵杆的水动力扭矩与操舵方向一致,正值表示二者方向相反。即当舵杆扭矩为负值时,舵叶压力中心位于舵杆之前,舵叶作用于舵杆的水动力扭矩与操舵方向一致,这种情况下,理论上舵机无需提供使舵叶转动的反向扭矩;当舵杆扭矩为正值时,舵叶压力中心位于舵杆之后,舵叶作用于舵杆的水动力扭矩与操舵方向相反,此时舵杆扭矩的值越小,意味着舵机需提供的反向扭矩越小。图6为20°舵角时3种方案的压力分布及流场流线示意图。
|
图 5 全浸没状态不同舵角下的舵杆扭矩计算值 Fig. 5 Torque on different attack angle for full immersion |
|
图 6 方案1~方案3(20°舵角)压力云图及流场流线示意图 Fig. 6 Pressure contours and streamline for program 1, 2, 3(20°) |
计算结果表明,对于3种典型的半悬挂舵布置方案,除方案1的20°以内舵角范围,舵杆扭矩基本为正值,即大多数情况下,舵叶压力中心位于舵杆之后。方案1在舵角不大于20°的情况下,舵杆扭矩在0位小幅波动,说明舵叶压力中心与舵杆中心基本重合,即压力中心系数Cp接近于方案1的平衡比(β=0.272)。当方案1的舵角大于20°时,压力中心后移,舵杆扭矩上升,但尽管如此,由于方案1的平衡比(β=0.272)明显高于方案2(β=0.235)和方案3(β=0.234),因此其整个舵角范围内的舵杆扭矩仍显著低于方案2和方案3。4)方案2和方案3的平衡比基本相同,二者各舵角下的舵杆扭矩计算值也基本相同,从另一方面说明了平衡比对舵杆扭矩存在直接影响。
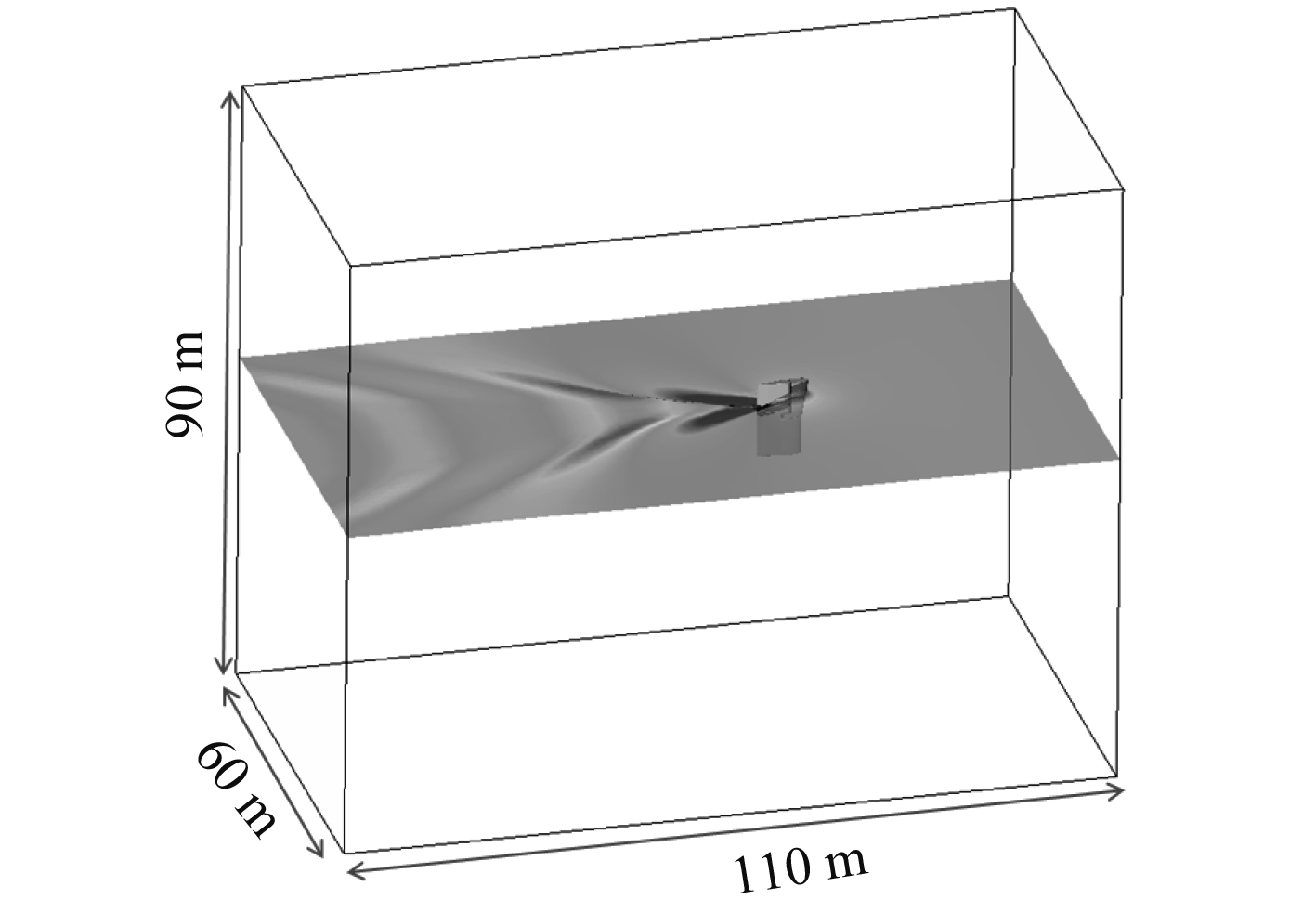
2.3 部分浸没状态CFD分析考虑大部分船舶在试航状态下都处于压载状态,达不到全浸没或95%以上,因此有必要对部分浸没状态下的舵系水动力进行分析。保持3种舵布置方案不变,参考与本尺寸舵叶相适配的10万吨级船舶的螺旋桨尺寸和压载工况,将舵浸没高度设定为距舵叶底端8 580 mm,3种方案浸没面积达77%~81%,3种方案浸没部分的舵叶平衡比分别为:β1=0.274,β2=0.238,β3=0.229。计算域及模型如图7所示。
|
图 7 部分浸没状态计算域及模型 Fig. 7 Calculation domain and model for partial immersion |
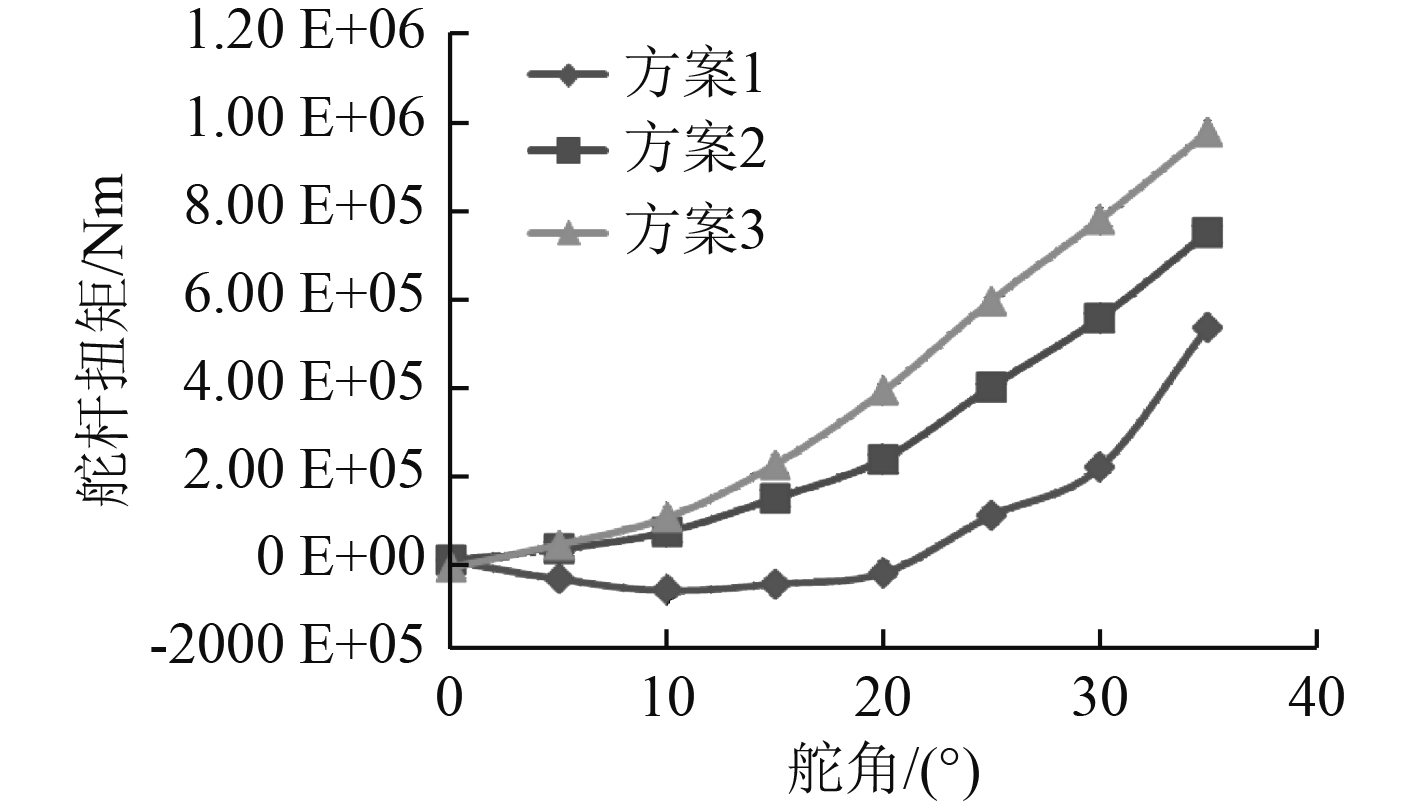
3种方案的舵杆扭矩计算结果如图8所示。方案1的舵杆扭矩最小,方案2次之,方案3最大,呈现出与全浸没状态计算结果相同的规律,即随着浸没部分舵叶平衡比的增大,舵杆扭矩减小。
|
图 8 部分浸没状态下不同舵角下的舵杆扭矩计算值 Fig. 8 Torque on different attack angle for partial immersion |
与全浸没状态计算结果有所不同的是,部分浸没状态方案2较比方案3的舵杆扭矩有所减小,而全浸没状态二者舵杆扭矩基本相同。这是由于全浸没状态下二者的平衡比基本相同,而在部分浸没状态下方案2中浸没舵叶的平衡比(β2=0.238)比方案3(β3=0.229)的要大,这也反映了平衡比对舵杆扭矩的直接影响。
上述计算结果直观地反映了舵叶平衡比在全浸没状态和部分浸没状态对半悬挂舵舵杆水动力扭矩的影响,即选取适当大的平衡比,使转舵中心尽可能接近压力中心的变化范围,可有效降低舵杆水动力扭矩。
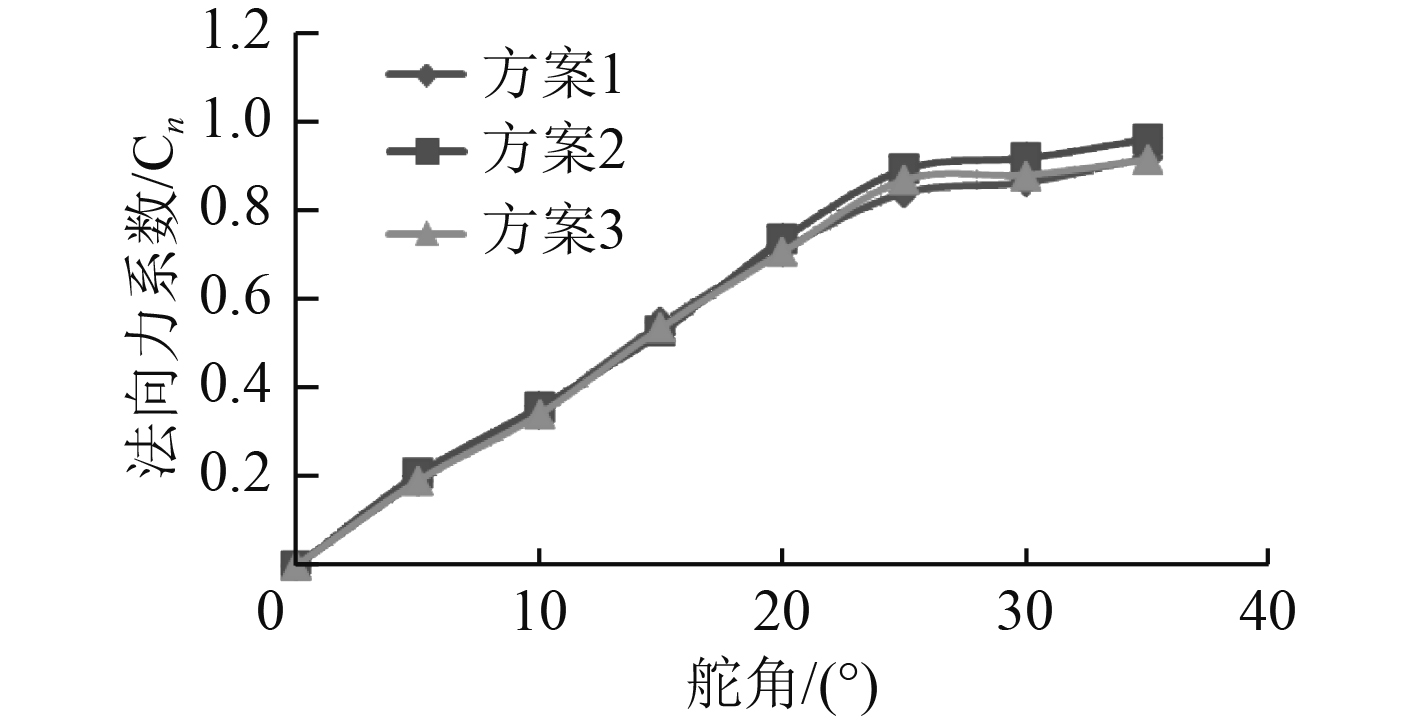
从舵效的角度而言,全浸没状态下方案2的展弦比最大,而方案1的展弦比最小,方案2将具有更大的法向力系数。图9反映了3个方案法向力系数Cn的比较。从中可见,当舵角大于20°时,方案2的Cn值具有一定的优势。
|
图 9 全浸没状态下3种方案的法向力系数Cn Fig. 9 Lift coefficient on different attack angle for full immersion |
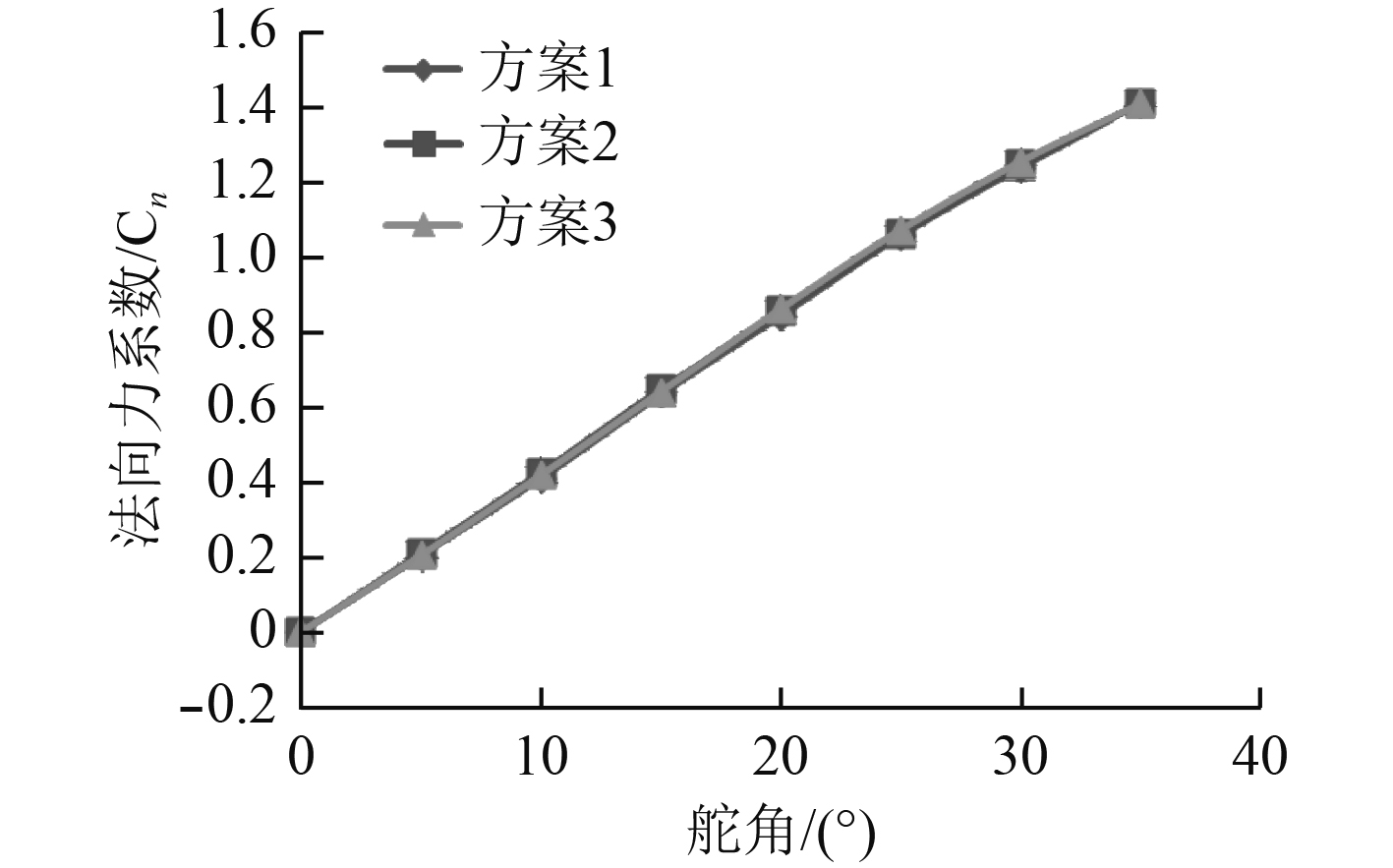
而部分浸没状态下3个方案的展弦比基本接近,图10反映了3个方案法向力系数Cn的比较,显而易见三者的法向力系数也几乎重合。因此实际设计中,应根据设计需求,综合考虑不同舵布置方案对舵杆扭矩和舵效的影响。
|
图 10 部分浸没状态下3种方案的法向力系数Cn Fig. 10 Lift coefficient on different attack angle for partial immersion |
上述对半悬挂舵舵杆扭矩的CFD分析表明,从减小舵杆水动力扭矩的角度,应尽可能避免方案2和方案3的小平衡比设计,而方案1所体现的大平衡比的设计可以有效减小舵杆水动力扭矩,使得舵机扭矩余量变大,这对舵机能力验证的换算是非常有利的。
将这一思路应用于前述散货船的后续船,其舵叶外形根据上述方案1的布置方案进行优化设计,优化后的舵叶外形如图11所示。平衡比由原来的0.21调整为0.239,舵面积保持不变。实际选用的转叶式舵机最大工作扭矩仍为845 kNm,舵机液压泵为定量泵,但由于生产厂商不同,液压系统配设有所区别,系统压力参数如下:
|
图 11 某散货船后续船的舵外形尺寸图 Fig. 11 The rudder blade outline of sister vessel |
最大工作压力240 Bar,设计压力(安全阀设定压力)300 Bar。
后续船试航操舵试验结果如表3所示。
|
|
表 3 某散货船后续船操舵试验结果 Tab.3 Steering test results of ballast trial for sister vessel |
根据式(4),可对PF做如下推算:
PF=1.25×(30.0/25.1)×(15.5/15.5)2×150=224 Bar。
可以看出,后续船在最大航海吃水和以最大营运前进航速条件下推算出的将舵叶自一舷35°转至另一舷30°时舵机系统压力并没有超过舵机设定的最大压力值,试航换算结果满足SC246的要求。
由于两船的船型尺度、舵叶面积、舵机扭矩均相同,唯一区别在于某散货船舵机的最大工作压力略低,但是即使将其舵机的工作压力提高为240 Bar,而换算结果PF=276 Bar,仍然不能满足UI SC246 Rev.1的换算结果。因此可以判断,舵叶平衡比的增大是后续船能够满足SC246舵机能力验证的原因。
此外,两船的舵机扭矩在舵杆扭矩规范计算值的基础上预留的余量都高达50%,即使考虑摩擦扭矩等因素,扭矩余量也是充裕的。但原船的舵机能力验证仍不能通过SC246的换算,可见其公式偏于简单化,并不能涵盖全部、多样化的舵系设计。挪威船级社(DNV)出具的评估报告[6]也注意到公式的保守性,这一问题还有待规范和相关研究作进一步深入探讨。
4 结 语本文利用CFD方法计算舵杆扭矩,更加直观地反映了不同舵设计方案舵杆水动力扭矩的高低,为舵系设计提供定性的参考。计算得到的数值结果、压力云图可以为舵系优化设计提供方向;实尺度的舵系数值计算也可以最大程度地消除因尺度效应给模型试验带来的影响,不会因为雷诺数的巨大差异对结果产生较大的偏差。
本文借助CFD方法研究典型船型不能通过SC246舵机能力验证的问题,为后续基于CFD方法研究舵系问题提供了方向。验证了舵叶平衡比对舵杆水动力扭矩存在直接影响,适当大的舵叶平衡比设计,可以显著降低舵杆的水动力扭矩,为设计者在进行舵系优化设计时提供了依据。
需要指出的是,本文对半悬挂舵进行CFD分析得到的舵杆扭矩并不能直接作为舵系构件强度计算的受力依据。在现有的规范框架内,规范强制规定了舵力的臂矩不得低于0.1c[7]。也就是说,用于舵系构件强度计算的舵杆扭矩,无论如何应不低于按规范计算得到的最小扭矩值,这一最小扭矩值并不代表舵杆的实际水动力扭矩。但从实用角度出发,通过舵系优化设计获得适当小的舵杆实际水动力扭矩,对舵系优化设计以及试航状态舵机能力换算,都是十分有利的。
| [1] |
孙华伟, 孙大虎. 对IACS UI SC246关于操舵试验推算公式的应用探讨[J]. 船舶设计通讯, 2016(S2). |
| [2] |
KARIM M. M, SHAKIL M. Ahmmed. numerical study of periodic cavitating flow around NACA0012 hydrofoil[J]. Ocean Engineering, 2012, 55: 81-87. DOI:10.1016/j.oceaneng.2012.06.034 |
| [3] |
Ok-Sok Gim, Gyoung-Woo Lee. Flow characterisitics and trip vortex formation around a NACA 0018 foil with an endplate[J]. Ocean Engineering, 2013, 60: 28-38. DOI:10.1016/j.oceaneng.2012.12.009 |
| [4] |
李胜忠, 赵峰, 杨磊. 基于CFD的翼型水动力性能多目标优化设计[J]. 船舶力学, 2010, 11: 1241-1248. DOI:10.3969/j.issn.1007-7294.2010.11.007 |
| [5] |
周广礼, 董文才, 姚朝帮.半悬挂舵敞水水动力性能数值计算方法研究[C]. 2013.
|
| [6] |
TORGRIM D. Calculation procedure for equivalent steering gear performance[R]. DNV, 2013.
|
| [7] |
中国船级社, DNV-GL, BV等. 钢质海船入级规范[S].
|
 2019, Vol. 41
2019, Vol. 41
