2. 必维船级社(中国)有限公司,上海 200011
2. Bureau Veritas Marine China Co., Ltd, Shanghai 200011, China
钻井船是进行深远海油气资源开发的重要装备,其结构强度是关键安全因子。钻井船结构不但需要规范校核,同时需要设计波法直接强度计算[1-4]。随着钻井船创新型设计的不断涌现,船体功能设计的拓展,船体变地更加复杂、独特。因此,工程中迫切需求新的设计波方法,可针对独特的船体结构更加全面、精准的进行强度极限的校核,以保证结构安全。本文针对超深水钻井船总强度评估的等效设计波方法进行探索研究,对比了传统主控载荷设计波和应力设计波法。在传统设计波强度评估的同时,针对月池角隅探索了以应力为目标的设计波法。通过比较传统设计波和应力设计波2套结果,探索了应力设计波法在超深水新型钻井船上的应用,进一步保证结构安全。
1 基本理论方法与设计波方法 1.1 水动力理论本文采用基于三维势流理论[5]的水动力求解器对船体波浪载荷进行计算。船舶在微幅(波高波长比远小于1)规则波中做微幅运动,流场速度势Φ(x,y,z,t)满足:
| $ {\nabla ^2}{\rm{\Phi }}\left( {x,y,z,t} \right) = 0{\text{,}} $ | (1) |
速度势满足线性自由面条件:
| $ \frac{{{\partial ^2}{\rm{\Phi }}\left( {x,y,z,t} \right)}}{{{\partial ^2}{t^2}}} + g\frac{{\partial {\rm{\Phi }}\left( {x,y,z,t} \right)}}{{\partial z}} = 0,\left( {z = 0} \right){\text{。}} $ | (2) |
速度势可划分为入射波和扰动势两部分,记
| $ {\rm{\varPhi }} = {\varphi _0} + {\varphi _p}{\text{,}} $ | (3) |
其中:φ0为入射波的一阶速度势;φp为扰动势。
在无限水深情况下,入射波速度势为:
| $ {\varphi _0} = \frac{{{\rm{g}}A}}{{i\omega }}{e^{{k_0}z}}{e^{i{k_0}\left( {x\cos \beta + y\sin \beta } \right)}},\left( {{k_0} = \frac{{{\omega ^2}}}{{\rm{g}}}} \right){\text{,}} $ | (4) |
扰动势φP在物面SH上适合物面条件:
| $ \frac{{\partial {\varphi _P}}}{{\partial n}} = \mathop \sum \nolimits_{j = 1}^6 {v_j}{n_j} - \frac{{\partial {\varphi _0}}}{{\partial n}}{\text{。}} $ | (5) |
根据势流理论,将物面条件离散,通过数值方法求解整个流场的速度势,进一步可求解流场所有信息,如附连水质量、水动压力及船体运动[6]等,进而计算船体的水动力载荷。
1.2 水动力-结构耦合方法水动力载荷包括惯性力和水动压力,需精确传递到结构上,并达到自平衡。惯性力通常可直接加载。为实现精确的传递水动力载荷,必维船级社研发的水动力-结构耦合软件Homer[7]采用最新研究成果,在有限元网格高斯积分点上直接计算水动压力[8],即在船体需要的位置点直接计算流体势函数:
| $ {\rm{\varphi }}\left( {{{\rm{x}}_s}} \right) = \mathop \iint \nolimits_{S_B^H}^\square \sigma \left( {{{\rm{x}}_h}} \right)G\left( {{{\rm{x}}_h};{{\rm{x}}_s}} \right){\rm d}S{\text{。}} $ | (6) |
其中:xs=(xs,ys,zs)表示结构上的点,xh=(xh,yh,zh)表示水动力网格上的点。
之后进一步求解船体的水动压力载荷:
| $ F_i^{D{I^S}} = i\omega \rho \mathop \iint \nolimits_{S_B^S}^\square \left( {\varphi _I^S + \varphi _D^S} \right){n_i}{\rm d}S{\text{,}} $ | (7) |
| $ {\omega ^2}A_{ij}^S + i\omega B_{ij}^S = \rho {\omega ^2}\mathop \iint \nolimits_{S_B^S}^\square \varphi _{Rj}^S{n_i}{\rm d}S{\text{。}} $ | (8) |
其中:上标“s”为结构计算对应的物理量
此方法可将水动力载荷“完美”传递到结构模型。由于直接在结构模型上求解运动方程,可达到自平衡。
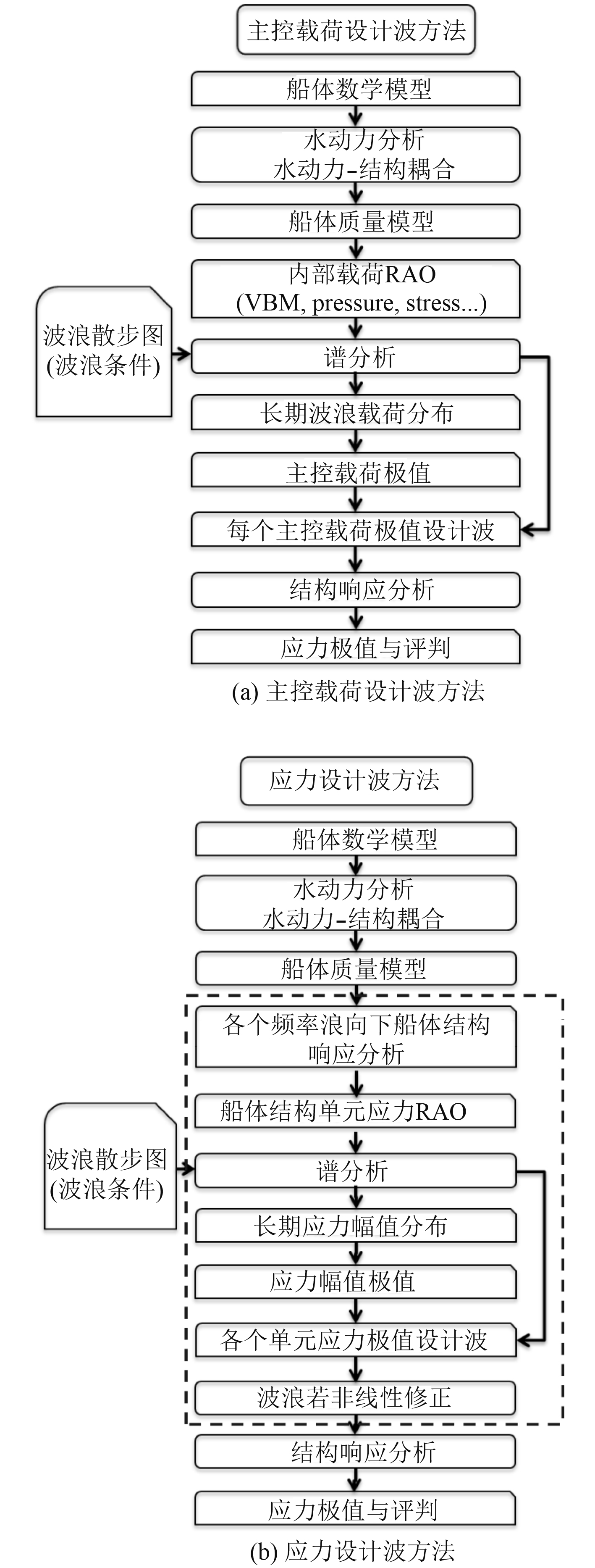
1.3 应力设计波方法主控载荷设计波法中,选取若干船体典型主控载荷为目标,根据主控载荷的RAO峰值、峰值频率、相位等参数构造等效设计波。传统主控载荷设计波法流程简单、明确、计算量小,适合成熟船型。然而,对结构新颖的船型,某些结构的受力是多重载荷综合作用结果,如月池角隅等结构。单一最大主控载荷可能难以覆盖最危险情况,这就需要应力设计波方法进行进一步分析。
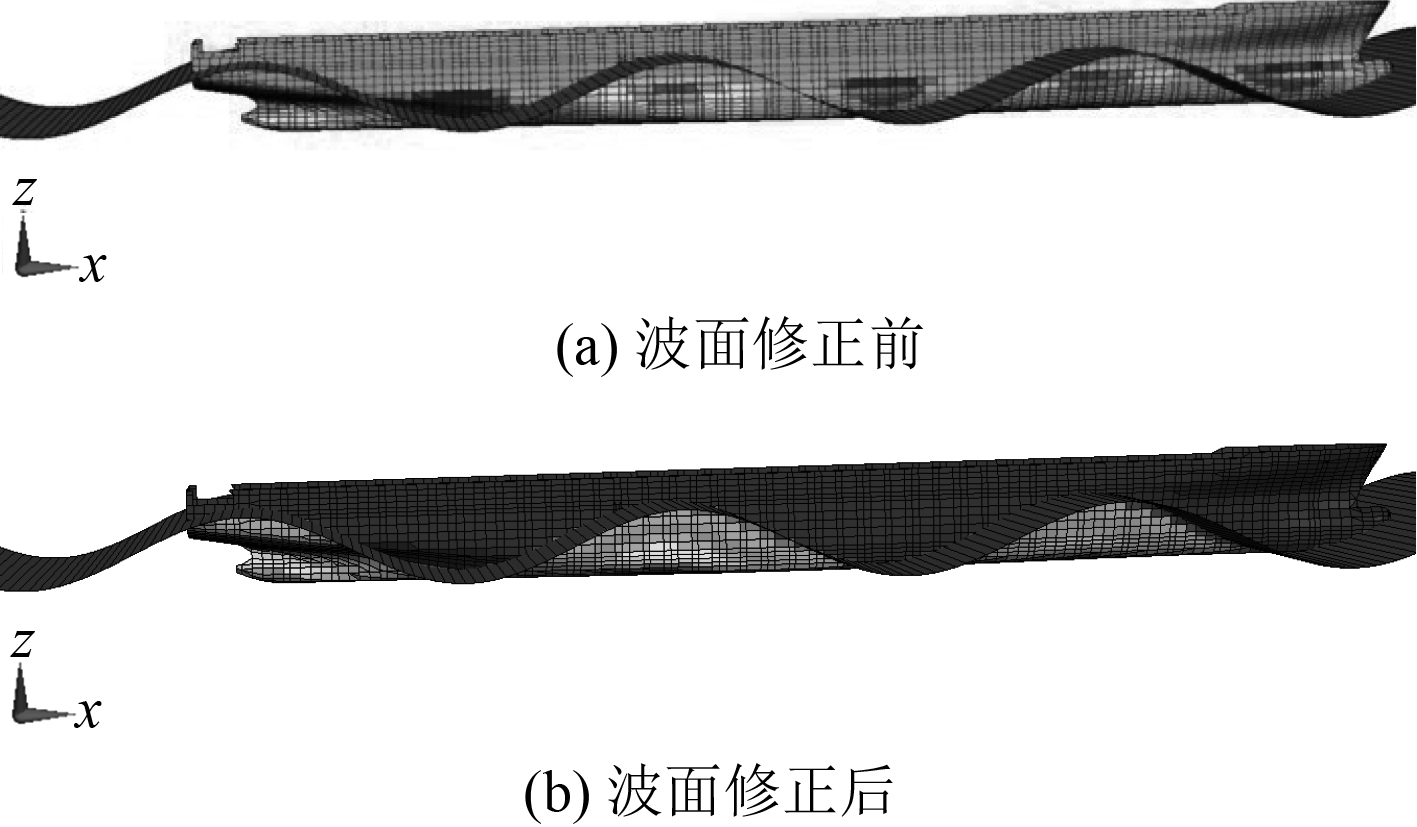
应力设计波法以关键结构处应力为目标,是目前船舶与海工领域较为前沿的设计波方法。首先,确定船体结构的关键结构节点,构建应力RAO曲线。再通过谱分析获得应力极值,作为设计波目标值。图1为对比主控载荷设计波与应力设计波流程。与主控载荷设计波加载不同,应力设计波法需在时域中进行弱非线性修正以精确表达波面起伏(见图2),求解整个波浪周期内结构响应,进行强度校核。
|
图 1 主控载荷设计波与应力设计波方法流程对比 Fig. 1 Comparison of the design wave approach based on main loads and based on stress |
|
图 2 波面若非线性修正前后船表压力对比 Fig. 2 Comparison of Wave surface pressure before and after correction |
应力设计波法计算量大,代价高。由于计算中针对特定结构进行了全浪向和全频率范围的计算和筛选,并考虑了波面修正,计算得到的应力结果更符合实际情况,对结构的评判期望更加合理。
2 超深水钻井船应力主控设计波研究本文研究了生存工况下某超深水钻井船的强度。超深水钻井船的主尺度参数如表1所示。
|
|
表 1 超深水钻井船主尺度 Tab.1 Main parameters of ultra-deep-water drilling ship |
本船特点在于月池比一般钻井船大,月池上方井架结构比一般钻井船重很多,且结构形式更复杂。因此,针对月池结构尤其是月池角隅位置,在传统设计波法之外,进一步采用应力设计波方法,全面深入研究角隅处极限强度,以保证船体强度安全。
2.1 船体载荷与结构响应计算按船体型线和结构,采用有限元软件FEMAP建立水动力计算模型和有限元模型,如图3所示。
|
图 3 水动力计算模型和有限元模型 Fig. 3 Hydrodynamic calculation model and finite element model |
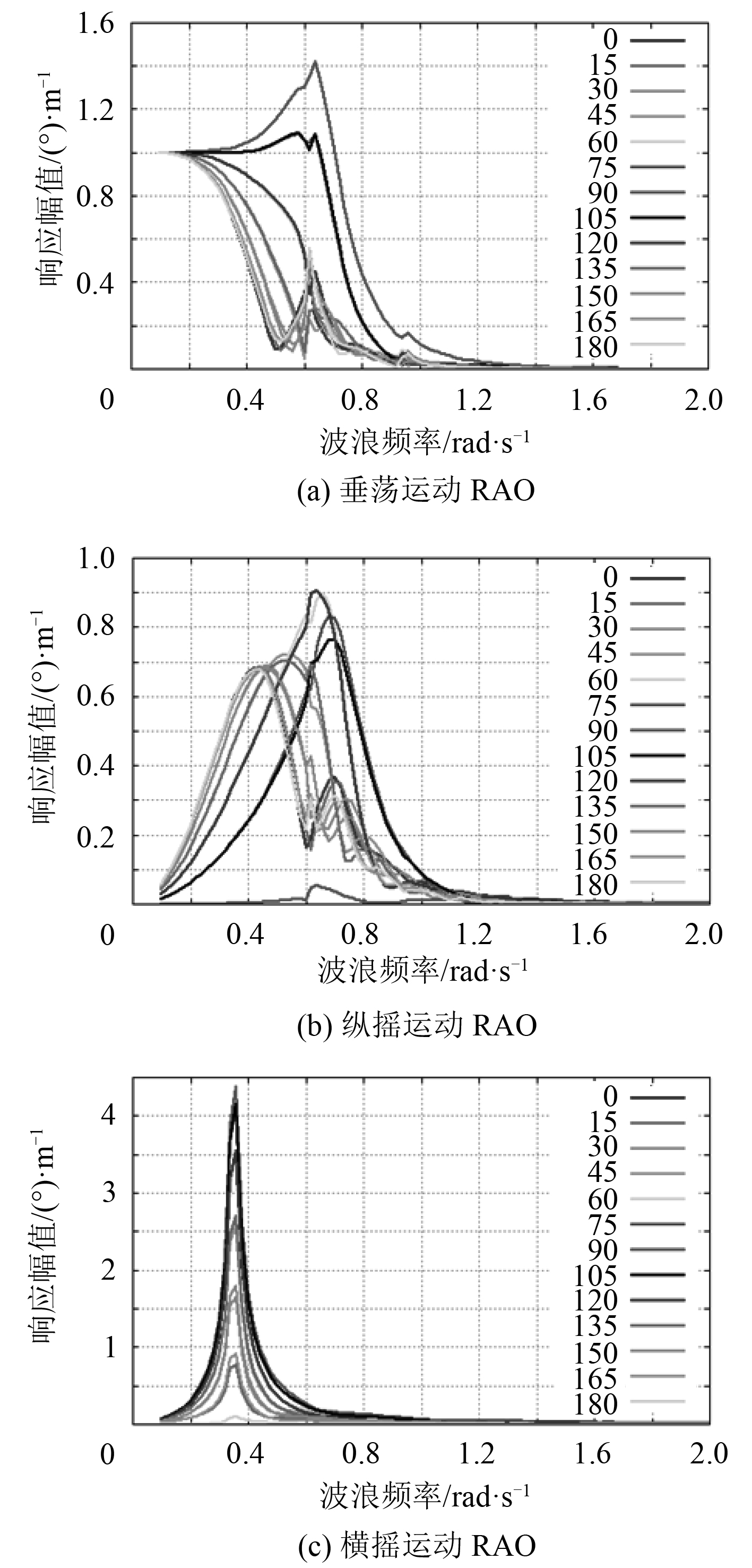
采用三维势流理论水动力软件HydroSTAR[9]开展水动力性能计算。计算得到船体在生存工况下的运动响应RAO如图4所示。90°(横浪)时,船体垂荡、横摇运动RAO峰值最大,但垂荡和横摇峰值频率不同。0°(随浪)或180°(迎浪)时,船体纵摇运动RAO峰值最大。
|
图 4 船体运动RAO Fig. 4 RAO of ship motion |
船体主控载荷RAO,如图5所示。包括船中垂向波浪弯矩RAO、1/4船长和3/4船长处垂直波浪剪力、船中扭矩RAO和井架重心加速度RAO。对比运动RAO和主控载荷RAO可看出,两RAO峰值紧密相关。垂直剪力Fz、垂向弯矩VBM的峰值发生在与垂荡、纵摇峰值频率相近区域;船舯剖面的扭矩RAO峰值频率与横摇RAO峰值频率、井架重心加速度峰值频率接近。船中井架质量巨大,其横摇对船中的扭矩产生较大影响。

|
图 5 船体主控载荷RAO Fig. 5 RAO of ship main loads |
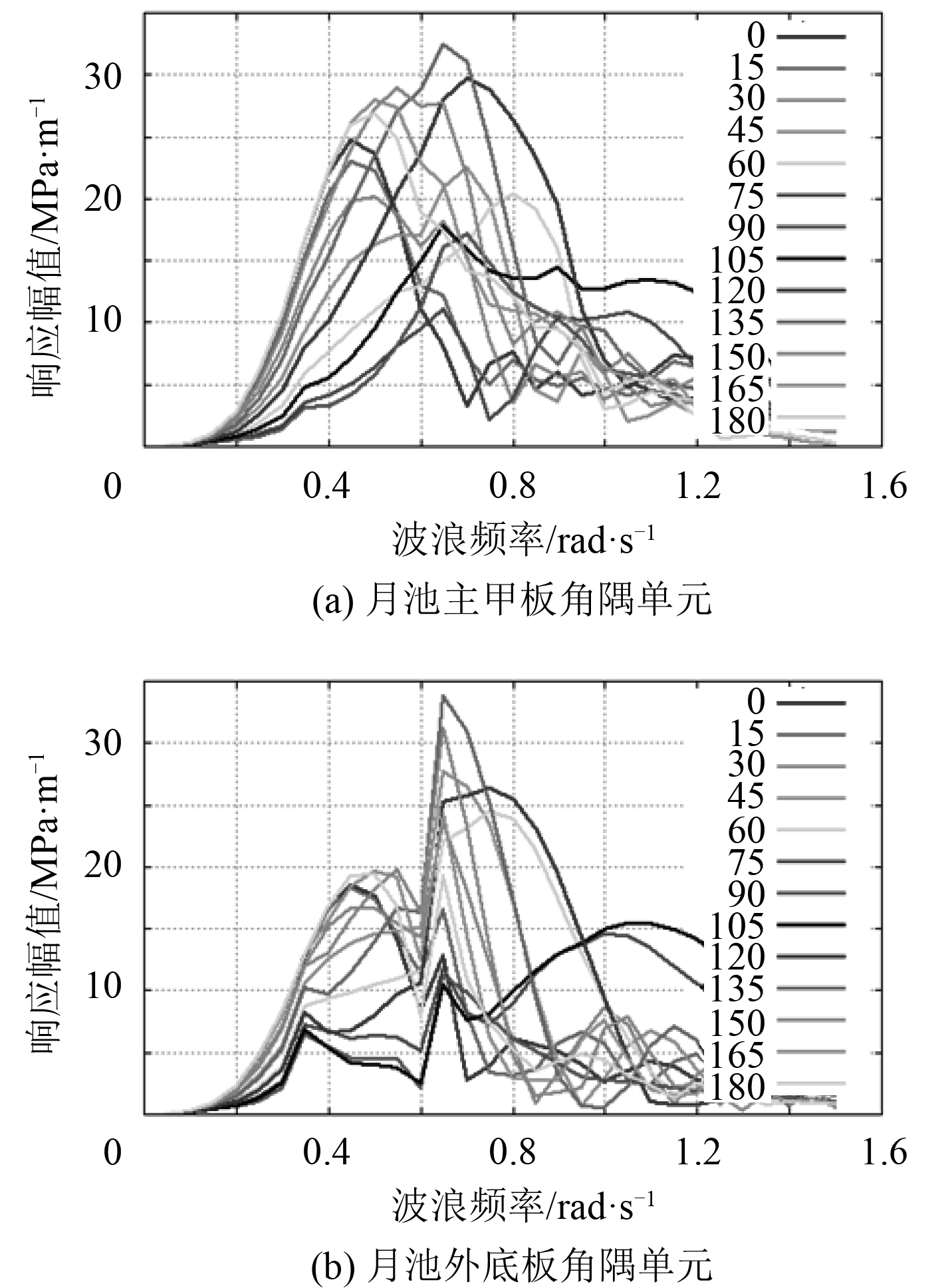
利用水动力-结构耦合软件HOMER,结合FEM模型,将水动力载荷加载到有限元模型,求解各个浪向、各个频率下的结构单元的应力响应RAO。本文选择月池甲板角隅和外底板角隅处的系列单元作为主控单元,图6为两处单元中面Von Mises应力RAO曲线。
|
图 6 月池角隅单元应力RAO Fig. 6 Stress RAO of element at moonpool corner |
在月池角隅处单元,其应力RAO同样呈明显“双峰”形态,即应力RAO峰值和峰值频率随浪向不同而改变,第1个峰值在波浪频率0.5 rad/s附近,此时入射波浪向为180°(迎浪);第2个峰值在波浪频率0.65 rad/s附近,入射波浪向为135°(顶斜浪)。结合船体运动和主控载荷:第1个应力峰值出现的频率、浪向与船舯垂向波浪弯矩的频率、浪向相同。如果以船舯垂向波浪弯矩为主控载荷,获得的等效设计波将使得月池角隅应力产生峰值。第2个应力峰值产生的频率、浪向与所有主控载荷设计波中频率、浪向都不相同:浪向135°时,多种载荷综合作用下的月池角隅应力水平更高,月池角隅应力对波浪力的作用更为敏感。
2.2 主控载荷极值分析结合实际工况对应波浪谱和海况信息进行谱分析,预报波浪载荷[10]在实际海况条件下的最大载荷,及最大载荷对应的浪向。生存工况对应的短期海况如表2所示,对应的波浪谱为JONSWAP谱。
|
|
表 2 生存工况短期海况参数 Tab.2 Short term sea state parameters for survival condition |
对船体波浪载荷RAO结果进行谱分析,得到百年一遇主控载荷极值及对应的浪向,如表3所示。表3同时给出了主控载荷极值对应的RAO峰值和峰值频率。
|
|
表 3 主控载荷的谱分析结果 Tab.3 Spectral analysis results of main loads |
根据谱分析获得主控载荷极值、浪向角,结合相应的RAO曲线,可以获得波浪的频率、相位。线性波浪幅则根据载荷极值和RAO峰值的比率进行计算:
| $ A = \frac{{{\text{载荷目标极值}}}}{{\left| {{\rm{RAO{\text{峰值}}}}} \right|}}{\text{,}} $ | (9) |
等效规则设计波的最终表达形式为:
| $ EDW = A\cos \left( {\omega t + \varepsilon } \right){\text{。}} $ | (10) |
以垂直剪力、垂向弯矩、扭矩、月池角隅应力等极值为目标的设计波如表4所示。
|
|
表 4 主控载荷、主控应力设计波参数 Tab.4 Design wave parameters for main load and main stress |
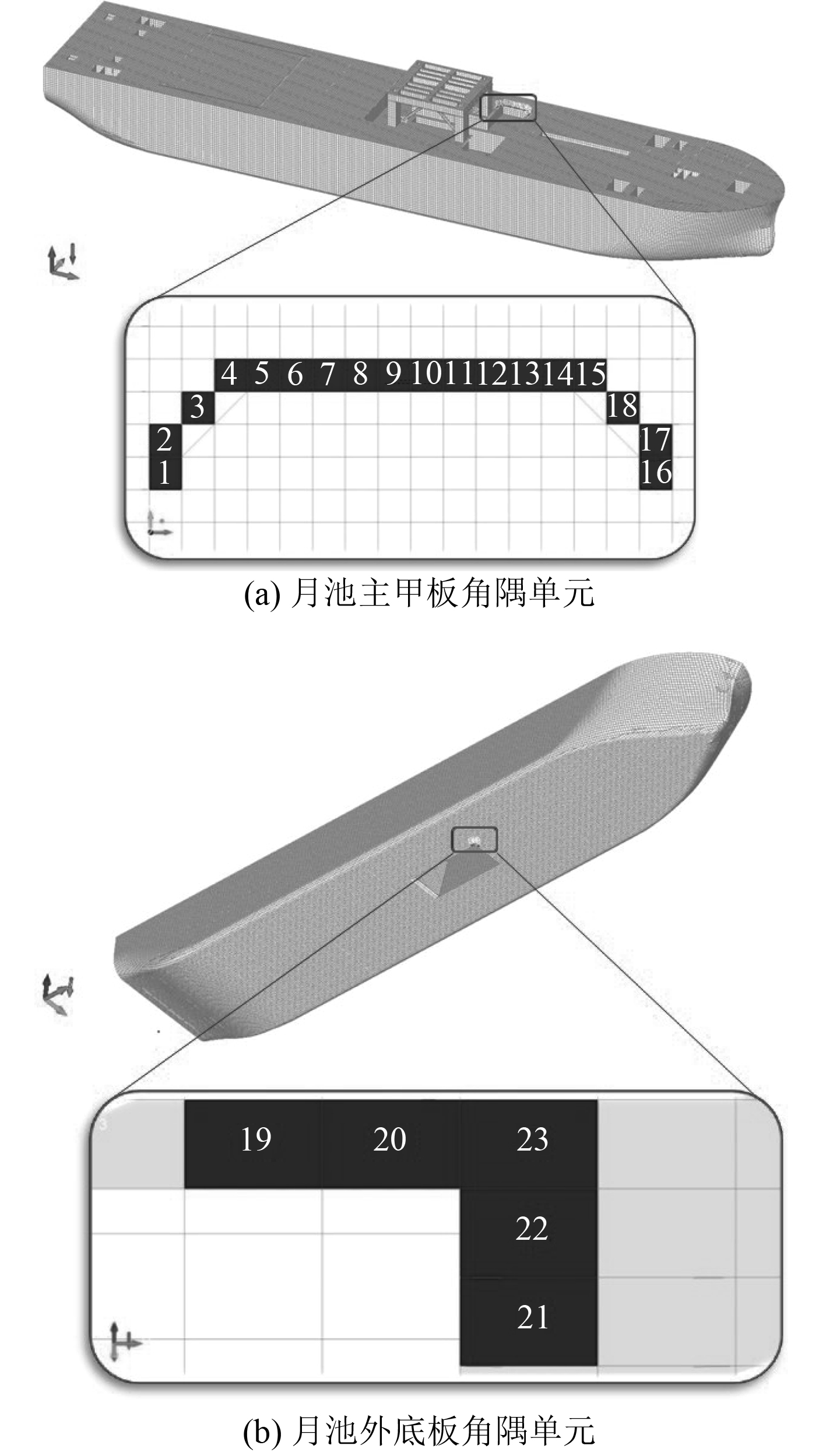
分别将2套设计波加载到船体,进行分析,得到结构响应。2套设计波在相同结构单元位置如图7所示。
|
图 7 月池角隅单元位置信息 Fig. 7 Location information of elements at moonpool corner |
表5给出了应力设计波法计算月池角隅应力极值及应力设计波参数。表6和表7给出了2种设计波方法的结果对比,可看出利用应力设计波法得到的单元极限强度所对应的设计波浪向、频率与单元应力幅值,都与主控载荷设计波法有所不同。从浪向看,由于主控载荷设计波中,没有斜浪设计波,故利用主控载荷设计波得到的是单元应力RAO的第1个峰值所产生的应力极值。而利用应力设计波方法,单元响应的极值浪向发生在顶斜浪,不仅受船体梁载荷影响,更是各种载荷综合作用的结果。
|
|
表 5 月池角隅单元应力设计波参数 Tab.5 Design wave parameters for stress of moonpool corner elements |
|
|
表 6 月池主甲板角隅单元应力计算结果比较-Von mises stress Tab.6 VM-Stress at the of main deck corner of moonpool |
|
|
表 7 月池外底板角隅单元应力计算结果比较-Von mises stress Tab.7 VM-Stress of bottom outer shell corner of moonpool |
应力设计波得到各个单元的应力极值基本上大于或等于主控载荷设计波结果,如图8所示。仅在月池外底板横向单元上,应力水平稍低。从应力极值的对比可看出,利用应力设计波法得到的应力水平通常更高,基本涵盖主控载荷设计波结果。应力随浪向、频率的分布,以及得到的对应最大屈服应力,对结构设计的加强具有更加明确的针对性和指导意义。

|
图 8 月池角隅单元总应力对比 Fig. 8 Total stress of elements at moonpool corner |
从计算量和计算时间上看,应力设计波的计算量与耗时远大于主控载荷设计波。因此,利用应力设计波法对创新型、高附加值船型进行强度分析和校核,更有效果。
3 结 论本文针对超深水钻井船总强度评估的等效设计波法进行探索研究,比较分析主控载荷设计波法和应力设计波新方法的结果,探索了应力设计波法在超深水钻井船上的应用。
1)针对关键结构,应力设计波法更全面的对浪向、频率展开搜索,获得的应力极值对应135°顶斜浪,与传统方法的应力极值浪向180°(迎浪)存在差异。传统方法以船体梁截面扭矩为主控载荷时,基于本船型得到的设计波为90°横浪,此时总扭矩主要由钻井模块(重量大、重心高)惯性力引起。然而,此扭矩导致的应力更直观体现在井架支撑结构,由45°斜浪船体梁扭转引发的月池角隅应力却被忽略,这是传统设计波法在超大型钻井船(钻井模块重量大、重心高)总强度评估中的缺陷,应力设计波法直接以目标区域应力为关注点,弥补了此漏洞。
2)从屈服结果的对比分析来看,应力设计波法得到的单元屈服应力普遍大于传统设计波法,说明目前工业界从船体梁整体失效目标考虑的设计波法在屈服评估时的极值涵盖还不够全面,关键结构最大屈服应力的搜索存在可能遗漏和不足,尽管传统方法较大程度上可满足船舶与海工结构设计需求。
3)对比结果显示,应力设计波法得到的应力中,存在极少数不符合规律的点(屈服应力小于传统方法),有必要针对该方法进一步开展全流程影响因素研究。
4)应力设计波法目前仅限屈服评估,对屈曲和疲劳还无法应用。一方面,屈曲和疲劳基于的应力分量更多,另一方面,屈曲和疲劳还受应力和材料属性之外的多个因素影响,更复杂,以屈曲、疲劳为目标的应力设计波法还有待进一步研究,以推广此方法在更广范围的应用,发挥其在结构评估中的精确性优势。
| [1] |
顾永宁, 滕小青, 戴立广, 等. 大开口船波浪载荷长期预报和弯扭强度整船[J]. 中国造船, 1998, 2(141): 63-79. |
| [2] |
阚涛, 刘加一, 向琳玲, 等. 基于设计波法的FLNG整船强度评估[J]. 舰船科学技术, 2017, 39(9): 32-37. KAN Tao, LIU Jia-yi, XIANG Lin-ling. Overall strength assessment of flng based on design wave approach[J]. Ship Science and Technology, 2017, 39(9): 32-37. |
| [3] |
肖桃云, 樊佳, 梅国辉, 等. 基于设计波法的舰船整船有限元强度分析[J]. 舰船科学技术, 2010, 32(6): 14-19. XIAO Tao-yun, FAN Jia, MEI Guo-hui. Strength analysis of overall ship fem model based on design wave approach[J]. Ship Science and Technology, 2010, 32(6): 14-19. |
| [4] |
段雷杰, 张少雄, 杨洋. 基于设计波法的FPSO全船有限元分析[J]. 船海工程, 2017, 46(2): 48-53. DOI:10.3963/j.issn.1671-7953.2017.02.011 |
| [5] |
戴遗山. 船舶在波浪中运动的频域与频域势流理论[M]. 北京: 国防工业出版社, 2005.
|
| [6] |
刘应中, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1987.
|
| [7] |
Bureau Veritas, User guide of Homer 2.1.7[R]. 2017.
|
| [8] |
MALENICA S, STUMPF E, SIRETA F X, et al. Consistent hydro-structure interface for evaluation of global structural responses in linear seakeeping[C]. Proceedings of OMAE 2008, 26th international conference on Offshore Mechanics and Artic Engineering. June 15-20, 2008, Estorill, Portugal.
|
| [9] |
BUREAU V. User manual of hydrostar for experts[R]. 2016.
|
| [10] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.
|
 2019, Vol. 41
2019, Vol. 41
