2. 国家海洋局 北海海洋技术保障中心,青岛 266033
2. North China Sea Marine Technical Support Center, State Oceanic Administration, Qingdao 266033, China
随着海洋资源的开发与利用,自主水下机器人作用愈发突出,而精细化作业的需求对潜器智能控制及自主导航的要求也越来越高。路径规划作为关键技术之一,直接影响到潜器的性能。潜器的路径规划具体可描述为:在具有障碍物的水下环境中,依据预设的评价标准,规划出一条从起点到终点最优或准优的无碰撞路径。
Dijkstra算法是最早被发明出来的规划搜索算法,它主要利用贪心思想在图里寻找最短路径;1968年,Hart在Dijkstra算法的基础上加入了启发式函数而创造出了A*算法,加快了搜索速度[1];Wang Z在2017年成功的将A*算法应用在水下机器人全局路径规划上[2]。Fast Marching(FM)算法用到了非线性程函方程的一阶数值近似,它可被认为是Dijkstra算法的连续版本;Yu H在2015年实现了FM算法在水下机器人路径规划上的应用[3]。人工势场法是一种虚拟力法,它是假设目标点对机器人存在吸引力,障碍物对机器人存在斥力,由此建立一个虚拟的势场,并让机器人沿着势场下降最快的方向前进直到目标点;然而该算法存在局部最小值问题[4],杨建在2017年成功的将人工势场法应用到了水下机器人避障运动上[5]。继而有学者提出进化算法,例如粒子群算法,蚁群算法和遗传算法,这些算法在智能潜器中也得到了相关的应用[6 – 10]。PRM算法和RRT算法则是在许可范围内,通过牺牲最优、随机采样实现快速可行的路径规划算法。PRM算法的基本思想是在空间里随机撒点并连线形成一个图,然后在该图上运行A*等搜索算法来寻找路径。RRT算法则是以起始点作为一棵树的根节点,通过不断的随机扩展这棵树上的节点,直到扩展的节点接近目标点,则认为在这棵树上找到了一条唯一的路径到达目标点,该算法的优点是计算速度较快,且可以在规划过程中加入动力学约束。但也有明显的缺点,找到的路径不一定最优。Yu L在2017年成功地将RRT算法应用到水下机器人的路径规划里[11]。2010年,S.Karaman通过引入代价函数来优化RRT算法,经过逐次迭代来改善之前的路径,优化后的算法被定义为RRT*算法[12]。RRT*算法不仅继承了RRT算法的优点,还克服了RRT算法的缺点,最终会得到一条最优或准优的路径,这额外的最优性使得RRT*算法在高维和实时工况下能快速有效的实现规划。RRT*算法在水下机器人路径规划中的应用鲜有实现。
实际应用中海洋环境比较复杂,有时还会存在洋流因素,洋流的速度和方向都会对水下机器人的能量消耗产生影响。因此在路径规划时,除了要考虑路径长度、障碍物信息外,还应考虑能耗问题。本文根据RRT*算法的优点,考虑洋流对水下机器人能耗的影响,设计实现基于RRT*的路径最短和能耗最低的路径规划算法,并通过相应的仿真模拟和实验室平台的真机实现验证了该算法的可行性。
1 RRT算法 1.1 问题定义让
问题1(可行路径):在非障碍物区域内找到一条从
问题2(最优路径):在非障碍物区域内找到一条从
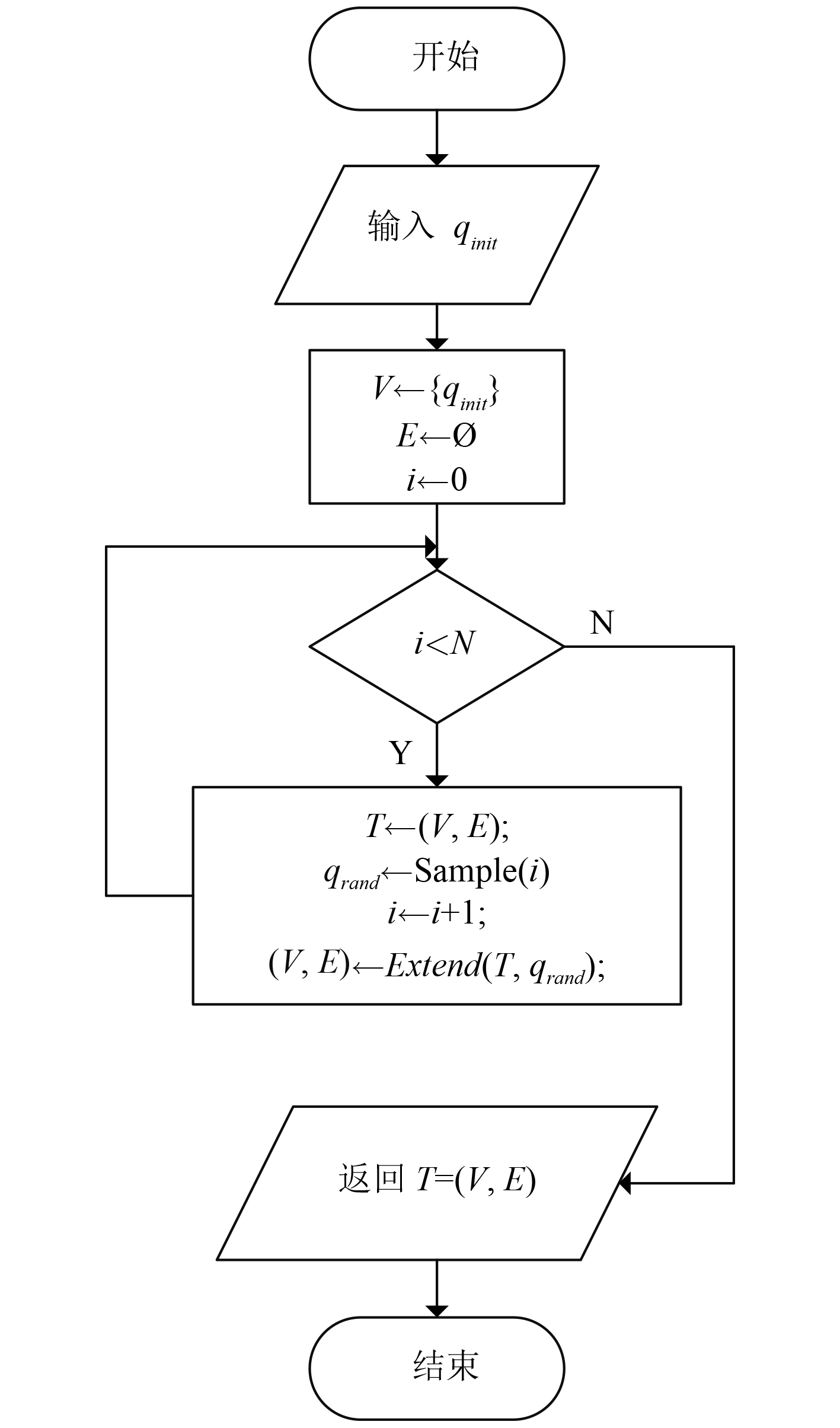
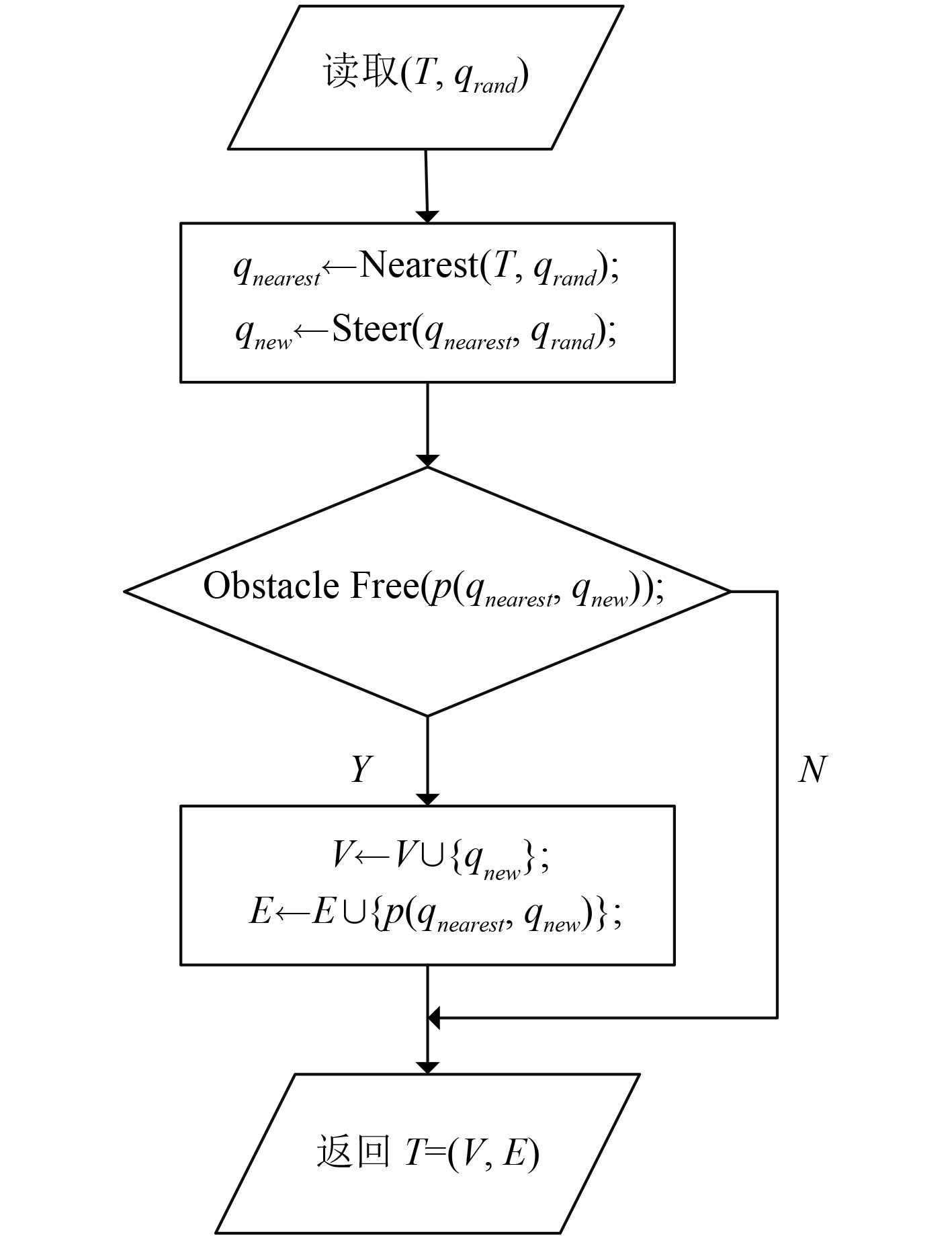
RRT算法是一种基于概率采样的搜索方法,图1为RRT算法程序流程图,具体实现如算法1所示。图2为随机树的关键扩展过程(Extend函数)程序流程图,具体实现如算法2所示。
|
图 1 RRT算法程序流程图 Fig. 1 Program flow diagram of RRT algorithm |
|
图 2 扩展过程(Extend函数)程序流程图 Fig. 2 Program flow diagram of Extend function |
算法1:
1
2 while
3
4
5
6 return
算法2:
1
2
3 if
4
5
6 return
其中,各函数含义及作用如下:
从RRT算法过程中可以看出随机树的扩展偏向于未被访问过的区域。这使得随机树在刚开始时扩展得很快,并能完全覆盖结构空间。随机树上的节点在结构空间里是均匀的。如果可行路径存在,那在节点数量足够的前提下,RRT算法就一定能找到一条从起始点到目标点的可行路径。通过上述分析可知,RRT算法所找到的可行路径不一定最优。
2 基于RRT*的路径规划算法针对RRT算法存在的问题,S.Karaman提出通过引入代价函数来优化,经过逐次迭代来改善之前的路径,从而得到一条最优或准优的路径。
2.1 RRT*算法在RRT算法内容基础上扩展定义如下:1)
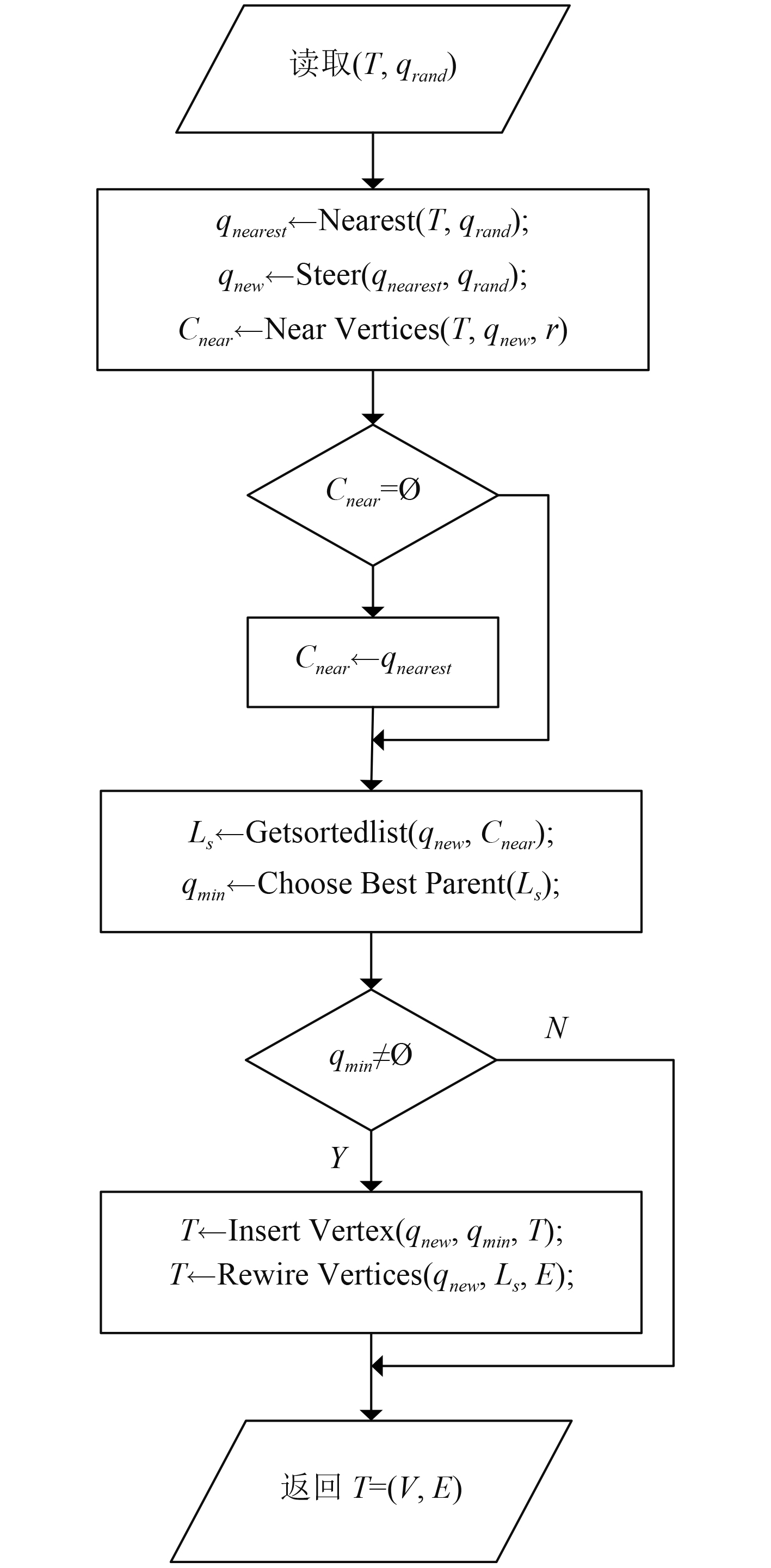
RRT*算法的初始化过程同算法1中一致,而不同的是RRT*算法在它的扩展过程中引入了代价函数,并通过代价函数来判断是否会更新之前的路径,以此来改善路径。图3则为RRT*算法中扩展过程(Extend函数)程序流程图,具体实现如算法3所示,接下来的则是一些在扩展过程中被调用的函数。
|
图 3 扩展过程(Extend函数)程序流程图 Fig. 3 Program flow diagram of Extend function |
算法3:RRT*
1
2
3
4 if
5
6
7
8 if
9
10
11 return
算法4:
1
2 for
3
4
5
6 return
算法5:
1 for
2 if
3 return
4 return
算法6:
1
2
3
4 return
算法7:
1 for
2 if
3 if
4
5
6
7 return
其中,各函数含义及作用如下:
如同算法1的开始一样,在初始化后RRT*算法开始它的迭代过程。先通过从非障碍物空间里随机采样
本文只考虑欧式空间,两点间的路径距离代价则为两点间的正欧式距离,可表示为:
| ${\rm{d}}({q_{\rm{i}}},{q_j}){\rm{ = }}{\left\| {{q_i} - {q_j}} \right\|_2} \text{。}$ | (1) |
基于Fossen模型[13],对于左右对称的低速水下机器人来说,非线性阻尼矩阵可以被忽略,而忽略垂荡、横摇和纵摇后的线性化的阻尼矩阵可被写成:
| $ {{D}} = - \left[ {\begin{array}{*{20}{c}} {{X_u}}&0&0 \\ 0&{{Y_v}}&{{Y_r}} \\ 0&{{N_v}}&{{N_r}} \end{array}} \right] \text{。} $ | (2) |
式中,
在真实的海洋环境中,有时还会存在洋流因素,而洋流的速度和方向都会对水下机器人路径上的能量消耗产生影响。
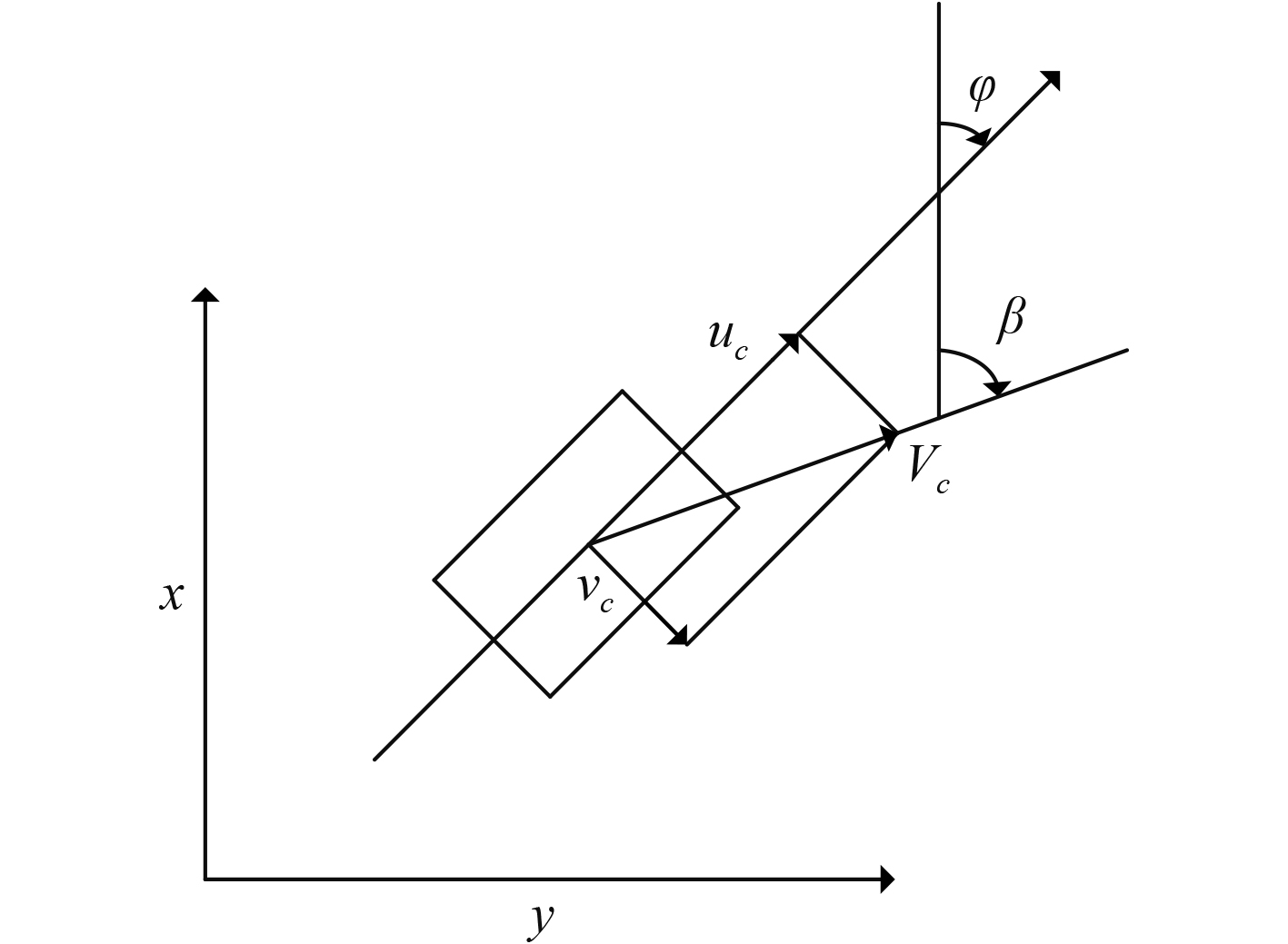
如图4所示,当存在一个缓变的速度为
|
图 4 水下机器人体坐标系下2D无旋洋流速度分量示意 Fig. 4 The velocity component of 2D irrotational ocean current in ROV body coordinate system |
| $\begin{align} {u_c} = {{{v}}_c} \cdot \cos (\beta - \varphi ) {\text{,}}\\ {v_c} = {{{v}}_c} \cdot \sin (\beta - \varphi ) {\text{,}} \\ \end{align} $ | (3) |
其中
设
| $ \begin{align} {{\bf{\tau }}_{{D}}} =& - {{D}} \cdot {{{v}}_r}= \\ &\left[ {\begin{array}{*{20}{c}} {{X_u} \cdot \left( {u - {{{v}}_c} \cdot \cos (\beta - \varphi )} \right)} \\ {{Y_v} \cdot \left( {v - {{{v}}_c} \cdot \sin (\beta - \varphi )} \right) + {Y_r} \cdot r} \\ {{N_v} \cdot \left( {v - {{{v}}_c} \cdot \sin (\beta - \varphi )} \right) + {N_r} \cdot r} \end{array}} \right]{\text{。}} \end{align} $ | (4) |
假设在水下机器人路径跟踪里会使水下机器人的艏向永远与规划出的路径方向保持一致,并保持匀速行驶,则水下机器人横向上没有位移,可认为水下机器人横向上的阻力不做功,则水下机器人在路径上的能量消耗只需要考虑水下机器人在纵向上所受到的阻力做功和原地旋转时受到的阻力矩做功。则从
| $\begin{split} e({q_i},{q_j}) = &\left( {{X_u} \cdot \left( {u - {{\bf{v}}_c} \cdot \cos (\beta - \varphi )} \right)} \right) \times {\left\| {{q_i} - {q_j}} \right\|_2}+ \\ & \left( {{N_v} \cdot \left( {v - {{\bf{v}}_c} \cdot \sin (\beta - \varphi )} \right) + {N_r} \cdot r} \right) \times \left( {{\varphi _2} - {\varphi _1}} \right){\text{。}}\\[-10pt] \end{split} $ | (5) |
式中:
若将式(1)与式(5)结合到一起,则可得到总的路径代价函数表示为:
| $ c({q_i},{q_j}) = \alpha \times e({q_i},{q_j}){\rm{ + }}\tilde \alpha \times {\rm{d}}({q_{\rm{i}}},{q_j}){\text{。}} $ | (6) |
当
基于前文理论分析及算法设计,利用Matlab编程实现RRT算法和RRT*算法(路径最短),并进行仿真对比,仿真结果如图5和图6所示。

|
图 5 RRT算法仿真结果 Fig. 5 Simulation results of RRT algorithm |
|
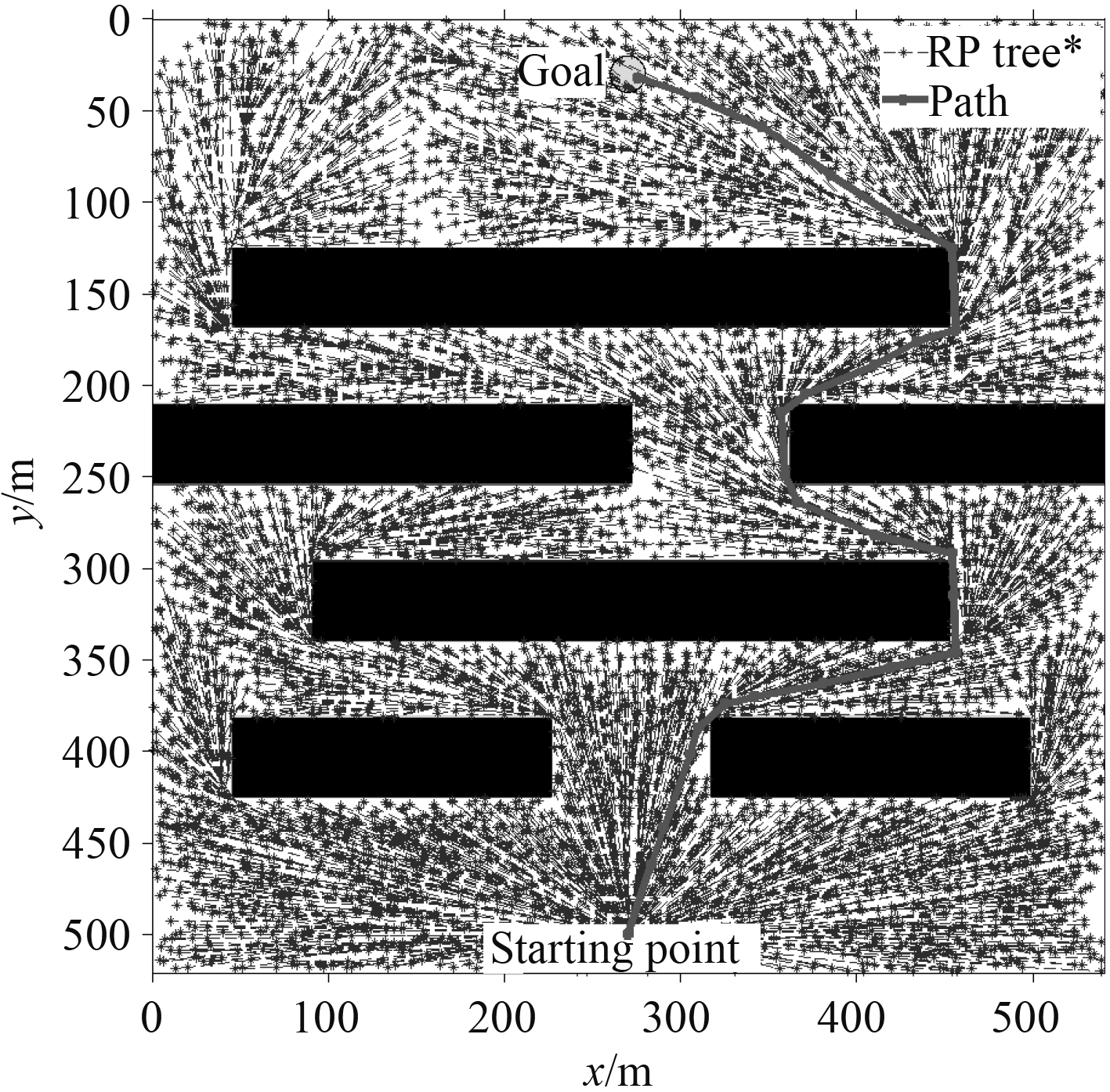
图 6 RRT*算法仿真结果 Fig. 6 Simulation results of RRT* algorithm |
图中矩形区域(黑色)代表障碍物,Starting Point代表起始点,圆形区域则代表目标区域,粗实线则为所寻找到的路径,将两图中的路径长度通过计算得到表1。
|
|
表 1 两种算法路径长度对比 Tab.1 Comparison of path length between two algorithms |
从仿真结果的对比可以看出,RRT算法能找到一条可行路径,但不一定是最优或准优路径;RRT*算法因代价函数的引入,找到的路径不仅是可行路径,相对RRT算法所得路径更优,可视为准优路径。
3.2 2D无旋洋流环境中路径最短与能耗最低路径规划的仿真模拟假设流场环境为2D无旋洋流,流速为
|
|
表 2 仿真参数表 Tab.2 Simulation parameter table |
|
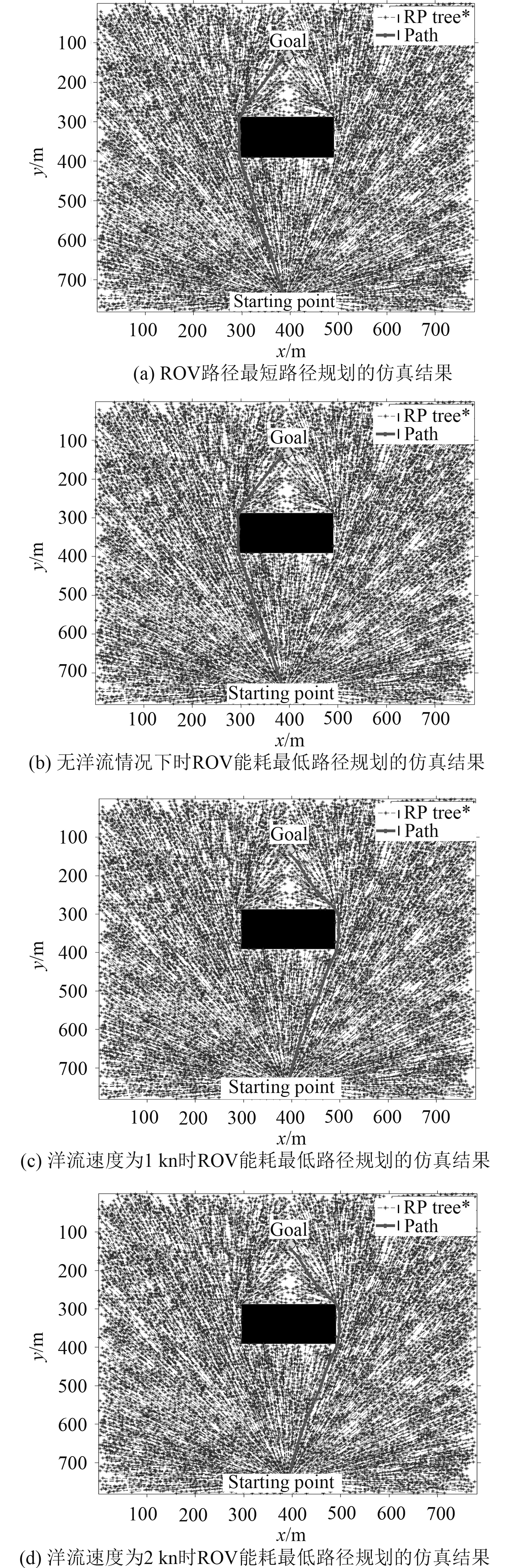
图 7 ROV两种路径规划的仿真结果 Fig. 7 Simulation results of two path planning of ROV |
从图7中可以看出,当无洋流因素影响时,ROV能耗最低路径规划得到的路径(b)与ROV路径最短路径规划得到的路径(a)一致,为左边路径。而当存在洋流时,ROV能耗最低路径规划得到的路径(c)和(d)则始终为右边路径。将这左、右2条路径在上述3种情况下的能耗和长度通过计算并整理得到表3。
|
|
表 3 两条路径的能耗和长度对比表 Tab.3 Comparison of energy consumption and length of two paths |
可以看出,左边路径的长度要比右边路径短。然而当洋流速度越大,左边路径所需要的能耗就越大,而右边路径所需要的能耗则越小。当不存在洋流影响时,左边路径的能耗要低于右边路径,故ROV能耗最低路径规划得到的路径是左边路径;当洋流速度为1 kn或2 kn时,左边路径的能耗要高于右边路径,故ROV能耗最低路径规划得到的路径是右边路径。该仿真结果验证了ROV路径最短和能耗最低路径规划算法可行有效。
4 RRT*算法的实验室实现 4.1 实验条件本次实验是在上海交通大学拖曳水池进行的,实验水池水深7.5 m,长300 m,宽16 m。实验对象则是采用实验室现有的水下机器人(ER3K,见图8),该水下机器人的基本性能参数见表4。地形环境则通过搭载在水下机器人本体上的声呐(Super SeaKing DST,见图9)获取,声呐性能参数见表5。

|
图 8 水下机器人 Fig. 8 Remote operated vehicle |
|
|
表 4 水下机器人基本性能 Tab.4 Basic performance of remote operated vehicle |

|
图 9 实验声呐 Fig. 9 Experimental sonar |
|
|
表 5 Super SeaKing DST声呐基本属性 Tab.5 Basic performance of sonar |
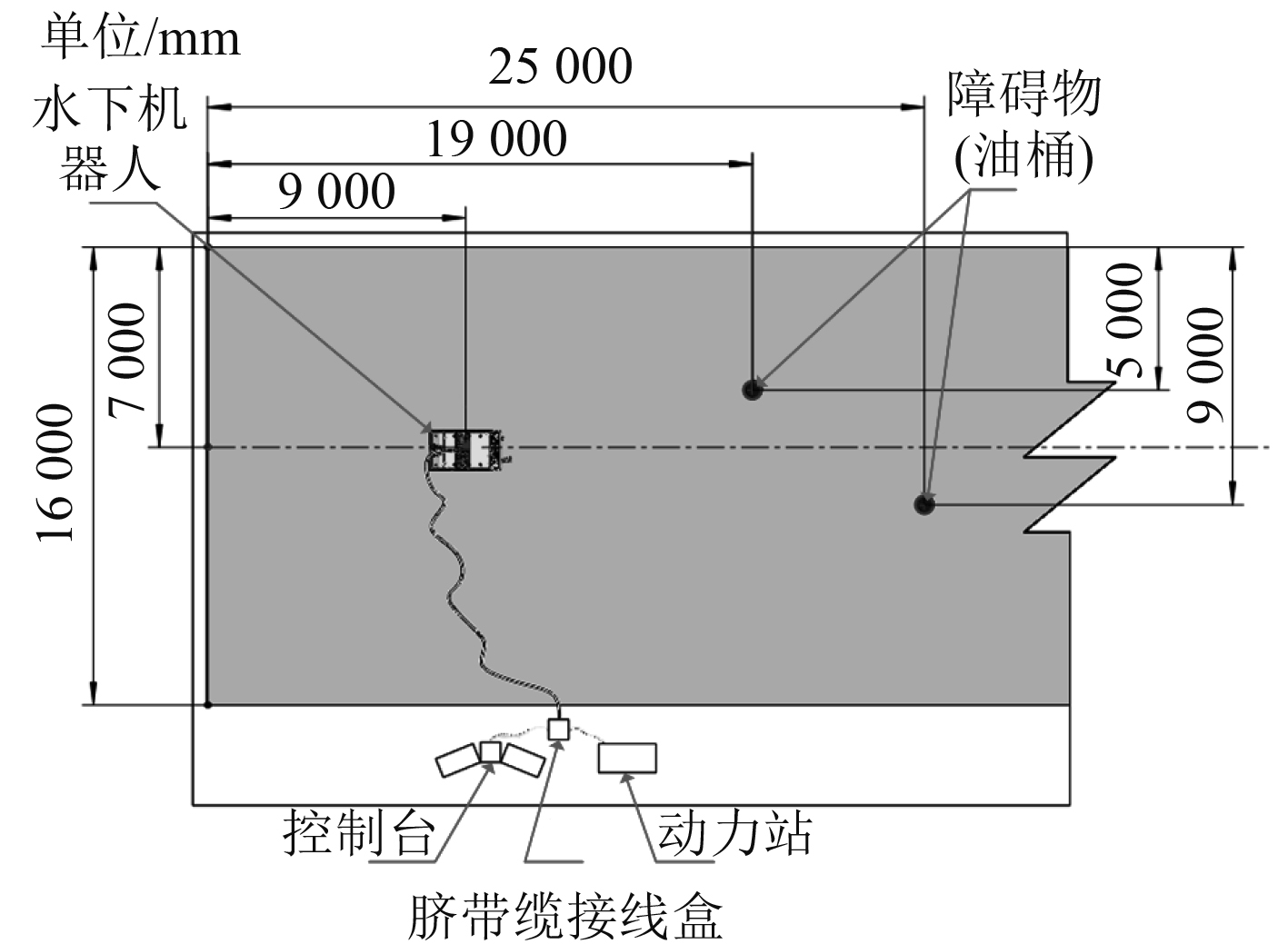
在本次实验中,采用2个油桶来充当障碍物,然后利用搭载在水下机器人上的实验声呐去扫描检测获取环境里的障碍物信息,最后再利用基于RRT*算法的路径最短和能耗最低路径规划算法得到准优路径。图10为本次实验示意图,图11为本次实验现场图。
|
图 10 实验示意图 Fig. 10 Experimental schematic diagram |

|
图 11 实验现场 Fig. 11 Experimental scene |
利用水下机器人上所搭载的实验声呐进行扫描检测,获得的声呐图像如图12所示。

|
图 12 声呐图像 Fig. 12 Sonar image |
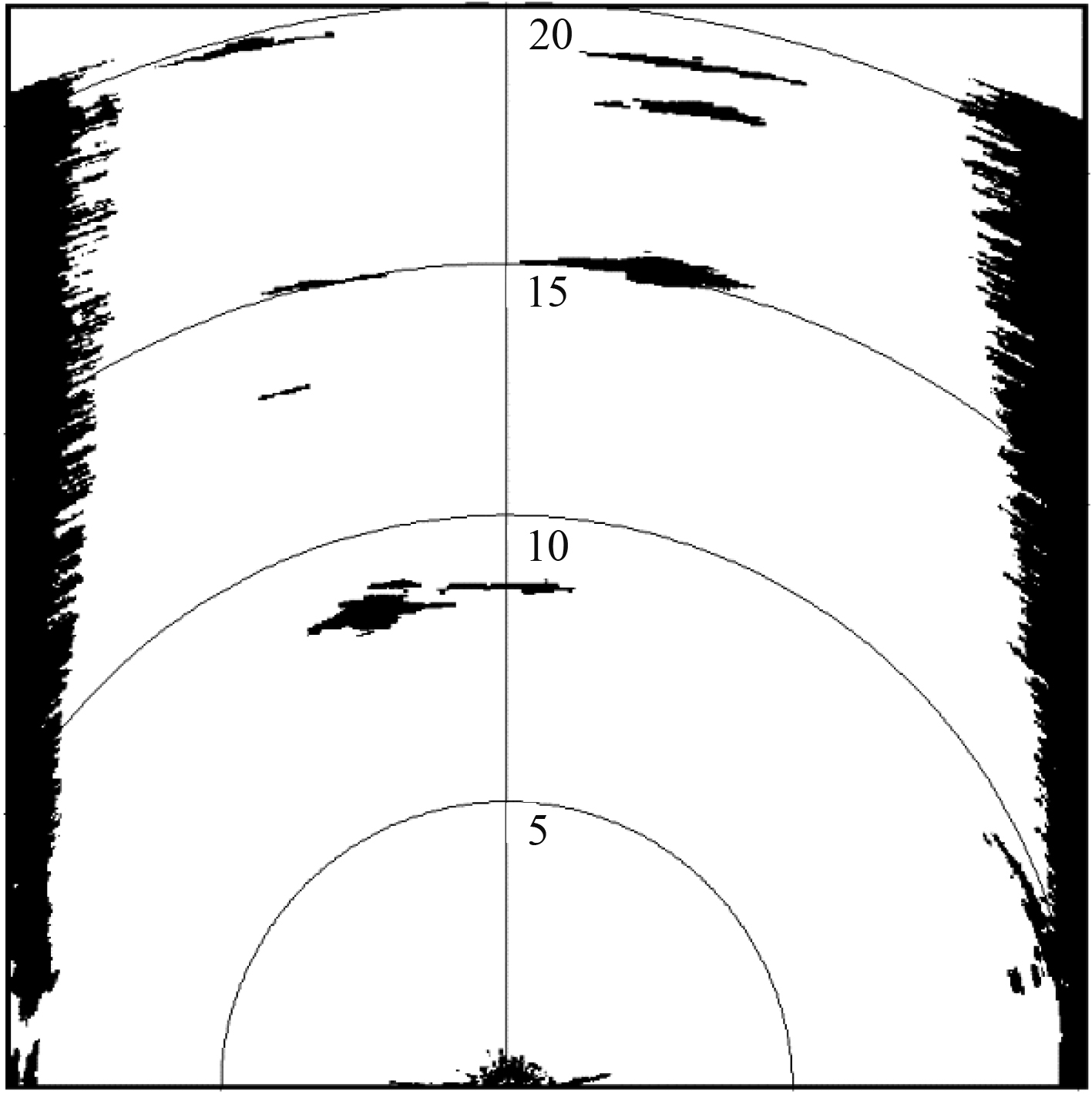
图12中,可看出图中深色区域为障碍物或杂波。在实际情况中,水下机器人并无法分辨出深色区域是障碍物还是杂波,所以此处将深色区域全部视为障碍物以此来规划路径。将声呐图像进行图像处理后得到如图13所示。
|
图 13 图像处理后的地图 Fig. 13 Map after image processing |
图中黑色区域被认为是障碍物,白色区域则被认为是可通行区域。进一步为了安全考虑,此处通过将图13中的障碍物扩大来保证水下机器人通行的安全距离,得到的最终地图如图14所示。受实验条件所限,实验环境为无流水池,则使水下机器人在图14上分别实施路径最短和能耗最低(无洋流情况下)路径规划算法,规划出的路径结果如图15所示。
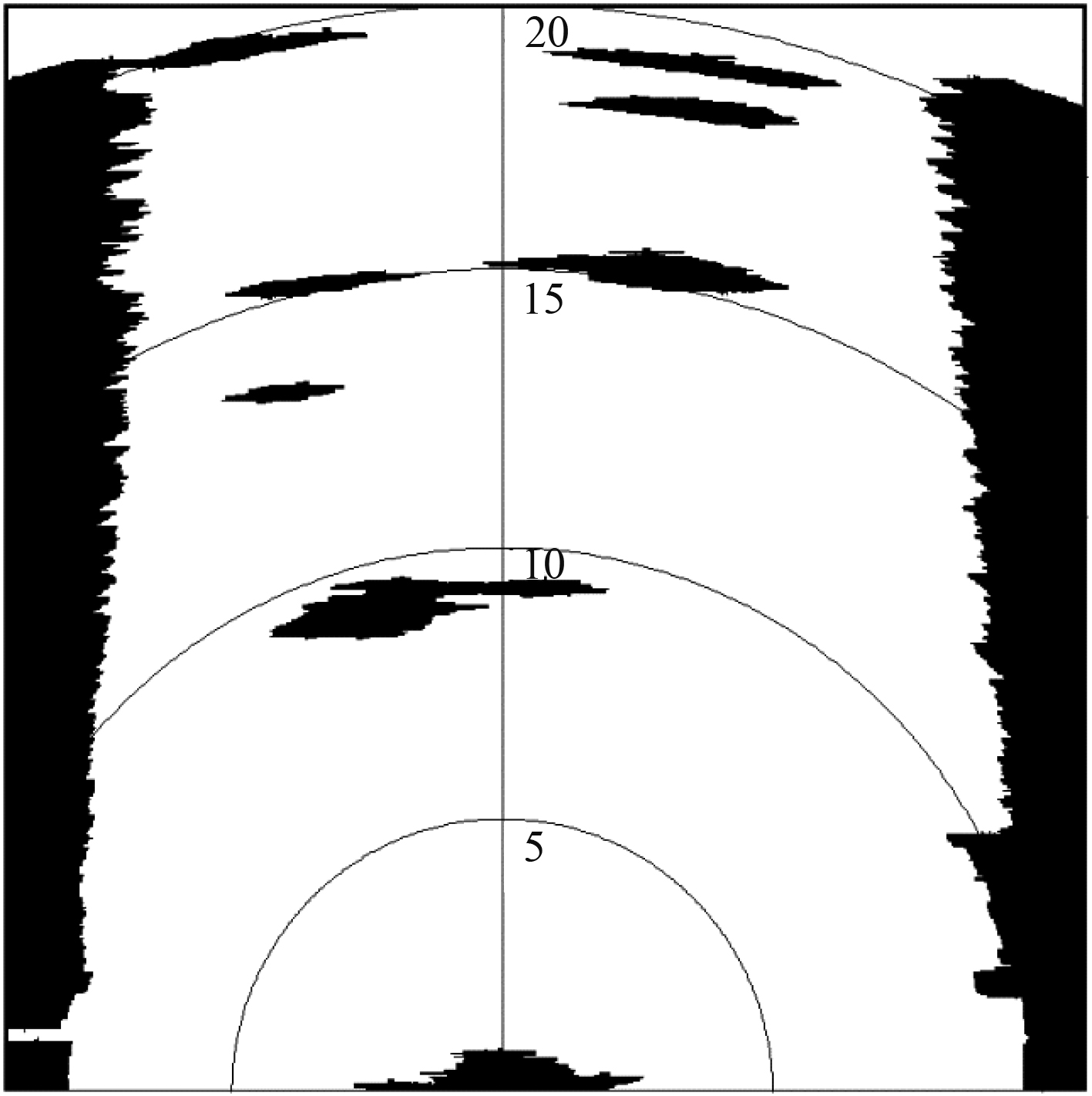
|
图 14 扩大障碍物后的地图 Fig. 14 Map after enlarging the obstacle |
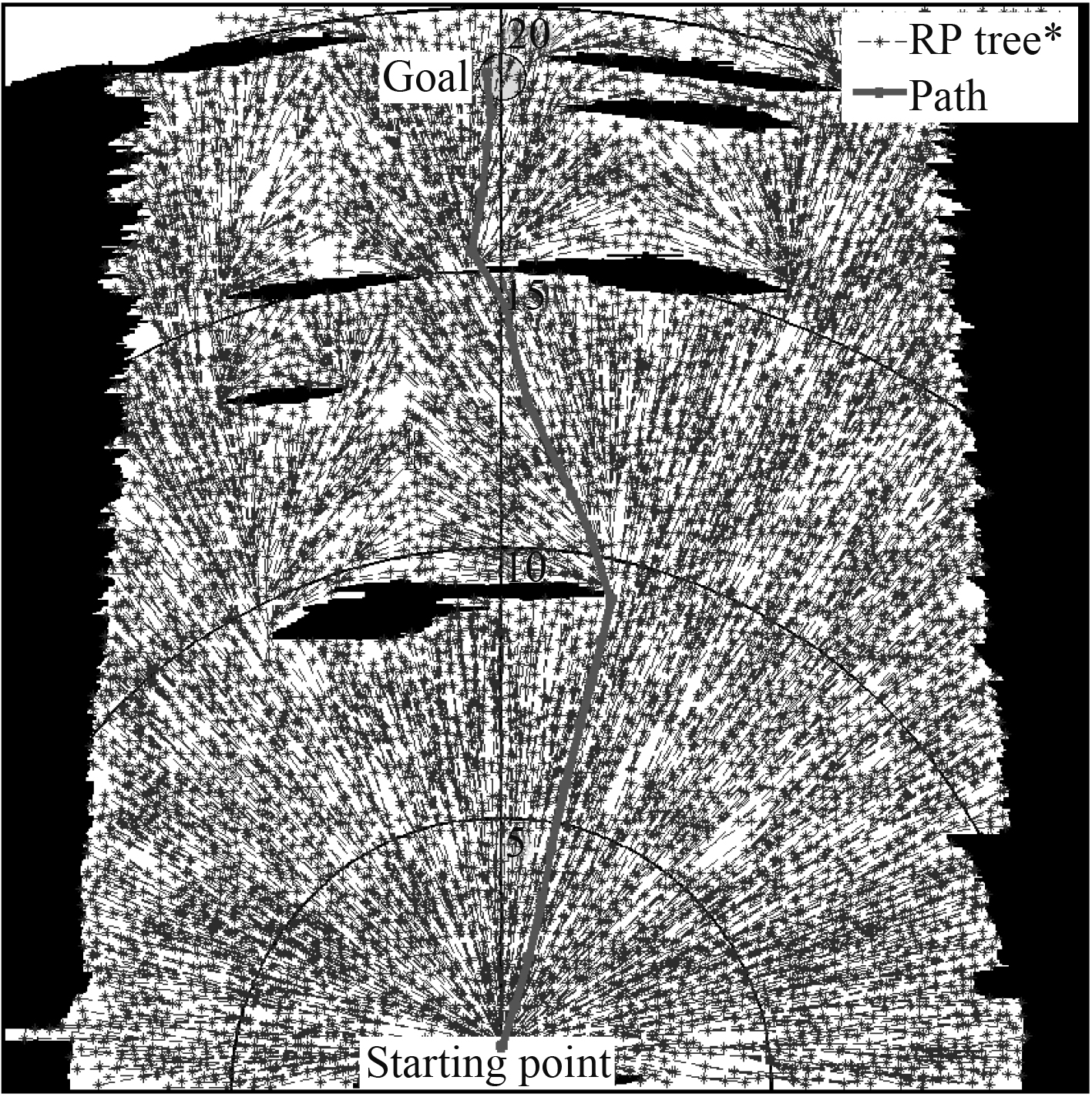
|
图 15 水下机器人路径规划结果 Fig. 15 Path planning results of underwater vehicle |
从图15可看出,水下机器人在该环境下实施路径最短路径规划和能耗最低路径规划得出的路径完全一致。该水池实验路径规划结果表明了所设计的基于RRT*的路径最短和能耗最低的路径规划算法可行有效。
5 结 语本文针对复杂海洋环境中水下机器人路径规划问题展开研究,综合考虑规划路径长度与全程能耗,设计出基于RRT*的路径最短和能耗最低的路径规划算法,继而进行仿真模拟和实验室现有水下机器人平台的真机实现,仿真及真机验证结果显示所设计的路径规划算法可行有效,为后期海上应用奠定基础。
| [1] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. DOI:10.1109/TSSC.1968.300136 |
| [2] |
WANG Z, XIANG X, YANG J, et al. Composite Astar and B-spline algorithm for path planning of autonomous underwater vehicle[C].Underwater System Technology: Theory and Applications (USYS), 2017 IEEE 7th International Conference on. IEEE, 2017: 1-6.
|
| [3] |
YU H, SHEN A, SU Y. CONTINUOUS MOTION PLANNING IN COMPLEX AND DYNAMIC UNDERWATER ENVIRONMENTS[J]. INTERNATIONAL JOURNAL OF ROBOTICS & AUTOMATION, 2015, 30(2): 192-204. |
| [4] |
Y. KOREN, J. BORENSTEIN, Potential field methods and their inherent limitations for mobile robot navigation, in: Robotics and Automation, 1991. Proceedings. 1991 IEEE International Conference on, IEEE, 1991, pp. 1398–1404.
|
| [5] |
杨健, 孟凡尘. 基于人工势场法的微小型AUV避障运动方法研究[J]. 水雷战与舰船防护, 2017, 4: 016. YANG Jian, MENG Fanchen. Research on Mini-AUV’s Avoiding Obstacle Motion Method Based on Artificial Potential Field Algorithm[J]. Mine Warfare & Ship Self-Defence, 2017, 4: 016. |
| [6] |
AMIRI Z, POUYAN A, MASHAYEKHI H. A topology control algorithm for autonomous underwater robots in three-dimensional space using PSO[J]. Journal of AI and Data Mining, 2015, 3(2): 191-201. |
| [7] |
WANG H, YUAN J, LV H, et al. Task allocation and online path planning for AUV swarm cooperation[C]. OCEANS 2017-Aberdeen. IEEE, 2017: 1-6.
|
| [8] |
LUAN X L, GONG F X, WEI Z Q, et al. Using Ant Colony Optimization and Cuckoo Search in AUV 3D Path Planning[C]. Software Engineering and Information Technology: Proceedings of the 2015 International Conference on Software Engineering and Information Technology (SEIT2015). 2016: 208-212.
|
| [9] |
TANAKITKORN K, WILSON P A, TURNOCK S R, et al. Grid-based GA path planning with improved cost function for an over-actuated hover-capable AUV[C]. Autonomous Underwater Vehicles (AUV), 2014 IEEE/OES. IEEE, 2014: 1-8.
|
| [10] |
AGHABABA M P, AMROLLAHI M H, BORJKHANI M. Application of GA, PSO, and ACO algorithms to path planning of autonomous underwater vehicles[J]. Journal of Marine Science and Application, 2012, 11(3): 378-386. DOI:10.1007/s11804-012-1146-x |
| [11] |
YU L, WEI Z, WANG Z, et al. Path optimization of AUV based on smooth-RRT algorithm[C]. Mechatronics and Automation (ICMA), 2017 IEEE International Conference on. IEEE, 2017: 1498-1502.
|
| [12] |
S. KARAMAN, E. FRAZZOLI. Incremental sampling-based algorithms for optimal motion planning[J]. Robotics Science and SYSTEMS VI, 2010, 104: 2. |
| [13] |
FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles[M]. Marine Cybernetics, 2002. P106-138.
|
 2019, Vol. 41
2019, Vol. 41
