2. 威海市机器人与智能装备产业研究院,山东 威海 264209
2. Weihai Robot and Intelligent Equipment Indastrg Research Institute, Weihai 264209, China
水下机器人是人类探索海洋的重要工具,能在水下复杂环境中完成有风险的作业和任务。便携式ROV以其体积小、重量轻、成本低、投放使用简单等特点在水文监测、水产养殖等领域具有广阔的应用前景[1]。与AUV相比,ROV的推进器数量及布局形式与其自由度数目、运动性能以及控制方式有着密切联系,常见的推进器数量有3个、4个、6个、8个,加上安装位置的不同,ROV演变出多种布局形式和结构外形。对运动性能要求较高的作业级、深海级ROV多数采用六推、八推的形式,全自由度运动能力使其能够在变幻莫测的水下抵抗各个方向的干扰,保证设备运动的稳定性和任务执行的可靠性。而观察级ROV主要应用于近海、湖泊、水库等浅水水域,且出于成本、体积重量的考虑,常被设计出少自由度或欠驱动系统[2],因此多采用三推、四推的布局形式。因此,研究推进器数量少于系统自由度的欠驱动水下机器人具有重要的现实意义。
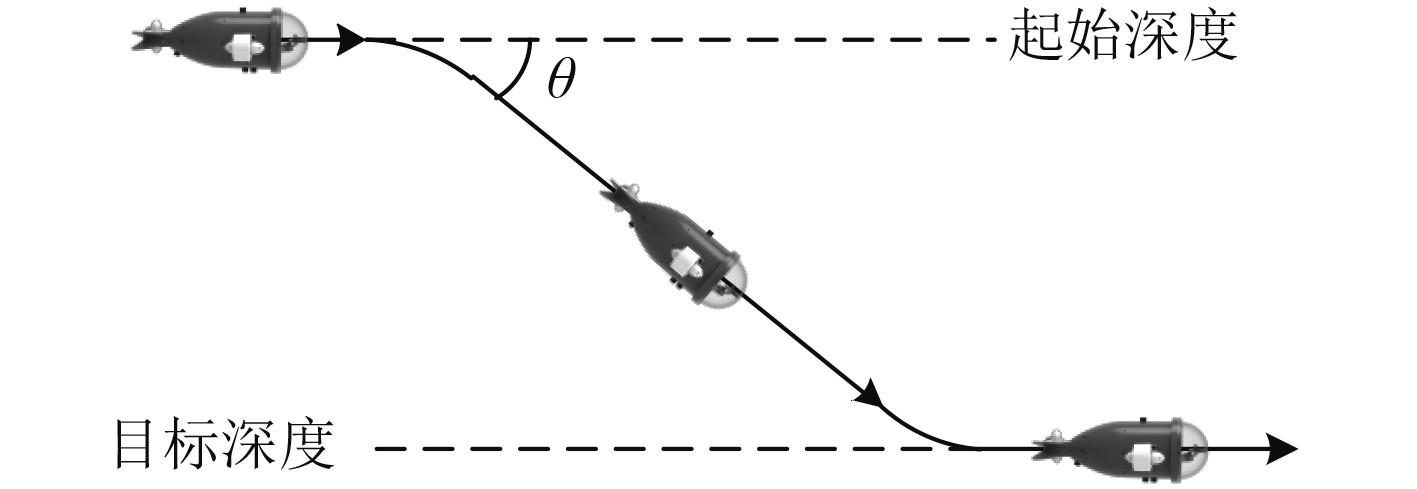
自动定深控制是水下机器人的关键技术之一,它可保证水下机器人自动到达并维持在指定深度,抵抗水下浪涌的干扰,实现水下稳定悬停观测及作业。本文研制的便携式ROV属于欠驱动系统,它安装有3个推进器,布置形式为中部两水平推进器和尾部单垂直推进器,这种布局使它的定深运动需要通过改变俯仰角的方式来实现,如图1所示。考虑到便携式ROV体积小、重量轻,容易受到波浪干扰,则分析其斜航定深过程中的航速、俯仰角度对运动稳定性的影响是十分必要。针对这种非定常运动,Fluent提供的动网格技术可对其进行模拟仿真,通过编写用户自定义函数预定义运动形式并导入Fluent中,便可实时获取水动力和运动参数[3 – 5]。
|
图 1 斜航定深示意图 Fig. 1 Oblique depth keeping of portable ROV |
为了实现水下机器人自动定深的稳定控制,国内外学者做了大量的研究工作,研究思路可划分为2种:一种是引进智能算法到水下机器人的运动控制中,另一种是将多种算法融合使用,取长补短以提升控制性能[6]。王建华等[7]构造了一种串级PID控制器并应用到ROV俯仰控制;乔磊等[8]提出了一种自适应鲁棒PID控制器用于水下近距离作业ROV的动态定位;董早鹏[9]针对欠驱动水下机器人直航跟踪控制问题提出了一种结合 BP 神经网络的T-S模糊控制器。但水下机器人运动控制器并非越复杂越好,应注重方便实用,易于实现[10]。
本文以研制的便携式ROV为研究对象,基于Fluent的动网格技术对其斜航定深运动特性进行分析,并设计了自动定深的双闭环模糊PID控制器。通过施加不同工况下的干扰,与传统PID控制器对比仿真。结果表明,双闭环模糊PID控制器具有有效性和适用性。本文可为小型ROV的研发设计与改进优化提供参考。
1 定深运动特性分析 1.1 控制方程与湍流模型对Navier-Stokes方程进行雷诺平均后得到RANS方程,其连续方程和动量方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0{\text{,}} $ | (1) |
| $ \begin{align} & \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \\ & \frac{\partial }{{\partial {x_j}}}\left[\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_l}}}{{\partial {x_l}}})\right] + \frac{\partial }{{\partial {x_j}}}( - \rho \overline {u_i'u_j'} ) {\text{。}} \end{align} $ | (2) |
采用的计算域总长为10 L,直径4 L,内流域总长为2 L,直径1.5 L,其中L为ROV长度,计算域入口距艇首3 L,艇尾距计算域出口5 L。计算域坐标系选取与ROV动系一致,坐标原点位于重心处。
网格划分采用结构与非结构网格相混合的划分方式,内流域采用适应能力好的非结构化网格划分,并对ROV复杂表面周围的网格进行细化处理,而形状规则的外流域采用质量可控的结构化网格划分。为了保证数值模拟计算的准确性和速度,划分网格数量共计130万,网格质量控制在0.65之上。各个计算域边界条件如表1所示。
|
|
表 1 边界条件 Tab.1 Boundary conditions |

|
图 2 网格划分图 Fig. 2 Mesh generation |
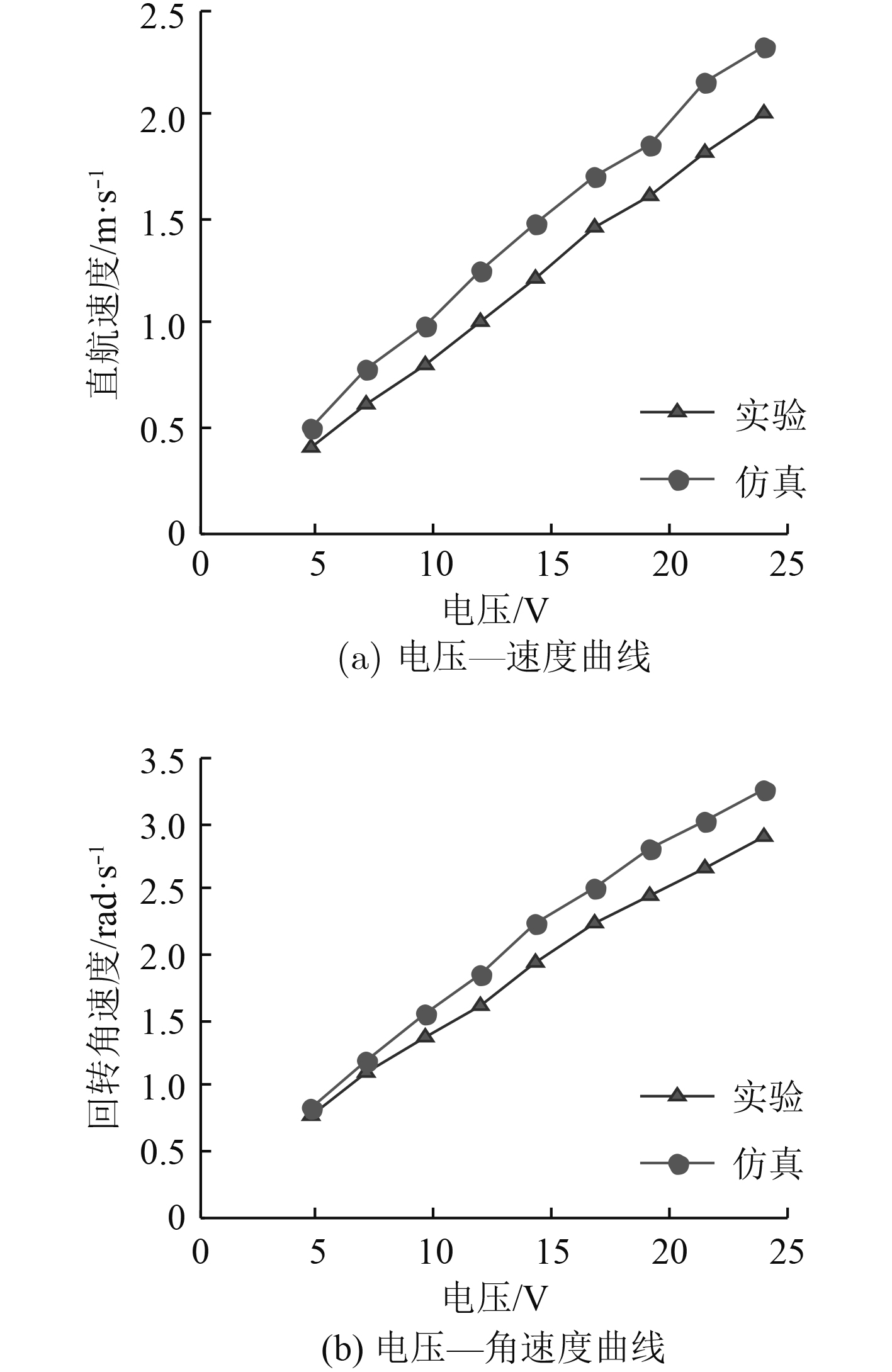
便携式ROV斜航定深属于非定常运动,可调用Fluent UDF中的DEFINE宏来自定义运动规律进行模拟并分析其运动特性。为了验证模拟计算的准确性,采用6DOF动网格模型对ROV水平面直航、转首简单定常运动进行了仿真计算,通过施加特定推力和力矩模拟计算出便携式ROV在不同电压的直航速度和回转角速度,并与实验结果进行对比,结果如图3所示。
|
图 3 数值模拟方法验证 Fig. 3 Validation of numerical simulation |
由图3可知,模拟计算结果与实验数据变化规律基本一致,且最大误差不超过10%,具有较高的可信度,验证了模型选择和参数设置的有效性和准确性。
便携式ROV斜航定深时的主要变量为俯仰角度和航行速度,影响其运动机动性和稳定性的主要参数是航行阻力和俯仰力矩。因此,基于以上模型编制UDF函数分别模拟了ROV在固定航速1 m/s,俯仰角度10°~45°(间隔
|
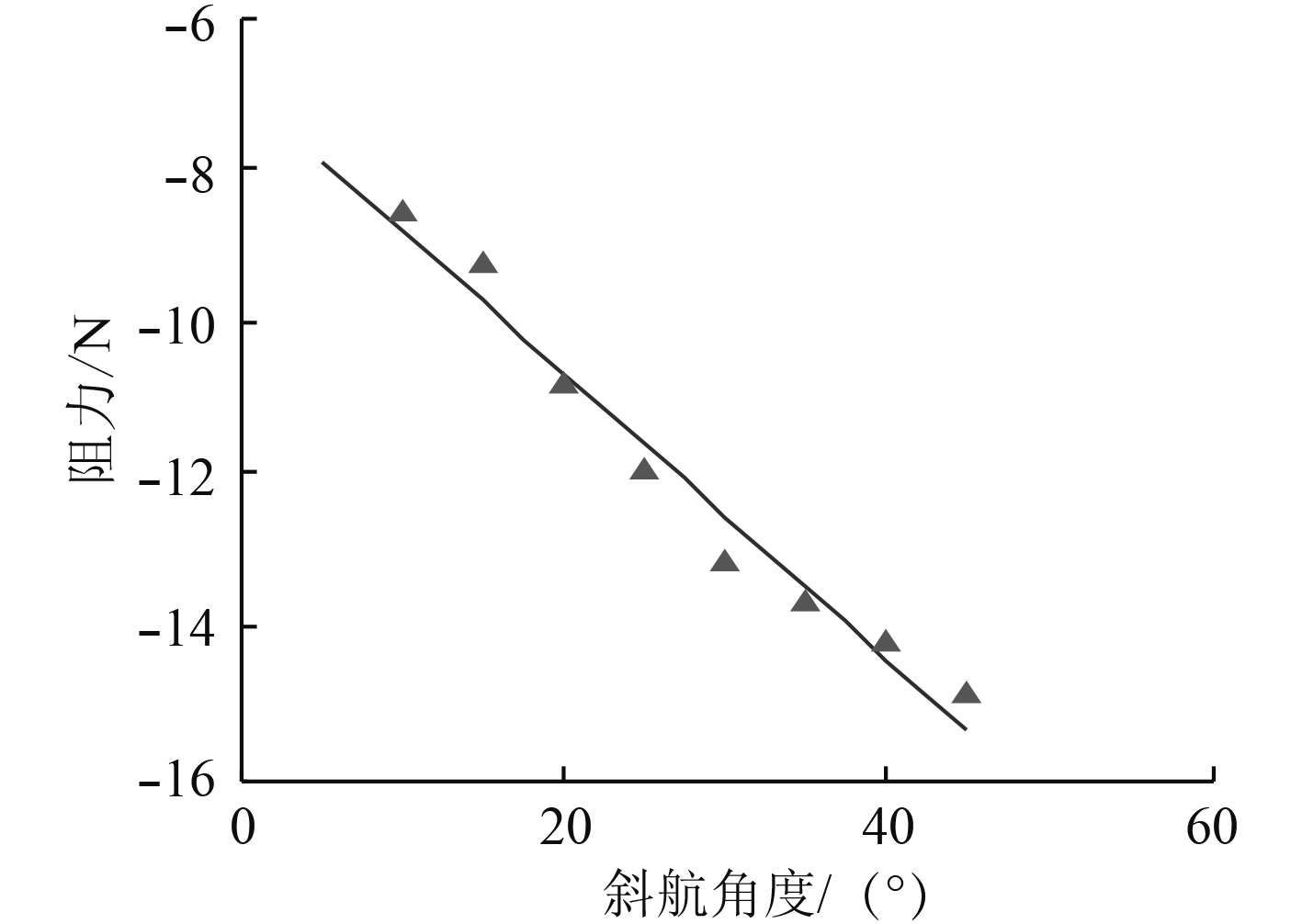
图 4 航行阻力随斜航角度变化曲线 Fig. 4 The curves of navigation resistance as pitch angle |
|
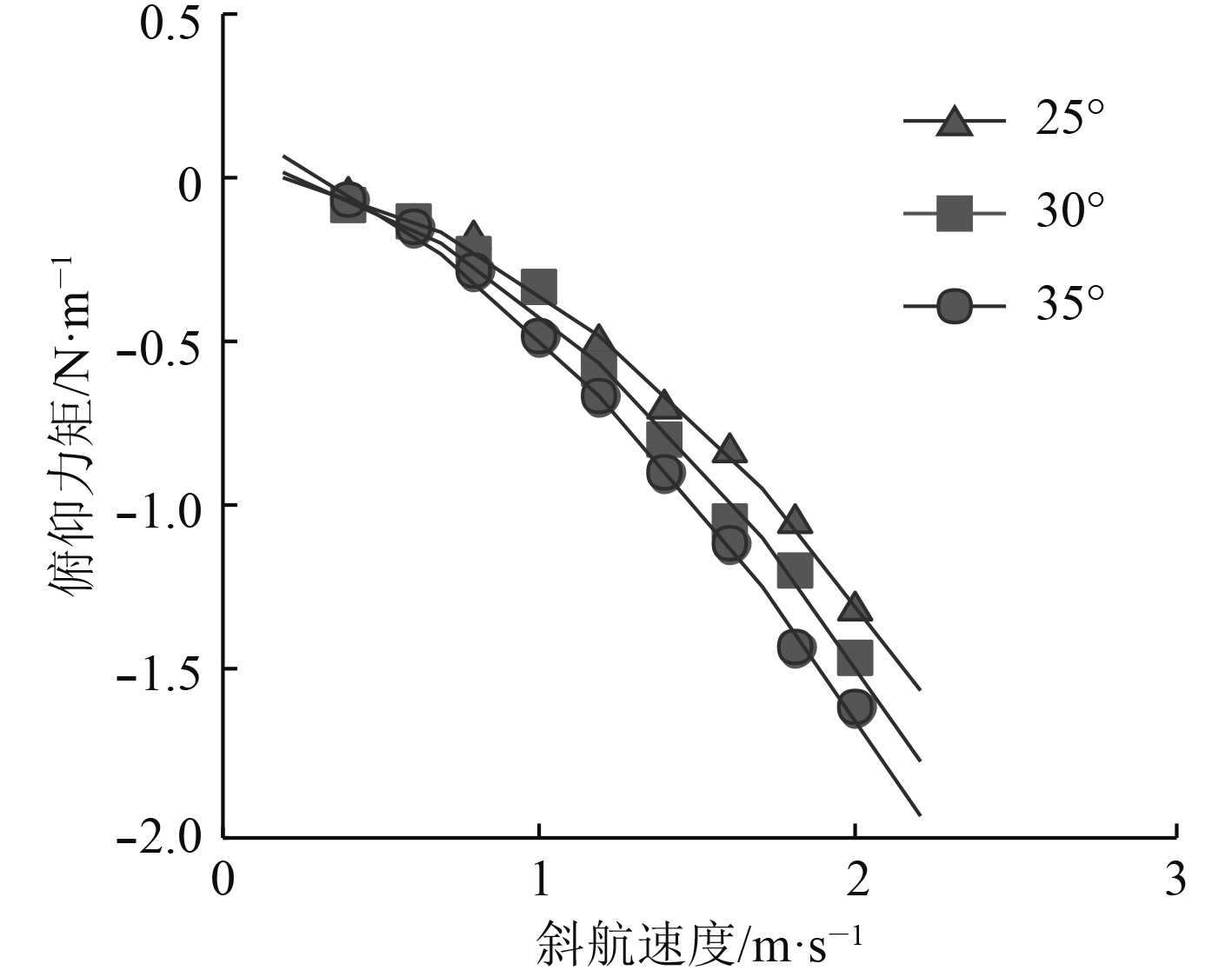
图 7 俯仰力矩随斜航速度变化曲线 Fig. 7 The curves of pitch moment as speed |
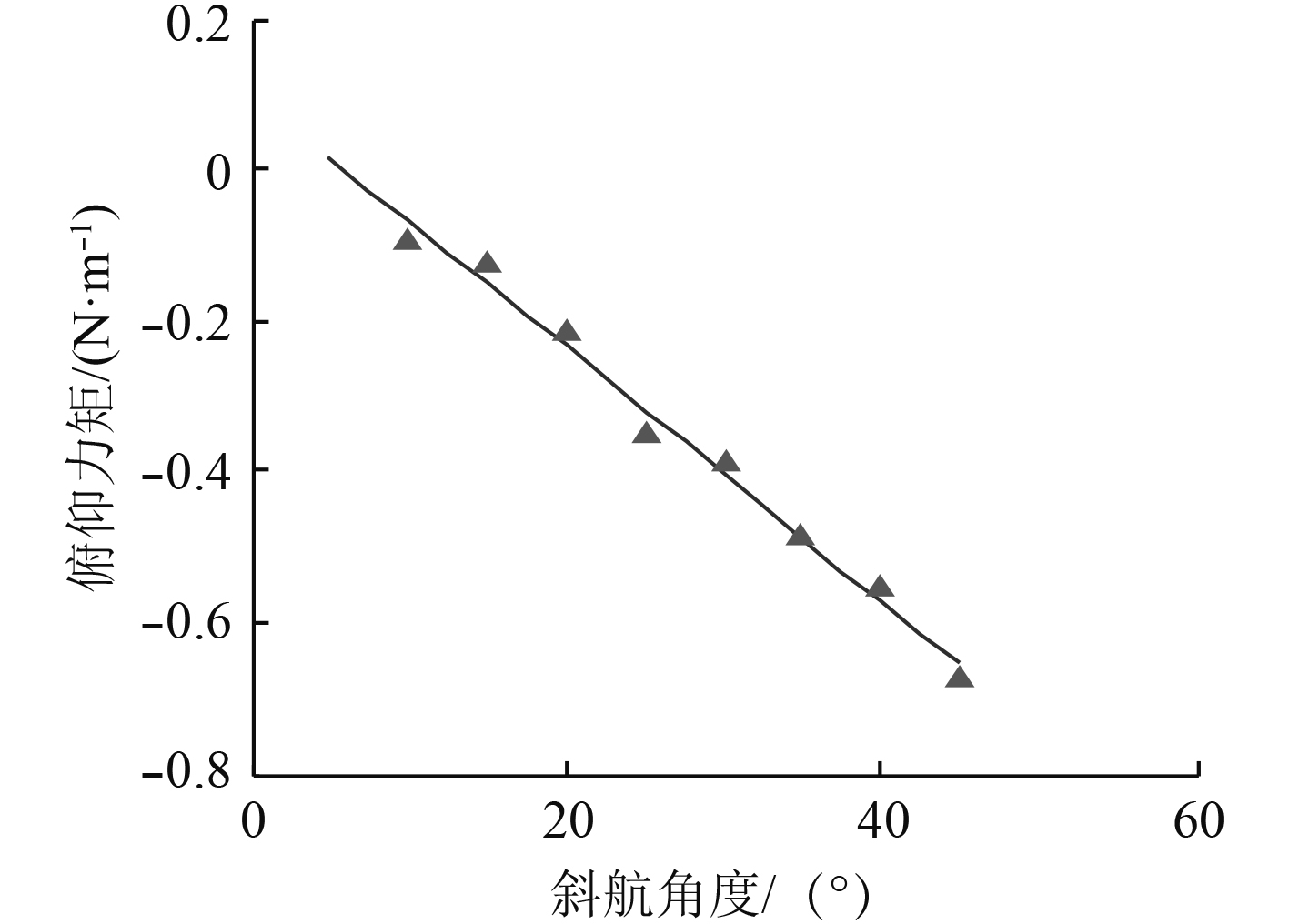
由图4和图5可知,ROV所受阻力和俯仰力矩与斜航角度呈线性关系,并随着斜航角度的增加而增大。航行阻力主要由压差阻力和粘性阻力组成,其中压差阻力占据主导地位。造成上述现象的原因在于ROV首部和尾部的深度差、流速差和湍流旋涡等因素造成前后压力分布不均匀,产生压差阻力和俯仰力矩,从而引起ROV的上下摇摆晃动和偏航。
|
图 5 俯仰力矩随斜航角度变化曲线 Fig. 5 The curves of pitch moment as pitch angle |
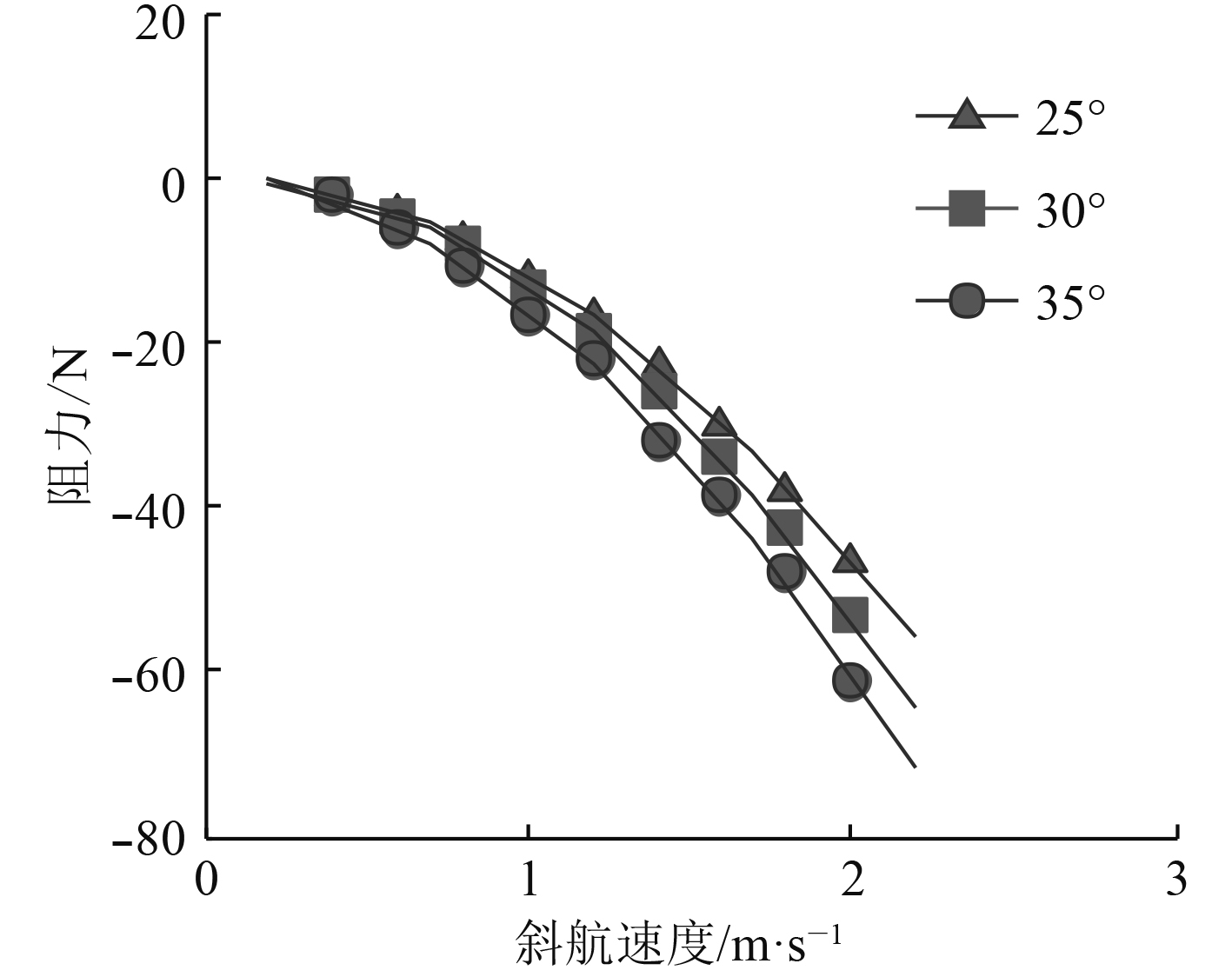
由图6和图7可知,ROV所受阻力与俯仰力矩与斜航速度呈二次函数关系,并随着斜航速度的增加而增大。由于斜航速度的变化导致便携式ROV周围的流场变化更为剧烈,首尾速度差、压力差也变化更大,造成航行阻力和俯仰力矩变化幅度较大,严重影响其航行稳定性。为确保便携式ROV在斜航定深过程中的机动性和稳定性,同时降低能量损耗和调控频率,本文选取便携式ROV定深运动的斜航角度不超过
|
图 6 航行阻力随斜航速度变化曲线 Fig. 6 The curves of navigation resistance as speed |
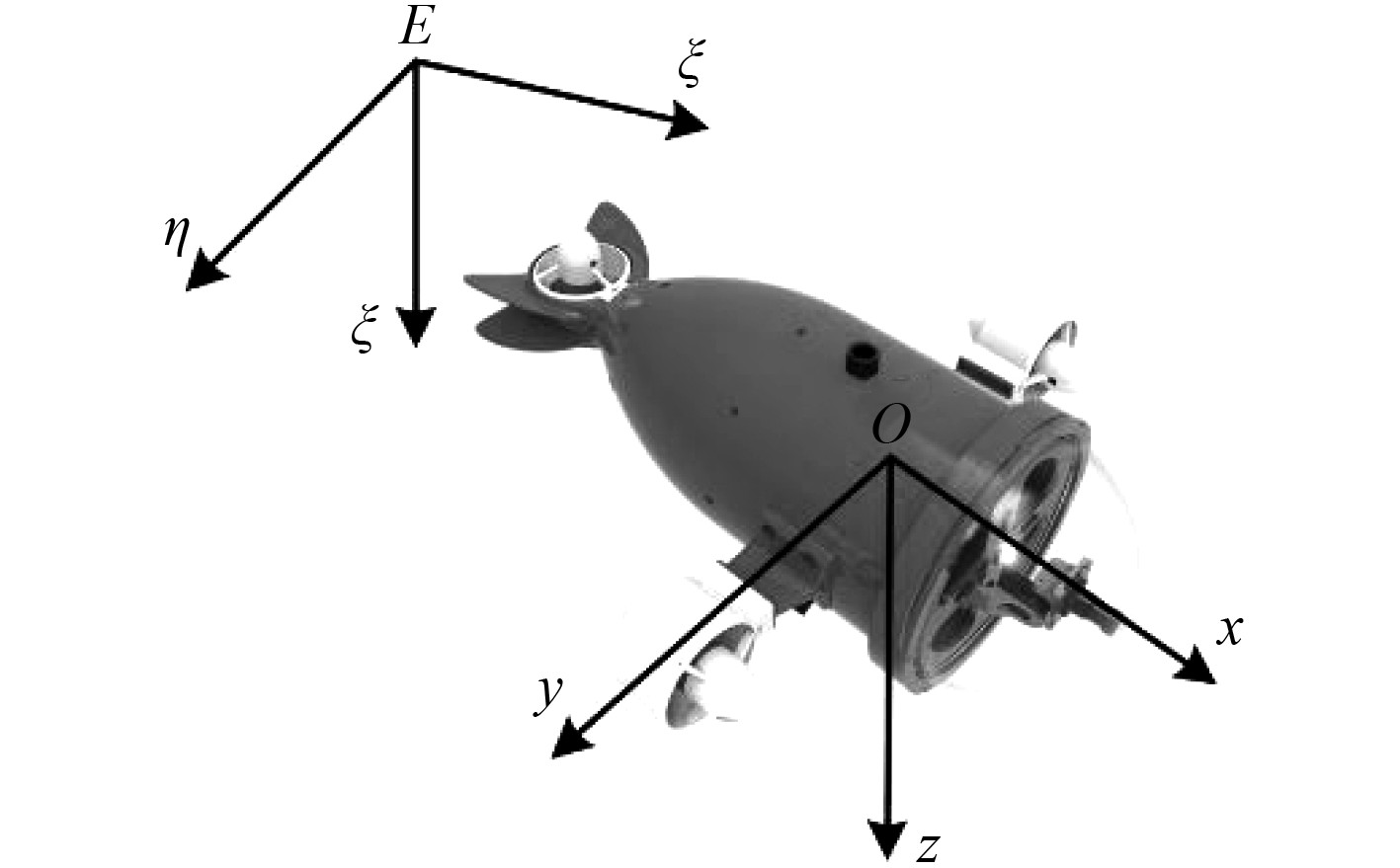
为了问题研究的方便,采用2个参考坐标系对便携式ROV进行位姿描述,即惯性坐标系
|
图 8 便携式ROV参考坐标系 Fig. 8 Reference coordinate of portable ROV |
| ${{\dot{ \eta }}_{\rm{1}}} = \left[ {\begin{array}{*{20}{c}} {\operatorname{c} \psi \operatorname{c} \theta } \!\!&\!\! { - \operatorname{s} \psi \operatorname{c} \phi + \operatorname{c} \psi \operatorname{s} \theta \operatorname{s} \phi } \!\!&\!\! {\operatorname{s} \psi \operatorname{s} \phi + \operatorname{c} \psi \operatorname{s} \theta \operatorname{c} \phi } \\ {\operatorname{s} \psi \operatorname{c} \theta } \!\!&\!\! {\operatorname{c} \psi \operatorname{c} \phi + \operatorname{s} \psi \operatorname{s} \theta \operatorname{s} \phi } \!\!&\!\! { - \operatorname{c} \psi \operatorname{s} \phi + \operatorname{s} \psi \operatorname{s} \theta \operatorname{c} \phi } \\ { - \operatorname{s} \theta } \!\!&\!\! {\operatorname{c} \theta \operatorname{s} \phi } \!\!&\!\! {\operatorname{c} \theta \operatorname{c} \phi } \end{array}} \right]{{{\upsilon }}}{\text{,}}$ | (3) |
| ${{{\dot \eta }}_{\rm{2}}} = \left[ {\begin{array}{*{20}{c}} 1&{\operatorname{s} \phi \tan \theta }&{\operatorname{c} \phi \tan \theta } \\ 0&{\operatorname{c} \phi }&{ - \operatorname{s} \phi } \\ 0&{\operatorname{s} \phi /\operatorname{c} \theta }&{\operatorname{c} \phi /\operatorname{c} \theta } \end{array}} \right]{{{\upsilon }}_{\rm{2}}}{\text{。}}$ | (4) |
出于运动分析方便的考虑,通常将水下机器人的空间运动划分为水平面运动和垂直面运动,本文只研究便携式ROV的垂直面运动。其动力学模型可表示为
| ${ M}{\dot{ \upsilon + }}{ C}({{\upsilon }}){{\upsilon + }}{ D}({{\upsilon }}){{\upsilon + }}{g}({{\eta }}) = {{\tau }}{\text{。}}$ | (5) |
式中:
便携式ROV定深控制需配合倾角变化来实现,因此采用双闭环模糊PID控制器,如图9所示。内环为倾角环,反馈装置为姿态传感器;外环为深度环,采用深度传感器作为反馈装置。倾角环与深度环采用同一模糊PID控制器,通过调整量化因子与比例因子以匹配两者物理论域的不同。

|
图 9 定深控制器结构 Fig. 9 Structure of depth controller |
模糊PID控制器由1个模糊控制器和1个PID控制器组成,模糊控制器的输入量为深度或倾角的偏差和偏差变化率,输出量为PID参数的修正量,从而实时在线整定PID参数,解决PID控制器全局最优参数设定困难的问题。模糊控制器的输入量和输出量的偏差变化范围,即论域为{–3,–2 –1,0,1,2,3},对应着模糊子集{NB, NM, NS, ZE, PS, PM, PB},隶属度函数两侧分别为Z型和S型,中部为对称的三角形函数。在斜航定深过程中,模糊PID控制器根据隶属度函数将深度和倾角的偏差和偏差变化率模糊化,并在线查询模糊控制规则表进行模糊推理,得到
本文以便携式ROV为研究对象,其本体重量为6.6 kg,外形尺寸(长×宽×高)为490 mm×395 mm×180 mm,最大工作深度可达30 m,利用流体仿真软件进行数值模拟得到便携式ROV的部分水动力系数如表2所示。
|
|
表 2 无因次水动力系数 Tab.2 Hydraulic coefficients of portable ROV |
根据上述简化运动模型和水动力系数进行Simlink仿真,定深策略为以固定俯仰角
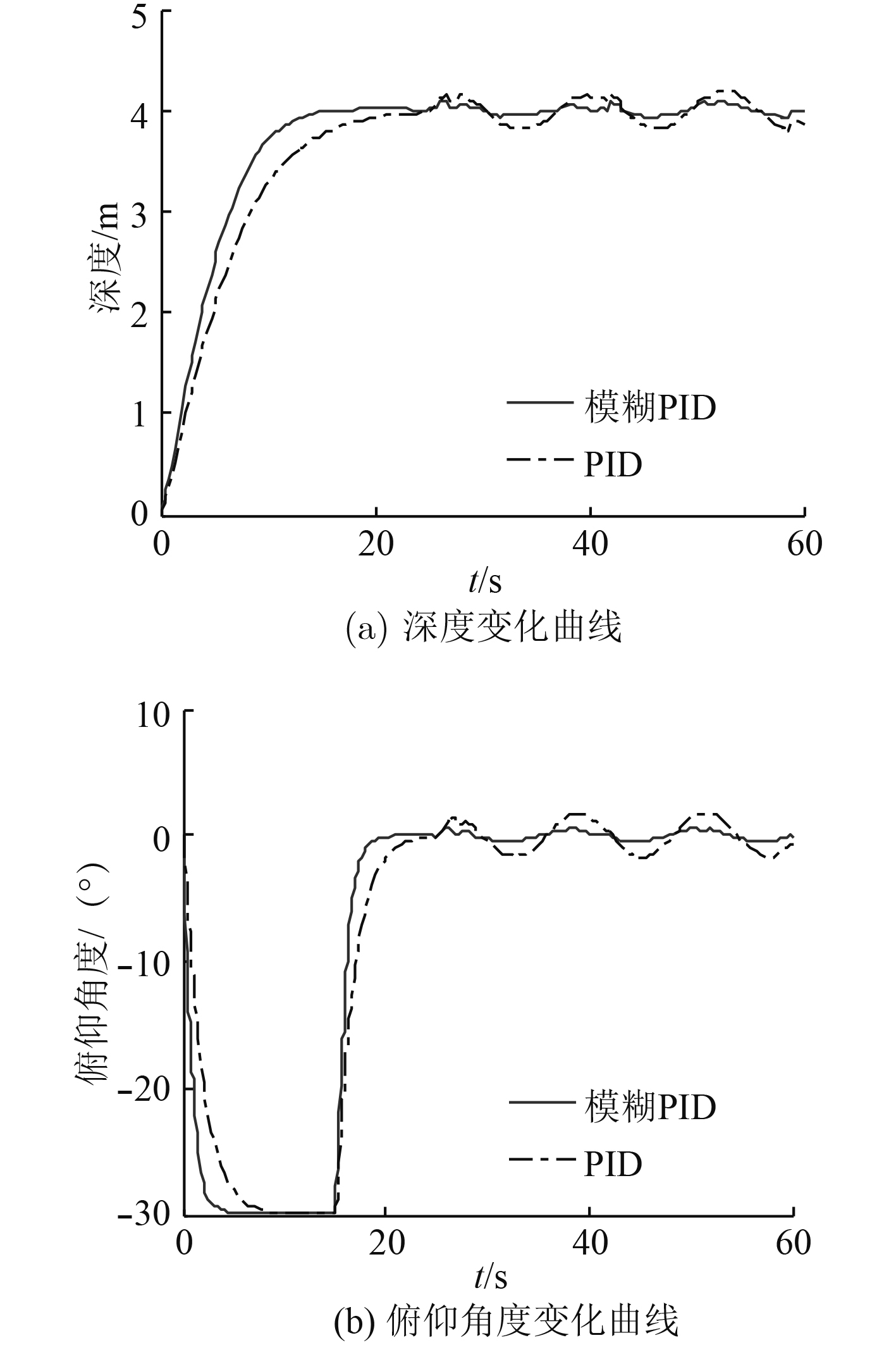
便携式ROV在浅水区工作时,易受海流和波浪的综合影响,因此施加由正弦信号和白噪声组成的随机信号,用于模拟ROV受到的外界环境干扰,仿真期望深度为4 m,仿真结果如图10所示。
由图10可知,2种控制器都能在浅水区实现定深控制,但模糊PID控制器可根据环境变化实时修正PID参数,具备更好的鲁棒性和适应能力。在到达指定深度后,基于PID控制的俯仰角由于海流与波浪的干扰在
|
图 10 浅水区定深控制的对比仿真结果 Fig. 10 Depth control in the disturbance of shallow water area |
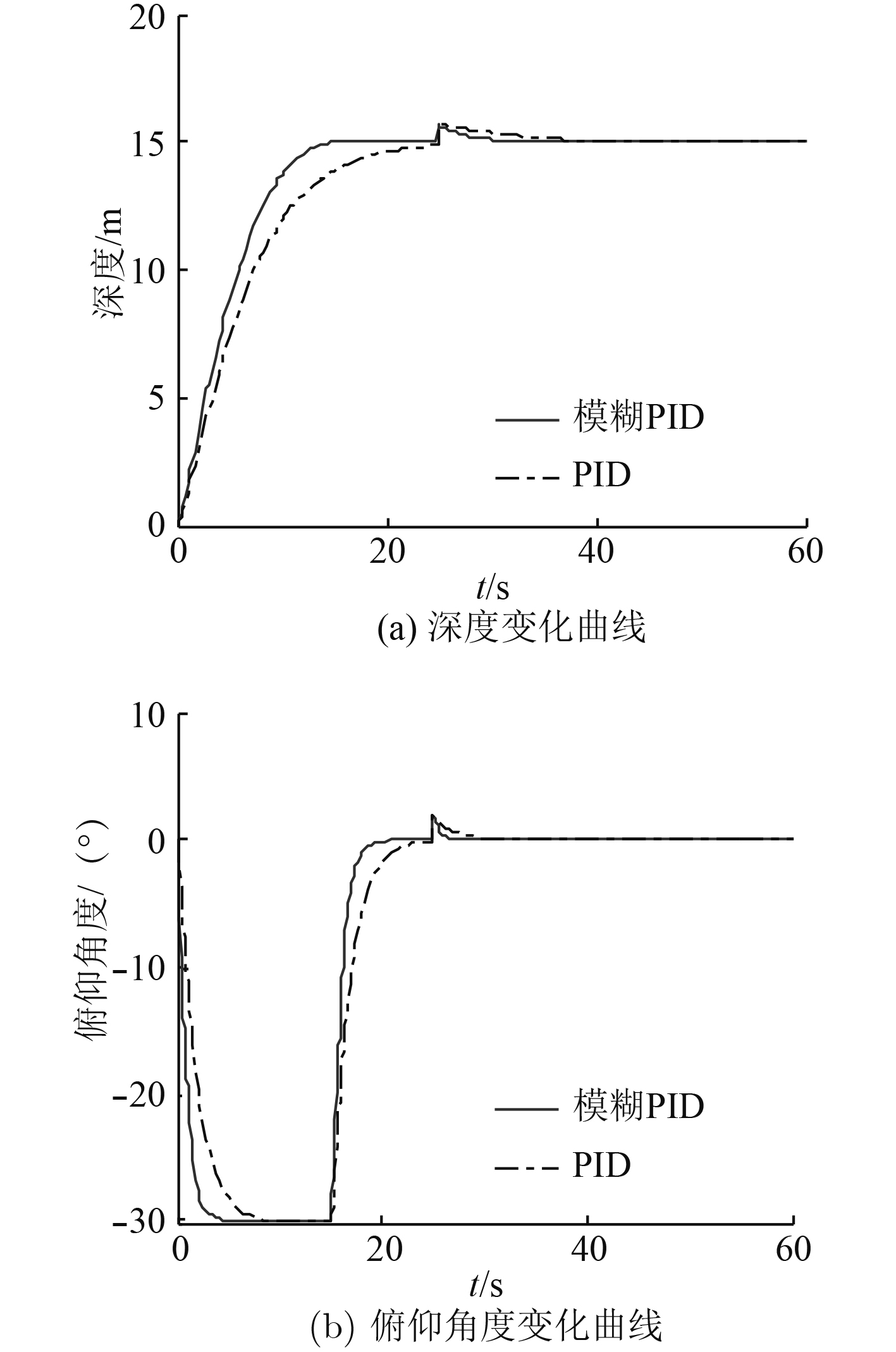
当便携式ROV深水区工作时,海流对其垂直面运动影响较弱,主要干扰为水底浪涌的瞬时干扰。因此在仿真过程中主要施加阶跃信号模拟浪涌造成的瞬时干扰,干扰起始时间为t=10 s,期望深度15 m,仿真结果如图11所示。
由图11可以看出,2种控制器均能抵御由浪涌造成的瞬时干扰,但相较于PID控制器,模糊PID控制器在受到瞬时干扰后能在较短的时间内消除超调影响,具有更好的响应能力和恢复能力。
|
图 11 深水区定深控制下的对比仿真结果 Fig. 11 Depth control in the disturbance of deep water area |
1)利用Fluent的动网格技术和用户自定义函数对便携式ROV斜航定深运动进行数值模拟,并研究分析了航速与俯仰角度对ROV稳定性的影响。仿真结果表明斜航阻力和俯仰力矩与俯仰角呈线性关系,与航速呈二次函数关系。考虑到能源损耗和稳定性,确定了便携式ROV斜航定深时的最大航速为1 m/s,倾角不超过
2)提出一种基于双闭环模糊PID的自动定深控制器,并与传统PID控制进行了对比仿真。仿真过程中施加了不同工况下的模拟干扰信号,结果显示该控制器具有更好的控制性能,可实现便携式ROV自动定深功能,为其执行任务提供更稳定的工作状态。
| [1] |
曾俊宝, 李硕, 李一平, 等. 便携式自主水下机器人控制系统研究与应用[J]. 机器人, 2016, 38(1): 91-97. |
| [2] |
毕凤阳, 张嘉钟, 魏英杰, 等. 模型不确定时滞欠驱动AUV的模糊变结构控制[J]. 哈尔滨工业大学学报, 2010, 42(3): 358-363. DOI:10.11918/j.issn.0367-6234.2010.03.005 |
| [3] |
李迎华, 吴宝山, 张华. CFD动态网格技术在水下航行体非定常操纵运动预报中的应用研究[J]. 船舶力学, 2010, 14(10): 1100-1108. DOI:10.3969/j.issn.1007-7294.2010.10.004 |
| [4] |
吴家鸣, 钟乐, 张恩伟, 等. 基于动网格技术研究海流对水下机器人运动特性的影响[J]. 舰船科学技术, 2017, 39(12): 20-25. DOI:10.3404/j.issn.1672-7649.2017.12.005 |
| [5] |
吴家鸣, 郁苗, 朱琳琳. 遥控水下机器人水动力数学模型及其回转运动分析[J]. 船舶力学, 2011, 15(8): 827-836. DOI:10.3969/j.issn.1007-7294.2011.08.001 |
| [6] |
万磊, 张英浩, 孙玉山, 等. 复杂环境下的欠驱动智能水下机器人定深跟踪控制[J]. 上海交通大学学报, 2015, 49(12): 1849-1854. |
| [7] |
王建华, 宋燕, 魏国亮. 串级PID控制在水下机器人俯仰控制系统中的应用[J]. 上海理工大学学报, 2017, 39(3): 229-235. |
| [8] |
QIAO Lei, ZHANG Li-xing, ZHANG Wei-dong. Robust adaptive PID control for positioning of remotely operated vehicle working in close proximity of an underwater structure[C]. Proceedings of the 35th Chinese Control Conference. Chengdu, 2016: 5780-5785.
|
| [9] |
董早鹏, 刘涛, 万磊. 基于 Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制[J]. 仪器仪表学报, 2015, 36(4): 863-870. |
| [10] |
张为民, 郭晨. 船舶航向PID型模糊控制器研究[J]. 中国造船, 2012, 53(1): 45-51. |
 2019, Vol. 41
2019, Vol. 41
