0 引　言

周期加肋板结构作为一类重要的工程结构形式，在舰船、机械、船舶及航空航天等领域的应用非常广泛。加肋板结构可以显著提高舰船及船舶等设备的力学性能及有效抵抗航行时的水流冲击作用，在船体的上、下层板及船侧外板中加肋板结构的应用较为普遍，因而其结构振动问题的相关研究在工程应用中具有重要作用，其中包含结构的声振耦合效应。由于加肋板结构声振领域问题的多样性与复杂性，其结构振动响应及相关声学性质是诸多工程领域的研究热点。Lamb^[1]，Maidanik^[2]和Heckl^[3]等对加肋板结构的振动响应或声学特性进行了早期相关研究。其中，Lamb分析了点力激励下的单周期加肋板的弯曲振动；Maidanik采用统计计算法分析了散射场内加肋板的振动响应性质，并探讨了加强肋对结构辐射阻抗的影响；Heckl研究了单周期加肋板结构的板内弯曲波的传播性质，并分析了加强肋对板的阻尼作用以及弯曲波的衰减特性。

在周期结构振动特性的相关研究中，Mercer^[4]较早采用传递矩阵法对单周期结构的振动性质进行了分析，Zhong和Williams^[5]则结合结构的周期特性进行分析，令其声振问题的分析求解更加简洁精确。Rumerman^[5]分析了单周期加肋板的振动响应及板内弯曲波的传播特性，并在文献中将周期加强肋的数学模型等效成周期线力和线矩。Mead^{[6 – 7]}和Mace^{[8 – 9]}基于谐波法，研究了单、双周期加肋板在谐振力激励下的振动响应及声辐射特性。其中，Mead^[7]分析了板内弯曲波在传播过程中由于结构振动及声辐射而导致的能量衰减损失，然而文献中所提出的方法没有实现加肋板与水流体的流固耦合作用。此后，基于有限元方法，Mead^[10]研究了一维耦合周期结构的振动响应性质，此方法在分析不同类型的周期结构时具有显著优势。结合离散傅里叶变换及结构周期理论，Maxit^[11]研究了单周期加肋板结构在点力作用下的振动响应及辐射声压。Zhou等^[12]通过谐波法和格林函数分析了双周期加肋板结构的振动特性及远场辐射声压。Lee和Kim^[13]则基于谐波法对单周期加肋板结构的振动及声透射特性进行了理论分析与计算。Legault等^[14]采用瑞利—李兹法(Rayleigh-Ritz method)等数学方法研究了周期加肋板结构在点激励、平面声波激励以及随机激励状况下的振动响应及声学特性。金叶青^[15]等通过数值截断的方法对均匀流中考虑剪切变形的加肋层合板的声振特性进行了研究。此外，Dozio^[16]、李凯^[17]和周俊平^[18]等通过半解析半数值的数学方法分析了加肋板的自由振动或声辐射特性。

对于无穷大模型的周期加肋板结构，考虑到结构的周期特性及流固耦合作用，在分析其相关声振问题时，可以在周期单元拓展分析的基础上，结合解析法或半解析法进行研究。本文通过谐波法和单、双重傅里叶变换相结合的方法对谐振激励力作用下的周期正交加肋板的振动性质进行理论分析，揭示了结构的振动响应特性，并分析了加强肋作用对结构的影响。

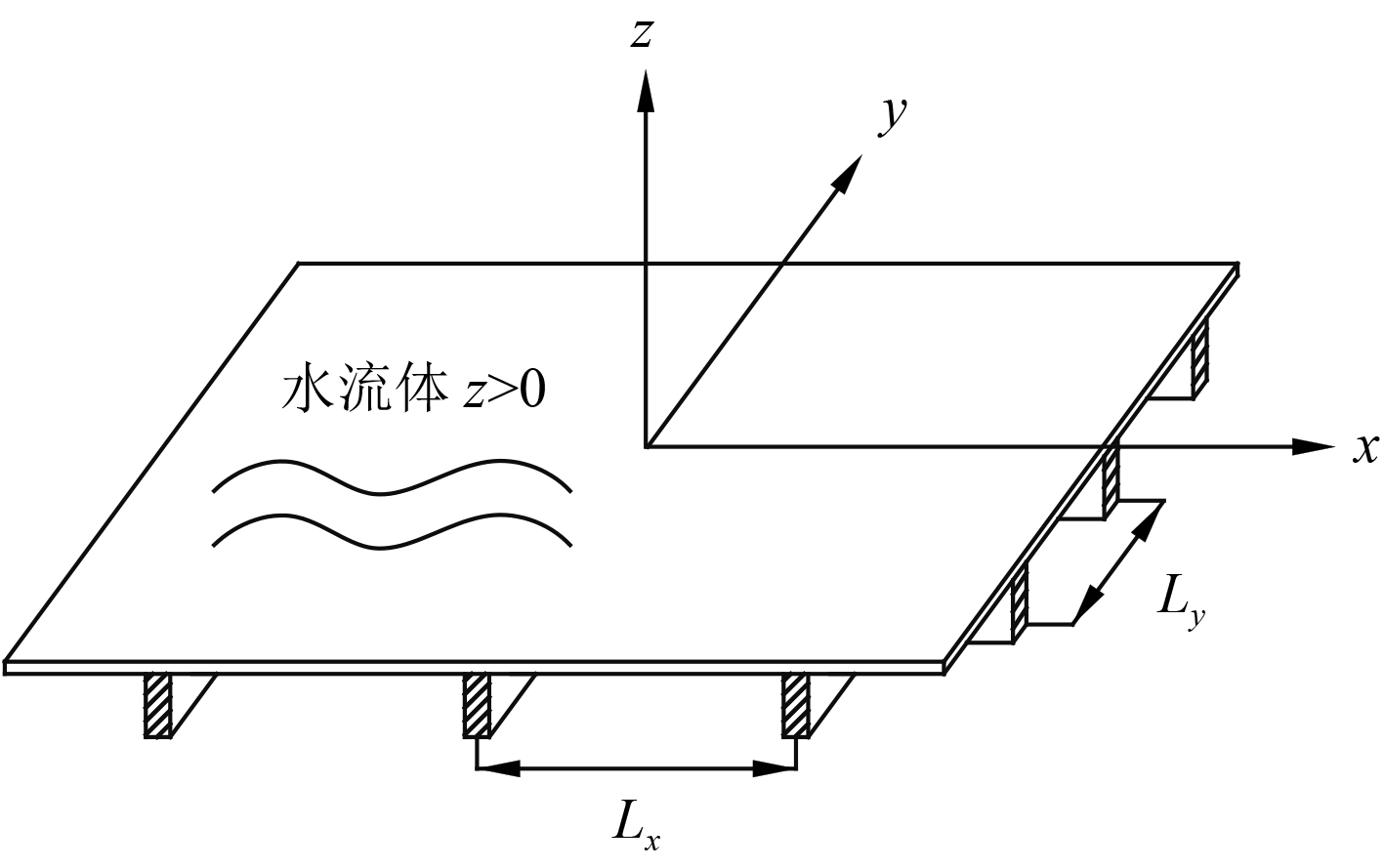
1 数学模型

无穷大模型的正交周期加肋板结构的上半空间充满水流体，下半空间是空气。在 $x$ 轴方向的加强肋沿直线 $x = m{L_x}$ 周期分布，在 $y$ 轴方向的加强肋沿直线 $y = n{L_y}$ 周期分布（ $m,n = 0, \pm 1, \cdots \pm \infty $ ）， ${L_x}$ 和 ${L_y}$ 分别是2个轴方向相邻加强肋间的周期间距，周期加肋板的局部结构示意图如图1所示。

周期加肋板结构受到随时间 $t$ 周期变化的谐振激励力 $f(x,y)\exp ({\rm{j}}\omega t)$ 的作用，其函数方程式为

$ f(x,y) = {P_{{f}}}\exp [ - {{j}}({k_x}x + {k_y}y)]{\text{。}} $

(1)

式中：

$ {k_x} = {k_0}\sin \theta \cos \phi ,{k_y} = {k_0}\sin \theta \sin \phi{\text{。}} $

(2)

式中： ${P_{{f}}}$ 为激励力幅值； $\omega $ 为圆频率； $\theta $ 为激励力与加肋板法向 $z$ 轴方向的夹角； $\phi $ 为激励力在 $x - y$ 平面上的分量与 $x$ 轴方向的夹角。

加肋板结构的振动方程为（为了简洁，均省略时间因子 $\exp ({\rm{j}}\omega t)$ ）：

$ \begin{gathered} \left( {D{\nabla ^2} - \rho h{\omega ^2}} \right)w(x,y) = f(x,y) - \sum\limits_{m = - \infty }^\infty {{F_1}(x,y)\delta (x - m{L_x})}- \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum\limits_{n = - \infty }^\infty {{F_2}(x,y)\delta (y - n{L_y})}- \\ {p_{{\rm{rad}}}}\left( {x,y,z} \right)\left| {_{z = 0}} \right. {\text{。}} \\[-10pt] \end{gathered} $

(3)

式中： $D = \dfrac{{E{h^3}}}{{12(1 - {v^2})}}$ ， ${\nabla ^2} = {(\dfrac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}})^2}$ ； $D$ ， $E$ ， $v$ 分别为薄板的弯曲刚度，杨氏模量，泊松比； $\rho $ ， $h$ 为薄板的密度，厚度。 ${F_1}(x,y)\delta (x - m{L_x})$ 和 ${F_2}(x,y)\delta (y - n{L_y})$ 为加强肋沿直线 $x = m{L_x}$ 和 $y = n{L_y}$ 方向与薄板间的法向作用力。将加强肋等效为欧拉梁，并根据薄板和加强肋的结合面间的位移连续条件，可以得到方程

$\left\{ \begin{gathered} {E_{\rm{b}}}{I_{\rm{b}}}\frac{{{\partial ^4}w(x,y)}}{{\partial {y^4}}} - {\omega ^2}{\rho _{\rm{b}}}{s_{\rm{b}}}w(x,y) = {F_1}(x,y){\text{，}} \\ {E_{\rm{b}}}{I_{\rm{b}}}\frac{{{\partial ^4}w(x,y)}}{{\partial {x^4}}} - {\omega ^2}{\rho _{\rm{b}}}{s_{\rm{b}}}w(x,y) = {F_2}(x,y) {\text{。}} \end{gathered} \right.$

(4)

式中： ${E_{\rm{b}}}$ , ${I_{\rm{b}}}$ , ${\rho _{\rm{b}}}$ , ${s_{\rm{b}}}$ 分别为加强肋的杨氏模量，惯性矩，质量密度和横截面面积。

可压缩流体中加肋板的辐射声压 ${p_{{\rm{rad}}}}(x,y,z)$ 满足Helmholtz方程，并满足加肋板结构与流体的边界连续条件^[10]

$ \left[ {\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right) + {{\left( {\frac{\omega }{c}} \right)}^2}} \right]{p_{{\rm{rad}}}}(x,y,z) = 0{\text{，}} $

(5)

${\rho _0}{\omega ^2}w(x,y) = \frac{{\partial {p_{{\rm{rad}}}}(x,y,z)}}{{\partial z}}\left| {_{z = 0}} \right.{\text{。}} $

(6)

式中： ${\rho _0}$ 为水流体的质量密度； $c$ 为水流体中的声速。

2 傅里叶变换分析

为便于分析求解方程(3)，这里将采用傅里叶变换。由傅里叶变换的定义可知，对满足傅里叶变换条件的任意函数 $g(x,y)$ ，其双重傅里叶变换是

$ \tilde g(\alpha ,\beta ) = \int\nolimits_{ - \infty }^\infty {\int\nolimits_{ - \infty }^\infty {g(x,y)\exp [{\rm{j}}(\alpha x + \beta y)]{\rm{d}}x{\rm{d}}y} } {\text{，}} $

(7)

由泊松迭加公式，可得

$\sum\limits_{m = - \infty }^\infty {\delta (x - m{L_x})} = \frac{1}{{{L_x}}}\sum\limits_{m = - \infty }^\infty {\exp \left({\rm{j}}\frac{{2m{{\text{π}}}}}{{{L_x}}}x\right)}{\text{，}} $

(8)

$\sum\limits_{m = - \infty }^\infty {\exp ({\rm{j}}m\alpha {L_x})} = \frac{{2{{\text{π}}}}}{{{L_x}}}\sum\limits_{m = - \infty }^\infty {\delta \left(\alpha + \frac{{2m{{\text{π}}}}}{{{L_x}}}\right)}{\text{，}} $

(9)

由式(4)、式(7)和式(8)可得

$ \begin{split} & \int\nolimits_{ - \infty }^\infty {\int\nolimits_{ - \infty }^\infty {\sum\nolimits_{m = - \infty }^\infty {{F_1}(x,y)\delta (x - m{L_x})} } } \exp [{\rm{j}}(\alpha x + \beta y)]{\rm{d}}x{\rm{d}}y= \\ & \int\nolimits_{ - \infty }^\infty {\int\nolimits_{ - \infty }^\infty {\sum\limits_{m = - \infty }^\infty {\left( {{E_{\rm{b}}}{I_{\rm{b}}}\frac{{{\partial ^4}}}{{\partial {y^4}}} - {\omega ^2}{\rho _{\rm{b}}}{s_{\rm{b}}}} \right)} } } w(x,y) \times \\ &frac{{\exp [{\rm{j}}({\alpha _{x,m}}x + \beta y)]}}{{{L_x}}}{\rm{d}}x{\rm{d}}y= \\ & \frac{{{J_{\rm{A}}}(\beta )}}{{{L_x}}}\sum\limits_{m = - \infty }^\infty {\tilde w({\alpha _{x,m}},\beta )} {\text{，}}\\[-20pt] \end{split} $

(10)

同理可得

$ \begin{split} & \int\nolimits_{ - \infty }^\infty {\int\nolimits_{ - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{F_2}(x,y)\delta (x - n{L_y})} } } \exp [{\rm{j}}(\alpha x + \beta y)]{\rm{d}}x{\rm{d}}y= \\ & \frac{{{J_{\rm{B}}}(\alpha )}}{{{L_y}}}\sum\limits_{n = - \infty }^\infty {\tilde w(\alpha ,{\beta _{y,n}})} {\text{，}}\\[-20pt] \end{split} $

(11)

在式（10）～式（11）中

$ {\alpha _{x,m}} = \alpha + {{2m{{\text{π}}}} / {{L_x}}},{\beta _{y,n}} = \beta + {{2n{{\text{π}}}} / {{L_y}}}\text{，} $

(12a)

$ \begin{split} & {J_{\rm{A}}}(\beta ) = {E_{\rm{b}}}{I_{\rm{b}}}{\beta ^{\rm{4}}} - {\omega ^2}{\rho _{\rm{b}}}{s_{\rm{b}}},{J_{\rm{B}}}(\alpha ) =\\ & {E_{\rm{b}}}{I_{\rm{b}}}{\alpha ^{\rm{4}}} - {\omega ^2}{\rho _{\rm{b}}}{s_{\rm{b}}}\text{。} \end{split} $

(12b)

对式（5）和式（6）进行傅里叶变换，整理可得

${\tilde p_{{\rm{rad}}}}(\alpha ,\beta ,z) = {{ - {\rho _0}{\omega ^2}\tilde w(\alpha ,\beta )\exp [ - \gamma (\alpha ,\beta )z]} / {\gamma (\alpha ,\beta )}}\text{，}$

(13)

式中， $\gamma (\alpha ,\beta ) = \sqrt {{\alpha ^2} + {\beta ^2} - {{({\omega / c})}^2}} $ ，且由Sommerfeld远场声辐射条件可知，当 $\operatorname{Re} \left( {\gamma (\alpha ,\beta )} \right) = 0$ 时，满足 $\operatorname{Im} \left( {\gamma (\alpha ,\beta )} \right) \geqslant 0$ 。

由谐波分析法可知，双周期加肋板结构的振动位移可表达为如下方程形式^[10]

$w(x,y) = \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{W_{mn}}} } \exp [ - {\rm{j}}({k_{x,m}}x + {k_{y,n}}y)]\text{，}$

(14)

式中， ${k_{x,m}} = {k_x} + {{2m{{\text{π}}}} / {{L_x}}}$ ； ${k_{y,n}} = {k_y} + {{2n{{\text{π}}}} / {{L_y}}}$ 。

对式(14)进行傅里叶变换，可得

$\tilde w(\alpha ,\beta ) = 4{{{\text{π}}}^2}\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{W_{mn}}} } \delta (\alpha - {k_{x,m}})\delta (\beta - {k_{y,n}})\text{。}$

(15)

3 加肋板振动方程的求解

对式（3）进行傅里叶变换，并根据式（10）、式（11）和式（13），可得

$ \begin{split} & \tilde w(\alpha ,\beta ) = \frac{1}{{Z(\alpha ,\beta )}}\{ \tilde f(\alpha ,\beta ) - \frac{{{J_{\rm{A}}}(\beta )}}{{{L_x}}}\sum\limits_{m = - \infty }^\infty {\tilde w({\alpha _{x,m}},\beta )}- \\ &\frac{{{J_{\rm{B}}}(\alpha )}}{{{L_y}}}\sum\limits_{n = - \infty }^\infty {\tilde w(\alpha ,{\beta _{y,n}})} \} \text{，} \end{split} $

(16)

$ {\text{式中，}}Z(\alpha ,\beta ) = D{\left( {{\alpha ^2} + {\beta ^2}} \right)^2} - \rho h{\omega ^2} - \frac{{{\rho _0}{\omega ^2}}}{{\gamma (\alpha ,\beta )}}\text{。}\hspace{10pt} $

(17)

由 $\delta $ 函数的性质，可知

$ \begin{split} & \sum\limits_{m = - \infty }^\infty {\tilde w({\alpha _{x,m}},\beta )} = \\ &\int\nolimits_{ - \infty }^\infty {\sum\limits_{m = - \infty }^\infty {\tilde w({\alpha ^*},\beta )} } \delta ({\alpha ^*} - {\alpha _{x,m}}){\rm{d}}{\alpha ^*}\text{，} \end{split} $

(18)

$\tilde w$ 的单重傅立叶逆变换是

$ {w^*}(m{L_x},\beta ) = \frac{1}{{2{{\text{π}}}}}\int\nolimits_{ - \infty }^\infty {\tilde w({\alpha ^*},\beta )} \exp ( - {\rm{j}}m{L_x}{\alpha ^*}){\rm{d}}{\alpha ^*}\text{，} $

(19)

因此，由式（9）和式（19）可得

$ \begin{split} & \sum\limits_{m = - \infty }^\infty {{w^*}(m{L_x},\beta )} \exp ({\rm{j}}m\alpha {L_x})= \\ & \frac{1}{{{L_x}}}\int\nolimits_{ - \infty }^\infty {\sum\limits_{m = - \infty }^\infty {\tilde w({\alpha ^*},\beta )\delta ({\alpha ^*} - {\alpha _{x,m}}){\rm{d}}{\alpha ^*}} } \text{。} \end{split} $

(20)

由式(14)得到周期加肋板结构振动位移的周期关系

${w^*}(x = m{L_x},\beta ) = {w^*}(x = 0,\beta )\exp ( - {\rm{j}}m{k_x}{L_x})\text{。}$

(21)

根据式（18）和式（20）间的数学关系，并结合式（21），可得

$ \begin{split} & \sum\limits_{m = - \infty }^\infty {\tilde w({\alpha _{x,m}},\beta )}= \\ & {L_x}\sum\limits_{m = - \infty }^\infty {{w^*}(0,\beta )\exp [{\rm{j}}(\alpha - {k_x})m{L_x}]} \text{。} \end{split} $

(22)

由振动位移式(14)可知，加肋板结构沿 $x = 0$ 直线上的振动位移关于变量 $y$ 的单重傅里叶变换是

$ {w^*}(x = 0,\beta ) = 2{\rm{{\text{π}}}}\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{W_{mn}}} } \delta (\beta - {k_{y,n}})\text{。} $

(23)

因此，根据式（9），式（22）和式（23）可得

$ \begin{split} & \sum\limits_{m = - \infty }^\infty {\tilde w({\alpha _{x,m}},\beta )} =\\ & 4{{{\text{π}}}^2}\sum\limits_{m = - \infty }^\infty {\sum\limits_{p = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{W_{pn}}} } \delta (\alpha - {k_{x,m}})\delta (\beta - {k_{y,n}})} \text{，} \end{split} $

(24)

同理可得

$ \begin{split} & \sum\limits_{n = - \infty }^\infty {\tilde w(\alpha ,{\beta _{y,n}})}= \\ &4{{{\text{π}}}^2}\sum\limits_{n = - \infty }^\infty {\sum\limits_{m = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{W_{mq}}} } \delta (\alpha - {k_{x,m}})\delta (\beta - {k_{y,n}})} \text{。} \end{split} $

(25)

将式（24）及式（25）代入式（16）中，可以得到方程

$ \begin{split} & \tilde w(\alpha ,\beta ) = \frac{{4{{{\text{π}}}^2}}}{{Z(\alpha ,\beta )}}\biggr\{ {p_e}\delta (\alpha - {k_x})\delta (\beta - {k_y}) -\\ & \frac{{{J_{\rm{A}}}(\beta )}}{{{L_x}}}\sum\limits_{m = - \infty }^\infty {\sum\limits_{p = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{W_{pn}}} } \delta (\alpha - {k_{x,m}})\delta (\beta - {k_{y,n}})}- \\ & { \frac{{{J_{\rm{B}}}(\alpha )}}{{{L_y}}}\sum\limits_{n = - \infty }^{ + \infty } {\sum\limits_{m = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{W_{mq}}} } \delta (\alpha - {k_{x,m}})\delta (\beta - {k_{y,n}})} }\biggr\}\text{，} \end{split} $

(26)

根据 $\delta $ 函数的性质，以及式(15)和(26)，可得

$ \begin{split} & {W_{mn}} = \frac{1}{{{Z_{mn}}}}\times \\ &\left\{ {{P_{\rm{f}}}{\delta _{mn}} - \frac{{J_{y,n}^{\rm{A}}}}{{{L_x}}}\sum\limits_{K = - \infty }^\infty {{W_{Kn}}} - } \right.\left. {\frac{{J_{x,m}^{\rm{B}}}}{{{L_y}}}\sum\limits_{K = - \infty }^\infty {{W_{mK}}} } \right\}\text{，} \end{split} $

(27)

$ \begin{split} & {\text{式中：}}{Z_{mn}} = Z({k_{x,m}},{k_{y,n}}),J_{y,n}^{\rm{A}} = {J_{\rm{A}}}({k_{y,n}}),J_{x,m}^{\rm{B}} =\hspace{19pt}\\ & {J_{\rm{B}}}({k_{x,m}}),{\delta _{0n}} = \left\{ \begin{gathered} 1,\;n = 0 \text{，} \\ 0,n \ne 0\text{。} \\ \end{gathered} \right.\\[-10pt] \end{split} $

(28)

式(27)是未知量 ${W_{mn}}$ 关于 $m$ 和 $n$ 的线性方程组。要求解 ${W_{mn}}$ ，则需要对 $m$ 和 $n$ 进行截断，令 $m,n = 0, \pm 1, \cdots \pm Q$ ， $Q$ 为最大截断整数项， $Q$ 必须保证加肋板振动位移的计算结果收敛。将 ${W_{mn}}$ 的值代入方程式(14)中，从而求解得到周期加肋板结构的振动位移。

4 算例分析

在算例分析中，所用到的物理参数为： $\rho = {\rho _{{b}}} = 7\;700\; {{{\rm{kg}}} / {{{\rm{m}}^{\rm{3}}}}}$ ， ${\rho _0} = 1\;000\; {{{\rm{kg}}} / {{{\rm{m}}^{\rm{3}}}}}$ ， $c = 1\;500\;{{\rm{m}} / {\rm{s}}}$ ， $E \!=\! {E_{{b}}} \!=\! 2.{\rm{0}}1 \times {10^{11}} \times {\rm{(1 + 0}}{{.02)}j}\;{\rm{Pa}}$ ， $v = 0.3$ ， $h \!=\!0.005\;{\rm{m}} $ ， ${P_{{f}}} = 1 \; 000\;{\rm{N}}$ ， ${k_0} = {\omega / c}$ 。加强肋的横截面为矩形，其宽度为 $0.005\;08\;{\rm{m}}$ ，高度为 $0.050\;8\;{\rm{m}}$ ， ${S_{{b}}} = 0.005\;08 \times $ $ 0.050\;8\;{{\rm{m}}^2}$ ，且 ${I_{{b}}} = 5.549\;8 \times {10^{ - 8}}$ 。通过计算分析发现当截断项参数 $Q = {\rm{2}}0$ 时，振动位移的计算结果已经收敛，误差不超过 $1\% $ 。

图2为薄板在激励力频率为 $2\;000$ Hz，角度分别为 $\theta = \phi = {{{\text{π}}} / 4}$ 和 $\theta = {{{\text{π}}} / 4},\phi = {{{\text{π}}} / 3}$ 的情况下，在 $ - 1 \leqslant x,y \leqslant 1$ 区域的振动位移。

图3为周期间距分别为 ${L_x} = {L_y} = 0.2$ 和 $ {L_x} = 0.2, $ ${L_y} = 0.1$ 的加肋板在激励力频率为 $2\;000$ Hz，角度分别为 $\theta = \phi = {{{\text{π}}} / 4}$ 和 $\theta = {{ {\text{π}}} / 4},\phi = {{{\text{π}}} / 3}$ 的情况下，在 $ - 1 \leqslant x,$ $ y \leqslant 1$ 区域的振动位移。

相对于图2中的薄板结构，图3中的正交周期加肋板结构的振动位移具有显著的二维周期特性，且由于加强肋的影响，加肋板的局部位置的振动位移变化较大。薄板及加肋板结构的振动受激励力的幅值和相位角影响。加肋板内的振动弯曲波传播角度的变化方向由角度 $\phi $ 决定，从图3(a)和图3(c)中可以看出当 $\phi = {{{\text{π}}} / 4}$ 时，薄板中的弯曲波的传播方向与 $x$ 和 $y$ 轴成相同的夹角。此外，由于加强肋沿2个轴方向的周期间距相等，因此3(a)中加肋板的振动位移沿 $x$ 和 $y$ 轴方向上是一致对应的。当相位角 $\phi $ 或某一个坐标轴上的加强肋的周期间距发生变化，如图3（b）～图3（d）所示，则加肋板沿 $x$ 和 $y$ 轴方向的振动位移将不再具有对称特性。与角度 $\phi $ 不同，角度 $\theta $ 可以改变结构的振动位移幅值大小，但不会改变板内弯曲波的传播方向。

图4为薄板和周期间距分别是 ${L_x} = {L_y} = 0.2$ 和 ${L_x} = {L_y} = 0.4$ 的加肋板在谐振力频率为 $100\sim 6\; 000$ Hz的范围内，在不同位置点处的振动位移。

由图4可知，薄板在 $(0,0)$ 点的振动位移非常小，且在整个频域区间其振动位移变化极小。在 $(0.2,0.4)$ 和 $(0.4,0.4)$ 位置点处，薄板的振动位移随频率的增加其变化较为明显，板内弯曲波可以顺利通过。加强肋在 $100\sim 3\;000$ Hz的范围内对薄板振动的影响作用较为显著。相对于薄板各点的振动，加肋板结构各对应点的振动位移波动较大。当增大加强肋的周期间距之后，加肋板结构的位移曲线在较多频率位置出现峰值或波谷，表明在一定范围内周期间距的增大将会导致加强肋在不同频率处增强对薄板的振动影响效果，并且由于加强肋周期间距的增大，使得加肋板结构的振动位移的峰值及波谷位置向低频偏移。在高于 $3\;000$ Hz的频率区间，加强肋对薄板的振动响应作用总体上减弱，加肋板振动位移的波动峰值减小，薄板与加肋板结构的振动位移曲线趋于一致。

5 结　语

研究了流体负载下的正交周期加肋板结构，在谐振力激励作用下的振动响应。根据薄板和加强肋的边界位移连续条件，以及泊松公式及傅里叶变换的应用，建立了周期加肋板结构的振动位移方程。通过谐波法，将加肋板的振动位移表达为关于无穷项谐波分量的迭加函数形式，并对谐波分量进行有限项数值截断计算，从而求解得到加肋板的振动位移。在算例分析里，研究了加强肋对薄板振动响应的影响。计算结果表明，在所研究频率范围的较低频域区间内，加强肋对薄板的振动响应影响较为显著，在中高频域区间的影响效果明显减弱。此外，适当增大加强肋的周期间距将会导致加肋板结构的振动位移在更多频率位置出现振动峰值或波谷。