2. 海军研究院,北京 100161;
3. 中国舰船研究设计中心,湖北 武汉 430064
2. Naval Academy of China, Beijing 100161, China;
3. China Ship Development and Design Center, Wuhan 430064, China
板壳结构的减重及声隐身性问题一直是军事领域的重要研究课题。与传统金属板相比,复合材料层合板结构以其比刚度大、比强度高等特性愈益广泛应用于舰船、潜艇等结构中,军事意义重大。复合材料带来减重优势的同时,其振动致声问题逐渐引起重视。对于这类问题,目前最普遍的做法是在结构表面敷设约束阻尼层来显著提高结构阻尼,增大剪切变形,从而达到减振降噪的目的[1 − 2]。但是目前关于复合材料约束阻尼板的研究主要局限在固有频率和模态阻尼等问题方面[3 − 7],而关于各参数对层合阻尼板声辐射的影响研究还远不如传统三明治结构那样充分[8 − 11]。面板厚度、芯层厚度和位置以及不同铺层角导致纤维长度的改变均可能对该结构声辐射产生影响。了解层合阻尼板的振声特性规律有助于充分利用阻尼材料,达到更高效地降低结构噪声的目的。
另一方面,有限元法在求解复杂几何和边界条件问题上的显著优势,愈益受到研究者们的青睐。由于各向异性复合材料以及粘弹性芯层材料的存在,结构剪切效应非常明显。因此如何基于有限元法准确高效的对该结构进行动力学分析是个难题[12 − 13]。针对这种结构,常用有限元离散方式有3种:1)基于一阶剪切变形理论(FSDT)或高阶剪切变形理论(HSDT)的壳单元;2)基于分层理论(Layerwise)的连续壳单元;3)基于三维弹性理论(3-D)的体单元。以上任意一种方式均不能兼顾准确性与计算量问题。而同时采用8节点三位移自由度的连续壳单元与8节点三位移自由度的体单元的有限元离散方式,既可以充分考虑结构的剪切变形,又可以降低计算量,2种单元之间还有很好的位移协调性。
本文在Li[14]基础上引入约束粘弹性阻尼层,采用连续壳单元离散约束面板和基板,而用体单元离散阻尼层,建立有限元模型,并结合声学无限元技术,通过算例验证了该方法振声分析的准确性。同时开展了面板厚度、芯层厚度和位置以及铺层角对结构振声特性影响规律的研究,从而为复层合阻尼板的低噪声设计提供依据。
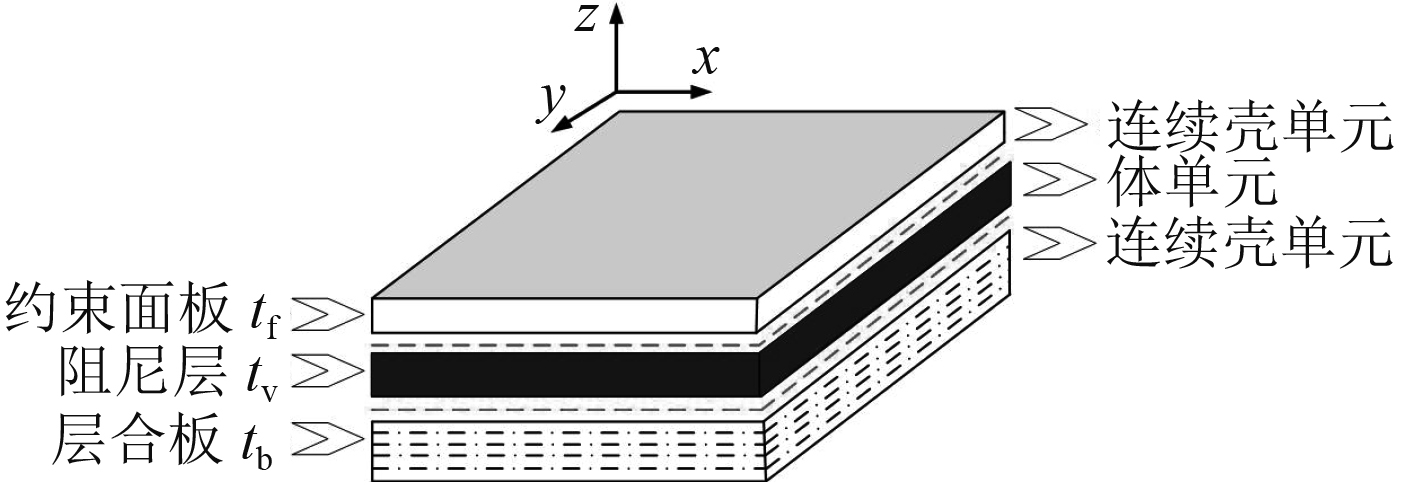
1 分层模型镶嵌在无限大刚性障板中的复合材料约束阻尼层合板结构如图1所示。板上表面位于平面
|
图 1 复合材料约束阻尼板结构示意图 Fig. 1 The figuer of a composite constrained damping plate |
以复合材料层合板为例,考虑建立基于线性分层理论的有限元模型,其位移模型如图2所示。假设层合板厚度方向分为

|
图 2 层合板线性位移模型 Fig. 2 Linear layerwise model of a laminated plate |
| $\begin{gathered} u(x,y,z) = \sum\limits_{i = 1}^N {{u_i}(x,y){\varPhi ^i}(z)}\text{,} \\ v(x,y,z) = \sum\limits_{i = 1}^N {{v_i}(x,y){\varPhi ^i}(z)}\text{,} \\ w(x,y,z) = \sum\limits_{i = 1}^N {{w_i}(x,y){\varPhi ^i}(z)}\text{。} \\ \end{gathered} $ | (1) |
其中:
| ${\varPhi ^i}(z) = \left\{ \begin{gathered} 0,{\rm{ z < }}{{\rm{z}}_{i - 1}} \text{,}\\ \varPsi _2^{i - 1} = \frac{{z - {z_{i - 1}}}}{{{z_i} - {z_{i - 1}}}},{\rm{ }}{z_{i - 1}} < z < {z_i} \text{,} \\ \varPsi _1^i = - \frac{{z - {z_{i + 1}}}}{{{z_{i + 1}} - {z_i}}},{\rm{ }}{{\rm{z}}_i} < z < {z_{i + 1}} \text{,}\\ 0{\rm{ }}{z_{i + 1}} < z \text{。} \\ \end{gathered} \right.$ | (2) |
为了建立基于线性分层理论的有限元模型,第i层上任意一点处位移,ui(x,y),vi(x,y)和wi(x,y)可通过二维线性拉格朗日插值多项式进行拟合:
| ${{{u}}_{{i}}}=\sum\limits_{n = 1}^{{m}} {u_i^n{\varphi ^n}(x,y),} {v_{{i}}}{{ = }}\sum\limits_{n = 1}^{{m}} {v_i^n{\varphi ^n}(x,y),} {{{w}}_{{i}}}{{ = }}\sum\limits_{n = 1}^{{m}} {w_i^n{\varphi ^n}(x,y)}\text{。} $ | (3) |
其中:m为每个单元的节点数目;
利用上述任意子层位移表达式并结合正交材料应力应变关系以及转应力轴公式,可得到层合板的单元刚度矩阵以及单元质量矩阵。同样可得到面板相应的单元刚度及质量矩阵。
为了精确描述低模量阻尼层的剪切变形,引入八节点三位移自由度的体单元来离散粘弹性芯层,具体可参考文献[3]。同时,体单元与连续壳单元3个位移自由度完全一样,因此基板、芯层与面板三者之间具有有很好的位移协调性。芯层弹性模量采用复数形式表示
利用不同类型单元离散得到的面板、芯层以及层合板的单元、质量刚度矩阵进行装配可得到结构整体的刚度矩阵K以及质量矩阵M。代入到欧拉拉格朗日运动方程以及虚功方程里并经过一系列积分简化,可得到在简谐力作用下在特定频率下的结构运动方程:
| $({{K}}(w) - {w^2}{{M}}){{U}}(w) = {{F}}(w)\text{。}$ | (4) |
其中:
声音在理想空气介质中传播时,若不考虑时域特性,则流场中声压要满足Helmholtz方程:
| ${\Delta ^2}p + {k^2}p = 0,$ | (5) |
式中:
声波在有限流场中传播时,由于边界阻抗的存在必然存在声波的反射,采用声学无限元技术,可在有限流体边界上覆盖一层无限单元来实现对无限流场的模拟。此时,声波就能够满足在流场无穷远边界条件上的Sommerfield辐射条件:
| $\mathop {\lim }\limits_{r \to \infty } r(\frac{{\partial p}}{{\partial r}} + jkp) = 0,$ | (6) |
若已知声辐射表面的速度分布,则声压速度关系满足的边界条件:
| ${\Delta ^2}p = - i\rho w{V_n},$ | (7) |
对Helmholtz方程应用Galerkin加权残值法,并分别对流体区域
| $ \begin{split} &\int_V {\nabla {W_i}\nabla p{\rm d}V - {k^2}\int_V {{W_i}p{\rm d}V} } - \int_{{\varGamma ^i}} {{W_i}\frac{{\partial p}}{{\partial n}}{\rm d}\varGamma - }\\ &\qquad\qquad \int_{{\varGamma ^e}} {{W_i}\frac{{\partial p}}{{\partial n}}{\rm d}\varGamma = 0},\end{split} $ | (8) |
其中:p为声压值函数;Wi为加权函数。
结合上式以边界条件,随着r→∞,有p→∞以及Γe→∞,通过线性插值函数,可得到
| $({\bar{ K}}(w) - {w^2}{\bar{ M}}){{p}}(w) = {\bar{ F}}(w),$ | (9) |
其中:
求得结构表面S上的声压和法向速度后,结构的辐射声功率可通过下式求得:
| $W = \frac{1}{2}\int_s {{R_{\rm{e}}}} (pv_n^*){\rm d}S$ | (10) |
式中:p和vn分别为结构表面声压和表面法向振速;
以四边固支的复合材料约束阻尼板为例,其基板、粘弹性阻尼层及面板的材料属性如表1所示。其中,基板为各向异性层合板,厚度tb=5 mm,包含5个厚度均为1 mm的单层板,初始铺设角度为[0/90/0/90/0]。阻尼层及面板为各向同性材料,初始厚度tv,tf均为0.5 mm。结构长宽尺寸为600 mm×400 mm。单位简谐激励力位于(0.1 m,0.1 m,0 m)位置处,其频率范围为50 Hz~1kHz。空气密度为1.21 kg/m3,空气中声速为343 m/s。基于LW理论的8节点连续壳单元离散基板及面板,基于三维弹性理论的8节点体单元离散阻尼层,建立面内及厚度方向上单元个数分别为60×40×7的混合有限元模型,应用声学无限元方法探究阻尼层厚度、面板厚度、阻尼层敷设位置以及与阻尼层直接接触的单层板纤维铺设方向对结构振声响应的影响。
|
|
表 1 复合材料约束阻尼板材料属性 Tab.1 Material properties of the composite constrained damping plate |
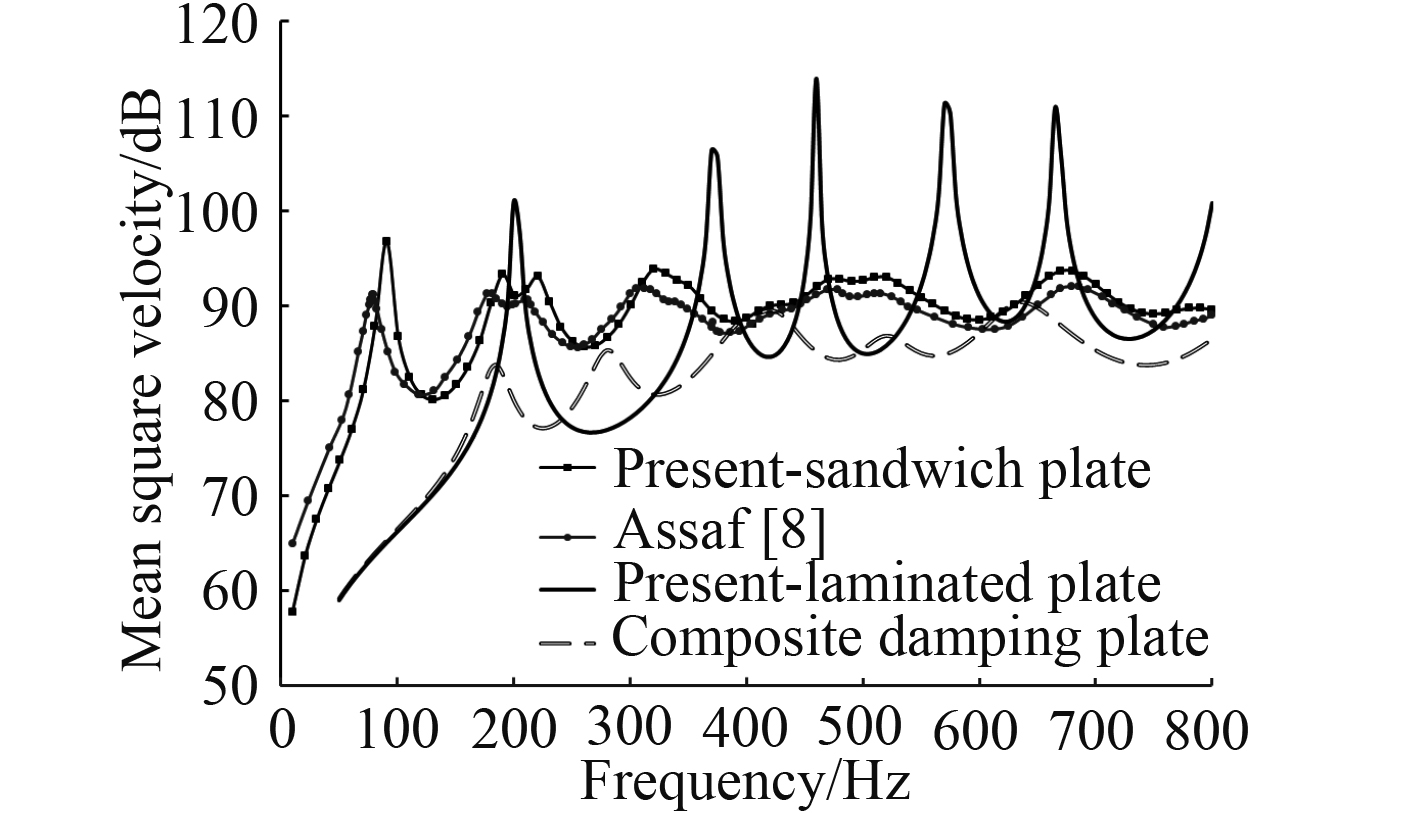
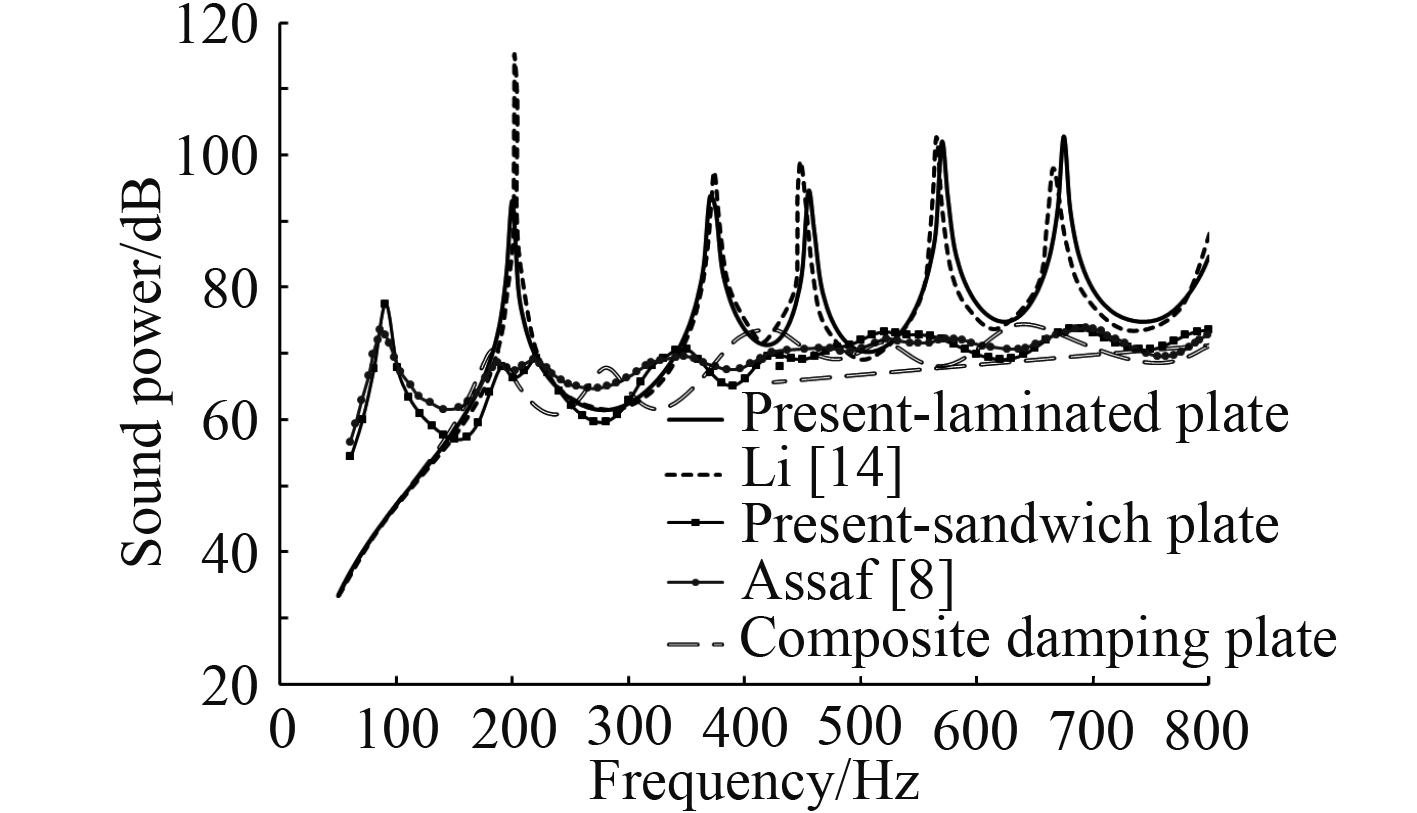
分别计算Li[14]中复合材料层合板以及Assaf[8]中三明治板的振声频响,并与文献结果进行对比,验算本文分析模型的准确性。其中,四边固支复合材料层合板材料属性、几何尺寸同上述基板一致,采用连续壳单元进行离散;简支三明治板长宽分别为0.48 m,0.42 m,各向同性上下面板厚度分别为3 mm,0.5 mm,采用连续壳单元进行离散;粘弹性芯层厚度为0.25 mm,用体单元进行离散。面板及芯层材料属性如表1所示。2种结构的表面均方振速计算结果如图3所示,辐射声功率结果如图4所示。
|
图 3 均方振速校验 Fig. 3 Validation of the mean square velocity |
|
图 4 辐射声功率校验 Fig. 4 validation of the sound power |
从图3和图4可知,本文建立的有限元模型计算结果分别与文献[8,14]中的结果一致,验证了该方法的准确性。基于此方法建立上述层合阻尼板的有限元混合模型并进行振声计算。由图3和图4可知,与无阻尼的层合板相比,敷设约束粘弹性阻尼层的复合材料层合板的表面均方振速以及辐射声功率均大幅降低。如在0~800 Hz范围内无阻尼板的平均均方振速以及辐射声功率分别为85.43 dB,71.17 dB,而层合阻尼板的平均均方振速以及辐射声功率分别为82.04dB,65.65 dB频率,二者分别相差3.39 dB,6.52 dB。由此可见,粘弹性材料对复合材料层合板结构有显著的减振降噪效果。
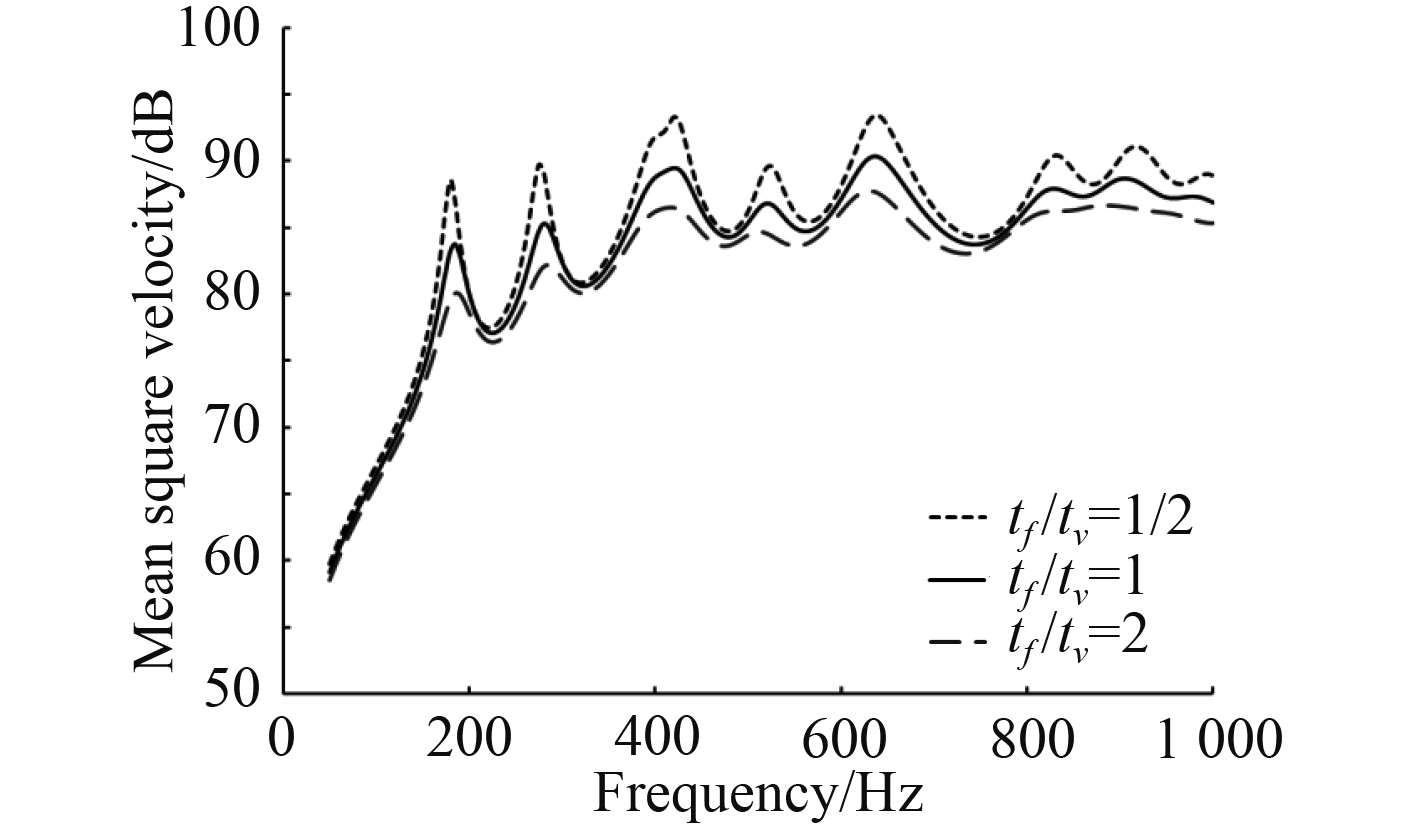
3.2 面板厚度影响考虑上述层合阻尼板,保持基板厚度tb、芯层厚度tv等其他条件不变,改变表层面板厚度tf,使得tf/tv分别为1/2,1以及2时分析结构振声频响特性。层合阻尼板结构在不同面板厚度下的均方振速、辐射声功率见图5和图6。
|
图 5 面板厚度对均方振速影响 Fig. 5 Influence of panel thickness on mean square velocity |

|
图 6 面板厚度对辐射声功率影响 Fig. 6 Influence of panel thickness on sound power |
从图5和图6可知,随着面板厚度增加,结构表面均方振速以及辐射声功率在整个频段范围内均有明显下降。如tf/tv分别为1和2时,相较于tf/tv为1/2,平均均方振速依次降低1.43 dB,2.86 dB,平均辐射声功率依次降低1.36 dB,2.83 dB。但在不同厚度面板下,各个峰值对应处的频率几乎无差别。这是由于增加的面板厚度对结构的比刚度影响较小,因此对固有频率影响不大,但是增大面板厚度能有效增加芯层的剪切变形,大量消耗结构振动时的能量,从而可以降低均方振速和声功率。
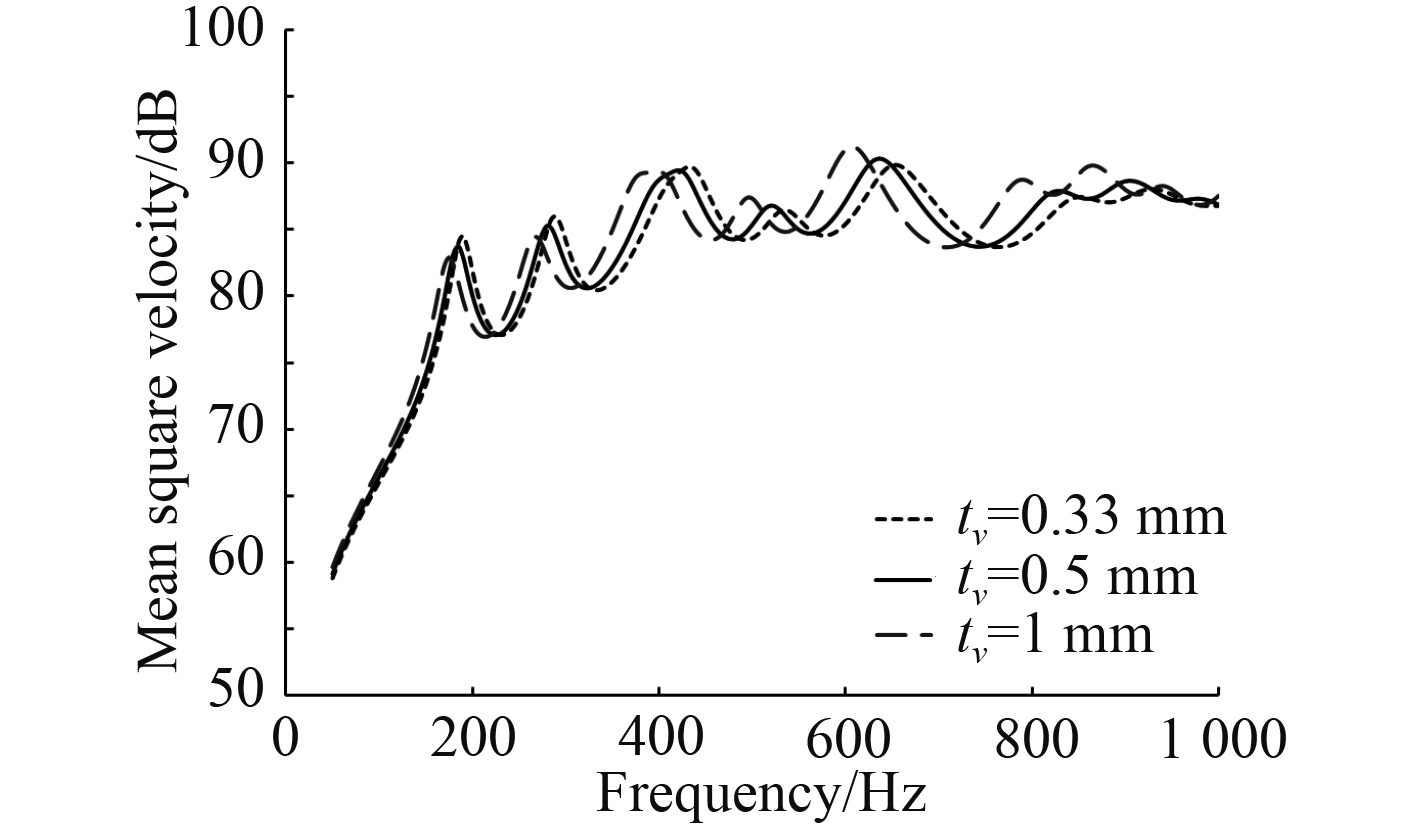
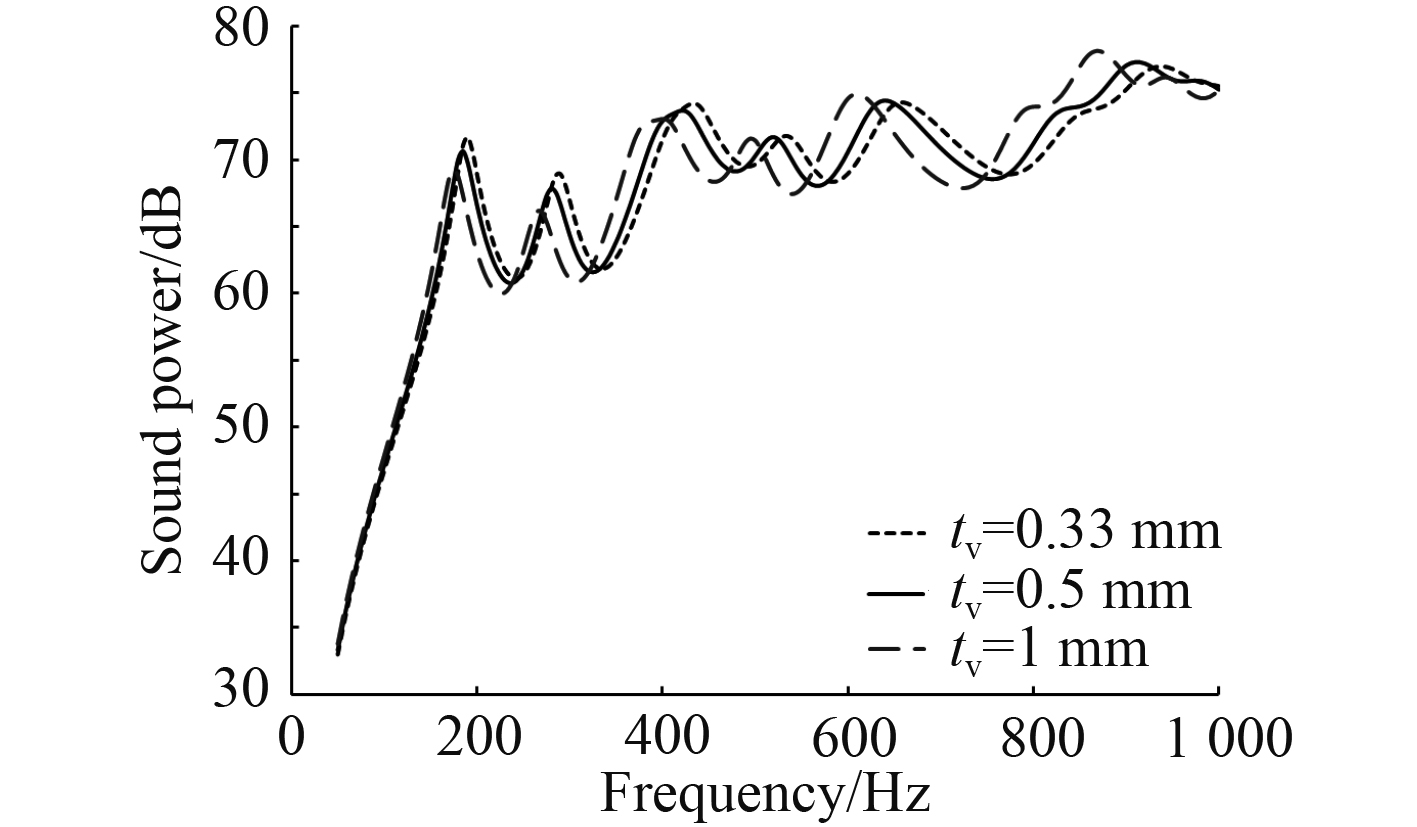
3.3 阻尼层厚度影响由3.1节可知,敷设粘弹性芯层材料的层合阻尼板可以显著降低振声水平,由此考虑阻尼层厚度将直接影响结构的振声响应。在初始面板、阻尼厚度均为0.5 mm的基础上,增加两组阻尼厚度分别为0.33 mm、1 mm的方案,探究阻尼层厚度对结构的均方振速及辐射声功率影响,分别如图7和图8所示。
|
图 7 阻尼层厚度对均方振速影响 Fig. 7 Influence of damping layer thickness on mean square velocity |
|
图 8 阻尼层厚度对辐射声功率影响 Fig. 8 Influence of damping layer thickness on sound power |
从图7和图8的均方振速及辐射声功率频率曲线可知,增加阻尼层厚度对各峰值大小无明显影响。在整个频率范围内,阻尼厚度分别为0.33 mm,0.5 mm,1 mm时的频域平均均方振速分别为82.94 dB,83.22 dB,83.68 dB,而平均辐射声功率分别为67.5 dB,67.68 dB,67.76 dB,可见,随着芯层厚度增加,结构的振声水平均有不同程度上升。另外,增加芯层厚度后,结构固有频率向低频段偏移,且低阶模态偏移较小,高阶模态偏移越来越显著。这是由于芯层厚度增加降低了结构的比刚度,导致结构固有频率有所降低。由上可见,增加芯层厚度,一方面降低了结构整体的比刚度,使得固有频率减小,另一方面,阻尼材料剪切变形所吸收的能量减小,使得振声水平略有上升。因此应当合理选择阻尼层厚度,过分追求阻尼层厚度对降低结构的声辐射水平无益,相反会增加结构重量。
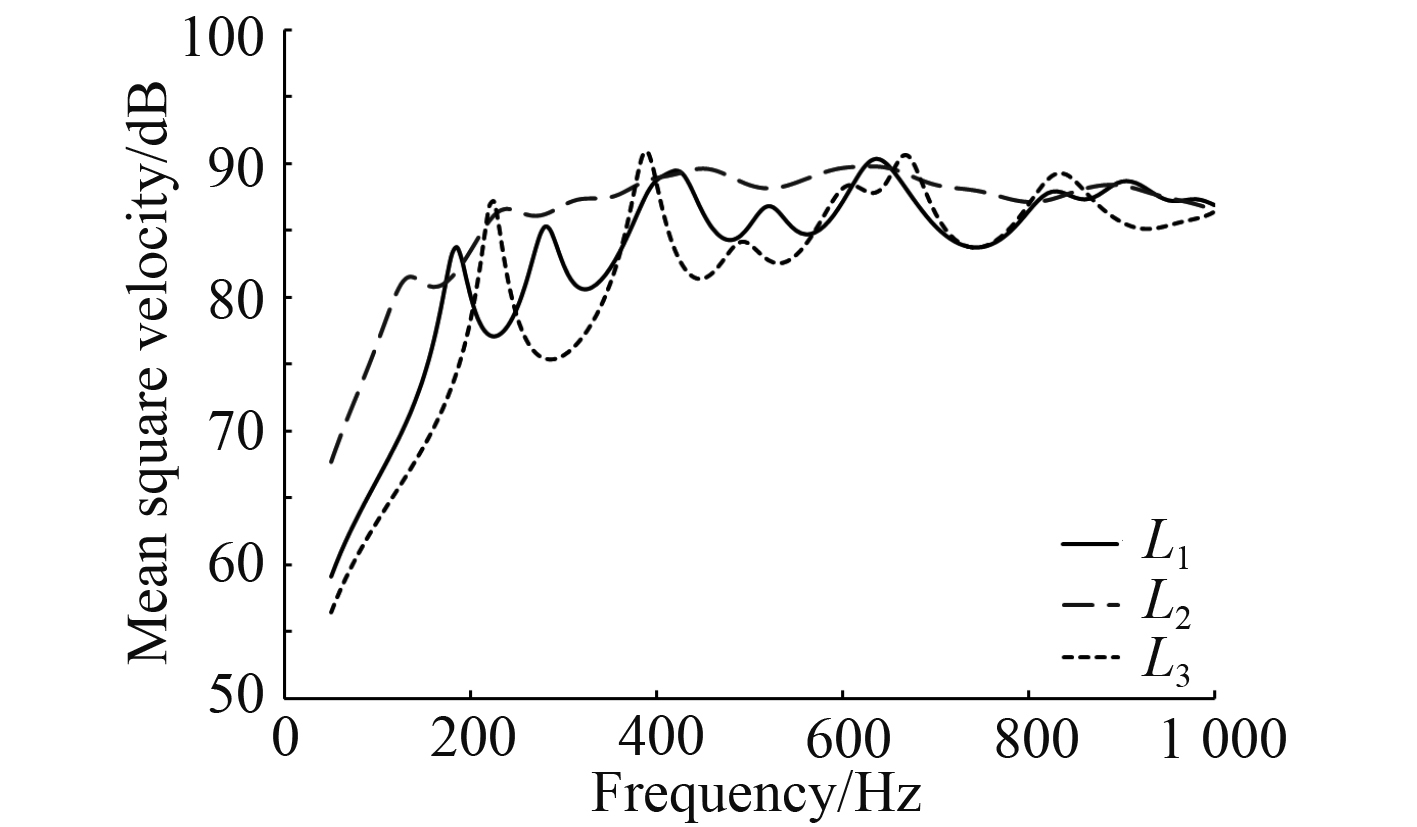
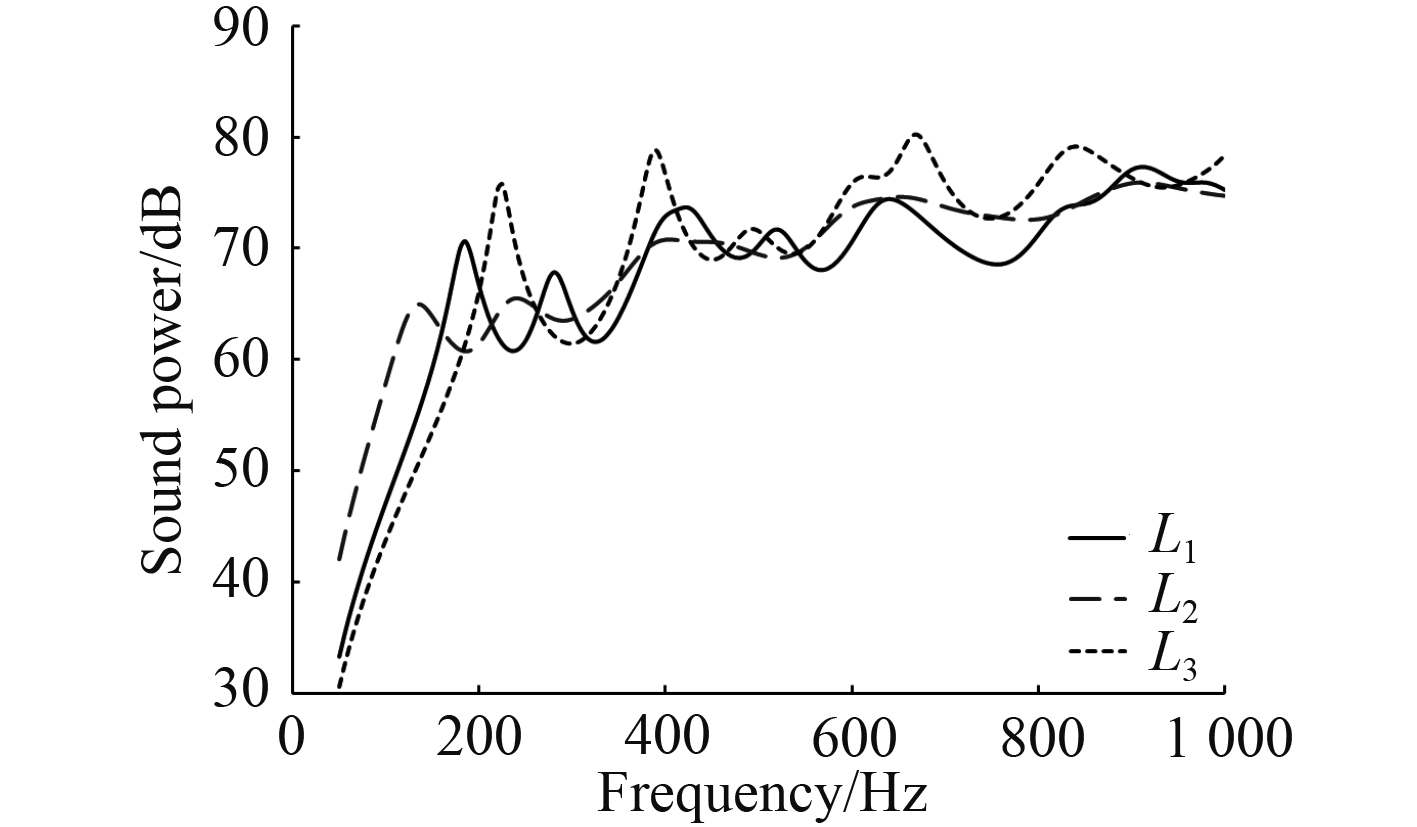
3.4 阻尼层位置影响保持阻尼层厚度等其他条件不变,考虑3种约束阻尼层敷设位置的情况:L1-层合板上表面、L2-层合板中面、L3-层合板上下表面各1/2。阻尼层位置示意图如图9所示。不同敷设方式对结构均方振速和辐射声功率的影响规律如图10和图11所示。

|
图 9 阻尼层敷设位置示意图 Fig. 9 The arrangement schemes of the damping layer |
|
图 10 阻尼层位置对均方振速影响 Fig. 10 Influence of damping layer locations on mean square velocity |
|
图 11 阻尼层位置对辐射声功率影响 Fig. 11 Influence of damping layer locations on sound power |
从图10和图11中可以看到,3种阻尼敷设方式对结构的振声规律影响较大。从平均均方振速方面来看,对于相同厚度的约束阻尼层,最优敷设方式依次为L3,L2,L1。如L3的平均均方振速为81.58dB,显著低于其他2种方式的平均均方振速值83.22 dB,86.39 dB。由此可见,此时分开敷设阻尼有利于提高了结构的整体刚度,使得振动水平降低。同时,分开敷设阻尼层方式的振动及声辐射频响曲线上的各共振峰频率均高于另外2种敷设方式,这同样证明了该敷设方式有利于增加结构刚度,从而增大结构固有频率。从平均敷设声功率方面来看,3种阻尼敷设方式L1,L2,L3的平均辐射声功率分别为67.68 dB,69.08 dB,69.07 dB。因此,约束阻尼层敷设在层合板表面最有利于降低结构的声辐射水平,在600~1 000 Hz范围内效果更为显著。
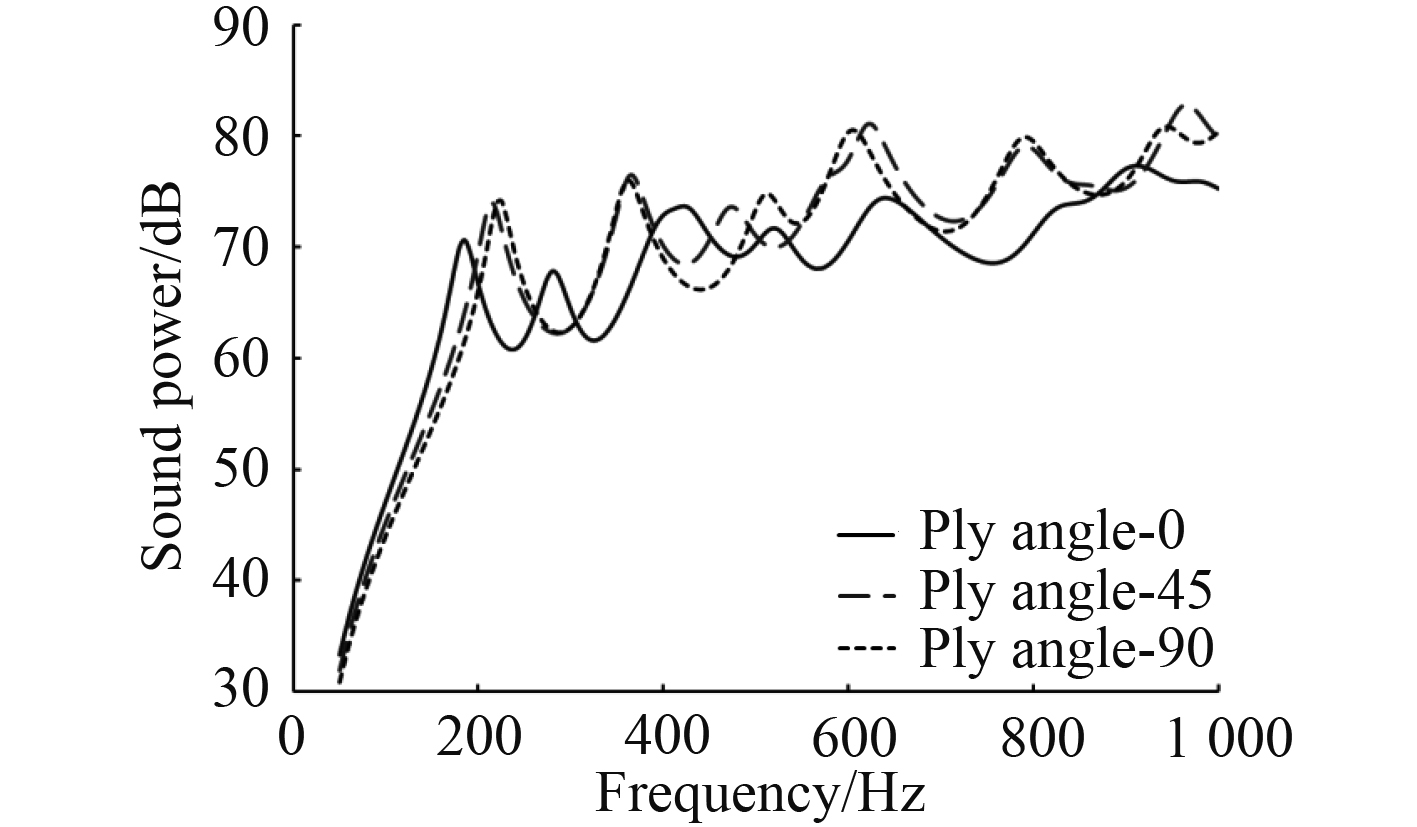
3.5 铺层角度影响为考虑与阻尼层直接接触的单层板铺设角度对该结构的振声影响,将原纤维铺设角度为0°、厚度为1 mm的单层板等分成0.25 mm的4层单层板,铺设角度为[θ/0/0/0],其中θ为与阻尼层毗邻的单层板铺设角度,分别取为0°,45°,90°。不同铺设角度下结构的均方振速和辐射声功率曲线分别如图12和图13所示。

|
图 12 铺设角度对均方振速影响 Fig. 12 Influence of ply angle on mean square velocity |
|
图 13 铺设角度对辐射声功率影响 Fig. 13 Influence of ply angle on sound power |
从图12和图13可知,与阻尼层直接相邻的单层板铺设角度对该结构的振声影响较大。具体来看,铺设角度为0°时的振声频响曲线与角度为45°,90°时差异较大,主要表现为峰值对应的固有频率向低段偏移较为明显,表明该铺设角度下结构的整体比刚度有所降低。但此时结构的平均辐射声功率较低,特别地,在600 Hz以上时效果较为显著,因此该铺设角度有利于提高结构的降噪能力。而铺设角度为45°,90°时的振声频响规律较为相似,比较二者的平均均方振速、平均辐射声功率,总体上铺设角度为90°时的振声水平要优于铺设角度为45°的情况。
4 结 语1)基于连续壳单元与体单元的混合有限元模型可以有效分析层合阻尼板的振声特性,约束粘弹性阻尼层对复合材料层合板有显著的减振降噪效果。
2)一定限度的增大约束面板厚度能有效提高芯层的剪切变形,从而显著降低均方振速和声功率;相反,过分追求阻尼层厚度不利于降低结构的振声水平,还会牺牲一部分重量。
4)阻尼层敷设在层合板表面,相较于板中面或在上下表面分开敷设方式,更能充分利用阻尼的降噪作用,提高声隐身的效率。
5)与阻尼层直接毗邻的单层板铺设角度对结构振声影响较大,当角度为0°时,平均辐射声功率低于另2种铺设角度。
| [1] |
李宁, 龙宇飞, 石崇. 粘弹性阻尼材料阻尼处理及在船体振动控制中的应用[J]. 材料开发与应用, 2015, 30(3): 47-52. |
| [2] |
任小逆, 洪玲, 高琛琪, 等. 船用阻尼材料研究进展[J]. 舰船科学技术, 2017, 39(21): 1-4. |
| [3] |
LI D, QING G, LIU Y. A layerwise/solid-element method for the composite stiffened laminated cylindrical shell structures[J]. Composite Structures, 2013, 98(3): 215-227. |
| [4] |
ZHANG S H, CHEN H L. A study on the damping characteristics of laminated composites with integral viscoelastic layers[J]. Composite Structures, 2006, 74(1): 63-69. DOI:10.1016/j.compstruct.2005.03.008 |
| [5] |
温华兵, 左言言, 彭子龙, 等. 船舶结构复合阻尼材料减振性能实验研究[J]. 船舶工程, 2013(4): 19-22. |
| [6] |
胡明勇, 王安稳, 章向明. 约束阻尼层合板的稳态响应[J]. 应用力学学报, 2010, 27(1): 214-218. |
| [7] |
高坚新, 沈亚鹏. 主被动阻尼层合板结构的自由振动和阻尼特性分析[J]. 应用数学和力学, 1999, 20(10): 1004-1014. DOI:10.3321/j.issn:1000-0887.1999.10.003 |
| [8] |
ASSAF S, GUERICH M, CUVELIER P. Vibration and acoustic response of damped sandwich plates immersed in a light or heavy fluid[M]. Pergamon Press, Inc. 2010.
|
| [9] |
LI X, YU K, ZHAO R. Vibro-acoustic response of a clamped rectangular sandwich panel in thermal environment[J]. Applied Acoustics, 2018, 132. |
| [10] |
王海英. 夹层结构振动声辐射特性研究[D]. 大连: 大连理工大学, 2009.
|
| [11] |
胡昊灏, 商德江. 黏弹性阻尼夹芯板水下声辐射数值计算[J]. 振动与冲击, 2014, 33(19): 206-210. |
| [12] |
JOHNSON C D, KIENHOLZ D A. Finite Element Prediction of Damping in Structures with Constrained Viscoelastic Layers[J]. Aiaa Journal, 1982, 20(20): 1284-1290. |
| [13] |
OH I K. Dynamic characteristics of cylindrical hybrid panels containing viscoelastic layer based on layerwise mechanics[J]. Composites Part B Engineering, 2007, 38(2): 159-171. DOI:10.1016/j.compositesb.2006.07.002 |
| [14] |
LI X, YU K, HAN J, et al. Buckling and vibro-acoustic response of the clamped composite laminated plate in thermal environment[J]. International Journal of Mechanical Sciences, 2016, 119: 370-382. DOI:10.1016/j.ijmecsci.2016.10.021 |
 2019, Vol. 41
2019, Vol. 41
