2. 高新船舶与深海开发装备协同创新中心(船海协创中心),上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
浅水域的海洋结构物通常采用的定位装置有:固定式装置、锚泊装置和动力定位系统。固定式海洋平台定位精度高,但不便于平台的转移,当遭遇极端海况时亦无法撤离平台易使平台遭受损坏酿成灾难。当平台在一个位置工作时间不是很久时不适用固定式装置,且其拆卸工作较为复杂。锚泊装置定位精度相对较低,对于如作为海上浮式机场或钻井平台的海洋结构物易引起事故,且下锚和起锚过程较为复杂,需要工程辅助船的协助,耗费大量时间和成本。动力定位系统在平台的整个工作期间均需启动动力定位装置,油耗高,既导致高昂成本也造成较严重的环境污染。
本文针对目前使用的定位装置的不足,提出了一种新型定位装置。该定位装置采用可伸缩桩进行定位,以半潜式平台为例,可伸缩桩安装于平台中,且相应地配套有用于升降可伸缩桩的装置。当平台到达工作地点时,可伸缩桩向下移动使桩低于平台甲板,以便平台在工作状况下可充分利用其平台区域。然后桩开始伸出直至触碰到海床,接着使可伸缩桩长度固定且平台注入压载水把桩压入海床一定距离。之后保持桩与土壤不脱离,边伸长可伸缩桩边排出平台压载水减小平台吃水,以增大桩顶部的垂向力加快进桩过程。重复这一过程直至桩达到设计插深,如图1所示。当平台完成工作任务或遇到极端海况需要转移时,排出平台内压载水使桩与土壤脱离,然后使桩收缩并存放回平台中。插桩和拔桩过程均可由浮体自身完成而无须工程辅助船协助,方便迅速,费用较低。定位装置定位精度高,机动性能好,适用于海上浮式机场或岛礁综合补给基地等。特别是对于作用海上浮式机场的超大型浮体[1 – 6],应用可伸缩桩定位装置后,浮体对于飞机起降所带来剧烈变化的载荷定位装置的运动响应较小,且工作状态下桩移至浮体甲板以下,不会干扰甲板作为飞机跑道。应用于生活平台上可提高平台上人员的舒适感。
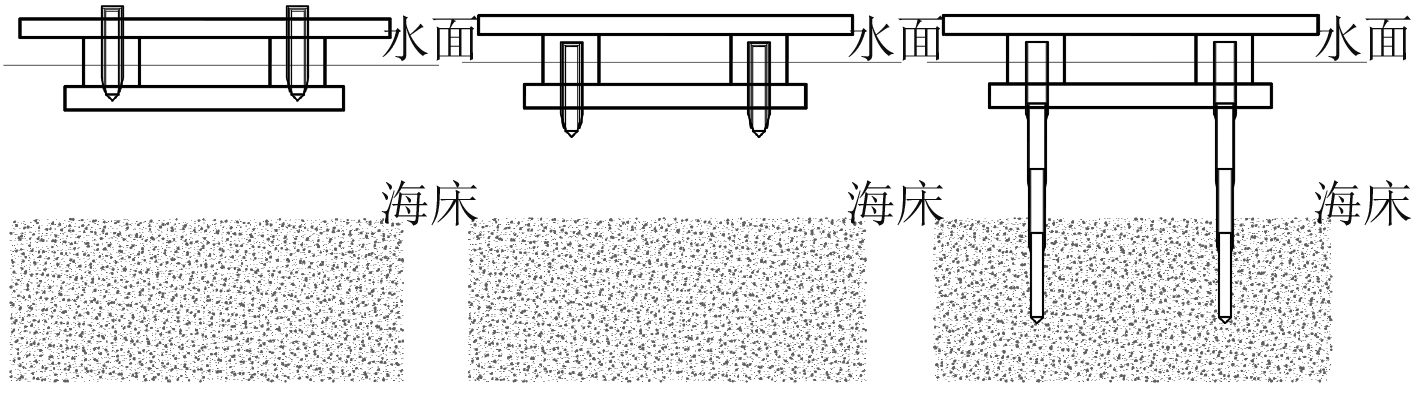
|
图 1 新型定位装置插桩过程示意图 Fig. 1 Plugging process of the novel positioning facility |
三维有限元分析可以较准确地模拟桩与土壤的相互作用,但为了保证计算精度,桩土接触面处的网格应足够细进而导致整个模型的网格数量很大,如本文中的三维有限元模型网格数量为几万,单次静力分析时间为几小时至几十小时,这对计算时间和计算机的内存要求很高。如果在后续同时研究整个平台所有桩的响应仍采用三维有限元法将需要更多的计算资源,为了减小计算资源,可采用p-y曲线法模拟土壤对桩的作用,该理论是用一系列沿深度方向分布,刚度与桩在相对应深度处p-y曲线吻合的非线性弹簧模拟土壤对桩的支承作用,如图2所示。采用该方法和三维有限元分析法计算桩在相同侧向载荷下得到桩的位移响应基本相同,进而可用于在后续研究中简化模拟土壤支承作用以提高计算效率。
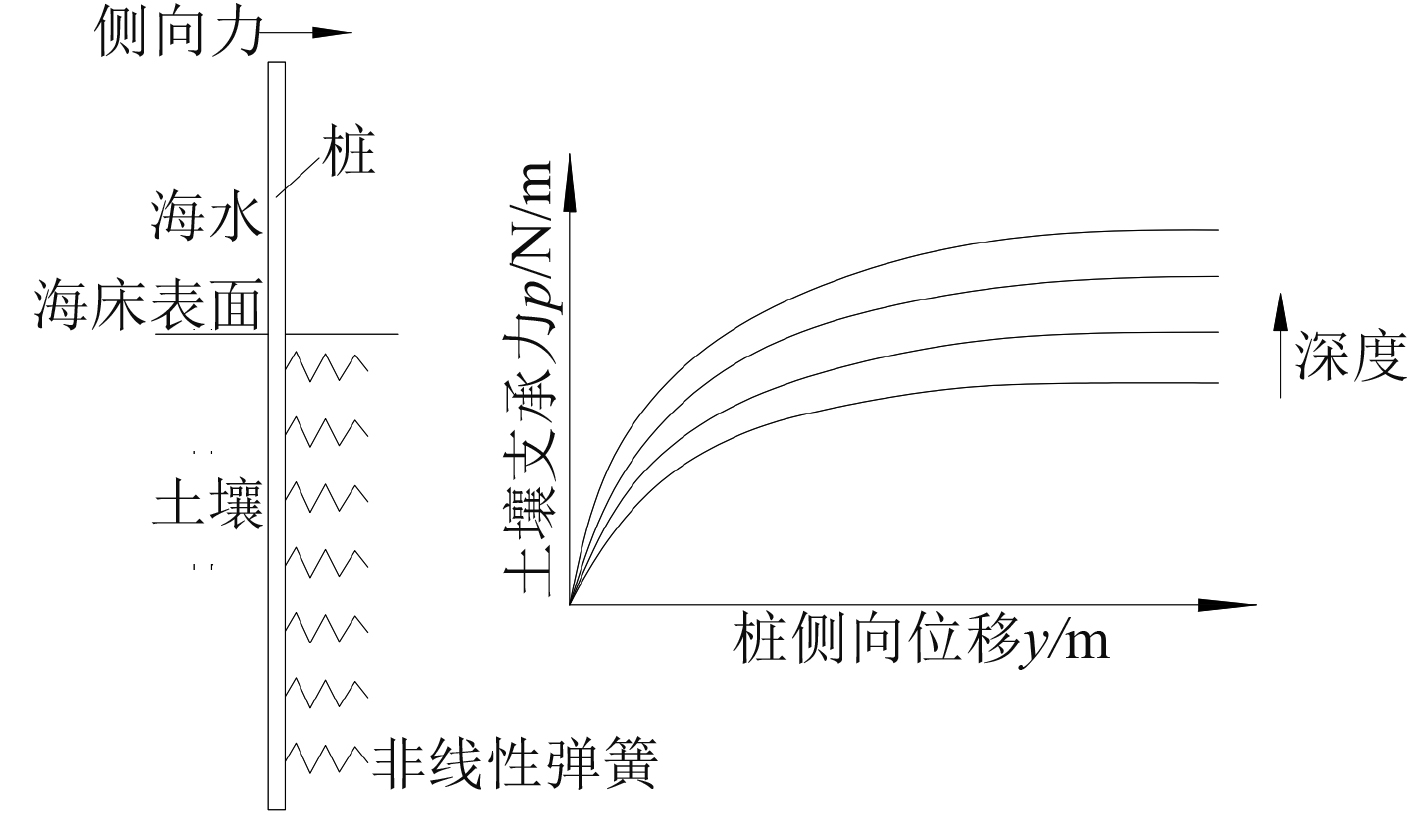
|
图 2 p-y曲线法模拟侧向承载桩原理图 Fig. 2 Diagram of the lateral loaded pile simulatedby p-y curve method |
自从McClelland 和 Focht[7]提出p-y曲线法模拟桩-土相互作用,p-y曲线法已被广泛运用于侧向承载桩的评估中。p-y曲线法已被美国石油学会(API)[8]和挪威劳氏船级社(DNV GL)[9]的海洋结构物设计规范所采纳,按照规范中的要求,桩的p-y曲线应通过桩的模型试验或半经验公式获得。但规范中提供的计算p-y曲线的经验公式是基于小桩径(小于3 m)均匀桩得到的,对本文的大桩径可伸缩桩不适用。文献[10 – 16]对侧向承载均匀桩在静态和动态侧向载荷下的响应进行了研究,并与模型试验结果比较验证了有限元法在计算桩的承载力上的适用性和准确性。但目前尚无针对可伸缩桩侧向承载力的研究,本文通过三维有限元法计算可伸缩桩的p-y曲线并分析其侧向承载能力。
1 p-y曲线法与三维有限元法比较本文以一个工作海域水深为50 m的超大型浮体为例,可伸缩桩定位装置布置于浮体中。在Abaqus中建立3 m桩径均匀桩和海床的三维有限元模型如图3所示,桩的插深为50 m。为模拟载荷为水面处平台传递到桩上,桩比海床表面高出50 m,且在海床上方50 m处建立参考点RP-1,与桩的上端建立刚体约束,模拟桩与平台间的刚性连接。平台传递到桩上的载荷通过加载在RP-1上传递给桩模型。
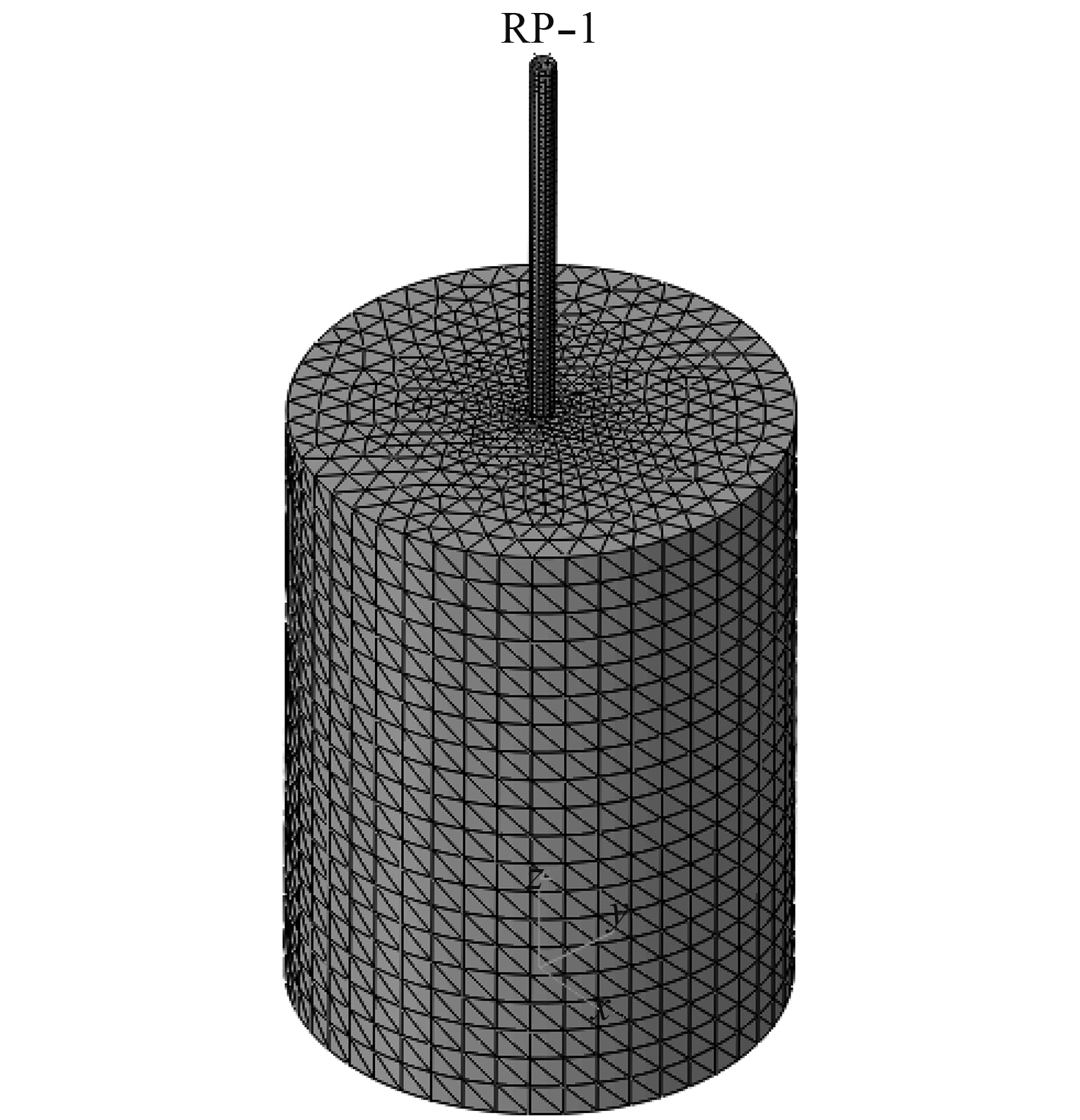
|
图 3 桩和土壤的三维有限元模型 Fig. 3 The 3D FE model of the pile and the soil |
桩模型采用弹性本构模型,由S4R单元组成,采用钢的材料属性,弹性模量为206GPa,泊松比为0.3,质量为7 840kg/m3。为减小边界效应的影响,土壤模型直径为20倍桩径,高度为桩插深加10倍桩径。土壤模型采用摩尔库伦本构模型,干重度为8.1 kN/m3,黏聚力为31.9 kPa,摩擦角为11.6°,弹性模量为5 MPa,泊松比为0.35。考虑到该加载过程是在不排水条件下完成的,设置土壤中的渗透率为1×10–6m/s,初始孔隙比为1.0,土壤孔隙流体重度为10 046 N/m3。土壤模型由C3D10单元组成,该类型单元只有平移自由度没有转动自由度。边界条件设置为土壤底部限制所有平移自由度,土壤侧面限制水平方向平移自由度。桩与土壤的接触面设置为“罚”接触,法线方向为硬接触,切线方向摩擦系数设置为0.25。
在三维桩-土有限元模型的参考点RP-1中施加水平侧向载荷进行静力分析,并从计算结果中提取出桩在不同深度位置处的p-y曲线,用梁和一系列非线性弹簧模拟桩和土壤支承力,将提取到的p-y曲线数据作为相应弹簧的刚度,比较在相同侧向载荷下三维模型桩和梁模型桩的侧向位移如图4和表1所示。
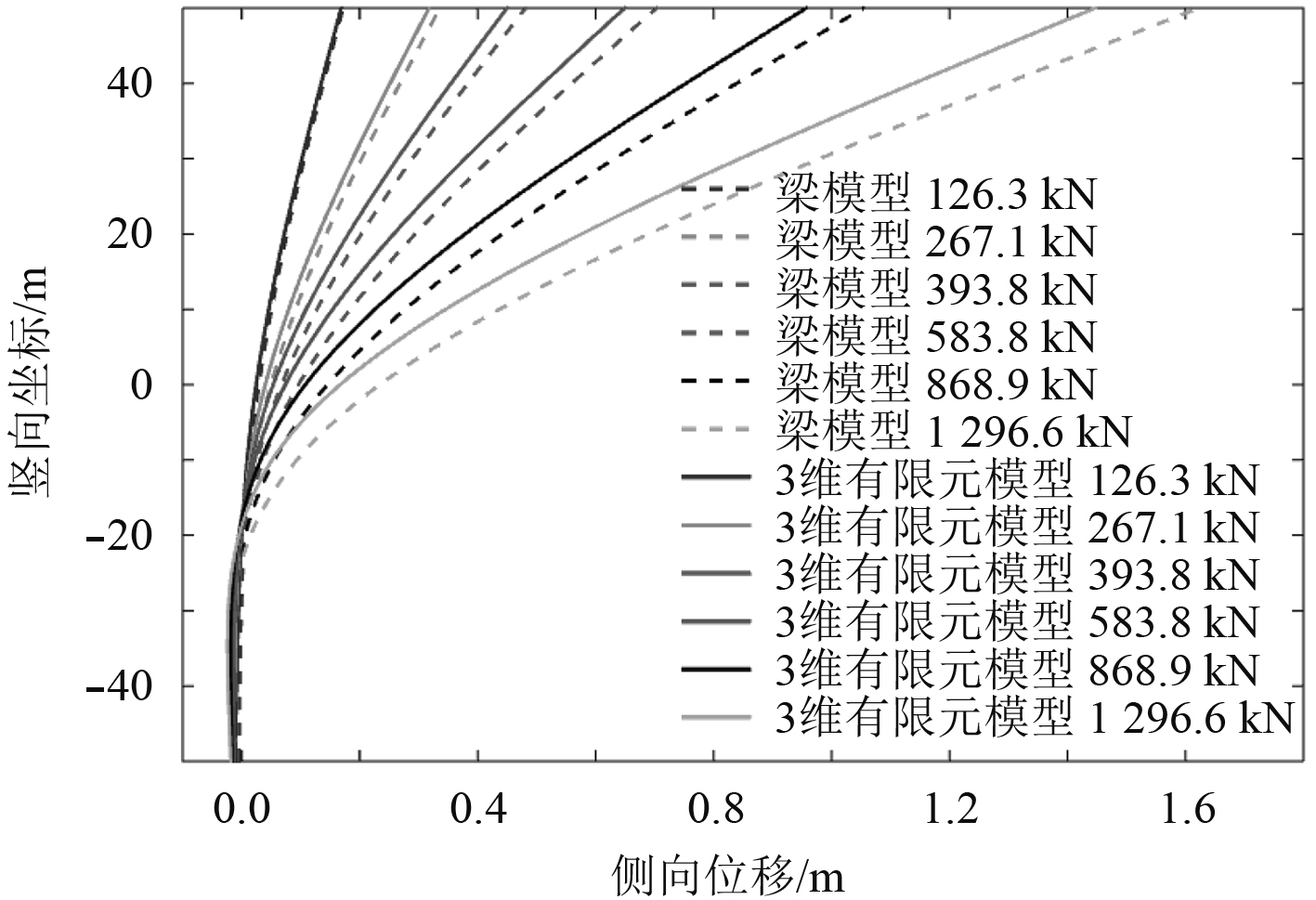
|
图 4 三维模型桩和梁模型桩侧向位移比较 Fig. 4 Comparison of the lateral displacement in the 3D pilemodel and the beam model |
|
|
表 1 三维模型桩与梁模型桩侧向位移特征值比较 Tab.1 Comparison of the lateral displacement in the 3D pilemodel and the beam model |
图3中纵坐标0代表海床表面,–50 m代表桩尖位置,50 m代表水面位置。三维模型中桩与梁模型中桩的在相同侧向载荷下的侧向位移符合较好,桩顶端位移差值最大不超过11%,证明p-y曲线法具有较高的准确性,可用于下文分析不同深度处的土壤侧向支承力。
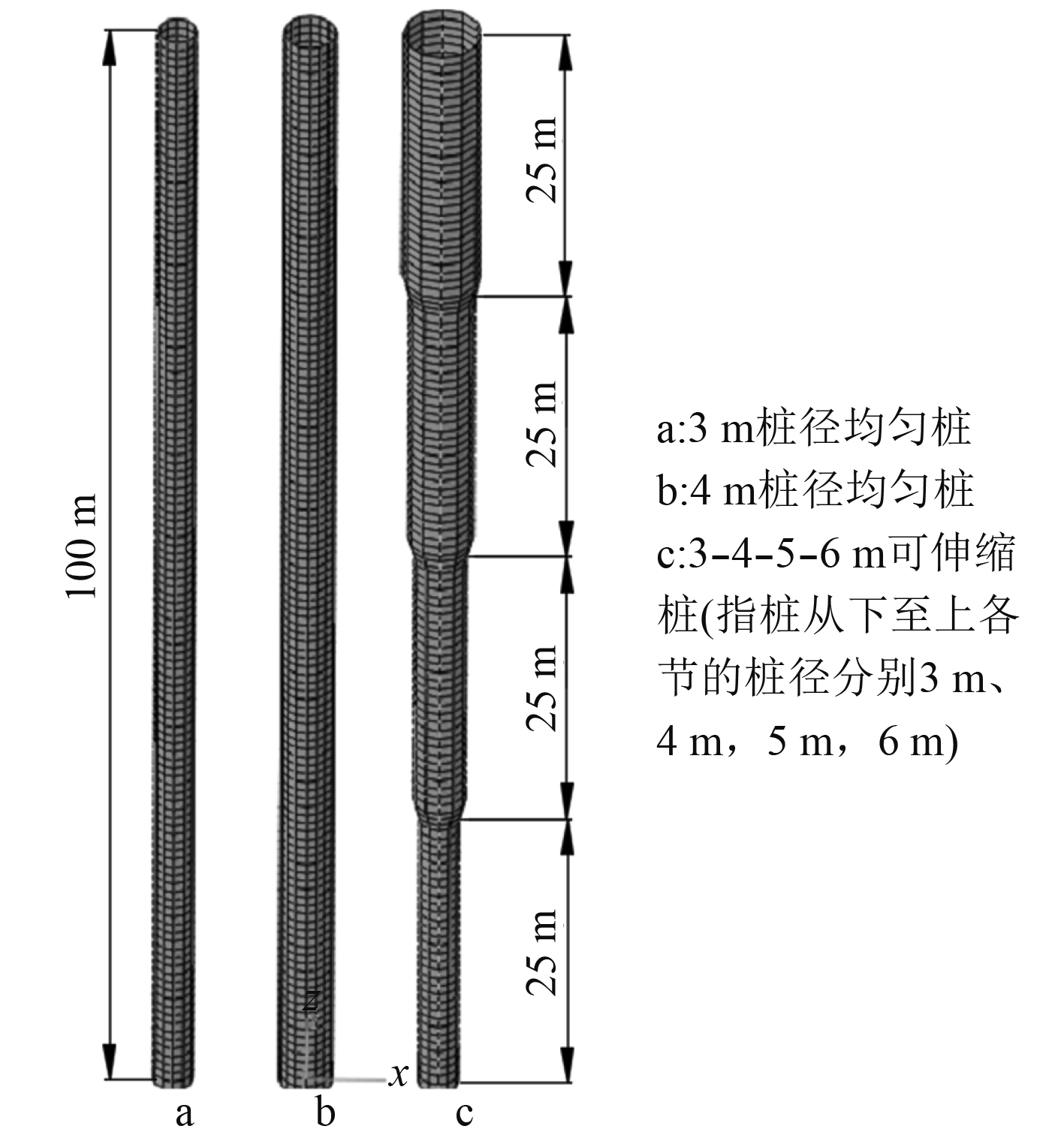
2 可伸缩桩与均匀桩的侧向承载力比较3-4-5-6 m可伸缩桩实际插入土壤中只有处于下方的2节,即桩径分别为3 m和4 m的2节,土壤对桩的支承力也是通过作用在这2节上实现的。本节主要研究3-4-5-6 m可伸缩桩与3 m桩径均匀桩和4 m桩径均匀桩的侧向承载能力对比,分析可伸缩桩结构在侧向承载力方面的表现状况。建立插深均为50 m的3 m桩径均匀桩、4 m桩径均匀桩和3-4-5-6 m可伸缩桩的三维有限元模型(见图5),通过加载侧向载荷比较其侧向位移响应和各深度处的p-y曲线。
|
图 5 3 m,4 m均匀桩和3-4-5-6 m可伸缩桩的三维有限元模型 Fig. 5 3D FE models of the 3m and 4m uniform piles and the 3-4-5-6m telescopic pile |
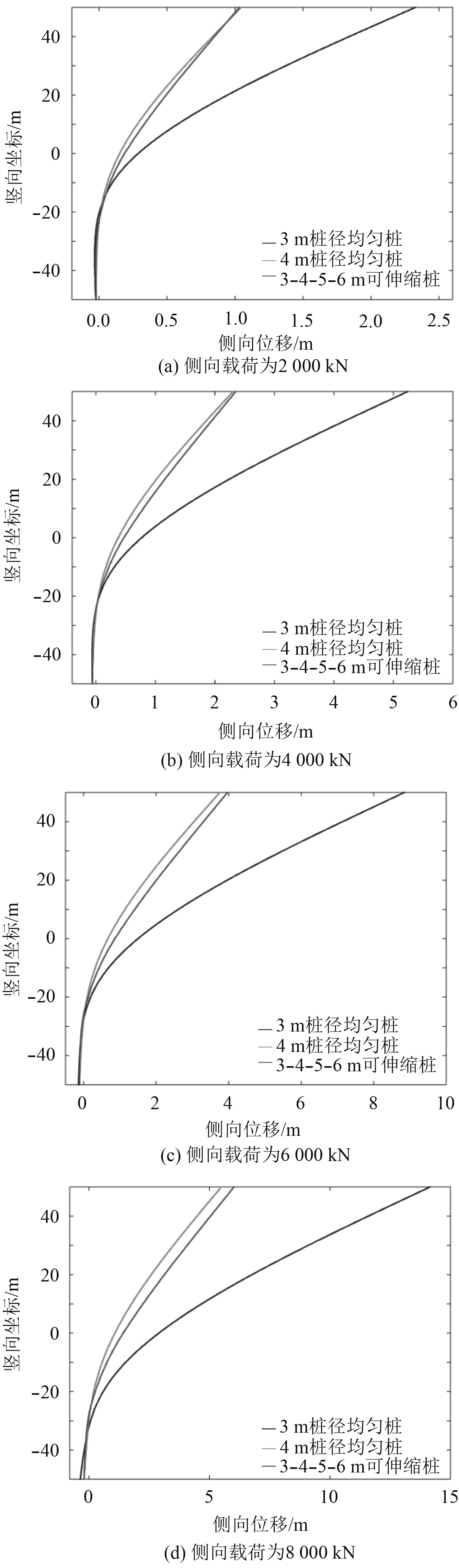
从图6可以看到,在侧向载荷较大(2 000 kN和4 000 kN)的2组工况中,3-4-5-6 m可伸缩桩的侧向位移与4 m桩径均匀桩的侧向位移非常相似;在侧向载荷较大(6 000 kN和8 000 kN)的2组工况中,3-4-5-6 m可伸缩桩的侧向位移比4 m桩径均匀桩的侧向位移略大。在所有4组工况中3-4-5-6 m可伸缩桩的侧向位移均明显小于3 m桩径均匀桩,所以3-4-5-6 m可伸缩桩的侧向承载能力与4 m桩径均匀桩接近,明显优于3 m桩径均匀桩。插入土壤部分的桩中,上半部分桩的侧向位移较大,而处于侧向位移拐点之下的桩侧向位移很小,拐点至海床表面这段桩所受到的土壤支承力对整个桩的侧向承载能力贡献较大,而拐点之下的部分桩对整个桩的侧向承载能力相对较小。所以3-4-5-6 m可伸缩桩的侧向承载能力更接近于4 m桩径均匀桩。桩所承受的侧向载荷越大,拐点位置越靠下,当侧向载荷大于6 000 kN时,拐点位于可伸缩桩最下方一节的位置,即此时最下方一节部分参与到对侧向承载能力贡献较大的那一段,而其桩径(3 m)比其上方一节桩径(4 m)小,该部分的侧向承载能力也会比较小。所以当侧向载荷大于6 000 kN(此时对应拐点位于可伸缩桩最下方2节的过渡处)时,侧向载荷越大,3-4-5-6 m可伸缩桩的侧向支承能力比4 m桩径均匀桩小越多。
|
图 6 3 m,4 m均匀桩和3-4-5-6 m可伸缩桩的侧向位移比较 Fig. 6 Comparison of the lateral displacements of the 3 m and 4m uniform piles and the 3-4-5-6 m telescopic pile |
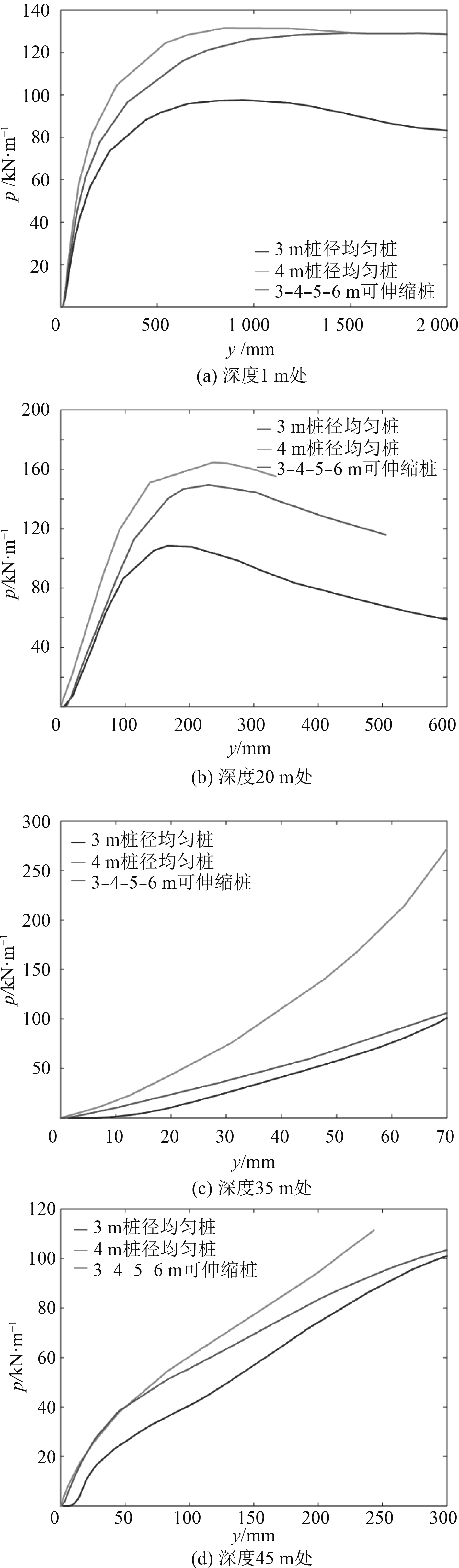
从图7可以看出,在插入土壤可伸缩桩的上方一节深度范围内(深度0~25 m),3-4-5-6 m可伸缩桩的p-y曲线形状接近于4 m桩径均匀桩,即在该范围内的侧向承载力与4 m桩径均匀桩相似。而在下方一节深度范围内(深度25~50 m),3-4-5-6 m可伸缩桩的p-y曲线形状接近于3 m桩径均匀桩,即该范围内的侧向承载力与3 m桩径均匀桩相似。这也为上文关于可伸缩桩侧向承载能力分析的猜测提供了佐证。
|
图 7 3 m,4 m均匀桩和3-4-5-6 m可伸缩桩在不同深度处的p-y曲线比较 Fig. 7 Comparison of p-y curves in various depths of the 3 m and 4m uniform piles and the 3-4-5-6 m telescopic pile |
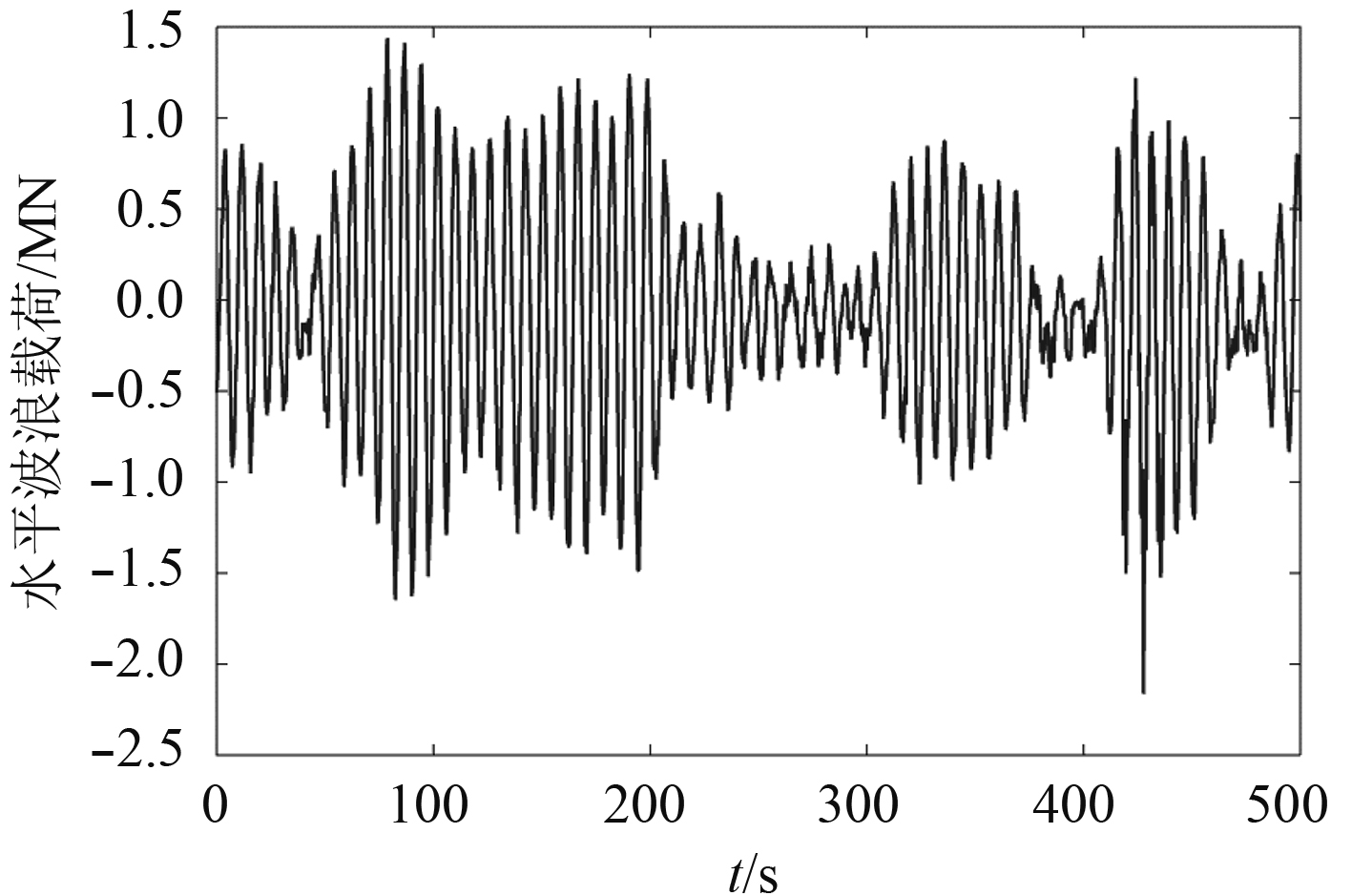
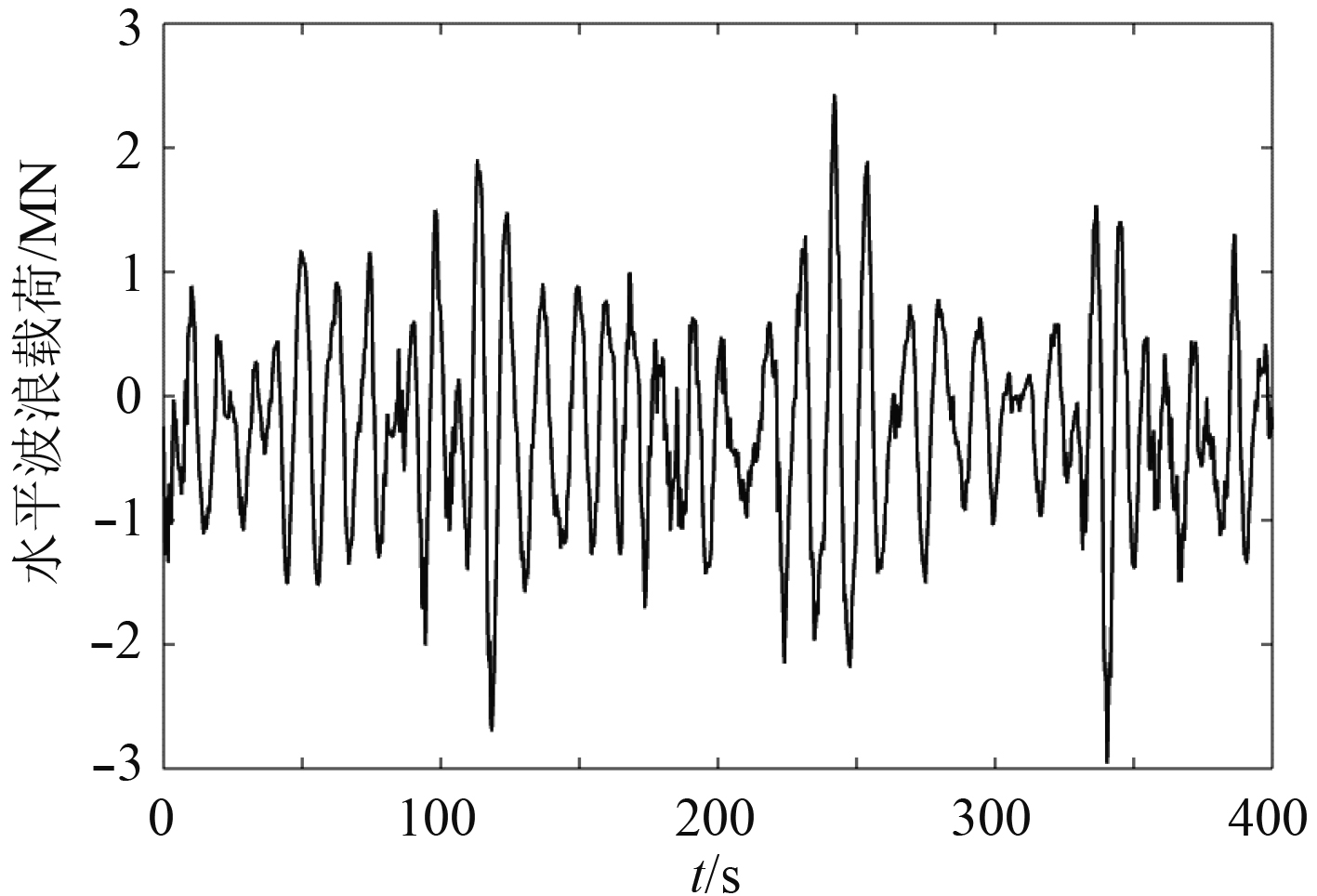
为分析可伸缩桩在实际工作当中受到往复变化波浪载荷下的运动响应,在有限元分析中加载波浪时历载荷。本文中可伸缩桩以安装于50 m水域超大型浮体为例,如图8和表2所示,相应的波浪载荷通过缩尺比为1∶ 100的模型实验测量获得,模型实验在上海交通大学国家海洋工程重点实验室进行。由于桩的定位精度高,采用桩定位的平台在波浪中的运动响应较小,实验中将平台设置为固定状态,分别试验超大型浮体在工作海况和生存海况所受到的波浪载荷。通过平台工作海域的观测统计,工作海况和生存海况中的波浪分别用有义波高3 m、谱峰周期7.48 s和有义波高5 m、谱峰周期9.66 s的Jonswap谱模拟。在工作海况和生存海况下,由浮体平均传递到每个可伸缩桩腿上的水平波浪载荷如图9和图10所示。
|
图 8 安装可伸缩桩腿的超大型浮体示意图 Fig. 8 Very large floating structure (VLFS) installed withtelescopic piles |
|
|
表 2 超大型浮体的主要参数 Tab.2 Basic parameters of the VLFS |
|
图 9 工作海况水平波浪载荷时历曲线 Fig. 9 Horizontal wave load in the operational condition |
|
图 10 生存海况水平波浪载荷时历曲线 Fig. 10 Horizontal wave load in the survival condition |
通过Abaqus/Standard的Implicit dynamic分析,计算桩在工作海况和生存海况的波浪载荷作用下的运动响应。分别提取工作海况和生存海况下,位于水面高度与桩连接的参考点RP-1和桩在海床表面高度处节点的水平时历响应,如图11和图12所示,位移响应统计值如表3所示。从图中可以看出桩在水平位移处的位移响应比参考点的位移响应小得多,大约是其1/5。即在波浪载荷作用下,插在土壤中桩的位移响应较小,但桩高于海床表面的长度较长(50 m),由于插于土壤中的桩发生转动和处于海水的部分桩发生弯曲导致参考点的水平位移远大于桩在海床表面位置处的水平响应。参考点代表了平台与桩的连接处,所以参考点的位移响应与平台的位移响应相似。工作海况下,桩在海床表面位置处的最大水平位移仅为0.23 m,不致引起土壤过大变形致使桩承载力下降,参考点的最大水平位移为1.2 m,定位精度远小于传统的锚泊定位装置,可满足对定位精度要求较高平台的设计要求。生存海况下,桩在海床表面位置处的最大水平位移为0.35 m,参考点的最大水平位移为1.78 m,由于生存海况下平台会停止工作,只需保证平台的安全,该运动响应一般也符合设计要求。

|
图 11 工作海况下桩的水平运动时历响应 Fig. 11 Horizontal motion response of the pilein the operational condition |
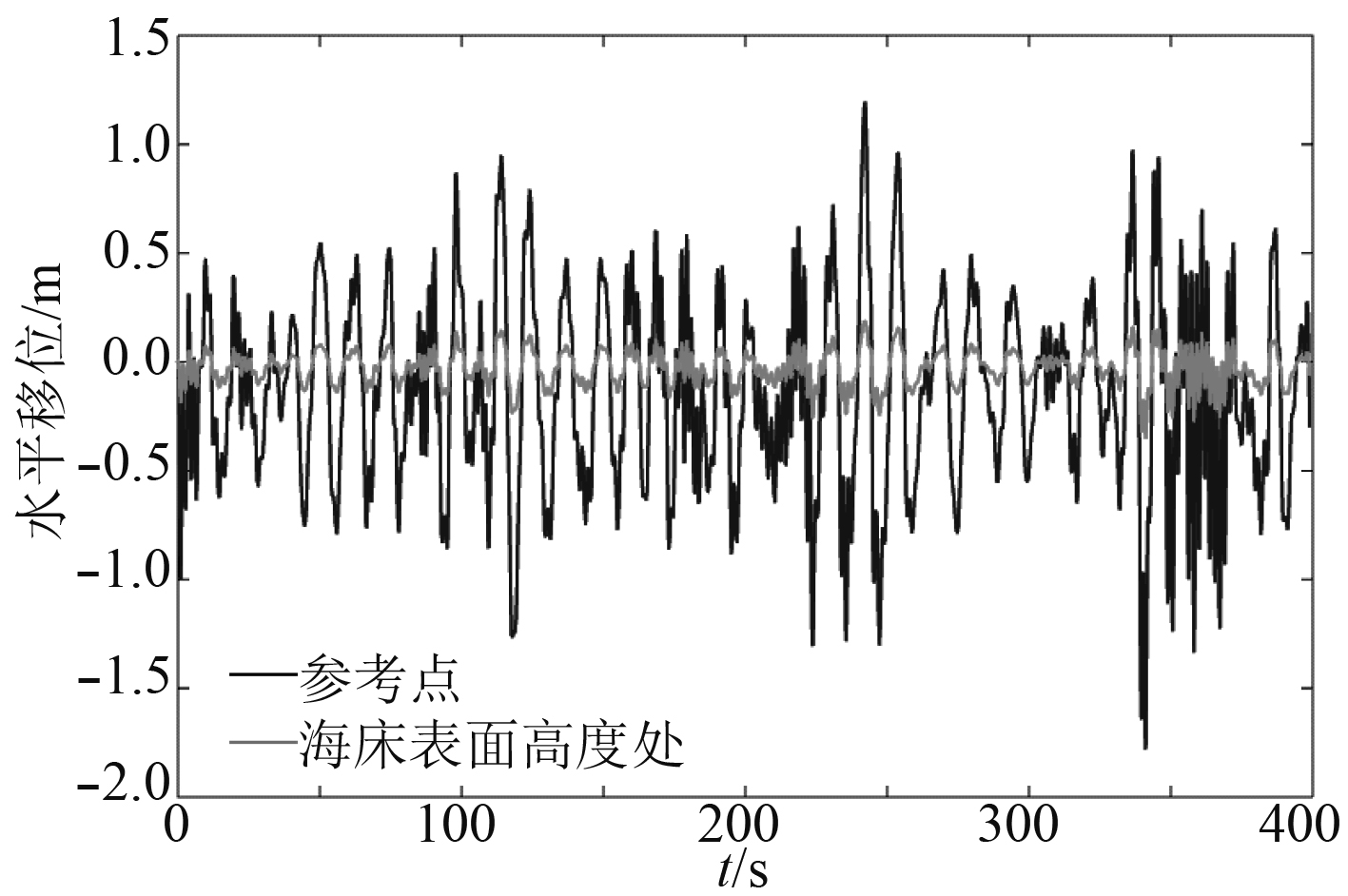
|
图 12 生存海况下桩的水平运动时历响应 Fig. 12 Horizontal motion response of the pilein the survival condition |
|
|
表 3 桩动态位移响应统计值 Tab.3 Statics of the pile motion response |
本文提出了一种适用于浅水域平台的新型定位装置,采用可伸缩桩进行定位。基于有限元法,通过商业软件Abaqus对可伸缩桩的侧向承载力进行分析。以3 m桩径均匀桩为例,比较了p-y曲线法和三维有限元法对桩侧向承载力的分析结果,验证了p-y曲线法的精确性。在此基础上用p-y曲线比较分析了3 m,4 m桩径均匀桩和3-4-5-6 m可伸缩桩在不同深度处的土壤支承力大小。通过比较相同侧向载荷下3种桩的侧向位移曲线,发现桩位移曲线拐点以上部分桩型对桩的侧向承载能力的影响比拐点以下部分桩型更大,3-4-5-6 m可伸缩桩的侧向承载能力接近于4 m桩径均匀桩。以可伸缩桩装置布置于超大型浮体为例,通过模型试验获得工作海况和生存海况下桩所承载的波浪时历载荷,计算得到桩的动态响应。结果显示可伸缩桩的动态响应较小符合工作和安全要求。可伸缩桩具有较好的侧向承载能力,该定位装置值得进一步研究以考虑应用到实际工程中。
| [1] |
ISSC. Committee VI.2: very large floating structures[C]. Southampton, UK: Proc 16th International Ship and Offshore Structures Congress, 2006.
|
| [2] |
MIGUEL L P, GREGORIOIGLESIAS L C. A review of very large floating structures (VLFS) forcoastal and offshore uses[J]. Ocean Engineering, 2015, 109(2015): 677-690. |
| [3] |
SUZUKI, H.. Overview of megafloat: concept, design criteria, analysis, and design[J]. Marine Structures, 2005, 18(2): 111-132. DOI:10.1016/j.marstruc.2005.07.006 |
| [4] |
SUZUKI H, et al. Very large floating structures[C]. International Offshore Mechanics and Arctic Engineering Conference, 2007, OMAE 2007-29758.
|
| [5] |
WANG CM, TAY ZY. Very large floating structures: applications, research and development[J]. Procedia Engineering, 2011, 14(3): 62-72. |
| [6] |
WATANABE E, WANG CM, UTSUNOMIYA T, et al. Very large floating structures: applications, analysis and design[J]. Centre for Offshore Research and Engineering, National University of Singapore, 2004, Core Report No. 2004-02.
|
| [7] |
MCCELLAND B, FOCHT J A. Soil modulus for laterally loaded piles[J]. Transactions ASCE, 1958, 123(1958): 1049. |
| [8] |
API. RP 2AWSD, 21st ed, recommended practice for planning, designing and constructing fixed offshore platforms – working stress design[S].
|
| [9] |
DNV-OS-J101, Design of Offshore Wind Turbine Structures [S]. |
| [10] |
DANNO, K. and KIMURA M.. Evaluation of long-term displacements of pile foundation using coupled fem and centrifuge model test[J]. Soils & Foundations, 2009, 49(6): 941-958. |
| [11] |
SUN Y. Experimental and numerical studies on a laterally loaded monopole foundation of offshore wind turbine[D]. Hangzhou: Dissertation of Zhejiang University, 2016.
|
| [12] |
MENG, Z.. Install effects and bearing capacity of drilled displacement piles with a screw-shaped shaft[D]. Hangzhou: Dissertation of Shanghai Jiao Tong University, 2017.
|
| [13] |
MANNA B. BAIDYA, DK. Nonlinear dynamic response of piles under horizontal excitation[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2010, 136(12): 1600-1609. |
| [14] |
KHODAIR Y, ABDEL-MOHTI A. Numerical analysis of pile–soil interaction under axial and lateral loads[J]. International Journal of Concrete Structures & Materials, 2014, 8(3): 239-249. |
| [15] |
HAIDERALI A, MADABHUSHI G. Evaluation of the p-y method in the design of monopiles for offshore wind turbines[C]. Offshore Technology Conference, 2013.
|
| [16] |
LESNY K,WIEMANN J. Finite-element-modelling of large diameter monopiles for offshore wind energy converters[C]. Proceedings, 2013, 1-6.
|
 2019, Vol. 41
2019, Vol. 41
