反后坐装置是舰炮发射系统的关键部位之一,某型大口径舰炮的驻退机为带沟槽的节制杆式驻退机,按照传统计算方法进行校核,舰炮的连发性能、驻退机腔内压力都没问题,但在射击试验中,当舰炮进行长连发射击时,出现后坐复进时间长的问题。在该问题上出现理论计算与射击试验结果不符现象,显示出传统设计方法在计算大口径舰炮长连发时存在不足,需要对驻退机流场重新进行计算分析。本文采用计算流体力学方法,通过CFD分析软件,重新研究驻退机内部流场的变化规律,分析驻退机出现该问题的原因,利用流体力学相关理论解决工程实际问题。
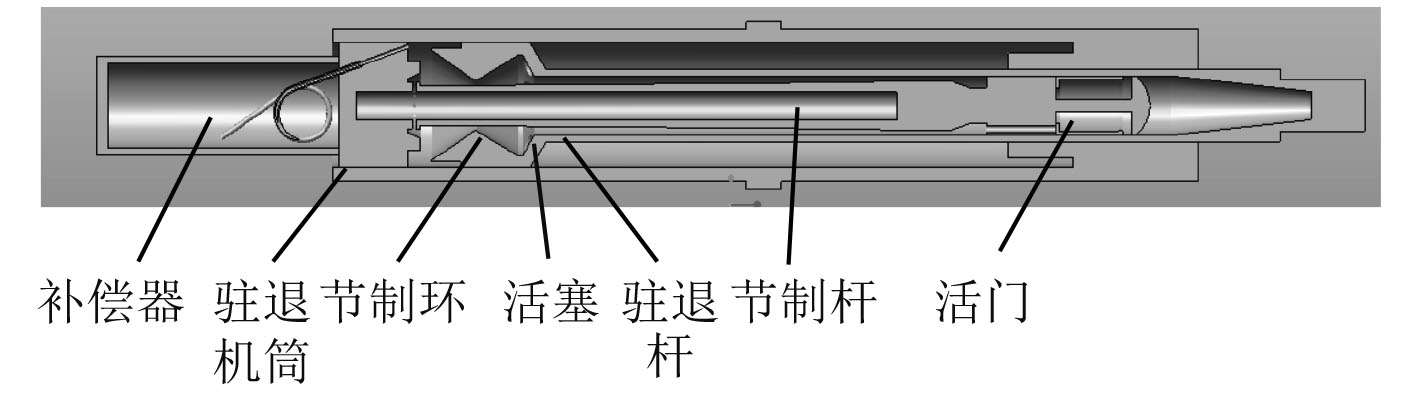
1 驻退机模型建立驻退机的主要功能是提供后坐阻力,控制火炮后坐部分按预先设定的力和运动规律运动,保证火炮射击时的稳定性。火炮使用驻退机大都是不可压缩液体的驻退机,节制杆式驻退机在火炮上有着广泛应用。图1为某型舰炮所采用的驻退机三维模型,这是一种典型的带沟槽的节制杆式驻退机。该制退机同时存在液量补偿器,可以防止液体因为温升膨胀影响驻退机正常工作[1]。
|
图 1 驻退机结构模型 Fig. 1 Structural diagram of recoil mechanism |
后坐过程驻退机的运动规律为:后坐部分带动驻退杆从驻退机筒中拉出来,液压油经过驻退杆活塞上的流液孔流出,一部分液体经节制环与节制杆间的环形间隙流到驻退杆的前腔,另一部分液体经驻退杆与节制杆间的环形间隙进入活门后内腔。液体经小孔高速流动时产生的阻尼抵消了部分后坐能量。节制环与节制杆间的环形间隙不断减小,液压油阻力逐渐增大,最终实现后坐部分的制动直至停止。
复进过程驻退机的运动规律为:在复进机的作用下后坐部分复进,带动驻退杆进入驻退机筒中。驻退杆前腔的液体经节制环与节制杆间的环形间隙以及驻退杆活塞上的流液孔流到驻退杆的后腔;驻退杆内腔的液压油经驻退杆内表面的可变深度的沟槽被挤向前,通过合理设计沟槽,可以确保驻退杆按照指定的规律复进[2]。
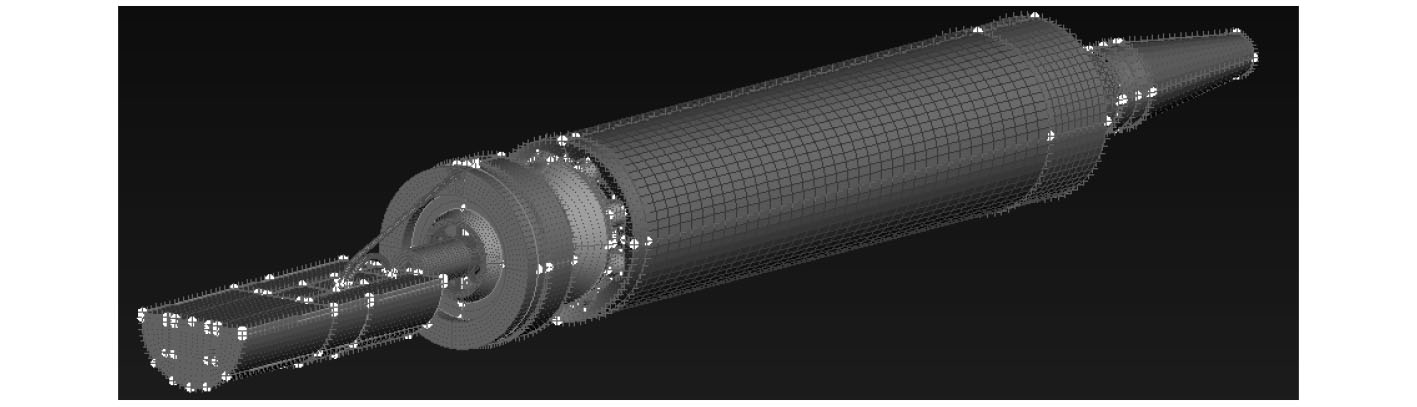
在实际仿真计算中,驻退机的结构过于复杂,需要进行简化处理,去掉一些无关的部件,带补偿器的主推机模型简化后划分网格如图2所示。
|
图 2 驻退机网格图 Fig. 2 Meshing diagram of recoil mechanism |
简化后的驻退机模型流场为三维对称不可压缩湍流,采用下面的数学模型:
| $ \begin{split} & \rho \left\{ {\frac{{\partial \varPhi }}{{\partial t}} + \frac{{\partial \mu \varPhi }}{{\partial x}} + \frac{{\partial \nu \varPhi }}{{\partial y}} + \frac{{\partial \omega \varPhi }}{{\partial z}}} \right\} = \frac{\partial }{{\partial x}}\left\{ {\Gamma \frac{{\partial \varPhi }}{{\partial x}}} \right\}+ \\ & \frac{\partial }{{\partial y}}\left\{ {\Gamma \frac{{\partial \varPhi }}{{\partial y}}} \right\} + \frac{\partial }{{\partial z}}\left\{ {\Gamma \frac{{\partial \varPhi }}{{\partial z}}} \right\} + S \text{。} \end{split} $ |
式中:
驻退机内部液体在非常短的时间内加速到最大速度,其速度变化非常剧烈,属于典型的非定常流动,驻退机节制杆流液孔处液体雷诺数高达上百万,形成高雷诺数湍流。湍流模型采用标准
| $ \rho \frac{{{\rm{D}}k}}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}{\text{,}} $ |
| $ \rho \frac{{{\rm{D}}\varepsilon }}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {C_{3\varepsilon }}{G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}} $ |
湍流粘性系数为:
该模型考虑到补偿器的作用,需要使用多相流模型,在补偿器连接空气部分使用压力边界入口,补偿器位置流体采用多相流模型,即VOF模型[4]。在后坐复进过程中,驻退杆往复运动,其内部运动边界不断变化,分析过程中使用动网格。其运动规律使用内弹道的计算数据,采用边界型函数(Profile文件)指定。在本模型中,运动变形区域为结构化网格,采用动态层技术可以快速实现动网格的实时更新[5] [6]。
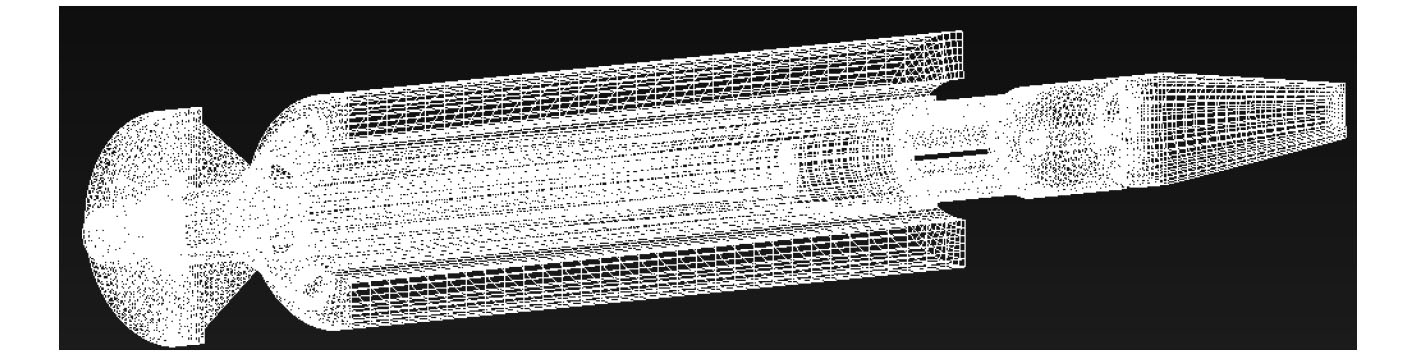
3 驻退机流场数值模拟分析本文分3步进行流场仿真,首先是不带补偿器单发后坐复进流场分析,之后是带补偿器单发后坐复进过程分析,最后是带补偿器连发后坐复进过程分析。不带补偿器的时候需要对模型进行处理,将补偿器去掉之后的模型如图3所示。此时驻退机内部全是液压油,在计算过程中认为是单相流运动,不必考虑空气的影响,从一定程度上可以对驻退机内部的流场进行简单的分析。
|
图 3 不带补偿器的驻退机网格模型 Fig. 3 Meshing diagram of recoil mechanism without compensator |
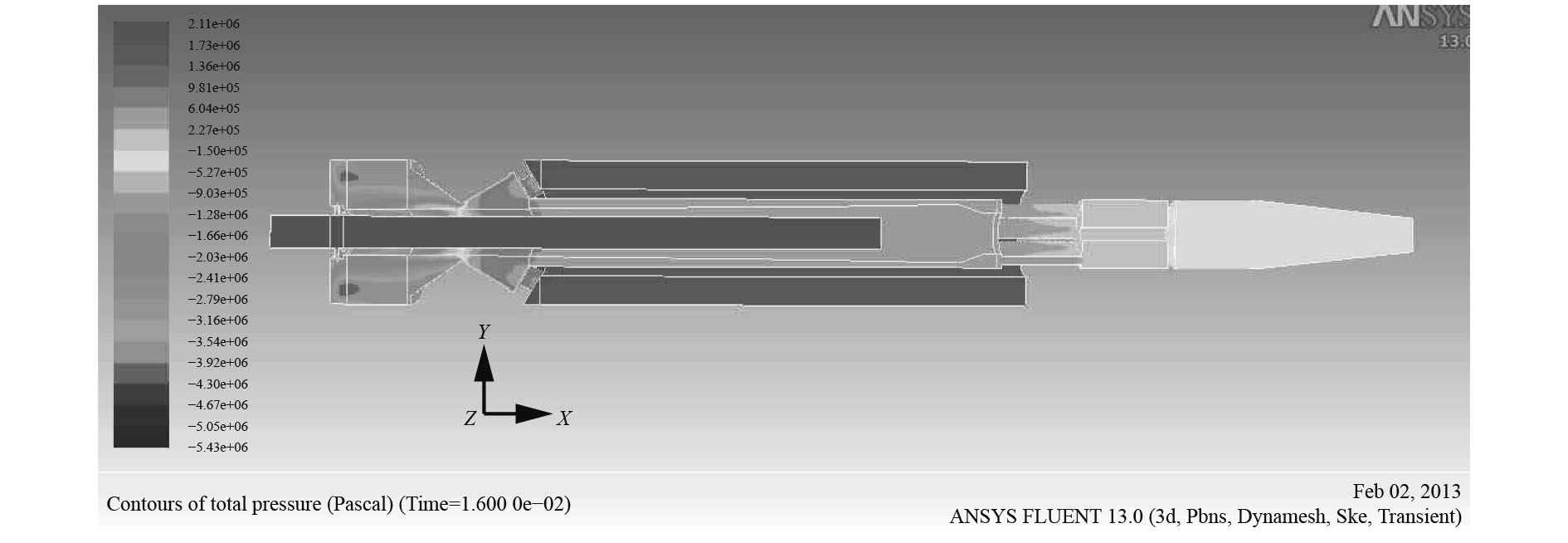
驻退机后坐复进过程共计0.6 s,其中后坐过程0.132 s,复进过程0.468 s,此处选取后坐过程中0.016 s,0.128 s;复进过程中0.16 s,0.32 s等4个时刻的驻退机内部流场压力数据,读取其对称面上的压力云图,如图4~图7所示。
|
图 4 0.016 s时压力云图 Fig. 4 Contours of dynamic pressure at 0.016 s |
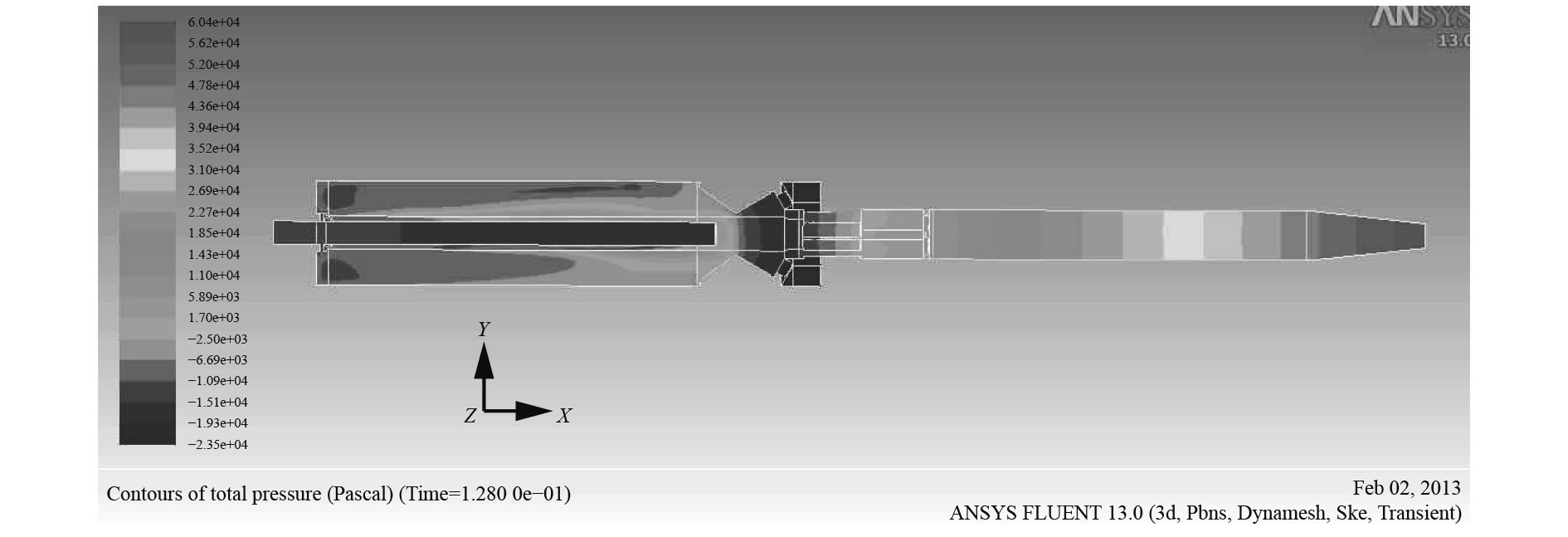
|
图 5 0.128 s时压力云图 Fig. 5 Contours of dynamic pressure at 0.128 s |
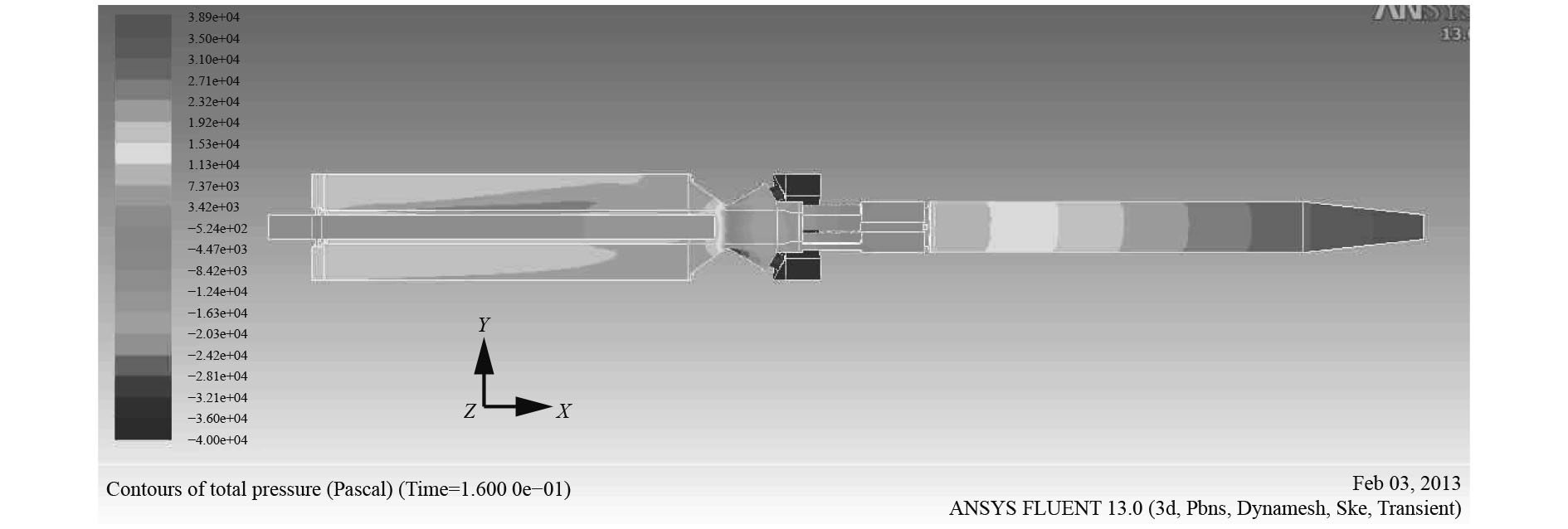
|
图 6 0.16 s时压力云图 Fig. 6 Contours of dynamic pressure at 0.16 s |
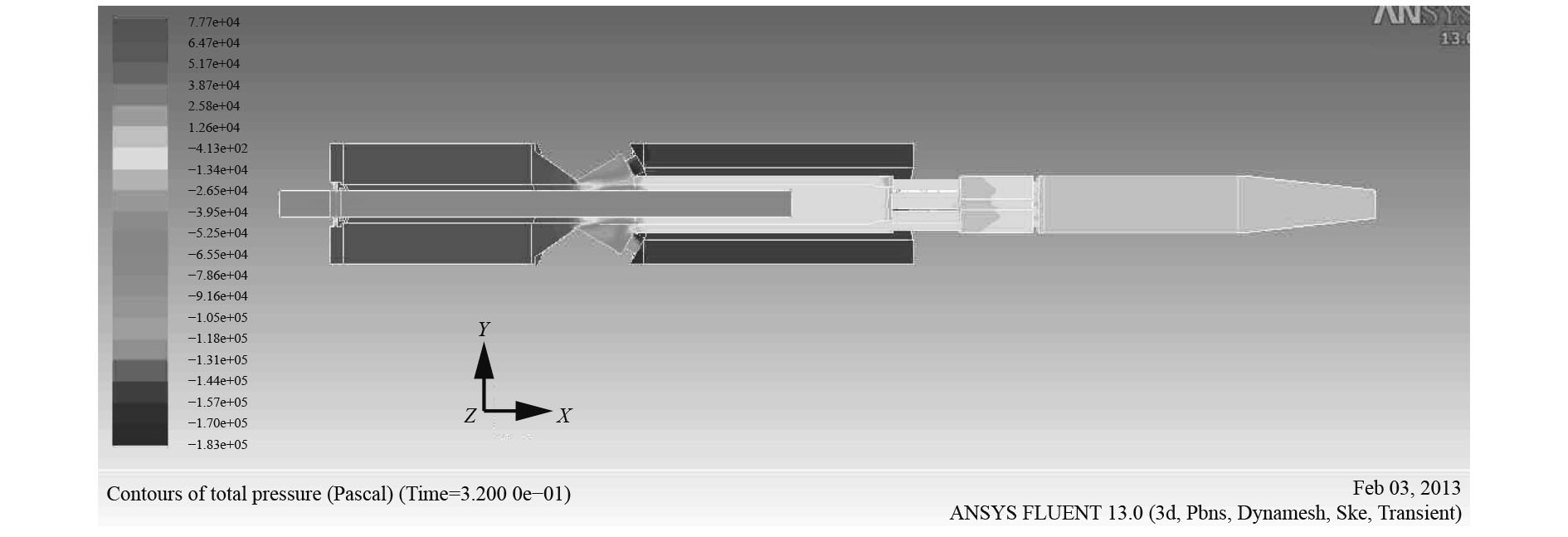
|
图 7 0.32 s时压力云图 Fig. 7 Contours of dynamic pressure at 0.32 s |
从图中可知,不同时刻驻退机内流场压力有很大差别,基本规律大致相似,活塞前部出现很大压力,活塞后部压力很小并出现负压,分析认为是液体局部压力下降到饱和蒸汽压或空气分离压以下,导致液体内部产生了气穴现象[7]。液压油中的空泡溃灭时间极短,局部会出现非常大的压强,不断溃灭的空泡产生极高的压强反复冲击碰撞驻退机壁面以至造成破坏,形成气蚀[8 – 9]。为避免该现象发生,驻退机前部添加了补偿器,补偿器与大气相连,可避免这种现象。
3.2 带补偿器的驻退机单发后坐复进模拟分析带补偿器的模型见图2。补偿器内上部为空气,仿真模型变为两相流,设置空气入口为压力入口,即press-inlet边界条件,并设置一个很小的湍流参数,保证计算后不会有较大误差。运动过程0.6 s,后坐0.132 s,复进0.468 s,选取流场体积分数、压力场两个角度进行分析。
1)驻退机内部流场体积分数
某一相的体积分数表示了该相在两相流中所占的比例[7],对单发运动,选择0.08 s时的体积分数云图,如图8所示。可以看出,驻退机前部区域空气体积分数都位于0.05以下,可以认为活塞环运动前部区域全部是液压油,活塞环运动后侧,气相体积分数开始逐渐增大,特别是驻退机内壁上部弯管入口处在到驻退机节制环周围,气体积分分数比较大,可以认为此处进入了空气,补偿器底部有体积分数小于0.05的区域,说明在补偿器中液压油并没有全部被抽入驻退机内。
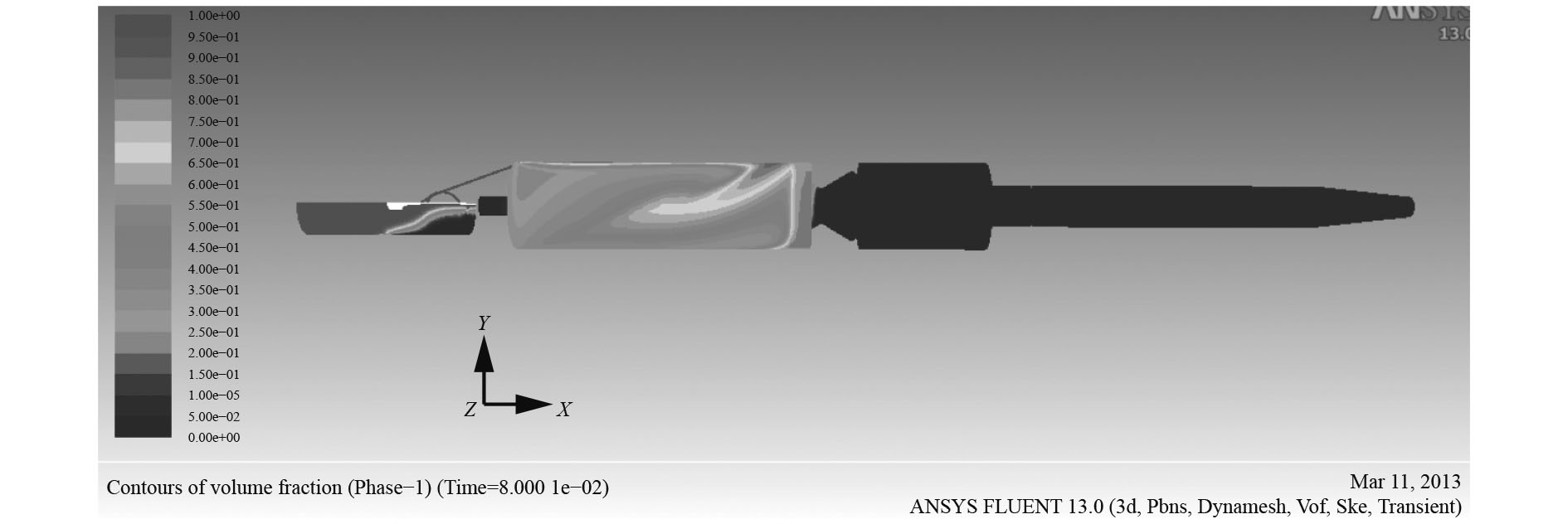
|
图 8 0.08 s时体积分数云图 Fig. 8 Contours of volume fraction at 0.08 s |
作为对比,可以参照0.12 s时的气体体积分数,此时后坐运动基本结束,补偿器内腔中有液压油没有被抽入到内腔中,驻退机内空气所占比重有所上升,认为有空气通过弯管进入驻退机内。
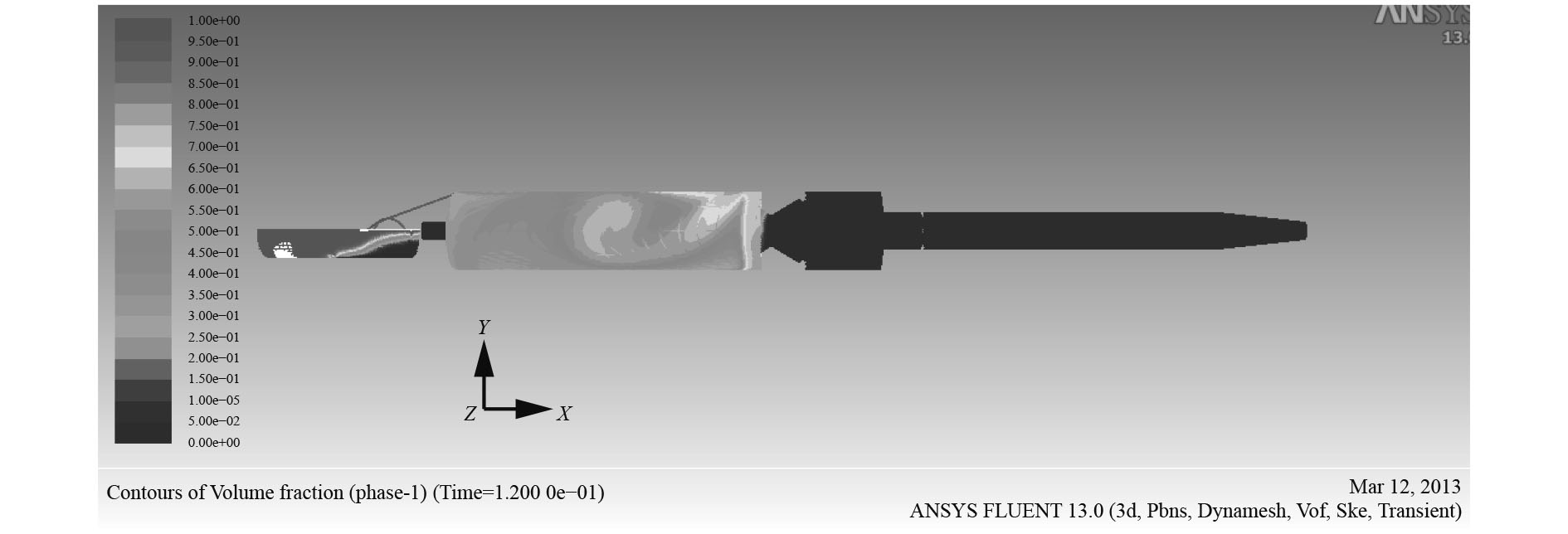
|
图 9 0.12 s时体积分数云图 Fig. 9 Contours of volume fraction at 0.12 s |
复进过程选取0.5 s时进行分析,如图10所示。此刻复进基本到位,驻退机内部液压油所占比例明显增多,液压油逐步占据了空气的空间,气体也逐渐返回补偿器,补偿器内底部有部分液压油。全过程中节制杆内腔没有空气进入,空气的影响区域主要是活塞运动方向前部。
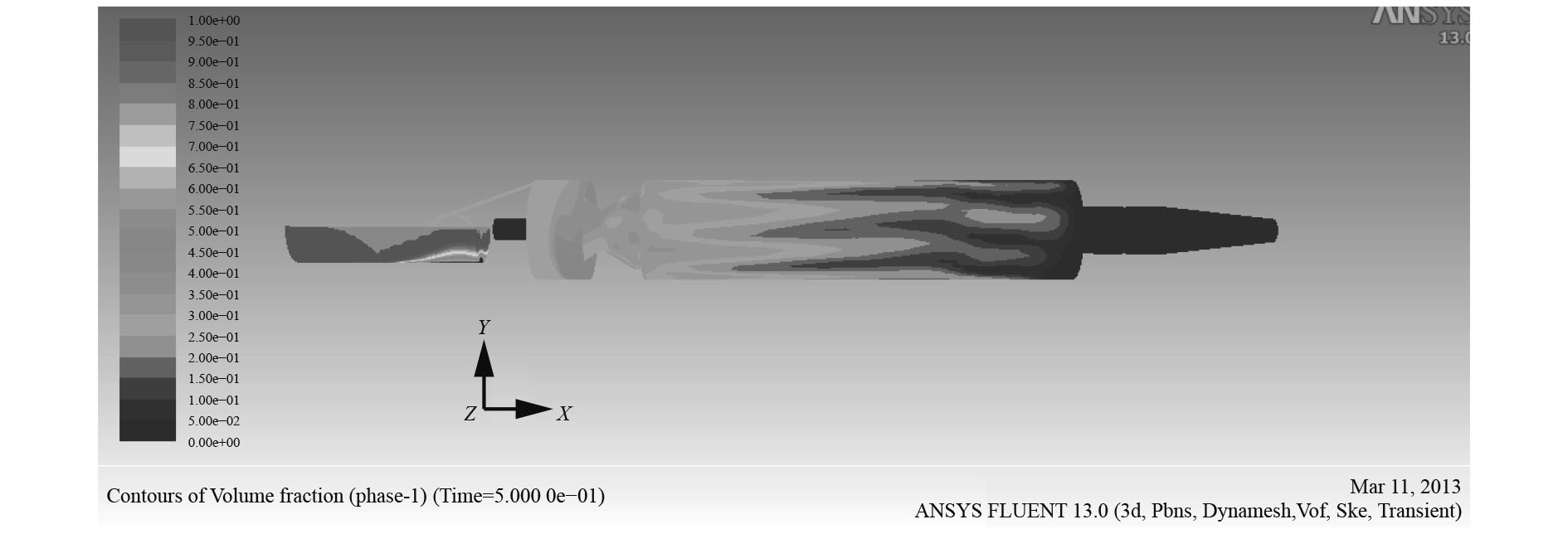
|
图 10 0.5 s时体积分数云图 Fig. 10 Contours of volume fraction at 0.5 s |
2)驻退机内部流场压力分析
后坐过程选取0.08 s时压力分析,由于两相流的作用,带补偿器的驻退机流场负压力已经消失(见图11),最大压力位于管道壁面处,压力值为0.28 MPa。
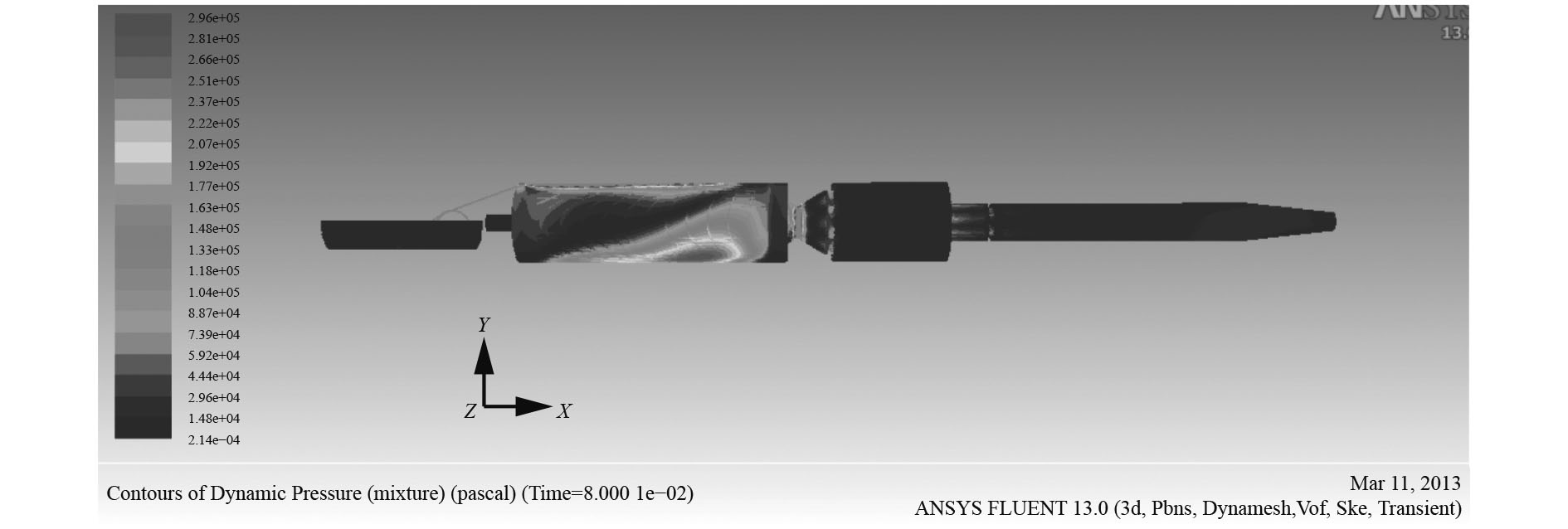
|
图 11 0.08 s时压力云图 Fig. 11 Contours of dynamic pressure at 0.08 s |
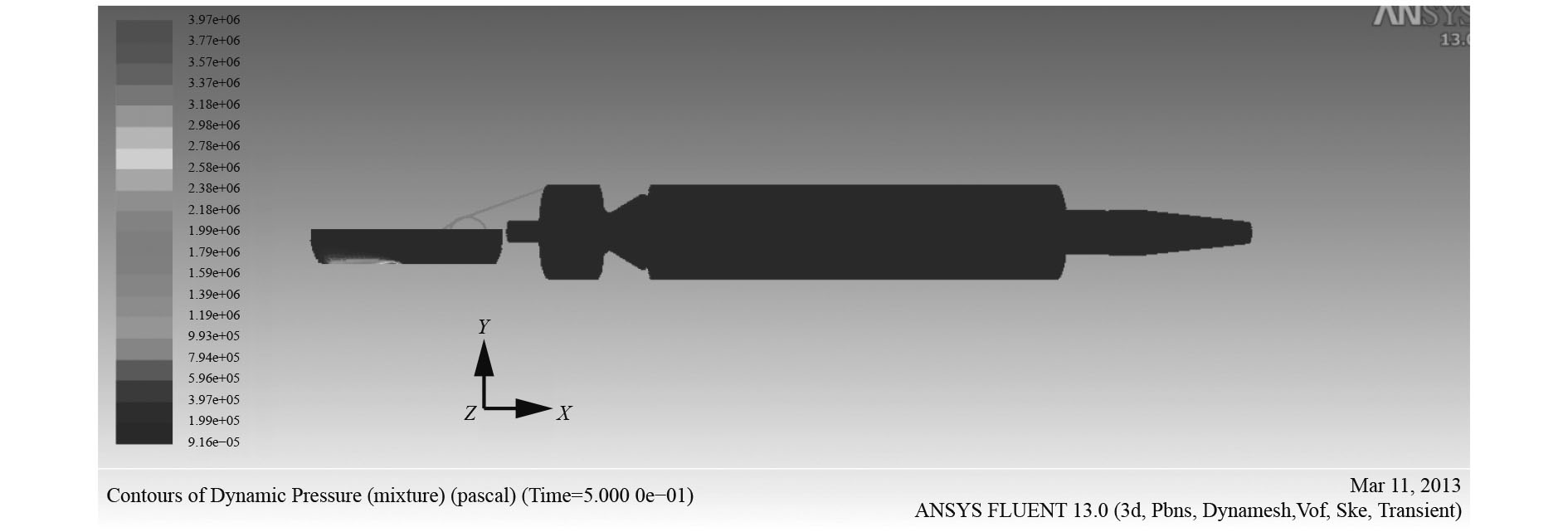
|
图 12 0.5 s时压力云图 Fig. 12 Contours of dynamic pressure at 0.5 s |
对于复进过程,选取0.5 s时分析压力变化规律,此时接近复进尾声,最大压力值为3.97 MPa,位于补偿器底部接近弯管处,其余部位压力位于0.2 Mpa以下。
3.3 带补偿器的驻退机连发后坐复进模拟分析本文选择了4次连发进行仿真计算,其中单发运动的后坐时间0.132 s,复进过程0.468 s,4次连发时间总计2.3 s。文中选取流场体积分数、有效粘度、压力场3个角度来进行分析。
1)驻退机内部流场体积分数和有效粘度分析
在长连发运动过程中,0.7 s时体积分数如图13所示。活塞环运动前部区域空气体积分数小于0.13,运动区域后部体积分数较大,在与弯管相连的上部区域,甚至达到0.6~0.75之间,说明通过弯管有相当数量的空气进入了驻退机内部。图14为1.9 s时驻退机内流场空气体积分数云图,此时活塞环运动位置和0.7 s时大致相同,在活塞环前部区域,空气体积分数有了很大提高,大致范围为0.4~0.45,节制杆内腔中空气体积分数也有一定提高,此时空气的影响已经到了节制杆内腔。在节制环后部流体区域从连接弯管处到活塞后部位置,空气体积分数比较高。
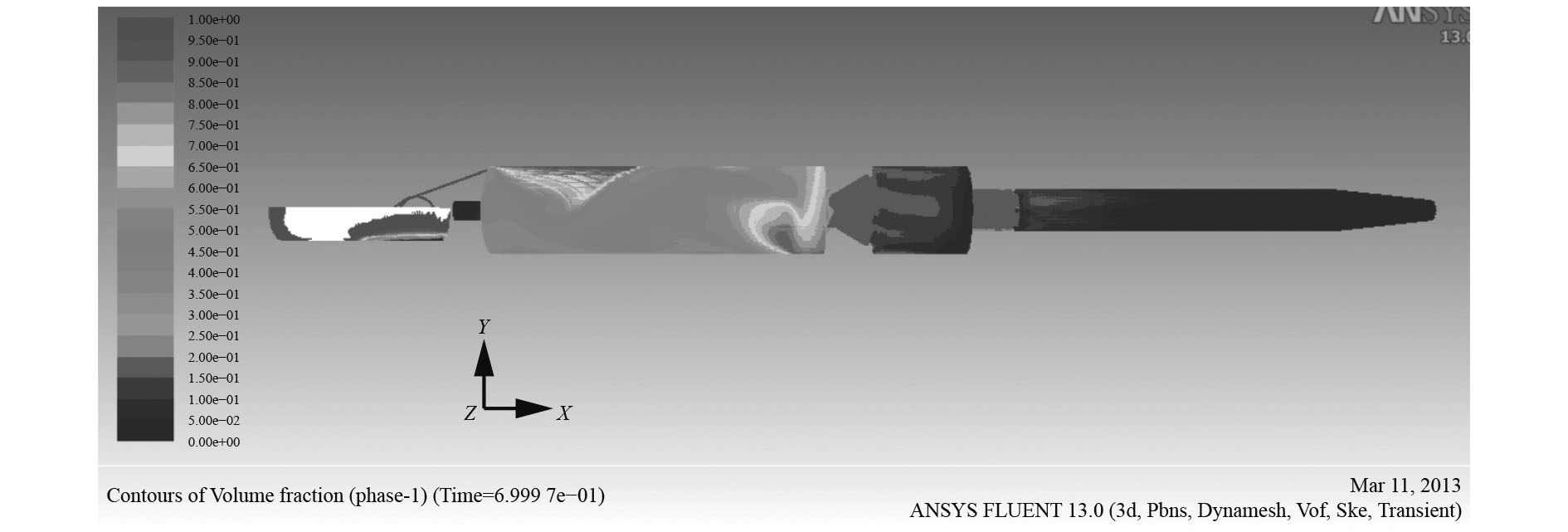
|
图 13 0.7 s时体积分数云图 Fig. 13 Contours of volume fraction at 0.7 s |

|
图 14 1.9 s时体积分数云图 Fig. 14 Contours of volume fraction at 1.9 s |
空气从弯管进入驻退机内后沿着上部壁面扩散,碰到活塞尾部后向活塞周围扩散,随着连发后坐复进运动的积累,后坐复进过程中空气的体积分数逐渐变大,而且扩散的区域也逐渐扩大,甚至进入到节制杆内腔中,大量空气会形成直径为0.05~0.5 mm的小气泡状态悬浮在液体中,这种气泡对液压油的体积弹性模量和液压油的粘度产生严重影响。
如果混入的空气继续增加,受到影响的液压油弹性模量急剧下降,液压油中的压力波传播速度减慢,动力粘度开始呈线性增高,对驻退机内的复进运动会造成严重影响,这里给出1.1 s,1.9 s时和2.26 s时的有效粘度云图(见图15~图17)。从1.9 s时和2.26 s时云图上分析,在1.9 s时最大粘度值为8.92 kg/m·s,2.26 s时最大粘度值为10.1 kg/m·s,粘度的整体分布情况也有了一些提高,在1.9 s时,大部分区域粘度数值集中在0.2~0.35 kg/m·s之间,而到了2.26 s时,大部分区域粘度数值集中在0.40~0.5 kg/m·s之间。粘度的增加有可能会造成复进不到位的现象。
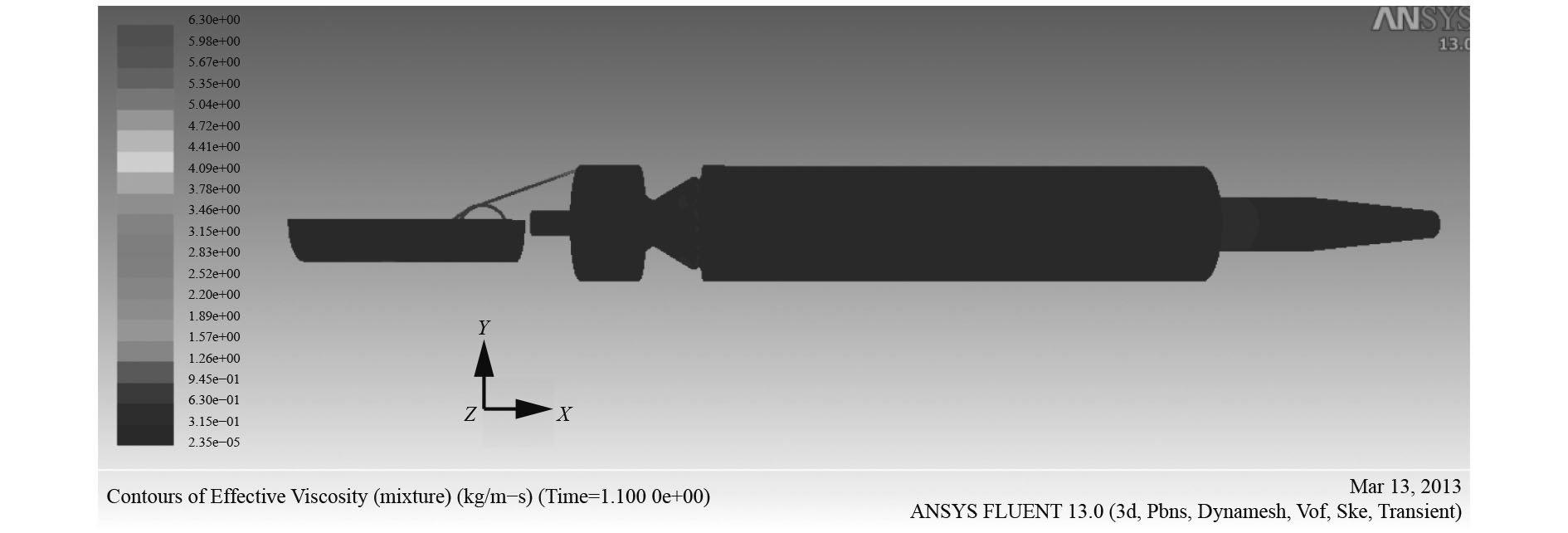
|
图 15 1.1 s时有效粘度云图 Fig. 15 Contours of effective viscosity at 1.1 s |
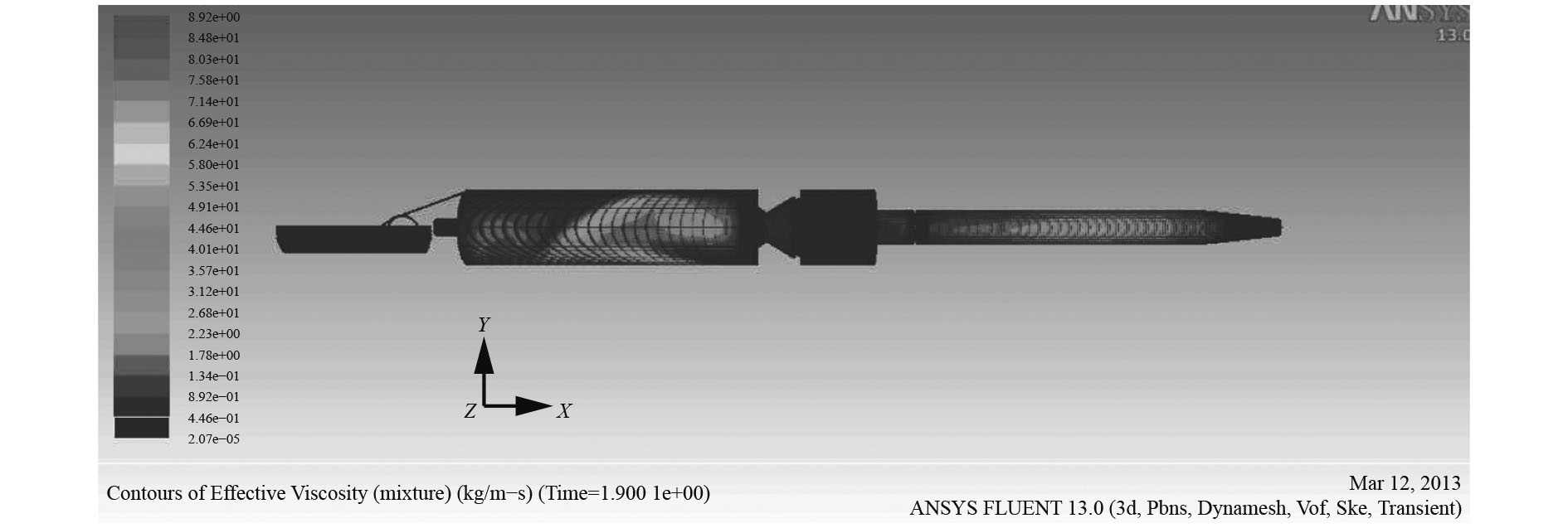
|
图 16 1.9 s时有效粘度云图 Fig. 16 Contours of effective viscosity at 1.9 s |
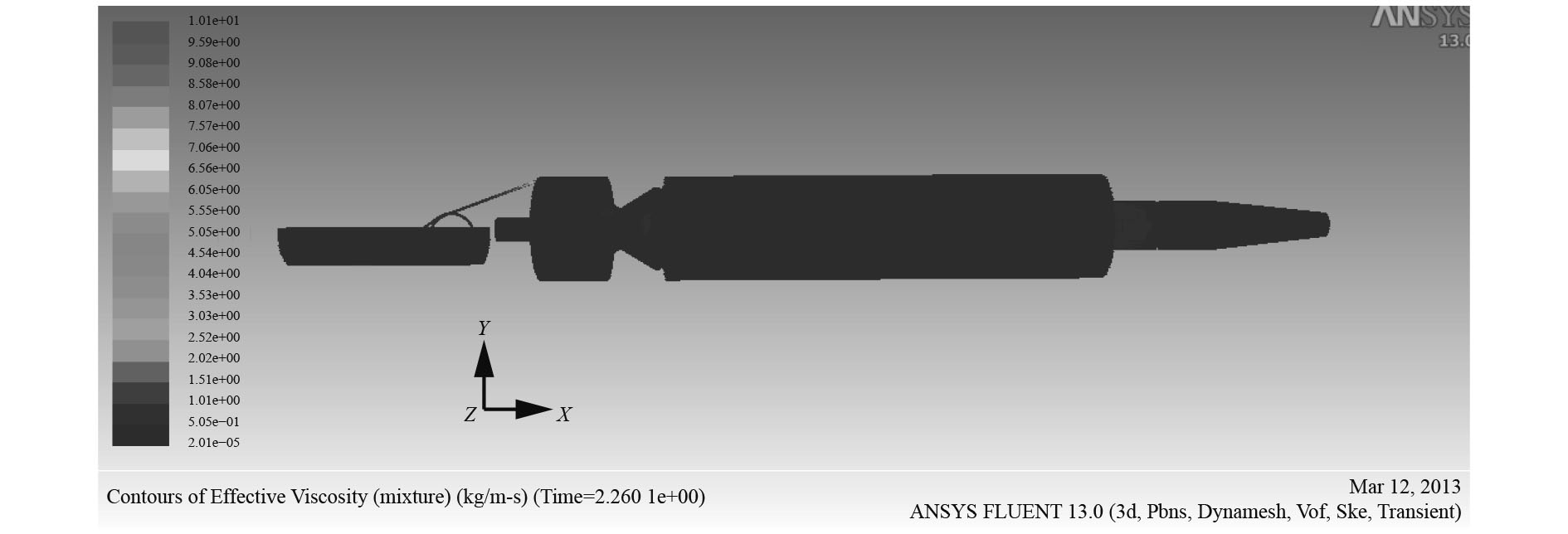
|
图 17 2.26 s时有效粘度云图 Fig. 17 Contours of effective viscosity at 2.26 s |
2)驻退机内部流场压力分析
随着后坐复进运动的增加,压力分布也出现了变化,这里选取1.3 s时和1.9 s时的压力场来进行分析,1.3 s时的压力云图如图18所示,最大压力为0.782 MPa,位于弯管与驻退机连接处,其中节制环处的最大压力为0.0392 MPa。1.9 s时的压力云图如图19所示,相比较而言,最大值减小为0.334 MPa,分析认为压力的减小是空气进入的缘故,随着后坐复进的继续进行,压力会继续减小。压力的减小对液压油没有显著的影响。
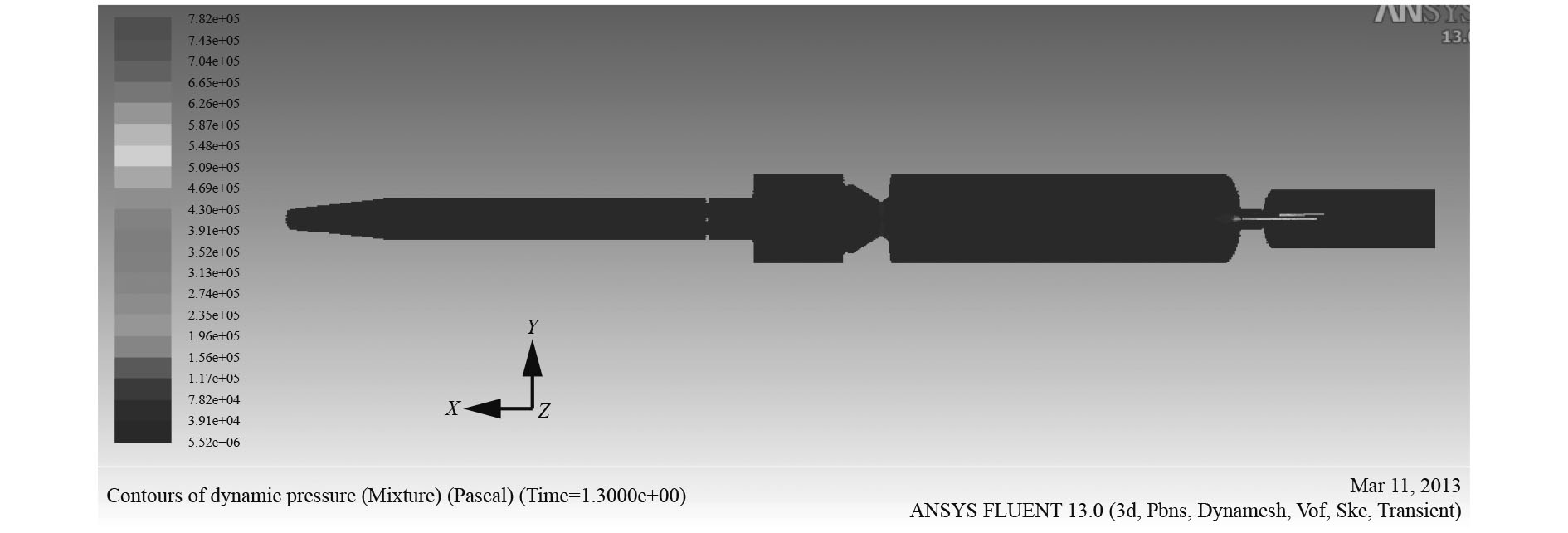
|
图 18 1.3 s时压力云图(顶视图) Fig. 18 Contours of dynamic pressure at 1.3 s(top view) |
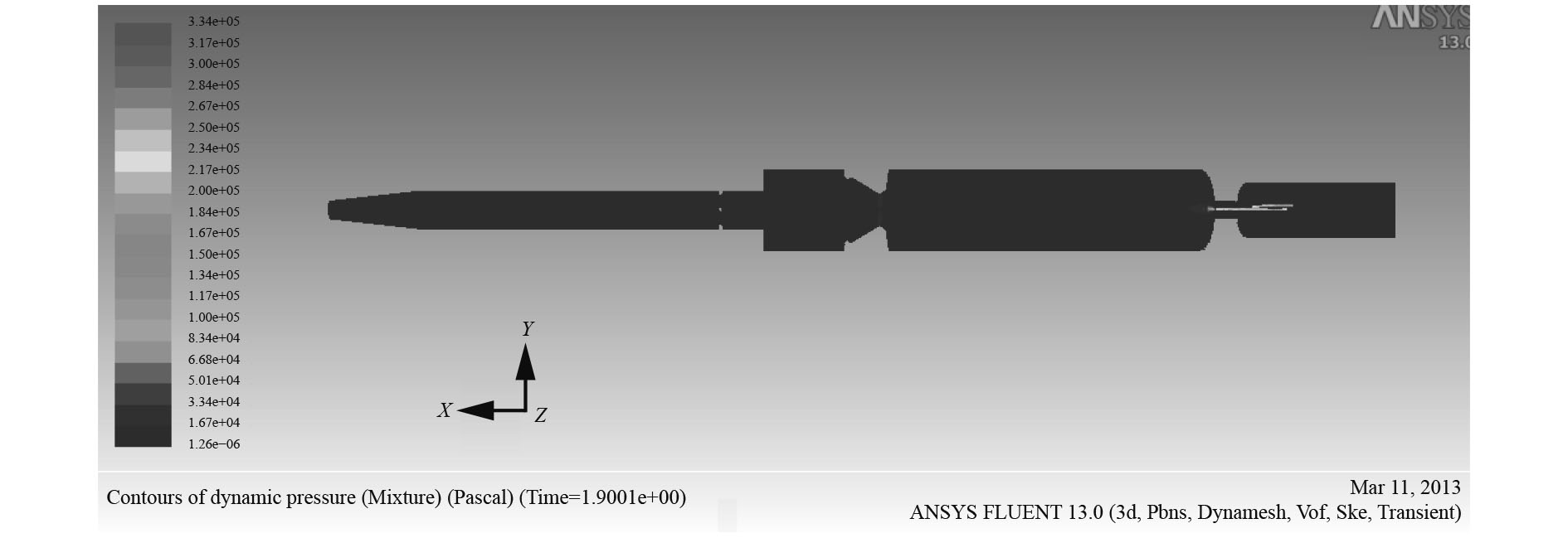
|
图 19 1.9 s时压力云图(顶视图) Fig. 19 Contours of dynamic pressure at 1.9 s(top view) |
不带补偿器的驻退机单发后坐复进过程主要从一般的计算角度对流场进行了分析,目前大部分对驻退机流场的仿真都不考虑补偿器的作用,文中对其进行计算主要便于之后同带补偿器的驻退机流场仿真结果进行对比。
带补偿器的后坐复进过程,不论单发还是连发,都需要考虑空气的作用,将问题扩展到多相流。由于补偿器直接与空气相连,导致空气从弯管处进入驻退机内腔,这一点对于驻退机长连发工作不利,会在驻退杆复进过程中增大粘度,粘度的增大对复进过程不利,解决方法可以从减小空气进入量,减小复进阻力等角度出发,具体措施有增大补偿器内部液压油的体积,增大驻退杆内表面沟槽尺寸等。本文对含补偿器的驻退机连发运动流场数值模拟为驻退机设计改进提供了一定的参考和借鉴作用。
| [1] |
高跃飞. 火炮反后坐装置设计[M]. 北京: 国防工业出版社, 2010.
|
| [2] |
胡胜海, 宋洪侠, 曲东越, 等. 舰炮缓冲技术的研究[J]. 哈尔滨工程大学学报, 2000, 21(1): 76-78. HU Sheng-hai, SONG Hong-xia, QU Dong-yue, et al. Research on Buffering Technique of Nun Gun[J]. Journal of Harbin Engineering University, 2000, 21(1): 76-78. DOI:10.3969/j.issn.1006-7043.2000.01.018 |
| [3] |
郑建国. 火炮制退机性能的数值预测[J]. 火炮发射与控制学报, 2000(2): 10-13. ZHENG Jian-guo. Digital value prediction for perfomance of gun muzzle brake[J]. Journal of gun launch & Control, 2000(2): 10-13. DOI:10.3969/j.issn.1673-6524.2000.02.003 |
| [4] |
杨猛. 计算流体力学两相流流动的模拟及两相流模型的研究[D]. 天津: 天津大学. 2005: 36-38. YANG Meng. Two-phase flow CFD simulations and its study[D]. Tianjin: Tianjin University 2005: 36-38. |
| [5] |
孙磊. 含动边界的燃气射流数值模拟[D]. 南京: 南京理工大学. 2006: 8-11. SUN Lei. Numercal simulation of gas plume including movable bullet[D]. Nanjing: Nanjing university of technology. 2006: 8-11. |
| [6] |
翟晓超, 陈亚军, 姜毅. 动网格在仿真发射装置内弹道中的应用[J]. 现代防御技术, 2006, 34(2): 24-28. ZHAI Xiao-chao, CHEN Ya-jun, JIANG Yi. Using dynamic grid to simulate interior trajectory of the launching container[J]. Modern defence technology, 2006, 34(2): 24-28. DOI:10.3969/j.issn.1009-086X.2006.02.006 |
| [7] |
周成. 某火炮驻退机流场数值模拟及冲蚀磨损预测[D]. 南京: 南京理工大学. 2006: 21-29. ZHOU Cheng. Numerical simulation of flow field and prediction of erosion wear in a gun recoil mechanism[D]. Nanjing: Nanjing university of technology. 2006: 21-29. |
| [8] |
狄长春, 顾赵强, 崔凯波, 等. 基于液固两相流的某驻退机冲蚀磨损过程模拟研究[J]. 润滑与密封, 2017, 42(2): 81-86. DI Chang-chun, GU Zhao-qiang, CUI Kai-go, et al. Simulation Research on Erosion Wear of mechanism based on liquid-solid Two-phase flow[J]. Lubrication engineering, 2017, 42(2): 81-86. DOI:10.3969/j.issn.0254-0150.2017.02.016 |
| [9] |
陈朝军. 火炮驻退机流场数值模拟[D]. 南京: 南京理工大学. 2013: 47-50. CHEN Chao-jun. Numerical simulation of flow field in a gun recoil mechanism[D]. Nanjing: Nanjing university of technology. 2013: 47-50. |
 2019, Vol. 41
2019, Vol. 41
