0 引　言

舰船辐射噪声中包含了大量反映舰船特征的信息，利用其对目标舰船进行分类与识别是水声研究范围内一个重要的研究课题。但是因为海洋环境的复杂多变，水下信道也极易受到磁场，海底火山运动等原因的干扰，想要在辐射噪声里提取出一种普遍适用于远距离目标舰船类型判断的物理特征，一直都是研究的难点。线谱作为舰船辐射噪声谱中的重要组成部分，其中含有大量特征信息，除了低频线谱外，中高频端的线谱由于受到螺旋桨叶片频和轴频的影响，具有明显的振幅调制现象。根据其调制深度以及调制频率可推算出叶片频，轴频，航速等舰船固有特征，对调制信息的准确提取，可有效地应用于目标舰船的识别与分类，具有重大意义。

文献[1]讨论了多频带分析以及小波包方法，并利用最小信息熵准则对小波包分解进行了优化，但因为信号经小波包分解后计算量激增，利用传统的希尔伯特解调法效果并不理想。文献[2]利用了高阶统计量中1（1/2）维谱对高斯型加性噪声抑制作用，提取舰船噪声的耦合线谱，但未对目标频带进行有效划分，存在大量杂波与虚假信息干扰，实验效果有待提高。文献[3]研究了Duffing振子的混沌运动规律，改进了其状态方程，提出利用Duffing振子检测舰船辐射噪声线谱的方法，但是在求解混沌临界状态的阈值时，计算量过大。

本文综合考虑调制信号的分布频段，信噪比以及计算量等因素的影响，利用Morlet小波的带通滤波能力及其实部与虚部正交特性提供的信号解调功能，以及高阶累积量对加性噪声的抑制作用，提出基于复Morlet小波的小波解调与1（1/2）维谱的联合分析方法，提高了调制特征的解调效果以及解调质量，实现了自适应频带选取以及在低信噪比条件下良好的调制特征提取效果。

1 方法原理 1.1 Morlet小波解调

Morlet小波是高斯包络下的复指数小波，其定义式为：

$ {{h}}\left( t \right) = \frac{1}{{\sqrt {{\text{π}} {f_b}} }}{e^{\left( {j2{\text{π}} {f_c}t - {t^2}/{f_b}} \right)}} {\text{，}}$

(1)

相应的 $\rm Fourier$ 变换为：

$ {{H}}\left( {{f}} \right) = {e^{ - {{\text{π}} ^2}{f_b}{{\left( {f - {f_c}} \right)}^2}}}{\text{。}} $

(2)

其中： ${f_c}$ 为小波的中心频率； ${f_b}$ 为带宽参数，其大小影响着Morlet小波的波形构造， ${f_b}$ 变小，小波带宽增大，边缘衰减速度增加，最后近似于脉冲信号；而当 ${f_b}$ 增大时，变化正好相反，最终退化为余弦信号。因而，在实际应用中选择适当的 ${f_b}$ 取值，用以优化小波与调制特征的匹配程度。

根据式（2），由 $\rm Fourier$ 逆变换可知Morlet小波 ${{h}}\left( t \right)$ 的实部 ${{{h}}_{{r}}}\left( t \right)$ 与虚部 ${h_i}\left( t \right)$ 分别为时间 ${{t}}$ 的实偶函数与实奇函数，进而可以得出它们的频谱 ${{{H}}_{{r}}}\left( f \right)$ 和 ${H_i}\left( f \right)$ 分别为实偶函数和纯虚奇函数。于是可推得 ${{{H}}_{{r}}}\left( f \right)$ 和 ${H_i}\left( f \right)$ 满足下列关系：

${H_i}\left( f \right) = - j{\rm{sgn}} \left( f \right){H_r}\left( f \right){\text{。}}$

(3)

其中： ${\rm{sgn}} \left( f \right)$ 为符号函数。式（3）可以看作一个时间函数Hilbert变换式的等价频域表示，即 ${{{H}}_{{r}}}\left( f \right)$ 与 ${H_i}\left( f \right)$ 是一对Hilbert变换对。

由小波分析理论，信号的连续小波变换（CWT）的定义为：

$cwt\left( {s,t} \right) = \frac{1}{s}\int_{ - \infty }^{ + \infty } {x\left( f \right)} h\left( {\frac{{t - f}}{s}} \right){\rm d}f{\text{。}}$

(4)

其中： $s$ 为尺度因子； $f$ 为位移因子。

设以 $s$ 为尺度的展缩函数 ${h_s}\left( t \right) = \dfrac{1}{s}h\left( {\dfrac{t}{s}} \right)$ ，则上式可以简化为：

$cwt\left( {s,t} \right) = x\left( t \right) * {h_s}\left( t \right){\text{，}}$

(5)

推至Morlet小波可得：

$\begin{gathered} cwt\left( {s,t} \right) = x\left( t \right) * h_s^r\left( t \right) + x\left( t \right) * jh_s^i\left( t \right) =\\ {\rm{Re}} \left( {cwt\left( {s,t} \right)} \right) + {\rm{Im}} \left( {cwt\left( {s,t} \right)} \right){\text{。}} \end{gathered} $

(6)

从信号分析的角度可知，Morlet小波可看作一个复数滤波器，其实部 $h_s^r\left( t \right)$ 近似于一个零相移的带通滤波器，虚部 $h_s^i\left( t \right)$ 则近似于一个存在90°相移的带通滤波器。因而，信号经Morlet小波进行复小波变换后的小波系数虚部 ${\rm{Im}} \left( {cwt\left( {s,t} \right)} \right)$ 较其实部 ${\rm{Re}} \left( {cwt\left( {s,t} \right)} \right)$ 相移了90°。根据包络检波原理^[5]，用解调的方法可以提取所选尺度下小波系数中的包络分量

$\mu \left( {s,t} \right) = \sqrt {{\rm{Re}} {{\left( {cwt\left( {s,t} \right)} \right)}^2} + {\rm{Im}} {{\left( {cwt\left( {s,t} \right)} \right)}^2}}{\text{。}} $

(7)

最后，对 $\mu \left( {s,t} \right)$ 进行 $\rm Fourier$ 变换后，即可得到信号调制特征频谱。

1.2 1（1/2）维谱特性分析

对于某一小波空间的小波系数为 $d\left( t \right)$ ，其3阶累积量定义为：

$R\left( {{\tau _1},{\tau _2}} \right) = E\left\{ {d\left( t \right)d\left( {t + {\tau _1}} \right)d\left( {t + {\tau _2}} \right)} \right\}{\text{，}}$

(8)

3阶累积量 $R\left( {{\tau _1},{\tau _2}} \right)$ 的对角线切片为：

$c\left( \tau \right) = c\left( {\tau ,\tau } \right) = E\left\{ {d\left( t \right)d\left( {t + \tau } \right)d\left( {t + \tau } \right)} \right\}{\text{，}}$

(9)

对 $c\left( \tau \right)$ 作一维 $\rm {\text{，}}Fourier$ 变换，即可得到小波系数 $d\left( t \right)$ 的1（1/2）维谱

$C\left( \omega \right) = \sum\limits_{\tau = - \infty }^\infty {c\left( \tau \right)} {e^{ - j\omega \tau }}{\rm d}\tau{\text{。}} $

(10)

设待处理信号 ${x_N} = \left\{ {{x_1},{x_2}, \cdots ,{x_{N = KM}}} \right\}$ 中共有 $N$ 个数据，每个数据分成 $K$ 段，每段长度为 $M$ ，则1（1/2）维谱的具体计算方法如下：

1）去除各数据段中的直流分量；

2）参照式（9），计算各个数据的3阶累积量，并得到其对角线切片 ${c_i}\left( \tau \right)$ ；

3）取所有数据段的 ${c_i}\left( \tau \right)$ 的均值，可到 $\mathop c\limits^ \wedge \left( \tau \right) = $ $ \dfrac{1}{K}\sum\limits_{i = 1}^k {{c^{\left( i \right)}}} \left( \tau \right)$ ；

4）对均值 $\mathop c\limits^ \wedge \left( \tau \right)$ 作一维Fourier变换，即可得到待处理信号的1（1/2）维谱。

本文利用高阶累积量对高斯噪声天然的抑制特性，选用1（1/2）维谱的方法对解调后的信号包络进行分析，降低了计算量，加强了信号基频，剔除其中非谐波分量。

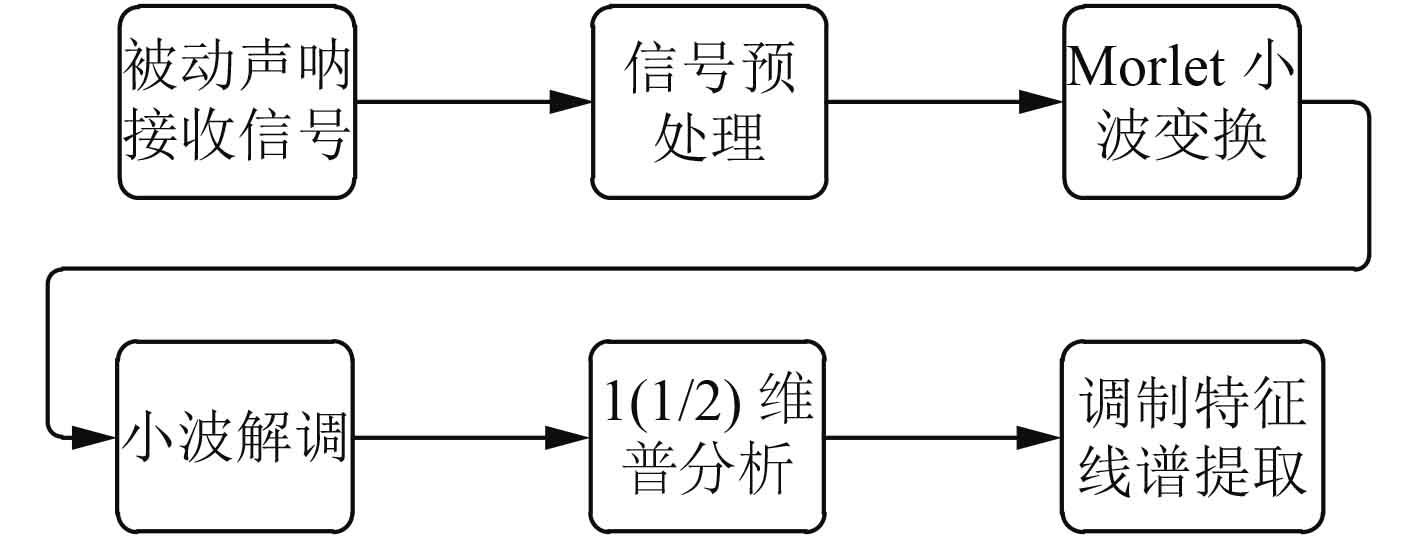
2 舰船辐射噪声调制特征提取 2.1 调制特征提取流程

由于水下低频端噪声复杂，极易将线谱淹没，难以准确分离提取辐射噪声中的有效信息。然而，其中高频端信号受水下背景噪声干扰较小，且线谱特征明显，可以提取出大量有效特征信息。中高频线谱由于受到螺旋桨叶片频率和轴频的影响，具有明显的振幅调制现象，提取其中的调制信息，可以直接计算出舰船的轴频，叶片频等，进而用于舰船的分类与识别。本文的具体工作流程如图1所示。被动声呐接收信号通过预处理进行初步降噪后，经Morlet小波的连续小波变换得到信号的尺度包络谱图，选取含有调制信息的小波分量进行小波解调，得到的调制信息经过1（1/2）维谱分析进一步滤除噪声，增强基频信号。最后，使用最大公约数法算法^[4]可以计算出轴频。

2.2 特征提取方法具体实现

在实际舰船信号处理中，包含带通滤波以及幅值解调两部分，利用Morlet小波解调的方法可以同时达到滤波与解调的效果，避免了多次滤波造成的信号混叠以及虚假信号的干扰。

根据连续小波变换理论，可知

${F_a} = \frac{1}{S} * {f_c} * {f_s}{\text{，}}$

(11)

其中： ${F_a}$ 为实际信号频率； ${f_c}$ 为小波中心频率； ${f_s}$ 为信号采样频率； $S$ 为小波变换尺度。根据奈奎斯特采样定理，为使小波尺度图的频率范围为 $\left( {0,{{{f_s}} / 2}} \right)$ ，其相应小波变换的尺度范围为 $\left( {2 * {F_c},\infty } \right)$ 。

从Morlet小波的幅频特性上看，其可以近似为一个1/1倍频程滤波器。为了方便实验，使得转换后的频率序列为一等差数列，那么相应的尺度序列可按如下形式划分：

${S_j} = {c / {\left( {m - j} \right)}}\;\;\;j = 0,1, \cdots ,m - 1{\text{。}}$

(12)

其中： $c$ 为一常数； $m$ 为小波变换时尺度序列长度，其大小可根据实验需求提前设定。由式（12）可知，当尺度为 ${c / m}$ 时所对应的信号实际频率为 ${{{f_s}} / 2}$ ，可以计算出 $c = 2 \times {F_c} \times m$ 。

根据上述方法，取合适的尺度序列进行计算，即可得到信号的包络谱图。选取有明显调制现象的小波分量进行解调，就可以提取其中的调制特征信息。最后，通过1（1/2）维谱分析的方法，提取其中的特征线谱。

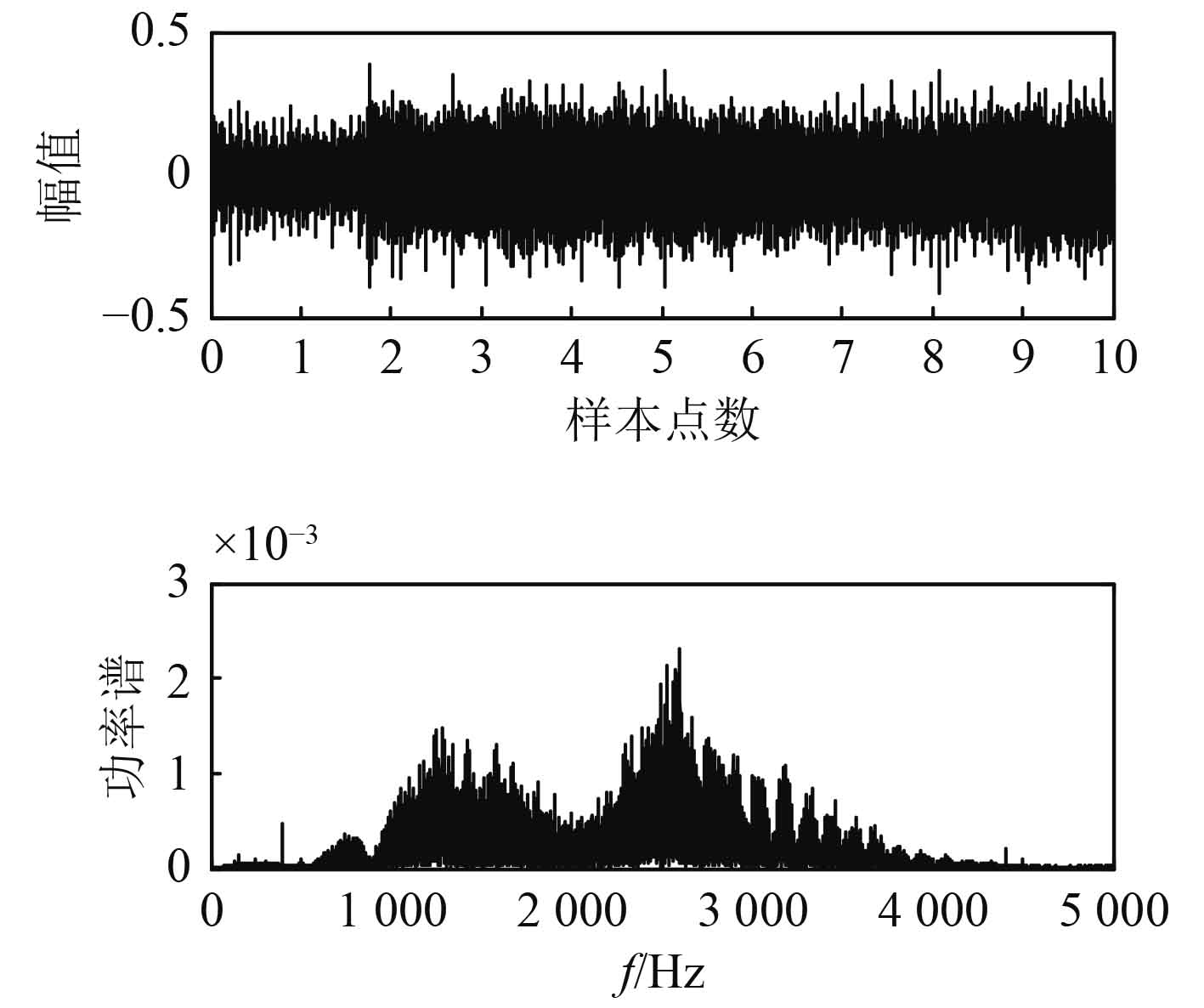
3 实验数据处理分析

本文的实测数据为某中型商船在稳定状态下顺风高速航行，原始信号频率为44 100 Hz，为了方便实验分析，去除不确定随机误差，选取中间较为稳定测量信号，其长度为10 s。由于该信号能量大多集中在5 000 Hz以下，为提高计算效率，将信号进行降采样处理，采样频率为10 000 Hz，利用加窗的快速傅里叶变换，得到该船辐射信号的功率谱图，如图2所示。

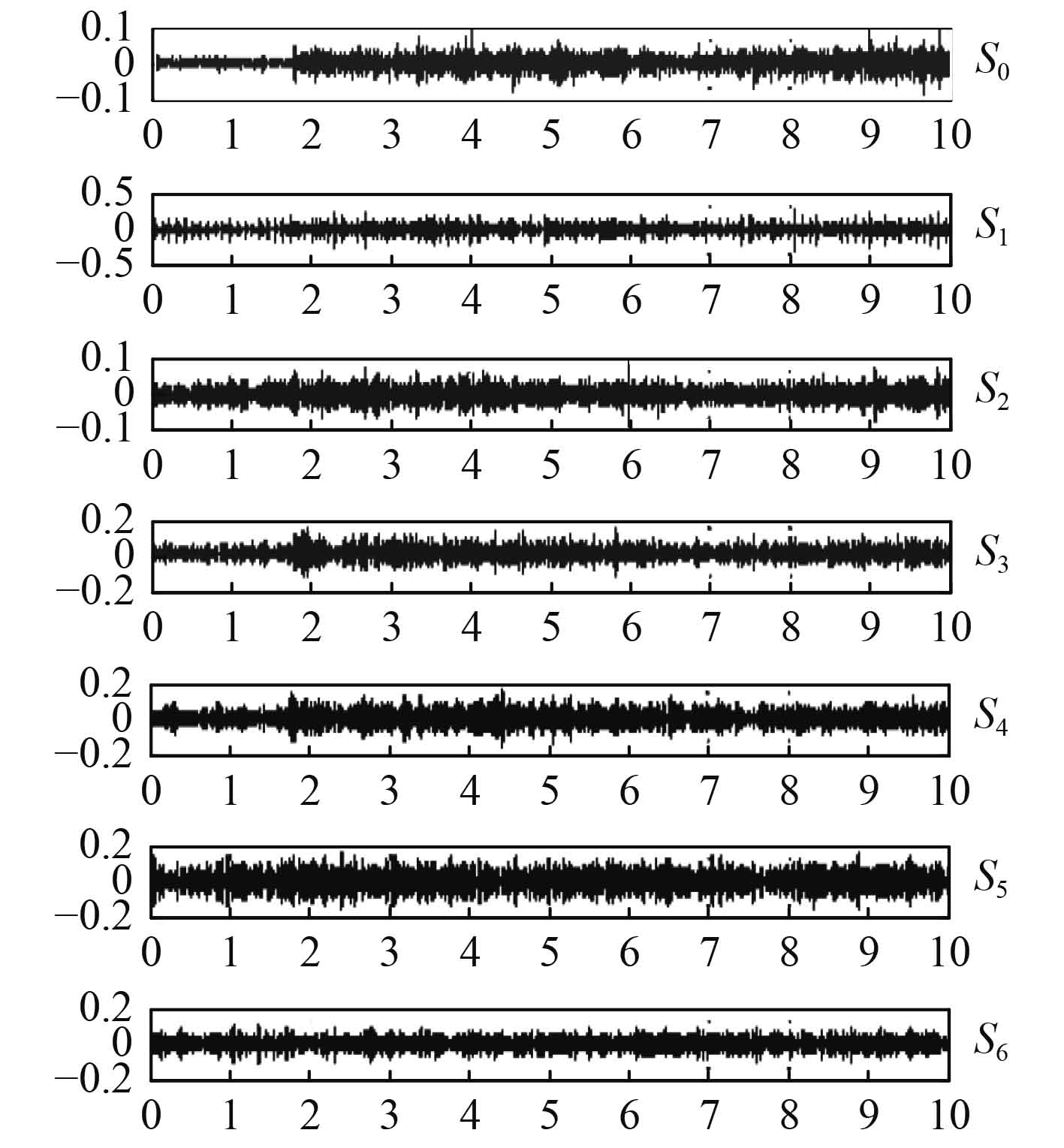
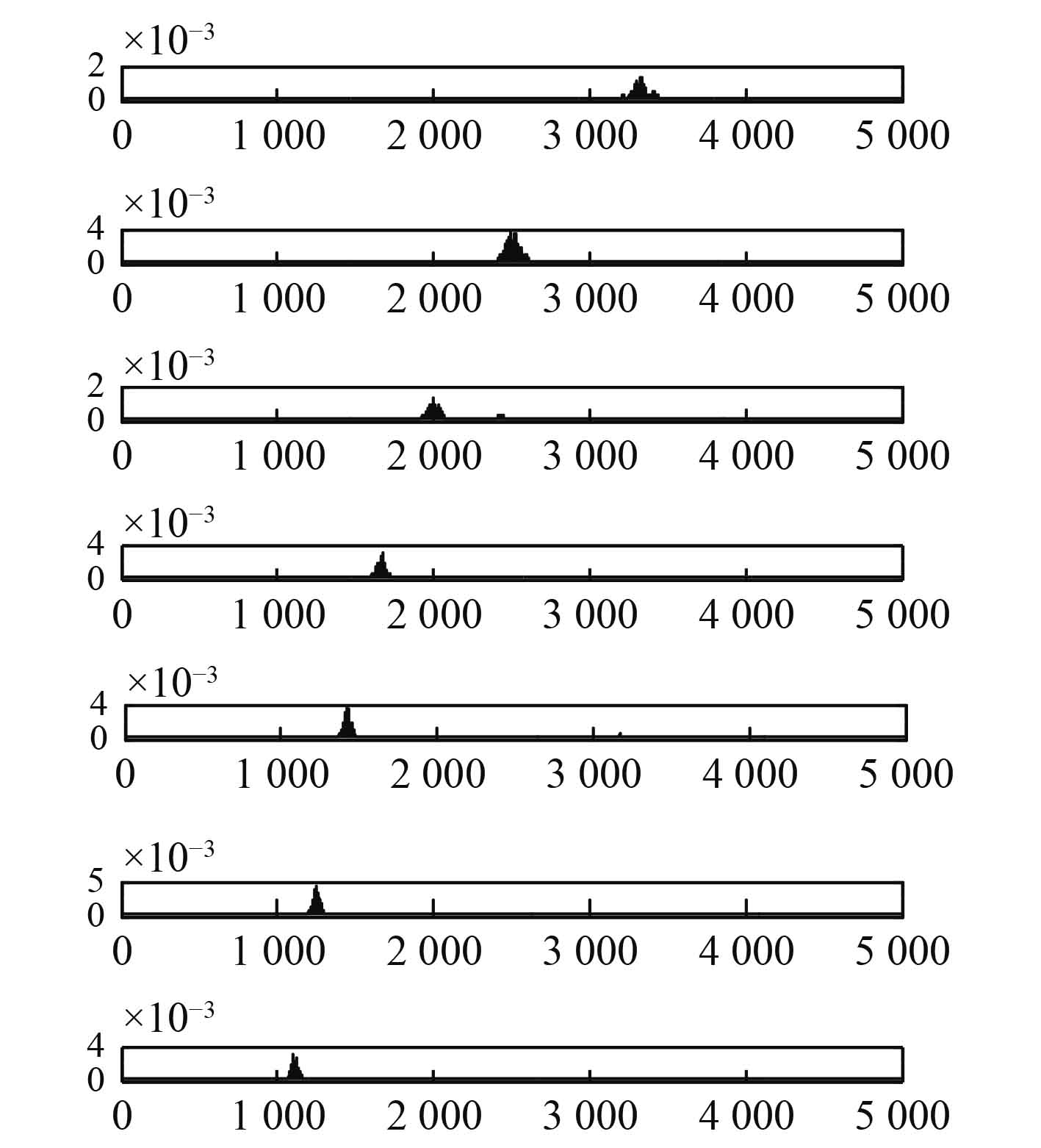
由图2可以明显看出，信号在中高频段处较为集中，采用复Morlet小波对信号进行连续小波变换，可以得到全频段的信号时-频分解图。为了方便实验，选取信号集中的中高频段分量显示，如图3所示，S₀～S₆为所取小波分量的尺度。图4是所取的各个小波分量功率谱，可以看出各分量所在的中心频带范围，并完全滤除了目标频带以外的信号。

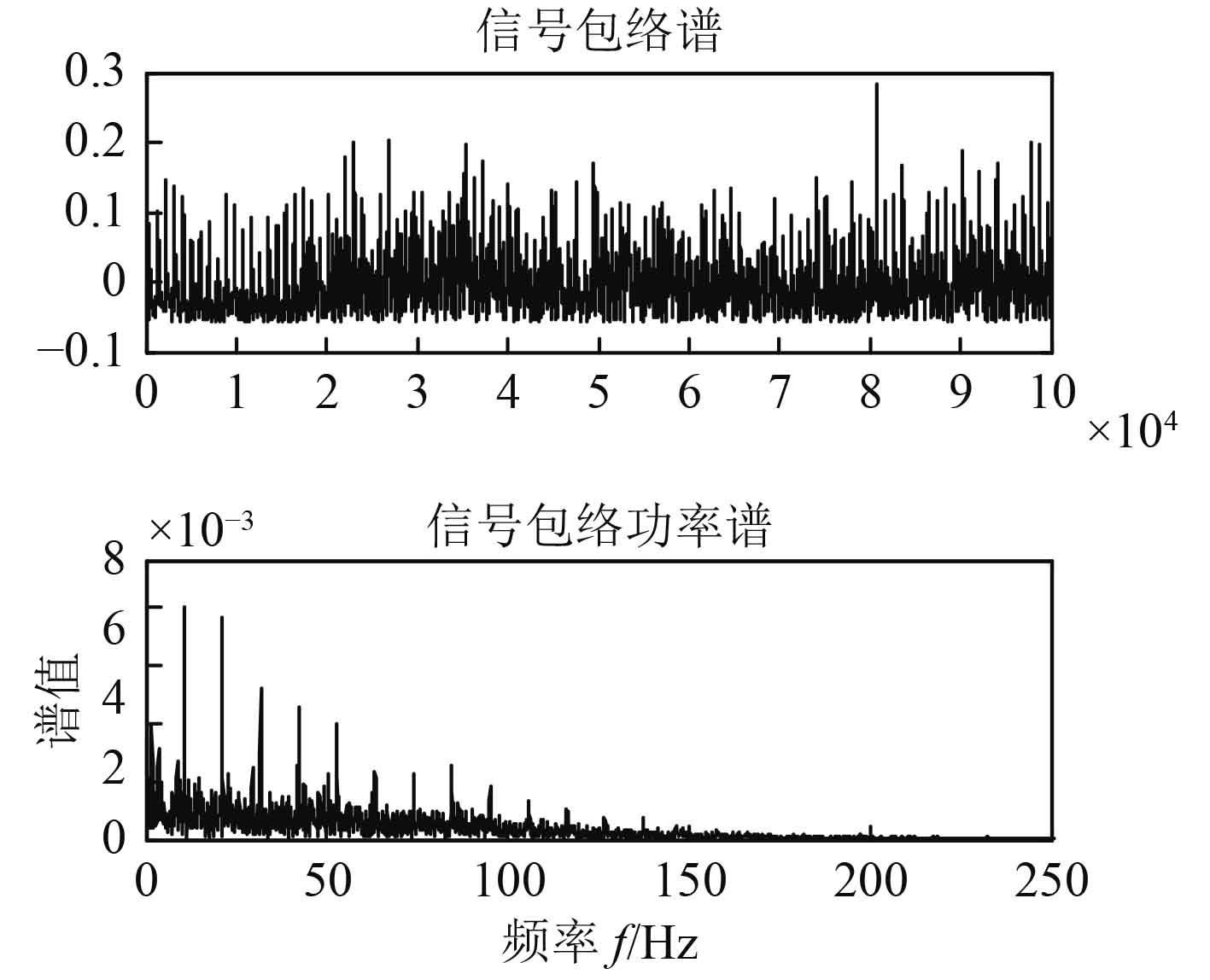
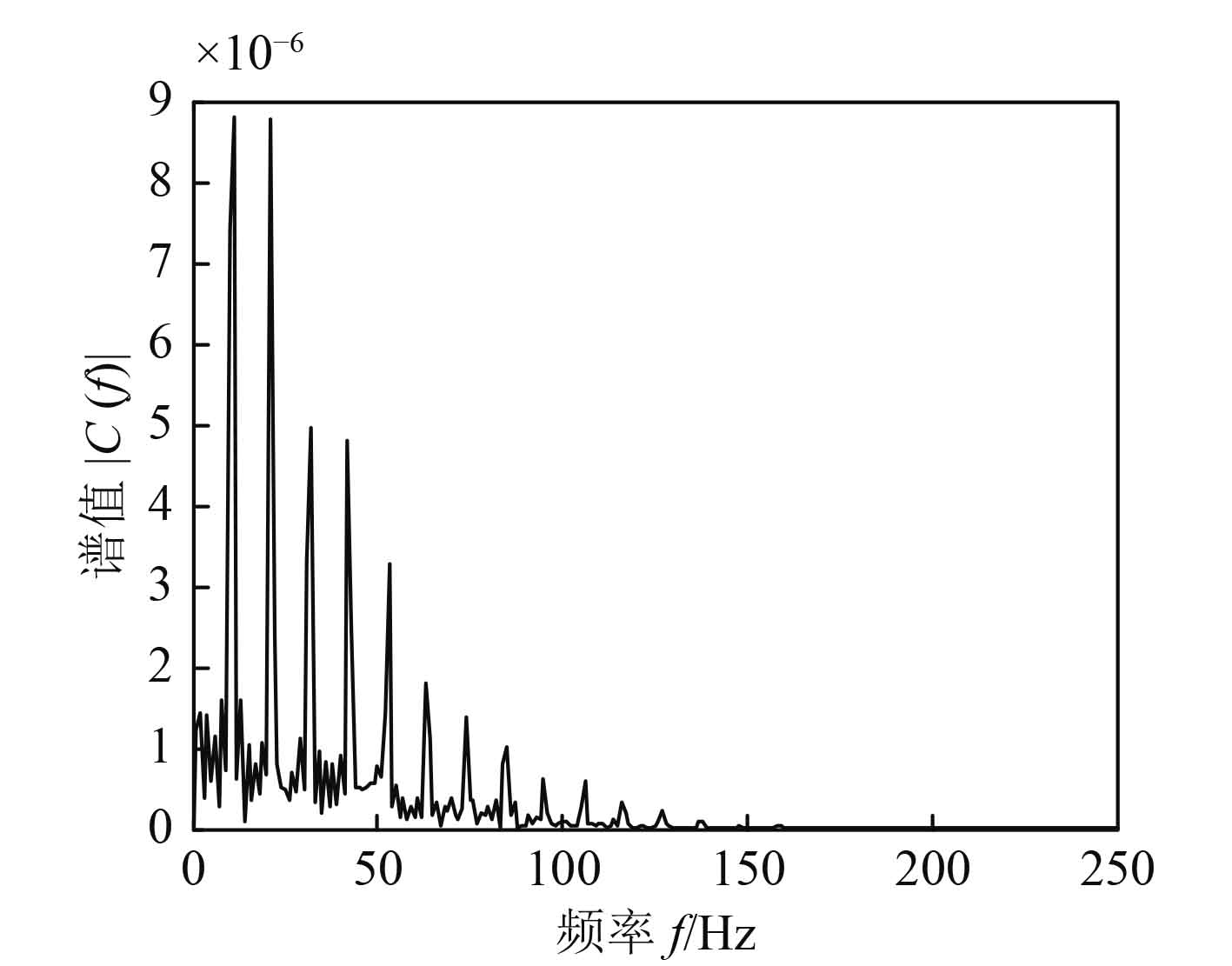
在尺度S₁，S₂，S₃上可以明显看到调制信号对应于舰船的调制信息，利用上文方法，对尺度S₂下的分量进行小波解调，并绘制出其功率谱图，如图5所示。可以明显看出在低频段（150 Hz以下）具有明显特征的线谱信息，但还存在较多杂波干扰。利用1（1/2）维谱进行谱分析，由于采样点数较多，因而进行降采样处理，采样频率为500 Hz。经过1（1/2）维谱分析后的线谱图，如图6所示。利用最大公约数法^[4]，可以算出轴频为11 Hz，谐波为22 Hz，33 Hz。

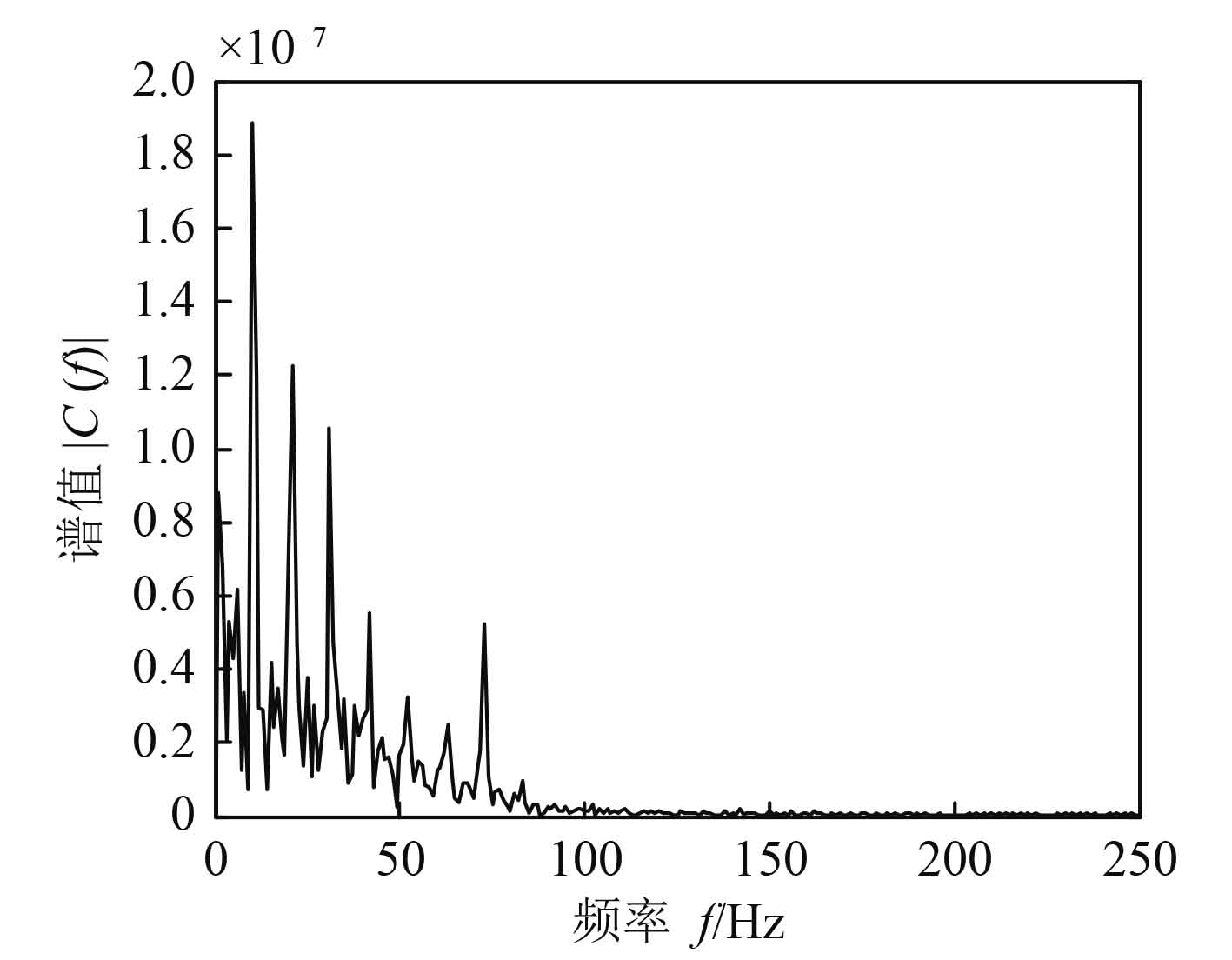
对该船舶在同等条件下以不同速度航行采集的信号重复上述实验分析，得到其调制线谱，如图7所示。利用最大公约数法^[4]，可以算出该轴频为9 Hz。显然，在不同航速下所提取出的轴频不同。

4 结　语

本文针对舰船辐射噪声中调制特征提取问题，提出一种基于复Morlet小波解调和1（1/2）维谱的联合分析方法，充分结合了两者的优点，得到理想的调制特征提取效果。利用复Morlet小波解调方法能在时-频两维空间内提取出信号的包络成分，得出反映信号全貌的尺度包络谱图，并且无需人工设定滤波中心频率，实现自适应滤波效果。用1（1/2）维谱方法对提取出的信号包络进行谱分析，对比传统的功率谱图，具有良好的抗高斯噪声以及加强信号基频的特点。实验结果显示，本方法可以稳定有效地提取舰船辐射噪声中的调制特征信息，为进一步确定舰船类型提供数据支撑。最后，用相同条件下不同航速下的船只进行相同方法提取的调制特征进行对比，验证了该方法的普适性与有效性。