2. 中国船舶重工集团公司第七二二研究所,湖北 武汉 430205
2. The 722 Research Istitute of CSIC, Wuhan 430205, China
液压缸作为液压系统中重要的执行元件,按结构形式可分为活塞式、柱塞式及摆动式三类。我国舰艇广泛应用的液压缸主要为前两类,用于船舶传动液压系统中[1]。在液压缸工作过程中,往往需要在短时间内带动大负载动作,容易在缸内产生瞬时液压冲击,导致液压系统中产生压力波动,从而影响系统的稳定性与可靠性[2],并引发较大噪声[3]。
国内外诸多学者围绕液压缸缓冲的动态特性展开大量研究工作。文献[4]通过动力学方程计算并设计出不同的缓冲结构,证明其具有吸收振动力与振动波的能力。文献[5]运用有限体积法分析建立非线性粘性流体在缓冲过程中的模型,并对其缓冲特性进行分析。文献[6]以液压冲击机理与缓冲方法研究为基础提出一种主动变阻尼的缓冲方法,通过在Simulation X中建立研究所用的系统仿真模型,并用试验研究对所提出的仿真结果进行验证。文献[7]以缓冲缸的缓冲压力与活塞速度2个参数为对象进行研究,运用控制变量法得到了不同参数条件下的敏感性与缓冲结构在缓冲过程中产生的作用。文献[8]提出一种新型缓冲制动缸,通过在安装缸套上固定活塞杆来满足位置要求,建立了关键缸体在最大受力作用下的数学模型,并基于模糊可靠度的设计方法对缸体的设计结构进行优化。从研究内容来看,大部分液压缸缓冲的研究集中在液压缸外部液压系统缓冲控制,对液压缸内部缓冲结构的研究仍是依靠经验公式、试验与仿真相结合的方式,需要进一步进行研究。
本文在分析液压缸缓冲理论的基础上,推导相应的液压缸缓冲数学模型,并在图形化仿真环境AMESim中建立对应仿真模型,分析在不同液压缸活塞结构参数下的缓冲特性。
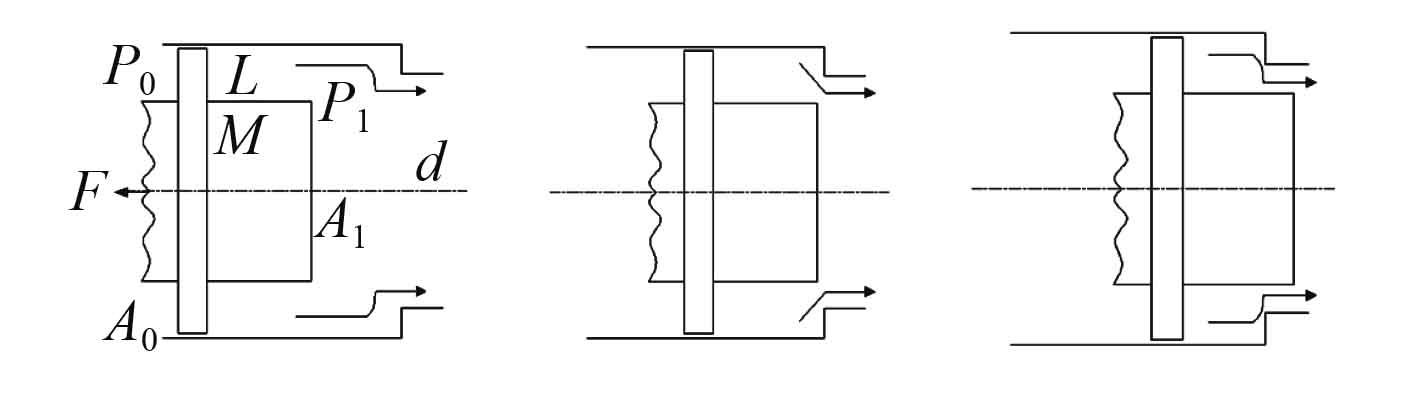
1 液压缸缓冲原理常用的圆柱形活塞液压缸缓冲过程如图1所示。
|
图 1 液压缸缓冲过程示意图 Fig. 1 Cushion process of hydraulic cylinder diagram |
在整个固定节流缓冲过程中,若忽略粘性阻尼与油液可压缩性的影响,活塞受力平衡方程和工作缸内流量方程如下:
| $ \left\{ \begin{array}{l} M\dfrac{{{\rm{d}}V}}{{{\rm{d}}t}} = {P_0}{A_0} - {P_1}{A_1} - F{\text{,}} \\ Q = {A_1}V = {C_d}d{\text{π}} \delta \sqrt {\frac{{2{P_1}}}{\rho }} {\text{。}} \\ \end{array} \right. $ | (1) |
式中:M为液压缸活塞质量;V为液压缸活塞运动速度;P0,P1分别为液压缸常压腔与控制腔的油液压力;A0,A1分别为液压缸两腔的有效受压面积;F为作用于液压缸活塞杆上的负载反力;Q为控制腔内流量;Cd为液压缸内流路变化下的流量系数;d为缓冲孔直径;δ为液压缸活塞与缓冲孔间的半径间隙;ρ为液压缸内油液密度。以液压缸活塞刚进入缓冲孔时刻对式(1)活塞运动V进行变形,得到缓冲微分方程如下式:
| $ \left\{ \begin{array}{l} \dfrac{{{\rm{d}}V}}{{{\rm{d}}t}} + {K_1}V - {K_2} = 0 {\text{,}}\\ {K_1} = \dfrac{{\rho A_1^3}}{{2M{{\left( {{C_d}d\text{π} \delta } \right)}^2}}} {\text{,}} \\ {K_2} = \dfrac{{{P_0}{A_0} - F}}{M} {\text{。}} \end{array} \right. $ | (2) |
液压缸活塞刚进入缓冲孔时t=0,此时液压缸活塞运动速度V=V0,为活塞运动的最高速度,下一时刻活塞开始缓冲制动。对式(2)进行求解可得速度的表达式如下式:
| $ V = \sqrt {\frac{{{K_2}}}{{{K_1}}}} \frac{{\left( {{V_0} + \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right){e^{2\sqrt {{K_1}{K_2}} t}} + \left( {{V_0} - \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right)}}{{\left( {{V_0} + \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right){e^{2\sqrt {{K_1}{K_2}} t}} - \left( {{V_0} - \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right)}}{\text{,}} $ | (3) |
将式(3)代入式(1)可求得控制腔缓冲压力的变化规律如下式:
| $ {P_1} = \frac{{\rho {A_1}^2}}{{2{{\left( {{C_d}d{\text{π}} \delta } \right)}^2}}}{V^2} {\text{,}}$ | (4) |
对式(3)求导可得活塞运动加速度的表达式如下式:
| $ a = - \frac{{4{K_2}{e^{2\sqrt {{K_1}{K_2}} t}}\left( {{V_0}^2 - \dfrac{J}{K}} \right)}}{{{{\left[ {\left( {{V_0} + \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right){e^{2\sqrt {{K_1}{K_2}} t}} - \left( {{V_0} - \sqrt {\dfrac{{{K_2}}}{{{K_1}}}} } \right)} \right]}^2}}}{\text{,}}$ | (5) |
对式(4)和式(5)联合求解,在t=0时刻有最大负加速度amax与最高缓冲压力Pmax如下式:
| $ \left\{ \begin{array}{l} {a_{\max }} = - \left( {{K_1}{V_0}^2 - {K_2}} \right) {\text{,}} \\ {P_{\max }} = \dfrac{{\rho {A_1}^2}}{{2{{\left( {{C_d}d{\text{π}} \delta } \right)}^2}}}{V_0}^2 {\text{,}} \end{array} \right. $ | (6) |
理想情况下,缓冲过程是控制腔内油液压力P1较低且保持不变,在负载反力的作用下活塞的缓冲过程是等减速过程,其速度与加速度应满足下式:
| $ \left\{ \begin{array}{l} V = \sqrt {{V_0}^2 - 2ax} \;{\text{,}} \\ a = \dfrac{{{P_1}{A_1} - \left( {{P_0}{A_0} - F} \right)}}{M} {\text{,}} \end{array} \right. $ | (7) |
将式(7)所示的理想运动规律代入式(1)求解,可得间隙δ与活塞在缓冲孔内行程的关系如下式:
| $ {\delta _{(x)}}^2 = \frac{{\rho {A_1}^2\left( {{V_0}^2 - 2ax} \right)}}{{2{{\left( {{C_d}d{\text{π}} } \right)}^2}{P_1}}}{\text{。}} $ | (8) |
从式(8)可以看出间隙方程满足抛物线规律,即表明理想情况下若不考虑粘性阻尼与油液可压缩性的影响,实现匀减速缓冲过程的活塞形状应为抛物线型。
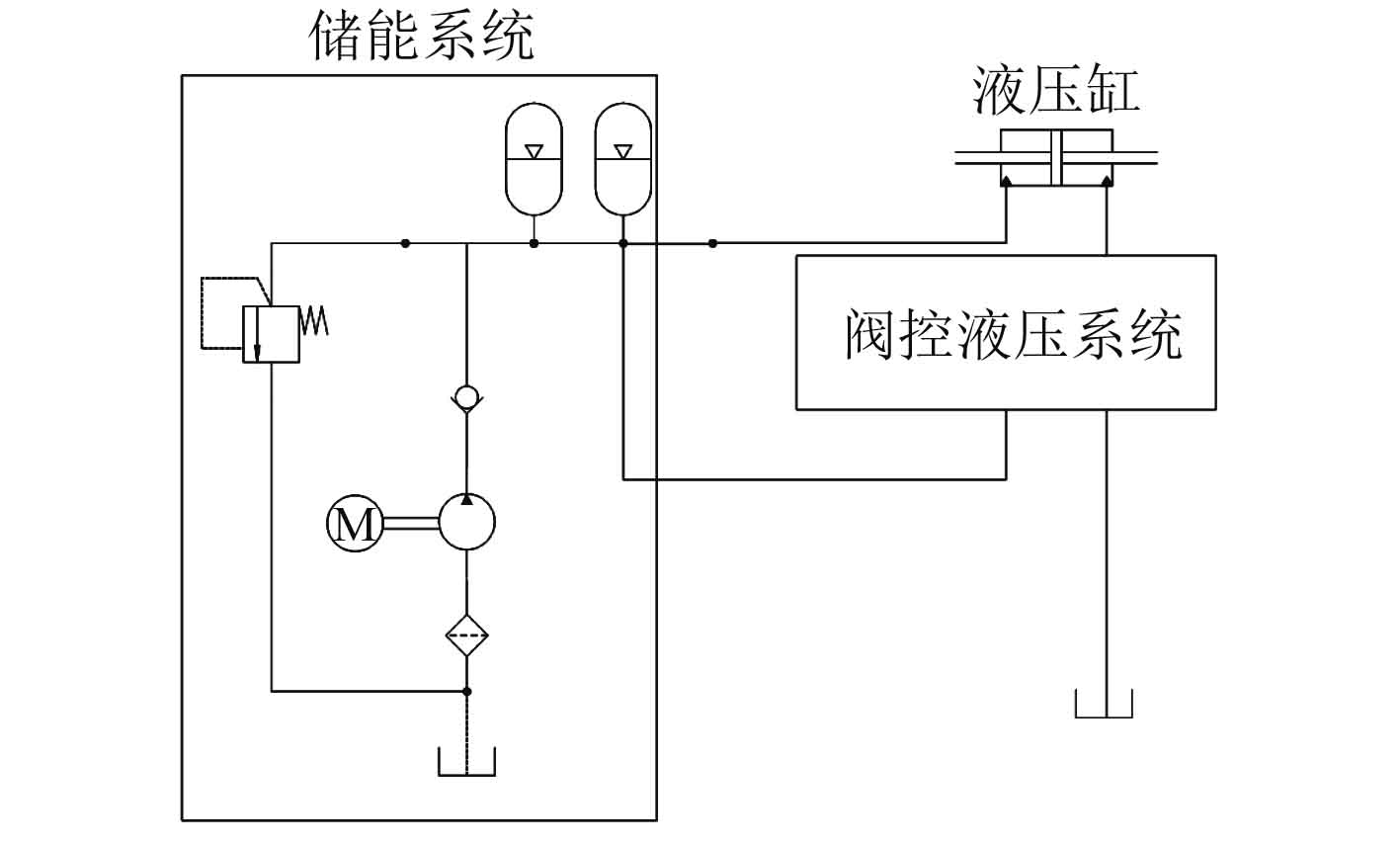
2 液压缸缓冲综合动力学仿真模型以某型号液压缸为例,其工作液压系统原理图如图2所示。
|
图 2 阀控液压缸系统原理图 Fig. 2 Principle diagram of valve controlling cylinder hydraulic system |
整个液压系统由储能系统、控制阀系统与液压缸组成。其中储能系统主要由泵与蓄能器组成,提供高压油。液压缸常压腔连通蓄能器,控制阀系统在接受动作指令后,通过多级控制阀控制高压油流入液压缸控制腔或将高压油泄回油箱,使液压缸按指令完成运动。
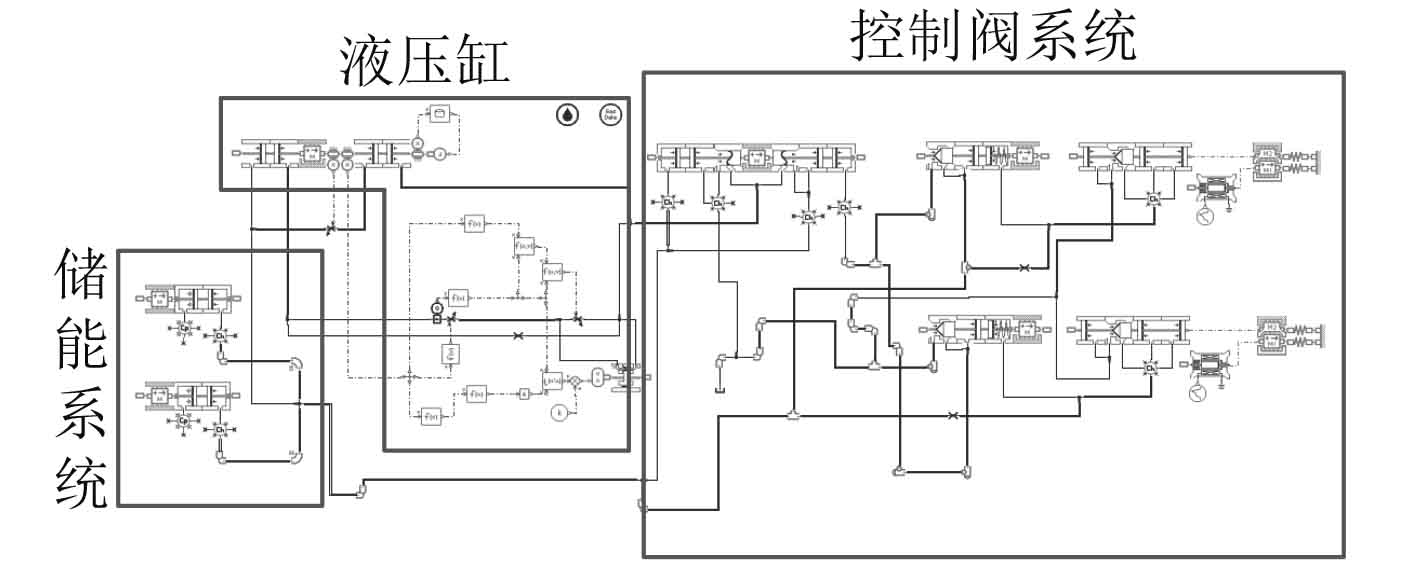
最终建立的动力学仿真模型如图3所示。其工作主要参数如表1所示。
|
图 3 阀控液压缸系统动力学仿真模型 Fig. 3 Simulation dynamic model of valve controlling cylinder hydraulic system |
|
|
表 1 计算所需主要参数 Tab.1 Main parameter of calculation |
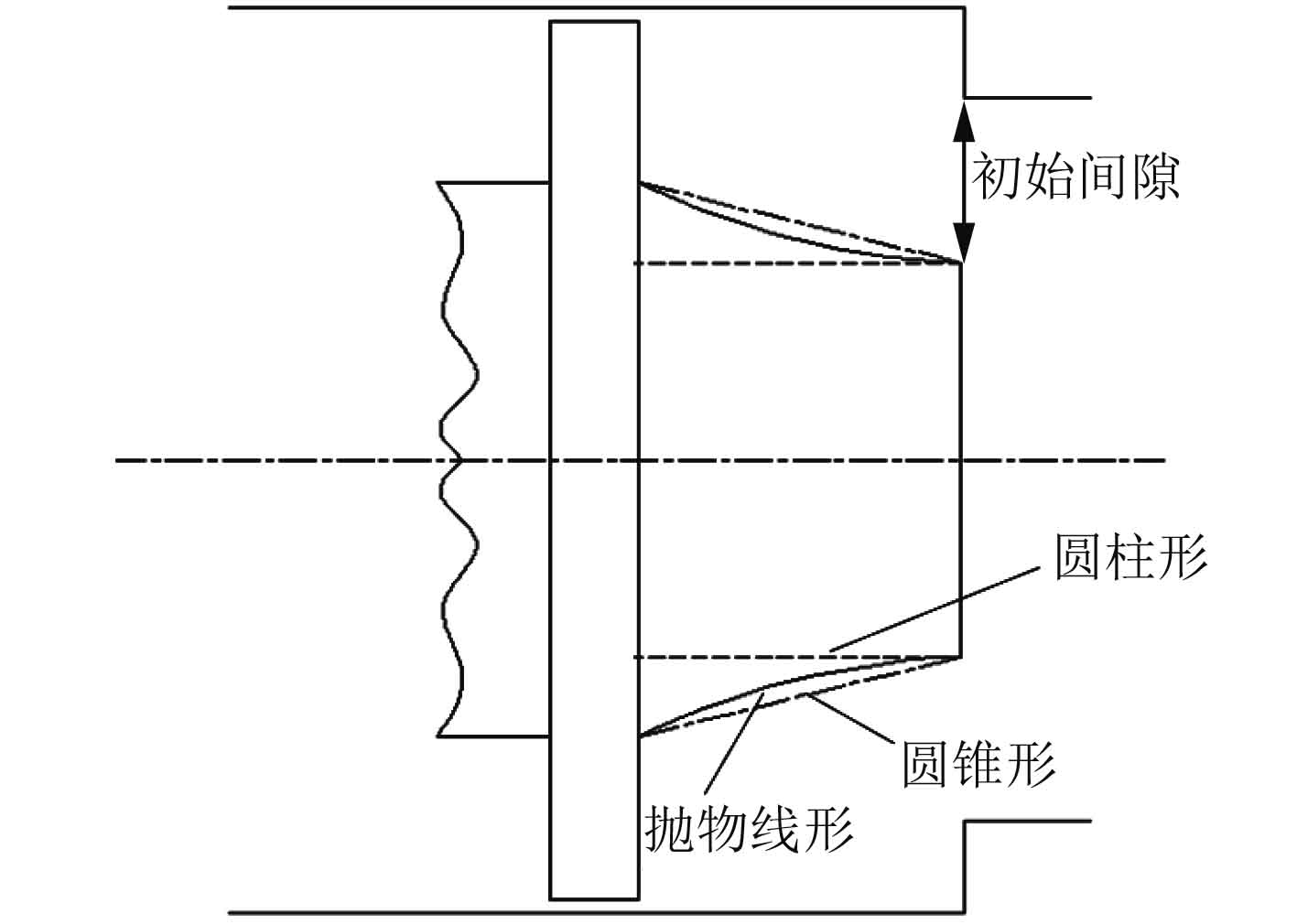
以圆柱形活塞模型为基础,分别建立同等活塞杆直径下的圆锥形、抛物线形活塞液压缸模型如图4所示。
|
图 4 不同结构形式液压缸活塞 Fig. 4 Different structure of hydraulic cylinder piston |
在活塞杆长度、缓冲孔直径、活塞直径等不变的条件下,通过改变初始间隙研究对缓冲特性的影响,可根据变参分析结果确定相同条件下的最优活塞杆结构。
根据初步的仿真计算并结合产品实际,活塞杆与缓冲孔的初始配合间隙在[1,2]范围内按照0.2 mm等值递增设计,经过多次计算对比分析,可根据计算结果得到效果较好的对比方案,较优的活塞杆结构方案选择主要原则是缓冲峰值压力低,缓冲末速度较小,且缓冲持续时间不能过长,活塞杆不应出现反向运动现象。
3种活塞杆在不同初始间隙时的计算结果如图5~图7及表2所示。
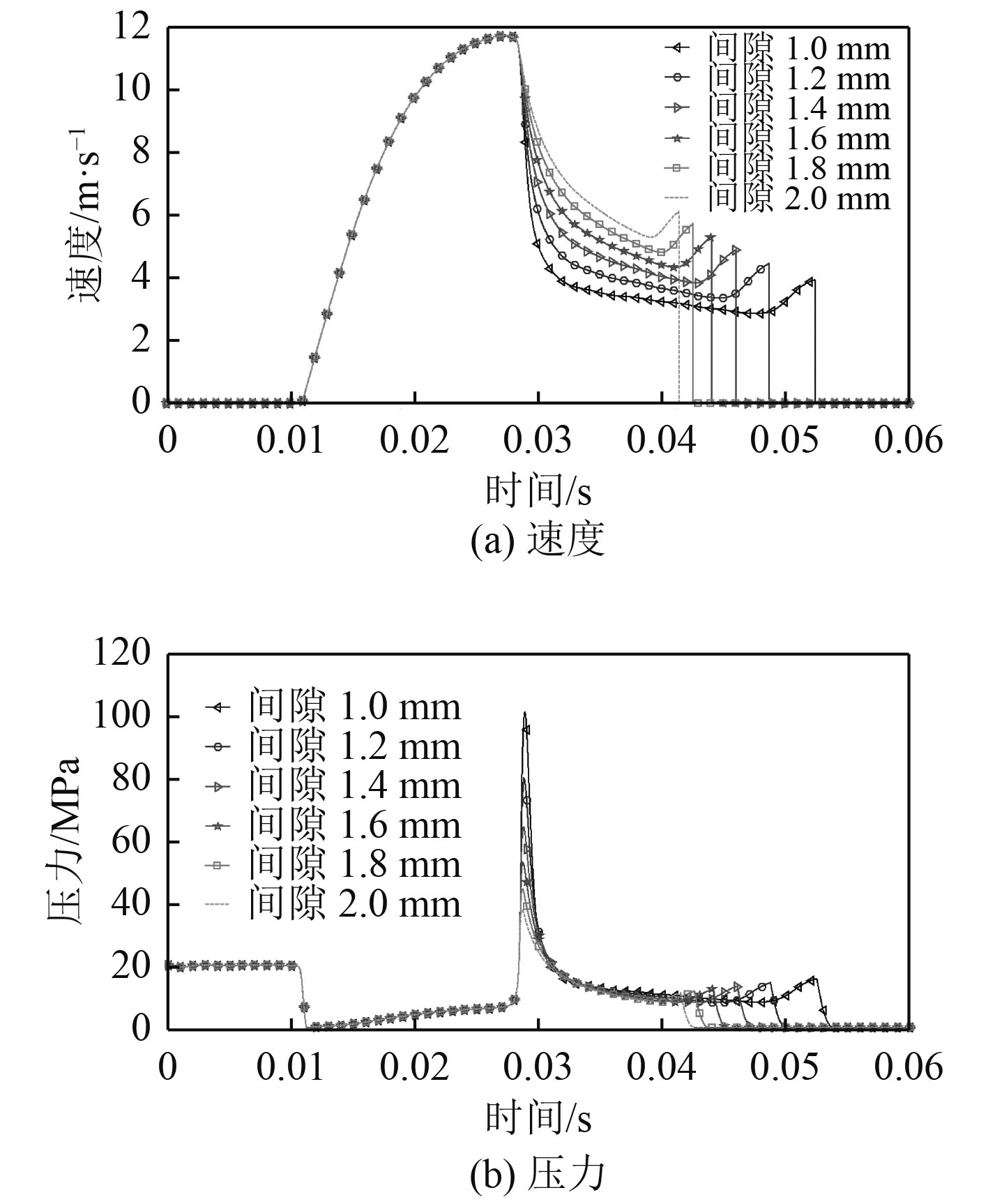
|
图 5 圆柱形活塞杆液压缸缓冲效果 Fig. 5 Cushion effect of cylindrical piston |
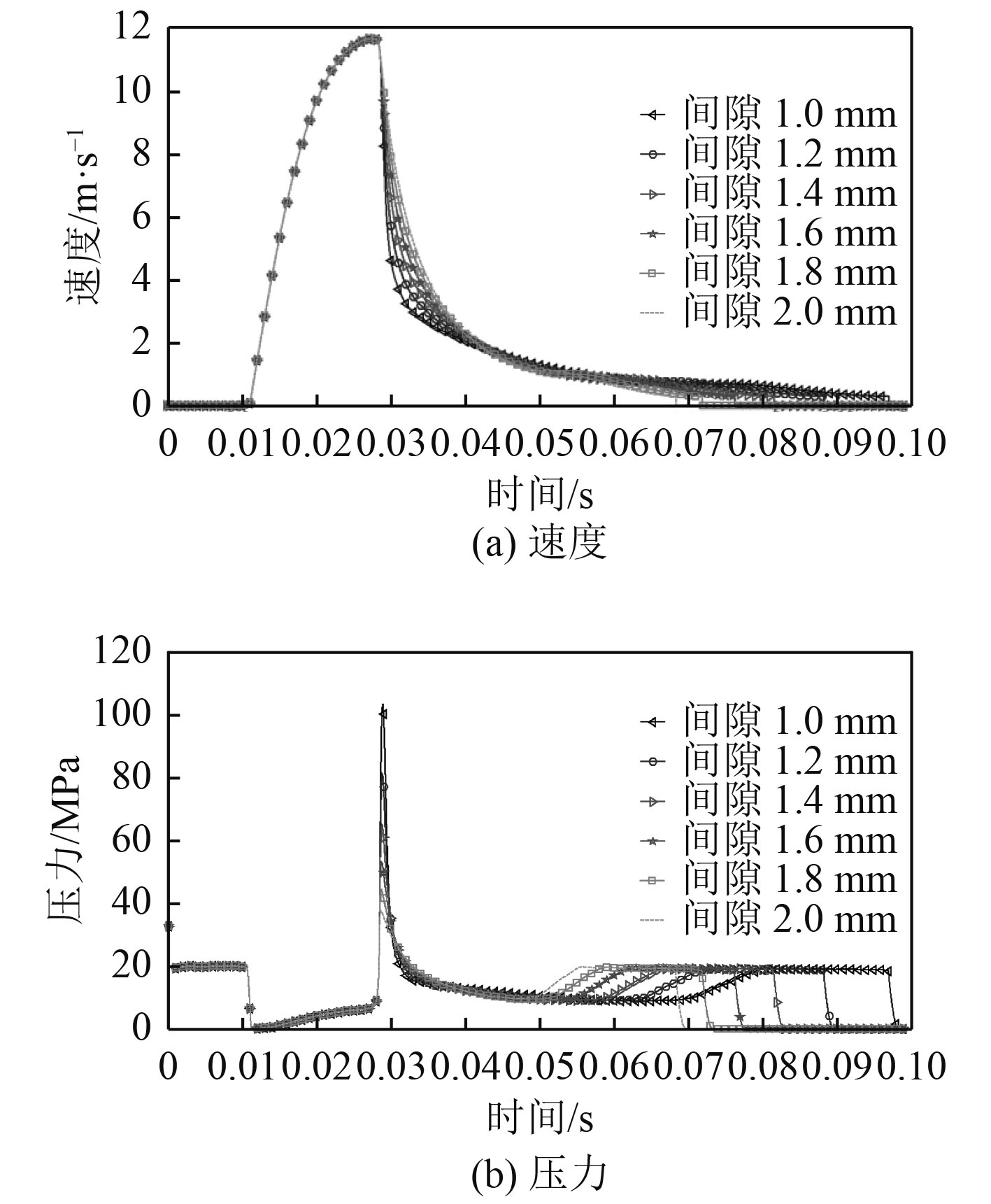
|
图 6 圆锥形活塞杆液压缸缓冲效果 Fig. 6 Cushion effect of conical piston |
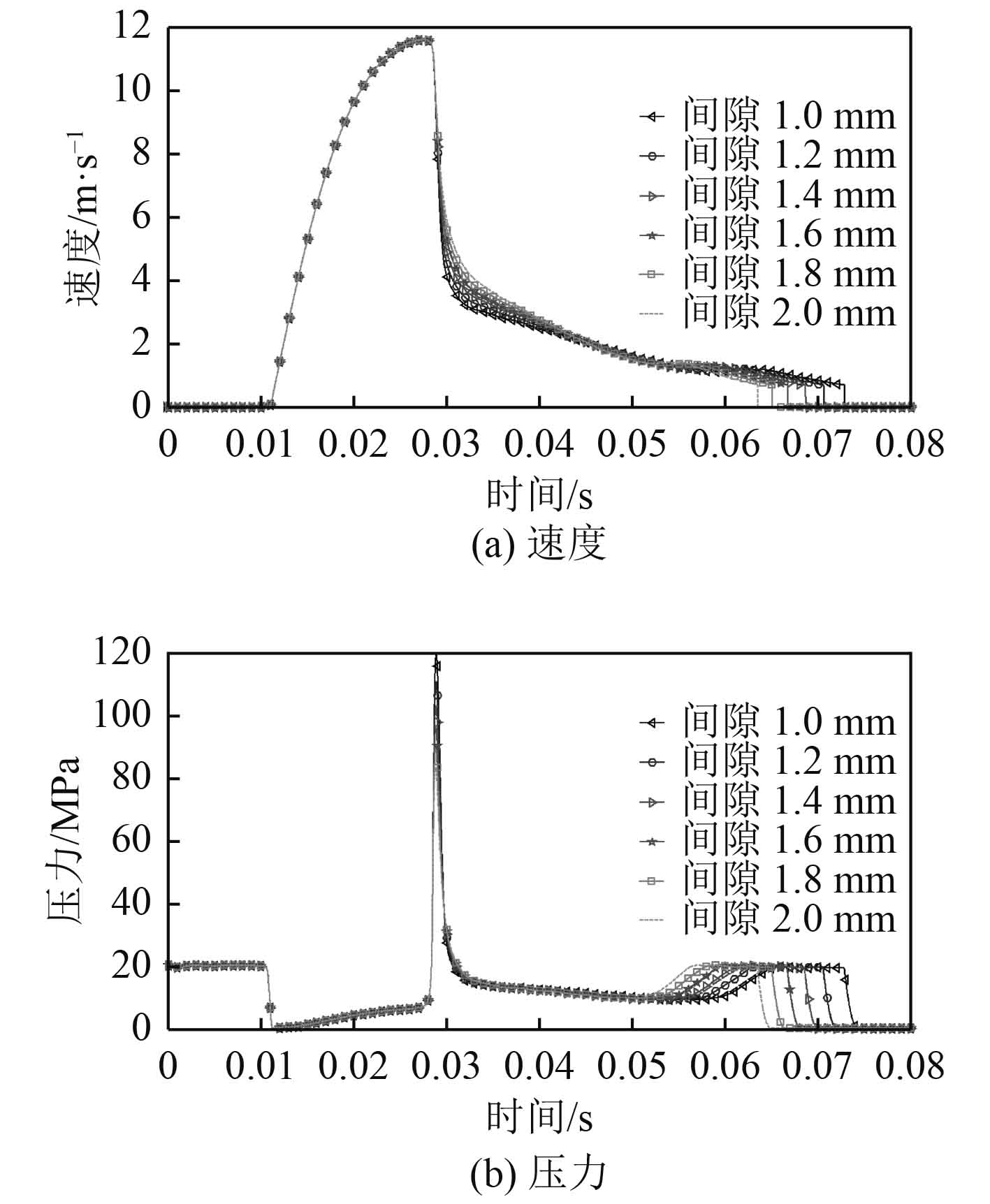
|
图 7 抛物线形活塞杆液压缸缓冲效果 Fig. 7 Cushion effect of parabolic piston |
|
|
表 2 不同结构形式活塞杆液压缸缓冲效果 Tab.2 Cushion effect of different piston structure |
从计算结果可看出:
1)对于圆柱形活塞杆,随着间隙增大,其缓冲末速度增大,且缓冲峰值压力减小。
2)对于圆锥形活塞杆,随着间隙增大,其缓冲末速度变化不明显,且缓冲峰值压力减小。相较于圆柱形活塞,圆锥形活塞杆末速度较低,但峰值压力略高。
3)对于抛物线形活塞杆,随着间隙增大,其缓冲末速度变化不明显,且缓冲峰值压力减小。其缓冲末速度普遍高于圆锥形活塞杆,但小于圆柱形活塞杆。其峰值压力普遍高于圆锥形和圆柱形活塞杆。
在液压缸的缓冲过程中,活塞运动的动能Ek、缓冲腔的压力势能Ep以及活塞与缓冲套撞击后的能量损耗Ew之间相互转换,且转化过程中的总能量保持不变,如下式:
| $ \left\{ \begin{array}{l} {E_k} + {E_p} + {E_w} = {E_{const}}{\text{,}} \\ {E_k} = \dfrac{1}{2}{M_1}V{(t)^2} {\text{,}} \\ {E_p} = \dfrac{{{M_2}P(t)}}{\rho } {\text{。}}\\ \end{array} \right. $ | (9) |
其中:M1和M2分别为活塞及其传动机构等效到活塞上的当量质量、缓冲腔高压油液的质量;Ew的数值大小与碰撞的剧烈程度相关,可通过末速度的大小进行衡量。
综合分析可知,理论最优的抛物线形活塞杆能够从一定程度上降低缓冲末速度,但缓冲峰值压力较高;圆锥形活塞杆虽然缓冲峰值压力略高,但其缓冲末速度较低,运行平稳。且圆锥形活塞杆相较于抛物线形活塞杆更易加工,选择合适的间隙值能较大程度上优化缓冲效果,是3种结构形式中最优的选择。
4 结 语本文通过推导液压缸的缓冲过程数学模型,得到理论最优的活塞杆结构形式为抛物线形。基于AMESim建立圆柱形、圆锥形、抛物线形液压缸活塞的缓冲液压系统动力学仿真模型,通过仿真结果分析得到液压缸在不同结构形式、不同初始间隙下的液压缓冲特性:
1)初始间隙值越大,不同结构形式的活塞杆均表现出缓冲峰值压力越小。间隙值对圆锥形、抛物线形缓冲末速度影响不大。
2)考虑初始间隙变化的条件下,圆锥形活塞杆具有最优的缓冲效果。
3)在工程实际中,可结合初始间隙值的计算结果,综合考虑活塞杆长度、缓冲孔直径、活塞直径来设计活塞杆结构形式,以达到最优缓冲效果。
| [1] |
王洪波, 王邦勤, 王旭东. 船用活塞式液压缸故障分析[J]. 中小企业管理与科技, 2010(2): 207-208. |
| [2] |
SOCHACKI W. Modelling and analysis of damped vibration in hydraulic cylinder[J]. Mathematical & Computer Modelling of Dynamical Systems, 2015, 21(1): 23-37. |
| [3] |
陈宗斌, 何琳, 徐荣武. 船用操舵系统低噪声设计及特性分析[J]. 舰船科学技术, 2016, 38(7): 49-53. CHEN Zong-bin, HE Lin, XU Rong-wu. Low noise design and characteristics analysis for marine steering system[J]. Ship science and Technology, 2016, 38(7): 49-53. DOI:10.3404/j.issn.1672-7619.2016.07.011 |
| [4] |
TENG C K, HSIAO C Y, WANG C S. The effect of the guiding directions of the guiding cylinders of an area ratio modified machine cushion on the capability of suppressing impact and vibration[J]. Advances in Engineering Software, 2009, 40(10): 991-999. DOI:10.1016/j.advengsoft.2009.03.014 |
| [5] |
GHADIMI, PARVIZDASHTIMANESH, ABBASDJEDDI, et al. Study of water entry of circular cylinder by using analytical and numerical solutions[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2012, 34(3): 225-232. |
| [6] |
王成斌, 权龙. 大惯量负载液压冲击的主动变阻尼抑制方法[J]. 机械工程学报, 2014, 50(8): 182-188. |
| [7] |
陈勋, 李丽红, 周军, 等. 高压斗杆缸缓冲性能影响参数的分析与优化研究[J]. 机电工程, 2014, 31(7): 833-838.
|
| [8] |
方秀荣, 范海峰. 液压缓冲制动缸的设计研究[J]. 机床与液压, 2010, 38(10): 43-45. FANG Xiu-rong, FAN Hai-feng. Design of the cushion and brake hydraulic cylinder[J]. Machine Tool & Hydraulics, 2010, 38(10): 43-45. DOI:10.3969/j.issn.1001-3881.2010.10.015 |
 2019, Vol. 41
2019, Vol. 41
