齿轮传动系统具有寿命长、传动比恒定、效率高、运行平稳、结构紧凑等诸多优点,被广泛运用于航天航空、车辆工程、船舶运输、风电等领域,是现代机械传动中的重要组成部分,其可靠性将直接影响到机械设备的稳定运转。其中,作为评价齿轮系统的关键因素之一,系统的振动特性一直受到人们的广泛关注和研究。在传动过程中,齿轮系统不仅将受到来自原动机与负载带来的外部激励,还存在由时变啮合刚度、传动误差、齿侧间隙、轴承刚度及间隙等因素引起的内部激励。一直以来,国内外学者就齿轮传动系统做了大量研究[1 – 4]。张建云等[5]建立了斜齿轮传动的多平行轴转子系统动力学模型,模型综合考虑了弯扭耦合、陀螺力矩、滑动轴承支承刚度及阻尼因素的影响。唐进元等[6]利用有限元法研究了螺旋锥齿轮刚度的计算方法,得到了单齿啮合和多齿综合啮合刚度,分析了载荷影响下刚度曲线的变化。马辉等[7]对斜齿轮传动进行精确建模,研究了斜齿轮传动的模态特性和响应。徐向阳等[8]利用有限元法分析了某大型船用齿轮箱传动系统,通过分析表明齿轮箱系统转频、啮合频率远低于固有频率,不存在共振现象。陈小安等[9]建立了多间隙耦合齿轮传动系统模型,在考虑齿侧间隙、轴承间隙、齿面摩擦影响的基础上,首次利用有限元法分析了支撑状态下齿轮耦合系统的非线性动态特性。相对于数值仿真法与解析法,有限单元法与复杂的实际情况更为贴合,可以处理多种任意复杂结构,求解过程简便,求解精度高。本文以某多级斜齿轮传动对为研究对象,通过大型通用有限元分析软件Ansys建立耦合系统动力学模型,分析耦合与非耦合情况下多级传动系统的模态特性,并研究了不同齿轮啮合刚度与支撑轴承刚度对系统模态特性的影响规律。
1 齿轮-轴承耦合系统动力学模型利用线性弹簧单元对齿轮副啮合过程进行模拟,在此过程中,首先要计算弹簧刚度。考虑到齿轮传动过程中刚度是个动态变化的过程,以平均啮合刚度代替时变啮合刚度。
1.1 齿轮啮合刚度及轴承刚度对于刚性外啮合齿轮,在负载作用下,单对齿轮啮合刚度
| $ k_{12}' = \frac{{8 \times {{10}^8}b\cos \beta }}{{0.04723 + \dfrac{{0.15551}}{{{Z_{v1}}}} + \dfrac{{0.25791}}{{{Z_{v2}}}}}}{\text{。}} $ | (1) |
式中:
对于斜齿轮而言,其当量齿数为:
| ${Z_{v1}} \approx \frac{{{Z_1}}}{{{{\cos }^3}\beta }},{Z_{v2}} \approx \frac{{{Z_2}}}{{{{\cos }^3}\beta }}{\text{,}}$ | (2) |
同时,由于齿轮传动是周期运动,轮齿接触对数随时间改变,刚性外啮合齿轮平均啮合刚度
| ${k_{12}} = (0.75{\varepsilon _\alpha } + 0.25)k_{12}'{\text{,}}$ | (3) |
式中,
在斜齿轮中,其重合度关系如下式:
| $ {\varepsilon _\alpha } = \frac{1}{{2{\text{π}} }}\left[ {{Z_1}(\tan {\alpha _{a1}} - \tan {\alpha _t}) + {Z_2}(\tan {\alpha _{a2}} - \tan {\alpha _t})} \right]{\text{。}} $ | (4) |
其中:
由于斜齿轮传动中会产生轴向力,因此采用角接触滚动轴承,在手册[11]中根据相应准则确定轴承刚度,如表1所示
|
|
表 1 滚动轴承刚度 Tab.1 Stiffness of rolling bearing |
在三维CAD软件UG中建立齿轮传动对模型,后将几何模型导入Hypermesh进行前处理。网格划分过程中,首先对齿轮与轴进行切割,齿轮平面建立二维网格后进行拉伸,齿轮轴与齿轮采用共节点连接方式。为了定义传动系统中角接触轴承受到的力,在定义边界条件时将其简化成x,y,z三个方向上的弹簧单元。就齿轮之间啮合关系而言,同样利用弹簧单元来模拟齿面之间的啮合力,弹簧刚度由前文计算的齿轮啮合刚度确定。由于齿轮对的齿数相同,故传动比为1:1,刚度值也相同,取
|
|
表 2 斜齿轮几何参数 Tab.2 Geometric parameters of helical gear |

|
图 1 齿轮啮合对有限元模型 Fig. 1 Finite element model of gear meshing |
对于多级齿轮传动系统,先对单对啮合齿轮进行模态特性分析,然后分析耦合状态下齿轮系统的模态特性,通过比较,得到单对啮合传动与耦合传动模态上的区别和联系。
2.1 单对啮合齿轮-轴模态特性分析由于2对齿轮几何、材料参数均相同,因此结果对称,只需要1对齿轮啮合对即可,前10阶模态参数如表2所示,其中第1阶为刚体模态,振型为齿轮的绕轴扭转。
|
|
表 3 单对齿轮啮合对的前10阶模态频率及振型描述 Tab.3 Description of the first ten order modal frequencies and modes of gear meshing pairs |
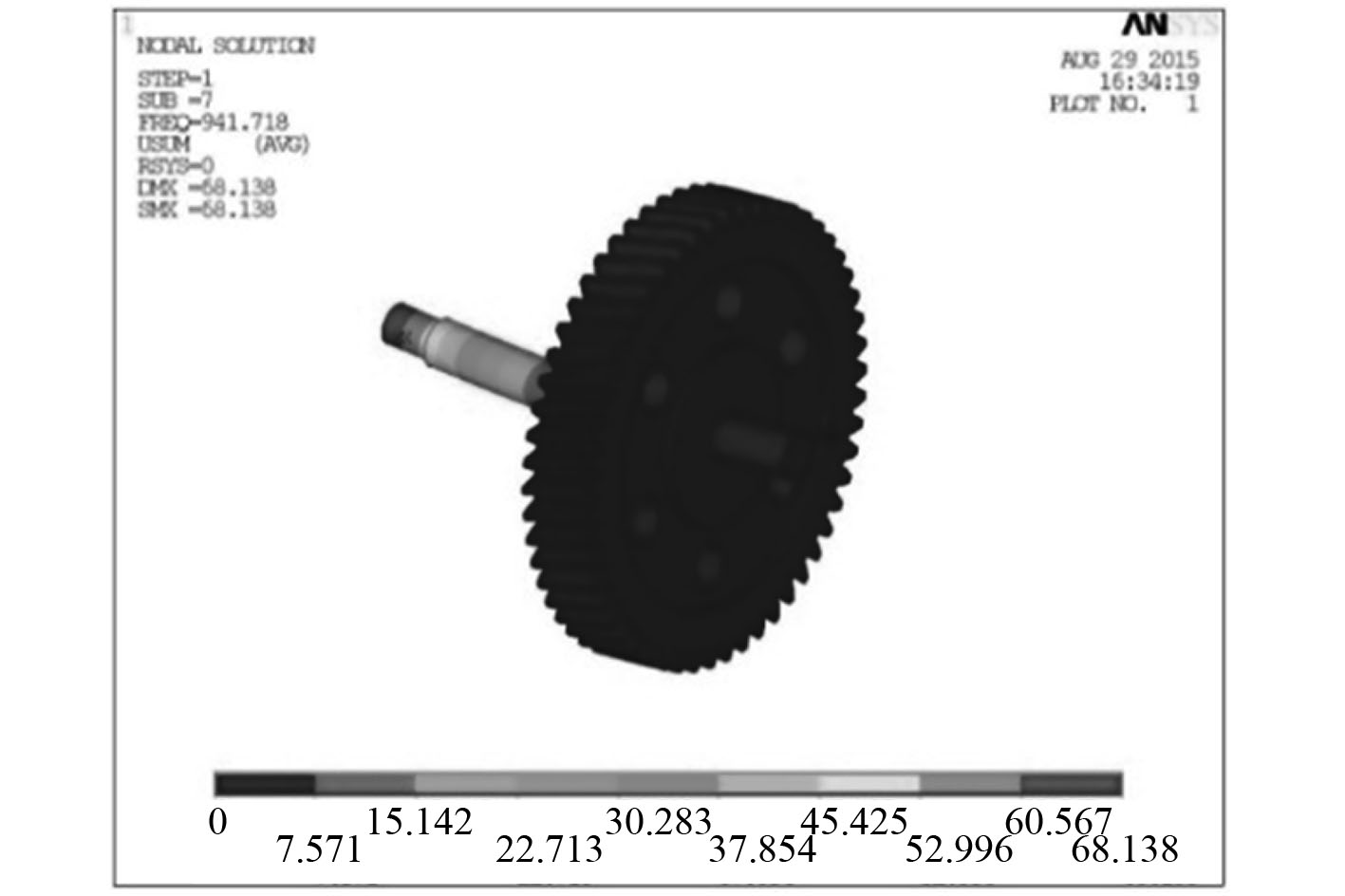
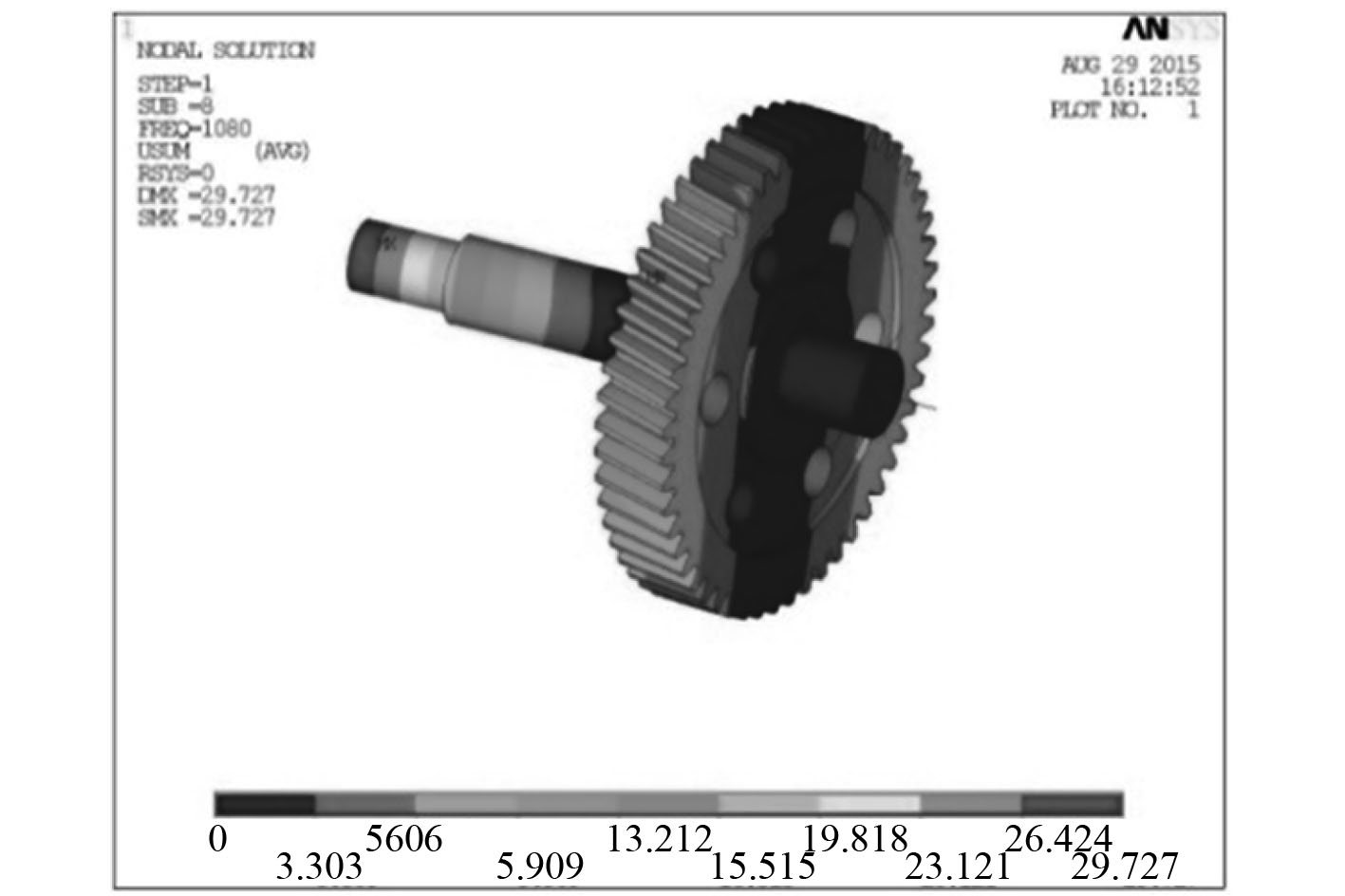
除第7和第8阶模态振型不同外其他的阶数都相同,图2和图3为第8阶输入、输出端齿轮振型图。
|
图 2 输入轴第8阶振型图 Fig. 2 Eighth order mode diagram of the input shaft |
|
图 3 输出轴第8阶振型图 Fig. 3 Eighth order mode diagram of the output shaft |
可以看出,由于齿轮轴几何材料参数相同,且对称分布,两轴在Y方向和Z方向的弯曲和摆动模态对称,除去前1阶和2阶模态外,相邻阶模态都存在振型和频率值接近的情况。
2.2 耦合齿轮-轴系统模态特性分析利用建立好的有限元模型,综合考虑耦合情况下,2对齿轮啮合对,分析其模态频率特征和振型。
|
|
表 4 耦合系统的模态频率及振型描述 Tab.4 Modal frequency and mode description |

|
图 4 模型第15阶振型图 Fig. 4 Model fifteenth order mode diagram |

|
图 5 模型第16阶振型图 Fig. 5 Model sixteenth order mode diagram |

|
图 6 模型第17阶振型图 Fig. 6 Model seventeenth order mode diagram |

|
图 7 模型第18阶振型图 Fig. 7 Model eighteenth order mode diagram |
根据单对啮合齿轮模态特性,比较耦合模态特性数据,得到以下结论:
1)在耦合情况下,除了第19阶和20阶模态为输出轴端的振动外,其他情况下都存在1对或多对的对称频率。
2)单对齿轮传动振动模态在耦合中得以保留存在,例如,如在耦合状态下,第15到18阶模态与输入轴的第7和第8阶模态频率接近,振型对应,耦合系统下模态可看作是单体模态的叠加。
3)当系统耦合振动时,产生了振型描述为三轴耦合扭转的新模态,频率为249.23 Hz。而对于单个轴而言,第1阶模态频率几乎为0,前后振型均为齿轮扭转,但模态频率变化很大。
3 刚度对系统模态的影响 3.1 齿轮啮合刚度对模态的影响分别考虑不同齿轮啮合刚度影响下,单对啮合齿轮模态特性的变化。保持模型其他参数不变,分别取啮合刚度为
|
|
表 5 不同啮合刚度下模态频率 Tab.5 Modal frequency of different meshing stiffness |
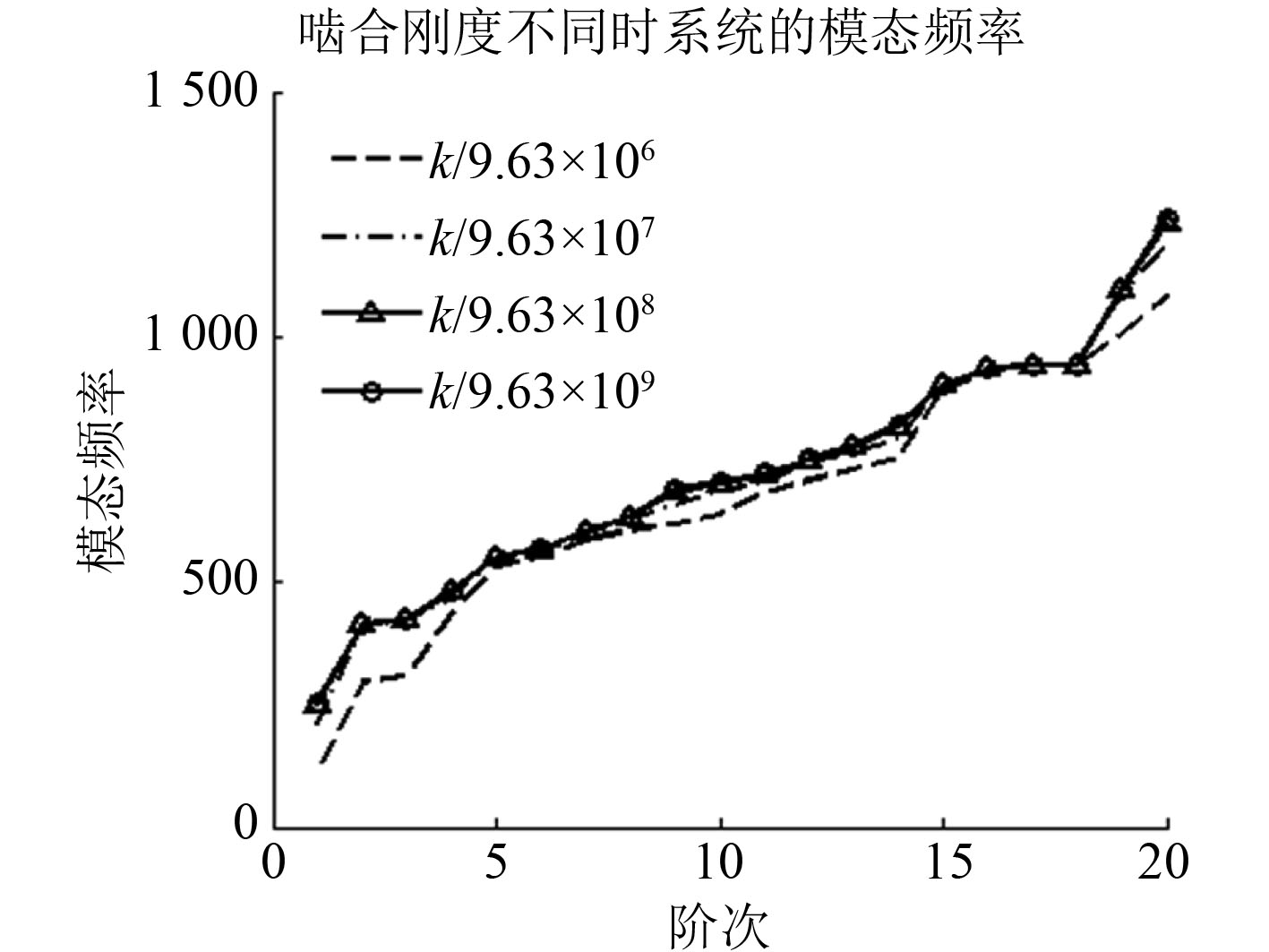
|
图 8 不同啮合刚度下模态频率变化曲线 Fig. 8 Modal frequency variation curve under different meshing stiffness |
1)随着设定啮合刚度的不断增大,模态频率呈上升趋势,但当刚度值大于
2)当刚度值变化时,低阶模态频率受影响程度最大,而对于14阶的模态频率而言,刚度的变化对其影响有限,敏感程度远低于低阶频率。
3) 结合耦合状态下的模态频率可知,啮合刚度的变化对于耦合模态影响较大,而对于非耦合情况,影响较小。
3.2 轴承支撑刚度对模态的影响保持齿轮的啮合刚度不变,通过改变轴承支撑刚度的数量级107,108,109,1010来考虑不同轴承刚度。
|
|
表 6 不同轴承刚度下系统的模态频率 Tab.6 Modal frequency under different bearing stiffness |
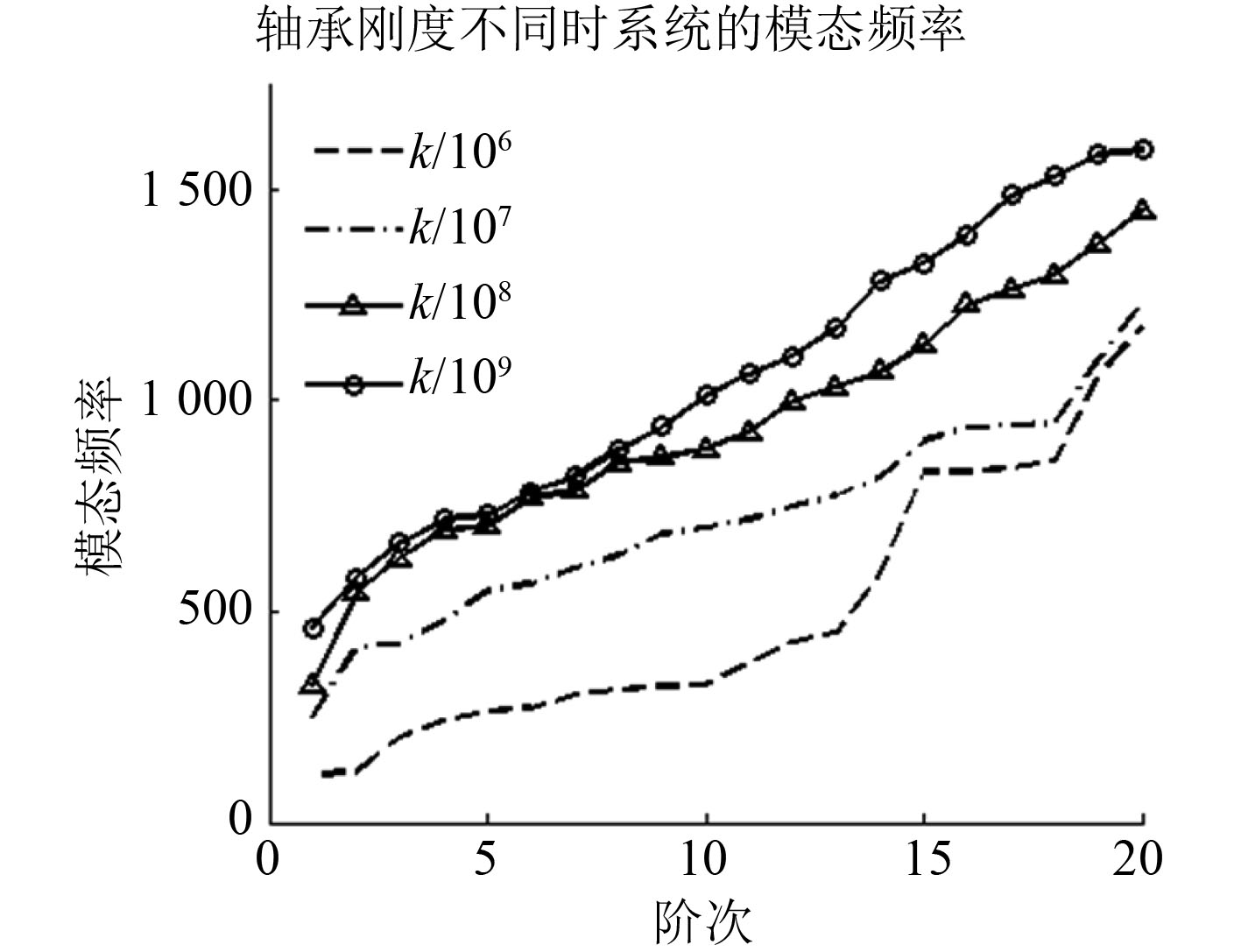
|
图 9 不同轴承刚度影响下模态频率变化曲线 Fig. 9 Modal frequency variation curve under theinfluence of different bearing stiffness |
1)当啮合刚度不变时,提高轴承刚度,系统的模态频率逐渐增大,不同轴承刚度下频率数值变化大,因此,在选取滚动轴承时就要综合考虑轴承对系统带来的影响,选取合适轴承规格,避免因不恰当的轴承刚度使系统处于共振频率。
2)结合振型图可知,系统前14阶为耦合振动状态,后6阶为单轴振动模态,因此,轴承刚度的大小变化不影响齿轮传动的耦合状态。
4 结 语1)建立了传动系统多级耦合传动模型,在考虑耦合情况下,齿轮对的模态会在单齿啮合叠加模态的基础上成对出现,并会产生新的模态。
2)齿轮对的模态频率会随着齿轮啮合刚度的增大而增大,当啮合刚度增大到一定程度时,啮合刚度将不再影响传动系统的模态。
3)当啮合刚度不变时,提高轴承刚度,系统的模态频率逐渐增大,不同轴承刚度下同阶模态数值变化大。轴承刚度的大小并不影响齿轮传动的耦合状态。
| [1] |
OZGUVEN H N, HOUSER D R. Mathematical models used in gear dynamic-a review[J]. J Sound Vib, 1998, 121(3): 381-411. |
| [2] |
王建军, 李润方. 齿轮系统动力学的理论体系[J]. 中国机械工程, 1998, 9(12): 61-64. |
| [3] |
李润方, 王建军. 齿轮系统动力学—振动、冲击、噪声[M]. 科学出版社, 1997.
|
| [4] |
王建军, 李其汉, 李润方. 齿轮系统非线性振动研究进展[J]. 力学进展, 2005, 35(1): 37-47. DOI:10.3321/j.issn:1000-0992.2005.01.005 |
| [5] |
张建云. 齿轮传动对多平行转子-轴承系统动力学特性影响的研究[D]. 西安: 西安交通大学, 1999.
|
| [6] |
唐进元, 蒲太平. 基于有限元法的螺旋锥齿轮啮合刚度计算[J]. 机械工程学报, 2011, 47(11): 23-29. |
| [7] |
马辉, 朱丽莎, 王奇斌, 等. 斜齿轮-平行轴转子系统模态耦合特性分析[J]. 中国电机工程学报, 2012, 32(29): 131-136. |
| [8] |
徐向阳, 朱才朝, 张晓蓉, 等. 大功率船用齿轮箱实验模态分析[J]. 振动与冲击, 2011, 30(7): 266-270. DOI:10.3969/j.issn.1000-3835.2011.07.052 |
| [9] |
陈小安, 缪莹赟, 杨为, 等. 基于有限单元法的多间隙耦合齿轮传动系统非线性动态特性分析[J]. 振动与冲击, 2010, 29(2): 46-49. DOI:10.3969/j.issn.1000-3835.2010.02.011 |
| [10] |
齿轮手册编委会. 齿轮手册[M]. 北京: 机械工业出版社, 2004.
|
| [11] |
罗继伟, 罗天宇. 滚动轴承分析计算与应用[M]. 北京: 机械工业出版社, 2009.
|
 2019, Vol. 41
2019, Vol. 41
