0 引　言

目前，海洋平台长期作业于恶劣海况下，其生产甲板上密集布置的工艺设备及管线系统易出现油气泄露，进而引发火灾、爆炸等事故，造成巨大的经济损失甚至人员伤亡^[1]。生活楼结构作业人员的生活区及极端环境下的避难场所，其结构在设计过程中应考虑油气爆炸载荷作用下的安全性问题。

数值仿真是分析爆炸下海洋平台结构响应问题的主流方法之一^{[1 – 6]}，但该方法需要针对不同的分析对象分别建模计算，效率较低。与之相比，理论方法则可以通过输入不同结构的相关几何参数快速预报结构在爆炸下的响应，大大提高了船体结构抗爆性能的计算效率，更加有利于工程设计及研究。其中，单自由度理论由于其系统构造简单，且能够较好地反映爆炸下结构的动态响应问题，国内外学者已将其应用在结构抗爆性能研究中^{[7 – 10]}，此外相关船级社规范^[11]也将单自由度理论作为分析爆炸载荷下船体结构的动态响应手段之一。

本文以某海洋平台生活楼端壁局部加筋板架结构为研究对象，基于单自由度理论，建立典型等效单自由度系统的弹塑性响应微分方程，求解得到系统响应表达式，并绘制单自由度最大响应图谱，分析爆炸载荷作用下局部加筋板架结构响应，以此评估平台生活楼局部板架结构的抗爆性能。

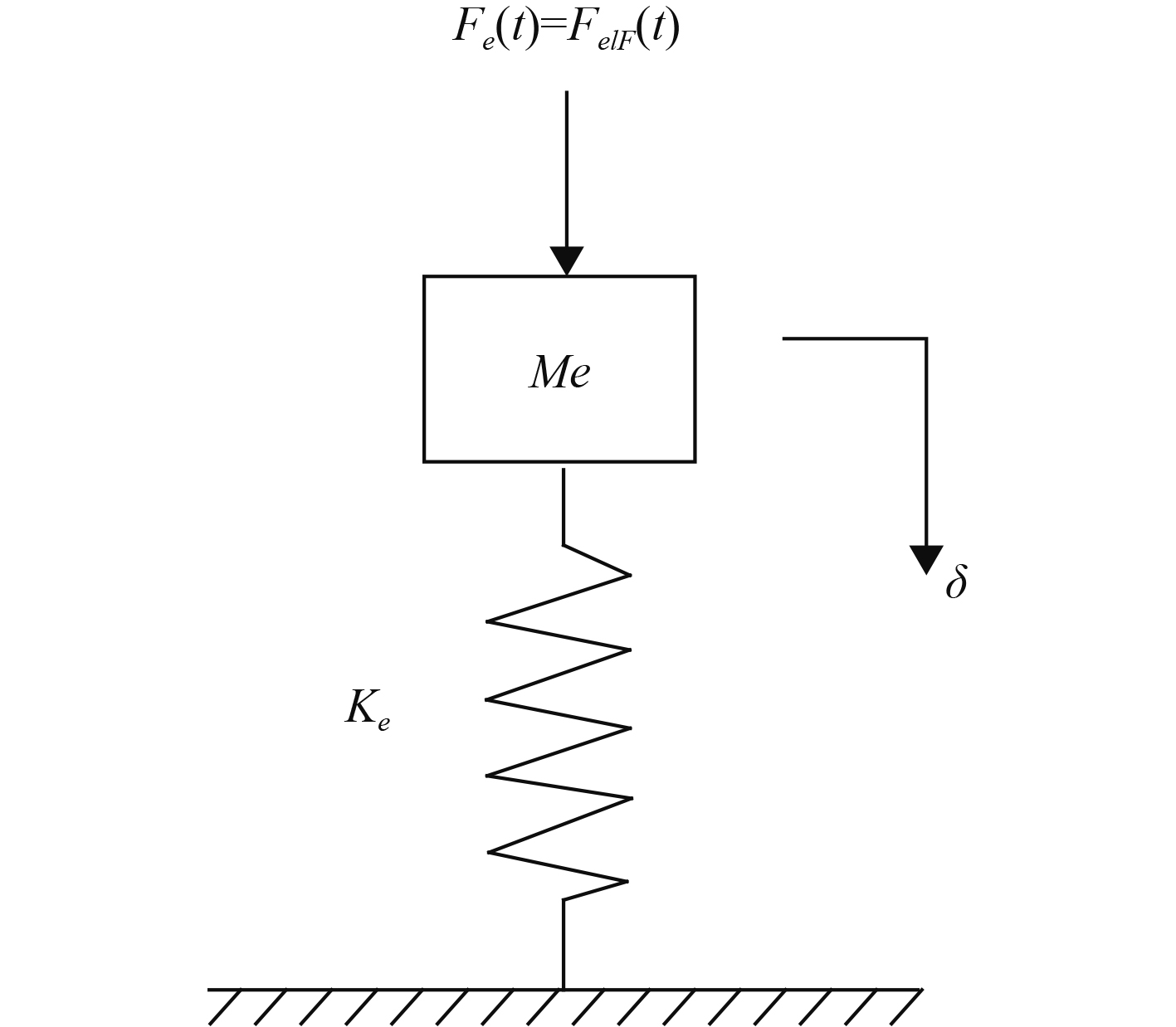
1 爆炸载荷作用下结构响应理论预报方法 1.1 等效单自由度系统分析法

对于船舶局部板架结构的抗爆设计及评估，可将结构简化为承受冲击载荷的无阻尼等效单自由度弹簧-质量系统（见图1）。通过分析爆炸载荷下结构等效单自由度系统的最大变形来评估结构的抗爆性能^[8]。单自由度方法整体分析流程如图2所示。主要分为3个步骤：1）通过结构与油气爆炸载荷的简化，得到结构等效单自由度系统运动方程，并对变量进行无量纲处理；2）求解等效系统运动微分方程，得到由无量纲变量表示的系统弹塑性响应表达式，绘制系统最大响应图谱；3）将实际结构等效为刚度为K的理想弹塑性模型，计算结构最大抗力R_m及弹性临界变形δ_el，基于响应表达式或响应图谱得到油气爆炸下结构的动态响应。

1.2 结构等效单自由度系统的简化

1）等效单自由度系统抗力-位移关系

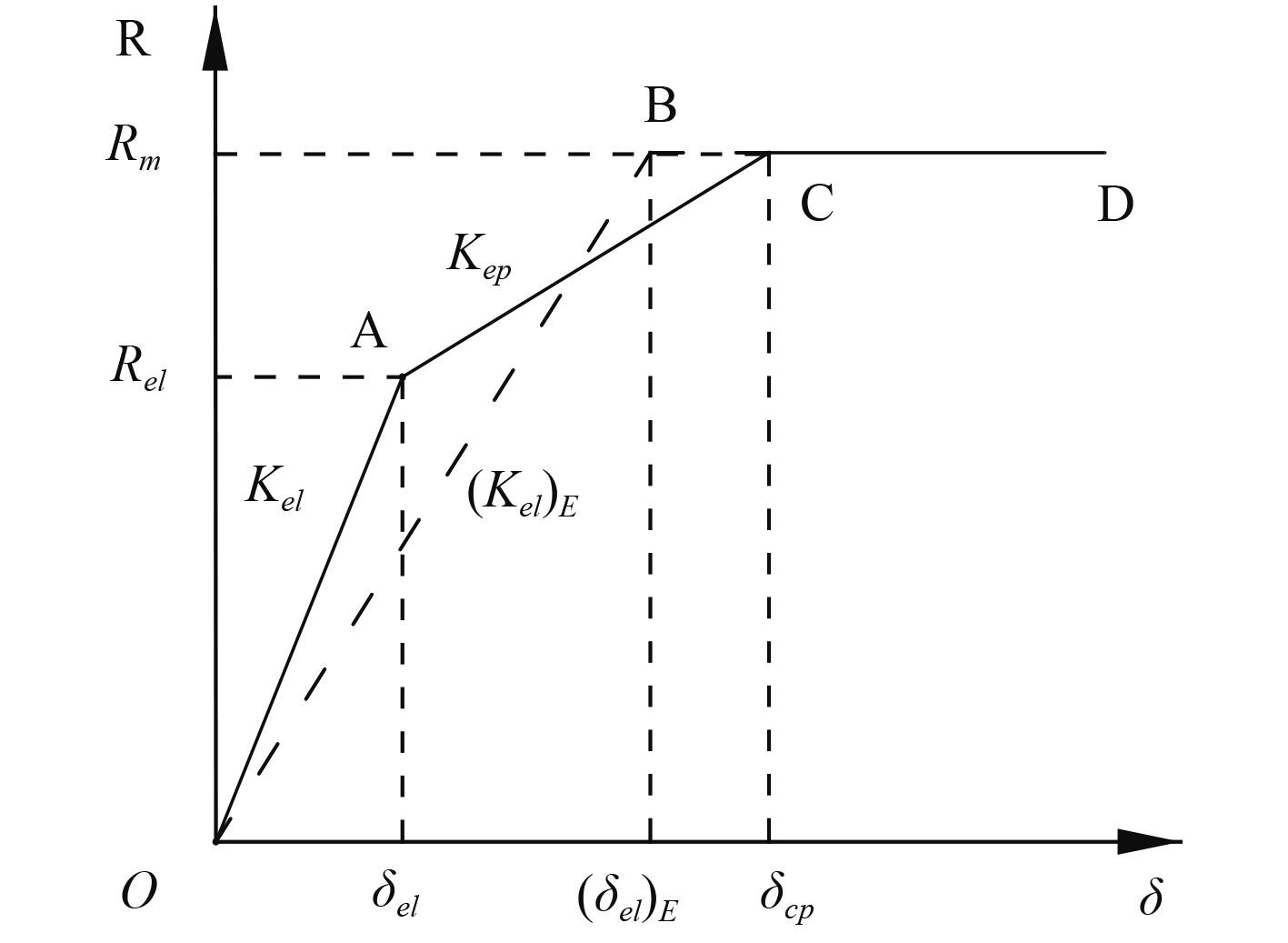
单自由度系统的抗力-位移关系决定着系统在外载荷作用下的运动响应情况，图3表示一个弹塑性单自由度系统的抗力-位移关系曲线。其中，抗力在OA段以弹簧刚度K_e为斜率线性增加，在A点达到最大值R_m，对应的位移为弹性极限δ_el；AB段为系统塑性变形阶段，抗力R_m保持不变，系统位移不断增加并在B点达到塑性极限δ_m；若系统在到达塑性极限δ_el前（失效前）卸载，则抗力-位移关系曲线会平行于OA段发生弹性恢复，抗力随着位移的减小不断降低，直至到达–R_m。

一般情况下，由实际结构简化得到的等效单自由度系统的抗力-位移关系曲线较为复杂。如图4所示，假设实际结构的抗力-位移关系为图中实线部分，其中OA为弹性阶段，AC为弹塑性过渡段，CD为塑性阶段。为了简化问题以提高计算效率，通常将塑性阶段前的OAC段简化为OBC段，即将实际结构等效单自由度系统的抗力-位移关系曲线简化为一个双线性函数。其中，将弹性刚度K_el与过渡段刚度K_ep简化为等效弹性刚度（K_el）_E，弹性临界变形δ_el与弹塑性临界变形δ_cp统一由等效弹性临界变形（δ_el）_E表示，系统弹性临界抗力R_el与塑性阶段最大抗力均由R_m表示。此时，可以基于实际结构与等效单自由度系统间的抗力-位移关系建立运动方程。

2）结构等效单自由度系统运动方程

爆炸载荷下，等效单自由度系统的运动方程表示为：

$ {{M}_{e}}\ddot{\delta }\left( t \right)+{{K}_{e}}\delta \left( t \right)={{F}_{e}}\left( t \right){\text{，}} $ $

(1)

式中， $ {{M}_{e}}={{\beta }_{M}}M$ ， $ {{K}_{e}}={{\beta }_{L}}K$ ， ${{F}_{e}}={{\beta }_{L}}F(t)$ 分别为等效质量、等效刚度与等效外载荷；M，K，F(t)分别为实际结构的质量、刚度及外载荷，β_M为质量系数，β_L为载荷系数，令载荷-质量系数 $ {{\beta }_{LM}}\text{=}{{\beta }_{M}}/{{\beta }_{L}}$ ，式（1）可改写为：

$ {{\beta }_{LM}}M\ddot{\delta }\left( t \right)+K\delta \left( t \right)=F\left( t \right){\text{。}} $

(2)

令固有角频率 $ \omega =\sqrt{{{K}_{e}}/{{M}_{e}}}=\sqrt{{{\beta }_{L}}K/{{\beta }_{M}}M}=$ $\sqrt{K/{{\beta }_{LM}}M}$ ，则周期T为：

$ T=2 {\text{π}}\sqrt{\frac{{{\beta }_{LM}}M}{K}}{\text{，}} $

(3)

式（2）即为结构等效单自由度系统的运动方程，通过载荷-质量系数β_LM实现实际结构与等效系统之间的转换。

1.3 等效单自由度系统弹塑性响应运动方程

根据图3所示的弹塑性单自由度系统的抗力-位移关系曲线，式（1）可改写为：

$ {M_e}\ddot \delta \left( t \right) + {K_e}\delta \left( t \right) - {F_e}\left( t \right) = 0{\text{，}}\;\;\;\;\;\;0 < \delta \left( t \right) < {\delta _{el}}{\text{；}} $

$ {M_e}\ddot \delta \left( t \right) + {R_m} - {F_e}\left( t \right) = 0{\text{，}}\;\;\;\;\;\;\;\;{\delta _{el}} < \delta \left( t \right) < {\delta _{\mathop{\rm m}\nolimits} }{\text{；}} $

$ \begin{split} & {M_e}\ddot \delta \left( t \right) + [{R_m} - {K_e}\left( {{\delta _{\mathop{\rm m}\nolimits} } - \delta \left( t \right)} \right)] - {F_e}\left( t \right) = 0{\text{，}}\\ & \left( {{\delta _{\mathop{\rm m}\nolimits} } - 2{\delta _{el}}} \right) < \delta \left( t \right) < {\delta _{\mathop{\rm m}\nolimits} }{\text{。}} \end{split} $

(4)

式（4a）、（4b）和（4c）分别适用于初始弹性范围、塑性范围以及系统达到最大变形δ_m后的弹性恢复。本文主要研究结构的最大响应δ_m，故不考虑系统达到最大变形后的弹性恢复。

令式（4）中 $ {F_e}({{t) = }}{F_1} \cdot f(t)$ ，其中F₁为载荷峰值，f(t)为载荷形函数。Biggs^[4]提出了4种常见的爆炸载荷简化形式，如图5所示，图5（a）～图5（d）分别为矩形爆炸载荷、直角三角形爆炸载荷、等腰三角形爆炸载荷及具有有限上升段的爆炸载荷。不同载荷形式下形函数分f（t）不同，会导致结构响应不同。参考相关海洋结构油气爆炸资料^[12]，选取图5（c）描述的三角形载荷为例对等效单自由度系统运动方程进行求解，三角形冲击载荷形函数f（t）表达式如下：

$ f\left( t \right) = \left\{ \begin{aligned} & \frac{{2t}}{{{t_{d}}}}{\text{，}} \quad\quad\quad\quad \quad 0 < t \text{≤} \frac{{{t_{d}}}}{2}{\text{；}}\\ & 2\left( {1 - \frac{t}{{{t_{d}}}}} \right){\text{，}}\quad\quad \frac{{{t_{ d}}}}{2} < t \text{≤} {t_{ d}}{\text{；}}\\ & 0{\text{，}} \quad\quad\quad\quad \quad t > {t_{d}}{\text{。}} \end{aligned} \right. $

(5)

式中，t_d表示载荷作用时间。

1.4 运动方程无量纲化

令无量纲时间参数τ = t/T，无量纲变形参数 $ \eta = \delta (t)/{\delta _{el}}$ ，式（4）中 $ \ddot \delta (t)$ 可表示为：

$ \ddot \delta (t) = \frac{{{{\rm d}^2}\delta (t)}}{{{\rm d}{t^2}}} = \frac{{{\delta _{el}}}}{{{T^2}}}\frac{{{{\rm{d}}^2}\eta (\tau )}}{{{\rm d}{\tau ^2}}} = \frac{{{\delta _{el}}}}{{{T^2}}}\ddot \eta (\tau ){\text{，}} $

(6)

又 $ {K_e}\delta = {R_m}$ ， $ {T^2} = 4{{\text{π}} ^2}M/k$ ，式（6）可改写为：

$ \frac{1}{{4{{\text{π}} ^2}}}\ddot \eta \left( \tau \right) + \eta \left( \tau \right) = \frac{{{F_1}}}{{{R_m}}} \cdot f(\tau ){\text{，}} $

(7)

在塑性范围内（即图3所示AB段）， $ {K_e}\delta \left( t \right) = {R_m}$ ，则等效单自由度系统的运动方程表示为：

$ \frac{1}{{4{{\text{π}}^2}}}\ddot \eta \left( \tau \right) + 1 = \frac{{{F_1}}}{{{R_m}}} \cdot f(\tau ){\text{，}} $

(8)

式（7）～式（8）为等效单自由度系统无量纲运动方程，对其进行求解可以得到爆炸载荷作用下系统弹塑性的响应情况。

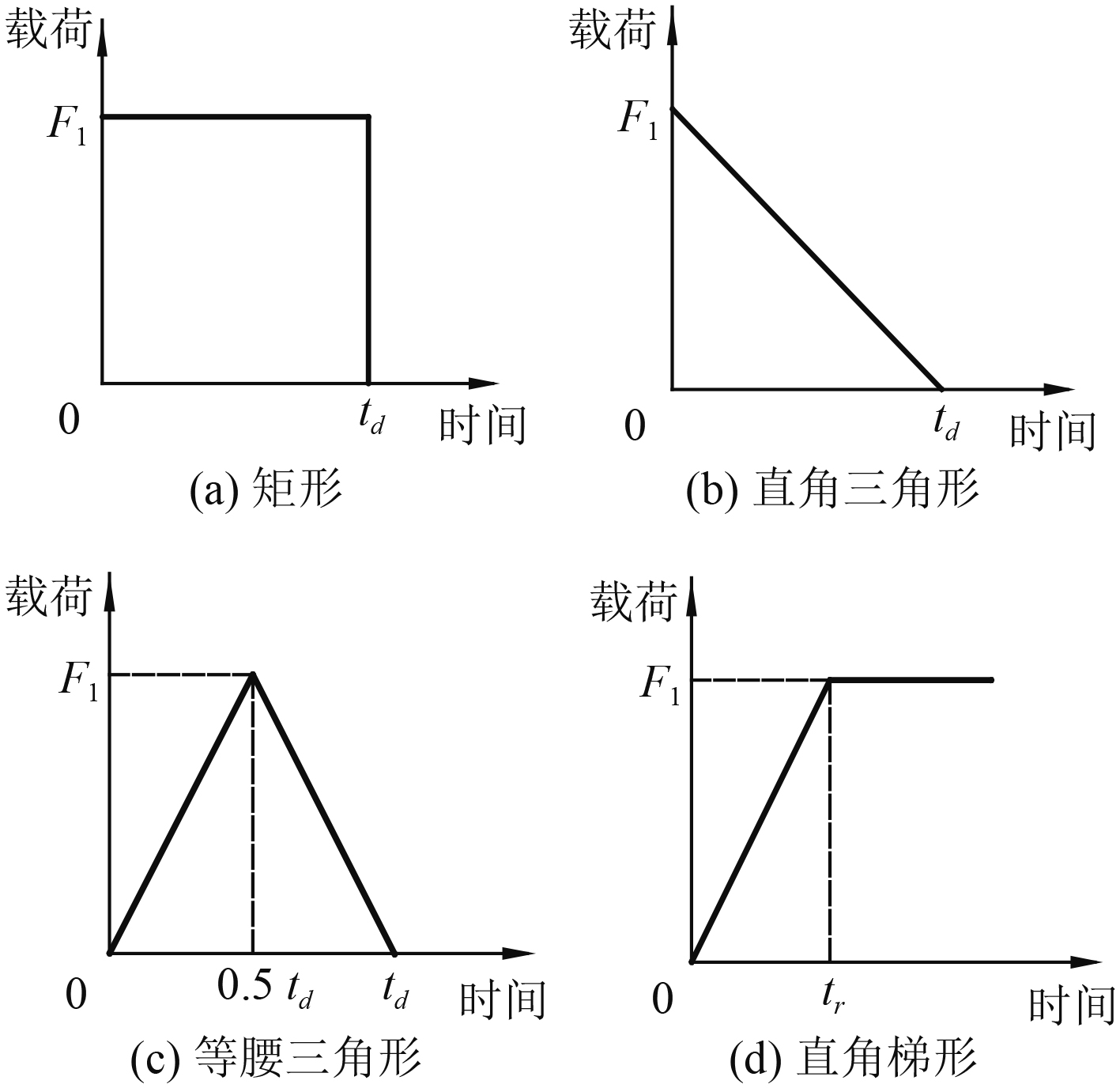
1.5 爆炸下等效单自由度系统的响应

以图5（c）中三角形载荷为例进行分析，其载荷形函数f（t）见式（5），等效单自由度系统运动方程求解过程如下：

1）弹性范围

当 $ \eta = \delta (t)/{\delta _{el}} \text{≤} 1$ 时，系统任意时刻的变形均小于δ_el，系统始终处于弹性响应阶段。等效单自由度系统在载荷第一阶段（ $ 0 < \tau \text{≤} 1/2\zeta $ ）的运动方程为：

$ \frac{1}{{4{{\text{π}} ^2}}}\ddot \eta \left( \tau \right) + \eta \left( \tau \right) = \frac{{{F_1}}}{{{R_m}}} \cdot \frac{{2\tau }}{\zeta }{\text{，}} $

(9)

式中， $ \zeta = {t_d}/T$ 。由初始条件 $ \eta (\tau ) = 0$ 、 $ \dot \eta (\tau ) = 0$ （即系统初始时刻速度、位移为0），解得等效单自由度系统的响应为：

$ {\eta _1}(\tau ) = \frac{{2{F_1}\tau }}{{{R_m}\zeta }} - \frac{{{F_1}\sin 2 {\text{π}} \tau }}{{{R_m}\zeta {\text{π}}}}{\text{，}} $

$ {\dot \eta _1}(\tau ) = \frac{{2{F_1}(1 - \cos 2 {\text{π}} \tau )}}{{{R_m}\zeta }}{\text{，}} $

(10)

等效单自由度系统在载荷第2阶段（ $ 1/2\zeta < \tau \text{≤} 1/\zeta $ ）的运动方程为：

$ \frac{1}{{4{{\text{π}} ^2}}}\ddot \eta \left( \tau \right) + \eta \left( \tau \right) = \frac{{2{F_1}}}{{{R_m}}} \cdot \left(1 - \frac{\tau }{\zeta }\right){\text{，}} $

(11)

将 $ {\eta _1}(1/2\zeta ) = {\eta _2}(1/2\zeta )$ 、 $ {\dot \eta _1}(1/2\zeta ) = {\dot \eta _2}(1/2\zeta )$ （即运动方程（9）与（11）在 $ \tau = 1/2\zeta $ 时刻的速度与位移相等）作为初始条件，系统在载荷第2阶段的响应为：

$ \begin{split} {\eta _2}(\tau ) =& \frac{{2{F_1}}}{{{R_m}}} - \frac{{2{F_1}\tau }}{{{R_m}\zeta }} -\\ & \frac{{{F_1}({C_1} \cdot \sin 2 {\text{π}} \tau + {C_2} - 2{C_3} - 2{C_4} \cdot \cos 2 {\text{π}} \tau )}}{{{R_m}\zeta {\text{π}} ({C_1} + {C_2})}}{\text{，}} \end{split} $

$ {\eta _2}(\tau ) = - \frac{{2{F_1}}}{{{R_m}\zeta }} - \frac{{2{F_1}({C_1} \cdot \cos 2 {\text{π}} \tau + 2{C_4} \cdot \sin 2 {\text{π}} \tau )}}{{{R_m}\zeta ({C_1} + {C_2})}}{\text{，}} $

(12b)

等效单自由度系统在载荷第3阶段（ $ \tau > 1/\zeta $ ）的运动方程为：

$ \frac{1}{{4{{\text{π}}^2}}}\ddot \eta \left( \tau \right) + \eta \left( \tau \right) = 0{\text{。}} $

(13)

同理，将 $ {\eta _2}(1/\zeta ) = {\eta _3}(1/\zeta )$ ， $ {\dot \eta _2}(1/\zeta ) = {\dot \eta _3}(1/\zeta )$ 作为初始条件，解得系统在载荷第3阶段的响应为：

$ \begin{split} & {\eta _3}(\tau ) = \\ & \frac{{{F_1}(\cos 2 {\text{π}} \tau \cdot {C_1}{D_2} - \sin 2 {\text{π}} \tau \cdot {C_1}{D_1} + {D_3}{D_4} + {C_2}({D_2} - {D_1}))}}{{{R_m}\zeta {\text{π}} \cdot {D_3}({C_1} + {C_2})}}{\text{，}} \end{split} $

$ {\dot \eta _3}(\tau ) = \frac{{ - 2{F_1}(\sin 2 {\text{π}} \tau \cdot {C_1}{D_2} + \cos 2 {\text{π}} \tau \cdot {C_1}{D_1})}}{{{R_m}\zeta \cdot {D_3}({C_1} + {C_2})}}{\text{，}} $

(14)

式中， $ {C_1} = \cos {\left(\displaystyle\frac{{{\text{π}} {t_{d}}}}{T}\right)^2}$ ， $ {C_2} = \sin {\left(\displaystyle\frac{{{\text{π}} {t_{d}}}}{T}\right)^2}$ ， $ {C_3} = \cos \left(\displaystyle\frac{{{\text{π}} {t_{d}}}}{T}\right)$ ， $ {C_4} = \sin \left(\displaystyle\frac{{{\text{π}} {t_{d}}}}{T}\right)$ ， $ {D_1} = \cos \left(\displaystyle\frac{{2{\text{π}} {t_{d}}}}{T}\right)$ ， $ {D_2} = \sin \left(\displaystyle\frac{{2{\text{π}} {t_{d}}}}{T}\right)$ ， $ {D_3} = $ $\cos {\left(\displaystyle\frac{{2{\text{π}} {t_{d}}}}{T}\right)^2}{\rm{ + }}\sin {\left(\displaystyle\frac{{2\pi {t_{d}}}}{T}\right)^2} $ ， $ {D_4} = 2{C_1}{\rm{ - }}2{C_2}{\rm{ - }}2{C_4}$ 。

联立式（12）、式（15）、式（18）即可得到等效单自由度系统在弹性范围内的运动轨迹。

2）塑性范围

当 $ \eta = \delta (t)/{\delta _{el}} > 1$ 时，系统变形 $ \delta (t)$ 超过弹性极限变形，系统进入塑性阶段。此时爆炸载荷持续时间 $ \zeta $ 的不同会对结构进入塑性的时间 $ \tau $ 产生影响，即当 $ \zeta $ 变化时，结构可能在爆炸载荷的3个阶段中的任一阶段进入塑性，因此需进行分类讨论。

假设结构在 $ \tau = {\tau _1}$ 时刻进入塑性，对式（8）两边积分，可以得到：

$ \left\{ \begin{array}{l} {{\ddot \eta }_p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{2{F_1}\tau }}{{{R_m}\zeta }} - 1\right){\text{，}}\\ {{\dot \eta }_p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\tau ^2}}}{{{R_m}\zeta }} - \tau \right){\rm{ + }}{{\rm{A}}_{\rm{1}}}{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{0 < }}\tau \text{≤} \displaystyle\frac{1}{{2\zeta }}{\text{，}}\\ {\eta _p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\tau ^3}}}{{3{R_m}\zeta }} - \displaystyle\frac{{{\tau ^2}}}{2}\right){\rm{ + }}{{\rm{A}}_{\rm{1}}}\tau {\rm{ + }}{{\rm{B}}_{\rm{1}}}{\text{，}} \end{array} \right. $

$ \left\{ \begin{array}{l} {{\ddot \eta }_p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{2{F_1}\zeta }}{{{R_m}\zeta }} - \frac{{2{F_1}\tau }}{{{R_m}\zeta }} - 1\right){\text{，}}\\ {{\dot \eta }_p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{2{F_1}\zeta \tau }}{{{R_m}\zeta }} - \displaystyle\frac{{{F_1}{\tau ^2}}}{{{R_m}\zeta }} - \tau \right){\rm{ + }}{{\rm{A}}_{\rm{2}}}{\text{，}}\;\;\;\;\;\;{\rm{}}\displaystyle\frac{1}{{2\zeta }}{\rm{ < }}\tau \text{≤} \displaystyle\frac{1}{\zeta }{\text{，}}\\ {\eta _p}\left( \tau \right) = 4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}\zeta {\tau ^2}}}{{{R_m}\zeta }} - \frac{{{F_1}{\tau ^3}}}{{3{R_m}\zeta }} - \displaystyle\frac{{{\tau ^2}}}{2}\right) + {{\rm{A}}_{\rm{2}}}\tau + {{\rm{B}}_{\rm{2}}}{\text{，}} \end{array} \right. $

$ \left\{ \begin{array}{l} {{\ddot \eta }_p}\left( \tau \right) = - 4{{\text{π}}^2}{\text{，}}\\ {{\dot \eta }_p}\left( \tau \right) = - 4{{\text{π}} ^2}\tau {\rm{ + }}{{\rm{A}}_{\rm{3}}}{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{}}\tau \text{≥} \displaystyle\frac{1}{\zeta }{\text{。}}\\ {\eta _p}\left( \tau \right) = - 2{{\text{π}} ^2}{\tau ^2} + {{\rm{A}}_{\rm{3}}}\tau + {{\rm{B}}_{\rm{3}}}{\text{，}} \end{array} \right. $

(15c)

若 $ 0 \text{≤} {\tau _1} \text{≤} 1/2\zeta $ ，结构在载荷第1阶段进入塑性，通过弹塑性临界点的速度、位移相等联立式（10a）、（15a）建立等式：

$ {\dot \eta _p}\left( {{\tau _1}} \right) = {\dot \eta _1}\left( {{\tau _1}} \right) = 4{{\text{π}} ^2}\left(\frac{{{F_1}{\tau _1}^2}}{{{R_m}\zeta }} - {\tau _1}\right){\rm{ + }}{A_1}{\text{，}} $

$ {\eta _p}\left( {{\tau _1}} \right) = {\eta _1}\left( {{\tau _1}} \right) = 4{{\text{π}} ^2}\left(\frac{{{F_1}{\tau _1}^3}}{{3{R_m}\zeta }} - \frac{{{\tau _1}^2}}{2}\right){\rm{ + }}{A_1}{\tau _1}{\rm{ + }}{B_1}{\text{，}} $

(16)

可得 $ {A_1} = {\dot \eta _1}\left( {{\tau _1}} \right) - 4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\tau _1}^2}}{{{R_m}\zeta }} - {\tau _1}\right)$ ， $ {B_1} = {\ddot \eta _1}\left( {{\tau _1}} \right) - $ $4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\tau _1}^3}}{{3{R_m}\zeta }} - \frac{{{\tau _1}^2}}{2}\right) - {A_1}{\tau _1} $ 。

将A₁，B₁代入式（15）可以得到载荷第1阶段内的塑性响应为：

$ {\eta _{p1}}{\left( \tau \right)_1} = 4{{\text{π}}^2}\left(\frac{{{F_1}{\tau ^3}}}{{3{R_m}\zeta }} - \frac{{{\tau ^2}}}{2}\right){\rm{ + }}{A_1}\tau {\rm{ + }}{B_1}{\text{，}} $

$ {\dot \eta _{p1}}{\left( \tau \right)_1} = 4{{\text{π}} ^2}\left(\frac{{{F_1}{\tau ^2}}}{{{R_m}\zeta }} - \tau \right){\rm{ + }}{A_1}{\text{，}} $

(17b)

将 $ \tau = 1/2\zeta $ 时刻的速度、位移（即 $ {\eta _{p1}}{\left( {1/2\zeta } \right)_1}$ 、 $ {\dot \eta _{p1}}$ ${\left( {1/2\zeta } \right)_1}$ ）作为初始条件代入式（15），可得系统在载荷第2阶段内的塑性响应为：

$ \begin{split} {\eta _{p1}}{\left( \tau \right)_2} =& {{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\zeta ^3}{\rm{ + }}12{F_1}\zeta {\tau ^2} - 6{F_1}{\zeta ^2} - 4{F_1}{\tau ^3}}}{{3{R_m}\zeta }} - 2{\tau ^2}\right){\rm{ + }}\\ & {A_1}\tau {\rm{ + }}{B_1}{\text{，}} \end{split} $

$ {\dot \eta _{p1}}{\left( \tau \right)_2} = {{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}{\zeta ^3}{\rm{ + }}24{F_1}\zeta \tau - 6{F_1}{\zeta ^2} - 12{F_1}{\tau ^2}}}{{3{R_m}\zeta }} - 4\tau \right){\rm{ + }}{A_1}{\text{，}} $

(18b)

同理，系统在第3阶段内的塑性响应为：

$ {\eta _{p1}}{\left( \tau \right)_3} = {{\text{π}} ^2}\left( - 2{\tau ^2}{\rm{ + }}\frac{{2{F_1}\zeta \tau }}{{{R_m}}} - \frac{{{F_1}{\zeta ^2}}}{{{R_m}}}\right) + {A_1}\tau {\rm{ + }}{B_1}{\text{。}} $

(19)

若 $ 1/2\zeta \text{≤} {\tau _1} \text{≤} 1/\zeta $ ，系统在 $ \tau \text{≤} {\tau _1}$ 内为弹性响应可直接由式（10）、式（12）表示，在载荷第2阶段内进入塑性响应阶段，根据前述方法，将 $ {\eta _2}({\tau _1})$ 、 $ {\dot \eta _2}({\tau _1})$ 代入式（15），得到载荷第2、第3阶段的等效单自由度系统响应为：

$ {\eta _{p2}}{\left( \tau \right)_2} = 4{{\text{π}} ^2}\left(\displaystyle\frac{{{F_1}(3\zeta {\tau ^2} - {\tau ^3})}}{{3{R_m}\zeta }} - \displaystyle\frac{{{\tau ^2}}}{2}\right){\rm{ + }}{A_2}\tau {\rm{ + }}{B_2}{\text{，}} $

$ {\eta _{p3}}{\left( \tau \right)_3} = 2{{\text{π}} ^2}\left(\displaystyle\frac{{2{F_1}\zeta (3\tau - \zeta )}}{{3{R_m}\zeta }} - {\tau ^2}\right){\rm{ + }}{A_2}\tau {\rm{ + }}{B_2}{\text{，}} $

(20)

式中， $ {A_2} = {\dot \eta _2}\left( {{\tau _1}} \right) - 4{{\text{π}} ^2}\left(\displaystyle\frac{{2{F_1}\zeta {\tau _1} - {F_1}{\tau _1}^2}}{{{R_m}\zeta }} - {\tau _1}\right)\;$ ， $ {B_2} = {\ddot \eta _2} $ $\left( {{\tau _1}} \right)- 4{{\text{π}} ^2}\left(\displaystyle\frac{{3{F_1}\zeta {\tau _1}^2 - {F_1}{\tau _1}^3}}{{3{R_m}\zeta }} - \displaystyle\frac{{{\tau _1}^2}}{2}\right) - {A_2}{\tau _1} $

若 $ {B_2} = {\ddot \eta _2}\left( {{\tau _1}} \right) - 4{{\text{π}}^2}\left(\displaystyle\frac{{3{F_1}\zeta {\tau _1}^2 - {F_1}{\tau _1}^3}}{{3{R_m}\zeta }} - \frac{{{\tau _1}^2}}{2}\right) - {A_2}{\tau _1}$ ，系统在第1、第2阶段及第3阶段部分区间（1/ζ≤τ≤τ₁）为弹性响应，可联立式（10）、式（12）及式（14）得到系统响应轨迹。将式（14）在 $ \tau = {\tau _1}$ 的值（即 $ {\eta _3}({\tau _1})$ 、 $ {\dot \eta _3}({\tau _1})$ ）作为初始条件代入式（15），得到区间（ $ \tau \text{≥} {\tau _1}$ ）内的塑性响应可表示为：

$ {\eta _{p3}}{\left( \tau \right)_3} = - 2{{\text{π}} ^2}{\tau ^2}{\rm{ + }}{A_3}\tau {\rm{ + }}{B_3}{\text{，}} $

(21)

式中， $ {A_3} = {\dot \eta _3}\left( {{\tau _1}} \right) - 4{{\text{π}} ^2}{\tau _1}$ ， $ {B_3} = {\ddot \eta _3}\left( {{\tau _1}} \right) - 2{{\text{π}} ^2}{\tau _1}^2 - {A_3}{\tau _1}$ 。

通过上述计算可知，若已知 $ {F_1}/{R_m}$ 和 $ {F_1}/{R_m}$ 的值，联立式（10）～式（21）即可求出等效单自由度系统在三角形爆炸载荷作用下的弹塑性响应轨迹。对于其余爆炸载荷形式，求解过程中仅需要改变式（7）–式（8）中的载荷形函数 $ f(\tau )$ ，求解方法与上述相同。

1.6 最大响应图谱

取 $ 0.1 \text{≤} \zeta \text{≤} 10$ 作为结构动态响应时间区间^[7]，若已知一对 $ \zeta $ 与 $ {R_m}/{F_1}$ ，则可由式（10）–式（21）计算得到与其对应的等效单自由度系统响应轨迹 $ \eta - \tau $ 曲线，每1条曲线对应一个最大响应 $ {\eta _{\max }}$ 及其时刻 $ {t_m}$ 。通过代入不同的 $ \zeta $ 与 $ {F_1}/{R_m}$ ，可以得到若干个延性比 $ \mu = {\eta _{\max }} = $ $ {\delta _m}/{\delta _{el}}$ 与最大响应时刻 $ {t_m}/{t_d}$ 的值。分别以 $ \mu $ ， $ {t_m}/{t_d}$ 为纵坐标， $ \zeta = {t_d}/T$ 为横坐标作图，如图6所示。

图6表示三角形爆炸载荷下等效单自由度系统的无量纲最大变形 $ \mu $ 与无量纲最大变形时刻 $ {t_m}/{t_d}$ 的响应图谱。从图中可知若已知 $ {R_m}/{F_1}$ 与 $ {t_d}/T$ 的值，可在图中得到对应无量纲最大变形 $ \mu = {\eta _{\max }} = {\delta _m}/{\delta _{el}}$ 与最大变形时刻 $ {t_m}/{t_d}$ ，此时仅需要给出系统弹性临界变形 $ {\delta _{el}}$ 与载荷作用时间 $ {t_d}$ ，就可以得到系统最大变形量 $ {\delta _m}$ 与最大变形时刻 $ {t_m}$ 。图6（a）中，当 $ {R_m}/{F_1} \text{≥} 1.5$ 时（即无量纲最大变形 $ \mu \text{≤} 1$ ），等效单自由度系统始终处于弹性响应阶段，而当 $ {R_m}/{F_1} \text{≤} 1.5$ 时（ $ \mu \text{≥} 1$ ），等效单自由度系统将发生弹塑性响应，因此可通过 $ {R_m}/{F_1}$ 的值快速判断系统是否进入塑性；从图6（b）中可以发现，最大变形时刻 $ {t_m}/{t_d}$ - $ \zeta $ 关系曲线随 $ {R_m}/{F_1}$ 的增加而增大，并在 $ {R_m}/{F_1} \text{≥} 1.2$ 后保持不变，这表明当 $ {R_m}/{F_1} \text{≥} 1.2$ 时，等效单自由度系统的无量纲最大变形时刻 $ {t_m}/{t_d}$ 相同，实际结构的最大变形时刻 $ {t_m}$ 仅与载荷作用时间 $ {t_d}$ 有关。

对于不同的单自由度系统，通过最大响应图谱便能够快速地找到其在爆炸载荷下的响应，将其运用于船舶结构抗爆设计中，可以有效提高工作效率。

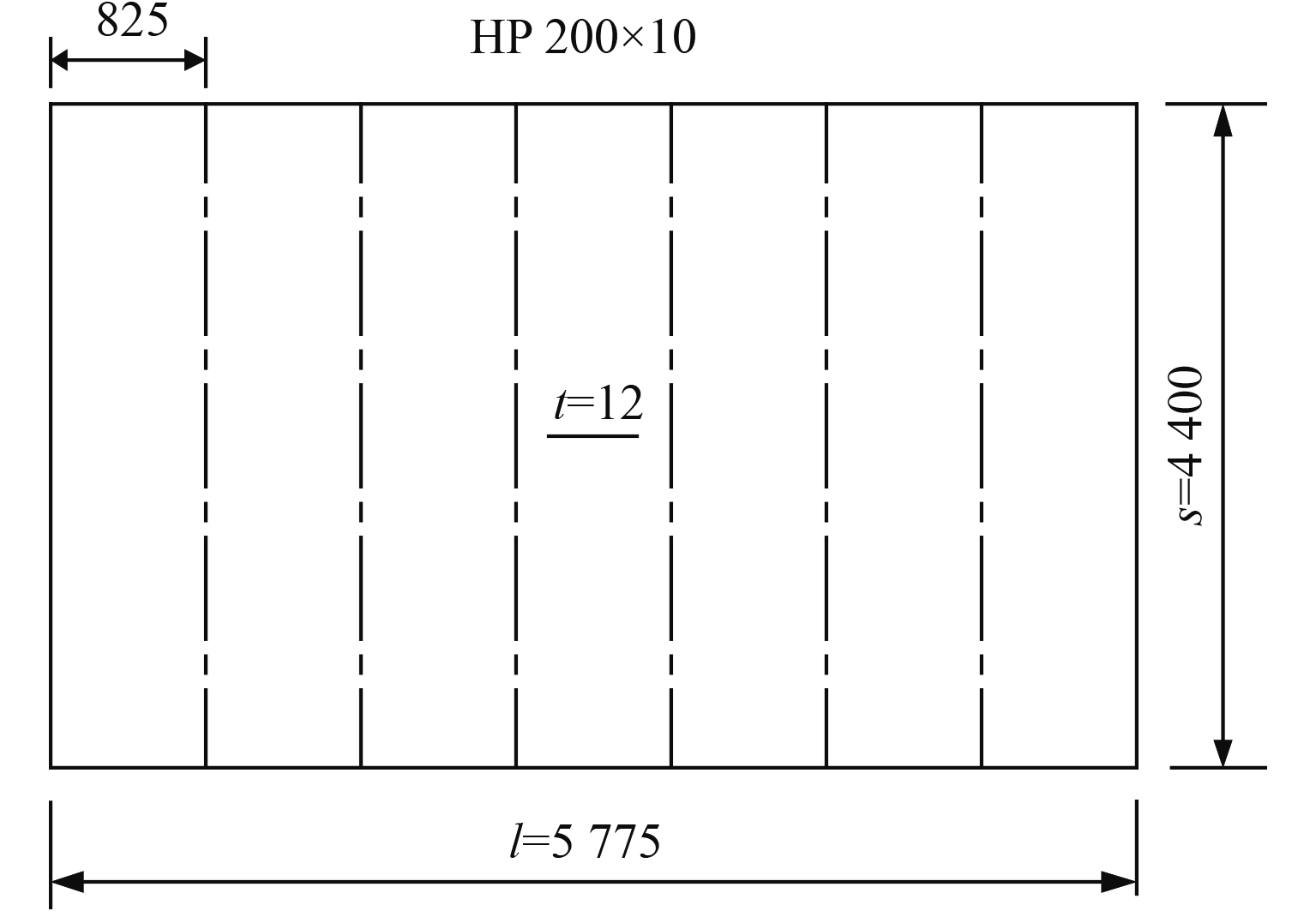
2 爆炸下平台生活楼板架结构的响应分析

以某海洋平台生活楼前端壁局部加筋板架为研究对象，利用单自由度方法分析爆炸载荷作用下结构的响应问题。结构尺寸如图7所示，板架长l=5 775 mm，宽s=4 440 mm，板厚t=12 mm，加强筋尺寸为HP200×10，加强筋间距825 mm。结构材料为普通低碳钢，弹性模量E=2.1×10⁵ MPa，屈服强度f_y=235 MPa。爆炸载荷为式5表示的简化三角形爆炸载荷，参照相关规范^[12]取超压峰值F₁=2 bar，持续时间t_d=20 ms。

2.1 加筋板的结构响应

对于理想弹塑性系统，若已知爆炸载荷形式下的等效单自由度最大响应图谱，则只需要计算出结构的抗力函数与固有周期T便能够快速得到结构的最大变形δ_m。通过等效单自由度法将图7所示的加筋板架简化为一个由单根加强筋与其有效带板组成两端刚性固定梁，分别计算其截面属性、固有振动周期及延性比，并以此分析生活楼局部加筋板架的最大响应。

1）截面属性

加强筋HP200×10的截面面积A_s=2.57×10^–3m²，质量m_s=20.14 kg/m，质心z_s=1.196×10^–1 m，加强筋的惯性矩为I=1.017×10^–5m⁴。为了避免屈曲和剪力滞后效应，需要计算加强筋的有效带板宽度。假设加强筋两端固支，其有效带板宽度系数s_e=0.86^[11]，有效带板的截面面积为： $ {A_{pe}} = 0.86lt = 8.51 \times {10^{ - 3}}{{\rm{m}}^2}$ 。因此，加强筋的抗弯截面系数可表示为：

$ W = \frac{I}{{{y_{\max }}}} = \frac{{1.017}}{{0.1811}} = 4.93 \times {10^{ - 5}}{{\rm{m}}^4}{\text{，}} $

式中：y_max为加强筋截面内点至中性轴的最大距离。

2）固有振动周期

由式3可知加筋板的固有振动周期 $ T = 2{\text{π}} \sqrt {{\beta _{LM}}{M_r}/{K_r}} $ 。其中 $ {\beta _{LM}}$ 为载荷-质量系数，根据DNV规范^[8]取 $ {\beta _{LM}} = $ 0.66。

含带板的加强筋总质量为：

$ {M_r} = ({m_s} + {m_{pe}})l = ({m_s}{\rm{ + }}0.825{s_e}\rho t)l = 382.69\;{\rm{kg}}{\text{，}} $

式中， $ {m_{pe}}$ 为有效带板质量。加筋板的弯曲刚度：

$ {K_r} = \frac{{307E{I_{pe}}}}{{{l^3}}}{\rm{ = 31}}{\rm{.2\;MN / m}}{\text{，}} $

式中， $ {I_{pe}} = 4.12 \times {10^{ - 5}}{{\rm{m}}^4}$ 为含带板的加筋板惯性矩。

因此，结构固有振动周期：

$ T = \frac{{2{\text{π}}}}{\omega } = 2{\text{π}} \sqrt {\frac{{{\beta _{LM}}{M_r}}}{{{K_r}}}} = 2{\text{π}} \sqrt {\frac{{0.66 \times 382.69}}{{31.2}}} = 17.9\;{\rm{ms}}{\text{。}} $

3）延性比

如图4所示，OBD段表示结构的抗力-位移关系。其中，结构弹性临界变形可表示为 $ {\delta _{el}} = {R_{{m}}}/{K_r}$ ， $ {R_{{m}}}$ 为加筋板结构塑性弯曲承载力，即系统的最大抗力。爆炸载荷作用下，加筋板结构塑性弯曲承载力为：

$ {R_{\rm{m}}} = \frac{{8{c_1}W{f_y}}}{l} = \frac{{8 \times 2 \times 4.93 \times {{10}^{ - 5}} \times 235}}{{4.4}} = 0.41\;{\rm{MN}}{\text{，}} $

式中， $ {c_1} = 2$ 为刚性固定约束系数，加筋板弹性临界变形：

$ {\delta _{el}} = \frac{{{R_{{m}}}}}{{{K_r}}} = \frac{{0.41}}{{31.2}} = 13.1{\rm{mm}}{\text{。}} $

根据图6所示，已知 $ {t_d}/T = 20/17.9 = 1.12$ ， $ {R_m}/{F_1} =$ $ 0.41/(0.2 \times 0.825 \times 0.86 \times 4.4) = 0.66$ ，延性比 $ \mu $ 表示为： $ \mu = {\delta _m}/{\delta _{el}} \approx $ 5.69。

4）结构的最大响应

在加筋板弹性临界变形 $ {\delta _{el}}$ 与延性比 $ \mu $ 已知的情况下，加筋板的最大变形：

$ {\delta _m} = \mu {\delta _{el}} = 5.69 \times 13.1 = 74.5\;{\rm{mm}}{\text{，}} $

达到最大变形 $ {\delta _m}$ 的时刻 $ {t_m}$ 可由图6读出 $ {t_m}/{t_d} = 1.04$ ，因此 $ {t_m} = 20.7{\rm{ms}}$ 。

2.2 数值仿真分析

利用有限元软件ABAQUS建立生活楼局部加筋板架有限元模型^[13]，如图8所示。单元类型为S4R（壳单元四边形缩减积分），网格大小50×50 mm。材料为普通低碳钢，屈服强度235 MPa。爆炸载荷为前述三角形脉冲载荷（ $ {F_1} = 2\;{\rm{bar}}$ ， $ {t_d} = 20\;{\rm{ms}}$ ），均布施加在带板上，加筋板两端刚性固定。

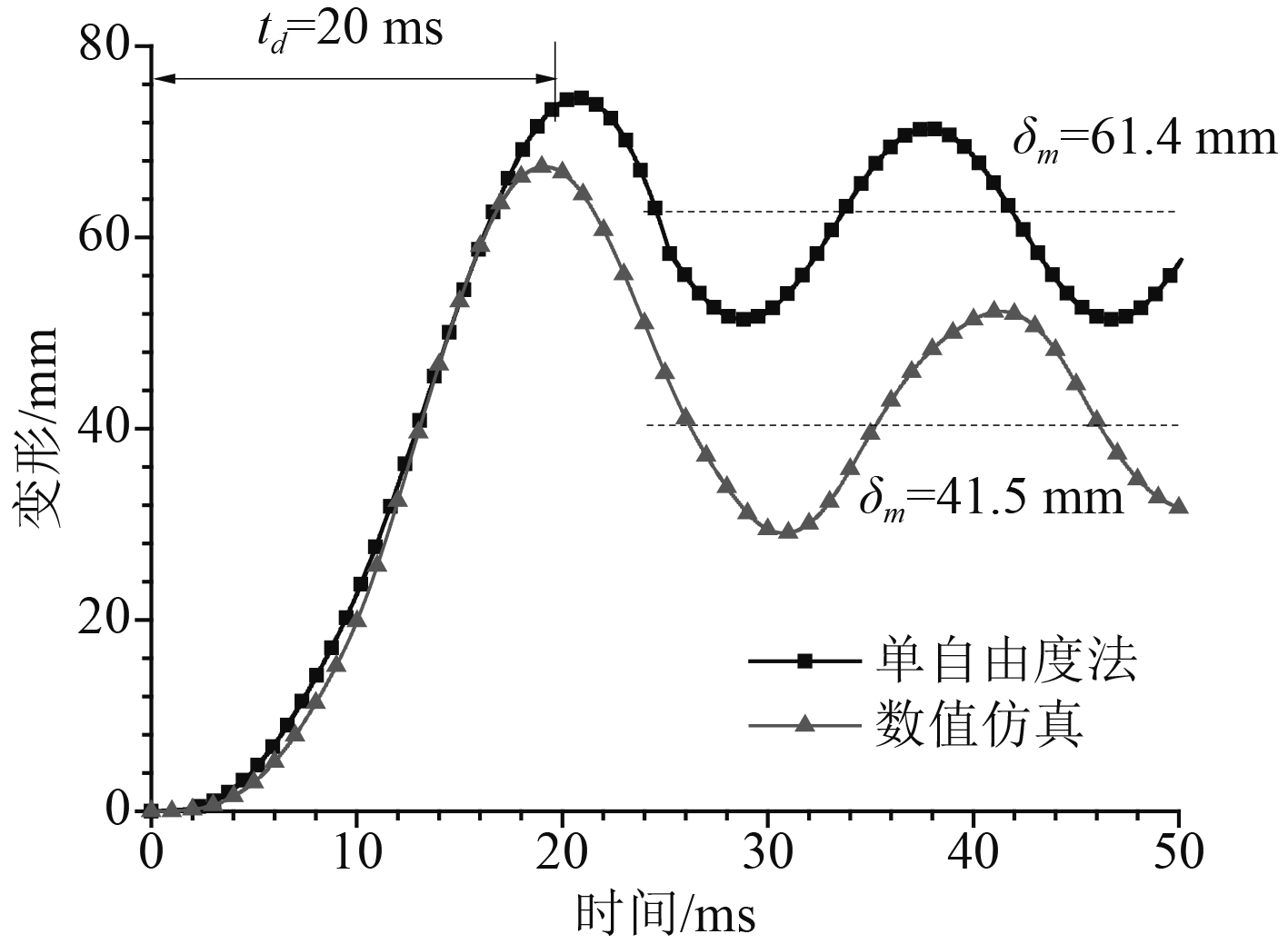
图9为单自由度分析法与数值仿真方法得到变形-时间关系曲线，可以看出2种方法得到的计算结果在载荷作用时间内的响应趋势高度一致，载荷作用结束后两者响应频率接近，但相比于数值仿真方法，单自由度法计算得到的加筋板塑性变形值略高，这是由于通过后者计算确定的结构等效刚度偏高，减少了结构的弹性变形，提高了结构塑性变形占比，使结果更为保守。为了进一步探究单自由度法在船舶板架结构抗爆分析中的适用性与可靠性，通过单自由度法与数值仿真分别对6种载荷工况下的加筋板动态响应进行计算，计算结果汇总于表1。

从上述结果中可以发现，2种方法计算得到的加筋板最大响应值及其对应时刻结果较为一致，最大变形值误差在10%内。在相同载荷工况下通过单自由度法得到的结构最大塑性变形均大于数值仿真方法，与此同时当载荷峰值较高时（2 bar），单自由度法得到的加筋板最大变形与塑性变形也均高于数值仿真结果，但随着载荷的减弱，前者计算的最大变形结果出现了个别低于数值仿真的情况，这和最大变形与延性比 $ \mu = {\delta _m}/{\delta _{el}}$ 有关，由于结构等效刚度值偏高导致从单自由度响应图谱读出的 $ \mu $ 值偏低，因此对加筋板最大变形产生了影响。对于工况LC2，尽管单自由度法计算得到的最大变形值偏低，但由于结构处于弹性范围内，且两者误差较低，因此可忽略其影响；而对于工况LC4，单自由度法得到的塑性变形大于数值仿真法，当结构弹性恢复后，仍可以认为前者的计算值较为保守，可以在用于船舶结构抗爆设计中。从加筋板出现最大响应的时刻来看，由单自由度法得到的时刻 $ {t_m}$ 普遍早于数值仿真结果，两者的误差保持在20%内，符合工程设计要求。

3 结　语

1）基于单自由度理论，根据等效单自由度系统运动方程及已知的三角形爆炸载荷函数表达式，求解了单自由度系统的响应表达式，并根据响应表达式绘制了单自由度系统最大响应图谱，形成了单自由度法分析流程。

2）利用单自由度法分析了爆炸下海洋平台生活楼局部板架结构的响应，并与数值仿真结构进行对比验证，两者结果误差较小，其中结构最大变形误差在10%内，最大响应时刻误差在20%内。

3）单自由度法考虑的结构等效刚度偏高，提高了爆炸载荷下结构变形中塑性变形的占比，使结果偏保守；在个别载荷较低的情况下会导致结构最大变形偏低，但该情况下多数处于弹性阶段或结构塑性变形仍偏保守，且误差较小，在工程设计中可以忽略其影响。

4）相对于数值仿真方法，单自由度法计算更为快捷且高效，但由于使用了大量的近似，其结果精确性不够高，适合将其运用在船舶结构抗爆初期设计，以提高设计效率。