岛礁中型浮式平台目前没有严格的定义,但大家普遍接受的观点是指那些可以以岛屿为依托,带有永久性或半永久性,具有多用途的海洋工程结构物[1]。岛礁中型浮式平台有以下独特优点[2]:1)结构简单,成本低廉,技术成熟,对周围环境的影响较小;2)不受海底地质条件约束;3)稳性好,波浪条件下结构依然保持平稳。
海洋工程领域,美国和日本对浮式结构物的研究较为领先。关西机场是日本在1973年正式提出的KIA计划[3],浮动跑道和辅助跑道是该计划的2个组成部分,为箱型结构形式。美国1992提出的海上基地“MOB——可移动式离岸基地”计划,整个结构由6个单独的半潜浮体拼接而成[4],但目前为止该计划并没有建造实物。国内最早开始涉及大型浮体研究工作的是中船重工第702研究所;2001年以来,上海交通大学开始进行水弹性方面的工作。Pinkster[5]以1艘LNG船浅水系泊系统为研究对象,发现浅水中束缚波对低频力的影响超过1阶波浪力;Y Kim[6]对锚泊线缆的张力进行研究,计算发现锚泊线的张力与平台的六自由度状态有关,同时考虑了海底对系泊缆的影响。
本文研究的平台位于南海岛礁附近,水深极浅、地势复杂。为了增加复杂受力情况下锚链和海底的摩擦力,本文为岛礁中型浮式平台设计了1套悬链线式锚泊系统,并详叙了平台的模型试验。对比分析平台在工作海况和生存海况下的数值计算和模型试验结果,并尝试分析了两者之间差异的主要原因。通过对比分析,本文验证数值计算的准确性与可行性,并对本文所涉及的锚泊方案的各项技术性能进行安全认证,为今后新平台和新锚泊方式的开发设计提供依据[7]。
1 模型试验方法及数值计算理论 1.1 相似理论模型和实际平台应该满足3个相似条件,即
1)几何相似:大小不同,形状却完全相似。
2)运动相似:模型和实体在运动时其对应点处在任意相同时刻的同类物理量,如流体速度、加速度等都有相同的比例。
3)动力相似:流体作用于模型和实体上的各种力,如重力、惯性力、粘性力和表面张力等互相成比例。
实践证明,完全相似不可能,通常都是根据具体的研究对象,选择合适的相似准则,这在相似理论中称为部分相似[8]。
1.2 模型制作与相关参数调节本次模型试验,选择的缩尺比为36。缩尺比确定后,根据几何相似的要求进行模型制作,模型试验中,对应实体和模型的参数见表1。
|
|
表 1 岛礁浮式平台主要参数 Tab.1 Main parameter of the platform |
模型制作完成以后,要分别对模型的重量、中心和惯量进行调节。此外,锚泊系统的锚链长度、重量和弹性系数也要进行相似模拟。
1.3 数值计算理论1)坐标系
随船坐标系
根据是否会产生回复力和回复力矩,可以将浮体六自由度运动分为2种。一是受到回复力和力矩作用的垂荡、横摇和纵摇,二是不会产生回复力的纵荡、横荡和首摇。
2)平台时域运动方程
在随船坐标系中, 平台时域运动方程为:
| $ \begin{split} & \left( {M + m} \right){ {\ddot x}}\left( t \right) + \int\nolimits_{ - \infty }^t \!\!\!\!{ {k\left( { {t - \tau} } \right)}} \mathop {{\rm{ }}{ x}}\limits^g \left( t \right){\rm d}\tau + C{ x}\left( t \right) = {\rm{ }}\\ &{F^{F - K}} + {\rm{ }}{F^D} + {\rm{ }}{F^w} + {\rm{ }}{F^C} + {\rm{ }}{F^{sn}}\left( t \right) + {\rm{ }}{F^m}\left( t \right)\text{。} \end{split} $ | (1) |
式中:
该部分介绍了悬链线式锚泊系统的设计以及模型试验的过程:模型重心的调节、锚泊系统的布置、风浪流的模拟、各种试验设备的调试与使用以及整个系泊系统在风浪流环境下的试验。
2.1 平台锚泊系统的设计考虑平台所在海域的地质地形特性、平台的使用特点和作业要求,平台的系泊方案采用悬链线式:8根悬链式系泊方案(工作海况)、12根悬链式系泊方案(生存海况)。
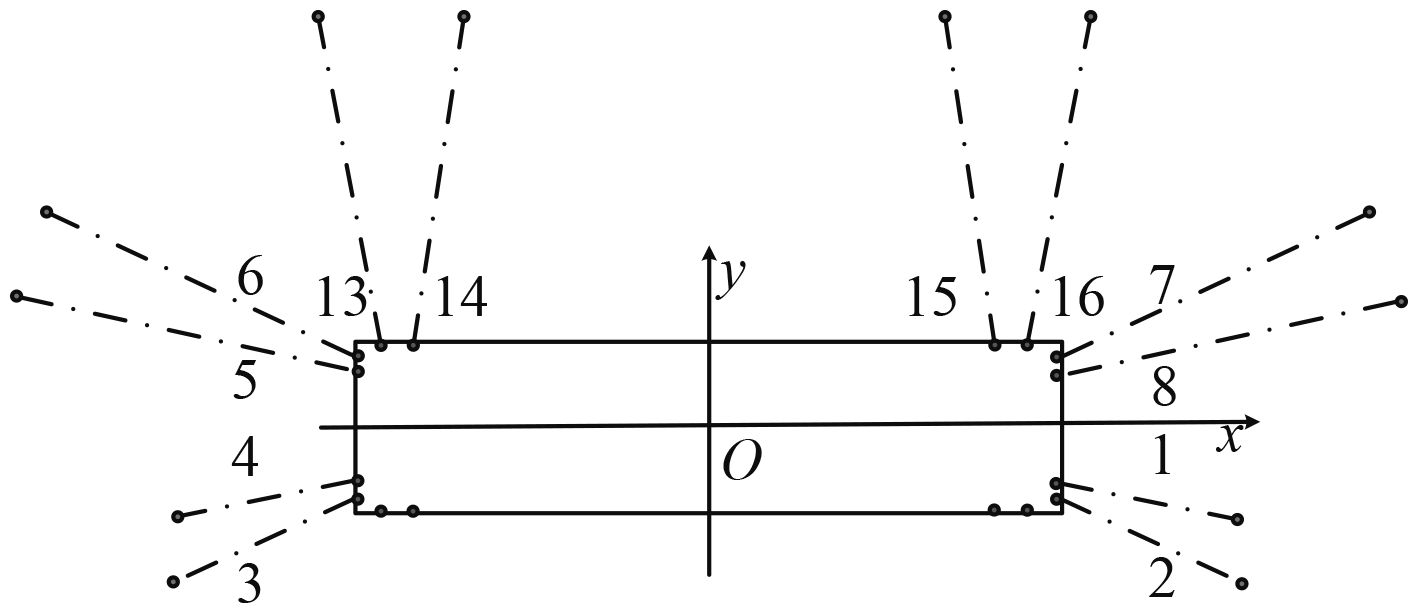
|
图 1 浮式平台12根悬链线式系泊系统示意图 Fig. 1 A schematic diagram of 12 catenary mooring systems for floating platform |
平台每根系泊缆绳都由系泊锚链加配重块组成,以期增加锚链与海底之间的摩擦力,锚链采用铸铁锚链[11]。系泊缆主要参数如表2所示。本浮式平台位于南海近岛礁极浅海域,主要试验条件为工作海况风速10 m/s,Hs=1 m,T=4.32 s;生存海况即风速36 m/s,Hs=3 m,T=7.48 s。模拟试验波浪谱使用北海联合海浪计划(JONSWAP)谱。
|
|
表 2 岛礁浮式平台系泊缆模型设计 Tab.2 Design of mooring cable for floating platform |
平台模型正式下水之前要对模型和环境做简单校对试验,依次是重量重心惯性矩调节试验、不规则海底模拟与布置、确定锚点位置安装力传感器、校波校风等,模型入水如图2所示。

|
图 2 模型入水 Fig. 2 Model into the water |
模型入水完成以后,要布置六自由度运动测量仪和锚链以及测力传感器等。之后,将平台模型置于规定的平衡位置,连接上系泊系统所有的锚泊线及拉力传感器。对每根锚泊线加上相同的预张力,使它们处于相同的张紧状态和具有同等的定位功能。布置好锚链和传感器之后,还要进行以下3个试验:系泊系统整体刚度测量、模型单自由度运动衰减试验和风浪环境下的系泊系统试验(见图3)。

|
图 3 横荡衰减试验 Fig. 3 Turbulence decay test |
1)工作海况
浮式平台水动力计算采用商业势流软件计算。由于该工况中环境力的方向是270°,平台在横荡、横摇和首摇方向的运动比较显著,而其在纵荡、纵摇和垂荡方面的运动相对不太明显。本节给出平台在横荡和横摇方向的运动时历,如图4所示。对于平台运动时历的统计结果,则给出了平台6个自由度的结果,分别包括其平均值、最大值和标准差,如表3所示。
|
|
表 3 工作海况下系泊系统平台6自由度运动统计结果 Tab.3 Operation condition 6-DOF statistical result |
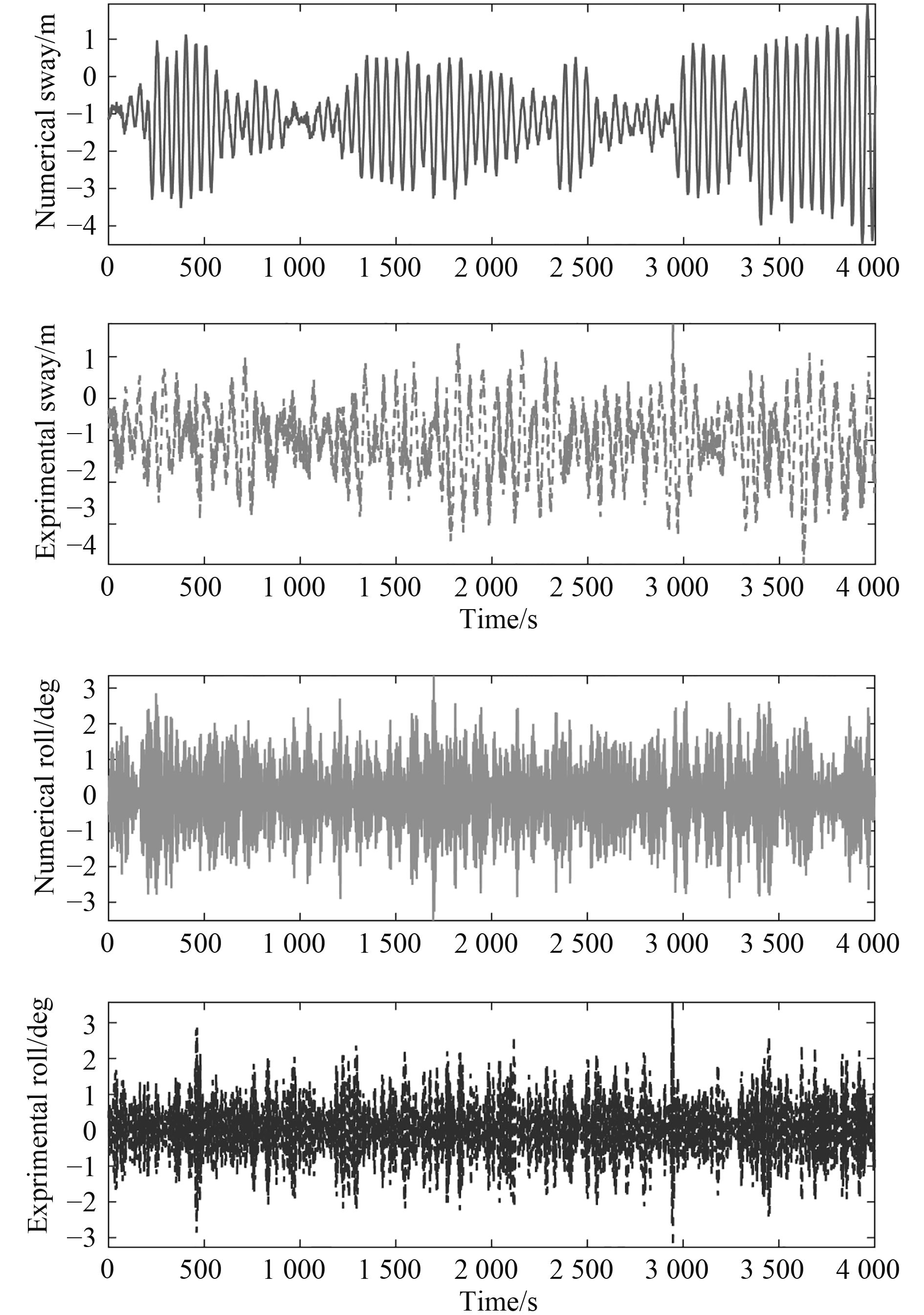
|
图 4 工作海况下平台横荡、横摇运动时历曲线对比 Fig. 4 Operation condition sway, roll time history |
由图5结果可知平台数值计算和模型试验的横荡和横摇结果,可以发现平台在数值计算和模型试验中的平均值和最大值非常接近,平均值误差在0~7.14%。两者的运动时历均显示平台在该工况下的定位非常稳定。数值计算的结果大体上反映了模型试验的结果。平台横荡运动的平均值在–1~4 m左右,横摇运动的平均值在0°左右,最大值在3°附近,其运动在可接受范围内。
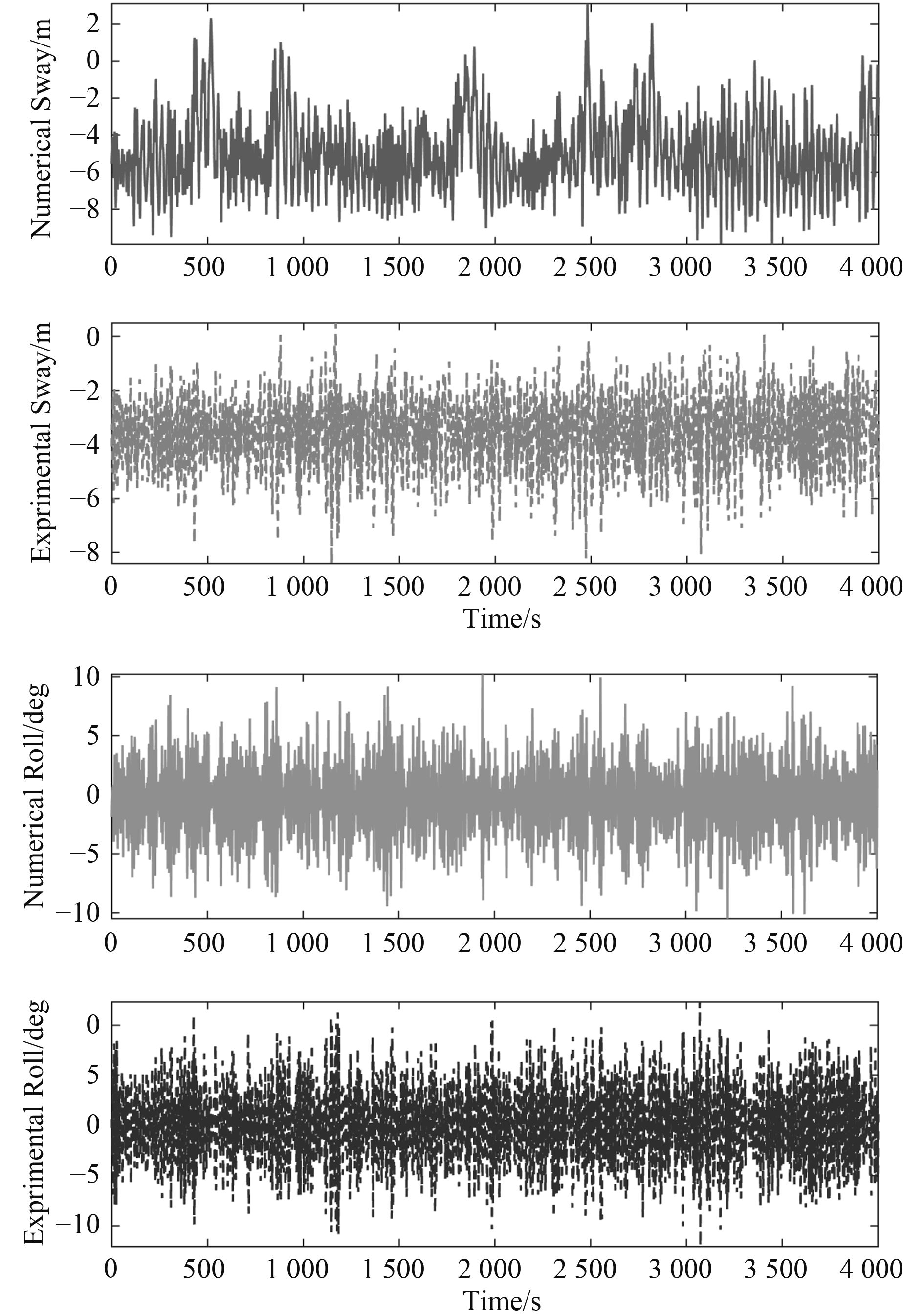
|
图 5 生存海况下平台横荡、横摇运动时历曲线对比 Fig. 5 Survival condition sway, roll time history |
通过以上数值计算和模型试验的横荡、横摇运动时历和六自由度运动统计结果的比较,数值计算结果与模型试验结果吻合较好。平台六自由度运动均在合理范围内。可以认为,在该工况下,平台可以非常好地保持定位。
2)生存海况
同样,本节仅给出了平台在横荡和横摇方向的运动时历(见图5)。对于平台运动时历的统计结果,则给出了平台6个自由度的结果,分别包括其平均值、最大值和标准差,如表4所示。
|
|
表 4 生存海况下系泊系统平台六自由度运动统计结果 Tab.4 Survival condition 6-DOF statistical result |
由图6的结果可知平台数值计算和模型试验的横荡和横摇结果,同样可以发现平台在数值计算和模型试验中的平均值和最大值比较接近,平均值误差最大在10.53%。平台横荡运动的平均值在–5~9 m左右,横摇运动的平均值在0°左右,最大值在11°附近,对于台风海况,其运动在可接受范围内。
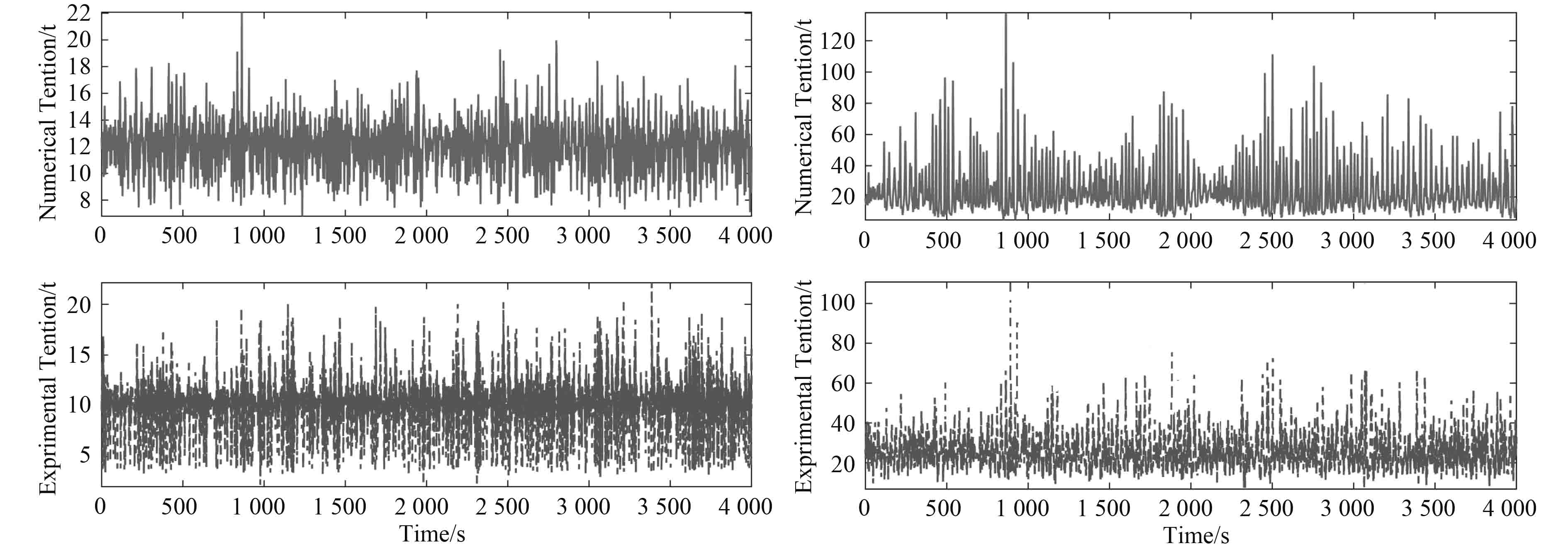
|
图 6 生存海况7号和12号的锚链张力 Fig. 6 Force of line 7 and 12 in survival condition |
通过以上数值计算和模型试验的横荡、横摇运动时历和六自由度运动统计结果的比较,数值计算结果与模型试验结果吻合较好。可以认为,在该工况下,平台可以安全地完成定位。
3.2 系泊缆张力时历分析生存海况下,系泊缆张力最大,故本节只讨论在生存海况下数值模拟和模型试验的对比。图6和表5为生存海况下锚链张力时历与统计结果。
|
|
表 5 生存海况下锚泊系统1~12号锚链张力(单位:t) Tab.5 Line 1~12 force(unit:t) |
模型试验中各系泊缆的张力的平均值均保持在10~26 t左右,在数值计算中其平均值保持在9~26 t左右,误差最大8%左右。生存海况中锚链受到的最大张力为139 t,使用准静态分析计算时,锚链最大张力的安全因子取2.0[12],安全系数为较高,不会有锚链破断的情况出现[13]。综合分析统计结果,数值计算中各系泊缆张力的结果与模型试验的结果差异较小。
3.3 锚点处锚抓力统计结果分析生存海况下,数值计算和模型试验中平台各锚点锚抓力统计结果如表6所示。
|
|
表 6 生存海况下1~12号锚抓力(单位:t) Tab.6 Line 1-12 anchor force(unit:t) |
可以发现,各点锚抓力的大小分为2组,迎风浪一侧9~12号锚点受力较大。平台各锚点锚抓力的平均值在模型试验中均保持在4~26 t,在数值计算中其平均值保持在4~24 t,且各锚点锚抓力平均值基本相同。综合分析统计结果,数值计算中各锚点锚抓力的结果与模型试验中的结果比较接近。锚链上的重块阻止了导缆孔处的拉力传递到锚点,因此不会有走锚危险[14]。
4 结 语对南海岛礁浮式平台的锚泊定位进行了锚泊系统设计和模型试验研究,并对比分析了数值计算和模型试验的结果。在工作海况下,平台在数值计算和模型试验中的平均值和最大值非常接近,平台六自由度运动均在合理范围内。可以认为,在该工况下,平台可以非常好地保持定位。生存海况下,平台可以安全地完成定位。
本文验证了数值模拟的准确性和可行性,可为平台在其他条件下数值计算的正确性提供理论依据。
锚泊定位的优化问题在极浅水中受到限制,通常做法是在锚链上配重以提高锚链与海底的摩擦力,保证平台稳定性,具有深远研究意义。
| [1] |
王志军, 舒志, 李润培, 等. 超大型海洋浮式结构物概念设计的关键技术问题[J]. 海洋工程, 2001(01): 1-6. WANG Zhijun, SHU Zhi, LI Runpei, YANG Jianmin. Key Technical Problems of Conceptual Design of Very Large Marine Floating Structures[J]. Ocean Engineering, 2001(01): 1-6. |
| [2] |
崔维成. 超大型海洋浮式结构物水弹性响应预报的研究现状和发展方向[J]. 船舶力学, 2002, 6(1): 73-90. CUI Wei-cheng. Research Status and Development Direction of Hydroelastic Response Prediction for Very Large Marine Floating Structures[J]. Journal of Ship Mechanics, 2002, 6(1): 73-90. DOI:10.3969/j.issn.1007-7294.2002.01.009 |
| [3] |
TOHMA, TOSHIAKI, SHUJI YAMAMOTO. Construction of the Kansai international airport[C]//Civil Engineering in Japan 1990, 29: 28–44.
|
| [4] |
刘璐. 超大型浮式结构物连接器的概念设计与分析[D]. 镇江: 江苏科技大学, 2013.
|
| [5] |
PINKSTER J. Wave drift forces in directional seas in shallow water[C]//In: ASME 2009 28th International Conference on Ocean, Offshore and Actic Engineering. American Society of Mechanical Engineers, 2009: 831–842.
|
| [6] |
KIM Y. A positioning mooring system design for barge ship based on PID control approach[J]. 2013, 17(5): 94–99.
|
| [7] |
史琪琪, 杨建民. 半潜式平台运动及系泊系统特性研究[J]. 海洋工程, 2010(04): 1-8. SHI Qi-qi, YANG Jian-min. Study on Characteristics of Semi-submersible Platform Motion and Mooring System[J]. Ocean Engineering, 2010(04): 1-8. |
| [8] |
徐胜. 半潜式平台运动耦合分析方法及水动力模型试验研究[D]. 镇江: 江苏科技大学, 2012.
|
| [9] |
刘珍. 波浪、水流与结构物耦合作用的时域模拟[D]. 大连: 大连理工大学, 2010.
|
| [10] |
张火明, 杨建民, 肖龙飞. 深海平台混合模型试验方法应用技术研究[J]. 中国海洋平台, 2006(01): 16-19. ZHANG Huo-ming, YANG Jian-min, XIAO Long-fei. Study on Application Technology of Hybrid Model Test Method for Deep Sea Platform[J]. China Ocean Platform, 2006(01): 16-19. DOI:10.3969/j.issn.1001-4500.2006.01.003 |
| [11] |
冯俐. 悬链式单点系泊立管设计与分析技术研究[D]. 大连: 大连理工大学, 2013.
|
| [12] |
浮式结构定位系统的设计与分析规范.
|
| [13] |
郑成荣. 深海系泊浮体的耦合分析及锚系的动力特性研究[D]. 上海: 上海交通大学, 2012.
|
| [14] |
唐尧. 船舶走锚运动方式的研究[D]. 大连: 大连海事大学, 2012.
|
 2019, Vol. 41
2019, Vol. 41
