0 引　言

变压器内部检测机器人是一款可进入变压器内部直接进行故障检测的微型球形机器人，其搭载摄像头、照明灯、深度计及姿态传感器，可在油浸式变压器内部拍摄绕组变形、绝缘材料劣化等故障情况，并实时将内部图像传输到控制端，实现变压器内部故障精准识别。该机器人外形结构设计为球形，由6路喷射泵推进，可实现四自由度运动，且具有零回转半径、运动灵活的特点^{[1 – 5]}，非常适用于变压器内部结构特殊、区域狭窄的复杂环境作业。

针对水下机器人的运动控制问题，研究者进行了大量研究并提出多种自适应控制方法，如模糊控制、滑模控制、神经网络控制以及多种控制方式结合的复合控制方法等，一定程度上解决了由于存在建模误差、水动力参数不确定性等造成的机器人控制困难问题。文献[6 – 7]分别采用神经网络小脑模型清晰度控制（CMAC）、模糊控制器对AUV的PID控制器进行了优化设计，增强了控制器的稳定性与抗干扰性；文献[8 – 11]针对非完整约束的AUV运动控制问题，分别基于解耦变换、反步控制、加幂积分、逻辑控制等方式建立了AUV的点镇定控制模型，有效实现了AUV的全局渐进稳定；文献[12]考虑了非线性系统的未知干扰因素，引入了动态干扰补偿器设计了滑模控制器，实现了AUV的运动控制；文献[13]通过采用反馈校正及Backstepping优化方式设计了AUV三维路径跟踪滑模控制器，具有良好的跟踪性能；文献[14]设计了一种模糊滑模控制器，有效提升了AUV的稳定性和鲁棒性。

尽管以上控制器具有相对较好的控制性能，但控制器的复杂化不适宜直接应用于机器人的底层控制中，复杂环境下微型水下机器人精准运动控制问题仍无最优控制方法。由于该款变压器内部检测机器人球体直径仅150 mm，任何外界扰动或控制误差都将极大影响机器人的运动控制效果，本文旨在解决微型球形机器人在未知干扰下的深度跟踪控制问题。针对球形机器人的运动特性及特殊应用环境，基于反步法设计了一种适用于球形机器人深度跟踪的控制方法，通过引入非线性干扰观测器实时补偿外界未知干扰，仿真及试验结果表明该控制系统能够快速稳定收敛，并有效抑制水平运动及外界未知干扰带来的扰动，具有很强的稳定性，能有效实现机器人保持目标深度运动。

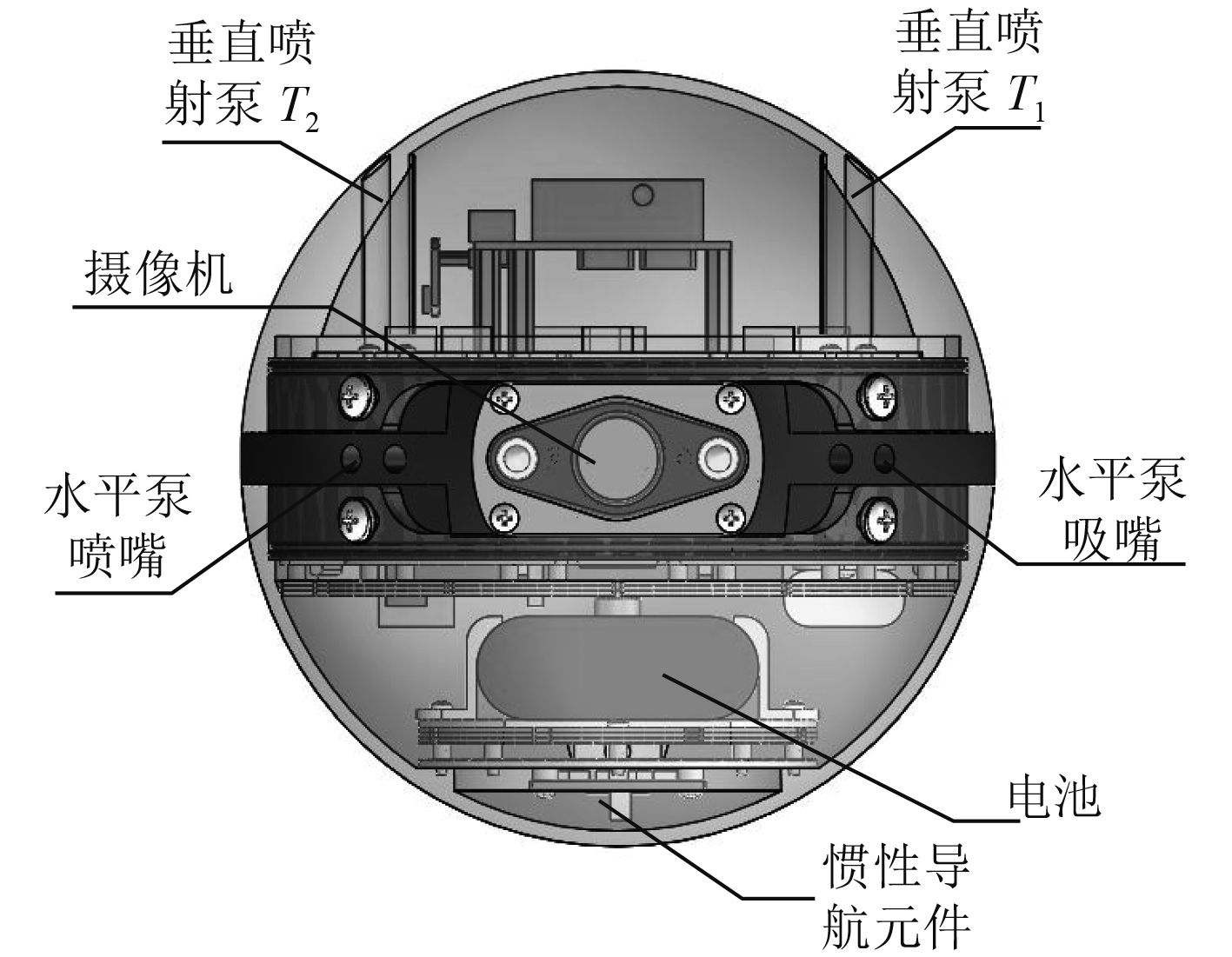
1 球形机器人模型描述

变压器油属于流动性较好的流体^[15]，机器人在油中受力情况可参考水下机器人在水中的分析。变压器内部检测球形机器人通过安装于球体中环的六路喷射泵实现姿态控制。机器人整体结构如图1所示。

机器人垂直方向主要受到推力、浮力、重力及水动力作用，为保证机器人安全，机器人需在无动力推动时悬浮于油表面，设计机器人具有微小正浮力，即浮力略大于重力，二者合力如式（1），其方向垂直向上。

$ {F_{bp}} = B - P\text{，} $

(1)

机器人在向下运动时，其垂直方向的喷射泵合力如式（2），推动机器人下潜。

$ {T_{\text{下}}} = {T_{\rm{1}}} + {T_{\rm{2}}}\text{。} $

(2)

由于喷射泵不能反向运动，只能向上喷射，因此机器人向上运动时只能依靠正浮力F_bp。机器人在垂直方向运动时属于欠驱动控制。

机器人在实际应用时，系统运动因受到外部碰撞产生干扰，将扰动项添加到系统动力学方程中，忽略式中3阶及以上的高阶项，得到机器人垂向运动的动力学模型表达式为：

$ \begin{split} &m[ - {z_g}({p^2} + {q^2}) + {x_g}(rp - {q^2}) + {y_g}(rq + {p^2})]+\\ & m[\dot w - uq + vp] = {Z_{\dot w}}\dot w{\rm{ + }}{Z_w}w + Z_q^{}q + Z_{uu}^{}{u^2} + Z_{uw}^{}uw+\\ &Z_{vu}^{}v|u| + {T_z} + (P - B)\cos \theta \cos \varphi {\rm{ + }}\Delta {f_z}\text{。} \end{split} $

(3)

式中：m为球形机器人的质量；p，q，r分别为沿x，y，z轴的角速度； $ {r_g} = {\left[ {\begin{array}{*{20}{c}}{{x_g}}&{{y_g}}&{{z_g}}\end{array}} \right]^{\rm{T}}}$ 为机器人重力中心坐标；u，v，w分别为机器人沿x，y，z轴方向的速度；Z_φ为流体阻尼系数；θ，φ分别为Eξ轴与Gx轴之间在垂直面和水平面的夹角；T_z为z轴上的推力；Δf_z为不确定干扰项。

机器人在油中的运动速度不高于0.1 m/s，由水平运动带来的油扰动不便于直接预测，与外界扰动类似，因此在进行机器人深度控制器设计时，可将由水平运动造成的油波动视为外界干扰，便于简化控制器设计，并增强系统的适应能力。球形机器人在变压器油中横倾及纵倾运动极弱，可忽略其造成的油流动扰动，则可将式（3）简化^[16]为：

$ \left( {m - {Z_{\dot w}}} \right)\dot w = {Z_w}w + {T_z} + \Delta {f_z}\text{，} $

(4)

令x₁=Z，x₂=w，则可得到欠驱动球形机器人的状态方程式为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}}\text{，}\\ {{{\dot x}_2} = A{x_2} + Bu + d}\text{。} \end{array}} \right. $

(5)

其中： $A =\displaystyle \frac{{{Z_w}}}{{\left( {m - {Z_w}} \right)}} $ ； $ B = \displaystyle\frac{1}{{\left( {m - {Z_w}} \right)}}$ ； $ d = \displaystyle\frac{{\Delta {f_z}}}{{\left( {m - {Z_{\dot w}}} \right)}}$ 。

2 控制器设计

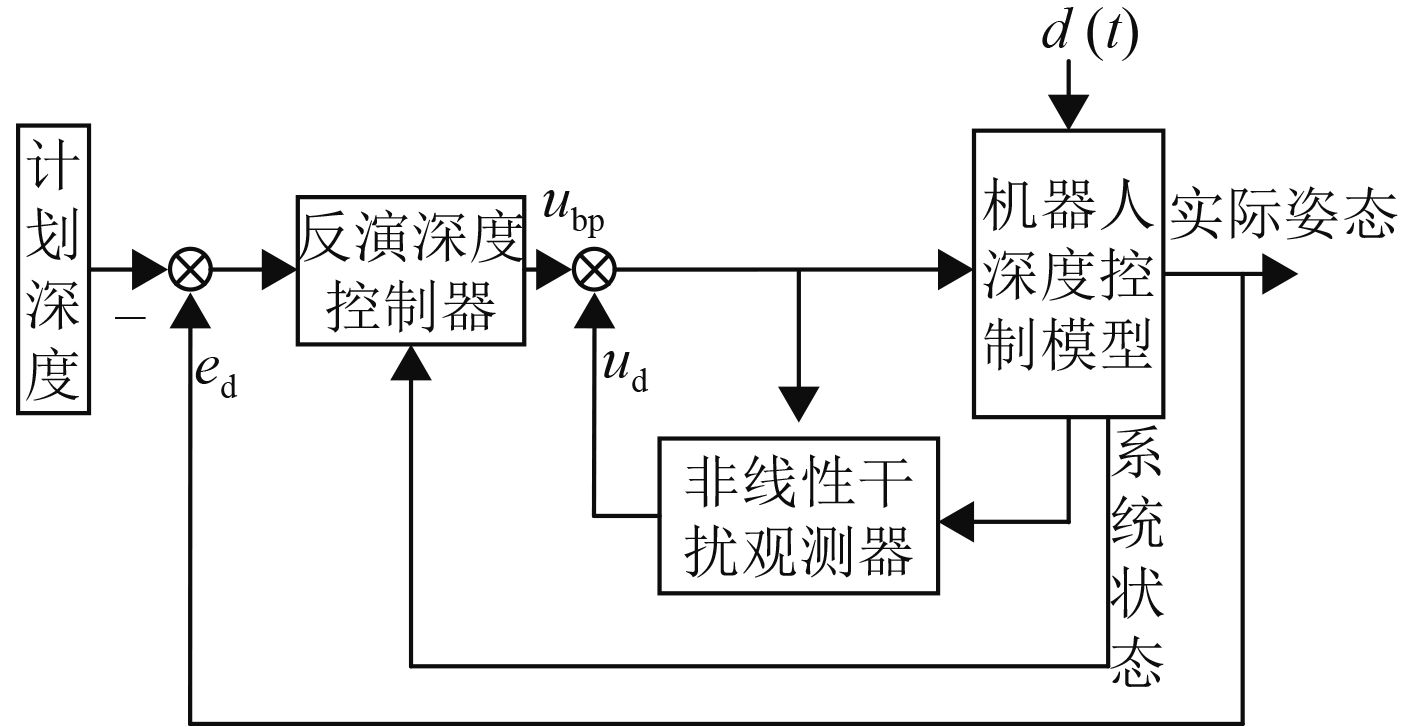
由于变压器内部空间狭窄，机器人在作业时不可避免会发生碰撞，引起机器人振荡，同时由于运动带来的变压器油扰动、控制误差等情况也会造成机器人深度控制困难。为保证球形机器人受外界干扰下能够有效实现精准深度控制，引入非线性干扰观测器对干扰进行跟踪估计，从而对输入进行补偿。机器人运动控制结构如图2所示。

2.1 非线性干扰观测器设计

根据系统状态方程式（5），定义非线性干扰观测器的状态形式：

$ \left\{ \begin{array}{l} g = \hat d - p(x)\text{，}\\ \dot g = - L(x)g + L(x)( - p(x) - Bu - A{x_2})\text{。} \end{array} \right. $

(6)

其中： $ \dot p(x) = L(x){\dot x_2}$ ； $ L(x)$ 为设计参数；选取 $ L(x) > 0$ 。

令观测误差 $\tilde d = d - \hat d $ ，由于没有干扰项d（x）的微分先验信息，为便于分析，假设相对于观测器的动态特性干扰变化时 $ \dot d = 0$ ，则观测动态误差方程为：

$ \dot{\tilde{d}}=\dot{d}-\dot{\hat{d}}=-\dot{g}-\dot{p}(x)=-L(x)\tilde{d}\text{。} $

(7)

设计非线性干扰观测器Lyapvnov函数为：

$ {V_{dis}} = \frac{1}{2}{\tilde d^2}\text{，} $

(8)

则 ${{\dot{V}}_{dis}}=\tilde{d}\dot{\tilde{d}}=-L(x){{\tilde{d}}^{2}}$ ，即该观测器全局渐进稳定。则非线性干扰观测器控制输出量为：

$ {u_d} = \frac{1}{B}\hat d\text{。} $

(9)

2.2 反步控制器设计

引入非线性干扰观测器后，系统状态方程（5）可描述为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}}\text{，}\\ {{{\dot x}_2} = A{x_2} + Bu + \hat d}\text{。} \end{array}} \right. $

(10)

设计z_d为目标深度，定义x₁为实际深度，系统跟踪误差为：

$ {e_1} = {x_1} - {z_d}\text{，} $

(11)

$ {e_2} = {x_2} - {\alpha _1}\text{。} $

(12)

定义虚拟控制量：

$ {\alpha _1} = - {k_1}{e_1} + {\dot z_d}\text{，} $

(13)

式中，k₁>0为反馈增益。

定义Lyapunov函数：

$ {V_1} = \frac{1}{2}e_1^2\text{，} $

(14)

则

$ {\dot V_1} = {e_1}{\dot e_1} = {e_1}({x_2} - {\dot z_d}) = {e_1}({e_2} + {\alpha _1} - {\dot z_d})\text{，} $

(15)

将式（13）代入式（15）可得：

$ {\dot V_1} = - {k_1}e_1^2 + {e_1}{e_2}\text{，} $

(16)

若e₂=0，则 ${\dot V_1} \text{≤} 0 $ 。进一步，定义Lyapunov函数：

$ {V_2} = {V_1} + \frac{1}{2}e_2^2\text{。} $

(17)

由于

$ {\dot e_2} = {\dot x_2} - {\dot \alpha _1} = A{x_2} + Bu + d + {k_1}{\dot e_1} - {\ddot z_d}\text{，} $

(18)

则

$ \begin{split} {{\dot V}_2} \!=\!& {{\dot V}_1} + {e_2}{{\dot e}_2} \!=\! - {k_1}e_1^2 + {e_1}{e_2} + {e_2}(A{x_2} \!+\!\\ &Bu + d + {k_1}{{\dot e}_1} - {{\ddot z}_d})\text{，} \end{split} $

(19)

设计反步控制律为：

$ {u_{bp}} = \frac{1}{B}( - A{x_2} - {e_1} - {k_1}{\dot e_1} - d + {\ddot z_d})\text{，} $

(20)

考虑非线性干扰观测器的干扰估计，则被控系统输入控制律为：

$ u = {u_{bp}} - {u_d}\text{。} $

(21)

2.3 稳定性分析

构建Lyapunov函数：

$ {V_3} = {V_2} + \frac{1}{2}{\tilde d^2}\text{，} $

(22)

对V₃求导，得

$ \begin{split} {{\dot V}_3} =& {{\dot V}_2} + {{\dot V}_{dis}} =- {k_1}e_1^2 + {e_1}{e_2} +\\ & {e_2}(A{x_2} + Bu + d + {k_1}{{\dot e}_1} - {{\ddot z}_d}) - L(x){{\tilde d}^2}\text{，} \end{split} $

(23)

将式（21）代入，得

$ {\dot V_3} = - {k_1}e_1^2 - L(x){\tilde d^2} \text{≤} 0\text{。} $

(24)

当且仅当 ${e_1} = \tilde d = 0 $ 时 $ {\dot V_3} = 0$ ，故系统全局渐进稳定。

3 仿真实验

设计的微型球形机器人质量为1.312 kg，球体直径R=150 mm，机器人实物图如图3所示。

选取非线性干扰观测器的参数为：L(x)=20，设计p(x)=20x₂；反演控制器参数k₁=8。系统初始深度为0，初始垂向速度为0。设定系统存在时变干扰：

$ d = \left\{ \begin{array}{l} 0,{\rm{ 0}} < t \text{≤} 20s\text{，}\\ 2\sin (t/20),{\rm{ 20 < t}} \text{≤} 100s\text{。} \end{array} \right. $

(25)

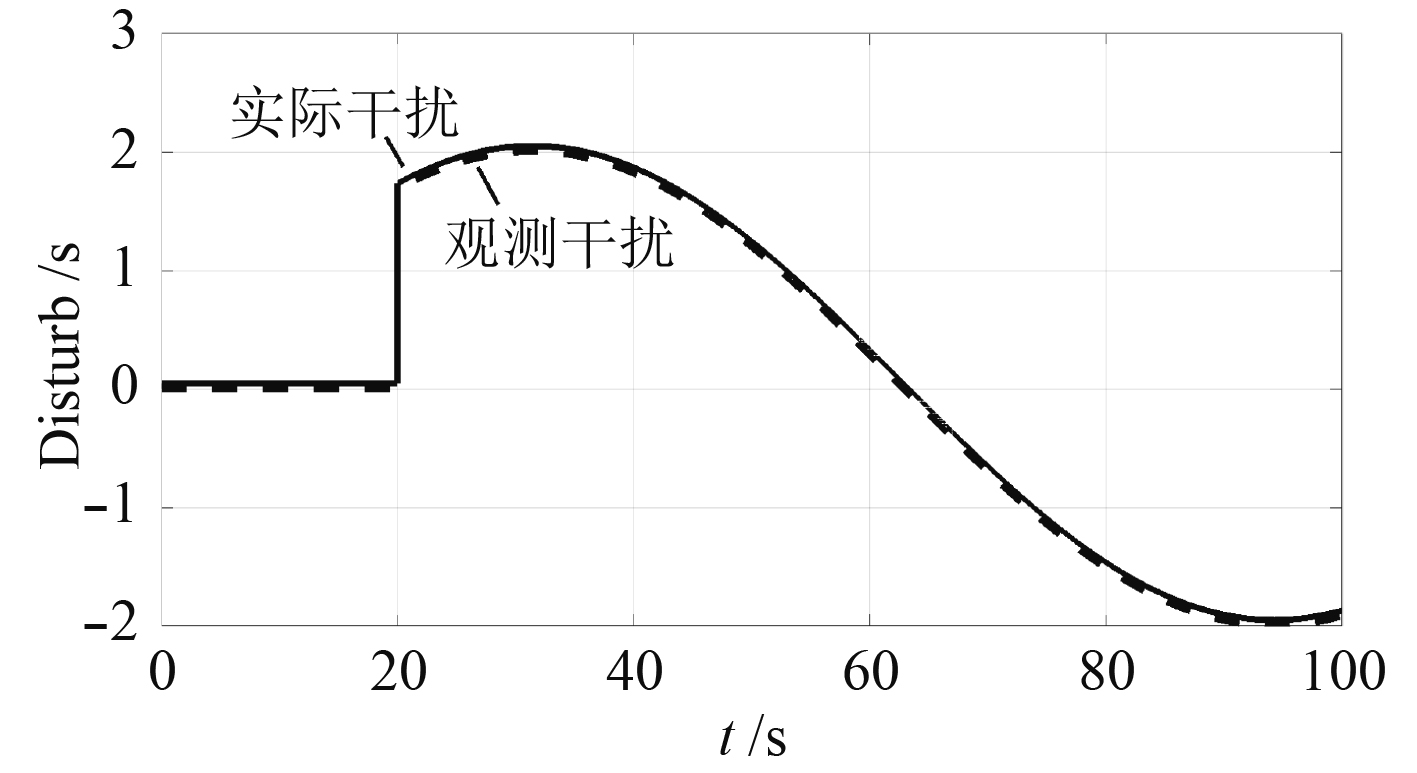
外界干扰值及干扰观测器估计值如图4所示。

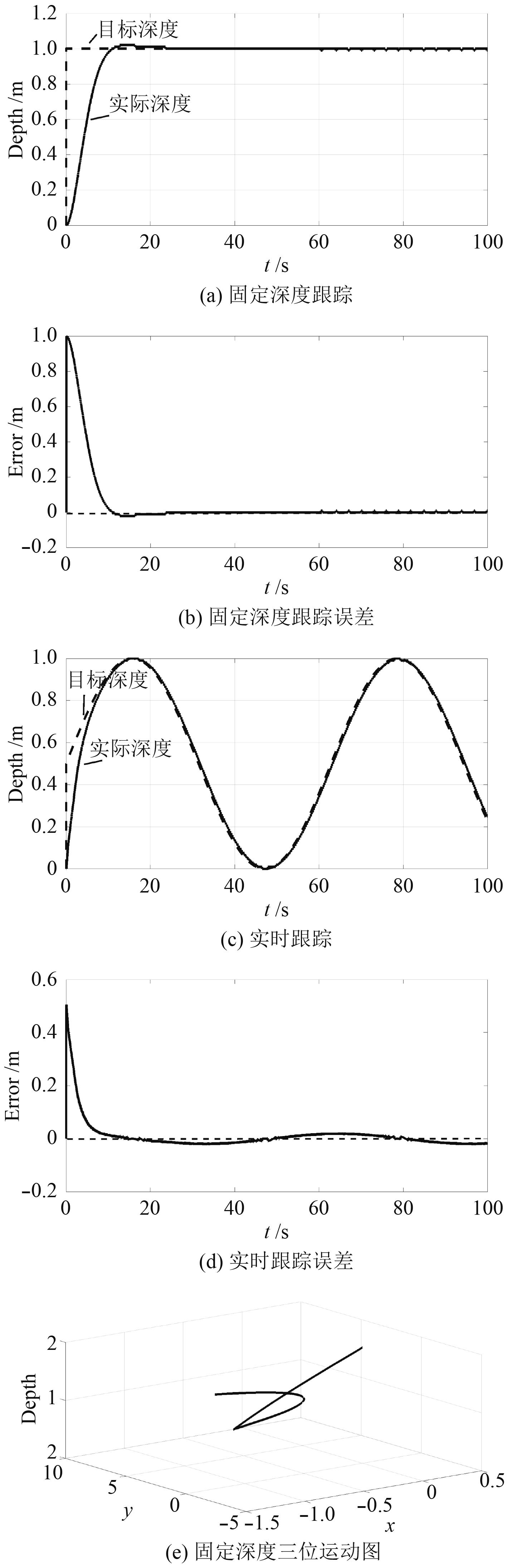
分别设定深度目标为定值1 m及实时变化曲线z_d=0.5+0.5sin（t/10），由图5可知，设计了干扰观测器的控制器受外部干扰影响较小，实现定深运动时无超调现象，调节时间较短，系统受扰动影响较小，调节误差不超过1 cm；系统在实现深度跟踪时，能及时调整输出补偿，受外界时变扰动影响较小，跟踪误差不超过2 cm，完全实现了目标深度跟踪，同时设定系统水平前进速度为0.05 m/s，前向角变化速度为1.5 °/s，系统实时运动三维图如图5（e）所示，可看出系统能有效实现定深航行运动，运动稳定平缓。

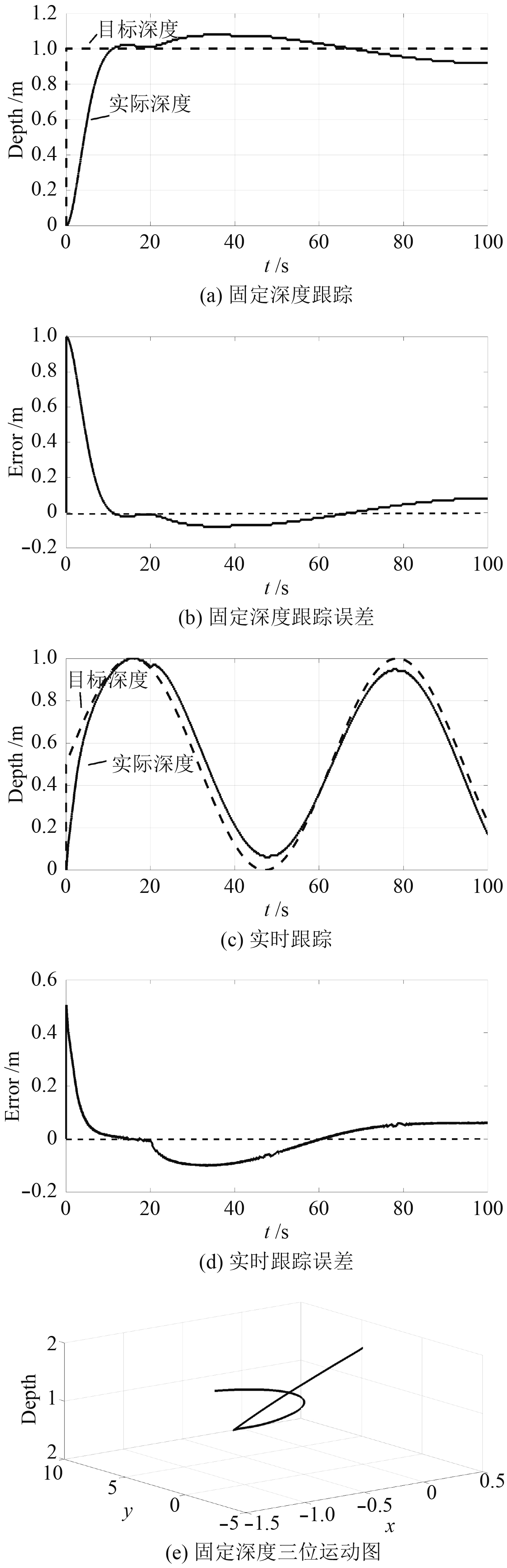
而未加干扰观测器的控制器则如图6所示，系统深度目标为定值时受突变干扰影响较大，无法有效调节回目标深度，误差最大为10 cm；系统实时变化深度目标时，控制器无法有效跟踪目标深度，系统受扰动后控制效果明显变差，跟踪误差最大超过13 cm。

综合以上仿真结果可知，当系统存在未知干扰时，所设计的干扰观测器能实时跟踪外界干扰，有效补偿外界干扰造成的扰动，降低控制器的抖动问题，控制性能明显改善。

4 结　语

本文分析了变压器内部检测微型球形机器人的运动特性，建立了机器人在油中的垂直面运动模型。针对该机器人易受自身运动及外界干扰影响情况，引入非线性干扰观测器，基于反步控制法设计了机器人的深度跟踪控制器，并做了相关仿真实验。仿真结果表明，该控制器在外界存在未知干扰情况下能有效逼近系统干扰，减小被控系统的受扰动量，并快速到达目标深度。所设计的控制器具有良好的跟踪性能，有效解决了干扰造成的控制器抖动现象，实现了机器人深度轨迹的精确跟踪，增强了系统的鲁棒性，适用于该球形机器人的作业环境。