2. 卫星海洋环境动力学国家重点实验室,浙江 杭州 310012;
3. 浙江水利水电学院 机械与汽车工程学院,浙江 杭州 310018
2. State Key Laboratory of Satellite Ocean Environment Dynamics, Hangzhou 310012, China;
3. Mechanical and Automotive Engineering College, Zhejiang Water Conservancy and Hydropower College, Hangzhou 310018, China
海洋工程领域中永久系泊系统的寿命一般长达20年之久,由于其自身所附带的特点,例如海洋环境复杂、造价昂贵、修复困难等,系泊系统设计过程中抗疲劳能力的分析是至关重要的一部分。现今,合成纤维缆广泛应用于深海领域,由于其复杂的特性,给系泊系统疲劳损伤带来了更大的挑战。目前广泛应用于海洋工程领域的疲劳分析方法为基于S-N曲线和Miner线性累积损伤准则的疲劳累积损伤法。
20世纪80年代初,结构的疲劳可靠性研究尚处于起步阶段,P. H. Wirsching[1]于1983年基于T-N曲线疲劳损伤分析方法建立了构件的疲劳可靠性计算模型。Han等[2]利用疲劳累积损伤法对一座半潜式平台锚泊系统的疲劳损伤进行计算,研究考虑了锚泊系统布置情况对疲劳损伤的影响。Omar等[3]分别利用Dirlik方法、雨流计数法、窄带谱分析法和宽带谱修正法,以某浮式采油平台系泊系统为例,对采用不同方法计算得到的疲劳疲劳损伤进行对比。乔东生[4 – 5]针对钢链-钢索-钢链和钢链-聚酯纤维缆-钢链2种形式系泊系统的疲劳展开研究,研究结果表明:2种形式的疲劳损伤都主要发生在钢链部分,聚酯纤维缆的疲劳损伤远小于钢索的疲劳损伤。曹菡等[6]借助于Harp软件,根据疲劳累积损伤法对系泊缆的疲劳寿命进行研究。研究结果表明:聚酯缆材料与锚链相比,具有更好的抗疲劳性能。王颢然[7]采用准动态方法对FPSO系泊系统进行动力分析,将低频运动响应和波频运动响应分离计算,采用疲劳累积损伤法对系泊缆不同位置的疲劳损伤进行研究,发现每根系泊缆的锚系点疲劳损伤最大。
1 基本理论对系泊缆疲劳损伤的研究采用基于T-N曲线和Miner线性累积损伤准则的疲劳累积损伤法。研究过程中假定聚酯缆破坏不受载荷历史的影响,系缆寿命可按照疲劳寿命分析法,通过对比聚酯缆的长期循环载荷和系缆的抗疲劳破坏能力得出,利用T-N曲线来确定缆绳的损伤量,利用Miner线性累积损伤准则来计算长期状况下的总损伤值。
1.1 T-N曲线系缆的疲劳性能以张力与达到破坏所需循环次数之间的关系表示,即T-N曲线。T-N曲线一般基于实验数据所得,给出了在某恒定载荷幅值作用下,聚酯系缆循环到破坏所需循环次数,反映了张力T和疲劳寿命N之间的关系。T-N曲线的形式如下所示:
| $ N{R^M} = K{\text{,}} $ | (1) |
其中:N为循环次数;R为张力范围与最小破断强度的比值。API-RP-2SM规范给出的基于数据点回归分析得到聚酯纤维缆的设计曲线中M=9.0,K=7.5。
1.2 疲劳累积理论系泊系统中每一次载荷的循环作用都会对缆绳造成一定的损伤,缆绳中产生的疲劳损伤不断的得到积累,当疲劳损伤累积到一定程度,系泊系统失效。Miner理论是现今在海洋工程中应用最为广泛的疲劳累积损伤理论。Miner[8]理论认为各个应力作用下,结构的疲劳损伤相互独立,总损伤则可以由相互独立的疲劳损伤线性叠加得到。
Miner理论假设一个循环造成的损伤为:
| $ D = \frac{1}{N}{\text{,}} $ | (2) |
其中N为对应载荷T作用下循环到破坏的次数;则等幅载荷作用下,n个循环造成的损伤为:
| $ D = \frac{n}{N}{\text{,}} $ | (3) |
常幅循环载荷下,当循环载荷的次数n等于其循环到破坏的次数N时,疲劳破坏发生,即n=N。
非等幅载荷作用下,n个循环造成的损伤为:
| $ D = \sum\nolimits_{i = 1}^n {\frac{1}{{{N_i}}}} {\text{。}} $ | (4) |
根据Miner线性累积损伤理论,缆绳在多级恒幅交变应力作用下总的疲劳损伤D,是各级应力范围水平下的损伤Dk之和,某一应力水平下的损伤度Dk等于该应力范围的实际循环次数nk与结构在该应力范围单一作用下达到破坏所需的循环次数Nk之比,即
| $ D = \sum {\frac{{{n_k}}}{{{N_k}}}} {\text{。}} $ | (5) |
由式(1)–式(5)整理得到,某短期海况作用条件下,系泊缆一年的疲劳损伤为:
| $ {D_j} = {p_j}\frac{{3.155\ 76 \times {{10}^7}}}{{{d_j}}}\sum\nolimits_k {\frac{{{n_{jk}}}}{{{N_k}}}} {\text{。}} $ | (6) |
式中:j为环境条件序号;Dj为环境条件j作用下系泊缆一年内的疲劳损伤;pj为环境条件j在长期海况中出现的概率;dj为环境条件j作用的时间;njk为环境条件j作用下第k个张力出现的循环次数;Nk为第k个张力使构件损坏所需的循环次数。
1.3 疲劳损伤计算步骤缆绳疲劳损伤的计算步骤如下:
1)将长期海况离散为多个短期平稳海况。对每个短期海况,利用波高、周期、谱形状、流速、风速等参数进行描述。并对长期海况下每个短期海况进行统计,确定短期海况发生的频率;
2)对每个短期海况下的系泊系统进行时域耦合动力分析,确定系缆时历载荷;
3)利用雨流计数法对步骤2中所得到的时历载荷进行统计,确定缆绳张力的张力范围;
4)选取合适的T-N曲线,确定M,K的值,按照上述公式计算每个短期海况下一年内张力作用下的累计损伤;
5)重复步骤2~步骤4计算所有短期海况的疲劳损伤,利用Miner线性累计损伤理论,求得长期海况下缆绳的疲劳损伤;
2 工程算例参数 2.1 半潜式平台模型选择海洋石油981深水半潜式钻井平台为原型,利用Ansys软件进行建模,其系泊系统采用绷紧式系泊系统。平台基本尺寸如表1和表2所示。
|
|
表 1 工况参数 Tab.1 Condition parameters |
|
|
表 2 半潜式模型尺寸 Tab.2 Se mi-sub mersible model di mensions |
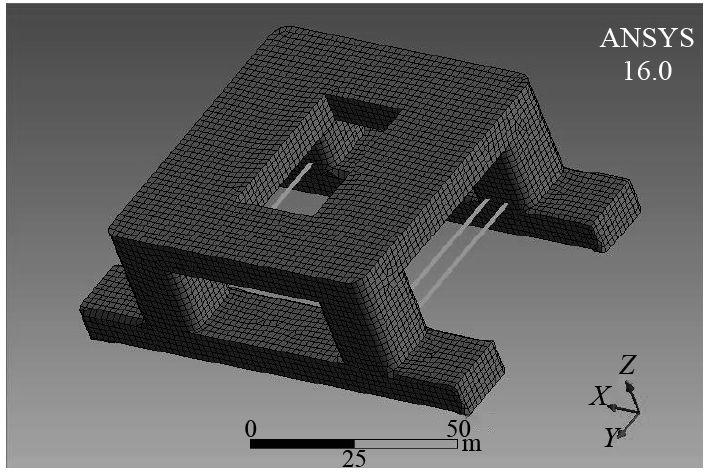
利用Ansys建立半潜式平台的水动力模型。运用面单元和杆单元为平台主体和水平撑杆进行建模,如图1所示。
|
图 1 半潜式平台水动力模型 Fig. 1 Semi-submersible platform hydrodynamic model |
半潜式平台的锚泊系统采用绷紧式系泊系统,系泊缆索数目为8根,对称分布,其中每根缆索均由3部分组成,上下两端采用钢缆,中间部分采用聚酯纤维缆。各部分材料参数如表3所示。
|
|
表 3 系泊材料参数 Tab.3 Mooring material parameters |
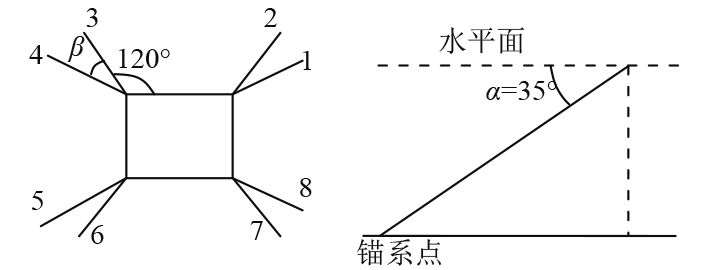
绷紧式系泊系统中初始时刻缆绳处于绷紧状态,系泊缆与水平面的夹角决定了缆绳水平与垂直方向所受到作用力的大小。缆绳与水平面的夹角为35°,即图2中α=35°,2条缆绳夹角为30°,即图2中β=30°,系泊缆布置方式如图2所示。
|
图 2 系泊缆布置方式 Fig. 2 Mooring cable arrangement |
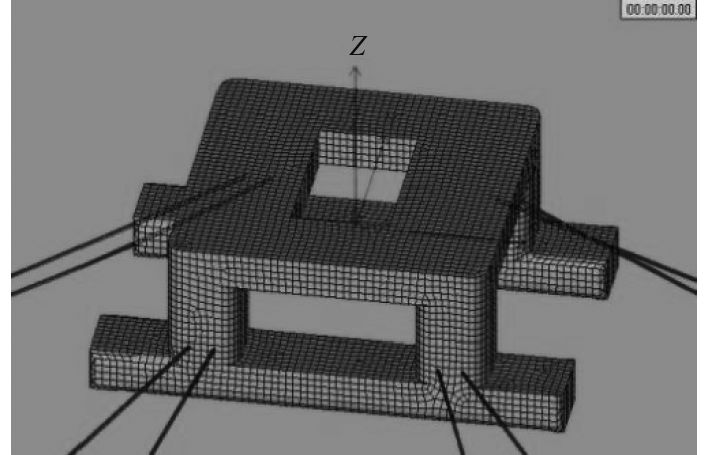
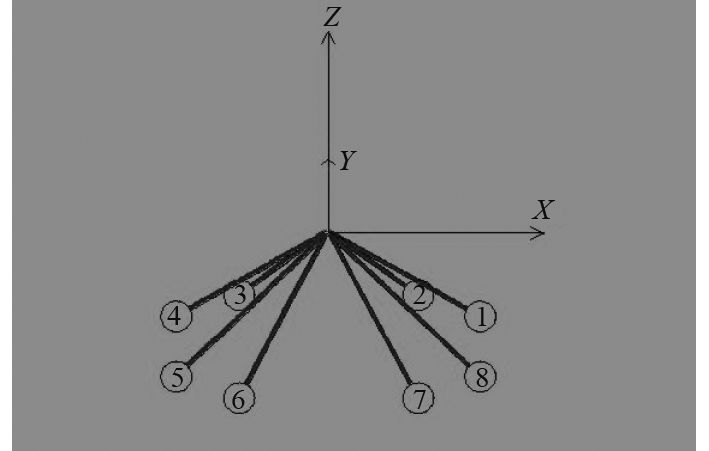
依据上述系缆参数,利用Ansys中的AQWA模块建立系泊系统模型,其中8条系缆的一端与半潜式平台模型4根立柱中的8个固定点相连接,上部连接如图3所示。8条系缆的另一端则与水深1 500 m处海底的锚系点相连接,构成完整的系泊,如图4所示。
|
图 3 缆绳-平台连接图 Fig. 3 Cable-platform connection |
|
图 4 系泊全局图 Fig. 4 Mooring overall |
由于疲劳载荷主要由波浪引起,疲劳分析中波浪的长期状态可看作由许多短期海况的序列所引起,每一海况由波浪特性的参数以及该海况出现的频率来描述,波浪谱采用JONSWAP谱,常用的波浪参数有有义波高Hs和平均跨零周期Tz。将南海某海域长期海况离散为表4中的56个短期海况。且假设所有波、浪、流的方向均为0°,即指向x轴正方向。
|
|
表 4 短期海况特征参数 Tab.4 Short - term sea conditions |
根据1.3节中疲劳寿命的计算步骤,对缆绳的疲劳损伤进行计算。
1)采用南海某海域海况,其一年内的海况离散为表4中的56个短期海况。
2)离散后的海况较多,选取海况44为例进行阐述。对44海况作用下的系泊系统与上部浮体进行时域耦合动力分析。
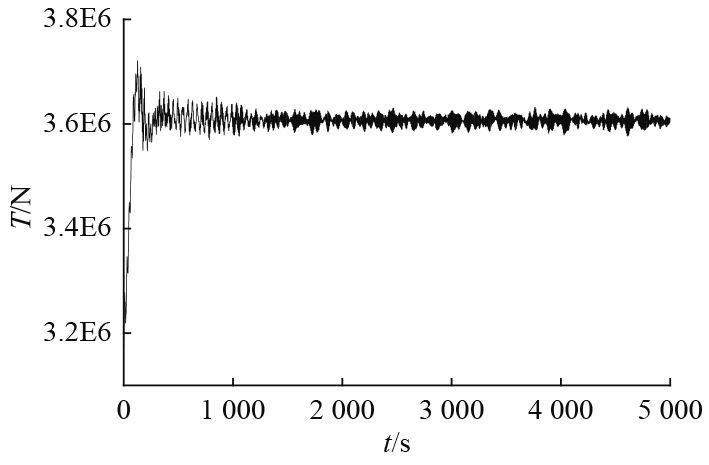
利用Ansys/AQWA,考虑风、浪、流联合作用,对平台及系泊缆绳进行耦合动力分析。在AQWA中设置步长为0.5 s,预张力为3 100 kN(20%的最小破断强度),时域模拟的总时长为5 000 s。选择4号缆绳作为研究对象展开分析,经过计算得到复合锚泊线中聚酯纤维缆顶端张力曲线如图5所示。
|
图 5 聚酯纤维缆顶端张力曲线 Fig. 5 Polyester fiber cable top tension curve |
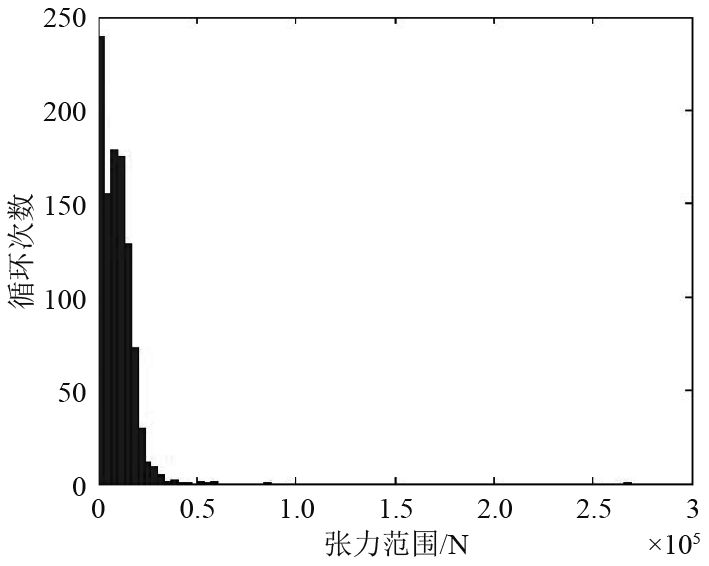
3)利用开发出的雨流计数法统计程序对图5中缆绳的张力载荷进行统计,经统计得到系缆张力范围分布结果如表5所示,分布直方图如图6所示。
|
|
表 5 张力范围统计结果 Tab.5 Tension range of statistical results |
|
图 6 张力范围及循环次数 Fig. 6 Tension range and number of cycles |
4)基于T-N曲线以及线性疲劳累积损伤理论,取M=9.0,K=7.5。经由疲劳损伤计算程序计算44海况纤维缆绳上端点的疲劳损伤,计算结果为:D44=5.91 E-09。
5)重复步骤2~步骤4,计算其余55中海况缆绳的疲劳损伤,经计算所得结果如表6所示。
|
|
表 6 各海况疲劳损伤 Tab.6 Fatigue of each sea condition |
6)计算得到缆绳的总损伤为:D=2.34 E-07。
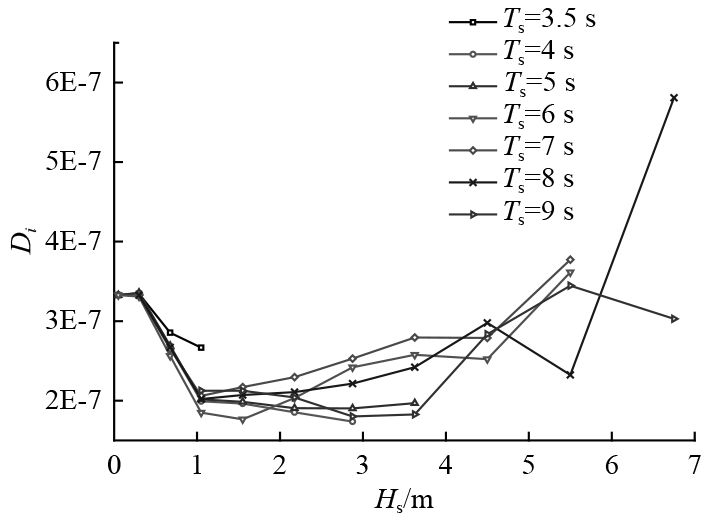
不考虑各短期海况的概率分布情况,计算56短期海况对应的不同周期、波高下纤维系缆的疲劳损伤,结果如图7所示。从图中可以观察到:曲线整体呈碗口形状,波高小于1 m时,缆绳的疲劳损伤随波高呈下降趋势;波高大于1 m时,缆绳的疲劳损伤随波高逐渐增大;Ts=3.5 s时的疲劳损伤则明显大于同幅值其他跨零周期的损伤;此曲线表明低频疲劳以及高幅值海况疲劳对系缆的损伤较大。
|
图 7 不同周期、波高缆绳的疲劳损伤 Fig. 7 Different periods, damage of wave height cable |
文中给出了缆绳疲劳寿命的详细计算步骤,借助仿真软件Ansys/Aqwa对绷紧式系泊缆绳的疲劳损伤展开研究。以“海洋石油981”为原型建立了半潜式平台模型,对1 500 m水深的绷紧式系泊系统聚酯纤维缆顶端的疲劳损伤展开研究。研究结果表明:波高小于1 m时,缆绳的疲劳损伤随波高呈下降趋势;波高大于1 m时,缆绳的疲劳损伤随波高逐渐增大;Ts=3.5 s时的疲劳损伤则明显大于同幅值其他跨零周期的损伤;表明低频疲劳以及高幅值海况疲劳对系缆的损伤较大。
| [1] |
WIRSCHING P H. Fatigue reliability for offshore structures[J]. Journal of Structural Engineering, ASCE, 1984, 110(10): 2340-2356. DOI:10.1061/(ASCE)0733-9445(1984)110:10(2340) |
| [2] |
HAN J S, KIM Y H, SON Y J, et al. A comparative study on the fatigue life of mooring systems with different composition[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(5): 452-456. |
| [3] |
OMAR V A, BRUNO E G, SUDATI S L V. Fatigue analysis and reliability of floating production systems mooring lines in deepwater[C]//Proceedings of the 17th International Conference on Ocean, Offshore and Arctic Engineering, Lisbon, Portugal. 1998.
|
| [4] |
乔东生, 欧进萍. 半潜式平台两种锚泊系统的疲劳损伤比较计算[J]. 振动与冲击, 2014(13): 1-5. QIAO Dong-sheng, OU Jin-ping. Comparative calculation on fatigue damage of two types of mooring systems for semi-submersible platform[J]. Journal of Vibration and Shock, 2014(13): 1-5. |
| [5] |
乔东生, 欧进萍. 深水悬链复合锚泊线疲劳损伤计算[J]. 船舶力学, 2012, 16(4): 422-432. QIAO Dong-sheng, OU Jin-ping. Calculation on fatigue damage of deepwater catenary hybrid mooring line[J]. Journal of Ship Mechanics, 2012, 16(4): 422-432. DOI:10.3969/j.issn.1007-7294.2012.04.012 |
| [6] |
曹菡, 强兆新, 苗文举, 等. 半潜式综合支撑平台系泊疲劳分析[J]. 中国海洋平台, 2016, 31(2): 62-67+74. CAO Han, QIANG Zhao-xin, MIAO Wen-ju, LIU Zhi-gang. Fatigue analysis for mooring lines of a semi-submerged platform[J]. China of Fshore Platform, 2016, 31(2): 62-67+74. |
| [7] |
王颢然, 魏跃峰, 潘方豪. 单点系泊FPSO系泊缆疲劳寿命研究[J]. 船舶, 2015(2): 101-105. WANG Hao-ran, WEI Yue-feng, PAN Fang-hao. On fatigue life of a single point mooring system on FPSO[J]. Ship & Boat, 2015(2): 101-105. DOI:10.3969/j.issn.1001-9855.2015.02.018 |
| [8] |
宋宪仓. 深水半潜式平台疲劳损伤评估技术研究[D]. 青岛:中国海洋大学, 2015. SONG Xian-cang. Research on technology of fatigue damage assessment for deepwater semi-submersible platform[D]. Qingdao: Ocean University of China, 2015. |
 2019, Vol. 41
2019, Vol. 41
