0 引　言

无人潜水器在水下特种作业任务中有着非常重要的作用，如海洋科考、深海搜寻与救援、石油和天然气勘探等。在复杂海况下，无人潜水器工程作业时的姿态保持和高度控制是一项艰难的任务^[1]。由于非结构化的水下环境导致的外部扰动、复杂外形无人潜水器水动力系数的不准确等问题的存在，传统的线性控制方法较难保证无人潜水器的控制性能^{[2 – 4]}。而滑动模态控制（SMC）是一种鲁棒控制方案，已广泛应用于线性和非线性系统，具有鲁棒性强、对模型误差不敏感、响应速度快等特点，因此可以利用该方法来解决参数不确定性和外部扰动不确定性带来的控制问题^{[3, 5 – 6]}。

基于不确定性、扰动补偿的自适应模糊算法的滑模控制器解决了在具有外部扰动的状态下的控制性能问题，但是其抖振现象依然存在^{[5, 7]}。滑动模态控制器工作过程中的抖振现象会导致执行机构过度磨损和能量消耗，甚至可能激发高频未建模动态，从而导致控制性能下降^[8]。在已有多种克服抖振问题的方法中，最常用的方案是利用边界层函数或一个近似的符号函数代替符号函数，来减弱在系统状态接近滑模面时执行机构的控制作用，进而减少抖振现象^{[9 – 10]}。但由于无人潜水器惯性较大，该方案的抖振减小效果是有限的。基于神经网络算法的滑模控制器能够产生连续信号从而可有取代边界层的作用，因此可以有效消除抖振现象^[11]。但是神经网络算法需要大量数据支撑，在工程实际中有一定难度。

本文提出的通过调节输出增益的变增益滑动模态控制器不仅可以抑制传统滑动模态控制器的抖振现象，同时具有良好的动态和稳态性能。通过调节控制器输出增益来实现控制力的调节，这样可以在充分利用推进器推力的同时减小抖振现象。在此基础上应用非线性状态观测器以实现对潜水器运动状态的高频观测，从而提升控制信号的时效性，进而实现潜水器高度的有效控制。

1 潜水器动力学建模

潜水器在一定的水深作业时，可以只考虑垂荡运动，运动方程可写为

$\left\{ {\begin{aligned} & {\dot z = w}, \\ &{\dot w = \frac{1}{{m - {Z_{\dot w}}}}\left( {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|} \right)w + \frac{1}{{m - {Z_{\dot w}}}}{T_z}} , \end{aligned}} \right.$

(1)

其中：m为质量；w为垂荡速度；z为深度；T_z为垂向推力；Z_w， ${Z_{w\left| w \right|}}$ 为阻尼系数； ${Z_{\dot w}}$ 为附加质量系数。

记水深为H，潜水器高度为h，则z = H–h，从而得到用高度描述的垂荡运动方程

$\left\{ {\begin{aligned} & {\dot h = - w}, \\ & {\dot w = \frac{1}{{m - {Z_{\dot w}}}}\left( {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|} \right)w + \frac{1}{{m - {Z_{\dot w}}}}{T_z}} {\text{。}} \end{aligned}} \right.$

(2)

2 控制器设计及稳定性分析

高度控制系统由变增益滑动模态控制器和非线性状态观测器组成，结构如图1所示。其中变增益滑动模态控制器的输入为高度偏差以及垂荡速度估计值，输出为推力信号；状态观测器输入为高度计测量值，输出为高度及垂荡速度观测值。

需要指出的是，图1中变增益滑模控制器输出的垂向推力需要转换为垂向推进器控制电压，该控制电压再输入到垂向推进器驱动器进而控制垂向推进器产生所需推力。由于推进器动态响应时间远远小于ROV本体垂荡运动的动态响应时间，因此在控制器设计中忽略了推进器的动态特性。

2.1 变增益滑模控制器设计

由于滑动模态控制具有鲁棒性强、对模型误差不敏感、响应速度快等特点，因此其在非线性系统中已经有了较多的应用，可以用来解决潜水器参数不确定性和外部扰动不确定性带来的控制问题。滑动模态控制器通过判断系统状态偏离滑模的程度进而进行切换控制，因此滑动模态控制器需要设计合理的切换函数和趋近律从而实现系统控制。

根据滑动模态控制理论，首先设计高度控制系统。

设计切换函数

$s = \dot e + \lambda e, $

(3)

其中：e = h_d–h为高度偏差；λ > 0为指数收敛速度。

采用趋近率

$\dot s = - ksat\left( s \right), k > 0, $

(4)

其中饱和函数 $ sat\left( s \right) = \left\{ {\begin{array}{*{20}{c}} 1,&{s > \Delta }, \\ {s/\Delta },&{\left| s \right| \leqslant \Delta }, \\ { - 1},&{s < - \Delta }{\text{。}} \end{array}} \right. $ 其中∆ > 0为边界层厚度。

由式（2）～式（4）可得控制律为

${T_z} = - \left( {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|} \right)w + \left( {m - {Z_{\dot w}}} \right)\left[ { - \lambda w + ksat\left( s \right)} \right]{\text{。}}$

(5)

由式（5）可知，在滑动模态控制中，当切换函数进入边界层之后，控制力T_z的改变使系统状态不断接近设计的滑模面。如果减小边界层，控制力T_z可以快速变化，但执行机构会剧烈抖振，容易造成设备磨损，影响使用寿命。如果增大边界层厚度，可以使控制力变化趋缓，进而减小抖振现象。但是随着边界层厚度的增加，垂向推进器无法得到充分利用。

针对该问题，本文在传统滑动模态控制器的基础上提出了输出变增益的方法，即在原有控制输出的基础上引入可调节的增益，表达式为

$T_z' = \sigma {T_z}, $

(6)

其中增益σ根据是否进入边界层以及深度误差是否小于设定范围进行变化，即

$\sigma = \left\{ {\begin{aligned} & {{\sigma _1}, {\rm{when}}\left| s \right| > \Delta }, \\ & {{\sigma _2}, {\rm{when}}\left| s \right| \leqslant \Delta {\rm{and}}\left| e \right| \leqslant 0.1m} {\text{。}} \end{aligned}} \right.$

(7)

2.2 变增益滑模控制器稳定性分析

由式（5）和式（6）可得

${T_z}^{'} = - \left( {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|} \right)w + \left( {m - {Z_{\dot w}}} \right)\left[ { - \lambda 'w + k'sat\left( s \right)} \right], $

(8)

其中 $\lambda ' = \left( {\sigma - 1} \right)\frac{{{Z_w} + {Z_{w\left| w \right|}}\left| w \right|}}{{m - {Z_{\dot w}}}} + \sigma \lambda $ ，k' = σk。显然λ' > 0，k' > 0。

比较式（5）和式（8）可以看出，变增益控制T_z'和T_z有相同的表达形式，不同之处在于T_z'中的λ'和k'为可变正数，所以这不会影响其稳定性。

2.3 状态观测器设计

由式（8）可见，高度控制器需要垂向运动的状态信息，即垂荡速度以及高度。

对于仅配备高度传感器的ROV而言，由于高度计更新率较低且通常存在野值，基于高度差分得到的垂荡速度存在较大失真。

为了克服此问题，引入状态观测器来对ROV垂荡运动的状态进行估计，以得到高更新率和可靠性的高度及垂荡速度反馈信息^[12]。

记状态变量 $x = \left[ {\begin{aligned}& {{x_1}} \\ & {{x_2}} \end{aligned}} \right] = \left[ {\begin{aligned}& h \\ & w \end{aligned}} \right]$ ，控制输入U（t）= T_z，且由于h可由高度计测量，式（2）可写为

$\left\{ {\begin{aligned} & {\dot x = f\left( x \right) + g\left( x \right)U\left( t \right)}, \\ & {y = h\left( x \right)} , \end{aligned}} \right.$

(9)

其中：

$f\left( x \right) = {\left[ { - {x_2}, \frac{1}{{m - {Z_{\dot w}}}}\left( {{Z_w} + {Z_{w\left| w \right|}}\left| {{x_2}} \right|} \right){x_2}} \right]^{\rm T}}, $

(10)

$g\left( x \right) = {\left[ {0, \frac{1}{{m - {Z_{\dot w}}}}} \right]^{\rm T}}, h\left( x \right) = {x_1}{\text{。}}$

(11)

应用文献[12]单输入单输出的非线性状态观测器理论，设计状态观测器为

$\left\{ {\begin{aligned} & {\dot {\hat x} \left( t \right) \!=\! f\left( {\hat x\left( t \right)} \right) \!+\! g\left( {\hat x\left( t \right)} \right)U\left( t \right) + {{\left[ {Q\left( {\hat x\left( t \right)} \right)} \right]}^{ - 1}}K\left[ {y\left( t \right) \!-\! h\left( {\hat x\left( t \right)} \right)} \right]}, \\ & {\hat x\left( 0 \right) = \bar x}, \end{aligned}} \right.$

(12)

其中：

$Q\left( x \right) = \frac{{{\rm{d}}\varPhi \left( x \right)}}{{{\rm{d}}x}}, $

(13)

且

$\varPhi \left( x \right) \!\approx\! \zeta \!=\! \left[\! {\begin{array}{*{20}{c}} {{\zeta _1}} \\ {{\zeta _2}} \end{array}} \!\right] \!=\! \left[\! {\begin{array}{*{20}{c}} {h\left( x \right)} \\ {{L_f}h\left( x \right)} \end{array}} \!\right] \!=\! \left[\! {\begin{array}{*{20}{c}} {{x_1}} \\ { - {x_2}} \end{array}} \!\right], K \!=\! \left[\! {\begin{array}{*{20}{c}} {{K_1}} \\ {{K_2}} \end{array}} \!\right], $

(14)

因此由式（13）和式（14）可得

$Q\left( x \right) = \frac{{{\rm{d}}\varPhi \left( x \right)}}{{{\rm{d}}x}} = \left[ {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & { - 1} \end{array}} \right]{\text{。}}$

(15)

根据文献[12]，待设计的有限增益向量K的参数选取需满足

$\left( {\mu - {\mu _1}} \right)\left( {\mu - {\mu _2}} \right) = \mu + {K_1}\mu + {K_2}, $

(16)

μ₁和μ₂根据Re{μ_i}<–γ，i = 1，2选取后代入式（16）可计算得到K。γ需满足

$\gamma \geqslant \left| {\frac{{{\rm{d}}a\left( {{\zeta _2}} \right)}}{{{\rm{d}}{\zeta _2}}}} \right|, $

(17)

其中 $a\left( {{\zeta _2}} \right) = \displaystyle\frac{1}{{m - {Z_{\dot w}}}}\left( {{Z_w} + {Z_{w\left| w \right|}}\left| {{\zeta _2}} \right|} \right){\zeta _2}$ 。

由于 $\displaystyle\frac{{{\rm d}a\left( {{\zeta _2}} \right)}}{{{\rm d}{\zeta _2}}} = \frac{{{Z_w} + 2{Z_{w\left| w \right|}}\left| {{\zeta _2}} \right|}}{{m - {Z_{\dot w}}}}$ ，且 ${Z_w}, {Z_{w\left| w \right|}} < 0$ ，所以取 $\gamma = - \displaystyle\frac{{{Z_w} + 2{Z_{w\left| w \right|}}{{\left| w \right|}_{\max}}}}{{m - {Z_{\dot w}}}}$ ，其中|w|_max为可能的最大垂荡速度值。

3 实验验证

为了检验高度控制系统的控制性能，以DOE HD2+2 ROV（图2）为试验平台在上海交通大学船舶海洋与建筑工程学院水下工程实验室水池进行实验。

DOE HD2+2 ROV的主要尺寸数据如表1所示。该潜水器在水下具有零浮力，配有一个最大推力为7 kg的垂向推进器。此外还配有高度传感器、惯性导航传感器等设备，用于测量ROV高度和姿态等数据。

基于计算流体力学（CFD）软件计算得到DOE ROV的水动力学系数等模型参数^[13]，如表2所示。

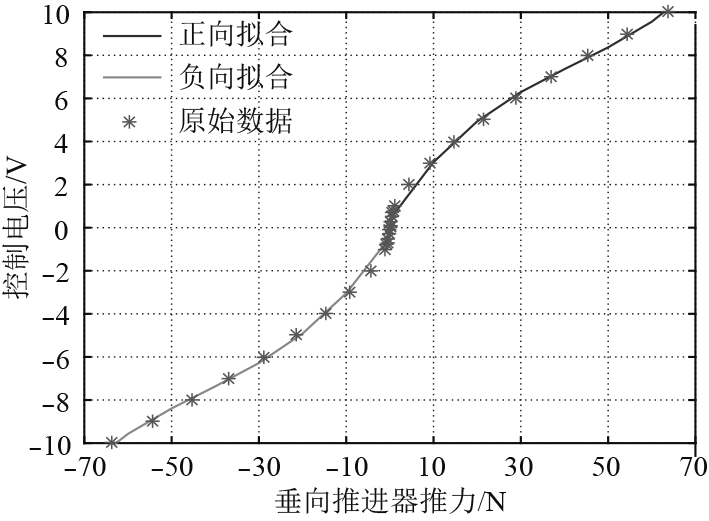
根据推进电机动力学以及机翼理论可以计算得到推进器推力与控制电压之间的非线性关系^[14]，如图3所示。

实验验证可分为状态观测器的性能验证和高度控制系统的性能验证2个部分。

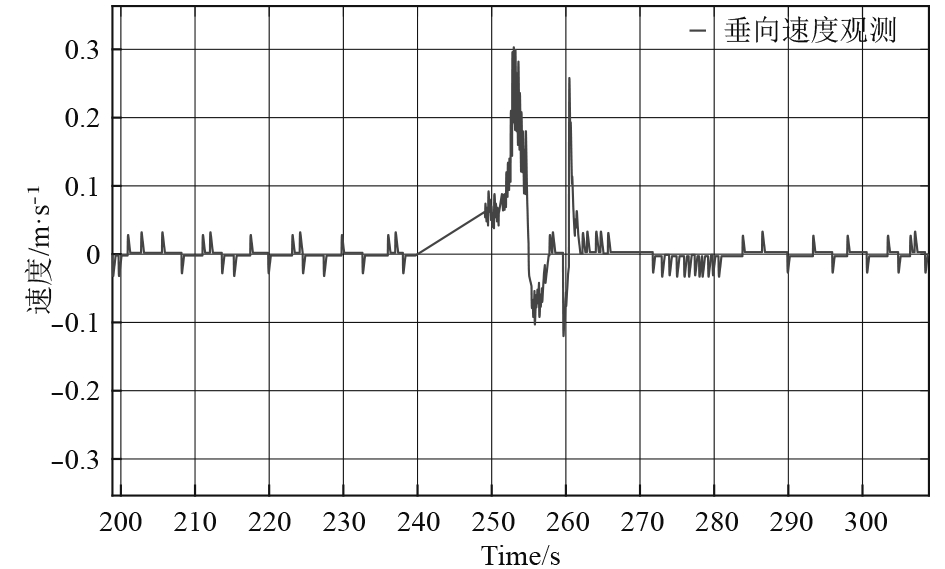
3.1 状态观测器性能实验验证

从图4可以发现在水下实验过程中，高度传感器原始数据有非常明显的缺失现象，在长达10 s的时间内没有有效数据。这是因为高度传感器在潜水器运动状态发生快速变化的时候产生了大量超出试验水池尺寸的不合理数据，因此被剔除。高度传感器不稳定性问题会对控制系统产生不利影响，因此状态观测器的反馈观测数据回路成为控制系统不可缺失的一部分。从图4和图5中可以看出，ROV的垂荡速度状态观测器有效地提供了垂荡速度信息；高度状态观测器不仅可以解决由野值导致的高度数据缺失，并提高了数据反馈频率。

3.2 变增益SMC高度控制性能实验验证

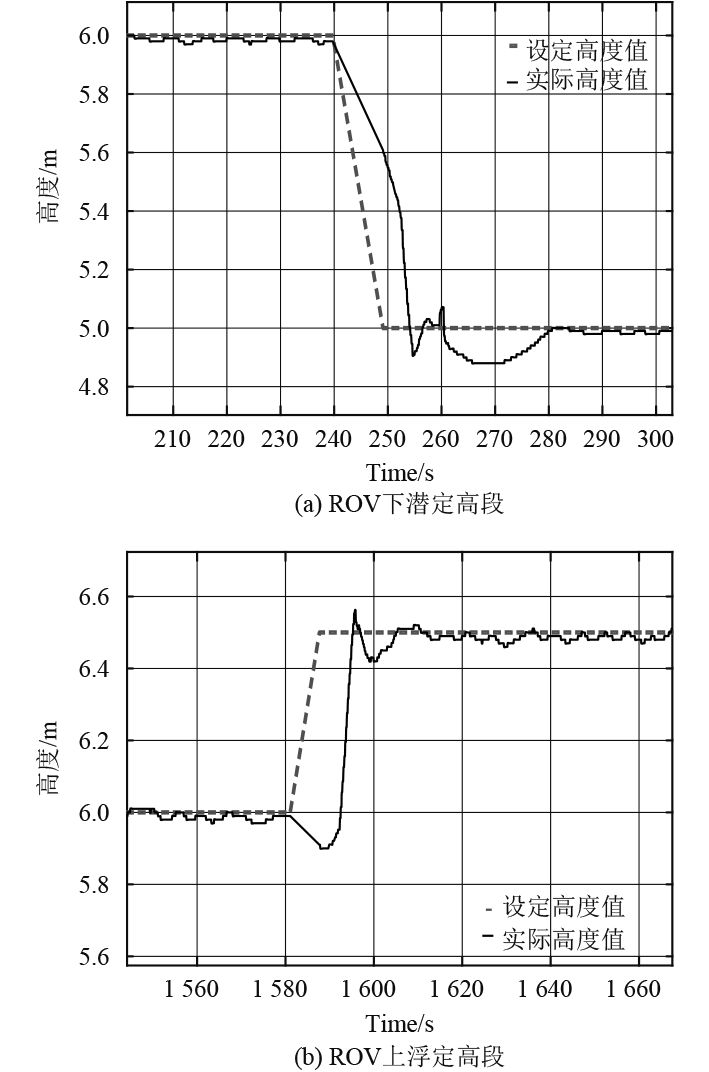
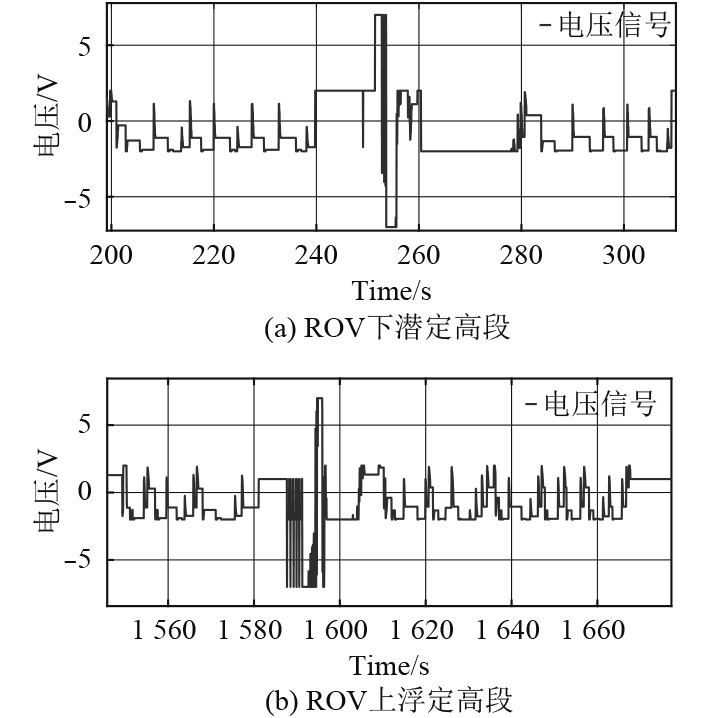
高度控制验证过程可以分为2个部分，即ROV下潜定高和ROV上浮定高。实验过程中参数σ₁取为1，参数σ₂取为0.2，w_max取为2 m/s，部分实验结果如图6所示。从图6（a）可以看出，ROV在下潜前，即处于静态控制过程时，其控制精度在1 cm内。随后将目标高度值由6 m设定为5 m，ROV进入动态调节过程约40 s后高度值达到稳态，其控制精度在1 cm左右。从图6（b）可以看出，ROV高度设定值从6 m调至6.5 m后经过30 s，其高度进入稳态，误差在2 cm左右。垂向推进器的控制电压信号输出如图7所示，可以看出控制系统没有出现严重的抖振现象，因此变增益方法改善了传统滑动模态控制器的抖振问题。

4 结　语

本文以潜水器高度控制为研究对象，基于变增益滑动模态控制方法设计了高度控制系统，实验结果表明该方法不仅有效地抑制了抖振现象，起到了降低执行机构（垂向推进器）机械损耗的作用。通过状态观测器观测潜水器运动状态，有效解决了传感器更新频率低的限制，从而加快了有效控制指令的输出，进而提升了控制效果。通过水池控制试验结果表明：1）垂向自由度的速度和高度状态观测器能够较好地观测出无人遥控潜水器的垂向速度和高度状态；2）基于变增益滑动模态控制的高度控制系统能够在实现高度的精确控制的基础上大幅减少抖振现象。