2. 中国船舶重工集团公司第七一四研究所,北京 100101;
3. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. The 714 Research Institute of CSIC, Beijing 100101, China;
3. Harbin Engineering University, Harbin 150001, China
水下航行器尾部舱段内置主机、辅机、发电机等大功率振动噪声源设备,是船舶航行的动力舱,其振动声辐射特性直接决定整船结构振动声辐射水平[1]。因此,开展水下航行器尾部结构振动声辐射特性研究具有重要的理论价值与工程意义。
Ramachandran[2]基于统计能量法开展了纵肋加强圆柱壳模态密度、辐射效率和声辐射响应等方面的研究,并与试验进行了对比分析。汤渭霖、何兵蓉[3]通过附加阻抗的形式引入环肋结构,讨论了加筋对圆柱壳振动声辐射的影响。艾海峰[4]将FEM/BEM方法应用到双层加肋圆柱壳数值计算中,发现结构刚度增大导致圆柱壳结构声辐射水平降低;吴文伟等[5]通过计算各参数对双层圆柱壳水下声辐射的影响,发现可通过增加内壳的厚度、增加实肋板的间距和优化舷间距离控制水下声辐射特性。
上述研究多聚焦于圆柱壳结构振动声辐射特性,对锥柱组合结构垂向激励力作用下的振动声辐射研究较少。为此本文以锥柱组合结构为研究对象,基于声固耦合方法,开展垂向激励力作用下结构振动声辐射特性研究,旨在为水下航行器振动声辐射控制提供参考。
1 理论基础假设结构周围流体是理想的声学介质,将其离散化,借助形函数可以获得单元内任意一点的声压和质点振速及其对时间的各阶导数,约去声压的变分得流体区域内声场的有限元方程为:
| ${{{M}}_f}{{\ddot {{P}}}} + {{{C}}_f}{{\dot {{P}}}} + {{{K}}_f}{{P}} + {\rho _f}{{{ R}}{\ddot {{U}}}} = \left[ 0 \right]\text{。}$ | (1) |
式中:
当结构置于水下时,流体介质与结构在两者交界面处相互作用,根据虚功原理可将该面力等效至单元节点上,得到结构与声场的耦合振动方程:
| ${{{M}}_s}{\ddot {{U}}} + {{{C}}_s}{\dot {{U}}} + {{{K}}_s}{{U}} = {{{F}}_s} + {{{F}}_f}\text{。}$ | (2) |
式中:
将式(1)和式(2)两式联立,得到结构与流体相互耦合的离散化方程:
| $ \begin{align} & \left( {\begin{array}{*{20}{c}} {{{{M}}_s}}&{\left[ 0 \right]}\\ {{\rho _f}{{R}}}&{{{{M}}_f}} \end{array}} \right)\left\{ \begin{array}{l} {{\ddot {{U}}}}\\ {{\ddot {{P}}}} \end{array} \right\} + \left( {\begin{array}{*{20}{c}} {{{{C}}_s}}&{\left[ 0 \right]}\\ {\left[ 0 \right]}&{{{{C}}_f}} \end{array}} \right)\left\{ \begin{array}{l} {{\dot {{U}}}}\\ {{\dot {{P}}}} \end{array} \right\}+ \\ & \left( {\begin{array}{*{20}{c}} {{{{K}}_s}}&{ - {{{R}}^{\bf{T}}}}\\ {\left[ 0 \right]}&{{{{K}}_f}} \end{array}} \right)\left\{ \begin{array}{l} {{U}}\\ {{P}} \end{array} \right\} = \left\{ \begin{array}{l} {{{F}}_s}\\ \left[ 0 \right] \end{array} \right\}\text{。} \end{align} $ | (3) |
当流场边界为全吸收即无声波反射时,可近似计算在无界流体区域内结构与流体的耦合振动和声辐射问题[6]。
2 计算模型简介锥柱组合结构基准模型示意图如图1所示。圆柱壳一侧舱壁为简支边界。L1,L2分别为圆柱壳段、圆锥壳段长度,D1,D2分别为圆柱壳段直径、圆锥壳段最小直径,d,D分别为壳体、舱壁板厚度,
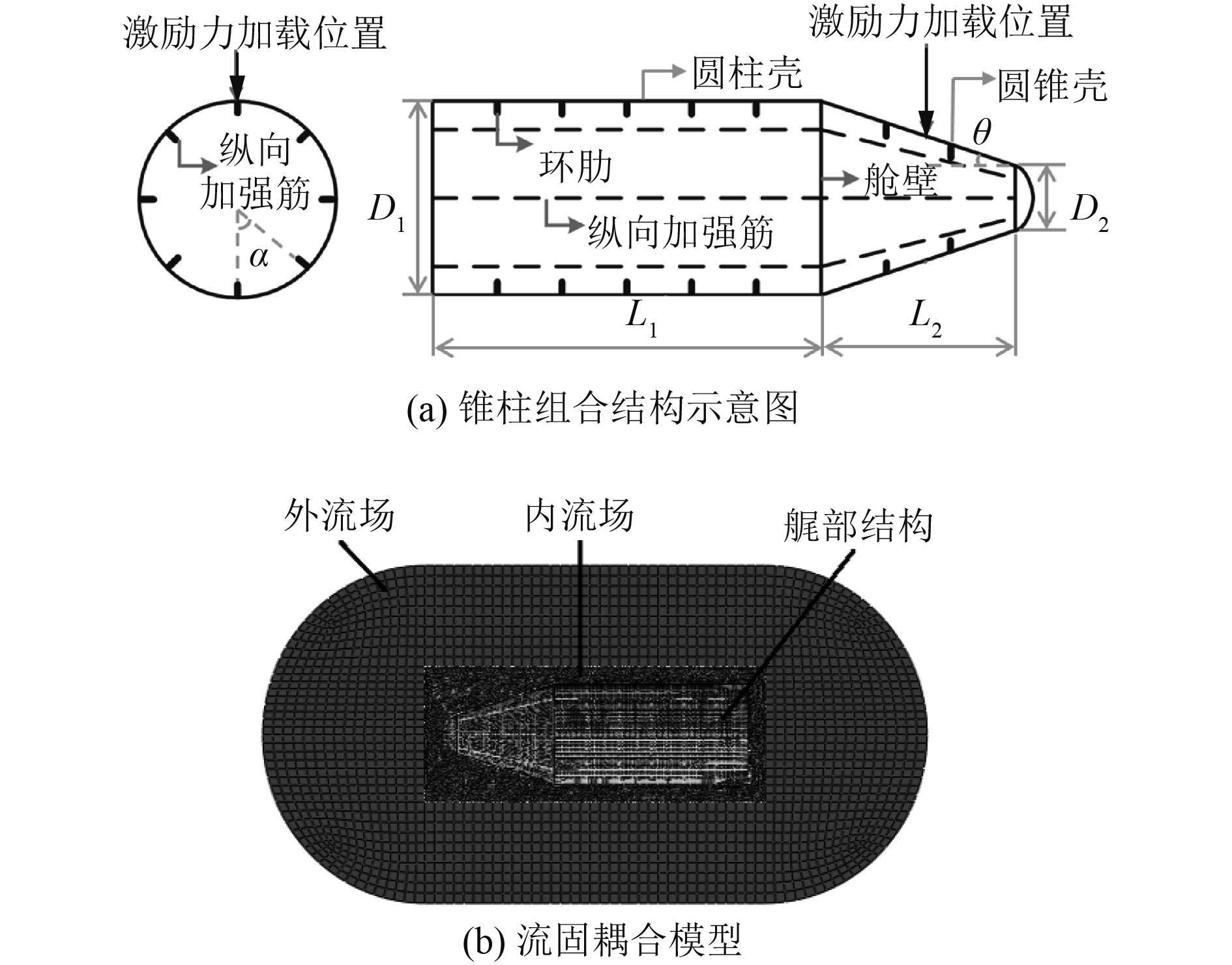
|
图 1 垂向激励力作用下锥柱组合结构基准模型 Fig. 1 A reference model of cone-column combined structure under vertical force |
在基准结构基础上,为探究增设舱壁对锥柱组合结构振动声辐射性能的影响,设置圆柱壳段增设舱壁、圆锥壳段增设舱壁、圆锥壳段与圆柱壳段均增设舱壁等3组工况作为对比(见图2)。
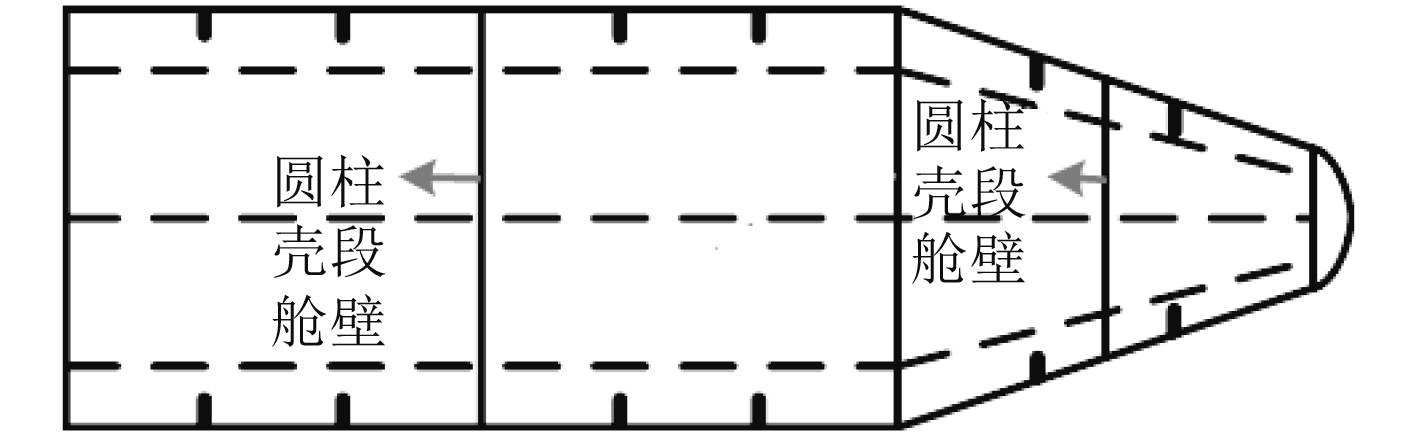
|
图 2 工况示意图 Fig. 2 The schematic diagram of working conditions |
垂向激励力作用下,不同舱壁布置形式下锥柱组合结构壳体表面均方振速和辐射声功率计算结果如图3所示。
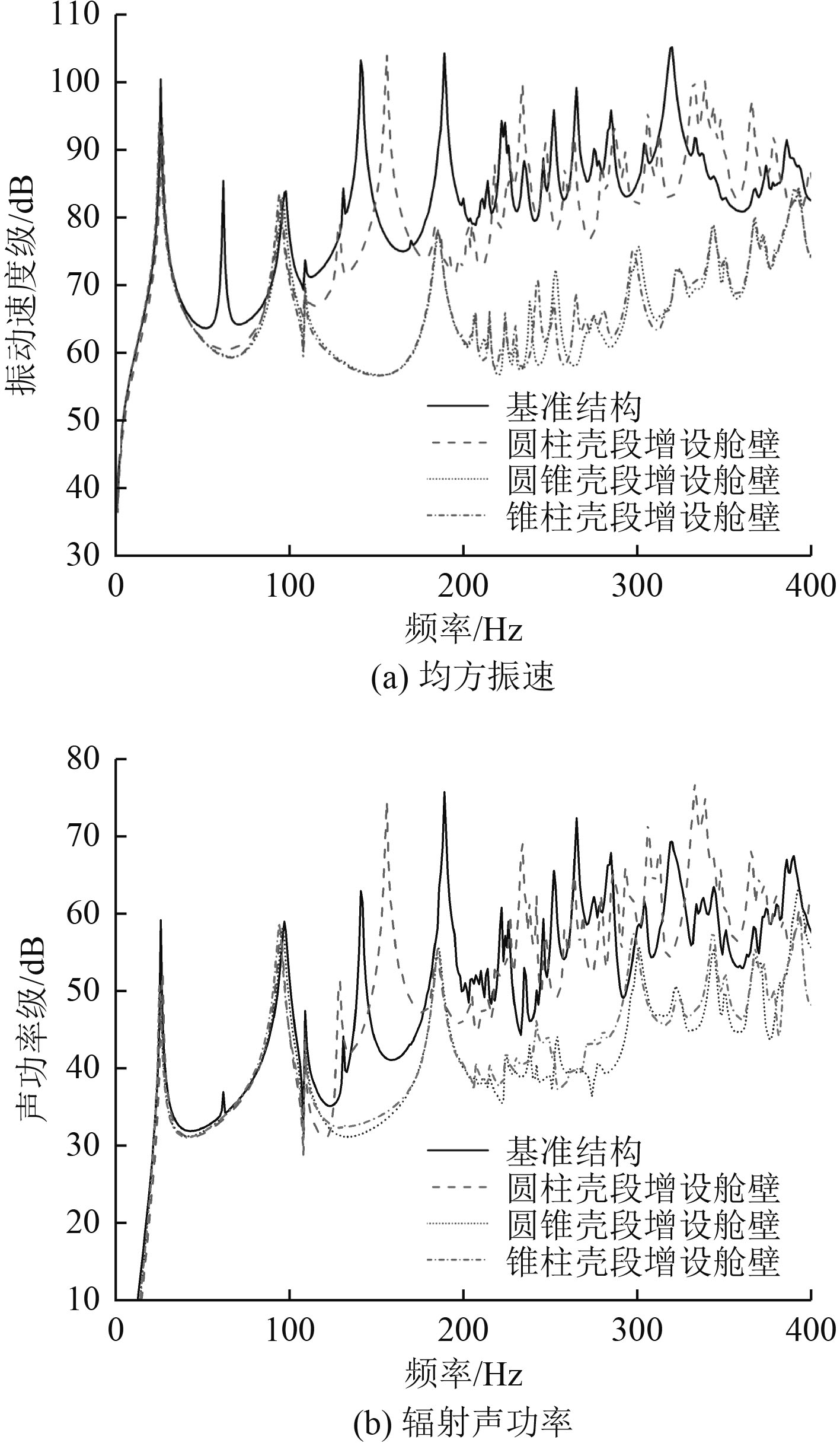
|
图 3 舱壁布置形式对振动声辐射的影响 Fig. 3 The influence of bulkhead layout on vibration and acoustic radiation |
由图3可知,圆柱壳段增设舱壁使锥柱组合结构振动噪声频谱峰值出现了微小的偏移与幅值变化,主要表现在25 Hz,100 Hz,140 Hz,190 Hz附近;圆锥壳段增设舱壁实现了锥柱组合结构振动和噪声数值的大幅下降,尤其是100 Hz以下频段,结构振动速度和声功率总级分别减少16.2 dB,10.6 dB,起到了较好的抑振降噪效果;锥柱壳段均增设舱壁与仅在圆锥壳段增设舱壁的振动噪声频谱曲线基本一致。可见,在垂向激励力作用位置增设舱壁可以有效地达到减振降噪效果,在远离激励力作用位置增设舱壁仅会对锥柱组合结构振动噪声频谱的峰值位置和幅值产生小幅影响。此外,在垂向激励力作用位置增设舱壁导致62 Hz振动峰消失,实现了对单一频点的有效控制。
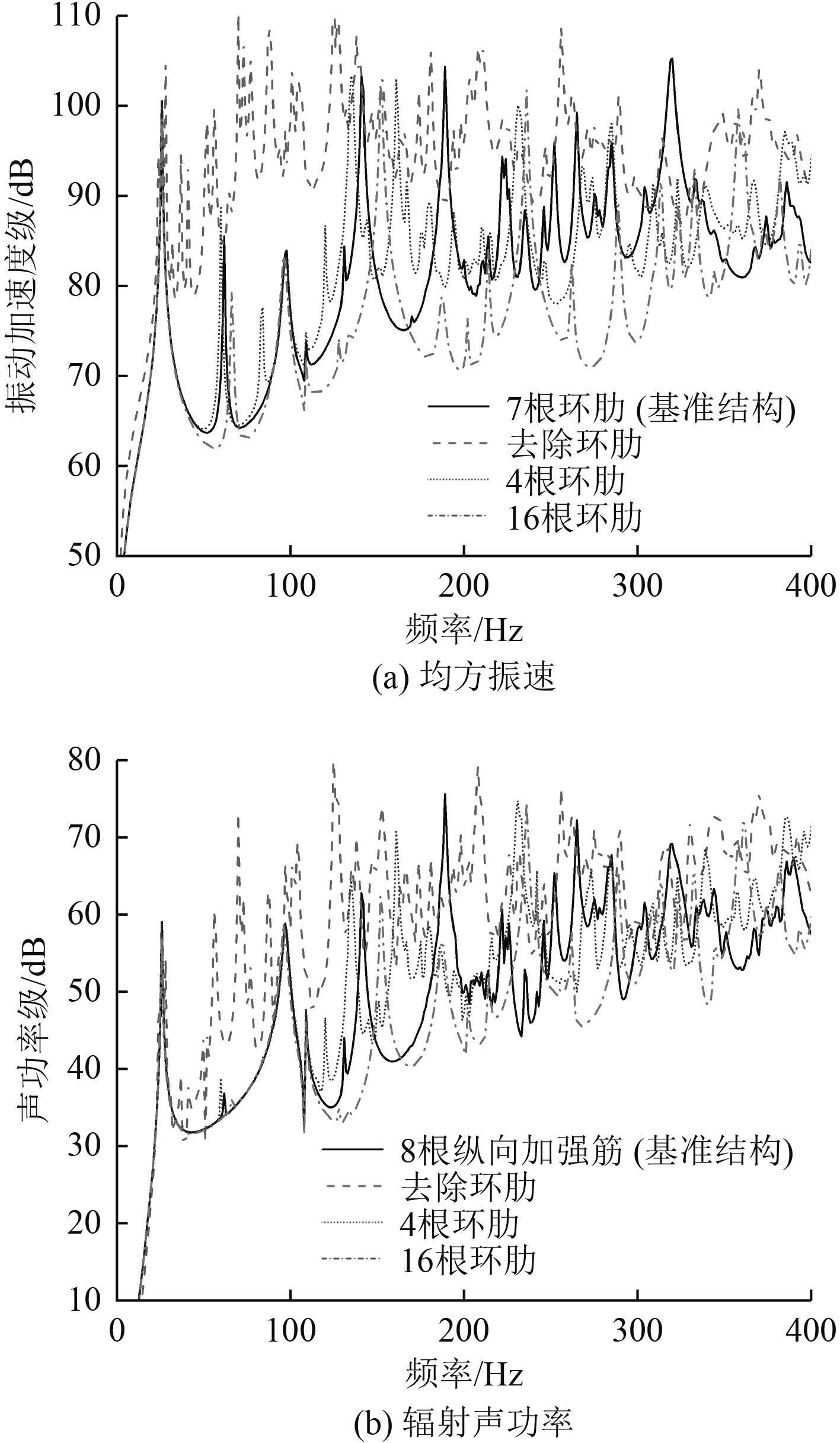
3.2 环肋数目的影响在基准结构基础上,为探究环肋数目对锥柱组合结构振动声辐射的影响,设置去除环肋、4根环肋、16根环肋等3组工况作为对比(见图4)。垂向激励力作用下,不同环肋数目下锥柱组合结构壳体表面均方振速和辐射声功率计算结果如图5所示。
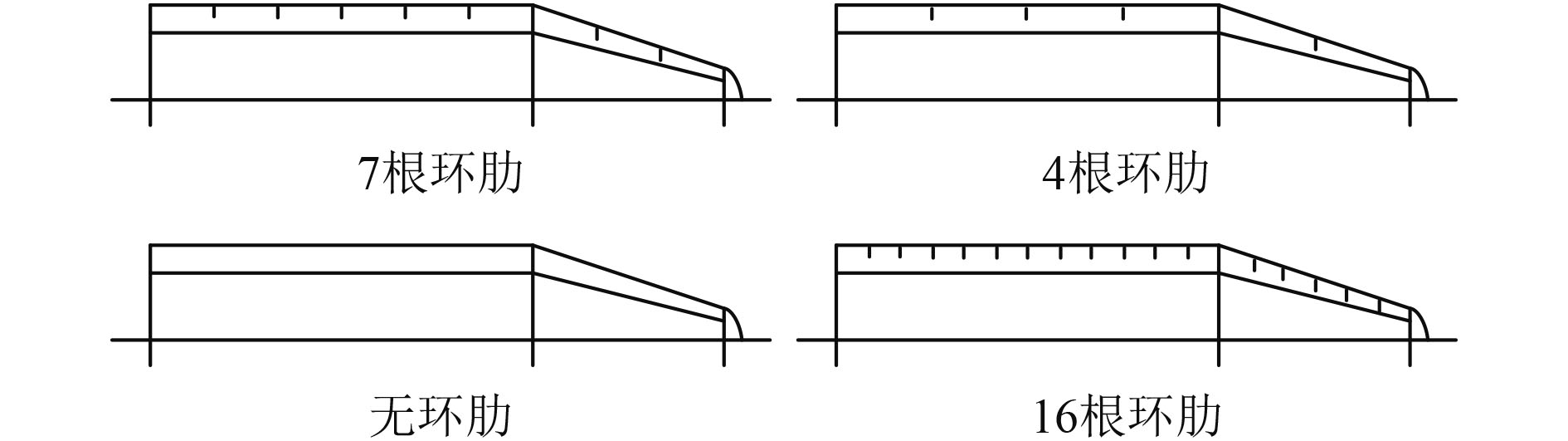
|
图 4 工况示意图 Fig. 4 The schematic diagram of working conditions |
|
图 5 环肋数目对振动声辐射的影响 Fig. 5 The influence of the number of ring ribs on vibration and acoustic radiation |
由图5可知,与基本结构相比,去除环肋导致锥柱组合结构振动噪声频谱在25~250 Hz频段更加丰富,幅值响应大幅增加;改变环肋数目,锥柱组合结构振动的峰值出现了位置偏移与幅值升降现象,体现在62 Hz,140 Hz,190 Hz,250 Hz,320 Hz等频点位置处,表现出环肋数目越多整体振动响应越小的趋势;环肋数目对锥柱组合结构声辐射的影响趋于复杂化,无明显趋势。可见,设置环肋可达到锥柱组合结构整体减振降噪效果,控制振动噪声频谱的丰富度、大幅降低振动噪声绝对数值;环肋数目增加在一定程度上降低了锥柱组合结构的振动响应,对噪声性能的影响无明显规律。
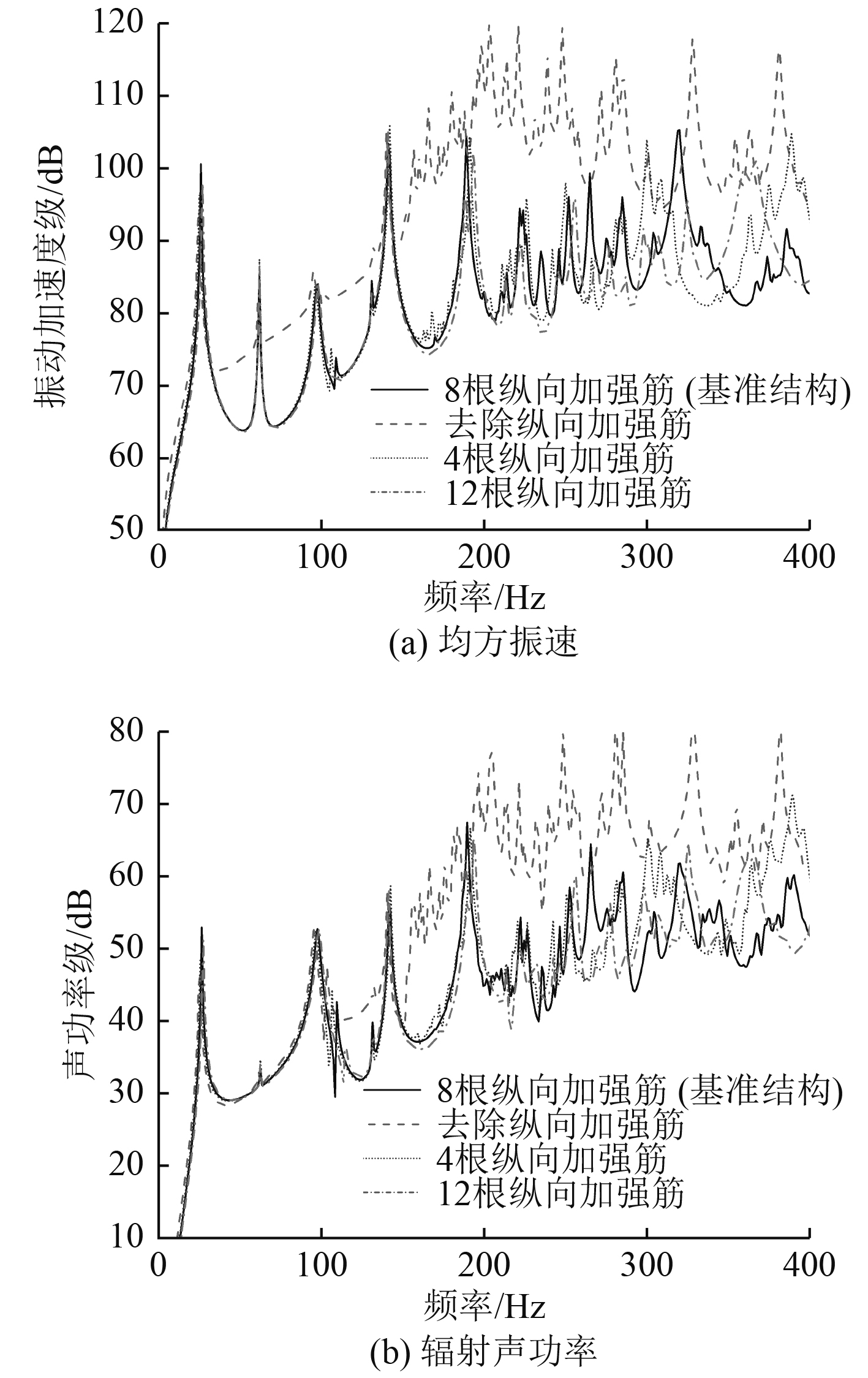
3.3 纵向加强筋数目的影响在基准结构基础上,为探究纵向加强筋数目对锥柱组合结构振动声辐射性能的影响,设置去除纵向加强筋、4根纵向加强筋、12根纵向加强筋等3组工况作为对比(见图6)。垂向激励力作用下,不同纵向加强筋数目下锥柱组合结构壳体表面均方振速和辐射声功率计算结果如图7所示。
|
图 6 工况示意图 Fig. 6 The schematic diagram of working conditions |
|
图 7 纵向加强筋数目对振动声辐射的影响 Fig. 7 The influence of the number of longitudinal stiffeners on vibration and acoustic radiation |
由图7可知,与基本结构相比,去除纵向加强筋使锥柱组合结构振动噪声频谱幅值在400 Hz频段范围大幅增加;而改变纵向加强筋数目,对锥柱组合结构振动噪声频谱影响较小。可见纵向加强筋有无对锥柱组合结构的振动声辐射特性有较大影响,但当其布置数量超过一定限值时,继续增加纵向加强筋数目对锥柱组合结构振动声辐射的影响可忽略不计,此时,继续增加锥柱组合结构纵向加强筋布置数目,不能有效降低结构振动声辐射水平。
4 结 语本文基于声固耦合方法,计及流体负载的影响,开展了垂向激励力作用下舱壁、环肋和纵向加强筋等结构形式变化对锥柱组合结构整体振动声辐射的影响研究,得出如下主要结论:
1)在激励位置附近布置横舱壁可明显改善锥柱组合结构振动声辐射水平,但随舱壁布置位置逐渐远离激励位置,锥柱组合结构振动声辐射频谱曲线出现明显的峰值偏移和幅值变化。
2)去除环肋导致锥柱组合结构振动噪声频谱更加丰富,且幅值响应大幅增加;环肋数目增加可有效降低锥柱组合结构振动响应,但对噪声特性影响较小。
3)纵向加强筋有无对锥柱组合结构振动声辐射特性有较大影响,但当其布置数量超过一定限值时,继续增加纵向加强筋数目对锥柱组合结构振动声辐射影响较小。
| [1] |
陈志坚. 舰艇振动学[M]. 北京: 国防工业出版社, 2010.
|
| [2] |
RAMACHANDRAN P., NARAYANAN S. Evaluation of modal density, radiation efficiency and acoustic response of longitudinally stiffened cylindrical shell[J]. Journal of Sound and Vibration, 2007, 304(1-2): 154-174. DOI:10.1016/j.jsv.2007.02.020 |
| [3] |
汤渭霖, 何兵蓉. 水中有限长加肋圆柱壳体振动和声辐射近似解析解[J]. 声学学报, 2001, 26(1): 1-5. DOI:10.3321/j.issn:0371-0025.2001.01.001 |
| [4] |
艾海峰, 陈志坚, 孙谦. 降低双层加肋圆柱壳低频噪声的声学设计技术[J]. 噪声与振动控制, 2007(3): 106-109. DOI:10.3969/j.issn.1006-1355.2007.03.028 |
| [5] |
吴文伟, 吴崇健, 沈顺根. 双层加肋圆柱壳振动和声辐射研究[J]. 船舶力学, 2002, 6(1): 44-51. DOI:10.3969/j.issn.1007-7294.2002.01.006 |
| [6] |
缪旭弘, 钱德进, 贾地, 等. 基于ABAQUS的船舶水下声辐射仿真计算[J]. 航天与装备仿真, 2012, 343-347. |
 2019, Vol. 41
2019, Vol. 41
