2. 船舶振动噪声重点实验室,江苏 无锡 214082;
3. 江苏省绿色船舶技术重点实验室,江苏 无锡 214082;
4. 沪东中华造船(集团)有限公司,上海 200129
2. National Key Laboratory on Ship Vibration and Noise, Wuxi 214082, China;
3. Jiangsu Key Laboratory of Green Ship Technology, Wuxi 214082, China;
4. Hudong-Zhonghua Shipbuilding (Group) Co., Ltd., Shanghai 200129, China
液化气船(LNG船)是一种高技术高附加值船舶,属于全冷式薄膜型液化天然气船。为了解LNG船的振动特性,需要对新型首制船进行船舶结构振动测量,包括船体振动特性(如固有频率、振型等)、航行时的总振动以及局部振动等,对于一些重要的局部构件或航行中振动大的结构,还需要进行局部结构的振动特性测试。通常获取被测结构固有频率的方法是进行激振试验,如激振机激励或敲击下的振动响应测量[1 – 2]。但对于有的场合,由于种种原因激振试验难于进行。针对这种情况,本文通过船舶在航行中不同运行工况下的振动响应测试,提取到了结构的固有频率。
对于大型LNG船的重点局部区域,如上层建筑、机舱、机舱棚、泵塔等,在设计阶段需要进行局部结构的振动计算。为了验证结构的振动特性,需要在建造中或试航期间进行一些振动试验[3]。在LNG船的液化气封闭舱内部有一泵塔,它垂直于舱内,其振动特性是LNG船的一项重要测试内容。为了测试某型LNG船液化舱内部的泵塔在空气中的振动特性,在船舶建造期间,采用冲击激振的方式进行了泵塔固有频率的测试[4]。在船舶试航期间进行了船舶航行总振动的测量,主要是检验其振动是否满足船舶舒适性的要求,了解船舶在主机转速航行范围内是否存在转速禁区[5],为后续LNG船的改进设计提供可靠的依据。在航行振动试验中同时对泵塔进行了振动测量,由不同运行工况下的振动测试信号中,提取到了泵塔结构在空气中的固有频率,为一些难以开展激振试验的场合提供了一种振动特性的测试方法。
1 泵塔激振试验 1.1 测试方法分别在船的纵向和横向冲击使泵塔产生自由振动,同时采集所有测点的振动加速度信号,重复几次测量。然后对振动信号进行FFT分析,得到平均后的信号均方谱,即各测点的频率—幅值曲线图。曲线上的峰值频率为结构共振频率,即固有频率。其中一测点作为参考点,根据其他测点相对参考点的相位谱得到对应频率的振型。
1.2 激励方式及测点位置激振试验在某型LNG首制液化气船内进行,在试验开始前船上的所有设备都已安装到位,测试时船舶在厂方码头处于锚泊状态。
测试系统包括加速度计和数据采集分析仪,其中数据采集分析仪采用国内东华测试公司的DH5920分析仪。
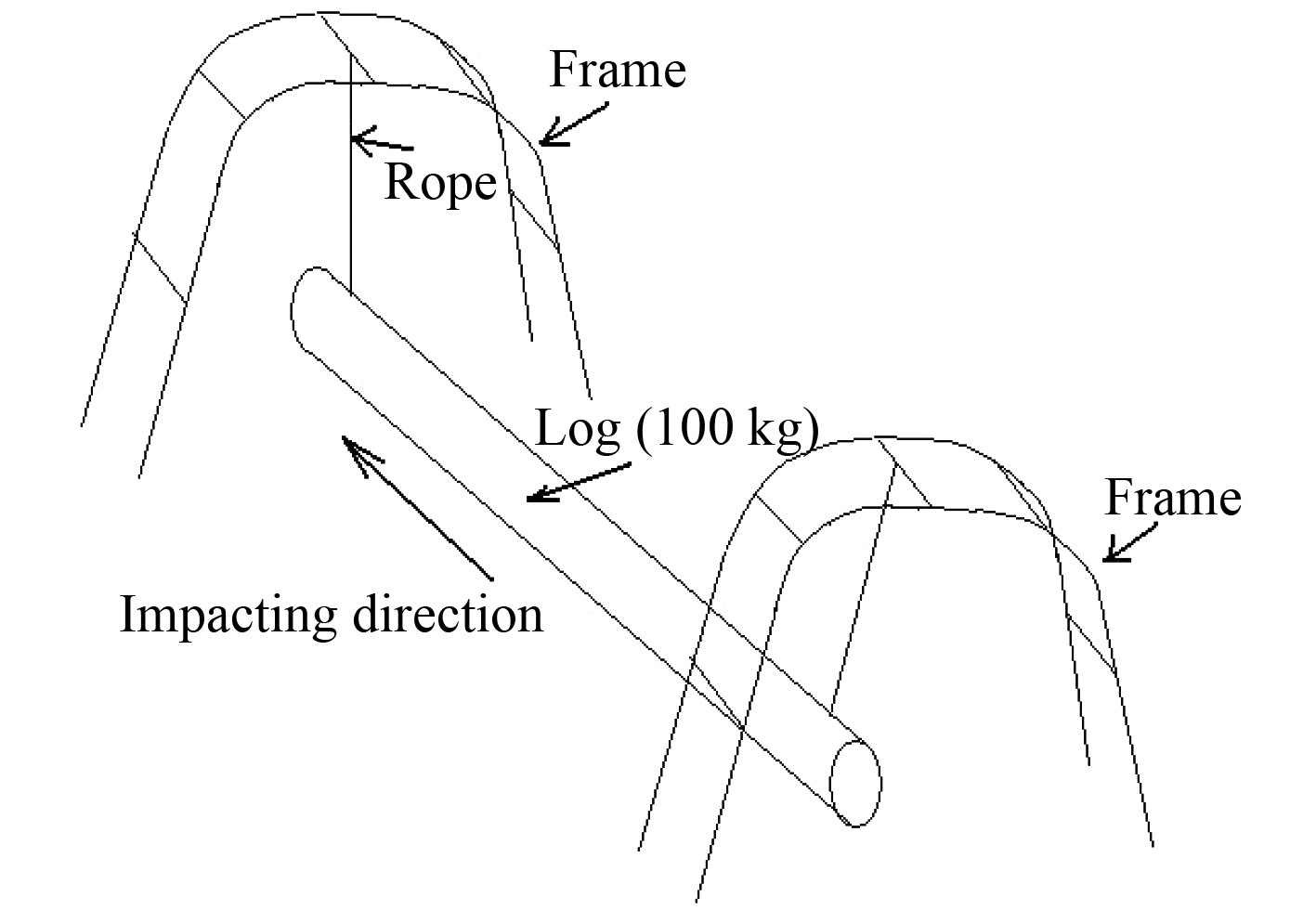
采用木棒对泵塔下端施加激励,分别在纵向和横向冲击泵塔,这时泵塔产生自由振动。图1为激振示意图。其中框架高约2 m,用约1.7 m长的绳索与木棒绑定,木棒重100 kg。冲击时速度逐渐由低到高,直到泵塔产生自由振动。通常冲击测试需要重复3次以上。
|
图 1 激振示意图 Fig. 1 Excitation vibration sketch |
|
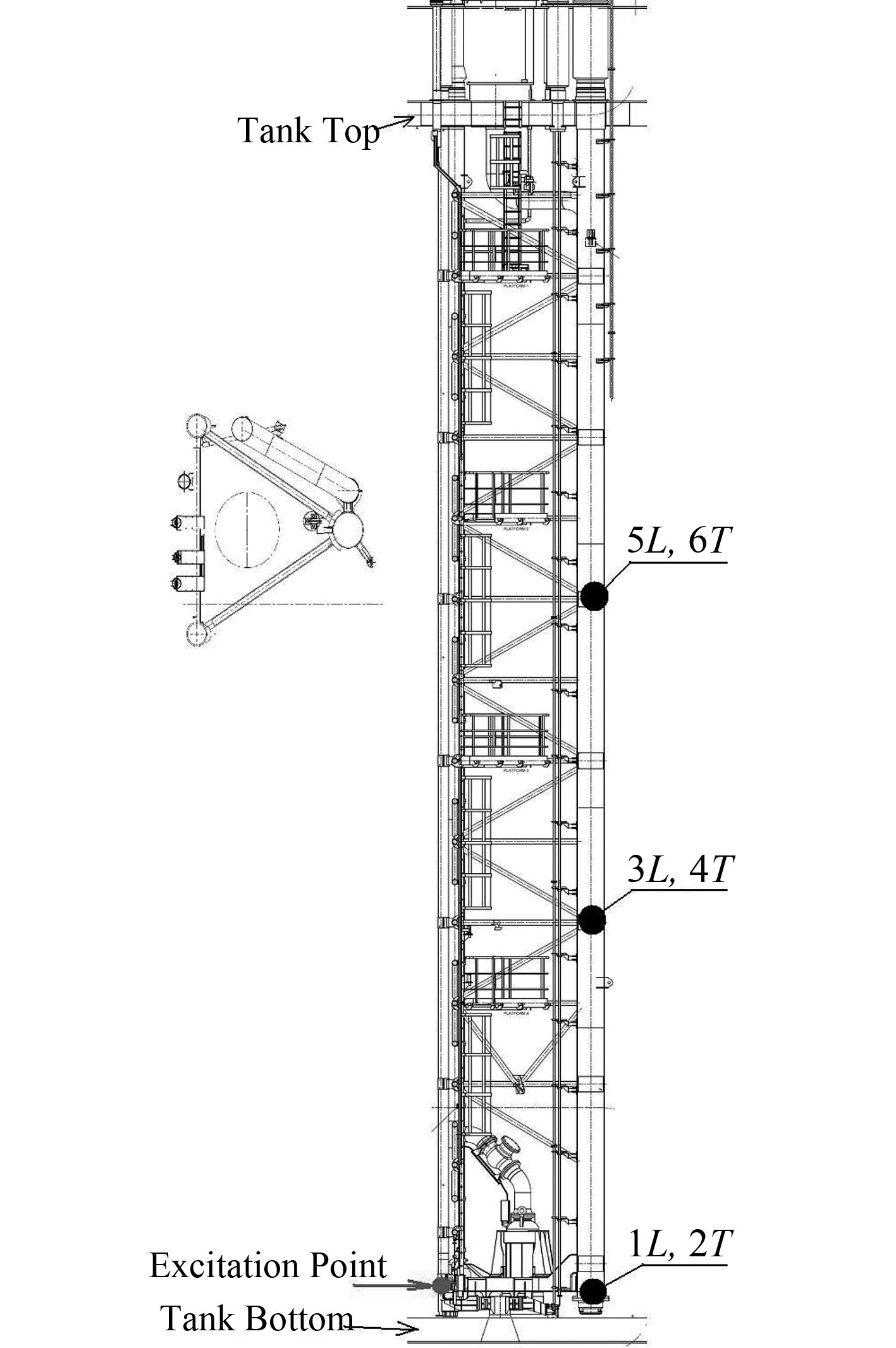
图 2 泵塔振动测点图 Fig. 2 Vibration measure points of pump tower |
|
|
表 1 测点位置 Tab.1 Location of measuring points |
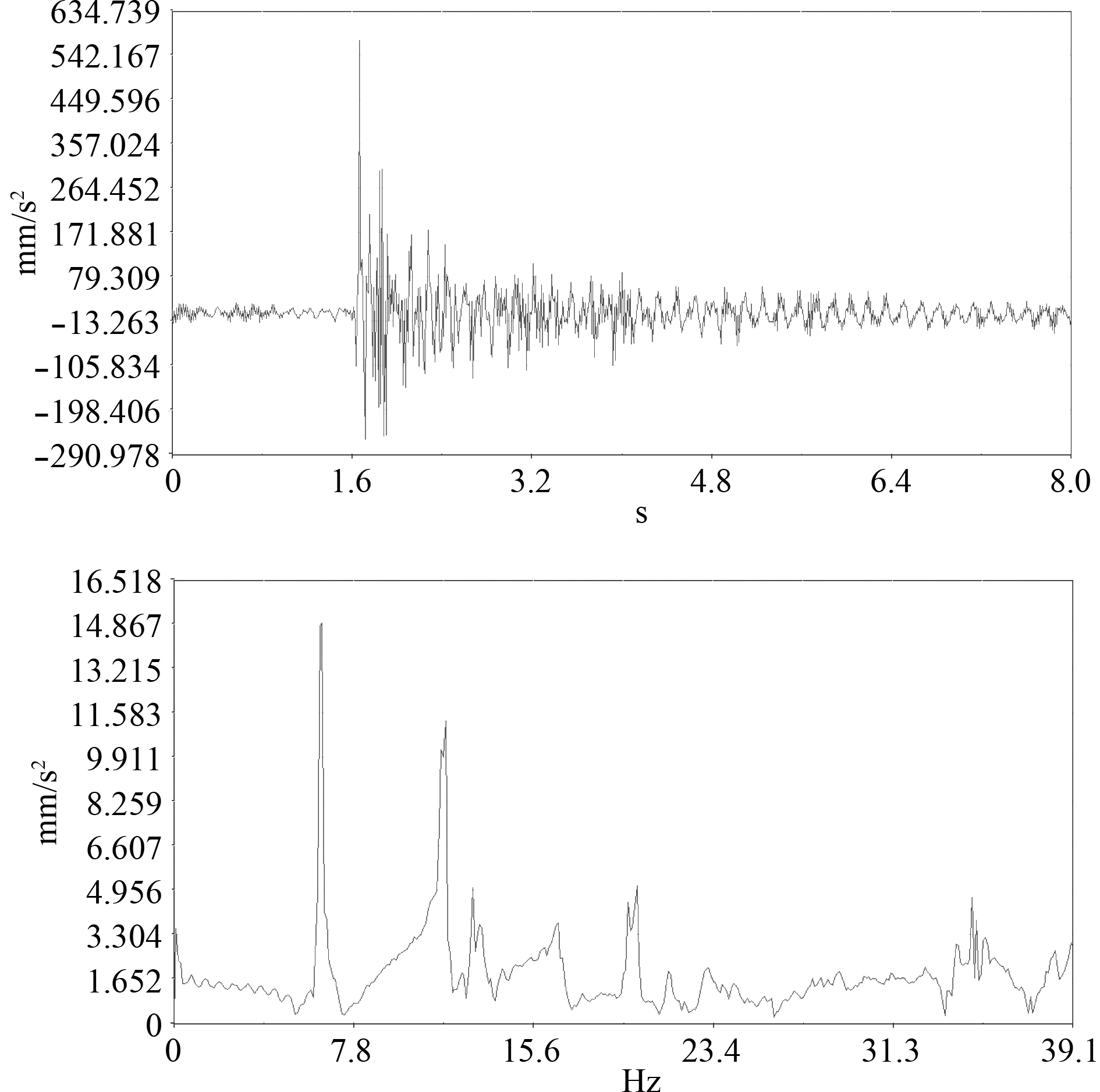
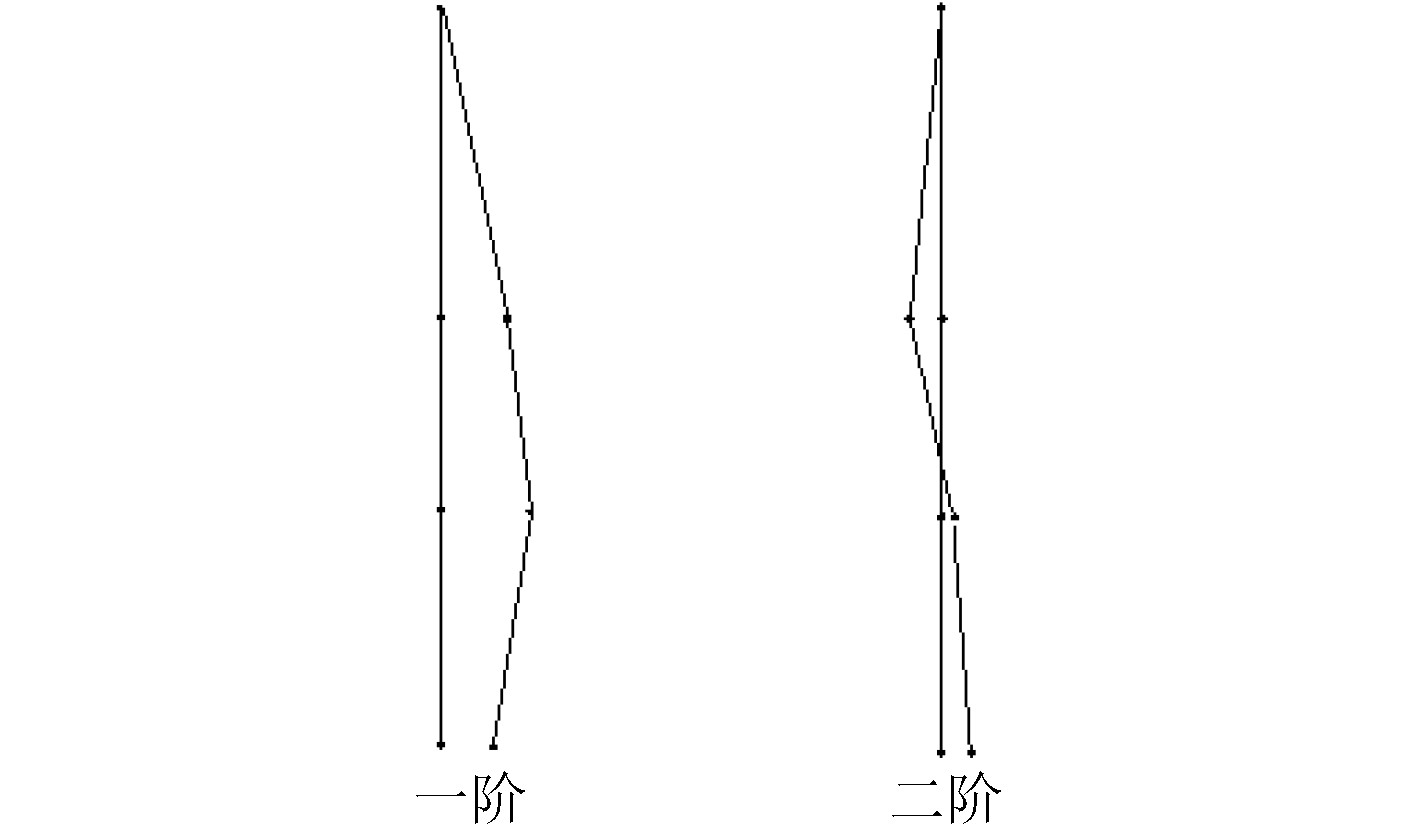
由激振试验测试得到各测点的振动信号,图3给出了激励时测点5的时域曲线和频谱曲线。图3的频谱曲线显示了泵塔纵向有2个固有频率。根据频谱曲线得到的泵塔固有频率见表2,由测点之间的相位关系识别出泵塔相应模态的振型见图4所示。
|
图 3 测点5的时域曲线和频谱图 Fig. 3 Time domain curve and spectrum plot of measuring point No.5 |
|
|
表 2 泵塔固有频率结果 Tab.2 Natural frequency results of pump tower |
|
图 4 纵向振动模态振型图 Fig. 4 Longitudinal vibration mode shapes |
利用运行时结构的振动响应信号提取结构的振动特性参数,已有一些相应的方法,包括ODS(运行变形形状)和OMA(运行模态分析)。但这些新方法都假设结构所受激励为稳态白噪声[6~8]。
对于一个实模态系统,激励和响应之间的频响函数为:
| $\begin{split} {h_{ik}}(\omega ) = \dfrac{{{x_i}}}{{{f_k}}} &= \displaystyle\sum\limits_{i = 1}^N {\dfrac{{{\phi _{ir}}{\phi _{kr}}}}{{{k_r} - {\omega ^2}{m_r} + j\omega {C_r}}}}= \\ &\displaystyle\sum\limits_{i = 1}^N {\dfrac{{{\phi _{ir}}{\phi _{kr}}}}{{(j\omega - {\lambda _r})(j\omega - {\lambda _r}^*)}}} {\text{。}} \end{split} $ | (1) |
式中:N为模态阶数;Φir,Φpr为结构第r阶模态振型在测点i和k处的分量值;λr,
在只有结构响应可测的情况下,假设结构上某一点为参考点,其响应作为输入,其他测点与参考点有某种线性相关性,可建立响应点与参考点的传递函数进行系统识别。假设结构上每个测点的振动响应信号为xi(t)(i=0,1,2,...,n),在结构上取一个固定参考点p,传递率可以表示为:
| ${a_i}(\omega ) = \dfrac{{{x_i}(\omega )}}{{{x_p}(\omega )}}{\text{。}}$ | (2) |
式中:xi(ω)为i测点响应的傅里叶变换。
结构上任一点的振动响应xi(ω)可以用k点的激励力fk(ω)和系统的传递函数hk(ω)表示为:
| ${x_i}(\omega ) = \sum\limits_{k = 1}^m {{h_{ik}}(\omega )} {f_k}(\omega ){\text{。}}$ | (3) |
式中:m为结构的激励点数。
在船舶航行时结构的响应xi(ω)能够测量、而激励力fk(ω)不可测量,利用传统的模态参数识别方法是行不通的。
假设对结构施加的激励力为平稳随机信号,则它的功率谱密度函数在整个频域内为近似的均匀分布,则结构上各点的激励力满足:
| ${f_k}(\omega ) = f(\omega ){\text{,}}$ | (4) |
则式(3)可以改为:
| ${x_i}(\omega ) = f(\omega )\sum\limits_{k = 1}^m {{h_{ik}}(\omega )} {\text{。}}$ | (5) |
将式(5)代入式(2)可得:
| ${a_i}(\omega ) = \frac{{f(\omega )\displaystyle\sum\limits_{k = 1}^m {{h_{ik}}(\omega )} }}{{f(\omega )\displaystyle\sum\limits_{k = 1}^m {{h_{pk}}(\omega )} }} = \frac{{\displaystyle\sum\limits_{k = 1}^m {{h_{ik}}(\omega )} }}{{\displaystyle\sum\limits_{k = 1}^m {{h_{pk}}(\omega )} }}{\text{。}}$ | (6) |
对比式(6)和式(1)可知,传递率ai(ω)与结构的模态参数直接相关。假设结构的各阶实模态彼次能有效分开,它们之间不存在耦合或耦合很小,则式(6)可以近似为:
| ${a_i}(\omega ) = \dfrac{{\dfrac{{{\phi _{ir}}}}{{(j\omega - {\lambda _r})(j\omega - {\lambda _r}^*)}}\displaystyle\sum\limits_{k = 1}^m {{\phi _{kr}}} }}{{\dfrac{{{\phi _{pr}}}}{{(j\omega - {\lambda _r})(j\omega - {\lambda _r}^*)}}\displaystyle\sum\limits_{k = 1}^m {{\phi _{kr}}} }} = \dfrac{{{\phi _{ir}}}}{{{\phi _{pr}}}}{\text{。}}$ | (7) |
式中,p为参考点固定不动,所以对于确定的固有频率ωr=|λr|处,Φpr是定值,故式(7)可以表示为:
| ${a_i}(\omega ) = \dfrac{{{\phi _{ir}}}}{{{\phi _{pr}}}} = C{\phi _{ir}} = {\phi _{ir}}^*{\text{。}}$ | (8) |
式中,C为常数。
由式(8)可知,通过直接读取曲线ai(ω)在固有频率ωr处的幅值和相位,就可以得到对应频率结构的工作振型,它可近似地看作是结构的第r阶振型。
在船舶航行时,船舶主要的结构振动是由主机及螺旋桨激励引起的,此外设备还会受到海浪环境的随机激励。因此可将其假设为随机激励和周期激励同时存在。如果结构的固有频率与航行时的激励频率恰好重合,则就无法识别出该峰值频率是否为结构的固有频率。因此,仅从一个运行工况下的振动响应频谱是难以判断出结构的固有频率。但在变工况下运行时,其激励频率将随之变化。在LNG船航行试验中,采用主机转速阶段递增的方式测量结构振动信号,从不同转速工况下的振动响应频谱中找出不随主机转速变化的振动峰值频率,该频率即为结构的固有频率。
在实际测试中,参考点不能选择靠近振型节点的位置,应尽量选择在各阶频率下响应都较大的点。式(2)振动传递率可表示为:
| ${a_i}(\omega ) = \frac{{{x_i}(\omega )}}{{{x_p}(\omega )}} = \frac{{x_p^*(\omega ){x_i}(\omega )}}{{x_p^*(\omega ){x_p}(\omega )}} = \frac{{{G_{pi}}(\omega )}}{{{G_{pp}}(\omega )}}{\text{。}}$ | (9) |
式中:i为结构上的测点,通过每次所测试的响应对xi(ω)和xp(ω)可以得到相应于测点i的动态曲线ai(ω),对于某阶固有频率,ai(ω)就是相应频率下的工作模态,由传递率谱图可确定对应固有频率处的振型。
2.2 测试方法及测点位置航行试验在东海进行,试验时LNG船保持自由直线航行状态。该船的桨叶数为5。测量过程中主机采用阶段递增的方式,从30%SMCR增至SMCR,具体转速如下:57.9(30%SMCR),61,64,67,70.2(50%SMCR),73,76,79.6(70%SMCR),83(80%SMCR),84.6(NOP),88.7(100%)RPM,共测量了11个转速下的船体结构和泵塔振动响应,测量时船上2台主机转速保持一致,每一阶段的测量均应保持转速稳定在3 min以上,转速稳定后进行同步记录航行总振动试验所有测点的振动响应,包括泵塔的振动信号。
航行试验时泵塔振动测点位置、加速度计与激振试验时相同,测量导线引出液化舱外并与数据采集分析仪连接,数据采集分析仪采用丹麦B&K公司的PULSE 3660D分析仪。
2.3 测试结果通过对各测点在11个主机转速工况下的振动测试信号进行频谱分析,得到所有工况下的振动频谱曲线。由于测量工况多,为了方便直观显示测试的振动情况,将各测点振动响应随转速的变化规律以振动加速度频率-幅值-主机转速之间相互关系的瀑布图形式给出,本文给出了纵向振动测量结果,如图5~图7所示。
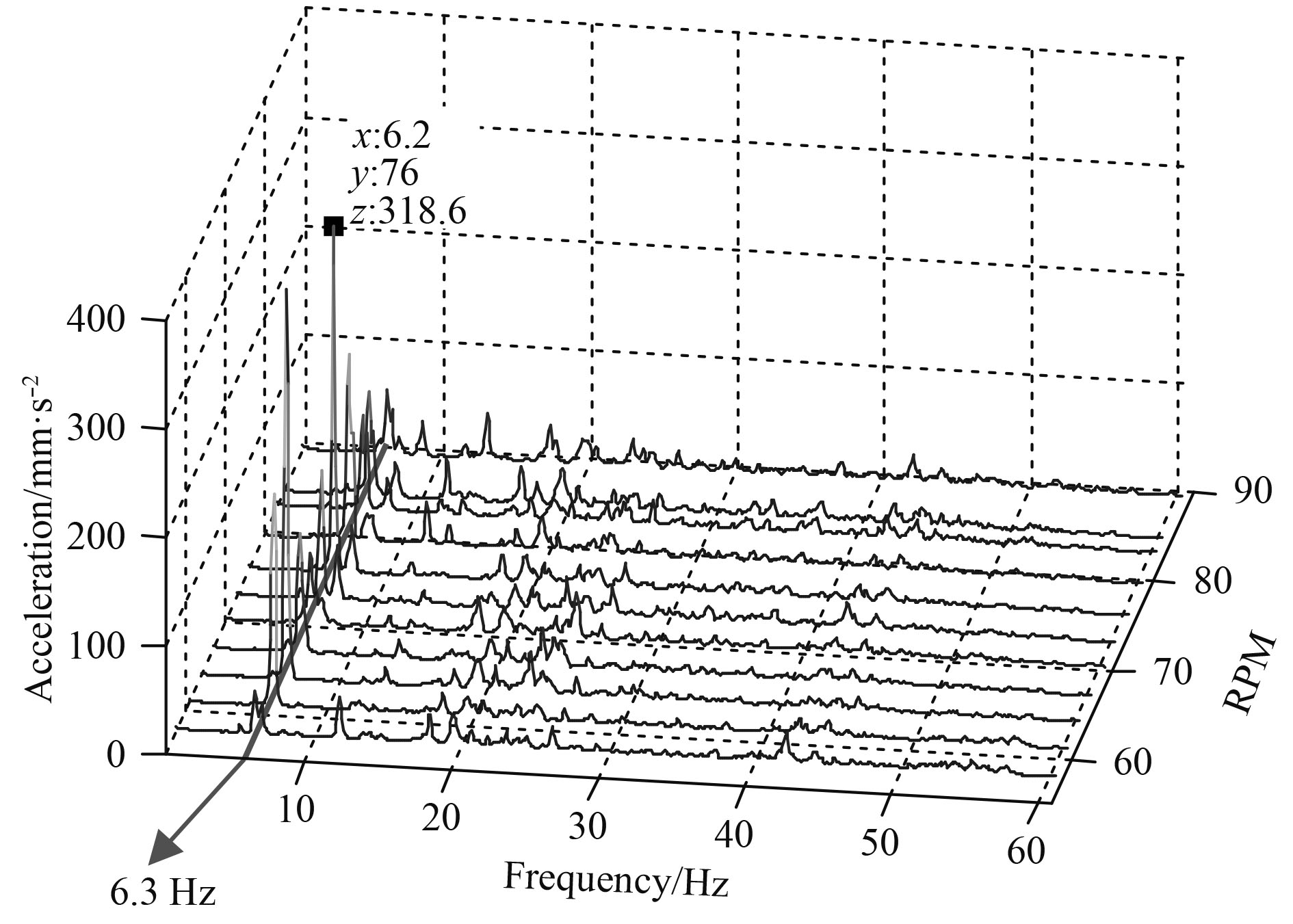
|
图 5 泵塔上部纵向的转速-频率-加速度瀑布图 Fig. 5 Waterfall plot of RPM-frequency-acceleration of upper pump tower(longitudinal) |
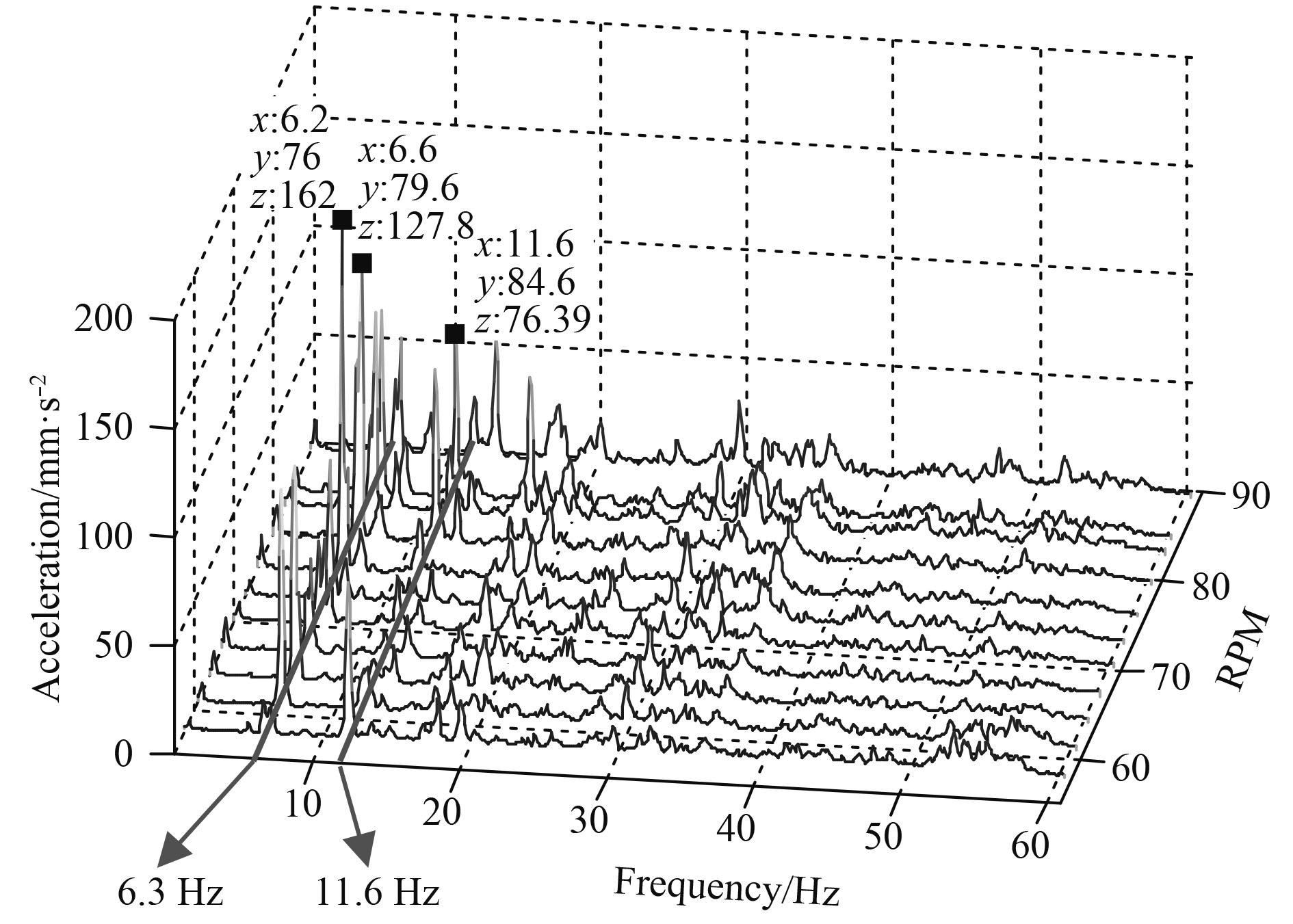
|
图 7 泵塔底部纵向的转速-频率-加速度瀑布图 Fig. 7 Waterfall plot of RPM-frequency-acceleration of bottom pump tower(longitudinal) |
从各转速下测得的振动曲线可以看出,泵塔的各个振动测点显示有一个不随主机转速变化的振动加速度峰值频率,说明该峰值频率为泵塔结构的固有频率。航行试验结果显示泵塔的纵向1阶固有频率为6.3 Hz、2阶固有频率为11.6 Hz。
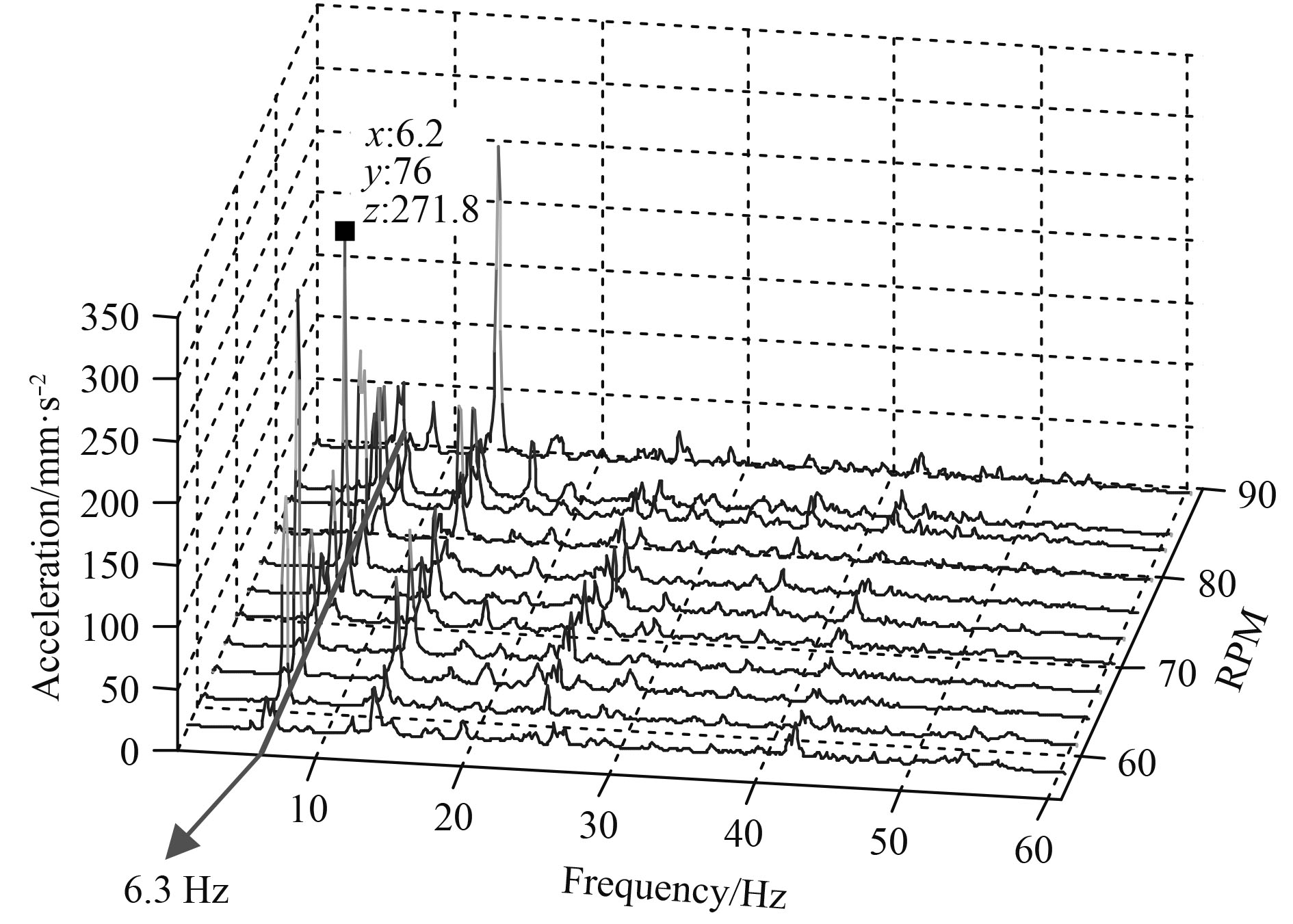
|
图 6 泵塔中部纵向的转速-频率-加速度瀑布图 Fig. 6 Waterfall plot of RPM-frequency-acceleration of middle pump tower(longitudinal) |
航行试验中测得的纵向测点上最突出的部分振动峰值结果如表3所示。可以看出,泵塔主要振动频率为5倍主机轴频,即为螺旋桨的叶频(5叶桨)。在主机转速76.0 r/min,79.6 r/min时桨叶频恰好与泵塔的1阶纵向固有频率和1阶横向固有频率重合,从而导致泵塔在这2个转速工况下的振幅相对大些,当然最大振幅还是位于纵向固有频率和螺旋桨叶频重合的频率上。测试结果表明,由于运行激励的影响,如果仅从单一运行工况测试中难以对结构的固有频率作出判断,只有在变工况运行下才能准确识别系统的振动特性。
|
|
表 3 泵塔纵向振动幅值测量结果 Tab.3 Measurement results of longitudinal vibration of pump tower |
由于大型LNG船航行的主机转速低,因此关心的是泵塔的低阶模态频率。根据激振试验和航行变工况试验两个方法的振动测量,得到泵塔前2阶的纵向固有频率结果对比,如表4所示。可以看出2种试验方法测得的固有频率结果吻合较好,频率偏差很小。频率的微小偏差是因为2次试验使用的数据采集仪不同,选择的频率分辨率不同所导致。由此说明在变工况试验中测试得到的结果可信,可作为获取结构固有频率的一种测试方法。
|
|
表 4 激振试验与航行试验的结果比较 Tab.4 Comparison of the results of excitation test and navigation test |
本文采用传统的激振试验方法、船舶在航行中不同运行工况下振动测试的方法,获得某大型LNG船泵塔结构的固有频率。对2种方法测试结果进行了比较,结果表明变工况振动测试方法的测试结果准确可信,能够识别结构存在的固有频率。该方法无需专门施加激励,尤其适用于难以开展激振试验场合的结构振动特性测量,比如液体介质中或特殊环境场合中的结构。通过对船舶结构的航行振动测试,还可发现振动较为强烈的部位和频率,采取适当的措施改善结构的动态性能,尽量避免固有频率与航行的激励频率重合,为后续船舶的结构设计和改进提供参考。
| [1] |
B/Z 805-2016, 实船激振试验规程[S]. CB/Z 805-2016, Test procedure of vibration excitation for full-scale ship[S]. |
| [2] |
龚君来. 某艇船体结构总振动测量及动力性能评估[J]. 舰船科学技术, 2008, 30(3): 60-63. GONG Jun-lai. A certain ship’s global vibration test trial and dynamical capability evaluation[J]. Ship Science and Technology, 2008, 30(3): 60-63. DOI:10.3404/j.issn.1672-7649,2008.03.010 |
| [3] |
柯耀星, 刘阳, 张晓彤, 等. 船体振动分析的实船验证及改进方案[J]. 舰船科学技术, 2016, 38(6): 105-109. KE Yao-xing, LIU Yang, ZHANG Xiao-tong. Ship vibration onboard verification and improvement[J]. Ship Science and Technology, 2016, 38(6): 105-109. DOI:10.3404/j.issn.1672-7619.2016.06.021 |
| [4] |
郎济才, 姚熊亮, 邵长青, 等. 船舶筒状桅杆的模态分析[J]. 舰船科学技术, 2006, 28(4): 26-28. LANG Ji-cai, YAO Xiong-liang, SHAO Chang-ging. Modal analysis for warship tubular masts[J]. Ship Science and Technology, 2006, 28(4): 26-28. |
| [5] |
傅仁华, 刘镇, 黄映云. 某船船体模态及振动测试[J]. 船海工程, 2007, 36(3): 14-16. FU Ren-hua, LIU Zhen, HUANG Ying-yun. Modal measurement and vibratio situation measurement of a ship[J]. Ship & Ocean Engineering, 2007, 36(3): 14-16. DOI:10.3963/j.issn.1671-7953.2007.03.005 |
| [6] |
KIM B H, STUBBS N, PARK T. A new method to extract modal parameters using output-only responses[J]. Journal of Sound and Vibration, 2005(282): 215-230. |
| [7] |
毛宽民, 李斌, 等. 基于响应信号的结构模态参数提取方法[J]. 华中科技大学学报(自然科学版), 2008, 36(7): 77-80. MAO Kuan-min, LI Bin. Response signals-based structural modal parameter identification (Natural Science Edition)[J]. J. Huazhong Univ. of Sci. & Tech(Natural Science Edition), 2008, 36(7): 77-80. DOI:10.3321/j.issn:1671-4512.2008.07.021 |
| [8] |
姜大正, 洪明, 周力. 运行模态分析技术在船舶结构中的应用[J]. 中国舰船研究, 2010, 5(3): 22-33. JIANG Da-zheng, HONG Ming, ZHOU Li. Application of operational modal analysis in vibration of ship structures[J]. Chinese Journal of Ship Research, 2010, 5(3): 22-33. DOI:10.3969/j.issn.1673-3185.2010.03.005 |
 2019, Vol. 41
2019, Vol. 41
