2. 中国海洋大学 工程学院,山东 青岛 266100;
3. 威海海洋职业学院,山东 荣成 264300
2. College of Engineering, Ocean University of China, Qingdao 266100, China;
3. Weihai Ocean Vocational College, Rongcheng 264300, China
船体极限强度的研究一般归结为对简化箱型梁结构的纵向极限强度计算,箱型梁的纵向强度可用横截面承受的最大弯矩来表示,因此线弹性理论一直被用来计算箱型梁的纵向强度。近些年来,包括屈曲在内多种失效形式的出现、结构部件失效产生的相互作用以及横截面受力重分布等,表明应考虑材料非线性及几何非线性对箱型梁的极限强度进行研究,因此非线性有限元法被广泛应用到船舶极限强度研究中。
国内外许多学者对箱形梁结构进行了详细广泛的研究,Nshihara,Dowling,Reckling[1 – 4]对不同的箱形梁结构进行了极限强度研究实验,通过对实验的结果进行比较分析,改进了箱形梁极限强度的理论算法。Hansen[5]采用有限元方法对Nshihara的几个箱形梁实验模型进行了简单的研究,其中模型采用的是4节点壳单元,通过不断增大荷载,使模型发生整体弯曲,通过对对比5种箱形梁极限强度实验结果和理论算法分别对应的的应力-应变曲线及弯矩-曲率曲线,发现结构崩溃段有很大的差异,反映了理论算法的缺陷。Guedes Soares等[6]详细研究了箱形梁在简支条件下受纯弯矩作用的受力变形过程,并用Ansys软件进行了模拟,实验结果与有限元结果符合较好。徐向东等[7]也对箱形梁进行了极限承载能力方面的实验与理论研究,推出了一个理论公式,并用实例进行了验证。贺双元等[8]基于Marc软件对Nshihara论文中的NST3箱形梁进行极限强度分析。白勇等[9]基于非线性有限元程序Sandy较全面讨论了包括屈服应力、杨氏模量、初始缺陷、焊接残余应力、板厚等因素对船体结构中拱极限强度影响程度,但仅采用一个算例进行分析,普遍性较小。
本文运用Abaqus提供的弧长法(RIKS)计算3个典型箱型梁极限强度值,并与已有实验数据比对,验证本文有限元算法的可靠性。通过计算考察边界条件类型、网格密度大小和初始缺陷幅值对数值计算结果的影响,给出具体的误差值。
1 弧长法加弧长法原理是通过设置一个弧长参数来控制平衡方程的增量迭代和收敛,可以将式(1)写成式(2)增量形式:
| $\{ P\} - \{ I\} = 0{\text{。}}$ | (1) |
式中:{P}为载荷列阵;{I}为内力列阵。
| $\left[ {{K_T}} \right]\left\{ {\Delta u} \right\} = \left\{ {\Delta P} \right\} - \left\{ R \right\}{\text{。}}$ | (2) |
式中:[KT] 为切线刚度矩阵;{Δu}为位移增量;{ΔP}为载荷增量;{R}为残差力。
设第i步迭代的载荷增量为{ΔP}i,由载荷增量因
| ${\left\{ {\Delta P} \right\}_i} = \Delta {\lambda _i}\left\{ {{P_{ref}}} \right\}{\text{。}}$ | (3) |
将式(3)代入式(2)得到第i步迭代的增量格式:
| $\left[ {{K_T}} \right]\left\{ {\Delta u} \right\} = \Delta {\lambda _i}\left\{ {{P_{ref}}} \right\} - {\left\{ R \right\}_i}{\text{。}}$ | (4) |
如图1所示,弧长法在求解中,是把上一步增量计算的平衡点看做圆心,弧长增量
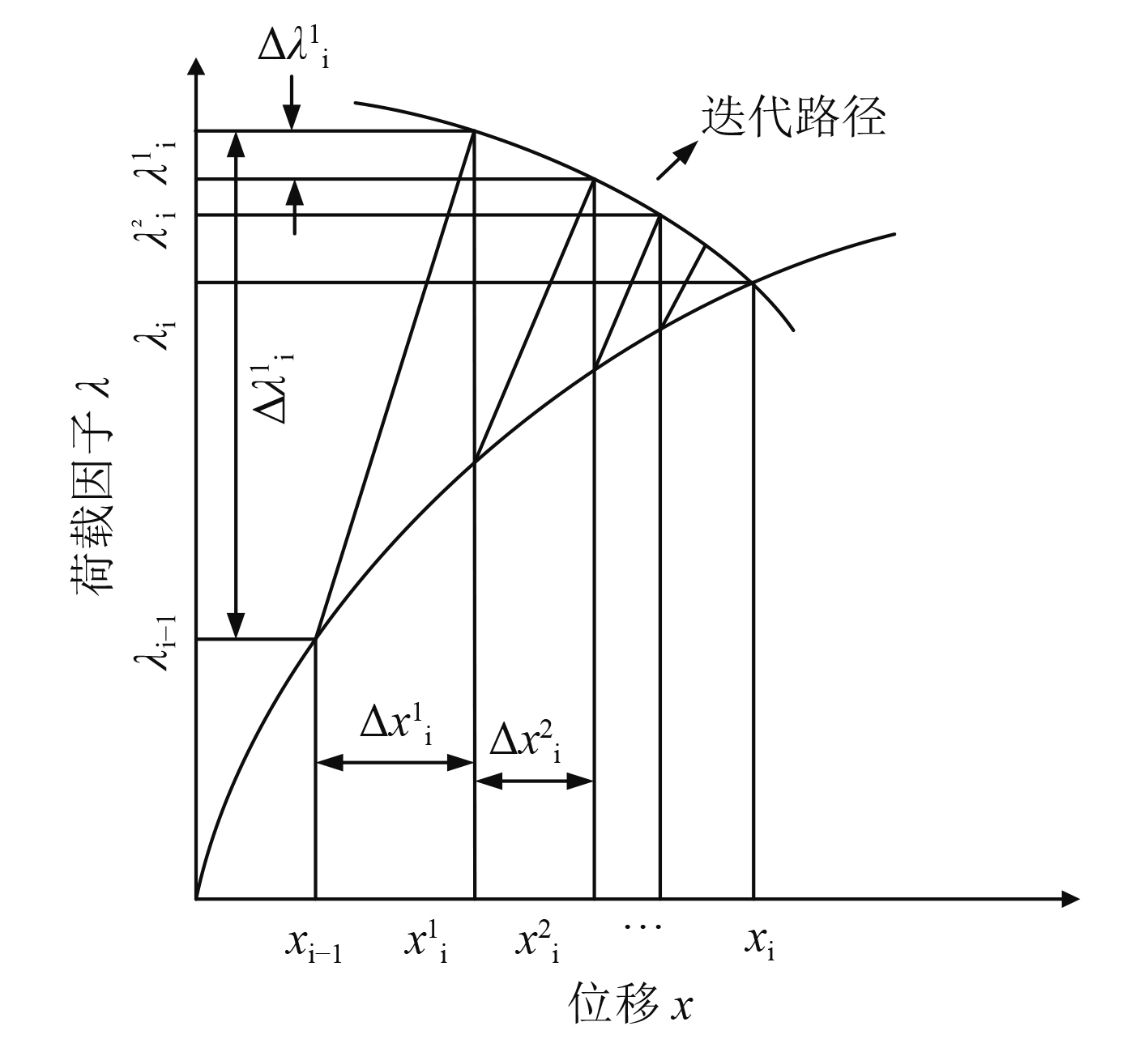
|
图 1 弧长法原理示意图 Fig. 1 Principle diagram of RIKS |
| $\left| {\Delta {l_i}} \right| = \sqrt {{{\left| {\left\{ {\Delta {u_i}} \right\}} \right|}^2} + {{\left| {\Delta {\lambda _i}\left\{ {{P_{ref}}} \right\}} \right|}^2}} {\text{。}}$ | (5) |
经过不断的迭代,一直到残差力控制在容差{R}i之内。第i步迭代完成时有:
载荷列阵
位移列阵
弧长
在弧长增量
本文选用Nishihara,Dowling,Reckling模拟实船钢箱梁设计的3种箱型梁结构,3位学者均对模型进行了实验研究,将本文有限元结果与实验结果进行对比,分析这3种箱型梁极限强度的影响因素及误差大小。
3种典型箱型梁即Nshihara的方形梁MST-3模型(简称Nshihara3模型)、Dowling2箱型梁模型、Reckling23箱型梁模型的剖面结构形式如图2所示。
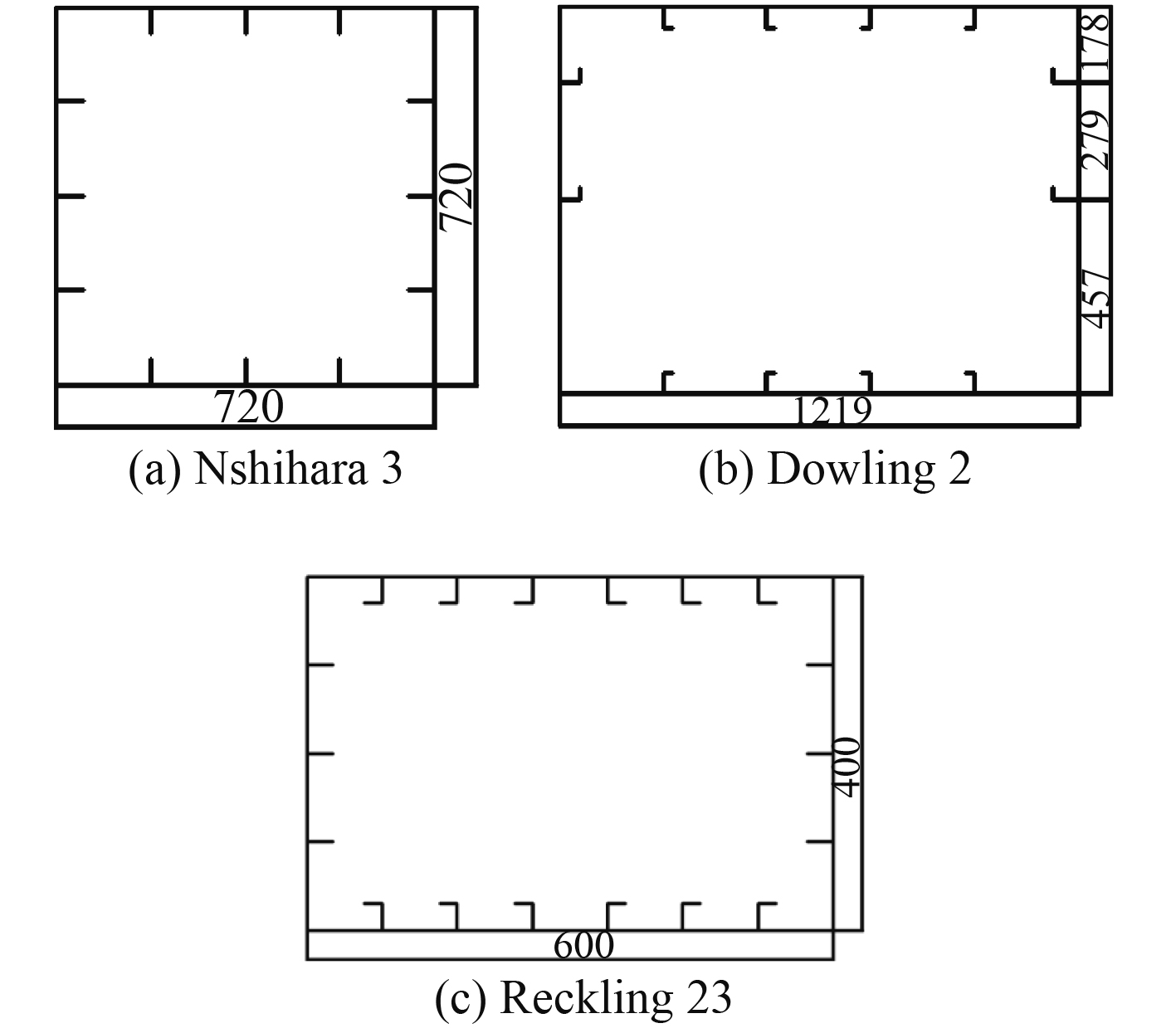
|
图 2 三种典型箱型梁剖面尺寸图 Fig. 2 Dimensions of three typical box girders |
3种模型构件的详细尺寸和材料特性见表1~表3,且3种模型的跨长L分别为540 mm,787 mm,500 mm。
|
|
表 1 Nshihara 3箱型梁结构尺寸表 Tab.1 Dimensions of Nshihara MST-3 box girder |
|
|
表 2 Dowling2箱型梁结构尺寸表 Tab.2 Dimensions of Dowling2 box girder |
|
|
表 3 Reckling23箱型梁结构尺寸表 Tab.3 Dimensions of Reckling23 box girder |
箱型梁有限元模型采用shell单元进行模拟,单元类型S4R5,Nshihara3箱型梁模型如图3所示,模型的两端均使用了相同的延长段,目的是应用St.Venant原理纠正边界条件的偏差,在延长段两端中心各设置一个参考点,两端节点采用MPC多节点约束,约束条件为:在左端面刚体约束的参考点上约束轴1、轴2、轴3方向的线位移Ul,U2,U3以及绕轴1、轴3的角位移UR1,UR3;右端面刚体约束的参考点上约束轴2、轴3方向的线位移U2,U3以及绕轴1、轴3的角位移URI,UR3,考虑箱型梁表面的初始缺陷,在两端参考点处施加连续的垂向弯矩,使梁发生纯弯曲破坏,据输出的弯矩-转角曲线可得到箱型梁的极限弯矩值。
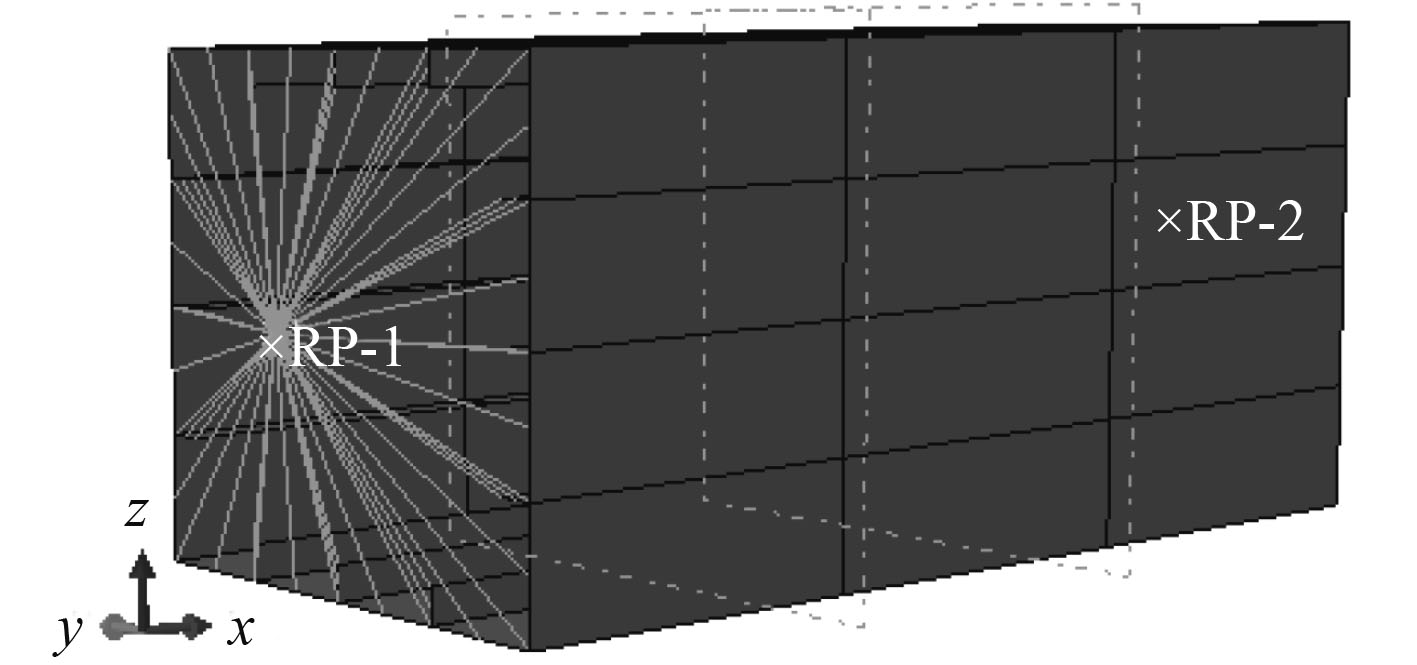
|
图 3 Nshihara 3箱型梁模型 Fig. 3 Model of Nshihara 3 box girder |
为了验证有限元计算结果的可信性,以Nshihara3箱型梁模型、Dowling2箱型梁模型、Reckling23箱型梁模型为例进行计算,初始缺陷为箱型梁跨长的0.01,网格密度为5 cm,其中Nshihara3箱型梁模型结果如图4所示。
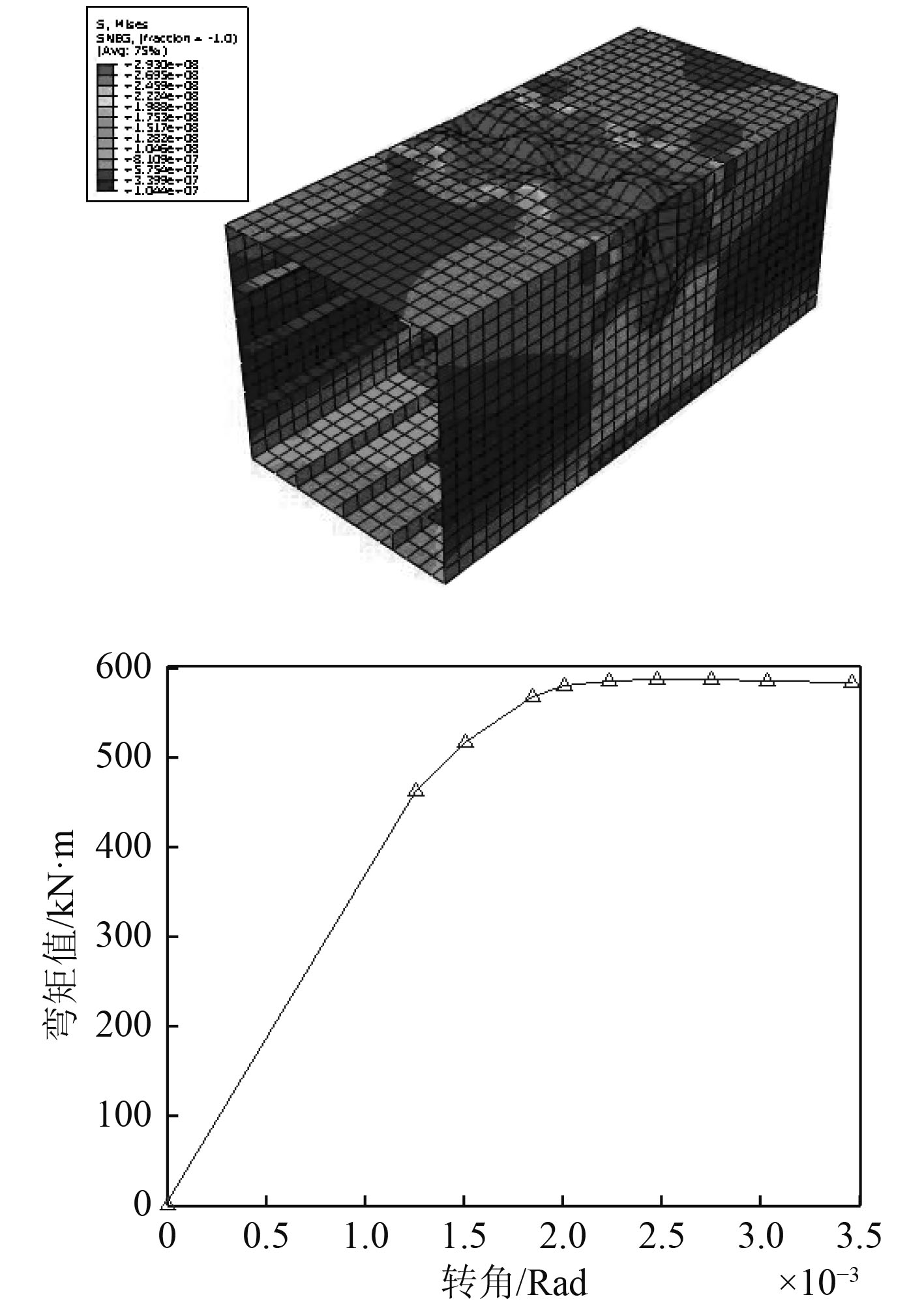
|
图 4 Nshihara3箱型梁损伤变形、应力云图及弯矩-转角曲线 Fig. 4 Damage deformation and stress cloud diagram bending moment - angle curve of Nshihara3 box girders |
3种箱型梁有限元计算结果和实验值比对如表4所示,3种箱型梁有限元解和实验值的误差分别为0.92%,0.84%,3.6%,满足精度要求,验证了有限元算法的可信性。
|
|
表 4 三种箱型梁有限元解和实验值对比(MPa) Tab.4 Comparison of finite element solutions and experimental values of three box girders(MPa) |
箱型梁极限强度有限元算法的影响因素主要为边界条件、初始缺陷、网格密度等,因此本节重点研究这3种箱型梁模型在有限元方法中,不同边界条件、初始缺陷、网格密度对其极限强度的影响程度及误差大小。
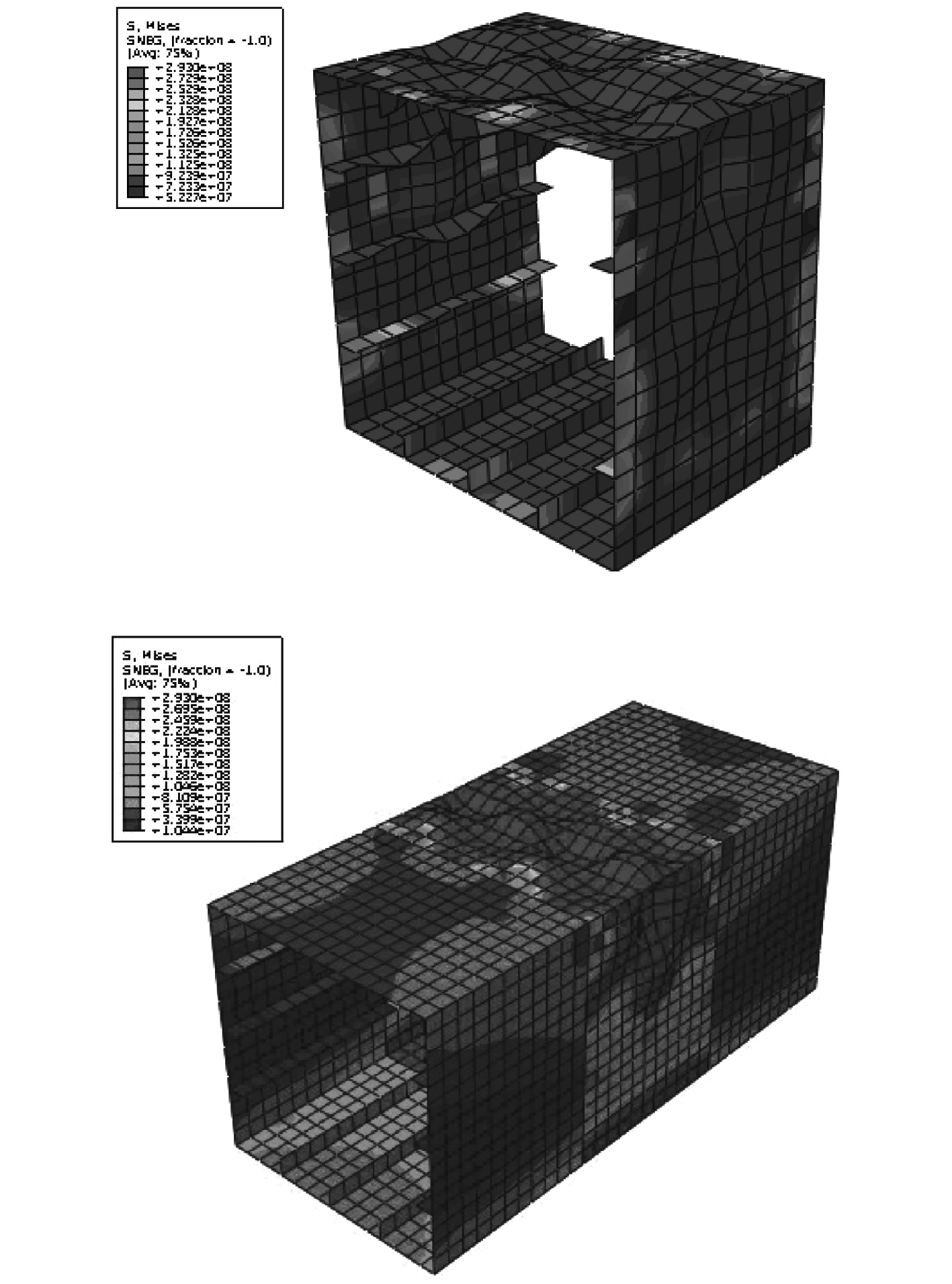
3.1 边界条件本文在箱型梁两端各设置一段与原模型等长的延长段,即1+1+1模型,延长段采用较高屈服强度的材料且增加板厚,目的防止延长段过早破坏。图5为Nshihara3箱型梁模型在无延长段边界条件、1+1+1边界条件下的损伤变形、应力云图,从图中看出模型延长段无明显变形且应力较小,变形与应力都集中在箱型梁中段,即设置延长段不影响原箱型梁的变形及应力分布,说明设置的延长段比较合理。
|
图 5 无延长段和1+1+1边界条件下Nshihara3箱型梁损伤变形、应力云图 Fig. 5 Damage deformation and stress cloud diagram of no extension and 1+1+1 Boundary conditions |
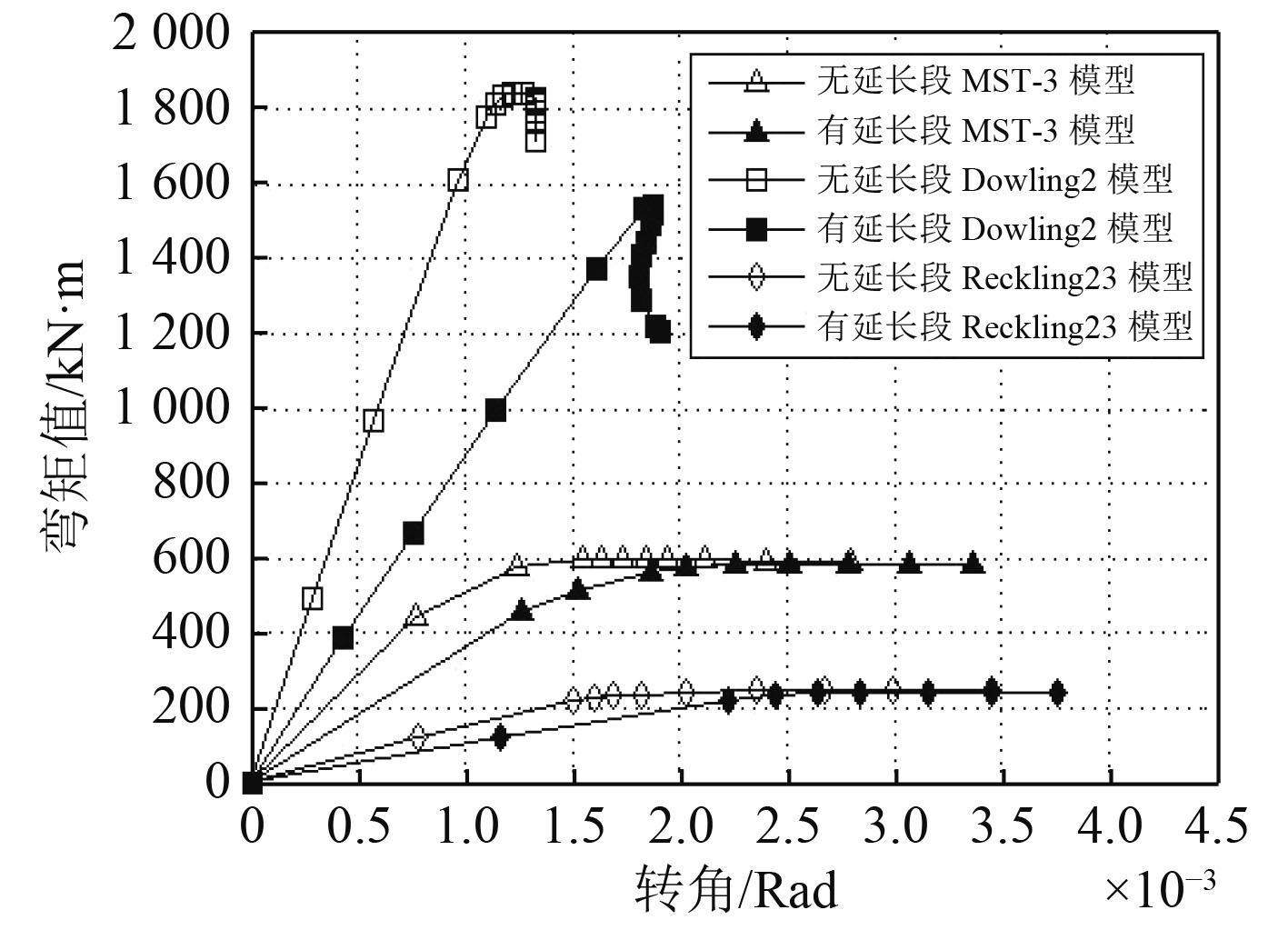
为比较Nshihara3模型、Dowling2箱型梁模型、Reckling23箱型梁模型在上述2种边界条件下计算结果的差异,分别计算这2种边界条件下3种模型的极限强度。图6为3种箱型梁模型的在上述2种边界条件下计算得到的弯矩-转角曲线图。
|
图 6 两种边界条件下各箱型梁的弯矩-转角曲线 Fig. 6 Bending moment - angle curve of each box beam under two boundary conditions |
可以看出,无延长段模型比1+1+1模型计算结果偏大,尤其对Dowling2箱型梁模型影响更为明显。表5为3种箱型梁结构在两种边界条件下极限强度有限元值与实验值对比。可以看出,2种边界条件下极限弯矩差距为19%左右,且1+1+1模型计算结果更接近实验值,因此采用具有延长段的边界条件可以更好地模拟箱型梁的纯弯屈曲变形。
|
|
表 5 两种边界条件箱型梁极限弯矩值(kN·m) Tab.5 The ultimate bending moment value of two boundary condition box girders(kN·m) |
在研究箱型梁的极限强度时,需要引入合适的初始缺陷,使数值模拟过程与计算结果更符合实际,初始缺陷的处理可采用傅里叶级数法,通过改变单元节点的位移进行施加,但施加过程比较复杂,为方便施加初始缺陷,本文引入初始缺陷的方法是采用Abaqus软件提供的Buckle分析步对加筋板模型进行特征值屈曲分析,通过对特征屈曲模态按照比例因子进行合适的缩放,将缩放后的变形结果作为初始缺陷引入到后屈曲分析中。
比例因子的取值影响着引入缺陷的大小,因此选取比例因子范围不应过大,考虑到实际初始缺陷的量级,本文按0.01~0.02 L(L为箱型梁跨长)大小选取比例因子,即初始缺陷5~10 mm,对3种箱型梁进行分析。
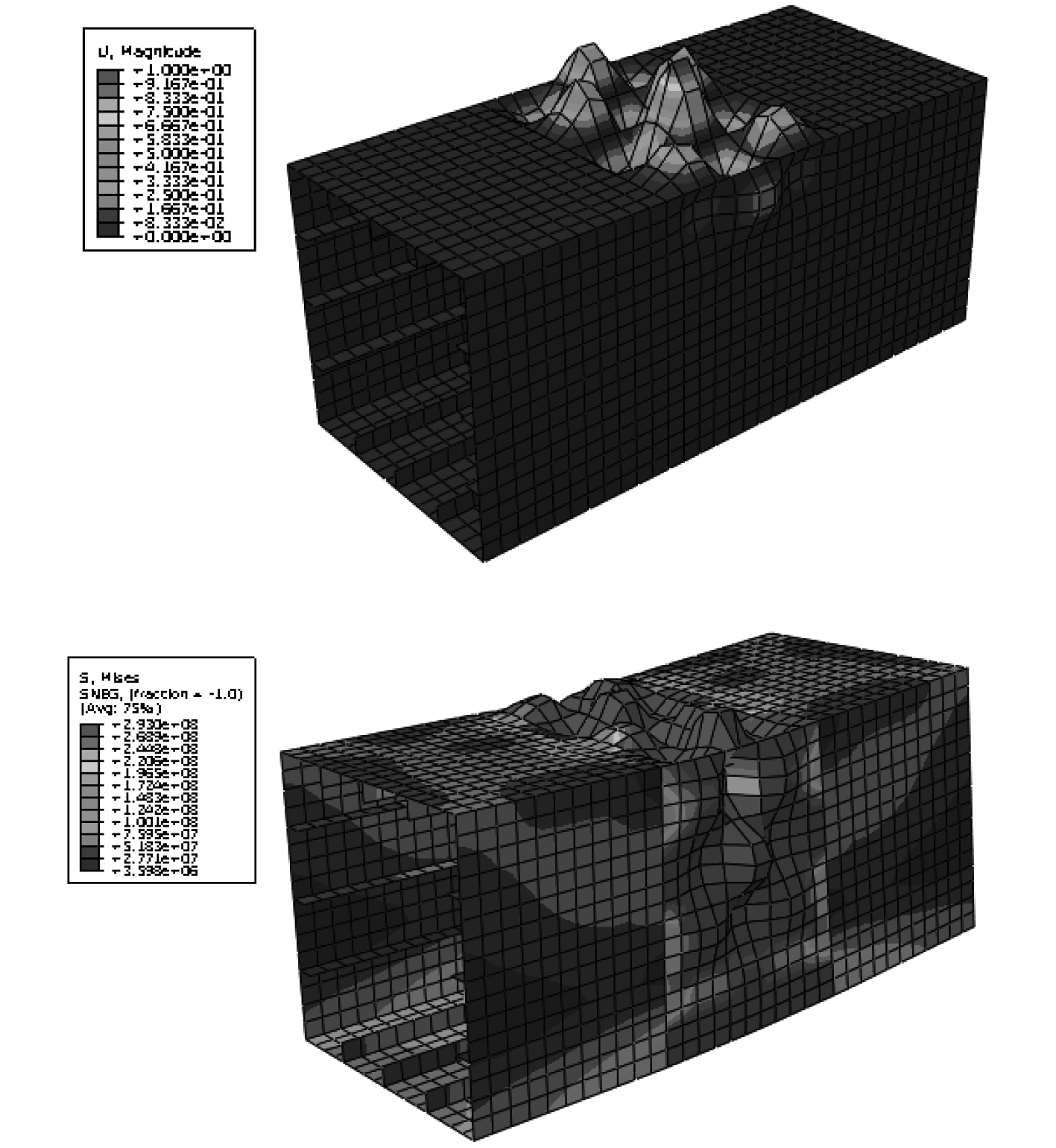
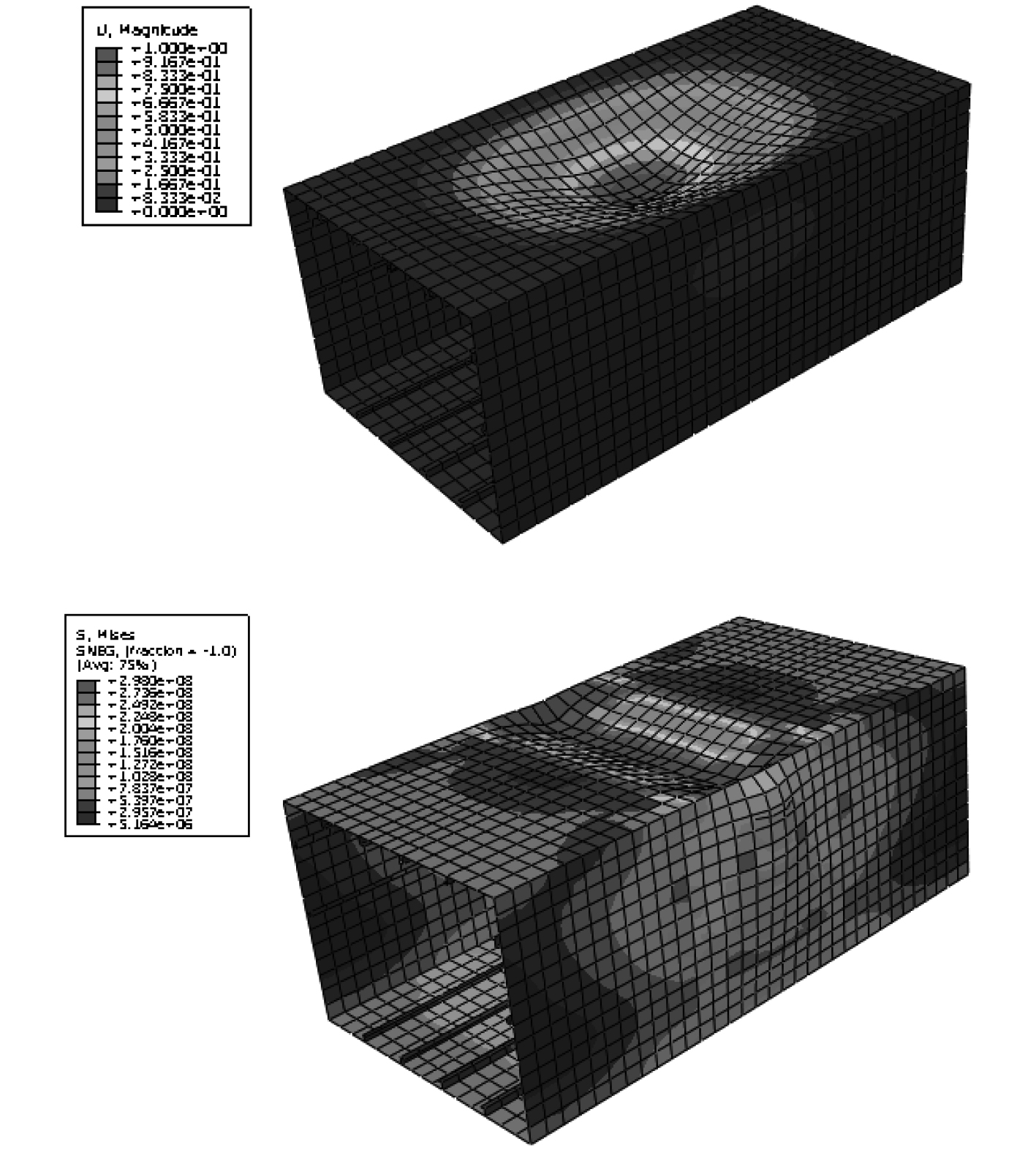
图7~图9分别为Nshihara3模型、Dowling2箱型梁模型、Reckling23箱型梁模型的屈曲模态与相应的箱型梁极限损伤变形、应力云图。可以看出,屈曲模态的变形区域与箱型梁最终变形云图基本一致,屈曲模态作为结构初始缺陷,决定模型的屈曲变形位置,并影响模型最终的破坏形态。
|
图 7 Nshihara3模型屈曲模态及损伤变形、应力云图 Fig. 7 Buckling mode of Nshihara3 model and Damage deformation、stress cloud diagram |

|
图 9 Reckling23箱型梁模型屈曲模态及损伤变形、应力云图 Fig. 9 Buckling mode of Reckling23 model and Damage deformation、stress cloud diagram |
|
图 8 Dowling2箱型梁模型屈曲模态及损伤变形、应力云图 Fig. 8 Buckling mode of Dowling2 model and Damage deformation、stress cloud diagram |
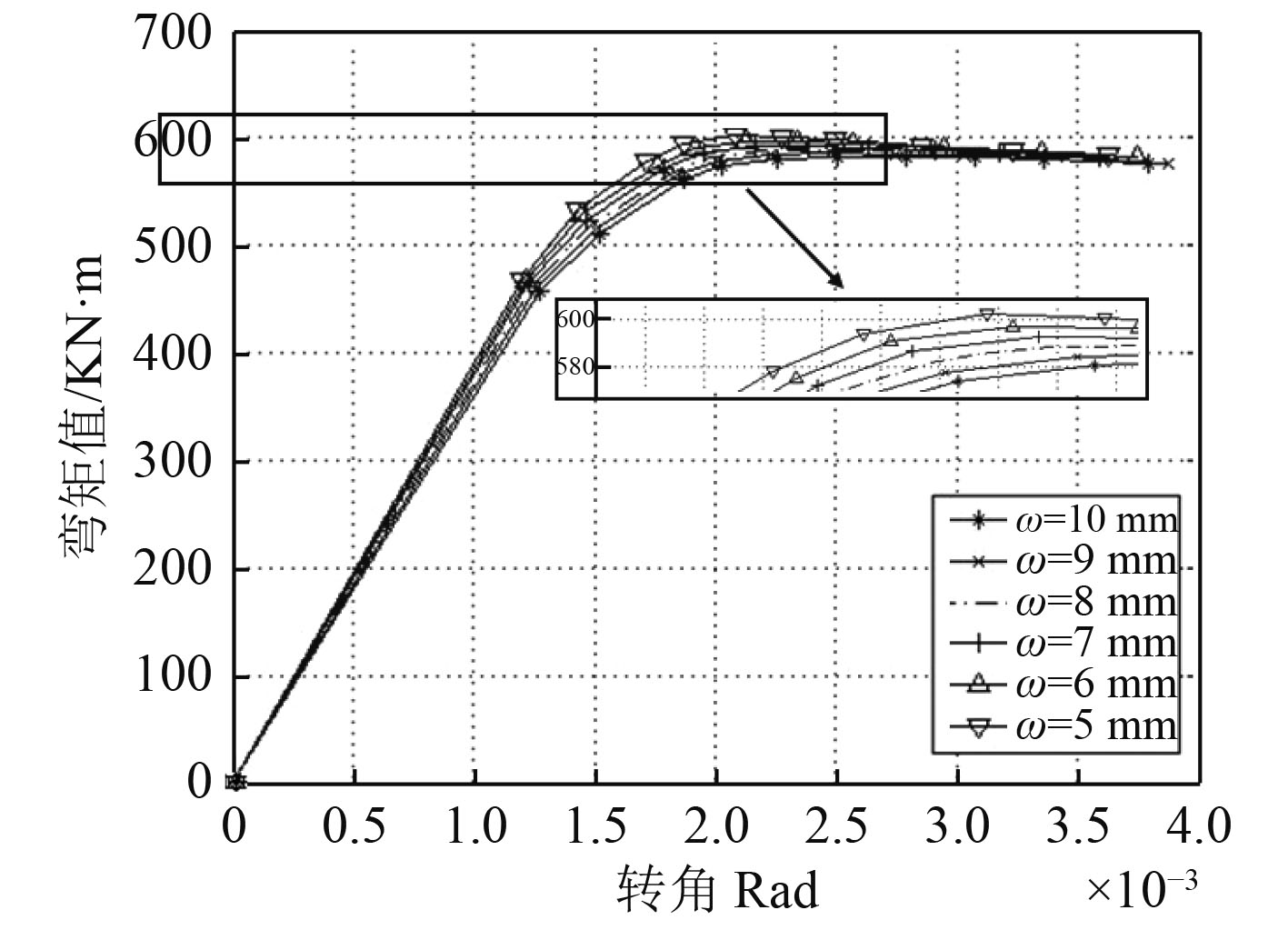
图10为Nshihara3模型的弯矩-转角图,从图中可以看出,随着初始缺陷的增大,极限弯矩呈减小趋势,且在初始缺陷为5~10 mm范围内,极限强度计算结果差距不大,其他箱型梁的弯矩-转角曲线差距类似。
|
图 10 Nshihara 3箱型梁不同缺陷下的弯矩-转角曲线 Fig. 10 Bending moment - angle curve of Nshihara 3 box girder under different defect |
表6为3种箱型梁在5~10 mm等不同缺陷大小下极限弯矩值,可以看到对应不同初始缺陷,各模型的极限弯矩值,从误差结果来看最大误差达到6%,最小误差为0.71%,说明在此范围内选择初始缺陷的大小是比较合理的,从坡度的变化趋势可以看出Nshihara3模型和Reckling23箱型梁模型均为减小的趋势,最适合的缺陷值为8 mm,Dowling2最适合缺陷为10 mm,均在0.01~0.02倍箱型梁跨长范围内。
|
|
表 6 三种箱型梁在不同缺陷大小下极限弯矩值计算值(kN·m) Tab.6 The ultimate bending moment of three kinds of box girders under different defect(kN·m) |
其中,误差坡度=
一般来说,模型网格越密计算的结果更精确。然而随着网格密度增加,相应的计算时间会更长。因此,合适的网格密度既能得到满足精度的结果又可削减计算时间,这一规律在大型结构中尤其明显。
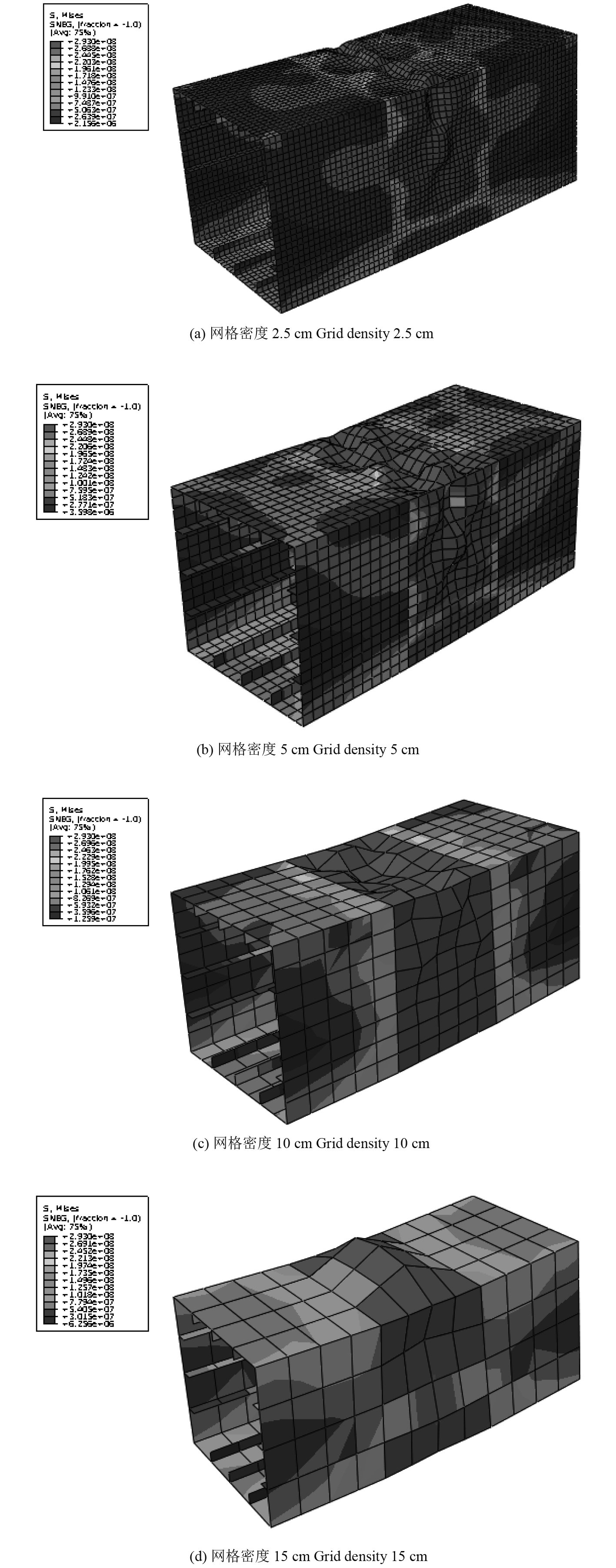
本文选取网格尺寸为2.5 cm,5 cm,10 cm,15 cm且均设为正方形网格。图11为4种网格密度下Nshihara3模型损伤变形、应力云图。
|
图 11 不同网格密度下Nshihara3箱型梁模型损伤变形、应力云图 Fig. 11 Damage deformation and stress cloud diagram of Nshihara3 box girder model under different grid densities |
图12为2.5 cm、5 cm、10 cm、15 cm 4种网格密度下Nshihara3模型弯矩-转角曲线,从图中可以看出网格密度为2.5 cm与5 cm极限弯矩大小基本相同,网格密度为10 cm与15 cm极限弯矩大小也基本相同,按网格密度从5 cm变大到10 cm,极限弯矩明显减小,可见网格粗糙程度对箱型梁极限弯矩有限元解具有较大影响。

|
图 12 四种网格密度下Nshihara箱型梁模型弯矩-转角曲线 Fig. 12 Bending moment - Angle curve of Nshihara box girder under four kind of grid densities |
表7为3种箱型梁在2.5 cm、5 cm、10 cm、15 cm网格密度下的计算结果,从表中可以看出网格密度越稀疏,计算值越大,在4种网格尺寸中,Nshihara3模型在网格为5 cm时误差最小,仅与实验值有0.41%的误差,但在网格尺寸增加到10 cm时,计算值有较大程度的增长,弯矩坡度从2.15增到38.13,说明网格大小在5~10 cm之间时,计算结果受网格密度影响很大,网格尺寸为2.5~5 cm之间值,弯矩坡度仅为2.15,综合误差值与弯矩坡度值可得出,Nshihara3模型网格大小为2.5~5 cm之间时可得到满足精度且比较稳定的结果,有限元结果在大于5 cm时出现跳跃,网格密度为10 cm以上时,Nshihara箱型梁模型极限强度误差值超过30%。
|
|
表 7 三种箱型梁在不同网格密度下的计算结果(kN·m) Tab.7 The ultimate bending moment of three kinds of box girders under different grid densities(kN·m) |
本文研究箱型梁极限强度有限元法的不稳定性,选取Nshihara的方形梁MST-3模型、Dowling2模型、Reckling23模型等3个典型箱型梁模型,通过对边界条件、初始缺陷、网格尺寸等因素进行分析,得到以下结论:
1)在相同荷载条件下,有延长段模型比无延长段模型极限弯矩值更接近实验值,且无延长段的Dowling2箱型梁模型计算值误差达到了20%,说明采用延长段的边界条件模拟箱型极限破坏得到的计算值更准确。
2)比例因子取5~10 mm时,3个模型在不同初始缺陷下计算误差为0.71%~6%,Nshihara模型和Reckling23模型最适合缺陷值为8 mm,Dowling2为10 mm,均在0.01~0.02倍箱型梁跨长范围内。
3)在2.5~15 cm网格密度内,有限元结果在大于5 cm时出现跳跃,此时Nshihara箱型梁模型极限强度误差值达到36%,当网格密度在0.1倍箱型梁跨长值以内时,计算结果更精确。
| [1] |
NISHIHARA S. Analysis of ultimate strength of stiffened rectangular plate (4th report) on the ultimate bending moment of ship hull girders[J]. Journal of the Society of Naval Architects of Japan, 1983, 154: 367-375. |
| [2] |
NISHIHARA S. Ultimate longitudinal strength of midship cross section[J]. Naval Arch. Ocean Eng, 1984, 22: 200-214. |
| [3] |
DOWLING P J, MOOLANI F M, FRIEZ PA. The effect of shear lag on the ultimate Strength of box girder[C]// Proc. Int. Con. On Steel Plated Structures. London, 1976: 108~147.
|
| [4] |
REKLING K A. Behaviour of box girder under bending and shear[A]. proc. ISSC[C], Paris 1997. Ⅱ. 2.46-11.2.49
|
| [5] |
HANSEN A M. Strength of midship section[J]. Marine Structures, 1996, 9: 471-494P. DOI:10.1016/0951-8339(95)00040-2 |
| [6] |
GORDO J M, SOARES C G, FAULKNER D. Approximate assessment of the ultimate longitudinal Strength of the hull girder[J]. Ship Research, 1996, 40(1): 60-59. |
| [7] |
徐向东, 崔维成, 冷建兴等. 箱型梁极限承载能力试验与现论研究[J]. 船舶力学. 2000, 4(5): 36~43
|
| [8] |
白勇, 徐向东, 崔维成. 船体结构极限强度的影响参数与敏感度探讨[J]. 船舶力学, 1998, 4(5): 35-43. |
| [9] |
贺双元, 吴卫国, 陆浩华, 运用MARC进行箱梁的极限强度分析[J]. 武汉理工大学学报(交通科学与工程版), 2006. 30(5): 889~891
|
 2019, Vol. 41
2019, Vol. 41
