2. 中国船舶重工集团有限公司,北京 100097;
3. 中国船级社上海规范研究所,上海 200135
2. China Shipbuilding Industry Corporation, Beijing 100097, China;
3. Shanghai Rules and Research Institute, China Classification Society, Shanghai 200135, China
近年来大型集装箱船发展迅速,最大箱位已达2万多箱,但2013年发生的“MOL COMFORT”号8110TEU集装箱船断裂沉没事故时刻提醒业界关注大型集装箱船结构强度[1 – 3]问题。集装箱船具有甲板开口大、抗扭刚度低的特点,航行过程中遭遇恶劣海况(如斜浪或不对称波浪),会产生较大的扭矩载荷[4 – 5],对船体结构安全构成威胁[6]。目前集装箱船结构强度校核[7 – 11]侧重于对组合载荷[12]和船舶整体强度的分析,一般采用波浪载荷数值预报[13 – 14]和结构有限元分析[15 – 17],忽略单个载荷的特殊作用。而针对斜浪工况下[18]的扭矩载荷的专门研究对集装箱船结构细节设计尤为重要,可提高船舶抗扭能力、改善舱口角隅设计和抗扭箱设计等。
本文以1艘大型集装箱船为研究对象,研究斜浪作用下的扭矩特性及结构响应:首先采用动态载荷直接计算方法(Dynamic Load Approach,DLA),计算了处于不同设计波参数下、不同横截面处的系列扭矩载荷传递函数,分析了扭矩载荷传递函数的规律;继而采用北大西洋波浪谱,对船舶扭矩载荷进行长期预报,得到基于不同主要载荷控制参数和超越概率水平下的设计波参数,分析了影响设计波参数的主要因素,并通过研究不同设计波条件下扭矩载荷沿船长的分布规律和包络值曲线,分析扭矩载荷沿船长的分布特性;研究美国船级社(ABS)集装箱船规范和结构共同规范(HCSR)中扭矩公式,通过算例比较规范计算值与DLA计算结果的差别,分析原因,提出大型集装箱船扭矩载荷计算与应用的建议;在此基础上,通过整船结构强度分析,计算45°、60°和70°浪向的船体结构应力分布,识别斜浪作用下船体结构响应的关键位置,可作为大型集装箱船结构设计过程中船体梁扭转强度计算、舱口角隅设计、抗扭箱强度评估等的参考。
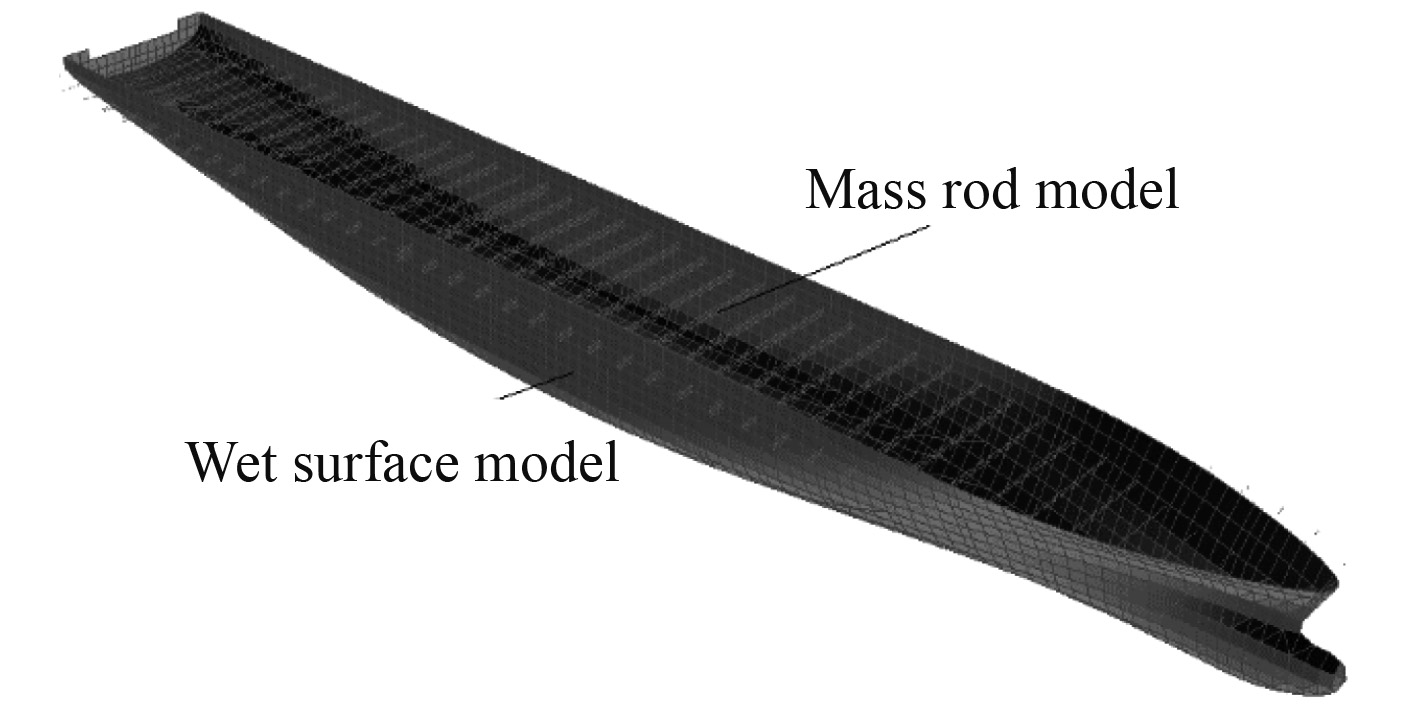
1 水动力分析 1.1 水动力模型水动力模型[19]分为船体湿表面模型和质量模型两部分(见图1):按照船舶型线图建立水线以下部分的船体湿表面模型;按照装载手册在全船重心高度处建立等效质量模型,质量棒长度按下式确定。
|
图 1 集装箱船水动力模型 Fig. 1 Hydrodynamic model of container ship |
| ${l_{beam}} = \sqrt {12} \cdot {r_{roll - gyr}}\text{。}$ | (1) |
式中:
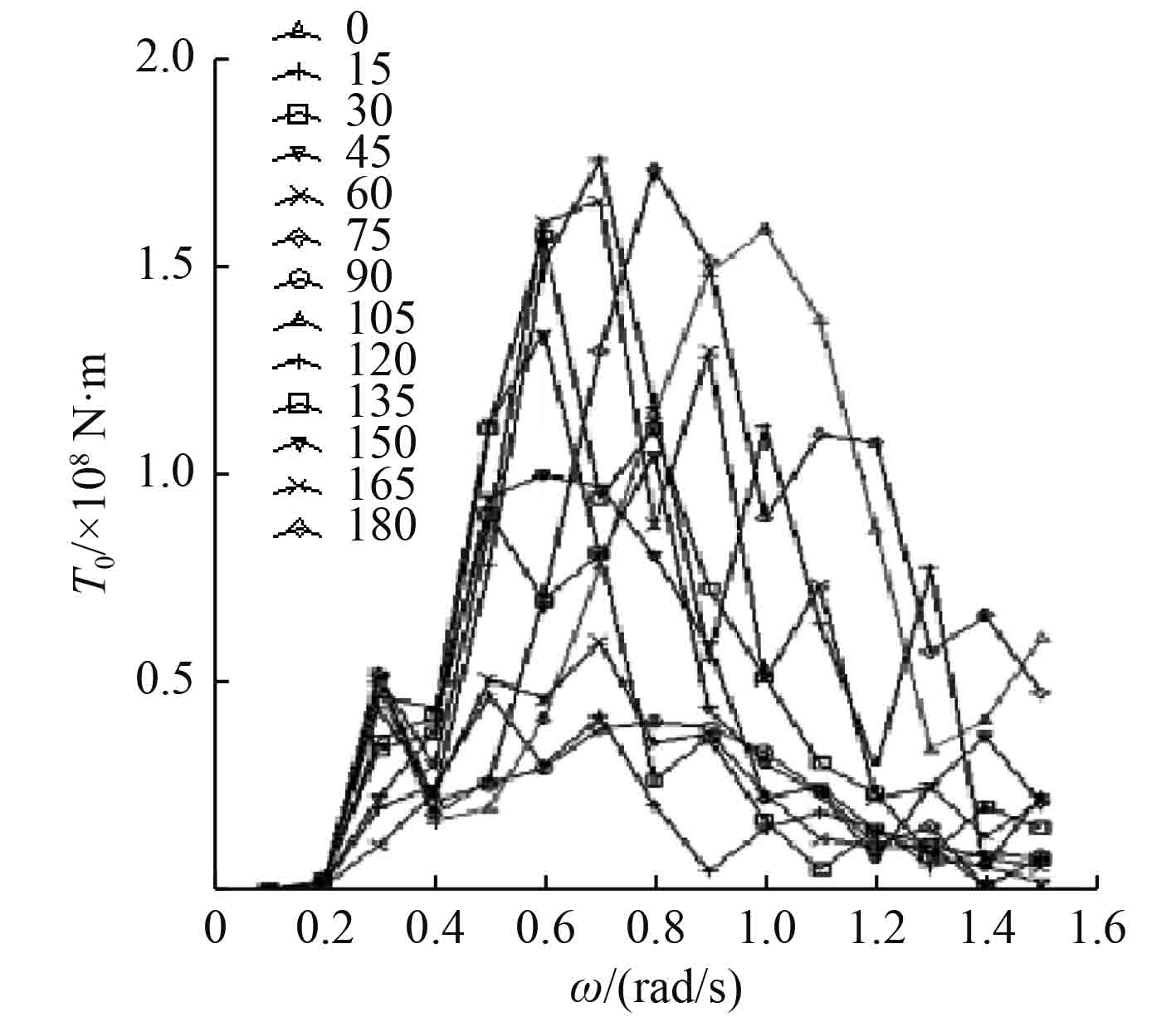
扭矩传递函数与船舶型线、浪向、作用位置相关,分别计算了1/20 L~20/20 L(L为船长)截面处的扭矩传递函数,其中5/20 L截面处的扭矩传递函数见图2。
|
图 2 扭矩载荷传递函数(5/20 L位置) Fig. 2 Torque load transfer function(5/20 L position) |
通过比较各个扭矩传递函数:船中偏后位置处扭矩传递函数的绝对值较大、且与浪向和波浪频率的敏感性最高,选择传递函数时需兼顾最大扭矩载荷和结构关键剖面的合理组合,这与文献[20 – 21]中的结论相一致。
1.3 主要载荷控制参数采用北大西洋波浪散布图,以扭矩作为主要载荷控制参数,按照船舶结构规范[22]确定设计波参数。
| $ \lambda = \frac{{2{\text{π}}g}}{{\omega _a^2}}\text{,} $ | (2) |
式中:
| ${\alpha _w} = \frac{L}{A}\text{。}$ | (3) |
式中:
取沿船长1/4 L、1/2 L和3/4 L位置附近的扭矩作为主要载荷控制参数,对应的设计波见表1。扭矩载荷与设计波参数密切相关:1)易产生较大扭矩的浪向角为45°,60°,75°,105°和120°,对应的设计波波长为76.1 m,125.8 m和684.9 m;2)对应超越概率为10–2、10–4和10–8的设计波波幅,可近似为2倍关系;3)当主要载荷控制参数取4/20 L,10/20 L和14/20 L处的扭矩载荷时,设计波波幅达到极值。
|
|
表 1 设计波参数确定 Tab.1 Determination of design wave parameters |
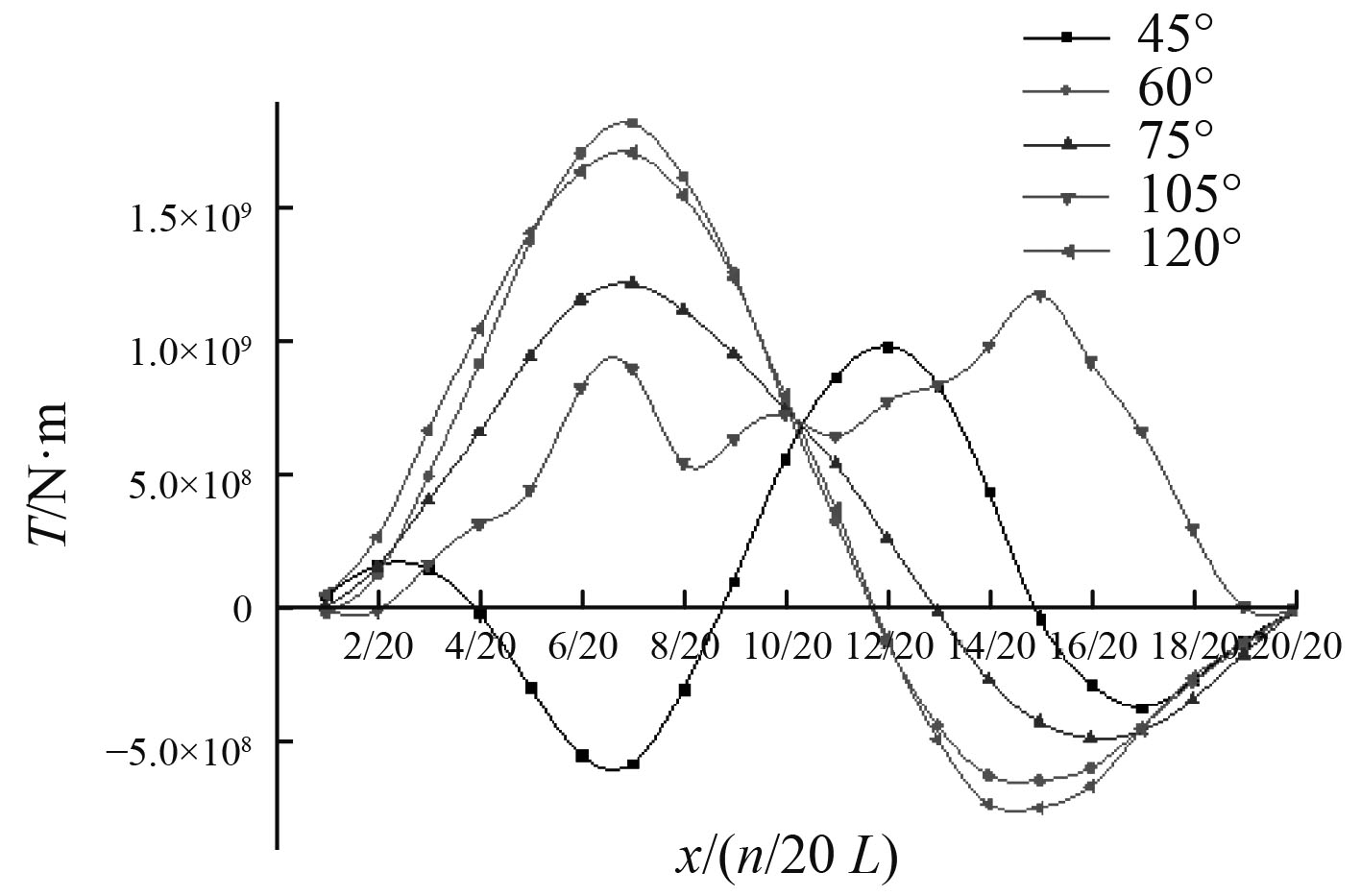
选择表1中45°,60°,75°,105°和120°的5个斜浪设计波,计算沿船长的“扭矩-位置”曲线见图3所示。
|
图 3 斜浪工况下扭矩沿船长的分布曲线 Fig. 3 Distribution of Ttorque along ship length under oblique wave |
设计波参数对扭矩影响较大:1)浪向角为60°或120°,波长约为1/4 L~1/3 L的设计波可能产生最大的扭矩载荷;2)扭矩沿船长分布曲线形似正弦,载荷最大值出现在位于7/20 L横截面处;3)45°和105°浪向角的扭矩曲线较为特别,沿船长出现多个扭矩极值,载荷最大值出现在12/20 L ~16/20 L横截面处。
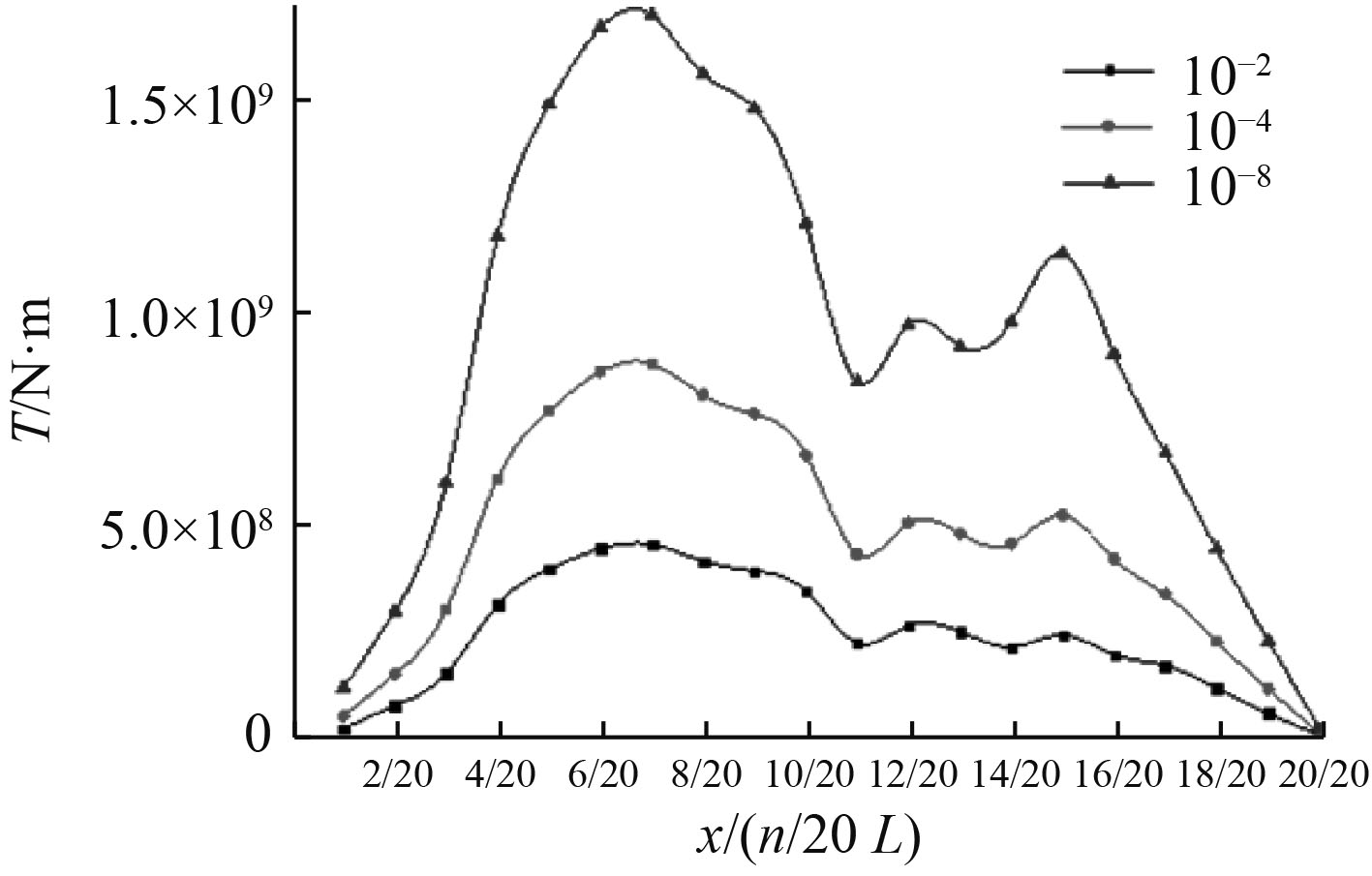
2.2 扭矩极值与超越概率的关系超越概率水平体现了不同的结构校核安全水平,通常总强度采用10–8超越概率、局部强度采用10–4超越概率,疲劳强度采用10–2超越概率。考虑10–2,10–4,10–8超越概率水平,计算各斜浪工况下扭矩的包络值,绘制沿船长分布的“扭矩极值-超越概率”曲线,如图4所示。
|
图 4 不同超越概率水平的扭矩极值曲线 Fig. 4 Torque extremum curves with different probability levels |
不同超越概率水平是的扭矩极值具有如下特征:1)不同概率水平的扭矩极值呈比例关系,可近似采用1.93倍换算;2)扭矩极值与船体型线有关,船体后半段的扭矩极值通常大于船体前半段;3)扭矩极值曲线的最大值通常出现在船中偏后7/20L位置,一般还会存在多个极大值。
2.3 与规范扭矩的对比分析美国船级社(ABS)集装箱船规范中扭矩载荷的计算公式[23]如下:
| $\begin{array}{l} {M_t} = {k_s}kL{B^2}d\left[ {{{\left( {{C_w} - 0.5} \right)}^2} + 0.1} \right]\\ \;\;\;\;\;\;\;\;\; \times \left[ {0.13 - \left( {e/D} \right){{\left( {{c_0}/d} \right)}^{0.5}}} \right] \end{array} $ | (4) |
式中:
虽然HCSR规范适用于油船和散货船,但其扭矩计算公式[24]考虑航向、型线、主尺度等参数,作为研究集装箱船扭矩的参考。
| ${M_t}\! =\!\! {f_\beta }\left( {0.4{f_{t1}}{C_W}\!\!\sqrt {\frac{L}{{{T_{LC}}}}} {B^2}D{C_b} \!+\! 0.22{f_{t2}}{C_W}L{B^2}{C_b}} \right)\text{。}\!\!$ | (5) |
式中:
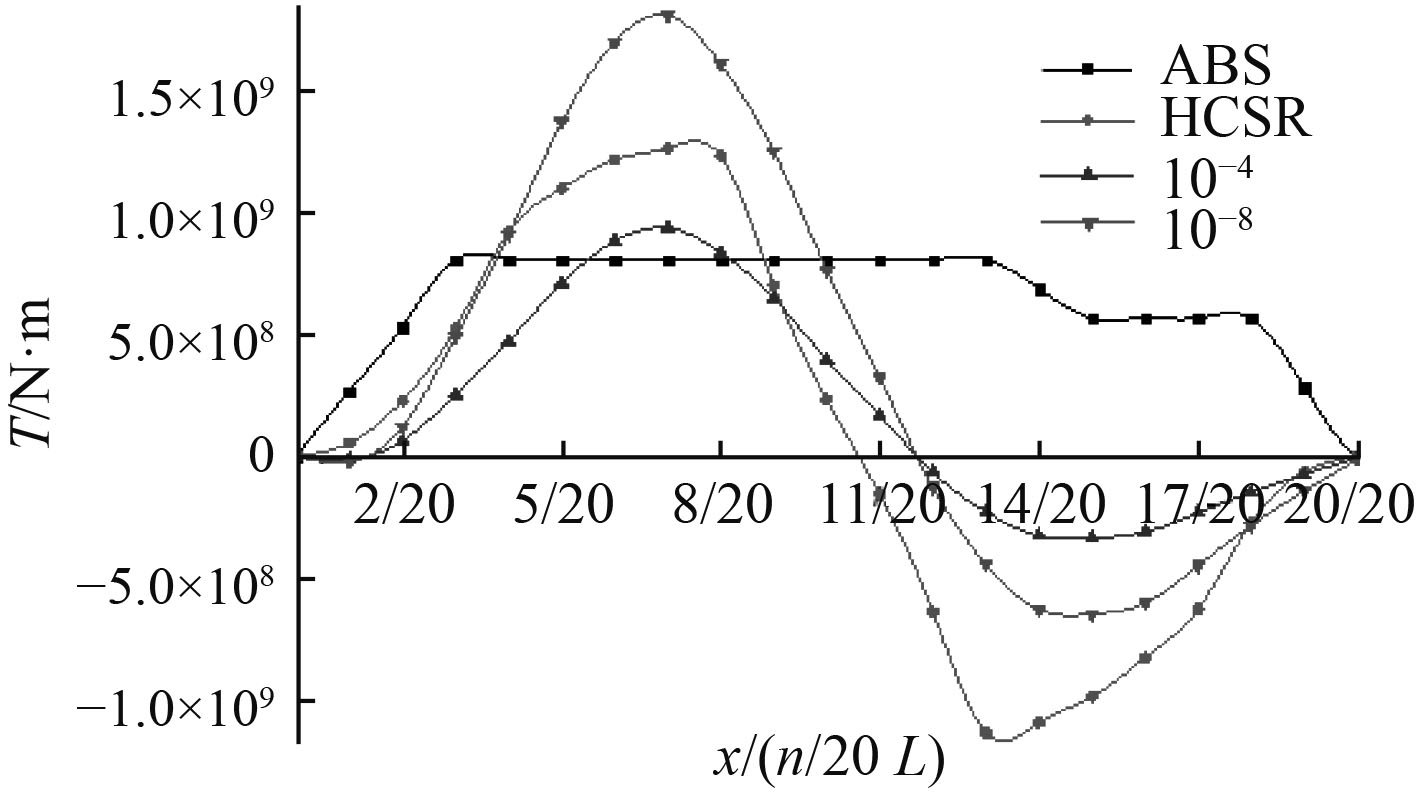
浪向角为60°时DLA计算扭矩值与ABS和HCSR规范扭矩载荷公式计算值的对比见图5。
|
图 5 规范扭矩和DLA计算扭矩对比 Fig. 5 Comparison of torque calculated by ship rule and DLA |
ABS规定该扭矩用于计算局部结构强度,扭矩曲线可近似为分段直线,在3/20 L~11/20 L处扭矩计算值最大,且最大值的作用范围大于DLA计算值,与超越概率10–4的DLA扭矩计算值大致相当,这也验证了“局部强度采用10–4超越概率水平”的观点。
HSCR规定该扭矩用于船体梁强度计算,规范扭矩曲线由多段曲线组合而成,曲线形状与DLA计算扭矩曲线相似,在船尾方向7/20 L ~8/20 L位置处出现扭矩最大值,该值较超越概率10–8的DLA扭矩计算值低30%左右,约与超越概率10–6.5的DLA扭矩计算值相当。
对比45°,60°和75°浪向下DLA扭矩计算曲线和HSCR扭矩计算曲线,如图6所示。

|
图 6 规范扭矩和不同浪向角DLA扭矩比较 Fig. 6 Comparison of torque under different wave directions |
ABS扭矩计算值约和45°浪向角时的DLA扭矩计算值相当,但曲线形状相反;HCSR扭矩计算值约和75°浪向角时的DLA扭矩计算值相当,曲线形状相似。
DLA扭矩计算值与船舶规范存在差异,可能的原因是:1)船型的差别,本文以集装箱船为研究对象,HSCR是散货船和油船规范,计算结果仅可作为借鉴;2)设计波和装载情况的差异,本文DLA计算考虑最恶劣斜浪和装载的组合,而ABS是综合多种因素的统计回归值;3)概率水平上的差异,本文DLA计算的超越概率水平分别为10–2,10–4和10–8,而规范中总强度主要考虑20年或25年一遇的概率水平、局部强度考虑10–4概率水平。
DLA计算扭矩最大值及作用范围与船舶规范要求存在一定差异,因此,对于大型集装箱船,在规范载荷的基础上,通过水动力分析直接预报扭矩值,具有必要性。
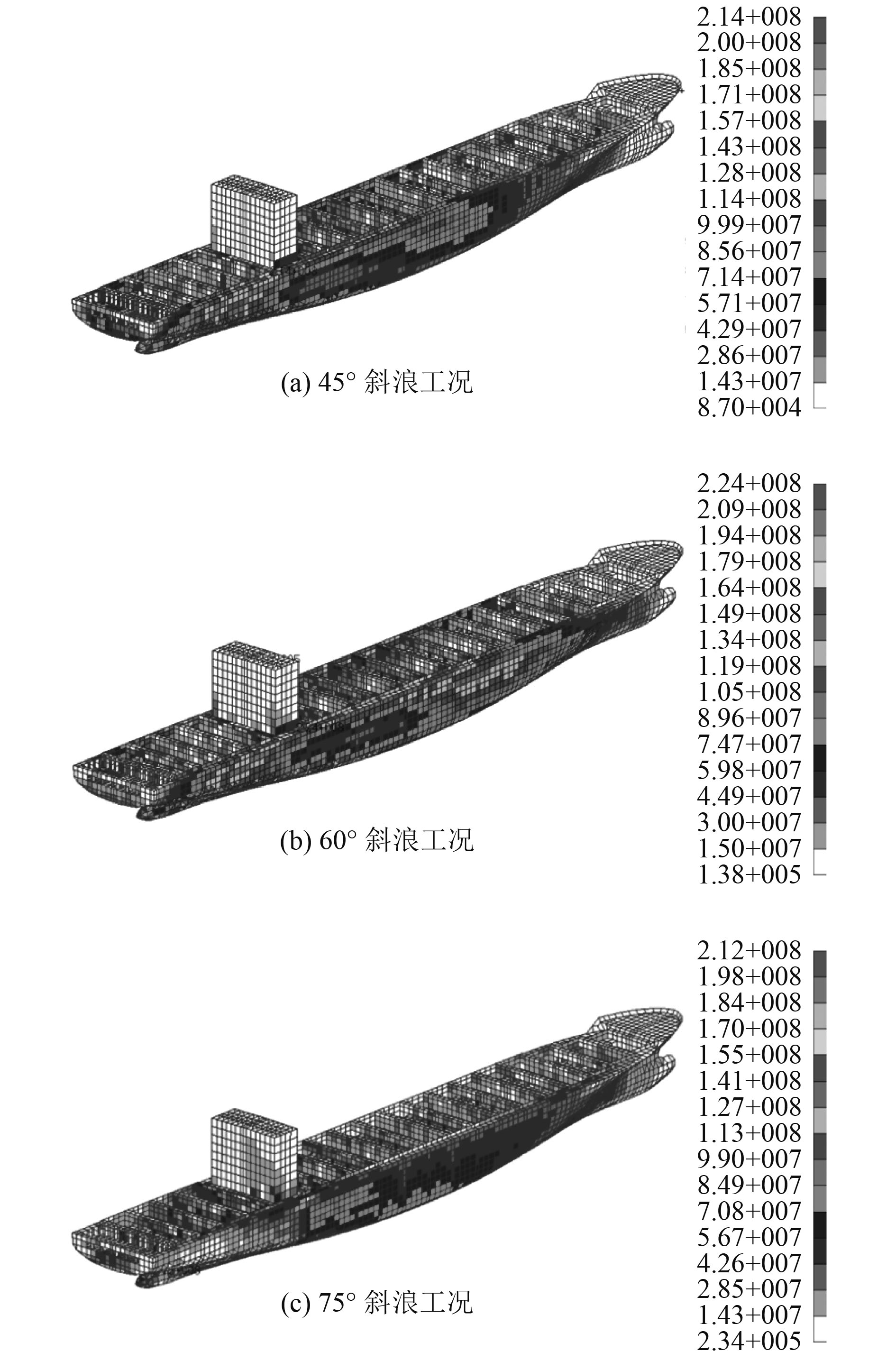
3 整船结构强度分析分别计算45°,60°和75°斜浪工况下的集装箱船的结构应力分布云图。
|
图 7 斜浪工况下集装箱船应力云图 Fig. 7 Stress of container ship under oblique wave condition |
斜浪工况下船体结构的最大应力通常出现在顶边舱、舱口角隅、机舱等位置,对应不同斜浪应力分布有所差别:当45°斜浪时,右舷的应力较大,最大应力出现在机舱后部的舱口角隅,达214 MPa;当60°斜浪时,顶边舱附近的应力都较大,最大应力出现在机舱附近,达224 MPa;当75°斜浪时,机舱附近应力较大,最大应力出现在机舱后舱壁,达212 MPa。
对于不同的结构强度校核目标,如典型横剖面的扭转强度、舱口角隅的翘曲应力、抗扭箱结构强度等,应通过水动力分析确定相对校核目标最恶劣的斜浪,包括浪向角、设计波长、超越概率水平等。
4 结 语1)斜浪设计波参数是扭矩载荷的关键要素,本文集装箱船水动力分析算例中,最恶劣斜浪对应的设计波参数为浪向角为60°或120°,设计波长为125.8 m(1/3 L~1/4 L),最大扭矩出现在船中偏后的7/20 L截面处;
2)超越概率水平体现了不同的结构校核安全水平,对应10–2,10–4和10–8超越概率,沿船长分布的扭矩载荷包络值曲线形状相似,计算值呈比例关系(约为1.93倍),开展总强度、局部强度和疲劳强度分析时,需根据不同的校核目标选择相应的超越概率;
3)ABS规范与超越概率为10–4的DLA的扭矩最大值相当,但分布趋势有所差异,HCSR规范与DLA的扭矩分布趋势相当,但最大值仅相当于超越概率为10–6.5的DLA扭矩计算值,建议集装箱船结构设计时,除满足规范要求,还应开展恶劣斜浪工况下的扭矩载荷直接计算;
4)集装箱船整船结构强度直接计算结果表明,斜浪设计波参数对集装箱整船结构应力分布具有重要影响,特别是顶边舱、舱口角隅和机舱前后端等位置,集装箱船结构设计时需引起重视。
| [1] |
ALFRED MOHAMMED E, BENSON S D, HIRDARIS S E, et al. Design safety margin of a 10, 000 TEU container ship through ultimate hull girder load combination analysis[J]. Marine Structures, 2016(46): 78-101. |
| [2] |
Ingrid Marie Vincent Andersen, Jørgen Juncher Jensen. Measurements in a container ship of wave induced hull girder stresses in excess of design values[J]. Marine Structures, 2014(37): 54-85. |
| [3] |
张聆玲, 钟进蓉. 船体梁结构强度的非线性有限元分析[J]. 舰船科学技术, 2019, 41(3A): 10-12. ZHANG Lingling, ZHONG Jinrong. Nonlinear finite element analysis of hull beam structural strength[J]. Ship Science and Technology, 2019, 41(3A): 10-12. |
| [4] |
王翀. 超大型集装箱船扭转强度研究[J]. 船舶工程, 2015(37): 28-30, 52. |
| [5] |
彭亚康, 王伟飞, 韩钰, 等. 超大型集装箱船载荷响应特性的数值研究[J]. 舰船科学技术, 2019, 41(3): 62-67. PENG Yakang, WANG Weifei, HAN Yu, et al. The numerical research for wave load response characteristic of ultra large container[J]. Ship Science and Technology, 2019, 41(3): 62-67. |
| [6] |
PAPANIKOLAOU A, ALFRED MOHAMMED E, SPYROS E, HIRDARIS. Stochastic uncertainty modelling for ship design loads and operational guidance[J]. Ocean Engineering, 2014(86): 47-57. |
| [7] |
ZHU Suji, MOAN T. Nonlinear effects from wave-induced maximum vertical bending moment on a flexible ultra large containership model in severe head and oblique seas[J]. Marine Structures, 2014(35): 1-25. |
| [8] |
TAKAMI T, MATSUI S, OKA M, et al. A numerical simulation method for predicting global and local hydroelastic response of a ship based on CFD and FEA coupling[J]. Marine Structures, 2018(59): 368-386. |
| [9] |
HONG-Il IM, VLADIMIR N, MALENICA S, et al. Hydroelastic response of 19, 000 TEU class ultra large container ship with novel mobile deckhouse for maximizing cargo capacity[J]. International Journal of Naval Architecture and Ocean Engineering, 2017(9): 339-349. |
| [10] |
RAJENDRAN S, GUEDESSOARES C. Numerical investigation of the vertical response of a container ship in large amplitude waves[J]. Ocean Engineering, 2016(123): 440-451. |
| [11] |
Wang Chonglei, Wu Jiameng, Wang Deyu. Numerical investigation of three-dimensional hull girder ultimate strength envelope for an ultra large container ship[J]. Ocean Engineering, 2018(149): 23-37. |
| [12] |
顾永宁, 滕小青, 顾立广, 等. 大开口船波浪载荷长期预报和弯扭强度整船有限元分析[J]. 中国造船, 1998, 39(2): 63-70. |
| [13] |
TEMAREL P, BAI W, BRUNS A, et al. Prediction of wave-induced loads on ships: Progress and challenges[J]. Ocean Engineering, 2016(119): 274-308. |
| [14] |
YONGHWAN K, HYUNKIM J. Benchmark study on motions and loads of a 6750-TEU container ship[J]. Ocean Engineering, 2016(119): 262-273. |
| [15] |
郭文, 王铁钢. 集装箱船上层建筑结构优化研究[J]. 舰船科学技术, 2019, 41(2A): 16-18. GUO Wen, WANG Tiegang. Research on optimization of superstructure of container ship[J]. Ship Science and Technology, 2019, 41(2A): 16-18. |
| [16] |
陈庆强, 朱胜昌. 大型集装箱船整船有限元分析计算技术研究[J]. 船舶力学, 2006, 10(1): 80-91. CHEN Qingqiang, ZHU Shengchang. Research on numerical technique of whole large container ship by FEM[J]. Journal of Ship Mechanics, 2006, 10(1): 80-91. DOI:10.3969/j.issn.1007-7294.2006.01.011 |
| [17] |
赵欣, 高茜. 超大型集装箱船全船结构强度分析[J]. 造船技术, 2018(3): 6-12. DOI:10.3969/j.issn.1000-3878.2018.03.002 |
| [18] |
Zhanyang CHEN, Jialong JIAO, Hui LI. Time-domain numerical and segmented ship model experimental analyses of hydroelastic responses of a large container ship in oblique regular waves[J]. Applied Ocean Research, 2017(67): 78-93. |
| [19] |
Sime MALENICA, Quentin DERBANNE. Hydro-structural issues in the design of ultra large container ships[J]. International Journal of Naval Architecture and Ocean Engineering, 2014(6): 983-999. |
| [20] |
Myung-Jae SONG, Kyong-HwanKim, YonghwanKim. Numerical analysis and validation of weakly nonlinear ship motions and structural loads on a modern container ship[J]. Ocean Engineering, 2011(38): 77-87. |
| [21] |
S. E. HIRDARIS, Y. LEE, G. MORTOLA, et al. The influence of nonlinearities on the symmetric hydrodynamic response of a 10, 000 TEU Container ship[J]. Ocean Engineering, 2016(111): 166-178. |
| [22] |
中国船级社(CCS). 钢质海船入级规范[S]. 北京: 人民交通出版社有限公司, 2015.
|
| [23] |
American Bureau of Shipping (ABS). Rules for Building and Classing Steel Vessels[S]. Houston: ABS, 2015.
|
| [24] |
International Association of Classification Societies (IACS). Common Structural Rules for Bulk Carriers and Oil Tankers[S]. London: IACS, 2018.
|
 2019, Vol. 41
2019, Vol. 41
