2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics (HUST), Wuhan 430074, China
随着各国对清洁能源的需求不断增加,全球范围内天然气运输量也在快速增长。与气态形式相比,LNG能量密度高、易于储存,非常适合陆上或海上长距离运输。LNG船液货舱通常可分为2种类型:薄膜型和独立型[1]。独立型液货舱又可以分为A型、B型和C型[2]。B型液货舱的货物维护系统主要包括液货舱和支撑结构,其特点在于液货舱具有部分次屏蔽且不作为压力容器。液货舱和船体通过弹性支撑结构连接。船体运动时,支撑可将作用力传递给液货舱,引起液货舱运动,进而激发舱内液体的晃荡。此时,晃荡载荷不仅会威胁液货舱的结构安全,也会使支撑结构受到的作用力增大。因此,在设计阶段,必须考虑晃荡载荷对支撑结构作用力的影响。
随着计算机性能的提高和相关理论的发展,越来越多的数值方法和求解技术被应用于液舱晃荡的研究[3],如有限元法(Finite Element,FE)[4],流体体积法(Volume of Fluid,VOF)[5],任意拉格朗日-欧拉法(Arbitrary Lagrangian-Eulerian,ALE)[6]等。
本文以1艘LNG船B型独立液货舱为研究对象,建立二维模型,基于ALE方法和体积模量缩减技术,运用有限元软件Abaqus对液舱晃荡进行分析,得到横摇状态下支撑结构作用力的时间响应。讨论了船体横摇幅值、货物状态以及液货舱挡板布置对支撑结构作用力的影响。
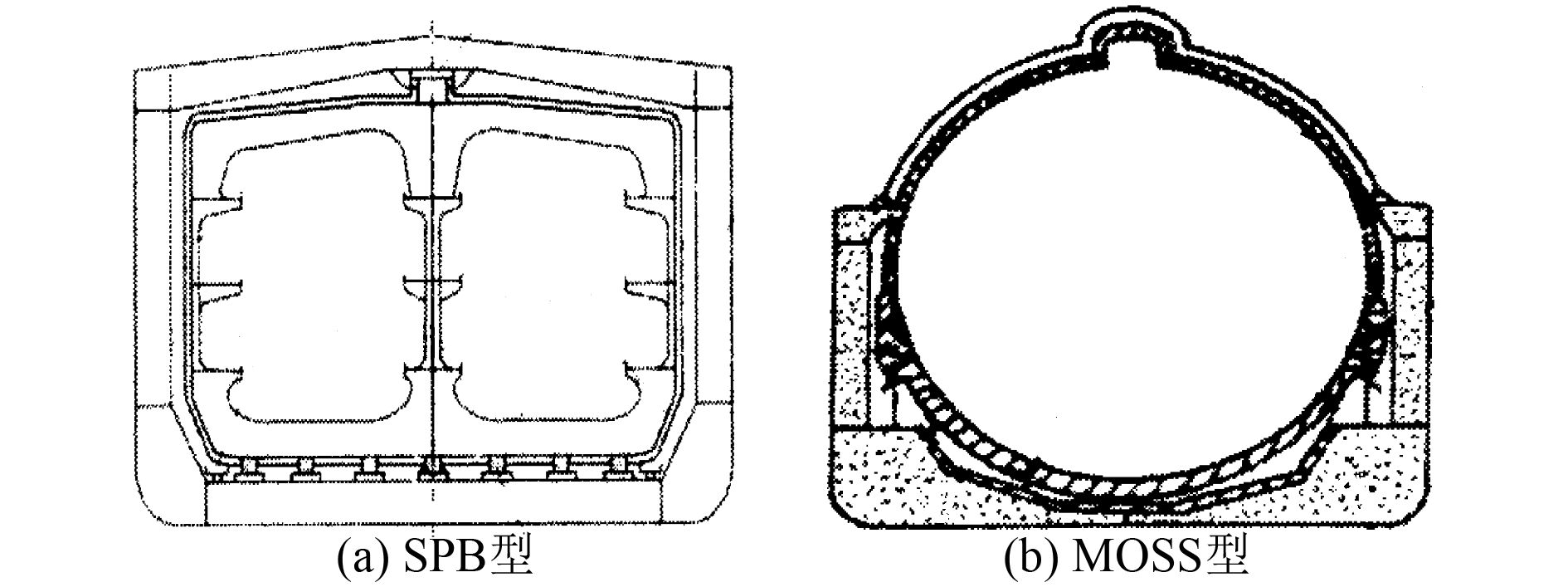
1 研究对象B型液货舱按形状可分为棱柱形(SPB型)和球形(MOSS型),如图1所示[7]。本文的研究对象是棱柱形液货舱,主要由耐低温的平面板材制成。
|
图 1 B型独立液货舱 Fig. 1 Independent type B tank |
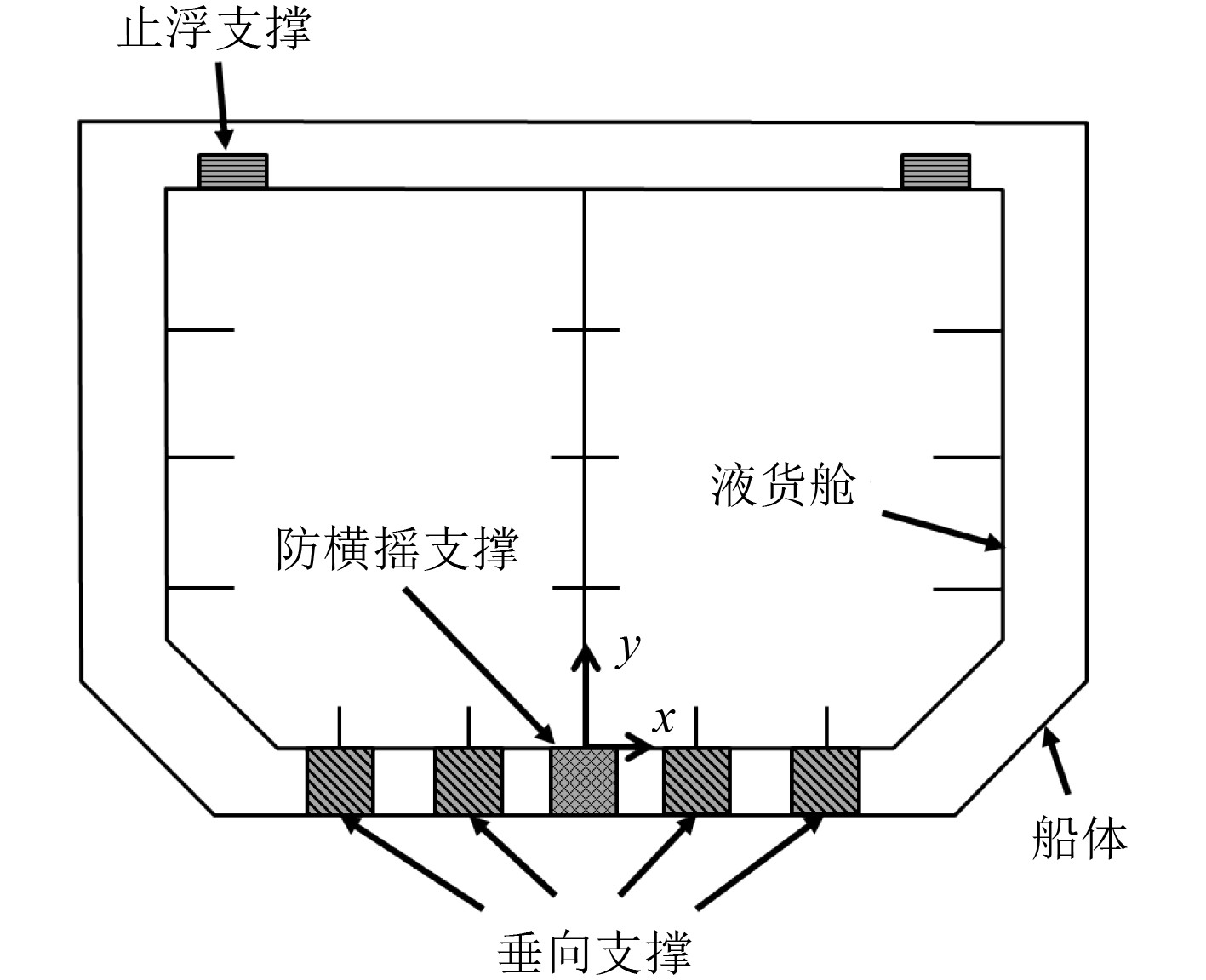
支撑结构用于连接船体和液货舱。根据其安装位置和功能的不同,支撑结构可分为垂向支撑、防横摇支撑、防纵摇支撑以及止浮支撑等,如图2所示。垂向支撑和止浮支撑用于支持液货舱,防止其与船体发生碰撞,可提供y方向的作用力,且只受压不受拉。防横摇支撑和防纵摇支撑用于减轻由船体运动引起的液货舱晃动,可提供x或z方向的作用力。
|
图 2 B型独立液货舱支撑结构 Fig. 2 Support structure of independent type B tank |
本文利用有限元软件Abaqus的显式动态分析模块(Abaqus/Explicit,Dynamic),采用任意拉格朗日-欧拉自适应网格技术(Arbitrary Lagrangian-Eulerian adaptive meshing technique)和体积模量缩减技术(Bulk modulus reduction technique),对B型独立液货舱的晃荡问题进行研究。
使用有限元法对液舱晃荡进行分析时,若流体单元变形过大则极易导致计算不收敛。ALE自适应网格技术可以有效解决这一问题,它结合了拉格朗日方法(网格点与物质点重合,网格之间没有物质的转移)和欧拉法(网格点固定,物质可以在网格间自由转移)的优点,能够在不改变网格原有拓扑结构的情况下保证网格质量,增大计算结果的收敛性和准确性。ALE方法的物质导数描述为[8]:
| $ \frac{{\partial f\left( {{X_i},t} \right)}}{{\partial t}} = \frac{{\partial f\left( {{x_i},t} \right)}}{{\partial t}} + \frac{{\partial f\left( {{x_i},t} \right)}}{{\partial {x_i}}}{w_i} {\text{。}}$ | (1) |
其中:
该方法的质量守恒、动量守恒和能量守恒控制方程分别为:
| $ \frac{{\partial \rho }}{{\partial t}} = - \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} - {w_i}\frac{{\partial \rho }}{{\partial {x_i}}}{\text{,}} $ | (2) |
| $ \rho \frac{{\partial {v_i}}}{{\partial t}} = {\sigma _{ij,j}} + \rho {b_i} - \rho {w_i}\frac{{\partial {v_i}}}{{\partial {x_j}}} {\text{,}}$ | (3) |
| $ \rho \frac{{\partial E}}{{\partial t}} = {\sigma _{ij,j}}{v_{i,j}} + \rho {b_i}{v_i} - \rho {w_j}\frac{{\partial E}}{{\partial {x_j}}}{\text{。}} $ | (4) |
其中:
本文将LNG假定为无粘性不可压缩流体,在Abaqus中使用Mie-Grüneisen状态方程对其建模。一种常见的Mie-Grüneisen状态方程表达为[9-10]:
| $ p - {p_{ref}} = \mathit{\Gamma} \rho \left( {e - {e_{ref}}} \right){\text{。}} $ | (5) |
其中:
| $ \Gamma = \frac{1}{\rho }{\left. {\frac{{\partial p}}{{\partial e}}} \right|_\rho }{\text{。}} $ | (6) |
Abaqus引入了线性
| $ {p_{ref}} = \frac{{{\rho _{ref}}c_0^2\eta }}{{{{\left( {1 - s\eta } \right)}^2}}}{\text{。}} $ | (7) |
其中:
| $ {U_S} = {c_0} + s{U_P}{\text{。}} $ | (8) |
在小应变情况下,有下式成立:
| $ K = {\rho _{ref}}c_0^2{\text{,}} $ | (9) |
其中,
数值分析中采用体积模量缩减技术能够在保证结果精度的情况下缩短计算时间。有限元分析时,稳态时间增量步长
| $ \Delta t \approx \frac{{{L_{\min }}}}{{{c_d}}}{\text{。}} $ | (10) |
其中:
| $ {c_d} = \sqrt {\frac{{E\left( {1 - \mu } \right)}}{{\rho \left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}}{\text{。}} $ | (11) |
考虑到体积模量的表达式为:
| $ K = \frac{E}{{3\left( {1 - 2\mu } \right)}}{\text{,}} $ | (12) |
将式(12)代入式(11),得到:
| $ {c_d} = \sqrt {K\frac{{3\left( {1 - \mu } \right)}}{{\rho \left( {1 + \mu } \right)}}}{\text{。}} $ | (13) |
可以看出,若减小材料的体积模量
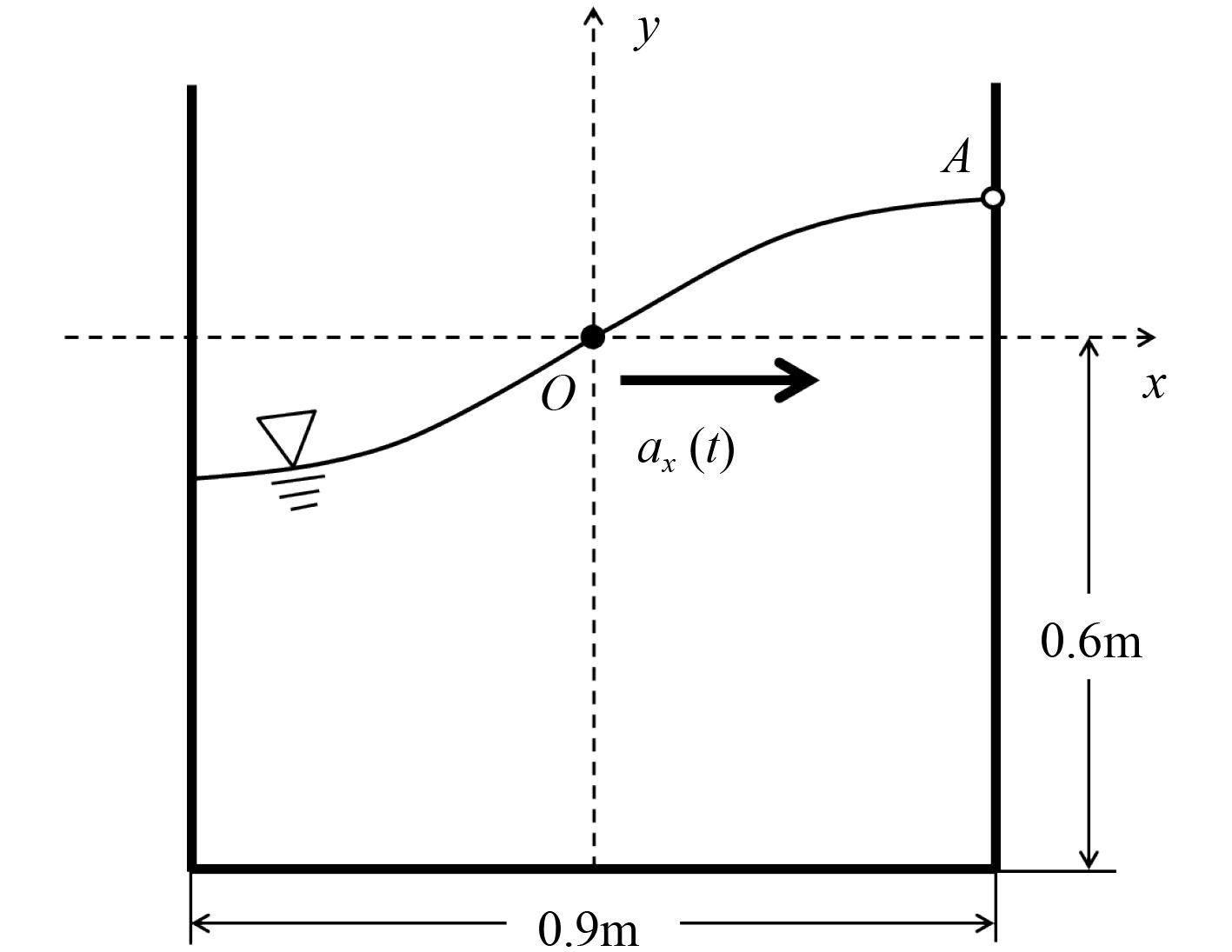
为验证上述数值方法的准确性,选取参考文献[15]中的二维矩形容器晃荡算例进行分析,如图3所示。
|
图 3 二维矩形容器晃荡算例 Fig. 3 Sloshing case of a two-dimensional container |
该矩形容器在水平方向外力作用下发生受迫振动,其水平加速度可表示为:
| $ {a_x}\left( t \right) = - {X_0}{\omega ^2}{\rm sin} \omega t{\text{。}} $ | (14) |
其中:加速度幅值X0=0.002 m;角速度ω=5.5 rad/s;重力加速度g=9.8 m/s2。容器内液体为水,密度
|
|
表 1 不同模型的计算时间 Tab.1 Computation time of different models |
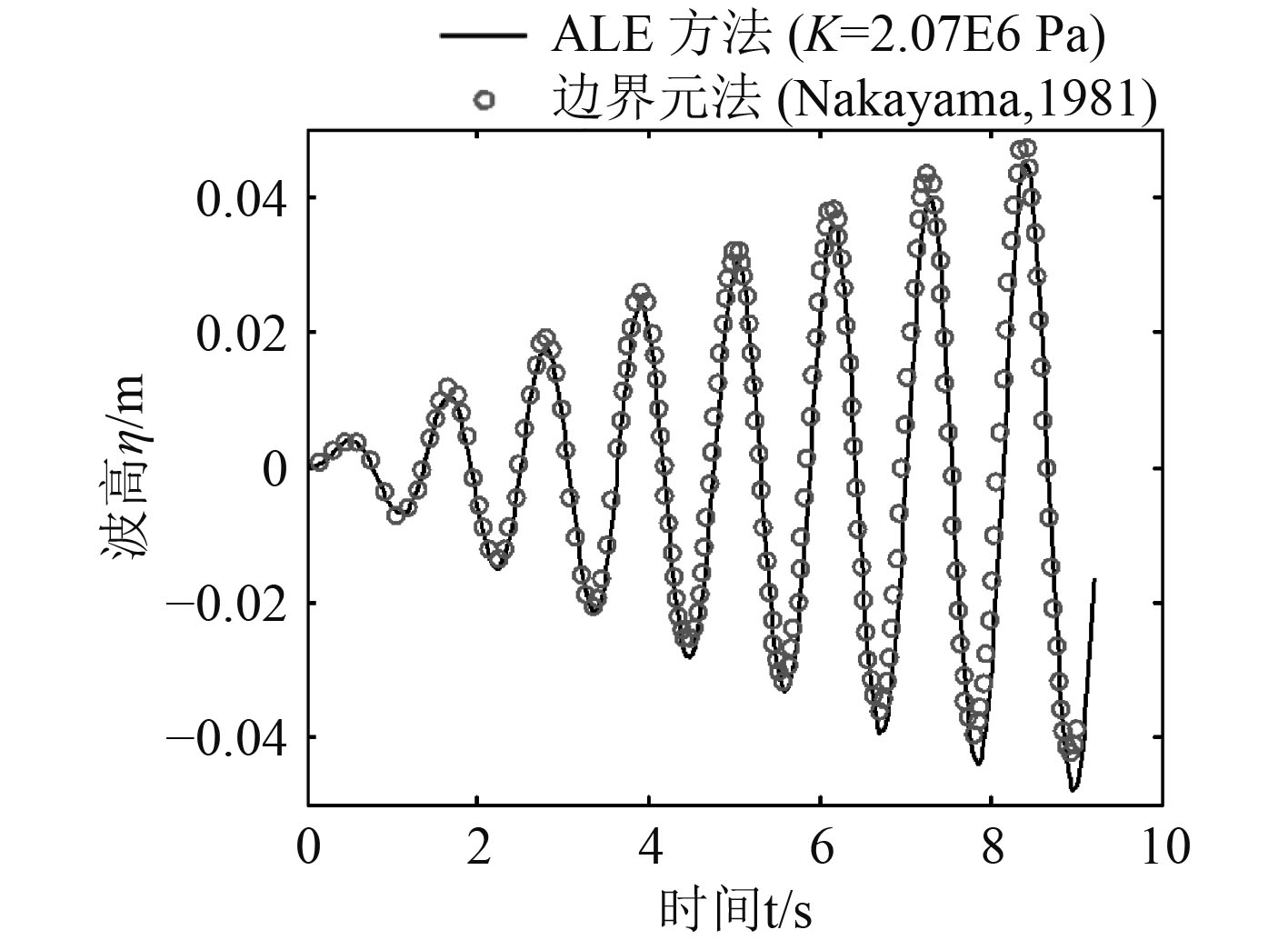
|
图 4 自由液面上A点的波高变化 Fig. 4 Variation of wave height at point A |
可以看出,随着体积模量的缩减,计算时间也在减少。将体积模量缩减为真实值的1/‰,即
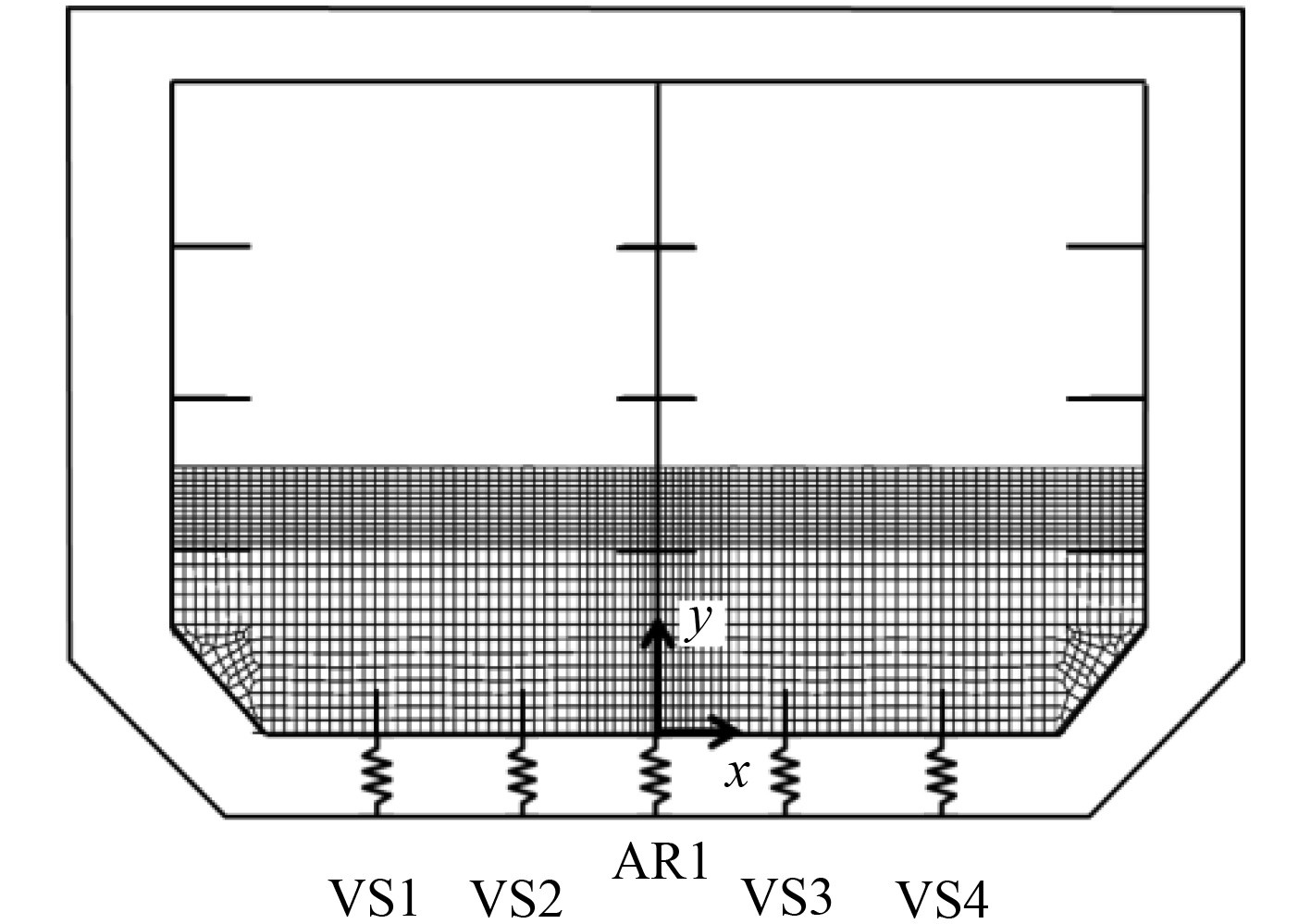
本文以1艘典型LNG船B型独立液货舱为例,建立横剖面二维模型。液货舱宽11.0 m,高6.0 m,位于中线处的纵向水密舱壁将其分为2个体积相等的舱室。液货舱主体结构,如外板、纵向舱壁、桁材等,均由刚体单元(R2D2)建模。模型包含5个支撑结构,中纵舱壁底部有1个防横摇支撑,液货舱底部关于中纵舱壁对称分布有4个垂向支撑。为方便计算,将这些支撑简化为弹性连接,由连接单元(CONN2D2)建模。防横摇支撑具有x方向刚度,垂向支撑具有y方向受压刚度,刚度系数取值见表2。有限元模型如图5所示。其中,VS1~VS4表示垂向支撑,AR1表示防横摇支撑。
|
|
表 2 支撑结构刚度系数 Tab.2 Stiffness coefficient of support structure |
|
图 5 B型独立液货舱有限元模型 Fig. 5 FE model of the independent type B tank |
液货舱装载率为40%,LNG由平面应变单元(CPE4R)建模。对自由表面附近的网格进行加密处理。不考虑液体和液货舱之间的摩擦力。LNG物理属性如表3所示[16]。
|
|
表 3 LNG物理属性 Tab.3 Material properties of LNG |
从运动状态、货物状态和液货舱内有无挡板3个方面考虑,选择7种计算工况,如表4所示。
|
|
表 4 计算工况 Tab.4 Computation case |
液货舱按如下正弦规律做横摇运动:
| $ \varphi = - {\varphi _0}\sin \omega t{\text{。}} $ | (15) |
其中,横摇幅值为φ0,角速度ω=0.748 rad/s,相应的运动周期T=8.4 s,为获得稳定结果,计算时长选为5个周期。
为验证连接单元的准确性与可靠性,计算LC1工况,比较支撑结构作用力与液货舱自身重力。为分析不同横摇幅值对支撑结构作用力的影响,分别对φ0=5°和φ0=8°两种情况下的液舱晃荡进行计算。为分析液体和固体货物对支撑结构作用力的影响,计算LC4和LC7工况,货物状态为液体表示装载LNG,货物状态为固体表示装载与LNG具有相同密度和体积的固体,计算时当作刚体处理。为分析液货舱内挡板对支撑结构作用力的影响,分别计算有挡板和无挡板2种情况。
3 计算结果对于LC1工况,液货舱静止时,仅有4个垂向支撑受到y方向的作用力。将计算得到的连接单元作用力与液货舱重力进行对比,结果如表5所示。
|
|
表 5 LC1工况下垂向支撑的作用力 Tab.5 Force on the vertical support structure in LC1 |
4个垂向支撑的总支持力与液货舱重力的误差小于1%,说明连接单元能够较好的模拟支撑结构,传递作用力。
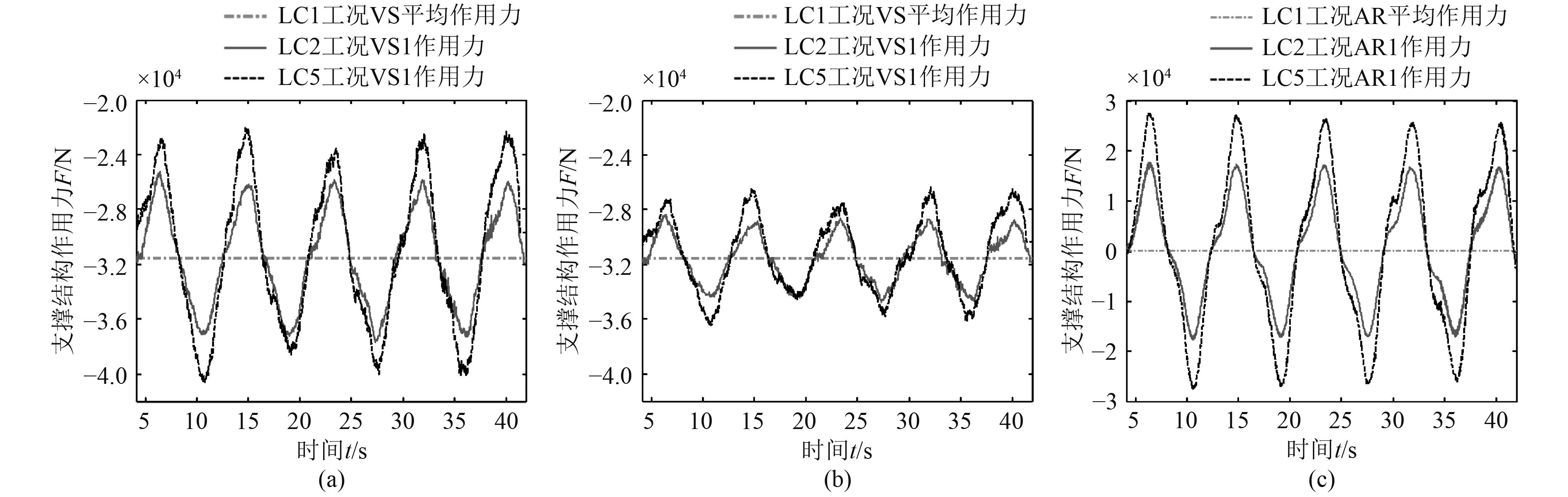
图6和图7分别对比了无挡板和有挡板的液货舱模型在不同横摇幅值下支撑结构的受力情况。可以看出,支撑结构的作用力随着船体横摇呈现出周期性变化。对于垂向支撑VS,液货舱静止时平均作用力
|
图 6 LC2和LC5工况支撑结构作用力对比 Fig. 6 Comparison of force on supports in LC2 and LC5 |
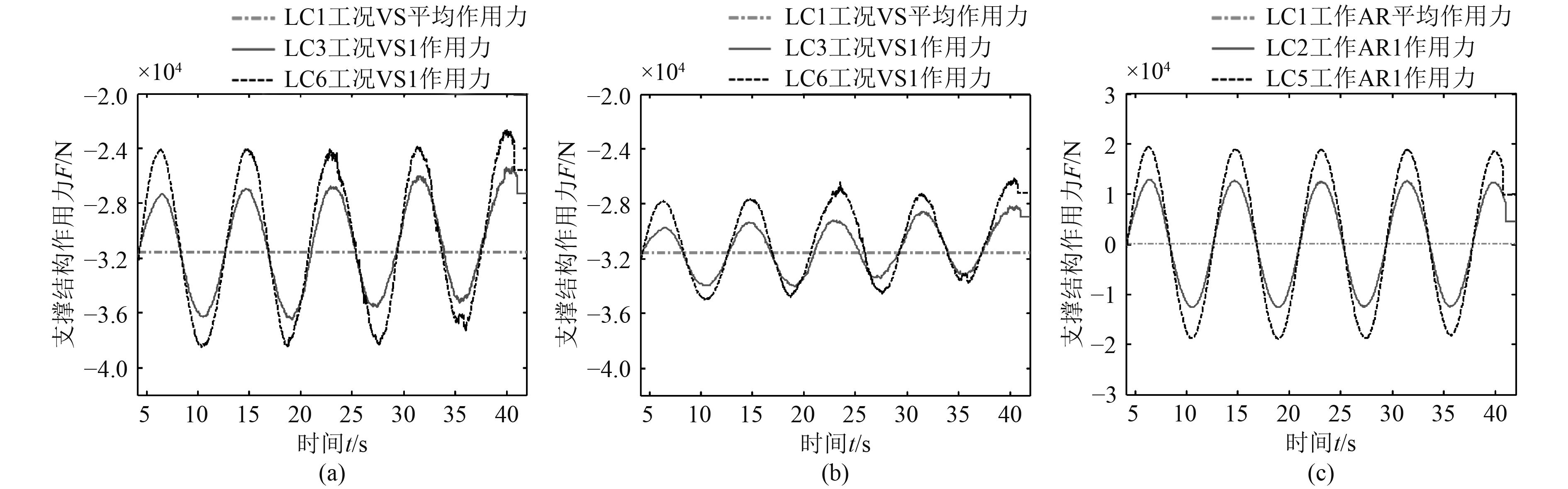
|
图 7 LC3和LC6工况支撑结构作用力对比 Fig. 7 Comparison of forces on supports in LC3 and LC6 |
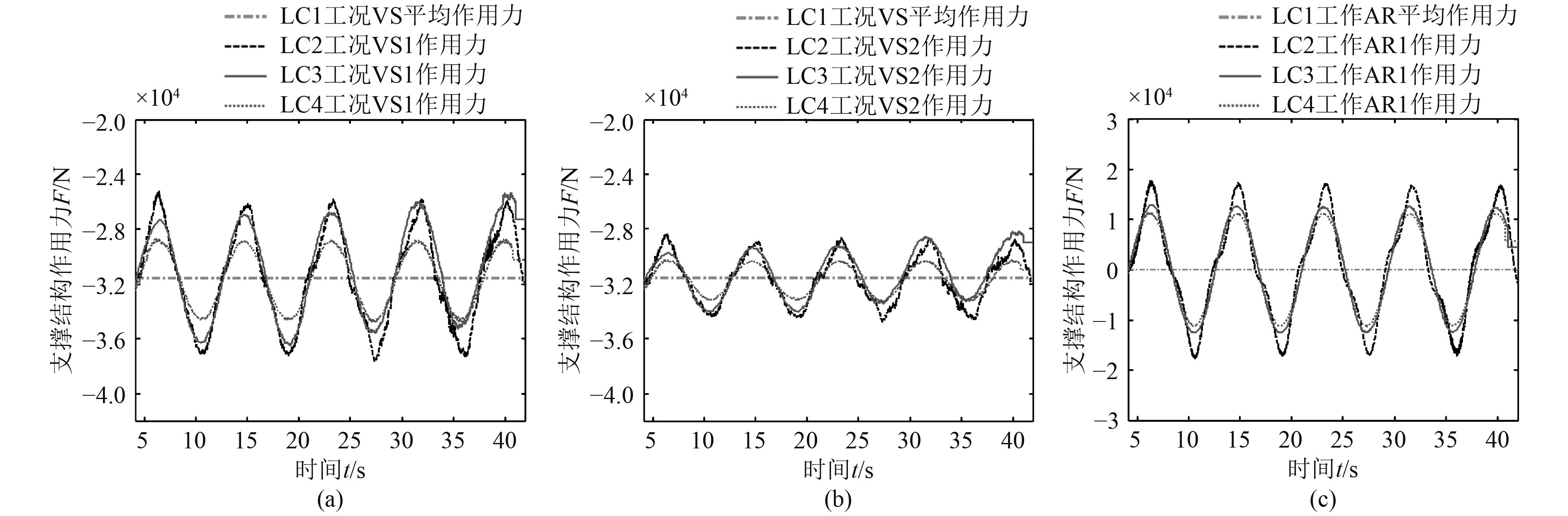
图8和图9分别对比了横摇幅值不同的液货舱模型在无挡板、有挡板以及装载固体货物时支撑结构的受力情况。可以看出,无论液货舱内有挡板还是没有挡板,装载液体还是固体,支撑结构作用力均具有类似的周期性变化规律。对于所有支撑,液货舱无挡板时支撑结构作用力变化范围最大,有挡板时次之,装载固体货物时最小。这说明,由于晃荡效应的存在,相对于固体货物,液体货物使支撑结构承受了更大的作用力。同时,在液货舱设置挡板能够有效降低作用力变化范围。
|
图 8 LC2,LC3和LC4工况支撑结构作用力对比 Fig. 8 Comparison of forces on supports in LC2,LC3 and LC4 |

|
图 9 LC5,LC6和LC7工况支撑结构作用力对比 Fig. 9 Comparison of forces on supports in LC5,LC6 and LC7 |
本文利用有限元法,采用任意拉格朗日-欧拉自适应网格技术和体积模量缩减技术,对LNG船B型独立液货舱进行晃荡分析,并探讨了晃荡对支撑结构作用力的影响。通过与文献数据对比,验证了数值方法的可靠性;建立有二维限元模型,根据横摇幅值、液货舱布置以及货物形态选取7个工况进行计算;比较不同工况下支撑结构作用力随时间的变化,得到以下结论:
1)船体做周期性横摇运动时,支撑结构作用力也呈现出周期性变化,且在平衡位置附近波动;
2)船体横摇幅值越大,支撑结构作用力的变化范围越大;
3)由于液舱晃荡,装载液体货物时支撑结构作用力的变化范围大于装载相同密度和体积的固体货物时的变化范围;
4)液货舱内设置挡板能够降低支撑结构作用力的变化范围。
| [1] |
刘文夫, 薛鸿祥, 唐文勇, 等. 独立B型LNG棱形液舱晃荡载荷数值分析[J]. 船舶工程, 2015(7): 22-25. LIU Wen-fu, XUE Hong-xiang, TANG Wen-yong, et al. Sloshing loads analysis of LNG carrier with independent Type B prismatic tanks[J]. Ship Engineering, 2015(7): 22-25. |
| [2] |
IMO, International code for the construction and equipment of ships carrying liquefied gases in bulk[S]. International Maritime Organization (IMO), 2012.
|
| [3] |
陆志妹, 范佘明. 船舶液舱晃荡研究进展[J]. 船舶与海洋工程, 2010(2): 14–16.
|
| [4] |
NAKAYAMA T, WASHIZU K. Nonlinear analysis of liquid motion in a container subject to forced pitching oscillation[J]. International Journal for Numerical Methods in Engineering, 1980, 15(8): 1207-1220. DOI:10.1002/nme.1620150808 |
| [5] |
HIRT CW, NICHOLS BD. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [6] |
HIRT CW, AMSDEN AA, COOK JL. An arbitrary Lagrangian-Eulerian computing method for all flow speeds[J]. Journal of Computational Physics, 1974, 14(3): 227-253. DOI:10.1016/0021-9991(74)90051-5 |
| [7] |
王永伟, 王晶. SPB储罐系统设计及特点[J]. 船舶物资与市场, 2007(6): 18–20.
|
| [8] |
丁峻宏, 金允龙, 王惠. 基于ALE的矿粉货物液化晃荡问题并行数值模拟[J]. 船舶力学, 2015(8): 927-933. DING Jun-hong, JIN Yun-long, WANG Hui. ALE-based parallel numerical simulation for sloshing problem of liquefied ore fines cargo[J]. Journal of Ship Mechanics, 2015(8): 927-933. DOI:10.3969/j.issn.1007-7294.2015.08.006 |
| [9] |
郑建国. 一般状态方程多流体界面数值方法研究[D]. 合肥: 中国科学技术大学, 2005.
|
| [10] |
吴宗铎, 严谨, 蒋颉, 等. 基于Mie-Grüneisen状态方程的水下爆炸数值模拟[J]. 舰船科学技术, 2017, 39(13): 29-33. WU Zong-duo, YAN Jin, JIANG Jie, et al. The numerical simulation of underwater explosion based on Mie-Grüneisen equation of state[J]. Ship Science and Technology, 2017, 39(13): 29-33. |
| [11] |
ABAQUS 6.10. Analysis user’s manual[M]. Dassault Systèmes, 2010.
|
| [12] |
莫建军, 孙承纬. 200 GPa压力范围内铝和铜的等熵压缩线计算[J]. 高压物理学报, 2006, 20(4): 386-390. MO Jian-jun, SUN Cheng-wei. Compression isentropes of aluminum and copper up to 200 GPa[J]. Chinese Journal of High Pressure Physics, 2006, 20(4): 386-390. DOI:10.3969/j.issn.1000-5773.2006.04.008 |
| [13] |
冉宪文. 混合物高压物态方程的理论研究[D]. 长沙: 国防科学技术大学, 2002.
|
| [14] |
程利冬, 王忠金. 高速锤击体积变形过程的有限元分析[J]. 哈尔滨工程大学学报, 2008, 29(2): 183-188. CHENG Li-dong, WANG Zhong-jin. Finite element analysis of the deformation process in high impact hammering[J]. Journal of Harbin Engineering University, 2008, 29(2): 183-188. DOI:10.3969/j.issn.1006-7043.2008.02.016 |
| [15] |
NAKAYAMA T, WASHIZU K. The boundary element method applied to the analysis of two-dimensional nonlinear sloshing problems[J]. International Journal for Numerical Methods in Engineering, 1981, 17(11): 1631-1646. DOI:10.1002/nme.1620171105 |
| [16] |
杜显赫. 预应力LNG储罐在地震作用下的流固耦合数值模拟[D]. 沈阳: 沈阳工业大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
