相比于航母宽阔的飞行甲板,航母上层建筑就像处于海洋中的岛屿,故称之为岛式上层建筑。岛式上层建筑均采用偏离主船体中心线的方式设置,一般总长度跨主船体4~5个站距,大致相当于一艘小型护卫舰的总长度,因而岛式上层建筑存在总强度问题,且是航母工程中一个重要的局部强度问题。
对于岛式上层建筑总强度,文献[1]推荐采用有限条法:按上层建筑长度取一段含上层建筑的船体结构,取该长度为有限条的长度,将纵向加强筋平摊在外板、侧壁板和纵向舱壁上,视船体(含上层建筑)横截面为沿纵向无变化的单一几何图形而进行有限条的横向划分,在有限条的两端作用总纵弯矩而求出各有限条的位移,在此基础上求出上层建筑的应力而得到其总强度。这种方法较简便,所需计算机内存小,计算工作量较小,在计算机硬件技术尚不发达且对上层建筑强度计算精度要求不高的前提下,是一种不错的选择。但岛式上层建筑其内外部结构非常复杂且不规则,不仅整体不对称且各层结构大小存在差异,因此将实船结构离散成有限条会导致强度计算结果出现较大的误差。随着科学技术的发展,使船体强度计算所受到的计算技术硬件约束得以解除,且船体结构设计过程中总有因结构优化要求需要较高的强度计算精度,因此有必要研究比有限条法更先进的上层建筑总强度计算方法。本文基于有限元理论、船体总强度理论提出一种新的岛式上层建筑总强度计算方法,该方法良好适应当前船体总强度计算现状,可有效利用船舶结构设计计算过程中的船体总强度计算结果,可克服有限条法的缺点、满足结构优化设计的要求。
1 上层建筑总强度计算理论及载荷分析上层建筑在外载荷的作用下,会产生强度问题[2 – 3]。研究上层建筑的受载、上层建筑结构应力计算方法(力学模型)及强度判别标准(许用应力),即为上层建筑强度理论[4]。上层建筑强度理论含有上层建筑结构局部强度和上层建筑结构总强度2个部分。
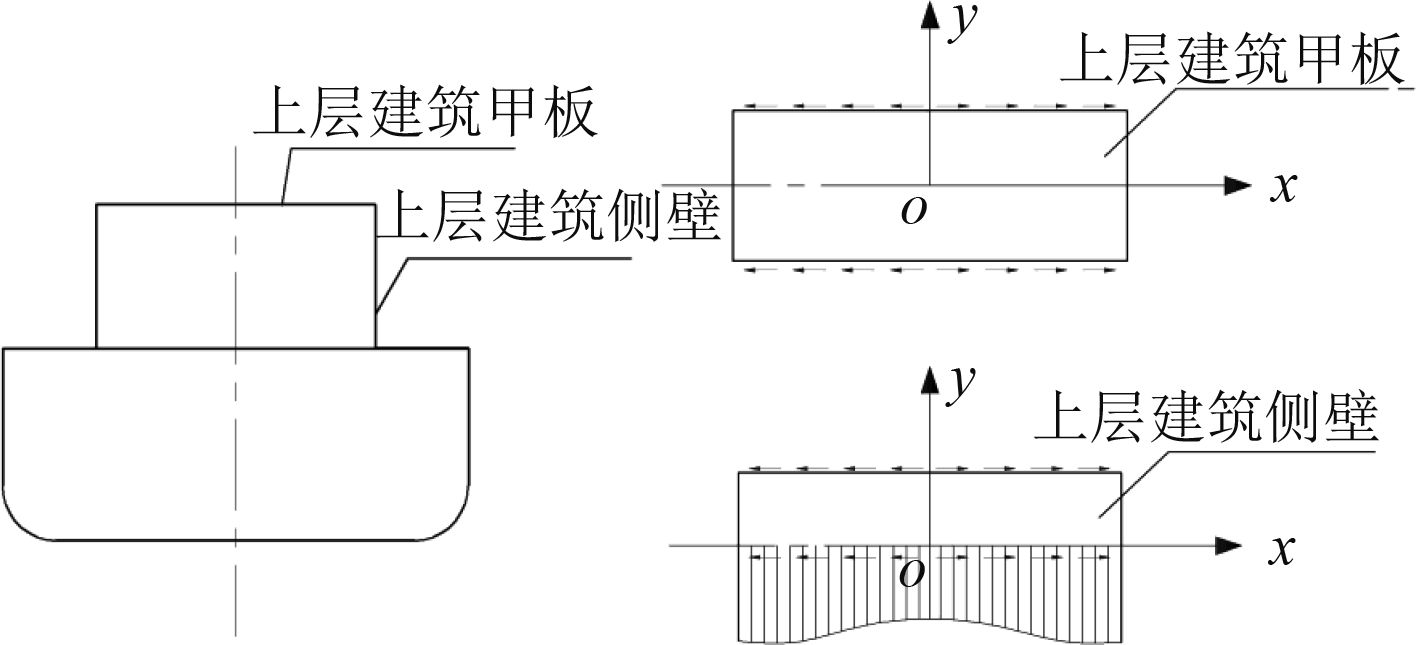
在上层建筑总强度计算方面,文献[5]提出由主船体对上层建筑侧壁的作用导致上层建筑受载而出现总强度问题。在边界条件已知的基础上,运用弹性力学的方法进行理论推导,分别求取各部分的应力,可称之为弹性力学法。该方法要求上层建筑侧壁结构、上层建筑甲板结构等必须处理成简单几何图形和板模型,这将与实际上层建筑结构形成极大的差异,从而使所得的计算结果只能是一个近似解,且近似的程度难以事先确定。
|
图 1 计算上层建筑总强度的弹性力学模型 Fig. 1 Elasticity model for calculating the total strength of superstructure |
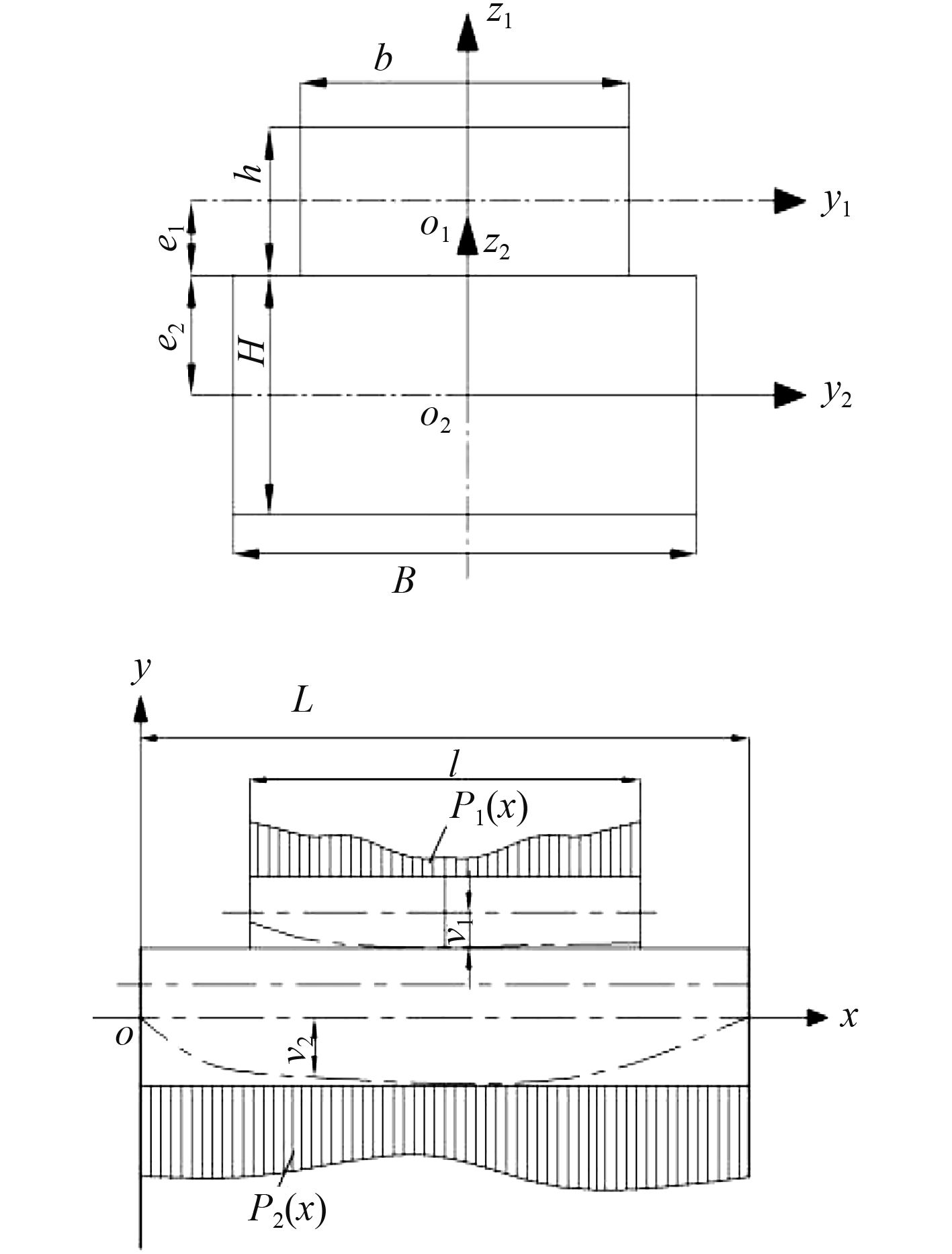
文献[5]介绍了一种组合梁法。将整个船体分离成主船体和上层建筑两部分,近似为两根梁,两者之间的相互作用用弹性支座来表示,运用弹性基础梁的理论,并计入水平剪力的影响,依据变形协调条件建立弯曲微分方程组进行求解。
|
图 2 计算上层建筑总强度的传统组合梁法力学模型 Fig. 2 The mechanical model of the traditional composite beam for calculating the total strength of the superstructure |
梁的弯曲方程为:
| $\left\{ {\begin{array}{*{20}{c}} {{E_s}{i_s}{v_1}^{\prime \prime }(x) = \int_0^x {\int_0^x {({p_1}(x) - p(x)){\rm{d}}x{\rm{d}}x + {e_1}\int_0^x {q(x){\rm{d}}x} } } } \text{,}\\ {{E_0}{I_0}{v_2}^{\prime \prime }(x) = \int_0^x {\int_0^x {({p_2}(x) - p(x)){\rm{d}}x{\rm{d}}x + {e_2}\int_0^x {q(x){\rm{d}}x} } } } \text{。} \end{array}} \right.$ | (1) |
式中:
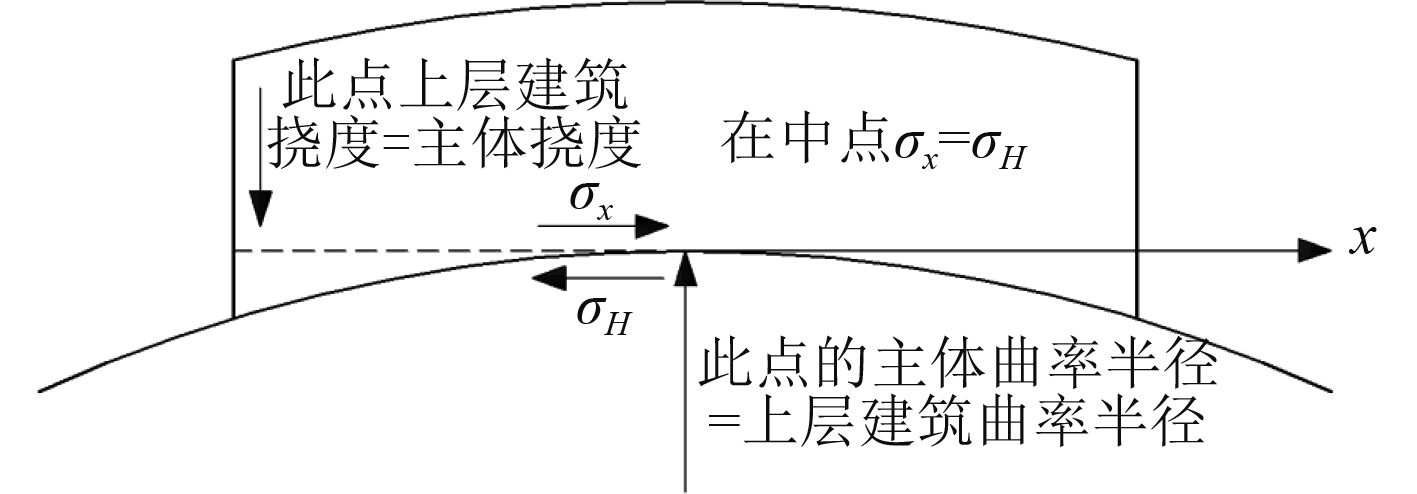
Crawford[6]提出了改进的“双梁理论”,即假定上层建筑和主船体都是单独的梁,各自承受垂向力和水平力,主船体梁还承受外力矩,从而可以求得双梁的正应力、挠度和曲率。相比于传统的组合梁法,双梁理论并未采用弹性基础梁的微分方程,而是对垂向拉压力与水平剪力作Fourier变换,然后在若干假定的基础上建立平衡方程求解,因此该方法更加简单。
|
图 3 计算上层建筑总强度的双梁理论模型 Fig. 3 Two-beam theoretical model for calculating the total strength of superstructure |
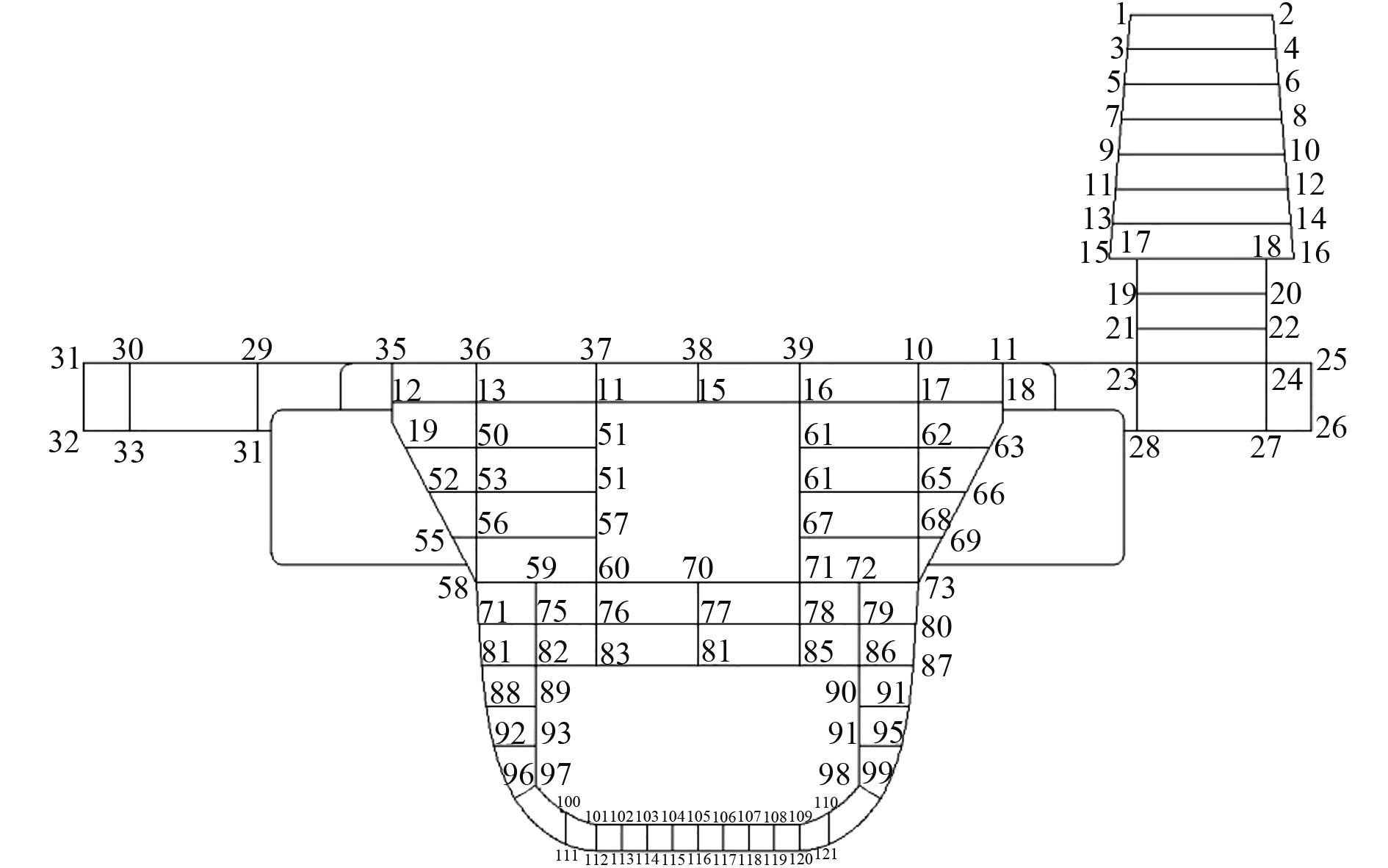
文献[7]介绍了计算上层建筑总强度的有限条法。如图4所示,将连续体割裂成部分连续部分离散的有限条,在条带内假设位移函数如下式:
|
图 4 主船体和上层建筑横剖面节点示意面 Fig. 4 Main hull and superstructure cross section node |
| $ \begin{gathered} f = \left\{ \omega \right\} = \sum\limits_{m = 1}^r {\left[ {\left[ {{C_1}} \right]\left[ {{C_2}} \right] \ldots } \right]} {\left\{ {\begin{array}{*{20}{c}} {\left\{ {{\delta _1}} \right\}} \\ {\left\{ {{\delta _2}} \right\}} \\ \vdots \end{array}} \right\}_m} \text{,}\hfill \\ {Y_m} = \sum\limits_{m = 1}^r {{Y_m}}\text{,} \sum\limits_{k = 1}^s {\left[ {{C_k}} \right]{{\left\{ {{\delta _k}} \right\}}_m}}\text{。} \hfill \\ \end{gathered} $ | (2) |
式中:
最终采用虚功原理或最小总势能原理得到刚度矩阵和载荷矩阵,从而可以得到总刚度方程。显然这种有限条法所逼近的结构只能是实际上层建筑结构的一个粗糙近似。
从上述多种上层建筑总强度计算理论可以看出,上层建筑的载荷和强度判别标准基本不变,变化的主要是计算结构应力的力学计算模型。
2 基于有限元理论的岛式上层建筑总强度计算传统的上层建筑总强度计算[8]的最大缺陷是所使用的结构力学模型过于简单,与实船结构有较大的差异,从而导致计算结果精度较低,对于主船体加上层建筑形成的复杂弹性体结构来说,想要求解出精确解十分困难[9]。本文尝试使用数值计算方法进行总强度的分析以克服上层建筑总强度传统计算方法的缺陷。
2.1 力学模型及基本理论目前使用最广泛、最有效率的数值计算方法是有限元法[10]。有限元的基本思想是将一个连续物体离散为有限个单元,单元之间通过节点相连接,对每个单元根据位移函数和能量原理,推导出单元平衡方程,再将所有单元的平衡方程组集合在一起,得到结构总平衡方程。有限元法可克服上层建筑总强度传统计算方法的缺陷,只要所取载荷精确,所得计算结果一定为问题的精确解。
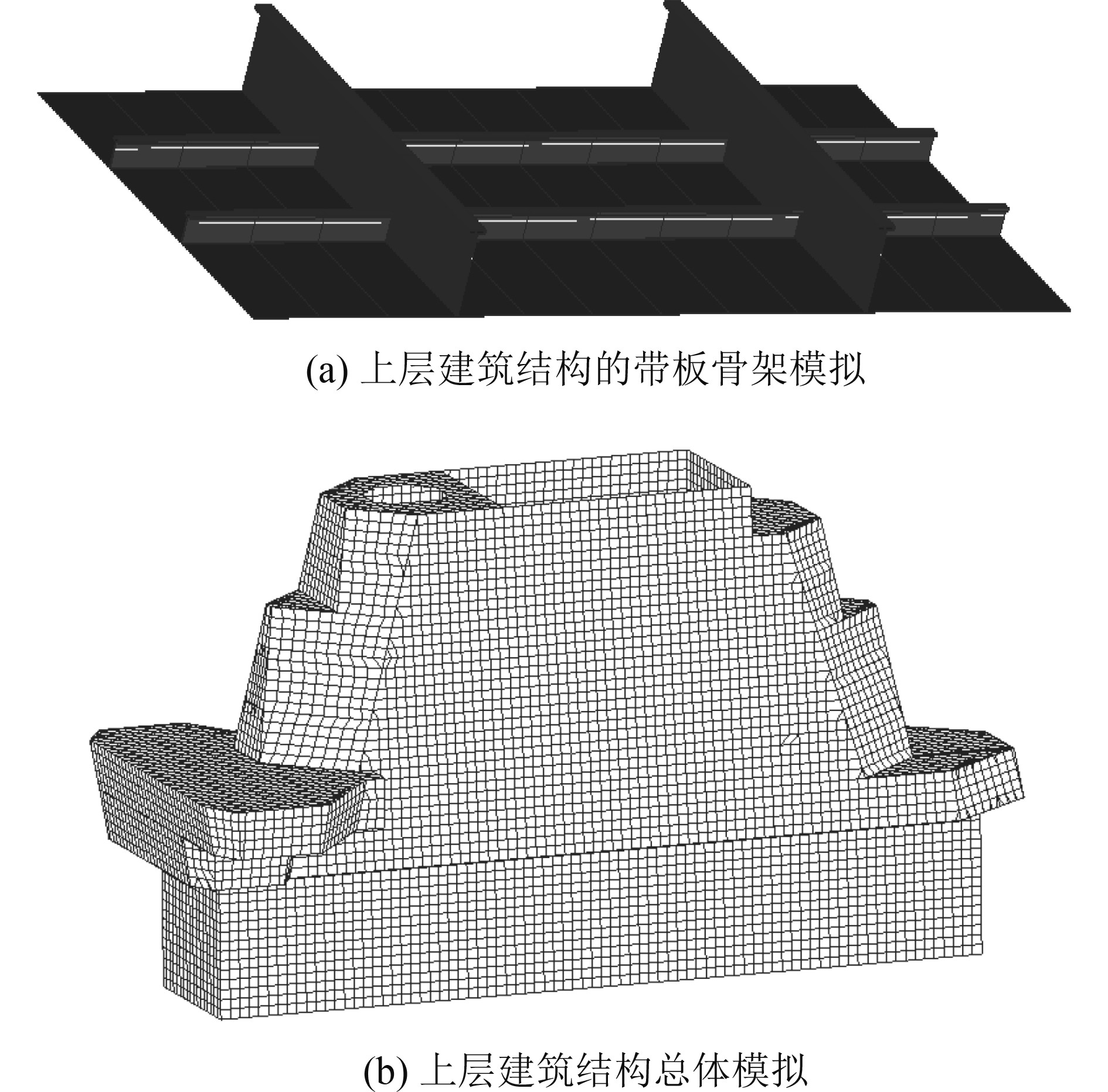
对某船岛式上层建筑结构,基于技术设计图纸,在不对结构进行任何简化的情况下,以板壳单元和梁单元离散上层建筑结构。板单元模拟上层建筑的甲板、侧壁板、横纵舱壁等板壳结构(构件),梁单元模拟骨材、桁材和桁架等,并考虑各构件的实际截面和偏心。建立上层建筑总强度有限元计算模型如图5所示。
|
图 5 计算上层建筑总强度的有限元模型 Fig. 5 Finite element model for calculating the total strength of superstructures |
上层建筑总强度载荷主要来源于主船体变形作用载荷。上层建筑结构与主船体连接在一起,主船体结构总纵弯矩作用下产生总纵弯曲挠度,该挠度产生时上层建筑亦将随之变形从而产生总强度问题。
在船体总强度计算中,总是首先确定船体所受到的弯矩曲线。当舰船所受弯矩曲线已知,船体各截面相对于船体两端的挠度值按下式计算:
| $V = \frac{{10\;000}}{E}\int_0^x {\int_0^x {\frac{{{M_y}(x)}}{{{I_{Z0}}(x)}}{\rm{d}}{x^2} - } } \frac{{10\;000x}}{{EL}}\int_0^L {\int_0^x {\frac{{{M_y}(x)}}{{{I_{Z0}}(x)}}} } {\rm{d}}{x^2} \text{,} $ | (4) |
| ${M_y}(x) = {M_s}(x) + {M_{w2}}(x) \text{。} $ | (5) |
式中:V为挠度值,m;L为正常排水量时的舰船设计水线长,m;E为弹性模量,MPa;
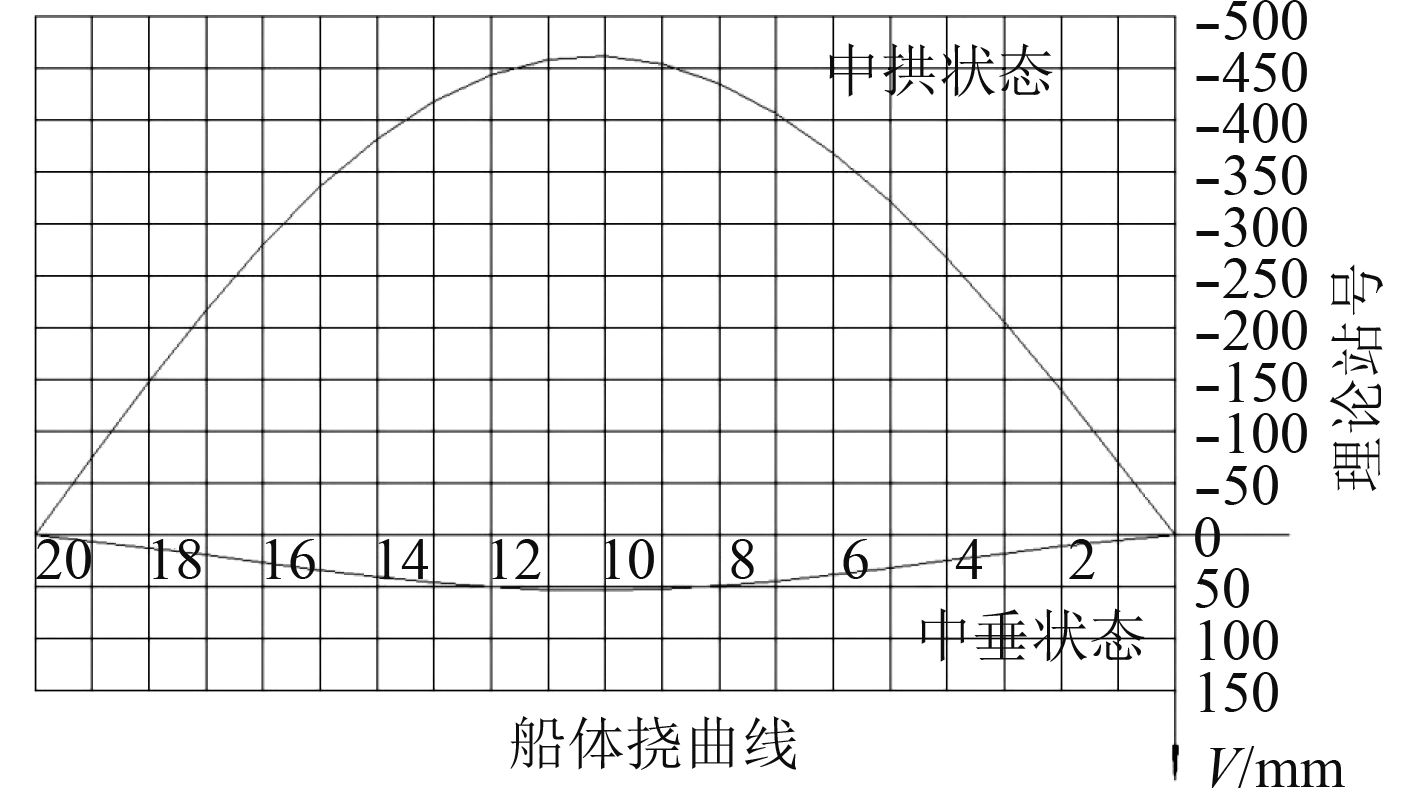
某船船体挠度曲线如图6所示。
|
图 6 中垂和中拱状态下的船体挠曲线 Fig. 6 In the middle and the arch state of the hull deflection curve |
截取船体挠度曲线中的上层建筑所在位置的值,以强迫位移边界条件的形式引入有限元模型中,即可实现对上层建筑结构的加载。本文将某船的上层建筑部分,沿纵向划分为13站,利用所截取的挠度值插值求出前述13站的绝对变形值和相对变形值如表1所示,施加到模型相应位置。
|
|
表 1 中拱状态下上层建筑各站处的挠度值 Tab.1 The deflection value of each building in the superstructure in the arch state |
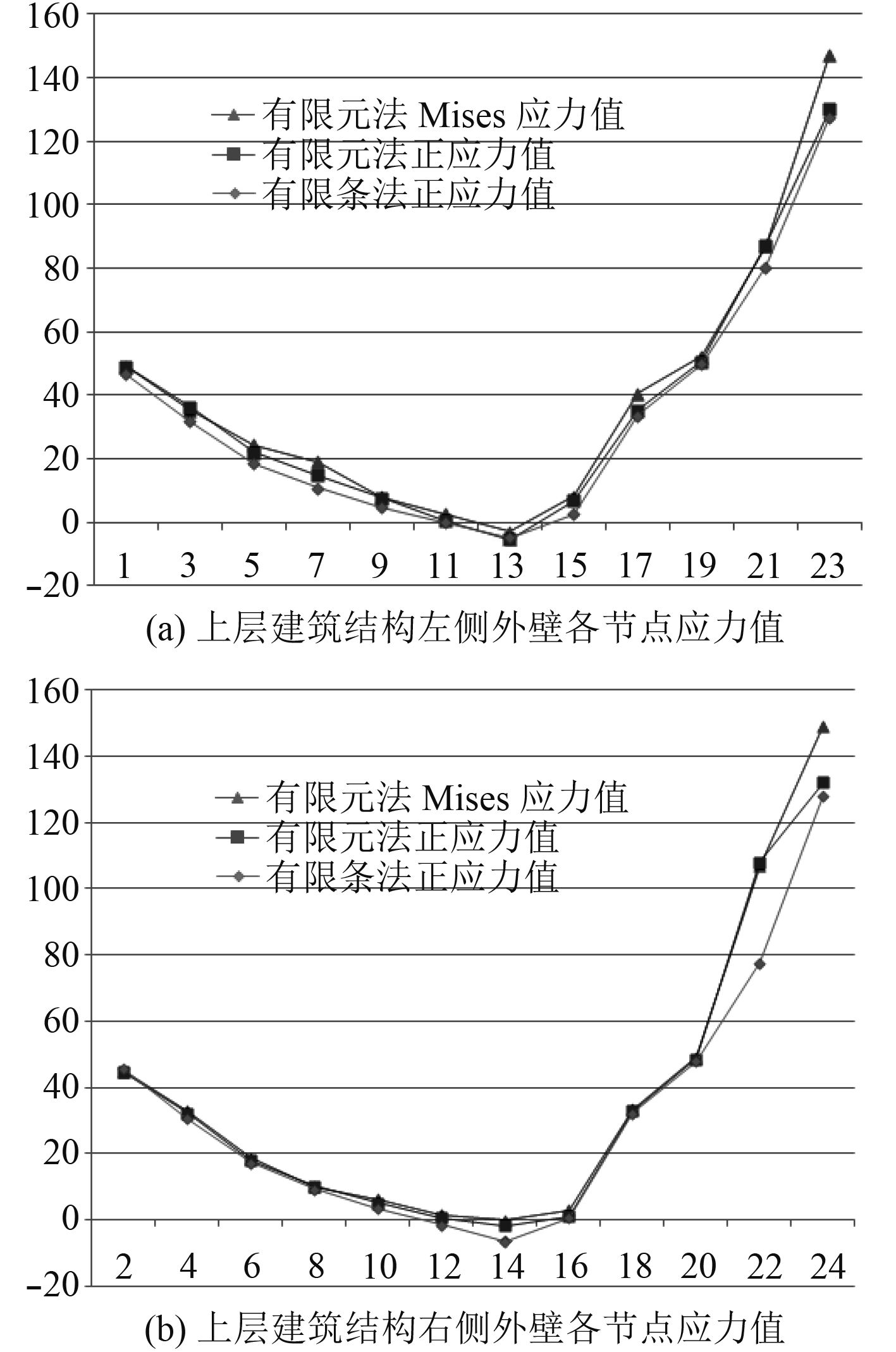
分别使用有限元法和有限条法对某船上层建筑总强度进行计算。有限条法及计算模型如第1节所述和图4所示,有限元法及计算模型如第2.1节所述及图5所示。有限条法与有限元法相应位置计算结果对比如图7和图8所示。
|
图 7 上层建筑结构应力计算结果[注] Fig. 7 Calculation results of stress in superstructure |

|
图 8 上层建筑总强度有限元法计算结果 Fig. 8 Finite element method for calculating the total strength of superstructure |
对建立好的上层建筑有限元模型进行静力分析,可以得到其总合正应力值,以及板、梁等局部结构的应力值。
有限条法计算结果表明,上层建筑总强度计算最大应力为128.1 MPa。有限元法计算结果表明,上层建筑总强度计算最大正应力和Mises应力分别为132.1 MPa和149 MPa。
有限条法的“节点”是代表实际结构的一条线,即“节线”。由有限条法理论和图4上层建筑有限条的离散图可知,有限条法的计算结果会让设计人员难以确定上层建筑结构最大应力的具体发生位置,如计算结果不符合要求需对结构进行改进设计时,显然使用有限条法在结构改进设计上不方便。
由图8可以看出,最大应力发生点(图中右侧1.49+005所对应标记)有明显的应力集中特征。这说明有限元法可以发现上层建筑结构中最大应力的发生特征(即是否有应力集中现象),而有限条法做不到这一点。
3 结 语本文首先认真分析了设计书中的有限条法计算过程,并提出将有限元法应用于计算上层建筑的强度。通过对比分析2种方法的过程和结果,讨论2种方法的优劣及实用性,得出以下结论:
1)采用有限条法进行计算时,输入和输出数据少、矩阵阶数少,在计算的简便上有较大的优越性。而有限元法计算时,需要首先建立上层建筑的三维有限元模型,过程复杂,但是考虑到设计书中的校验顺序,在前期进行的船舶总强度计算中,已经建立起了整船有限元模型,可以十分方便地从中截取上层建筑部分,因此采用有限元法计算岛式上层建筑的强度问题也有很好的实用性。
2)将本文的计算结果与有限条法的计算结果进行对比可以发现,有限条法计算出的应力值偏小,注意到有限条法对实际结构有较大的简化,可以断定误差较大;有限元法填补了有限条法中只能纵向分条无法横向离散的缺点,计算出的应力值更加真实。
3)有限条法是对整体结构的一种平均计算,无法细化到某个或者某些结构,而有限元法则弥补了这点不足,不仅能计算总合应力和局部结构的应力,还能计算结构中的集中应力,为结构强度预报提供依据。
| [1] |
海军装备部规范所. GJB.航母船体结构设计计算方法[S]. 北京: 总装备部军标出版社.
|
| [2] |
杨平, 吴凯. 上层建筑对船体总纵弯曲的效应分析[J]. 武汉交通科技大学学报, 1999(2): 31-36. YANG Ping, WU Kai. Analysis on the effect of superstructure on the longitudinal bending of hull[J]. Journal of Wuhan University of Communications Science and Technology, 1999(2): 31-36. |
| [3] |
郑杰, 谢伟, 骆伟, 等. 穿浪双体船横向强度与扭转强度的有限元计算[J]. 中国舰船研究, 2010(5): 14-18. ZHENG Jie, XIE Wei, LUO Wei, et al. Finite element calculation of transverse strength and torsional strength of wave–piercing[J]. Chinese Journal of Ship Research, 2010(5): 14-18. |
| [4] |
孙聪.内河船舶上层建筑对总纵强度的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [5] |
王西典.计入有效度的强力上层建筑设计研究[D]. 上海: 上海交通大学, 2015.
|
| [6] |
CRAWFORD L. Theory of long ship’s superstructures[J]. SNAME, 1950(4): 693. |
| [7] |
CHEUNG Y.K. 结构分析的有限条法[M]. 北京: 人民交通出版社, 1985.
|
| [8] |
陈庆强, 朱胜昌. 上层建筑一体化船型的船体梁总纵强度计算方法研究[J]. 船舶力学, 2011(10): 57-61. CHEN Qing-qiang, ZHU Sheng-chang. Study on calculating method of total longitudinal strength of hull girder with integrated building type[J]. Journal of Ship Mechanics, 2011(10): 57-61. |
| [9] |
陆鑫森. 船舶上层建筑的强度问题[J]. 交通大学学报, 1953(3): 184-215. LU Xin-sen. Strength of ship superstructure[J]. Journal of Traffic University, 1953(3): 184-215. |
| [10] |
陈庆强, 朱胜昌, 郭列, 等. 用整船有限元模型分析方法计算舰船的总纵强度[J]. 船舶力学, 2004(2): 79-85. CHEN Qing-qiang, ZHU Sheng-chang, GUO Lie, et al. Calculation of the total longitudinal strength of the ship by finite element model analysis method[J]. Journal of Ship Mechanics, 2004(2): 79-85. DOI:10.3969/j.issn.1007-7294.2004.02.011 |
 2019, Vol. 41
2019, Vol. 41

