0 引　言

随着船舶逐步趋向于大型化，船舶平面分段数量也逐步增大，因此船舶平面分段的调度问题研究具有十分重要的意义。在实际船舶生产建造过程中，受到机器因素、人工因素和其他不可控因素的影响^[1]，船舶平面分段的加工时间不可控。此外，船舶分段的具体加工时间和要求的交货期均为一个区间，很难确定其精确值。因此船舶平面分段在建造过程中的关键时间节点都具有模糊性，为了更好地吸收数据的模糊性，指导实际的生产计划，本研究对原始数据进行模糊化处理，从而开展模糊调度。平面分段由钢板及部件在流水线上进行焊接而成，各个船厂的平面分段流水线的功能设置各有不同，本文以一条面向纵骨先安装法的平面分段流水线为例。流水线上配置了拼板、底板焊接、纵骨安装、纵骨焊接、纵桁及肋板装配、纵桁及肋板焊接、检查运出等7个工位，其中拼板工位需要完成钢板的定位和预先电焊；纵骨安装通过安装门架机完成；纵桁及肋板装配由安装门架机并由工人辅助完成；检查运出工位需要对装配和焊接质量进行检查，最后由顶升装置和平板车将分段运出。

目前针对流水线调度问题，很多学者提出了蚁群算法、禁忌搜索法、模拟退火法等智能优化算法，主要的研究对象局限在流水车间调度问题和混合流水车间^{[2 – 3]}。众多的研究仅仅是针对流水线的静态调度进行研究，并没有考虑数据的模糊性和急件到达这种特殊工况。因此，本研究针对船舶平面分段单流水线面对急件任务情况下，设计一个多目标文化基因算法进行模糊调度。

1 问题描述

船舶平面分段单流水线反应式多目标调度问题考虑如下：流水线为单平面分段流水线，0时刻开始按照既定调度方案加工，t时刻急件任务到达。当急件任务到达时，正在流水线加工的分段继续完成加工，未进入流水线的分段等待重新调度。当流水线上最后一个分段离开第一个工位时开始重调度方案的生产，并要求急件任务和原任务以最小化最大完工时间完成，并保证急件任务和原任务在要求的工期内完成。分段的开始加工时间采用三角模糊数表达，分段加工时间采用梯形模糊数表达。

问题假设：对于所有重调度分段，均可在启动反应式调度时投入生产；加工过程中各工位持续可用；分段在各工位进行加工时不可中断；分段在各工位的加工时间及其交货时间模糊；分段在各工位上加工前的准备时间包含于加工时间；在建分段在各工位间的输送时间不计。

2 数学模型

基于以上描述与假设，建立平面分段单流水线反应式模糊调度问题的数学模型。

2.1 符号说明

$S$ 为重调度方案；

$S'$ 为原调度方案；

$n'$ 为原调度方案中参与重调度的分段（称为再调度分段）的数量；

$n''$ 为急件分段数量；

n 为重调度分段数量，重调度分段包括再调度分段和急件分段， $n = n + n''$ ；

$U$ 为重调度分段集合；

i 为重调度分段标号， $i \in U$ ；

m 为工位数量；

j 为工位标号， $j \in \left\{ {{\text{1}}，2，\ldots ，m} \right\}$ ；

f 为流水线标号， $f \in \left\{ {A，B} \right\}$ ；

P_b 为当前正在单流水线的工位1上加工的原调度方案中的分段；

$P{b_f}$ 为当前正在并行流水线f的工位1上加工的原调度方案中的分段；

${\tilde p_{i,j}}$ 为重调度分段i在工位j上的模糊加工时间；

${\tilde d_i}$ 为重调度分段i的模糊交货期；

${\tilde e_{i,j}}$ 为重调度分段i离开工位j的模糊时间，亦即分段i进入工位j+1的模糊时间；

${\tilde C_i}$ 为重调度分段i的模糊完工时间；

$AIC{D_i}$ 为重调度分段i的模糊完工时间与其模糊交货期的一致性程度^[4]。

${AISS '}_{i,j}$ 为重调度方案S和原调度方案 $S'$ 中分段i在工位j上的模糊开始加工时间的一致性程度（原调度方案中包含分段i）。

2.2 模糊调度变量

在模糊调度中，通常以三角模糊数来表述模糊加工时间和模糊完工时间，表示为 ${\tilde p_{i,j}}=\left( {p_{i,j}^L，{p_{i,j}}，p_{i,j}^U} \right)$ ，包含时间的最可能值 $\left({p_{i,j}}\right)$ 、时间的下限值 $\left(p_{i,j}^L\right)$ 和时间的上限值 $\left(p_{i,j}^U\right)$ 等3个参数。模糊加工时间的隶属函数表示如图1（a）。

通常以梯形模糊数刻画模糊交货期，表示为 ${\tilde d_i}=\left( {d_i^L, d_i^{{E_1}}, d_i^{{E_2}}, d_i^U} \right)$ 其中， ${\mu _{{{\tilde d}_i}}}$ 可理解为满意度（Satisfaction），表示为图1（c）。其中 ${ d}_i^U$ 和 ${ d}_i^L$ 分别表示交货期的上、下限，完工时间在上、下限之外，最不令人满意（满意度为0）； ${ d}_i^{{E_1}}$ 与 ${ d}_i^{{E_2}}$ 构成理想的交货期窗口 $\left( {{ d}_i^{{E_1}}, {\rm d}_i^{{E_2}}} \right)$ ，完工时间在此窗口内，最令人满意（满意度为1）。

2.3 数学模型

假设 ${b^R} = \left[ {{b^R}\left( 1 \right), {b^R}\left( 2 \right), \cdots , {b^R}\left( n \right)} \right]$ 表示重调度分段的加工序列，拟建分段i位列 ${b^R}$ 的第k位。各分段的模糊完工时间按式（5）~式（9）可以计算得到。考虑到有急件任务到达时，原调度方案的相关加工材料已经备好，为了充分利用现有资源，要求重调度方案尽量贴近原调度方案。鉴于模糊调度的特点，本研究定义了重调度方案S和原调度方案 $S'$ 中分段i在工位j上的模糊开始加工时间的一致性程度 ${AISS '}_{i,j}$ （原调度方案中包含分段i），最大化平均 ${AISS '}_{i,j}$ 即可从整体上尽量保持重调度方案与原调度方案的一致性。类似于AICD， ${AISS '}_{i,j}$ 定义如下：

$ \begin{split} & AIC{D_i} = \displaystyle\frac{{{\mathop{\rm area}\nolimits} \left( {{{\tilde C}_i} \cap {{\tilde d}_i}} \right)}}{{{\mathop{\rm area}\nolimits} \left( {{{\tilde C}_i}} \right)}}\text{，}\\ & {AISS '}_{i,j}{\rm{ = }}\displaystyle\frac{{{\mathop{\rm area}\nolimits} \left( {S{T_{i,j}} \cap {ST '}_{i,j}} \right)}}{{{\mathop{\rm area}\nolimits} \left( {S{T_{i,j}}} \right)}}\text{。} \end{split} $

(1)

式中： $S{T_{i,j}}$ 和 ${ST '}_{i,j}$ 分别表示重调度方案S和原调度方案 $S'$ 中分段i在工位j上的模糊开始加工时间。 ${AISS '}_{i,j}$ 具体指：分段i分别在重调度方案S和原调度方案 $S'$ 中时，在工位j上的模糊开始加工时间隶属函数图形的公共部分的面积，与分段i在重调度方案S中时，其在工位j上的模糊开始加工时间隶属函数图形的面积之比。

综上所述，平面分段单流水线反应式模糊调度以最小化模糊makespan、最大化平均AICD、最大化平均AISS′为调度目标，数学模型^[5]如下：

目标函数：

$ {\rm{Minimize}} \ {f_1} = makespan = \mathop {\max }\limits_{i \in U} {\tilde C_i}\text{，} $

(2)

$ {\rm{Maximize}} \ {f_2} = \overline {AICD} = \frac{1}{n}\sum\limits_{i \in U} {AIC{D_i}} \text{，} $

(3)

$ {\mathop{\rm Maximize}\nolimits} \ {f_3} = \overline {AISS'} = \frac{1}{{mn'}}\sum\limits_{i \in U} {\sum\limits_{j \in M} {AIS{{S'}_{i,j}} \cdot x_i^{S'}} } \text{，} $

(4)

约束条件：

$ {\tilde e_{{{\text{π}} ^R}\left( 1 \right), 0}} = \left( {{e_{Pb, 1}}, {e_{Pb, 1}}, {e_{Pb, 1}}} \right)\text{，} $

(5)

$ {\tilde e_{{{\text{π}} ^R}\left( k \right), 0}} = {\tilde e_{{{\text{π}} ^R}\left( {k - 1} \right), 1}}, \ k \in \{ 2, 3, \cdots , n\}s\text{，} $

(6)

$ \begin{split} {{\tilde e}_{{{\text{π}} ^R}\left( k \right),j}} =& \max \left( {{{\tilde e}_{{{\text{π}} ^R}\left( k \right),j - 1}} + {{\tilde p}_{{{\text{π}} ^R}\left( k \right),j}},\left( {1 - {{\rm{y}}_k}} \right){{\tilde e}_{{{\text{π}} ^R}\left( {k - 1} \right),j + 1}}}{\rm{ + }}\right. \\ & \left.{{{\rm{y}}_k} \cdot {{\tilde e}_{Pb,j + 1}}} \right),{\rm{ }}\\ & k \in \{ 1,2, \cdots ,n\} ,{\rm{ }}j \in \{ 1,2, \cdots ,m - 1\} \text{。} \end{split} $

(7)

$ {\tilde e_{{\pi ^R}\left( k \right), m}} = {\tilde e_{{\pi ^R}\left( k \right), m - 1}} + {\tilde p_{{\pi ^R}\left( k \right), m}}, \ k \in \{ 1, 2, \cdots , n\}\text{，} $

(8)

$ {\tilde C_i} = {\tilde e_{{\pi ^R}\left( k \right), m}}\text{。} $

(9)

式中： $x_i^{S'}$ 为0–1变量，若原调度方案 $S'$ 中包含分段i，则 $x_i^{S'}=1$ ，否则 $x_i^{S'}=0$ 。式（5）和式（6）表示分段进入流水线的时间，亦即在工位1上开始加工的时间，其中式（4）表示重调度加工序列中的第1个分段将于当前正在工位1上加工的分段P_b离开工位1时才进入流水线，此时间是确定的；式（6）表示重调度加工序列中的第 $k(k \in \{ 2, 3, \cdots , n\} )$ 个分段进入工位1的时间等于第k-1个分段离开工位1的时间。式（7）中， ${{\rm{y}}_k}$ 为0-1变量，当 $k=1$ 时 ${{\rm{y}}_k}=1$ ，否则 ${{\rm{y}}_k}=0$ ；式（7）表示重调度加工序列中的第k个分段离开工位j进入工位 ${{j+1}}\left( {j \in \left\{ {1,2, \cdots ,m - 1} \right\}} \right) $ 的时间为其在工位j上的完工时间 $({\tilde e_{\pi \left( k \right), j - 1}} + {\tilde p_{\pi \left( k \right), j}})$ 与其紧前分段离开工位j+1的时间的较大值；特别地，重调度加工序列中的第1个分段的紧前分段为分段P_b。式（8）表示加工序列中的第k个分段离开工位m（最后一个工位）的时间为其离开工位m-1进入工位m的时间加上其在工位m上的加工时间。式（9）表示分段i（加工序列中的第k个分段）的完工时间为其离开工位m（最后一个工位）的时间。

3 多目标文化基因算法

文化基因算法（Memetic algorithm，MA）将基于种群的全局搜索与基于个体的局部搜索有效结合，在保持遗传算法的全局搜索能力的同时提高了其局部搜索能力。因此，MA被广泛应用于求解各类优化问题，包括生产调度^{[6 – 7]}及其他工程领域的相关问题，如路径规划^[8]、资源分配^[9]以及特征选取^[10]等。本文提出一种多目标Memetic算法（Multi-objective Memetic algorithm，MOMA）以求解平面分段单流水线多目标模糊调度问题。作为多目标进化算法，MOMA基于Pareto最优的概念进行设计。MOMA以特定形式的向量表达调度解，引入2种启发程序生成初始解，并基于解的形式设计了交叉、变异等遗传操作和局部搜索算子。下面对MOMA解的表达、种群初始化、遗传操作和局部搜索等内容进行详细描述。

3.1 解的表达

本文以一个基因串来表示平面分段单流水线多目标调度的一个解。为了反映分段在流水线上的分配情况，在包含全部待加工分段的序列 $b = \left[ {b\left( 1 \right), b\left( 2 \right), \cdots , b\left( n \right)} \right]$ 中，b中工件的序列即为工件加工顺序。

3.2 遗传操作

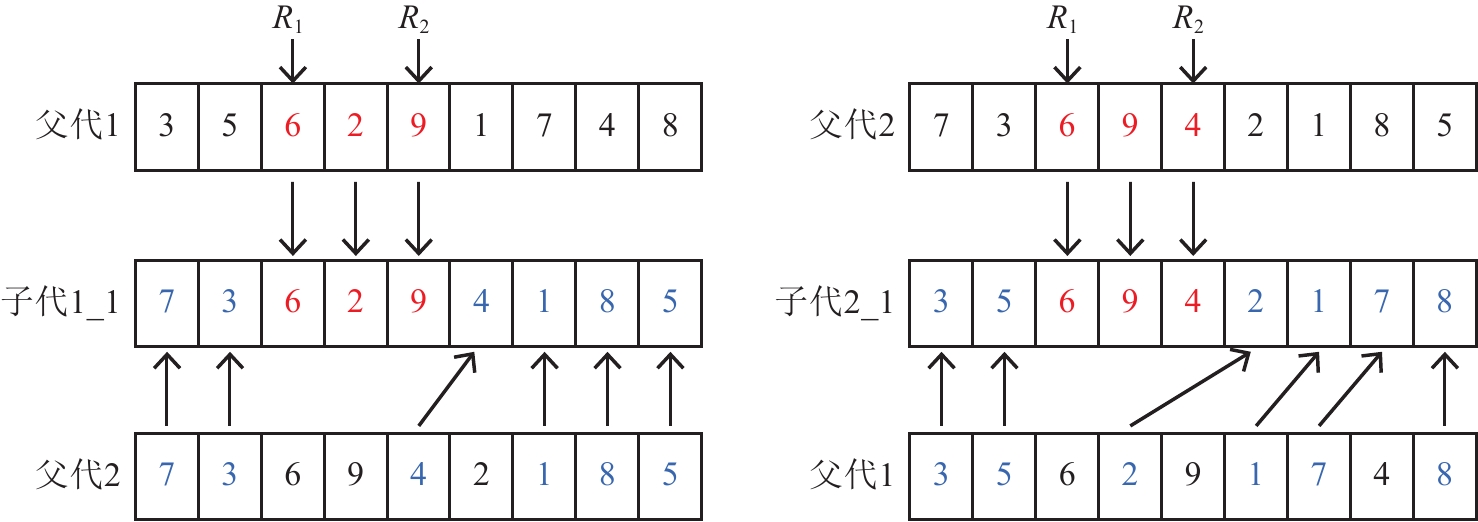
选择（selection）、交叉（crossover）和变异（mutation）是3个用于生成子代种群的遗传操作。选择操作采用基于非支配等级和拥挤距离的二元锦标赛方法，从父代种群中选出优秀个体。对于非支配等级不同的2个个体，优先选择非支配等级低的个体；对于非支配等级相同的2个个体，优先选择拥挤距离大的个体。随后，对选出的父代个体按概率p_c进行配对交叉。交叉操作如图2所示。

具体步骤如下：

步骤1　令子代1继承父代1的随机一段序列，子代2继承父代2的随机一段序列。

步骤2　填子代1的空位时，从左至右扫描父代2，将子代1中未继承的基因（平面分段号）依次填入空位；填子代2的空位时，从左至右扫描父代1，将子代2中未继承的基因（平面分段号）依次填入空位。

上述交叉操作能保留一个父代的某个子调度，同时能保留另一个父代中分段加工的相对先后关系，因此子代能较好地继承父代的性征。上述交叉操作能产生无数对子代，实际算法操作中只需随机产生其中的一对作为子代。

为保持种群的多样性，对交叉操作产生的子代按概率p_m实施变异操作，具体步骤如下：

步骤1　随机选择两位置d和k，要求 $1\text{≤} d, k \text{≤} n \wedge $ $d \ne k \wedge d \ne k - 1$ 。

步骤2　将位置d处的基因插入到位置k处的基因之前。

变异操作示例见图3。在变异前的序列中随机选择2个位置，分别命名为k，d。将d位置处的序列插入到k处序列的前面位置，保持其他序列的先后顺序不变，位置依次顺延。

3.3 局部搜索算子

Insert邻域结构能有效地构造流水车间调度问题邻域解。MOMA中，按概率p_ls对个体施加基于Insert邻域结构的局部搜索算子，局部搜索算子算法流程与参考文献[11]基本一致。

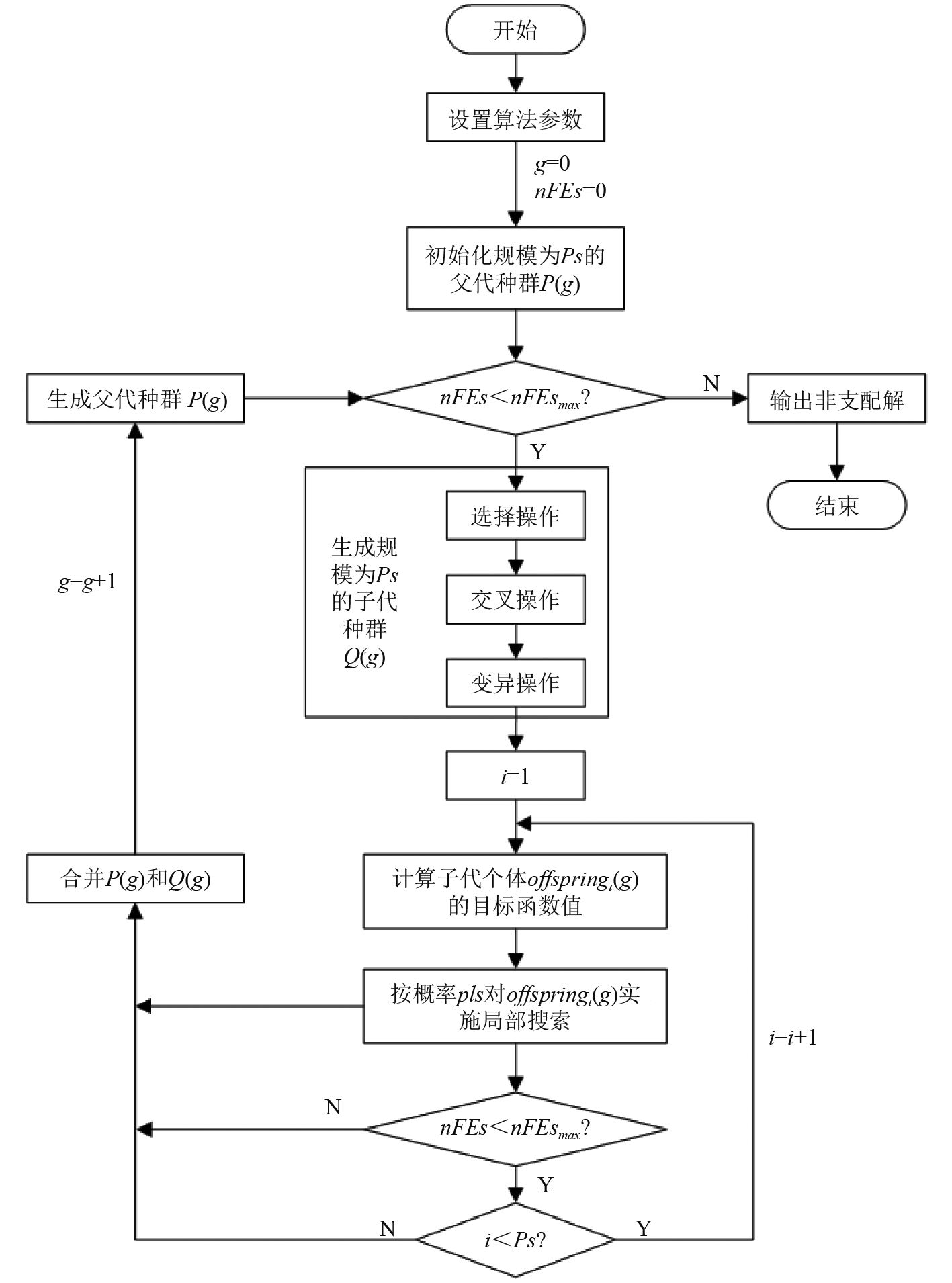
3.4 算法流程

基于上述各节对MOMA各部分内容进行的详细描述，该算法的流程如图4所示。

4 仿真试验

因为反应式调度是在一般式调度结果的基础上进行运算的，本研究收集到上海某船厂平面分段生产信息，计算单流水线的静态调度结果。假设在0时刻开始生产，且在1 800 min时接到急件任务如表1所示，利用上文所述的MOMA算法制定重调度方案。

因为MOMA算法是智能优化算法，运算结果具有一定的随机性，因此本研究通过多次计算，生成多组计算方案，并利用AHP法对多组调度方案进行选择，确定最终方案。利用MOMA算法对重调度任务独立求解10次，然后对求得的10组结果进行整合，剔除支配解，形成新的解集合。采用AHP发在新的非支配解集中选取重调度方案，输入AHP法的目标权重矩阵，计算出3个目标对应的权重为[0.5499，0.2402，0.2098]，选择出对应的调度方案为17→18→23→19→1→20→24→14→13→6→9→21→22→2→7，3个目标值对应为[8960，0.6382，0.7377]。

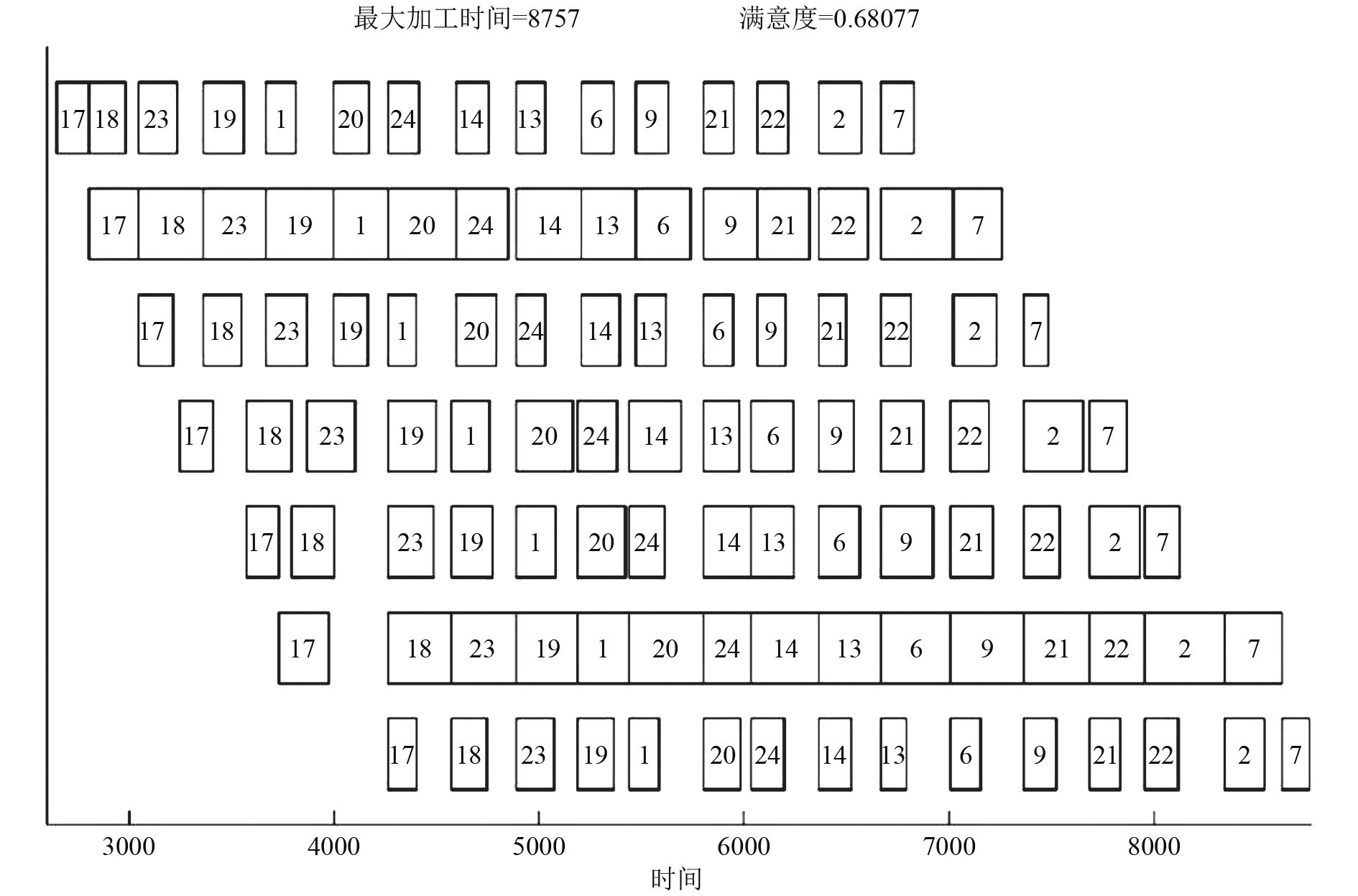
运用满意度的定义计算本算例的满意度为0.680 77，以AICD代替目标满意度，计算其相对误差为6.67%。最大完工时间makespan仿真结果为8 757，相对误差为2.27%。仿真得到的目标值与调度方案计划的目标值的相对偏差保持在较小的范围内，因此可认为求得的模糊调度方案能保证较高的可靠性。对调度方案进行仿真，绘制出仿真甘特图如图5所示，反映了调度方案仿真执行的进程状态，为船舶平面分段流水线反应式调度问题提供决策支持。

5 结　语

本文研究了船舶平面分段单流水线反应式模糊调度，面对急件任务的工况提出单流水线模糊调度的数学模型。通过设计一种多目标文化基因算法MOMA，对船舶平面分段模糊化加工信息数据进行计算。目标值与调度方案计划的目标值的相对偏差保持在较小的范围内，通过甘特图仿真分段加工过程，为船舶平面分段单流水线反应式调度问题提供决策支持。