2. 江苏新扬子造船有限公司,江苏 泰州 214500
2. Jiangsu New Yangzi Shipbuilding Co., Ltd., Taizhou 214500, China
随着全球平均气温的升高,冰层融化速度加快,北极资源开发和与之相关的北极航线建设成为当前的一个热点问题。对我国而言,正在“一带一路”倡议背景下,开展北极航道的开发和利用,打造“冰上丝绸之路”。然而,由于极地海域环境的复杂性,船舶与海冰发生碰撞不可避免,因此破冰船在保障极地资源开发和海洋活动的安全性和可持续性方面起着至关重要的作用。
由于船舶破冰是一种复杂的非线性动态响应过程,再加上海冰本构模型的复杂性,国内外还没有一种有效而准确的冰阻力预报方法。冰阻力主要受冰材料特性、船体形状、船舶运动和航速等多种因素的影响[1]。目前,计算冰阻力的方法主要有3种:基于模型试验或全尺度试验数据生成阻力经验关系的经验公式[2 – 5];基于船舶运动方程描述船舶与冰动态作用过程的数值模拟方法[6 – 7];模型或全尺度试验研究方法[8]。
1 冰材料及模型验证准确的海冰材料模型是保证数值模拟结果准确度的关键,然而由于冰材料的复杂性,国内外对冰材料本构模型的研究尚未形成共识。本文选取的冰材料模型为*MAT_124等向弹塑性材料[9]。该材料模型中需定义3种不同的材料曲线:定义2种不同的屈服应力与有效塑性应变曲线;一种用于拉伸,另一种用于压缩;第3条曲线是应变速率与比例压缩屈服应力因子(CYSF)曲线,用于说明应变速率对压缩强度的影响,将等效塑性应变值作为失效标准。
|
|
表 1 冰材料参数 Tab.1 The material parameters of ice |
通过模拟钢板挤压圆锥冰体,将碰撞力结果和现有试验结果进行比较,以验证所选冰材料的适用性。为与试验模型中冰锥形状尺寸基本保持一致,并模拟冰锥固定在试验装置上,建立直径为10 cm,锥角为30°的冰锥有限元模型,将冰锥底平面节点进行全约束。由于在钢板与冰锥的挤压试验中,钢板的厚度较大,表面无明显的变形,故将钢板设为刚体,这样不仅节约计算时间又不会产生较大误差。有限元模型如图1所示。

|
图 1 钢板与冰锥模型 Fig. 1 FE model of ice cone and steel plate |
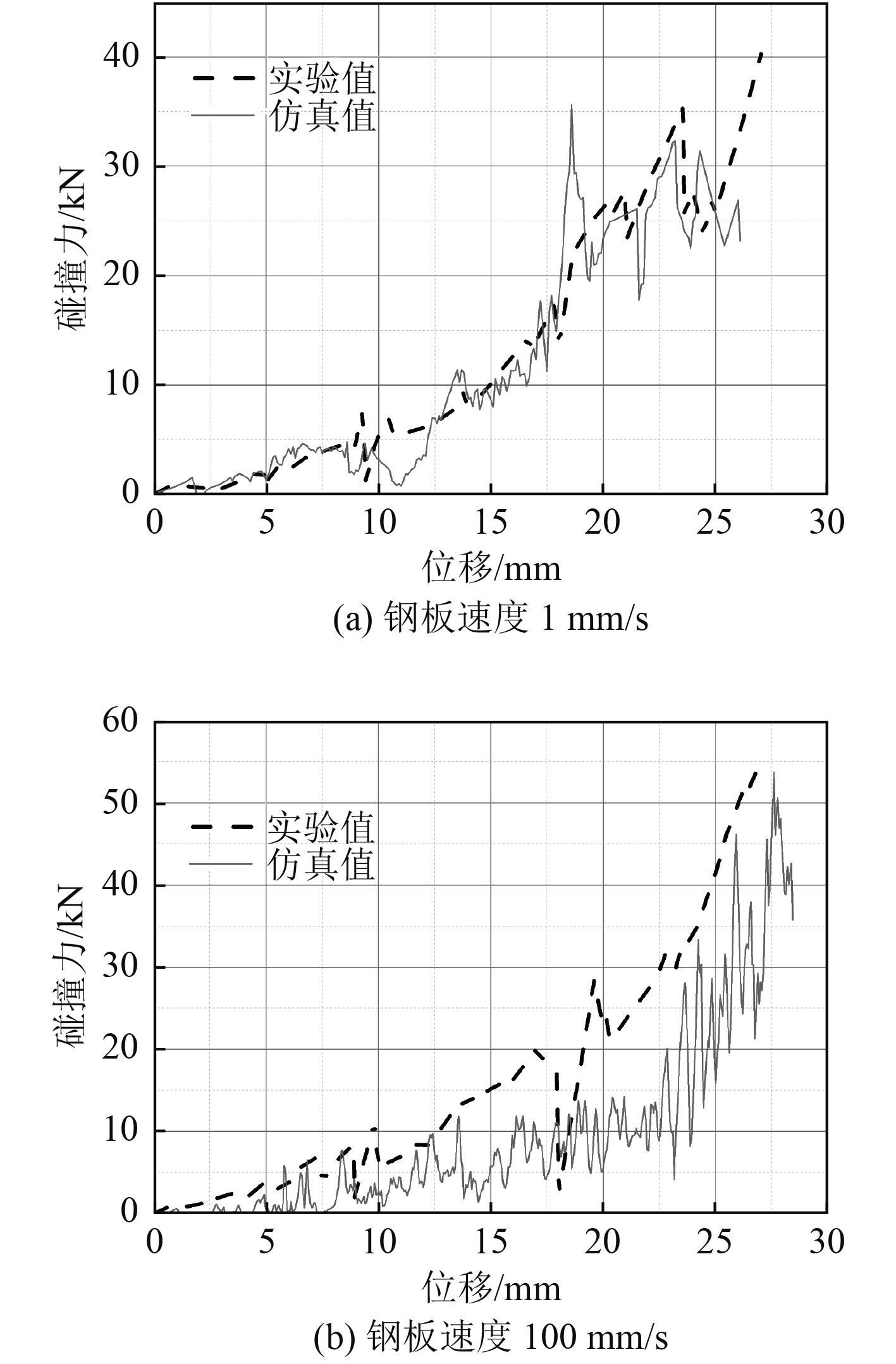
为验证该冰材料在不同应变率下的适用性,使钢板分别以1 mm/s和100 mm/s的速度挤压冰锥,图2为钢板以不同速度与冰锥相互作用的冰力-位移曲线,并和实验结果进行比较,相关实验数据来自文献[10]。
|
图 2 钢板不同运动速度下的冰力-位移曲线 Fig. 2 Curve of ice force-displacement at different steel plate speeds |
从图中可以看出,冰力随钢板位移波动上升,反映出钢板与冰锥碰撞过程是高度非线性运动。刚板在低速时冰力振幅较小,而刚板在速度相对较高时,冰力振幅较大,这是因为钢板在高速比低速时冰体破碎发生得更为频繁。不论是低速时的计算结果还是高速时的计算结果,都能反映出计算值和试验值的增长趋势基本相符,该海冰材料模型适合应用于破冰船破冰过程的数值模拟。
2 破冰船连续式破冰数值模拟 2.1 破冰船与冰排模型在冰厚不超过1.5 m时,破冰船通过船体首部特殊形状将冰层局部破碎,进行“连续式”破冰。本文以某极地破冰船在连续式破冰场景为对象,研究不同船速,不同冰厚对破冰阻力的影响。该船的主要参数包括:船长约123 m,型宽约24 m,吃水7.8 m,船首角23°以及外飘角58°。相关材料参数如表2所示。
|
|
表 2 极地破冰船材料参数 Tab.2 Polar icebreaker material parameters |
船体首部区域采用精细网格,在首部以后采用简化处理方法,对碰撞影响不大及远离碰撞区域的船体结构设为刚体。采用体单元建立120 m×60 m的冰层有限元模型,冰层前端面处于自由状态,左、右端面和后端面三面全约束。考虑到冰层浮于水面,根据冰层厚度的不同,使冰层上表面的略高于水线面。对冰层施加重力的同时在冰层底部施加相应的向上的浮力。其接触控制使用侵蚀接触,其关键字*CONTACT_ERODING_SURFACE_TO_SURFACE。为了不考虑破冰过程对船体运动的影响,对船体除x(定速运动方向)方向外的其他5个自由度进行刚性约束。破冰船与冰排模型如图3所示。

|
图 3 破冰船和冰排模型 Fig. 3 The model of icebreaker and ice row |
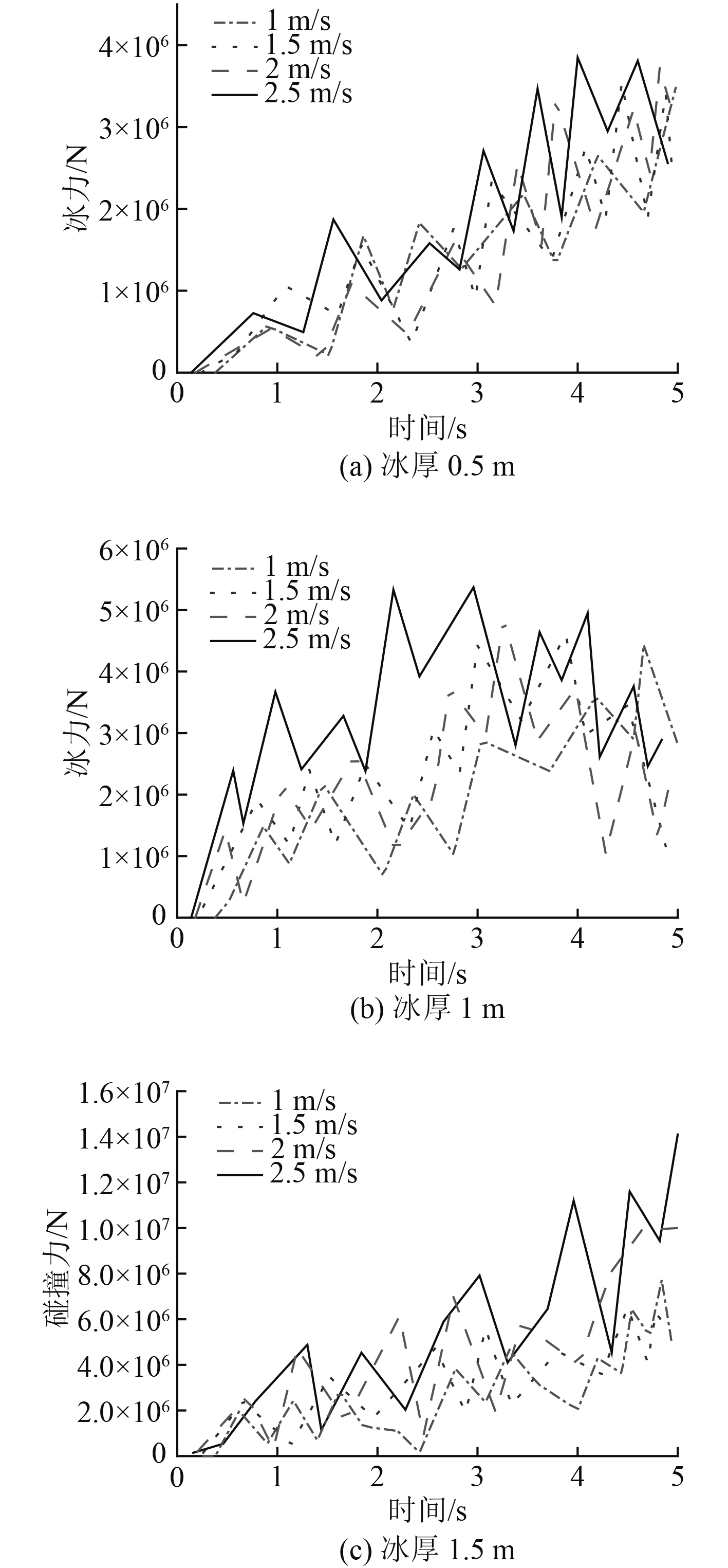
为了验证破冰船船速和冰厚对冰阻力的影响,本文就不同冰厚(0.5 m,1 m,1.5 m),不同船速(1 m/s,1.5 m/s,2 m/s,2.5 m/s)模拟破冰船在连续式破冰场景中的多个工况,得到的冰力曲线如图4所示。
|
图 4 不同船速冰厚下的冰力曲线 Fig. 4 Ice force curve under different ship speeds and ice thicknesses |
从图中整体冰力时程曲线可以看出,冰力曲线整体呈锯齿状波动上升或下降。在破冰船不断向前破冰过程中,起初由于船冰接触面积较小,因而冰力较小,随着船冰接触面积的逐渐增大,导致船冰摩擦力也增大,冰力也逐渐上升。但同时船舶破冰过程,冰排发生弯曲破坏,并伴随冰体不断失效,因而会产生不同程度的冰力卸载,冰力表现出锯齿状波动。不同工况下冰力值如表3所示。
|
|
表 3 不同工况下冰力值 Tab.3 Ice force values under different working conditions |
通过比较不同工况下冰力时程曲线和冰力表,发现冰力的波动振幅、冰力峰值和平均冰力都随着船速和冰厚的增大而增大。这是因为较大的速度和较大冰厚都会对冰排产生较大的碰撞力,冰力因冰单元失效而卸载,从而产生较大的振幅,而相比于船速,冰厚对冰阻力影响更大。
3 冰阻力经验模型 3.1 Lindqvist公式该公式是由Lindqvist[2]在波罗的海根据模型试验和实尺度观测结果,由冰的失效模式和运动状态,将冰阻力分成挤压冰阻力、弯曲破坏形成的冰阻力和冰浸没阻力3个部分。Lindqvist模型的冰阻力公式如下:
| ${R_{ice}} = \left( {{R_c} + {R_b}} \right)\left( {1 + 1.4\frac{V}{{\sqrt {g{h_i}} }}} \right) + {R_s}\left( {1 + 9.4\frac{V}{{\sqrt {gL} }}} \right){\text{,}}$ | (1) |
| ${R_c} = 0.5{\sigma _f}h_i^2\frac{{\tan \phi + \mu \cos \phi /\cos \psi }}{{1 - \mu \sin \phi /\cos \psi }}{\text{,}}$ | (2) |
| $ \begin{split} {R_b} =& \frac{{27}}{{64}}{\sigma _f}B\frac{{{h_i}^{1.5}}}{{\sqrt {\dfrac{E}{{12(1 - {\nu ^2})g{\rho _w}}}} }}\frac{{\tan \psi + \mu \cos \phi }}{{\cos \psi \sin \alpha }}\times\\ & \left(1 + \frac{1}{{\cos \psi }}\right){\text{,}} \end{split} $ | (3) |
| $ {R_s} = ({\rho _w} - {\rho _i})g{h_i}B\left(T\frac{{B + T}}{{B + 2T}} + k\right){\text{,}} $ | (4) |
| $ \begin{split} & k = \mu \biggr(0.7L - \frac{T}{{\tan \phi }} - \frac{B}{{4\tan \alpha }}+ \\ & T\cos \phi \cos \psi \sqrt {\frac{1}{{\sin {\phi ^2}}} + \frac{1}{{\tan {\alpha ^2}}}} \biggr){\text{,}} \end{split}$ | (5) |
| $\psi = \arctan \left( {\frac{{\tan \phi }}{{\sin \alpha }}} \right){\text{。}}$ | (6) |
式中:
该公式是由Riska[3]基于航行于波罗的海不同船舶的实船观测数据,对Lindqvist公式进行改进,从而提出有关平整冰的冰阻力经验公式。由于在平整冰环境下敞水阻力很小,通常忽略水动力与冰的相互作用。Riska模型的冰阻力公式如下:
| ${R_{ice}} = {C_1} + {C_2}V{\text{,}}$ | (7) |
| $ \begin{split} {C_1} =& {f_1}\frac{1}{{\dfrac{{2T}}{B} + 1}}B{L_{par}}{h_i} + (1 + 0.021\phi ) \times\\ & ({f_2}Bh_i^2 + {f_3}{L_{bow}}h_i^2 + {f_4}B{L_{bow}}{h_i}){\text{,}} \end{split} $ | (8) |
| $ \begin{split} {C_2} =& (1 + 0.063\phi )({g_i}h_i^{1.5} + {g_2}b{h_i}) +\\ & {g_3}{h_i}(1 + 1.2T/B)\frac{{{B^2}}}{{\sqrt L }}{\text{。}} \end{split} $ | (9) |
式中:
|
|
表 4 Riska模型经验系数 Tab.4 Empirical coefficient of Riska model |
该公式是由Jeong[4]在Spencer模型的基础上,根据模型实验提出的一种针对标准破冰船模型的冰阻力经验估算方法,冰阻力由破冰阻力、浮冰阻力和清除冰力3部分组成。Jeong模型的冰阻力公式如下:
| $ \begin{split} {R_i} =& 13.14{V^2} + {C_B}\Delta \rho g{h_i}BT + {C_C}F_h^{ - \alpha }{\rho _i}B{h_i}{V^2}+ \\ & {C_{BR}}S_N^{ - \beta }{\rho _i}B{h_i}{V^2}{\text{,}} \end{split} $ | (10) |
| $ {F_h} = \frac{V}{{\sqrt {g{h_i}} }}{\text{,}}\;\;\;\;{S_N} = \frac{V}{{\sqrt {\dfrac{{{\sigma _f}{h_i}}}{{{\rho _i}B}}} }}{\text{。}} $ | (11) |
式中:
|
|
表 5 各经验系数的取值 Tab.5 values of each empirical coefficient |
Edwards等[5]通过模型和实船试验结果推导,并对之前的经验公式重新进行分析和改进,得到下式:
| $ R = {\rho _w} \cdot B \cdot g \cdot {h_i}^2 \cdot \left(4.24 + 0.05 \cdot \frac{{{\sigma _f}}}{{{\rho _w} \cdot g \cdot {h_i}}} + 8.9{F_n}\right){\text{。}} $ | (12) |
式中:
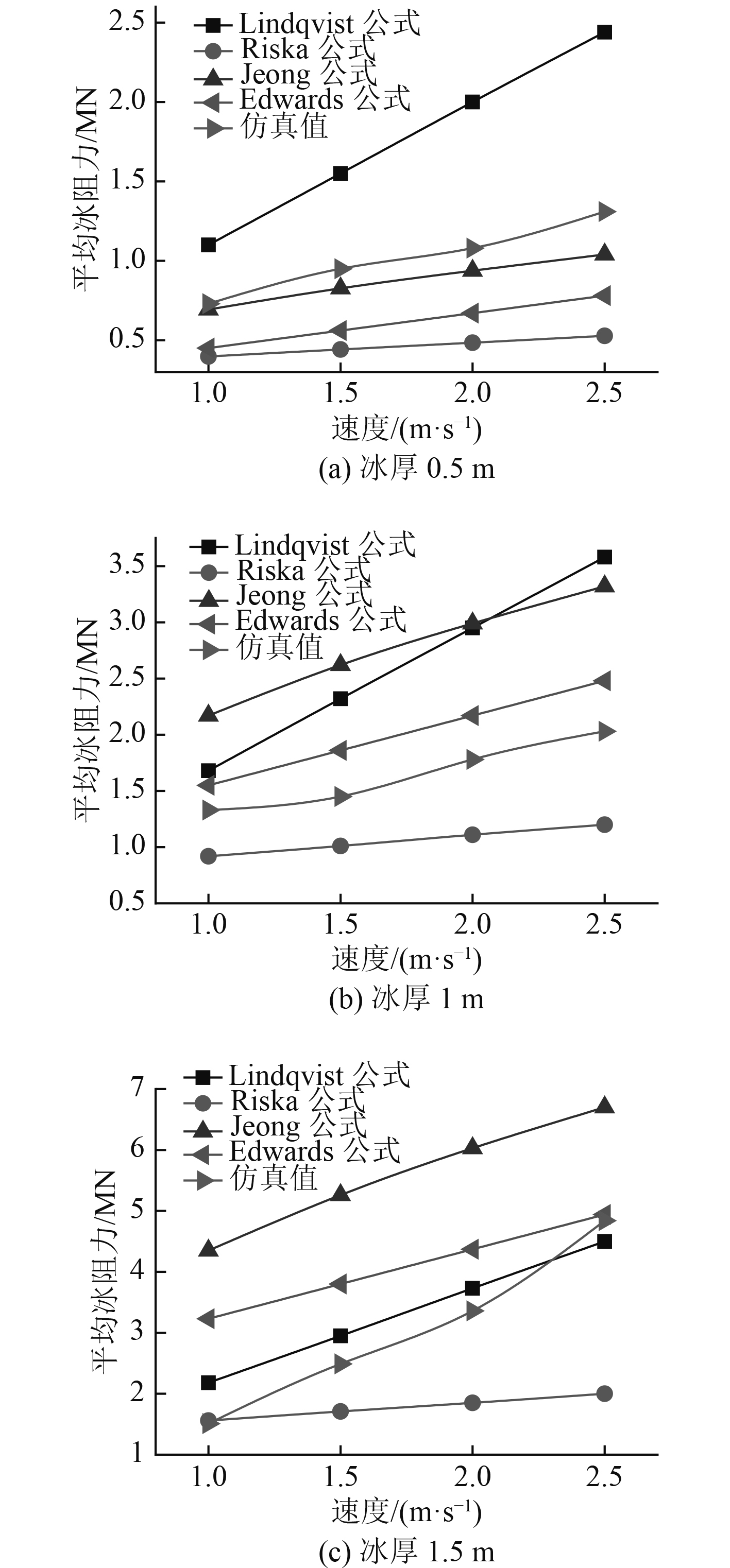
将经验公式计算得到的破冰船在连续破冰场景中不同工况下的平均冰力值,与数值模拟的平均冰力结果进行对比,得到不同工况下经验公式与数值模拟的冰力对比曲线,如图5所示。
|
图 5 不同工况下经验公式与数值模拟的冰力比较 Fig. 5 Comparison of empirical formula and numerical simulation results under different conditions |
可以看出,在不同船速和不同冰厚条件下,由各种经验公式和数值仿真得到的计算结果,都反映出了冰阻力随船速和冰厚的增大而增大的变化趋势。但各个经验解析公式和数值模拟对该破冰船在连续式破冰场景中的不同工况下的冰阻力预报,都存在不同程度的差异。Riska公式在各种工况下所计算出的冰阻力都最小。其中,在冰厚为0.5 m时,数值仿真结果与Lindqvist的冰阻力的计算结果偏差最大,而与Jeong公式计算值最为接近;在冰厚为1 m时,数值仿真结果与Lindqvist公式和Jeong公式的冰阻力计算结果偏差最大,而与Edwards公式计算值最为接近;在冰厚为1.5 m时,数值仿真结果与Jeong公式的冰阻力的计算结果偏差最大,而与Lindqvist公式计算值最为接近。
4.2 参数敏感性分析敏感性分析是分别将每个自变量在一定范围内进行变化,得到相应变化趋势和变化程度,最后得出自变量对结果的影响程度,而敏感性系数便是衡量影响程度的大小,敏感性系数越大,则该自变量对结果的影响便越大[11]。表6列出了不同冰阻力经验公式中涉及的主要参数,符号“√”表示冰阻力经验公式中所包含的相应参数。
|
|
表 6 相关主要参数 Tab.6 Related main parameters |
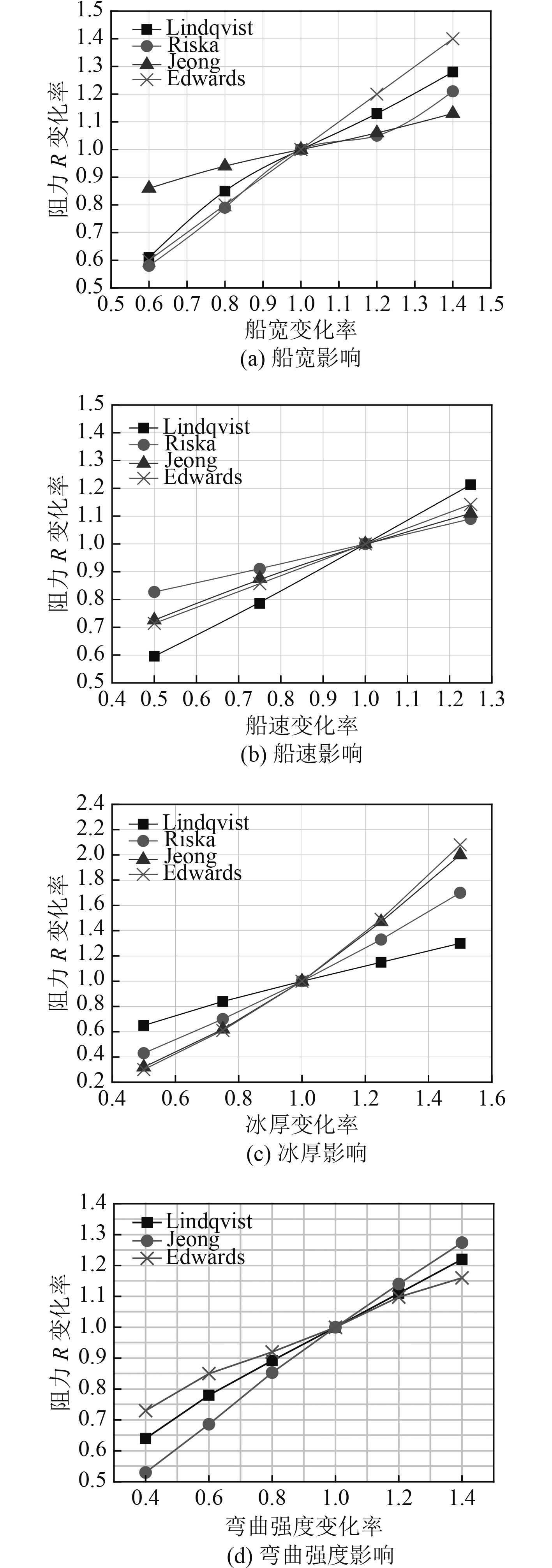
通过对冰阻力经验公式中的参数研究发现,计算结果由经验公式中各个参数值决定,而每个参数值对结果的影响程度也各有不同。针对在船速为2 m/s,冰厚为1 m,船宽为24 m,冰弯曲强度为1 MPa的初始条件下,相关参数敏感性分析如图6所示。
|
图 6 参数敏感性分析 Fig. 6 Parameter sensitivity analysis |
图6反映了冰阻力随各参数变化率增大而增大的变化趋势,但每个参数值对冰阻力的影响程度也各有不同。在初始条件下,船宽的变化对Edwards模型影响最大,若船宽增加20%,Lindqvist,Riska,Jeong,Edwards的冰阻力计算结果值分别增加了13.1%,5.3%,6.5%和20%;船速的变化对Lindqvist模型的冰阻力变化率影响最大,对Riska模型影响最小。若船速增加25%,Lindqvist,Riska,Jeong和Edwards的冰阻力计算结果值分别增加了21.3%,9.1%,11.2%和14.2%。冰厚的变化对各经验模型均有较大影响,其中对Edwards模型的冰阻力变化率影响最大,对Lindqvist模型影响最小,若冰厚增加20%,Lindqvist,Riska,Jeong和Edwards的冰阻力计算结果值分别增加了30.2%,70.1%,100.2%和108.1%。冰弯曲强度的变化对Jeong模型冰阻力变化率影响最大,对Edwards模型影响最小,若冰弯曲强度增加20%,Lindqvist,Jeong和Edwards的冰阻力计算结果值分别增加了22.1%,27.4%和16.2%。
5 结 语本文通过建立破冰船与冰排相关有限元模型,选取验证合适的冰材料模型,对破冰船在不同冰况下的破冰过程进行数值模拟分析,并对数值模拟和经验公式计算得到的冰阻力值作了比较分析,同时对各经验公式中的主要参数作了敏感性分析,得出以下结论:
1)在不同应变率下,由钢板与冰锥碰撞仿真计算所得的冰力-位移曲线与文献中的实验数据结果基本吻合,说明该海冰材料模型适用于破冰过程的数值模拟。
2)由数值仿真和各种经验公式计算结果,可以发现,在不同船速和冰厚条件下,冰阻力均随船速和冰厚的增大而增大,而在船速和冰厚2个参数中,冰厚对冰阻力影响更大。
3)经与数值仿真结果对比分析,不同的经验公式适用于不同冰厚条件下的冰阻力预报:冰厚为0.5 m时,数值仿真结果与Jeong公式计算值最为接近;冰厚为1 m时,数值仿真结果与Edwards公式计算值最为接近;冰厚为1.5 m时,数值仿真结果与Lindqvist公式的计算值最为接近,可以为进行快速冰阻力预报时选取适合的经验公式提供依据。
4)对不同经验公式中的不同参数进行敏感性分析,反映出了冰阻力随各参数变化率增大而增大的变化趋势,但船宽、船速、冰厚以及冰弯曲强度等参数对各经验公式冰阻力计算结果的敏感性也各有不同。船宽和冰厚的变化对Edwards公式影响最大,船速对Lindqvist公式影响最大,可以为船体结构设计提供参考。
| [1] |
韩端锋, 乔岳, 等. 冰区航行船舶冰阻力研究方法综述[J]. 船舶力学, 2017, 21(8): 41-54. HAN Duan-feng, QIAO Yue, et al. A review of ice resistance research methods for ice-going ships[J]. Journal of Ship Mechanics, 2017, 21(8): 41-54. |
| [2] |
LINDQVIST G. A straightforward method for calculation of ice resistance of ships[C]// Proceedings of the TenthInternational Conference on Port and Ocean Engineering under Arctic Conditions. Lulea, Sweden, 1989: 722-735.
|
| [3] |
RISKA K, WILHELMSON M, ENGLUND K, LEIVISKA T. Performance of merchant vessels in the Baltic[R]. Winter Navigation Research Board. Helsinki, Finland, 1997.
|
| [4] |
JEONG S Y, LEE C J, CHO S R. Ice resistance prediction for standard icebreaker model ship[C]// Proceedings of the Twentieth (2010) International Offshore and Polar Engineering Conference. Beijing, China, 2010: 1300-1304.
|
| [5] |
EDWARDS R Y, MAJOR R A. Influence of major characteristics of icebreaker hulls on their powering requirements and maneuverability in ice[R], 1976.
|
| [6] |
任奕舟, 邹早建. 破冰船在冰层中连续破冰过程的数值模拟[J]. 振动与冲击, 2016, 35(18): 210-223. REN Yi-zhou, ZOU Zao-jian. Numerical simulation of the continuous icebreaking by an icebreaker in level ice[J]. Jouranal of Vibration and Shock, 2016, 35(18): 210-223. |
| [7] |
刁峰, 陈京普, 等. 极地船舶冰阻力经验模型研究[J]. 中国造船, 2016, 57(2): 38-44. DIAO Feng, CHEN Jing-pu, et al. Study on ice resistance estimation using empirical models for polar ships[J]. Shipbuilding of China, 2016, 57(2): 38-44. DOI:10.3969/j.issn.1000-4882.2016.02.005 |
| [8] |
JIAN Hu, LI Zhou. Further study on level ice resistance and channel resistance for an icebreaking vessel[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8: 169-176. DOI:10.1016/j.ijnaoe.2016.01.004 |
| [9] |
DALEY C, KENDRICK A. Safe speed in ice [R]. Final report, prepared for BMT fleet technology, 2011 Reference: 6931DFR.Rev00, Ottawa, ON, Canada.
|
| [10] |
KIM M C. Study on icebreaking performance of the Korea icebreaker ARAON in the Arctic sea[J]. International Journal of Naval Architecture and Ocean Engineering, 2011, 3(3): 208-215. DOI:10.2478/IJNAOE-2013-0064 |
| [11] |
蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版), 2008(1): 9-16. CAI Yi, XING Yan, HU Dan. On sensitivity anaysis[J]. Journal of Beijing Normal University (Natural Science), 2008(1): 9-16. DOI:10.3321/j.issn:0476-0301.2008.01.003 |
 2019, Vol. 41
2019, Vol. 41
